Formule složenih funkcija. složene derivate. Logaritamski izvod. Derivat eksponencijalne funkcije

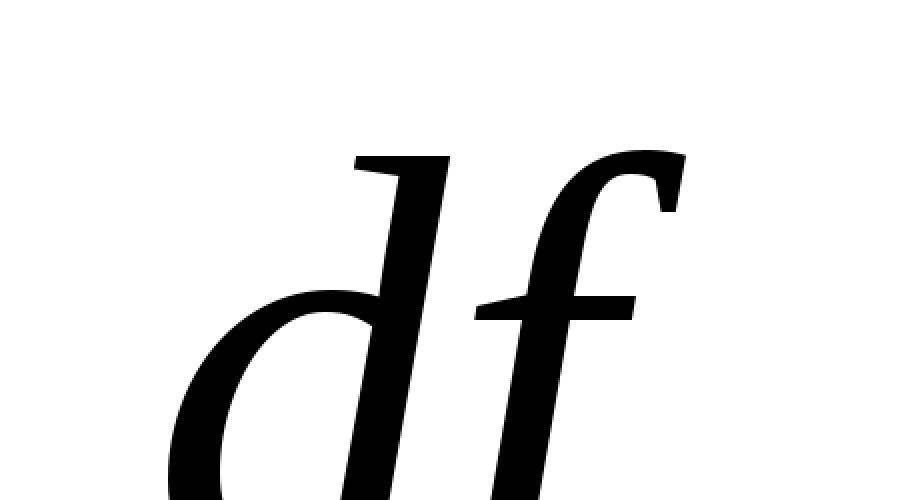
U "starim" udžbenicima to se naziva i "lančanim" pravilom. Sta ako y = f (u), i u = φ (x), to je

y = f (φ (x))

složena - složena funkcija (sastav funkcija) tada

gdje , nakon obračuna se smatra na u = φ (x).

Imajte na umu da smo ovdje uzeli "različite" kompozicije iz istih funkcija, a rezultat diferencijacije se prirodno pokazao da ovisi o redoslijedu "miješanja".

Pravilo lanca se prirodno proteže na sastav tri ili više funkcija. U ovom slučaju, postojaće tri ili više „karika“ u „lancu“ koji čini derivat, respektivno. Evo analogije sa množenjem: “imamo” - tablicu izvedenica; "tamo" - tablica množenja; “kod nas” je lančano pravilo, a “postoji” je pravilo množenja sa “kolona”. Prilikom izračunavanja takvih „složenih“ izvoda, naravno, ne uvode se pomoćni argumenti (u¸v, itd.), ali, pošto su sami zabilježili broj i redoslijed funkcija koje učestvuju u kompoziciji, oni „nizuju“ odgovarajuće veze u naznačenom redosledu.

. Ovdje se pet operacija izvodi sa "x" da bi se dobila vrijednost "y", odnosno, odvija se kompozicija od pet funkcija: "spoljna" (posljednja od njih) - eksponencijalna - e ; onda je obrnutim redosledom zakon stepena. (♦) 2 ; trigonometrijski sin(); moć. () 3 i konačno logaritamski ln.(). Zbog toga

Sljedeći primjeri će „ubiti parove golubova jednim udarcem“: vježbat ćemo razlikovanje složenih funkcija i dopuniti tablicu izvedenica elementarnih funkcija. dakle:

4. Za funkciju snage - y \u003d x α - prepisivanjem je koristeći dobro poznatu "osnovnu logaritamski identitet» - b=e ln b - u obliku x α = x α ln x dobijamo

5. Za proizvoljnu eksponencijalnu funkciju, koristeći istu tehniku, imat ćemo

6. Za proizvoljnu logaritamsku funkciju, koristeći dobro poznatu formulu za prijelaz na novu bazu, sukcesivno dobijamo

.

7. Za razlikovanje tangente (kotangensa) koristimo pravilo za razlikovanje količnika:

Da bismo dobili izvode inverznih trigonometrijskih funkcija, koristimo relaciju koju zadovoljavaju derivacije dvije međusobno inverzne funkcije, odnosno funkcije φ (x) i f (x) povezane relacijama:

Evo omjera

To je iz ove formule za međusobno inverzne funkcije

i
,

Na kraju, ove i neke druge, jednako lako dobijene derivate, sumiramo u sljedećoj tabeli.

Otkad ste došli ovdje, vjerovatno ste već uspjeli vidjeti ovu formulu u udžbeniku

i napravi facu ovako:

Prijatelju, ne brini! U stvari, sve je jednostavno za sramotu. Sigurno ćete sve razumjeti. Samo jedan zahtjev - pročitajte članak polako pokušajte razumjeti svaki korak. Napisao sam najjednostavnije i jasnije moguće, ali još uvijek morate proniknuti u ideju. I svakako riješite zadatke iz članka.

Šta je složena funkcija?

Zamislite da se selite u drugi stan i stoga pakujete stvari u velike kutije. Hajde da skupimo malo male stvari kao što je školski pribor. Ako ih samo bacite u ogromnu kutiju, između ostalog će se izgubiti. Da biste to izbjegli, prvo ih stavite, na primjer, u vrećicu, koju zatim stavite u veliku kutiju, nakon čega je zatvorite. Ovaj "najteži" proces je prikazan na dijagramu ispod:

Čini se, gdje je matematika? A osim toga, kompleksna funkcija se formira na POTPUNO ISTI način! Samo mi ne “pakujemo” sveske i olovke, već \ (x \), a služe različiti “paketi” i “kutije”.

Na primjer, uzmimo x i "upakujemo" ga u funkciju:

Kao rezultat, dobijamo, naravno, \(\cos⁡x\). Ovo je naša "vreća stvari". A sada ga stavljamo u "kutiju" - pakujemo ga, na primjer, u kubičnu funkciju.

Šta će se na kraju dogoditi? Da, tako je, postojaće "paket sa stvarima u kutiji", odnosno "kosinus od x kocke".

Rezultirajuća konstrukcija je složena funkcija. Po tome se razlikuje od jednostavnog NEKOLIKO „uticaja“ (paketa) se primjenjuje na jedan X u nizu i ispada, takoreći, "funkcija iz funkcije" - "paket u paketu".

AT školski kurs postoji vrlo malo tipova ovih istih "paketa", samo četiri:

Hajdemo sada prvo "pakirati" x eksponencijalna funkcija sa bazom 7, a zatim u trigonometrijsku funkciju. Dobijamo:

\(x → 7^x → tg⁡(7^x)\)

A sada hajde da "upakujemo" x dvaput trigonometrijske funkcije, prvo u , a zatim u :

\(x → sin⁡x → ctg⁡ (sin⁡x)\)

Jednostavno, zar ne?

Sada sami napišite funkcije, gdje je x:
- prvo se „pakuje“ u kosinus, a zatim u eksponencijalnu funkciju sa bazom \(3\);
- prvo na peti stepen, a zatim na tangentu;
- prvo do osnovnog logaritma \(4\) , zatim na stepen \(-2\).

Odgovore na ovo pitanje pogledajte na kraju članka.

Ali možemo li "pakirati" x ne dva, već tri puta? Nema problema! I četiri, i pet, i dvadeset i pet puta. Evo, na primjer, funkcije u kojoj je x "upakovano" \(4\) puta:

\(y=5^(\log_2⁡(\sin⁡(x^4)))\)

Ali takve formule se neće naći u školskoj praksi (učenici imaju više sreće - mogu biti teže☺).

"Raspakivanje" složene funkcije

Pogledajte ponovo prethodnu funkciju. Možete li shvatiti redoslijed "pakiranja"? U šta je X ubačen prvo, u šta onda i tako do samog kraja. To jest, koja funkcija je ugniježđena u koju? Uzmite komad papira i zapišite šta mislite. To možete učiniti lancem strelica, kao što smo gore napisali, ili na bilo koji drugi način.

Sada je tačan odgovor: prvo je x "upakovano" u \(4\)-tu potenciju, zatim je rezultat upakovan u sinus, on je zauzvrat stavljen u bazu logaritma \(2\), a u na kraju je cijela konstrukcija gurnuta u petice.

Odnosno, potrebno je odmotati sekvencu OBRATNIM REDOM. A evo i savjeta kako to učiniti lakše: samo pogledajte X - morate plesati od njega. Pogledajmo nekoliko primjera.

Na primjer, evo funkcije: \(y=tg⁡(\log_2⁡x)\). Gledamo X - šta se prvo dešava s njim? Oduzeto od njega. I onda? Uzima se tangenta rezultata. I redosled će biti isti:

\(x → \log_2⁡x → tg⁡(\log_2⁡x)\)

Drugi primjer: \(y=\cos⁡((x^3))\). Analiziramo - prvo je x kockan, a zatim je iz rezultata uzet kosinus. Dakle, niz će biti: \(x → x^3 → \cos⁡((x^3))\). Obratite pažnju, čini se da je funkcija slična prvoj (gdje sa slikama). Ali ovo je potpuno drugačija funkcija: ovdje u kocki x (to jest, \(\cos⁡((x x x)))\), a tamo u kocki kosinus \(x\) (to jest, \(\ cos⁡ x·\cos⁡x·\cos⁡x\)). Ova razlika proizlazi iz različitih sekvenci "pakiranja".

Posljednji primjer (sa važna informacija u njemu): \(y=\sin⁡((2x+5))\). Jasno je da smo ovdje prvo izvršili aritmetičke operacije sa x, a zatim je sinus uzet iz rezultata: \(x → 2x+5 → \sin⁡((2x+5))\). I to važna tačka: unatoč činjenici da aritmetičke operacije nisu funkcije same po sebi, ovdje djeluju i kao način "pakiranja". Udubimo se malo dublje u ovu suptilnost.

Kao što sam rekao gore, u jednostavnim funkcijama x se "pakuje" jednom, a u složenim funkcijama - dva ili više. Štaviše, bilo koja kombinacija jednostavnih funkcija (tj. njihov zbroj, razlika, množenje ili dijeljenje) je također jednostavna funkcija. Na primjer, \(x^7\) je jednostavna funkcija, kao i \(ctg x\). Dakle, sve njihove kombinacije su jednostavne funkcije:

\(x^7+ ctg x\) - jednostavno,
\(x^7 ctg x\) je jednostavno,
\(\frac(x^7)(ctg x)\) je jednostavan, i tako dalje.

Međutim, ako se na takvu kombinaciju primijeni još jedna funkcija, to će već biti složena funkcija, jer će postojati dva “paketa”. Pogledajte dijagram:

Ok, hajde da nastavimo s tim sada. Napišite slijed funkcija "omotavanja":
\(y=cos(⁡(sin⁡x))\)
\(y=5^(x^7)\)
\(y=arctg⁡(11^x)\)
\(y=log_2⁡(1+x)\)
Odgovori su opet na kraju članka.

Unutrašnje i eksterne funkcije

Zašto trebamo razumjeti ugniježđenje funkcija? Šta nam ovo daje? Stvar je u tome da bez takve analize nećemo moći pouzdano pronaći izvode funkcija o kojima smo gore govorili.

A da bismo nastavili dalje, trebat će nam još dva koncepta: unutrašnje i vanjske funkcije. Ovo je veoma jednostavna stvar, štoviše, u stvari, već smo ih analizirali iznad: ako se prisjetimo naše analogije na samom početku, onda je unutrašnja funkcija „paket“, a vanjska je „kutija“. One. ono u šta je X prvo "umotano" je interna funkcija, a ono u šta je interno "umotano" je već eksterno. Pa, razumljivo je zašto - to je spolja, znači eksterno.

Evo u ovom primjeru: \(y=tg⁡(log_2⁡x)\), funkcija \(\log_2⁡x\) je interna, i
- eksterni.

A u ovom: \(y=\cos⁡((x^3+2x+1))\), \(x^3+2x+1\) je interno, i
- eksterni.

Izvedite posljednju praksu analize složenih funkcija, i konačno, prijeđimo na točku za koju je sve započeto - naći ćemo derivate složenih funkcija:

Popunite praznine u tabeli:

Derivat kompleksne funkcije

Bravo za nas, ipak smo stigli do "gazde" ove teme - u stvari, izvedenice složena funkcija, a konkretno na onu jako strašnu formulu s početka članka.☺

\((f(g(x)))"=f"(g(x))\cdot g"(x)\)

Ova formula glasi ovako:

Izvod kompleksne funkcije jednak je proizvodu izvoda eksterne funkcije u odnosu na konstantnu unutrašnju funkciju i derivaciju unutrašnje funkcije.

I odmah pogledajte shemu raščlanjivanja, prema riječima, kako biste razumjeli na što se odnositi:

Nadam se da termini "derivacija" i "proizvod" ne izazivaju poteškoće. "Složena funkcija" - već smo demontirali. Kvaka je u "derivatu eksterne funkcije u odnosu na konstantu unutrašnju". Šta je to?

Odgovor: ovo je uobičajena derivacija vanjske funkcije, u kojoj se mijenja samo vanjska funkcija, dok unutrašnja ostaje ista. Još uvijek nejasno? U redu, uzmimo primjer.

Recimo da imamo funkciju \(y=\sin⁡(x^3)\). Jasno je da je unutrašnja funkcija ovdje \(x^3\), a vanjska
. Nađimo sada derivaciju spoljašnjeg u odnosu na konstantu unutrašnjeg.

Nakon preliminarne artiljerijske pripreme, primjeri s 3-4-5 dodataka funkcija bit će manje zastrašujući. Možda će se sljedeća dva primjera nekom učiniti komplikovana, ali ako se razumiju (neko će patiti), onda je gotovo sve ostalo diferencijalni račun izgledat će kao dječja šala.

Primjer 2

Pronađite izvod funkcije

Kao što je već napomenuto, pri pronalaženju derivacije kompleksne funkcije, prije svega, to je neophodno u pravu RAZUMIJETE INVESTICIJE. U slučajevima kada postoji sumnja, podsjećam korisna tehnika: uzimamo eksperimentalnu vrijednost "x", na primjer, i pokušavamo (mentalno ili na nacrtu) zamijeniti ovu vrijednost u "užasan izraz".

1) Prvo trebamo izračunati izraz, tako da je zbir najdublje ugniježđenje.

2) Zatim morate izračunati logaritam:

4) Zatim izrežite kosinus na kocku:

5) U petom koraku razlika:

6) I konačno, najudaljenija funkcija je kvadratni korijen:

Formula diferencijacije složenih funkcija primjenjuju se obrnutim redoslijedom, od najudaljenije funkcije prema unutrašnjoj. Odlučujemo:

Čini se da nema grešaka:

1) Uzimamo derivaciju kvadratnog korijena.

2) Uzimamo derivaciju razlike koristeći pravilo

3) Derivat trojke je jednak nuli. U drugom članu uzimamo derivaciju stepena (kocke).

4) Uzimamo derivaciju kosinusa.

6) I na kraju, uzimamo derivat najdubljeg gniježđenja.

Možda izgleda preteško, ali ovo nije najbrutalniji primjer. Uzmite, na primjer, kolekciju Kuznjecova i cijenit ćete sav šarm i jednostavnost analiziranog derivata. Primetio sam da vole da daju sličnu stvar na ispitu da bi proverili da li student razume kako da pronađe izvod kompleksne funkcije, ili ne razume.

Sljedeći primjer za nezavisno rešenje.

Primjer 3

Pronađite izvod funkcije

Savjet: Prvo primjenjujemo pravila linearnosti i pravilo diferencijacije proizvoda

Potpuno rješenje i odgovor na kraju lekcije.

Vrijeme je da pređete na nešto kompaktnije i ljepše.
Nije neuobičajeno da se u primjeru navede proizvod ne dva, već tri funkcije. Kako pronaći derivaciju proizvoda tri faktora?

Primjer 4

Pronađite izvod funkcije

Prvo, pogledamo, ali je li moguće pretvoriti proizvod tri funkcije u proizvod dvije funkcije? Na primjer, ako imamo dva polinoma u proizvodu, onda bismo mogli otvoriti zagrade. Ali u ovom primjeru, sve funkcije su različite: stepen, eksponent i logaritam.

U takvim slučajevima je neophodno sukcesivno primijeniti pravilo diferencijacije proizvoda dvaput

Trik je u tome što za "y" označavamo proizvod dvije funkcije: , a za "ve" - ​​logaritam:. Zašto se to može uraditi? Je li - ovo nije proizvod dva faktora i pravilo ne funkcionira?! Nema ništa komplikovano:

Sada preostaje primijeniti pravilo po drugi put u zagradu:

Još uvijek možete izopačiti i izvaditi nešto iz zagrada, ali unutra ovaj slučaj bolje je ostaviti odgovor u ovom obliku - bit će lakše provjeriti.

Gornji primjer se može riješiti na drugi način:

Oba rješenja su apsolutno ekvivalentna.

Primjer 5

Pronađite izvod funkcije

Ovo je primjer za nezavisno rješenje, u uzorku se rješava na prvi način.

Razmotrimo slične primjere sa razlomcima.

Primjer 6

Pronađite izvod funkcije

Ovdje možete ići na nekoliko načina:

ili ovako:

Ali rješenje se može zapisati kompaktnije ako, prije svega, koristimo pravilo diferencijacije kvocijenta , uzimajući za cijeli brojnik:

U principu, primjer je riješen, a ako se ostavi u ovom obliku, neće biti greška. Ali ako imate vremena, uvijek je preporučljivo provjeriti nacrt, ali da li je moguće pojednostaviti odgovor?

Dovodimo izraz brojioca na zajednički imenilac i riješite se trospratne frakcije:

Nedostatak dodatnih pojednostavljenja je u tome što postoji rizik od greške ne pri pronalaženju derivata, već prilikom banalnih školskih transformacija. S druge strane, nastavnici često odbacuju zadatak i traže da se „spomene” izvedenica.

Jednostavniji primjer rješenja uradi sam:

Primjer 7

Pronađite izvod funkcije

Nastavljamo da savladavamo tehnike pronalaženja derivacije, a sada ćemo razmotriti tipičan slučaj kada se za diferencijaciju predlaže "strašan" logaritam

Apsolutno je nemoguće riješiti fizičke probleme ili primjere iz matematike bez znanja o derivatu i metodama za njegovo izračunavanje. Derivat je jedan od najvažnijih pojmova matematička analiza. Odlučili smo posvetiti današnji članak ovoj temeljnoj temi. Šta je derivat, šta je njegov fizički i geometrijskog smisla kako izračunati derivaciju funkcije? Sva ova pitanja mogu se spojiti u jedno: kako razumjeti derivat?

Geometrijsko i fizičko značenje izvedenice

Neka postoji funkcija f(x) , dato u nekom intervalu (a,b) . Točke x i x0 pripadaju ovom intervalu. Kada se x promijeni, mijenja se i sama funkcija. Promjena argumenta - razlika njegovih vrijednosti x-x0 . Ova razlika je zapisana kao delta x i naziva se povećanje argumenta. Promjena ili povećanje funkcije je razlika između vrijednosti funkcije u dvije točke. Definicija izvedenice:

Derivat funkcije u tački je granica omjera prirasta funkcije u datoj tački i priraštaja argumenta kada potonji teži nuli.

Inače se može napisati ovako:

Koja je svrha u pronalaženju takve granice? ali koji:

derivacija funkcije u tački jednaka je tangenti ugla između ose OX i tangente na graf funkcije u datoj tački.

Fizičko značenje izvedenice: vremenski izvod puta jednak je brzini pravolinijskog kretanja.

Zaista, još od školskih dana svi znaju da je brzina privatan put. x=f(t) i vrijeme t . prosječna brzina za neko vreme:

Da biste saznali brzinu kretanja u datom trenutku t0 morate izračunati granicu:

Prvo pravilo: izbacite konstantu

Konstanta se može izvaditi iz predznaka derivacije. Štaviše, to se mora uraditi. Prilikom rješavanja primjera iz matematike uzmite po pravilu - ako možete pojednostaviti izraz, budite sigurni da ste ga pojednostavili .

Primjer. Izračunajmo derivaciju:

Drugo pravilo: derivacija zbira funkcija

Derivat zbira dviju funkcija jednak je zbroju izvoda ovih funkcija. Isto vrijedi i za derivaciju razlike funkcija.

Nećemo dati dokaz ove teoreme, već ćemo razmotriti praktični primjer.

Pronađite derivaciju funkcije:

Treće pravilo: derivacija proizvoda funkcija

Derivat proizvoda dvije diferencijabilne funkcije izračunava se po formuli:

Primjer: pronađite derivaciju funkcije:

Rješenje:

Ovdje je važno reći o izračunavanju izvoda složenih funkcija. Derivat kompleksne funkcije jednak je umnošku derivacije ove funkcije u odnosu na međuargument na derivaciju srednjeg argumenta u odnosu na nezavisnu varijablu.

AT gornji primjer srećemo izraz:

U ovom slučaju, srednji argument je 8x na peti stepen. Da bismo izračunali derivaciju takvog izraza, prvo razmatramo derivaciju eksterne funkcije u odnosu na međuargument, a zatim množimo derivacijom samog međuargumenata u odnosu na nezavisnu varijablu.

Četvrto pravilo: Derivat količnika dvije funkcije

Formula za određivanje derivacije kvocijenta dvije funkcije:

Pokušali smo razgovarati o derivatima za lutke od nule. Ova tema nije tako jednostavna kao što se čini, stoga budite upozoreni: u primjerima često postoje zamke, stoga budite oprezni pri izračunavanju izvedenica.

Za sva pitanja o ovoj i drugim temama možete se obratiti studentskoj službi. Per kratkoročno pomoći ćemo vam da riješite najteži test i da se nosite sa zadacima, čak i ako se nikada prije niste bavili proračunom izvodnica.

Funkcije složenog tipa ne odgovaraju uvijek definiciji složene funkcije. Ako postoji funkcija oblika y = sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, onda se ne može smatrati složenom, za razliku od y = sin 2 x.

Ovaj članak će pokazati koncept kompleksne funkcije i njenu identifikaciju. Poradimo s formulama za pronalaženje izvoda s primjerima rješenja u zaključku. Upotreba tablice izvedenica i pravila diferencijacije značajno skraćuje vrijeme za pronalaženje izvoda.

Yandex.RTB R-A-339285-1

Osnovne definicije

Kompleksna funkcija je funkcija čiji je argument također funkcija.

Označava se ovako: f (g (x)) . Imamo da se funkcija g (x) smatra argumentom f (g (x)) .

Definicija 2

Ako postoji funkcija f i kotangentna je funkcija, tada je g(x) = ln x funkcija prirodnog logaritma. Dobijamo da će kompleksna funkcija f (g (x)) biti zapisana kao arctg (lnx). Ili funkcija f, koja je funkcija podignuta na 4. stepen, gdje se g (x) = x 2 + 2 x - 3 smatra cijelom racionalnom funkcijom, dobivamo da je f (g (x)) = (x 2 + 2 x - 3) 4 .

Očigledno g(x) može biti nezgodno. Iz primjera y \u003d sin 2 x + 1 x 3 - 5, može se vidjeti da vrijednost g ima kockasti koren sa razlomkom. Ovaj izraz se može označiti kao y = f (f 1 (f 2 (x))) . Otuda imamo da je f sinusna funkcija, a f 1 je funkcija koja se nalazi ispod kvadratni korijen, f 2 (x) = 2 x + 1 x 3 - 5 - frakciona racionalna funkcija.

Definicija 3

Stepen ugniježđenja je definiran bilo kojim prirodni broj i zapisuje se kao y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .

Definicija 4

Koncept kompozicije funkcije odnosi se na broj ugniježđenih funkcija prema iskazu problema. Za rješenje, formula za pronalaženje derivacije kompleksne funkcije oblika

(f(g(x)))"=f"(g(x)) g"(x)

Primjeri

Naći izvod kompleksne funkcije oblika y = (2 x + 1) 2 .

Rješenje

Po konvenciji, f je kvadrirana funkcija, a g(x) = 2 x + 1 se smatra linearnom funkcijom.

Primjenjujemo formulu derivacije za složenu funkciju i pišemo:

f "(g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g "(x) = (2x + 1)" = (2x)" + 1" = 2 x" + 0 = 2 1 x 1 - 1 = 2 ⇒ (f(g(x))) "=f" ( g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

Potrebno je pronaći izvod sa pojednostavljenim početnim oblikom funkcije. Dobijamo:

y = (2x + 1) 2 = 4x2 + 4x + 1

Dakle, imamo to

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

Rezultati su se poklopili.

Prilikom rješavanja problema ove vrste važno je razumjeti gdje će se nalaziti funkcija oblika f i g (x).

Primjer 2

Trebali biste pronaći izvode složenih funkcija oblika y = sin 2 x i y = sin x 2.

Rješenje

Prvi unos funkcije kaže da je f funkcija kvadriranja, a g(x) sinusna funkcija. Onda to shvatamo

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x)" = 2 sin x cos x

Drugi unos pokazuje da je f sinusna funkcija, a g (x) = x 2 označava funkcija snage. Iz toga slijedi da se proizvod kompleksne funkcije može zapisati kao

y " \u003d (sin x 2) " \u003d cos (x 2) (x 2) " = cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

Formula za izvod y \u003d f (f 1 (f 2 (f 3 (. . (f n (x)))))) biće napisana kao y "= f" (f 1 (f 2 (f 3 (. . ( f n (x)))))) f 1 "(f 2 (f 3 (. . (f n (x))))) f 2 " (f 3 (. . . (f n (x) )) )) . . . f n "(x)

Primjer 3

Naći derivaciju funkcije y = sin (ln 3 a r c t g (2 x)) .

Rješenje

Ovaj primjer pokazuje složenost pisanja i određivanja lokacije funkcija. Tada y \u003d f (f 1 (f 2 (f 3 (f 4 (x))))) označava, gdje je f , f 1 , f 2 , f 3 , f 4 (x) sinusna funkcija, funkcija podizanja do 3 stepena, funkcija sa logaritmom i bazom e, funkcija tangente luka i linearna.

Iz formule za definiciju kompleksne funkcije imamo to

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Dobivanje šta pronaći

1. f "(f 1 (f 2 (f 3 (f 4 (x))))) kao derivacija sinusa u tabeli derivacija, onda f "(f 1 (f 2 (f 3 (f 4 (x ))))) ) = cos (ln 3 a r c t g (2 x)) .
2. f 1 "(f 2 (f 3 (f 4 (x)))) kao derivacija funkcije stepena, onda f 1 "(f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x) .
3. f 2 "(f 3 (f 4 (x))) kao logaritamski izvod, onda f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 "(f 4 (x)) kao derivacija tangente luka, tada je f 3 "(f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Prilikom pronalaženja derivacije f 4 (x) = 2 x, izvadite 2 iz predznaka derivacije koristeći formulu za izvod funkcije stepena s eksponentom koji je 1, a zatim f 4 "(x) = ( 2 x)" \u003d 2 x "\u003d 2 · 1 · x 1 - 1 = 2 .

Kombinujemo srednje rezultate i dobijamo to

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)

Analiza takvih funkcija podsjeća na lutke za gniježđenje. Pravila diferencijacije se ne mogu uvijek eksplicitno primijeniti korištenjem derivacijske tablice. Često morate primijeniti formulu za pronalaženje izvoda složenih funkcija.

Postoje neke razlike između složenog pogleda i složene funkcije. Uz jasnu sposobnost da se ovo razlikuje, pronalaženje derivata će biti posebno lako.

Primjer 4

Potrebno je razmisliti o dovođenju takvog primjera. Ako postoji funkcija oblika y = t g 2 x + 3 t g x + 1 , onda se može smatrati kompleksnom funkcijom oblika g (x) = t g x , f (g) = g 2 + 3 g + 1 . Očigledno je potrebno primijeniti formulu za složeni derivat:

f "(g (x)) \u003d (g 2 (x) + 3 g (x) + 1) " \u003d (g 2 (x)) " + (3 g (x)) " + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 = 2 g (x) + 3 1 g 1 - 1 (x) = \u003d 2 g (x) + 3 = 2 t g x + 3; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 t g x + 3 ) 1 cos 2 x = 2 t g x + 3 cos 2 x

Funkcija oblika y = t g x 2 + 3 t g x + 1 ne smatra se složenom, jer ima zbir t g x 2 , 3 t g x i 1 . Međutim, t g x 2 se smatra složenom funkcijom, tada dobivamo funkciju snage oblika g (x) \u003d x 2 i f, koja je funkcija tangente. Da biste to učinili, morate razlikovati po količini. Shvatili smo to

y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 cos 2 x

Idemo dalje na pronalaženje izvoda kompleksne funkcije (t g x 2) ":

f "(g (x)) = (t g (g (x)))" = 1 cos 2 g (x) = 1 cos 2 (x 2) g "(x) = (x 2)" = 2 x 2 - 1 = 2 x ⇒ (t g x 2) " \u003d f " (g (x)) g " (x) \u003d 2 x cos 2 (x 2)

Dobijamo da je y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Kompleksne funkcije mogu biti uključene u složene funkcije, a same složene funkcije mogu biti kompozitne funkcije složenog oblika.

Primjer 5

Na primjer, razmotrite kompleksnu funkciju oblika y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Ova funkcija se može predstaviti kao y = f (g (x)) , gdje je vrijednost f funkcija logaritma baze 3, a g (x) se smatra zbirom dvije funkcije oblika h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 i k (x) = ln 2 x (x 2 + 1) . Očigledno, y = f (h (x) + k (x)) .

Razmotrimo funkciju h(x) . Ovo je omjer l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 prema m (x) = e x 2 + 3 3

Imamo da je l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) zbir dvije funkcije n (x) = x 2 + 7 i p ( x) = 3 cos 3 (2 x + 1) , gdje je p (x) = 3 p 1 (p 2 (p 3 (x))) kompleksna funkcija s numeričkim koeficijentom 3, a p 1 je funkcija kocke, p 2 kosinusna funkcija, p 3 (x) = 2 x + 1 - linearna funkcija.

Otkrili smo da je m (x) = e x 2 + 3 3 = q (x) + r (x) zbir dvije funkcije q (x) = e x 2 i r (x) = 3 3 , gdje je q (x) = q 1 (q 2 (x)) je kompleksna funkcija, q 1 je funkcija s eksponentom, q 2 (x) = x 2 je funkcija stepena.

Ovo pokazuje da je h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

Kada se prijeđe na izraz oblika k (x) \u003d ln 2 x (x 2 + 1) \u003d s (x) t (x), jasno je da je funkcija predstavljena kao kompleks s (x) \ u003d ln 2 x \u003d s 1 ( s 2 (x)) sa cijelim racionalnim t (x) = x 2 + 1, gdje je s 1 funkcija kvadriranja, a s 2 (x) = ln x je logaritamska s bazom e .

Iz toga slijedi da će izraz dobiti oblik k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .

Onda to shvatamo

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Prema strukturama funkcije, postalo je jasno kako i koje formule se moraju primijeniti da bi se izraz pojednostavio kada se razlikuje. Da bismo se upoznali sa ovakvim problemima i razumjeli njihovo rješenje, potrebno je osvrnuti se na točku diferenciranja funkcije, odnosno pronalaženja njene derivacije.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter