Równania modulo. Moduł liczby (wartość bezwzględna liczby), definicje, przykłady, właściwości

Jednym z najtrudniejszych tematów dla studentów jest rozwiązywanie równań zawierających zmienną pod znakiem modułu. Zobaczmy na początek, z czym jest to związane? Dlaczego, na przykład, równania kwadratowe większość dzieci klika jak orzechy, ale przy tak dalekiej od najbardziej złożonej koncepcji, jak moduł, ma tak wiele problemów?

Moim zdaniem wszystkie te trudności wiążą się z brakiem jasno sformułowanych reguł rozwiązywania równań z modułem. Tak, decydując równanie kwadratowe, uczeń wie na pewno, że musi najpierw zastosować wzór na dyskryminację, a następnie wzory na pierwiastki równania kwadratowego. Ale co, jeśli w równaniu napotkamy moduł? Postaramy się jasno opisać niezbędny plan działania dla przypadku, gdy równanie zawiera niewiadomą pod znakiem modułu. Dla każdego przypadku podajemy kilka przykładów.

Ale najpierw pamiętajmy definicja modułu. Tak więc moduł liczby a sam numer nazywa się if a nieujemna i -a jeśli liczba a mniej niż zero. Możesz napisać to tak:

|a| = a jeśli a ≥ 0 i |a| = -a jeśli a< 0

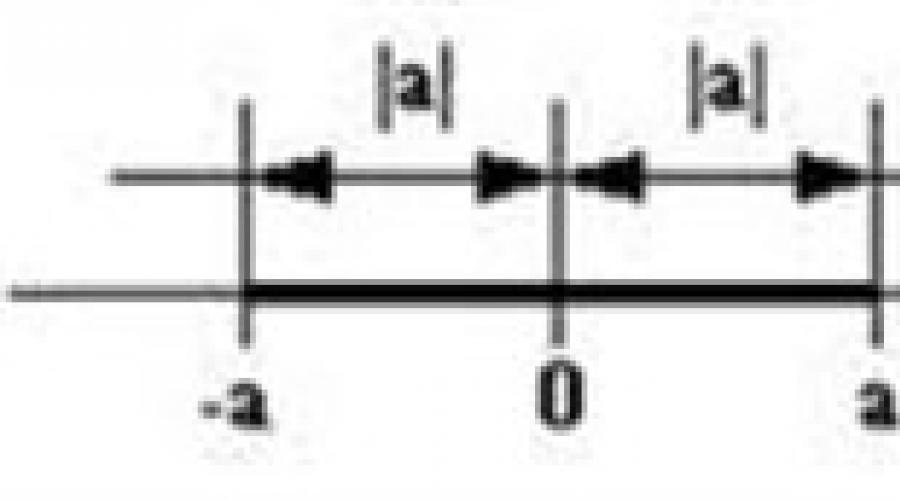
Mówiąc o zmysł geometryczny należy pamiętać, że każda liczba rzeczywista odpowiada określonemu punktowi na osi liczbowej - jej do koordynować. Tak więc moduł lub wartość bezwzględna liczby to odległość od tego punktu do początku osi liczbowej. Odległość podawana jest zawsze jako liczba dodatnia. Tak więc moduł dowolnego Liczba ujemna jest liczbą dodatnią. Nawiasem mówiąc, nawet na tym etapie wielu uczniów zaczyna się mylić. W module może znajdować się dowolna liczba, ale wynik zastosowania modułu jest zawsze liczbą dodatnią.

Przejdźmy teraz do rozwiązywania równań.

1. Rozważ równanie postaci |x| = c, gdzie c jest liczbą rzeczywistą. Równanie to można rozwiązać za pomocą definicji modułu.

Wszystkie liczby rzeczywiste dzielimy na trzy grupy: większe od zera, mniejsze od zera, a trzecia grupa to liczba 0. Rozwiązanie zapisujemy w postaci diagramu:

(±c jeśli c > 0

Jeśli |x| = c, to x = (0 jeśli c = 0

(bez korzeni, jeśli z< 0

1) |x| = 5, ponieważ 5 > 0, to x = ±5;

2) |x| = -5, ponieważ -5< 0, то уравнение не имеет корней;

3) |x| = 0, następnie x = 0.

2. Równanie postaci |f(x)| = b, gdzie b > 0. Aby rozwiązać to równanie, należy pozbyć się modułu. Robimy to tak: f(x) = b lub f(x) = -b. Teraz należy osobno rozwiązać każde z otrzymanych równań. Jeśli w pierwotnym równaniu b< 0, решений не будет.

1) |x + 2| = 4, ponieważ 4 > 0, to

x + 2 = 4 lub x + 2 = -4

2) |x 2 – 5| = 11, ponieważ 11 > 0, to

x 2 - 5 = 11 lub x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 bez pierwiastków

3) |x 2 – 5x| = -8 , ponieważ -osiem< 0, то уравнение не имеет корней.

3. Równanie postaci |f(x)| = g(x). Zgodnie ze znaczeniem modułu takie równanie będzie miało rozwiązania, jeśli jego prawa strona jest większa lub równa zero, tj. g(x) ≥ 0. Wtedy mamy:

f(x) = g(x) lub f(x) = -g(x).

1) |2x – 1| = 5x - 10. To równanie będzie miało pierwiastki, jeśli 5x - 10 ≥ 0. Tu zaczyna się rozwiązywanie takich równań.

1. ODZ 5x – 10 ≥ 0

2. Rozwiązanie:

2x - 1 = 5x - 10 lub 2x - 1 = -(5x - 10)

3. Połącz ODZ a rozwiązanie otrzymujemy:

Pierwiastek x \u003d 11/7 nie pasuje do O.D.Z., jest mniejszy niż 2, a x \u003d 3 spełnia ten warunek.

Odpowiedź: x = 3

2) |x – 1| \u003d 1 - x 2.

1. ODZ 1 - x 2 ≥ 0. Rozwiążmy tę nierówność metodą przedziałową:

(1 – x)(1 + x) ≥ 0

2. Rozwiązanie:

x - 1 \u003d 1 - x 2 lub x - 1 \u003d - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 lub x = 1 x = 0 lub x = 1

3. Połącz roztwór i O.D.Z.:

Tylko pierwiastki x = 1 i x = 0 są odpowiednie.

Odpowiedź: x = 0, x = 1.

4. Równanie postaci |f(x)| = |g(x)|. Takie równanie jest równoważne następującym dwóm równaniom f(x) = g(x) lub f(x) = -g(x).

1) |x 2 - 5x + 7| = |2x – 5|. To równanie jest równoważne dwóm następującym:

x 2 - 5x + 7 = 2x - 5 lub x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 lub x = 4 x = 2 lub x = 1

Odpowiedź: x = 1, x = 2, x = 3, x = 4.

5. Równania rozwiązywane metodą substytucji (zmiana zmiennej). Ta metoda rozwiązania najłatwiej wyjaśnić w konkretny przykład. Niech więc będzie podane równanie kwadratowe z modułem:

x 2 – 6|x| + 5 = 0. Według właściwości modułu x 2 = |x| 2 , więc równanie można przepisać w następujący sposób:

|x| 2–6|x| + 5 = 0. Zróbmy zmianę |x| = t ≥ 0, wtedy będziemy mieli:

t 2 - 6t + 5 \u003d 0. Rozwiązując to równanie, otrzymujemy to t \u003d 1 lub t \u003d 5. Wróćmy do wymiany:

|x| = 1 lub |x| = 5

x = ±1 x = ±5

Odpowiedź: x = -5, x = -1, x = 1, x = 5.

Spójrzmy na inny przykład:

x 2 + |x| – 2 = 0. Przez właściwość modułu x 2 = |x| 2 , więc

|x| 2 + |x| – 2 = 0. Zróbmy zmianę |x| = t ≥ 0, wtedy:

t 2 + t - 2 \u003d 0. Rozwiązując to równanie, otrzymujemy t \u003d -2 lub t \u003d 1. Wróćmy do wymiany:

|x| = -2 lub |x| = 1

Brak pierwiastków x = ± 1

Odpowiedź: x = -1, x = 1.

6. Innym rodzajem równań są równania o „złożonym” module. Takie równania obejmują równania, które mają „moduły w module”. Równania tego typu można rozwiązywać za pomocą właściwości modułu.

1) |3 – |x|| = 4. Postępujemy tak samo, jak w równaniach drugiego typu. Dlatego 4 > 0, to otrzymujemy dwa równania:

3 – |x| = 4 lub 3 – |x| = -4.

Wyraźmy teraz moduł x w każdym równaniu, wtedy |x| = -1 lub |x| = 7.

Rozwiązujemy każde z otrzymanych równań. W pierwszym równaniu nie ma pierwiastków, ponieważ -jeden< 0, а во втором x = ±7.

Odpowiedź x = -7, x = 7.

2) |3 + |x + 1|| = 5. Równanie to rozwiązujemy w podobny sposób:

3 + |x + 1| = 5 lub 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 lub x + 1 = -2. Nie ma korzeni.

Odpowiedź: x = -3, x = 1.

Jest również metoda ogólna rozwiązywanie równań z modułem. To jest metoda odstępów. Ale rozważymy to dalej.

blog.site, z pełnym lub częściowym skopiowaniem materiału, wymagany jest link do źródła.

W tym artykule szczegółowo przeanalizujemy wartość bezwzględna liczby. Damy różne definicje moduł liczby, wprowadzamy notację i dajemy ilustracje graficzne. Czyniąc to, rozważ różne przykłady znajdowanie modułu liczby z definicji. Następnie wymieniamy i uzasadniamy główne właściwości modułu. Na końcu artykułu porozmawiamy o tym, jak określa się i znajduje moduł liczby zespolonej.

Nawigacja po stronach.

Moduł liczby - definicja, zapis i przykłady

Najpierw przedstawiamy oznaczenie modułu. Moduł liczby a zapiszemy jako , to znaczy po lewej i prawej stronie liczby wstawimy pionowe linie tworzące znak modułu. Podajmy kilka przykładów. Na przykład modulo -7 można zapisać jako ; moduł 4,125 jest zapisany jako , a moduł jest zapisany jako .

Poniższa definicja modułu odnosi się do, a zatem do i do liczb całkowitych oraz do liczb wymiernych i niewymiernych, jako części składowych zbioru liczb rzeczywistych. Porozmawiamy o module liczby zespolonej w.

Definicja.

Moduł jest albo samą liczbą a, jeśli a jest liczbą dodatnią, albo liczbą −a, przeciwnie do liczby a, jeśli a jest liczbą ujemną, lub 0, jeśli a=0.

Dźwięczna definicja modułu liczby jest często napisana w następujący formularz , ten zapis oznacza, że ​​jeśli a>0 , jeśli a=0 i jeśli a<0 .

Rekord można przedstawić w bardziej zwartej formie . Ten zapis oznacza, że ​​jeśli (a jest większe lub równe 0 ) i jeśli a<0 .

Jest też rekord . Tutaj przypadek, w którym a=0 należy wyjaśnić osobno. W tym przypadku mamy , ale −0=0 , ponieważ zero jest uważane za liczbę przeciwną do siebie.

Przynieśmy przykłady znajdowania modułu liczby z podaną definicją. Na przykład znajdźmy moduły liczb 15 i . Zacznijmy od znalezienia . Ponieważ liczba 15 jest dodatnia, jej moduł jest z definicji równy tej liczbie, czyli . Jaki jest moduł liczby? Ponieważ jest liczbą ujemną, to jej moduł jest równy liczbie przeciwnej do liczby, czyli liczbie . W ten sposób, .

Na zakończenie tego akapitu podajemy jeden wniosek, który jest bardzo wygodny do zastosowania w praktyce przy ustalaniu modułu liczby. Z definicji modułu liczby wynika, że moduł liczby jest równy liczbie pod znakiem modułu, niezależnie od jego znaku, a z przykładów omówionych powyżej widać to bardzo wyraźnie. Stwierdzenie dźwięczne wyjaśnia, dlaczego moduł liczby jest również nazywany wartość bezwzględna liczby. Tak więc moduł liczby i wartość bezwzględna liczby są jednym i tym samym.

Moduł liczby jako odległość

Geometrycznie moduł liczby można interpretować jako dystans. Przynieśmy wyznaczanie modułu liczby w funkcji odległości.

Definicja.

Moduł to odległość od początku linii współrzędnych do punktu odpowiadającego liczbie a.

Definicja ta jest zgodna z definicją modułu liczby podaną w akapicie pierwszym. Wyjaśnijmy ten punkt. Odległość od początku do punktu odpowiadającego liczbie dodatniej jest równa tej liczbie. Zero odpowiada początkowi, więc odległość od początku do punktu o współrzędnej 0 wynosi zero (żadnego pojedynczego odcinka ani żadnego odcinka stanowiącego ułamek jednostkowego odcinka nie trzeba przełożyć, aby dostać się z punktu O do punktu ze współrzędną 0). Odległość od początku do punktu o ujemnej współrzędnej jest równa liczbie przeciwnej do współrzędnej danego punktu, ponieważ jest równa odległości od początku do punktu, którego współrzędna jest przeciwna.

Na przykład moduł liczby 9 wynosi 9, ponieważ odległość od początku do punktu o współrzędnej 9 wynosi dziewięć. Weźmy inny przykład. Punkt o współrzędnej -3,25 znajduje się w odległości 3,25 od punktu O, więc .

Brzmiona definicja modułu liczby jest szczególnym przypadkiem definiowania modułu różnicy dwóch liczb.

Definicja.

Moduł różnicowy dwóch liczb a i b są równe odległości między punktami linii współrzędnych o współrzędnych a i b .

To znaczy, jeśli dane są punkty na linii współrzędnych A(a) i B(b), to odległość od punktu A do punktu B jest równa modułowi różnicy między liczbami a i b. Jeśli przyjmiemy punkt O (punkt odniesienia) jako punkt B, to otrzymamy definicję modułu liczby podanej na początku tego paragrafu.

Wyznaczanie modułu liczby za pomocą arytmetycznego pierwiastka kwadratowego

Czasami znaleziony wyznaczanie modułu przez arytmetyczny pierwiastek kwadratowy.

Na przykład obliczmy moduły liczb -30 i w oparciu o tę definicję. Mamy . Podobnie obliczamy moduł dwóch trzecich: .

Definicja modułu liczby w postaci arytmetycznego pierwiastka kwadratowego jest również zgodna z definicją podaną w pierwszym akapicie tego artykułu. Pokażmy to. Niech a będzie liczbą dodatnią, a −a będzie liczbą ujemną. Następnie oraz , jeśli a=0 , to .

Właściwości modułu

Moduł posiada szereg charakterystycznych wyników - właściwości modułu. Teraz podamy główne i najczęściej używane z nich. Uzasadniając te własności, będziemy opierać się na definicji modułu liczby w kategoriach odległości.

Zacznijmy od najbardziej oczywistej właściwości modułu − moduł liczby nie może być liczbą ujemną. W postaci dosłownej ta właściwość ma postać dowolnej liczby a . Ta właściwość jest bardzo łatwa do uzasadnienia: modułem liczby jest odległość, a odległość nie może być wyrażona jako liczba ujemna.

Przejdźmy do kolejnej właściwości modułu. Moduł liczby jest równy zero wtedy i tylko wtedy, gdy ta liczba wynosi zero. Z definicji moduł zerowy wynosi zero. Zero odpowiada początkowi, żaden inny punkt na linii współrzędnych nie odpowiada zero, ponieważ każda liczba rzeczywista jest powiązana z pojedynczym punktem na linii współrzędnych. Z tego samego powodu każda liczba inna niż zero odpowiada punktowi innemu niż początek. A odległość od początku do dowolnego punktu innego niż punkt O nie jest równa zeru, ponieważ odległość między dwoma punktami jest równa zeru wtedy i tylko wtedy, gdy te punkty się pokrywają. Powyższe rozumowanie dowodzi, że tylko moduł zero jest równy zeru.

Pójść dalej. Liczby przeciwne mają równe moduły, to znaczy dla dowolnej liczby a . Rzeczywiście, dwa punkty na linii współrzędnych, których współrzędne są przeciwstawnymi liczbami, znajdują się w tej samej odległości od początku, co oznacza, że ​​moduły o przeciwnych liczbach są równe.

Następna właściwość modułu to: moduł iloczynu dwóch liczb jest równy iloczynowi modułów tych liczb, to znaczy, . Z definicji moduł iloczynu liczb a i b wynosi albo a b jeśli , albo -(a b) jeśli . Z reguł mnożenia liczb rzeczywistych wynika, że ​​iloczyn modułów liczb a i b jest równy albo a b , albo −(a b) , if , co dowodzi rozważanej własności.

Moduł ilorazu dzielenia a przez b jest równy ilorazowi dzielenia modułu a przez moduł b, to znaczy, . Uzasadnijmy tę właściwość modułu. Ponieważ iloraz jest równy iloczynowi, to . Na mocy poprzedniej własności mamy . Pozostaje tylko użyć równości , która jest ważna ze względu na definicję modułu liczby.

Następująca właściwość modułu jest zapisana jako nierówność: , a , b i c to dowolne liczby rzeczywiste. Zapisana nierówność to nic innego jak nierówność trójkąta. Aby to wyjaśnić, weźmy punkty A(a) , B(b) , C(c) na linii współrzędnych i rozważmy zdegenerowany trójkąt ABC, którego wierzchołki leżą na tej samej linii. Z definicji moduł różnicy jest równy długości segmentu AB, - długości segmentu AC, oraz - długości segmentu CB. Ponieważ długość dowolnego boku trójkąta nie przekracza sumy długości pozostałych dwóch boków, nierówność , zatem nierówność również się utrzymuje.

Udowodniona właśnie nierówność występuje znacznie częściej w formie . Pisana nierówność jest zwykle traktowana jako odrębna własność modułu ze sformułowaniem: „ Moduł sumy dwóch liczb nie przekracza sumy modułów tych liczb”. Ale nierówność wynika bezpośrednio z nierówności , jeśli wstawimy do niej −b zamiast b i przyjmiemy c=0 .

Moduł liczb zespolonych

Dajmy wyznaczanie modułu liczby zespolonej. Dajmy się Liczba zespolona, zapisany w formie algebraicznej , gdzie x i y są liczbami rzeczywistymi, reprezentującymi odpowiednio część rzeczywistą i urojoną danej liczby zespolonej z, i jest jednostką urojoną.

Tochilkina Julia

W artykule przedstawiono różne metody rozwiązywania równań z modułem.

Ściągnij:

Zapowiedź:

Miejska Budżetowa Instytucja Oświatowa

„Szkoła średnia nr 59”

Równania modulo

Praca abstrakcyjna

Wykonywane Uczeń klasy 9

MBOU „Szkoła średnia nr 59”, Barnauł

Tochilkina Julia

Kierownik

Zacharowa Ludmiła Władimirowna,

nauczyciel matematyki

MBOU „Szkoła średnia nr 59”, Barnauł

Barnauł 2015

Wstęp

Jestem w dziewiątej klasie. W tym roku akademickim muszę zdać maturę na kurs w szkole podstawowej. Aby przygotować się do egzaminu, zakupiliśmy kolekcję Matematyki D. A. Maltseva. Stopień 9 Przeglądając kolekcję znalazłem równania zawierające nie tylko jeden, ale i kilka modułów. Nauczyciel wyjaśnił mi i moim kolegom z klasy, że takie równania nazywane są równaniami „zagnieżdżonych modułów”. Ta nazwa wydawała nam się niezwykła, a rozwiązanie na pierwszy rzut oka dość skomplikowane. Tak powstał temat mojej pracy „Równania z modułem”. Postanowiłam pogłębić ten temat, zwłaszcza, że ​​przyda mi się on przy zdawaniu egzaminów na koniec roku szkolnego i myślę, że przyda mi się w klasach 10 i 11. Wszystko to decyduje o trafności wybranego przeze mnie tematu.

Cel :

1. Rozważ różne metody rozwiązywania równań z modułem.
2. Naucz się rozwiązywać równania zawierające znak wartości bezwzględnej różnymi metodami

Do pracy nad tematem sformułowano następujące zadania:

Zadania:

1. Przestudiować materiał teoretyczny na temat „Moduł liczby rzeczywistej”.
2. Rozważ metody rozwiązywania równań i skonsoliduj wiedzę zdobytą przez rozwiązywanie problemów.
3. Zastosuj zdobytą wiedzę w rozwiązywaniu różnych równań zawierających znak modułu w liceum

Przedmiot studiów:metody rozwiązywania równań z modułem

Przedmiot badań:równania modulo

Metody badawcze:

Teoretyczny : studium literatury przedmiotu badań;

Internet - informacja.

Analiza informacje uzyskane w badaniu literatury; wyniki uzyskane przez rozwiązywanie równań z modułem na różne sposoby.

Porównanie sposoby rozwiązywania równań, przedmiot racjonalności ich wykorzystania w rozwiązywaniu różnych równań modułem.

„Zaczynamy myśleć, kiedy na coś wpadamy”. Paul Valerie.

1. Pojęcia i definicje.

Pojęcie „modułu” jest szeroko stosowane w wielu sekcjach szkolnego kursu matematyki, na przykład w badaniu błędów bezwzględnych i względnych liczby przybliżonej; w geometrii i fizyce badane są pojęcia wektora i jego długości (modułu wektora). Pojęcie modułu jest stosowane na kierunkach matematyki wyższej, fizyki i nauk technicznych studiowanych w szkołach wyższych.

Słowo „moduł” pochodzi od łacińskiego słowa „modulus”, które w tłumaczeniu oznacza „miara”. Słowo to ma wiele znaczeń i jest używane nie tylko w matematyce, fizyce i technologii, ale także w architekturze, programowaniu i innych naukach ścisłych.

Uważa się, że termin ten został zaproponowany przez Kotsa, ucznia Newtona. Znak modułowy został wprowadzony w XIX wieku przez Weierstrassa.

W architekturze moduł jest początkową jednostką miary ustaloną dla danego obiektu architektonicznego.

W inżynierii jest to termin używany w różnych dziedzinach techniki, który służy do oznaczania różnych współczynników i wielkości, na przykład modułu sprężystości, modułu zaangażowania ...

W matematyce moduł ma kilka znaczeń, ale potraktuję go jako wartość bezwzględną liczby.

Definicja1 : Moduł (wartość bezwzględna) liczby rzeczywistej a sam numer nazywa się if a ≥0 lub przeciwna liczba - co jeśli a moduł zero wynosi zero.

Rozwiązując równania za pomocą modułu, wygodnie jest korzystać z właściwości modułu.

Rozważ dowody 5,6,7 właściwości.

Stwierdzenie 5. Równość │ jest prawdziwe, jeśliśr ≥ 0.

Dowód. Rzeczywiście, po podniesieniu do kwadratu obu części tej równości otrzymujemy, │ a+v │²=│ a │²+2│ ab │+│ do │²,

a² + 2 av + b² \u003d a² + 2│ av │ + b², skąd │ ​​av │ = av

A ostatnia równość będzie prawdziwa dlaśr ≥0.

Stwierdzenie 6. Równość │ a-c │=│ a │+│ c │ jest prawdziwe, kiedyśr ≤0.

Dowód. Aby to udowodnić, wystarczy równość

│ a + in │=│ a │+│ in │ zastąp in przez - in, potem a (- in) ≥0, skąd av ≤0.

Stwierdzenie 7. Równość │ a │+│ in │= a + in wykonywane w a ≥0 i b ≥0.

Dowód . Biorąc pod uwagę cztery przypadki a ≥ 0 i b ≥ 0; a ≥0 i b a przy ≥0; a w a ≥0 i b ≥0.

(a-c) w ≥0.

Interpretacja geometryczna

|a| to odległość na linii współrzędnych od punktu ze współrzędną a , do początku współrzędnych.

|-a| |a|

0 za x

Interpretacja geometryczna znaczenia |a| wyraźnie potwierdza, że ​​|-a|=|a|

Jeśli 0, to na linii współrzędnych znajdują się dwa punkty a i -a, równoodległe od zera, których moduły są równe.

Jeżeli a=0, to na linii współrzędnych |a| reprezentowany przez punkt 0.

Definicja 2: Równanie z modułem to równanie zawierające zmienną pod znakiem wartości bezwzględnej (pod znakiem modułu). Na przykład: |x +3|=1

Definicja 3: Rozwiązanie równania oznacza znalezienie wszystkich jego pierwiastków lub udowodnienie, że nie ma pierwiastków.

2. Metody rozwiązania

Z definicji i właściwości modułu wynikają główne metody rozwiązywania równań za pomocą modułu:

1. „Rozszerzenie” modułu (tj. za pomocą definicji);
2. Wykorzystanie geometrycznego znaczenia modułu (właściwość 2);
3. Metoda rozwiązania graficznego;
4. Użycie przekształceń równoważnych (właściwości 4.6);
5. Podstawianie zmiennych (używa właściwości 5).
6. metoda interwałowa.

Rozwiązałem dość dużą liczbę przykładów, ale w mojej pracy przedstawiam tylko kilka, moim zdaniem, typowych przykładów rozwiązywanych na różne sposoby, ponieważ reszta się powiela i aby zrozumieć, jak rozwiązywać równania za pomocą moduł, nie ma potrzeby rozpatrywania wszystkich rozwiązanych przykładów.

ROZWIĄZANIE RÓWNAŃ | f(x)| = a

Rozważ równanie | f(x)| = a i R

Równanie tego rodzaju można rozwiązać definiując moduł:

Jeśli a wtedy równanie nie ma pierwiastków.

Jeśli a= 0, to równanie jest równoważne f(x)=0.

Jeśli a>0, to równanie jest równoważne zbiorowi

Przykład. Rozwiąż równanie |3x+2|=4.

Rozwiązanie.

|3x+2|=4, potem 3x+2=4,

3x+2= -4;

X=-2,

X=2/3

Odpowiedź: -2;2/3.

ROZWIĄZANIE RÓWNAŃ Z WYKORZYSTANIEM WŁAŚCIWOŚCI GEOMETRYCZNYCH MODUŁU.

Przykład 1 Rozwiąż równanie /x-1/+/x-3/=6.

Rozwiązanie.

Rozwiązanie tego równania polega na znalezieniu wszystkich takich punktów na osi liczbowej Ox, dla których suma odległości od niego do punktów o współrzędnych 1 i 3 jest równa 6.

Żaden z punktów na liniinie spełnia tego warunku, ponieważ suma podanych odległości wynosi 2. Poza tym segmentem znajdują się dwa punkty: 5 i -1.

1 1 3 5

Odpowiedź: -1;5

Przykład 2 Rozwiąż równanie |x 2 +x-5|+|x 2 +x-9|=10.

Rozwiązanie.

Oznacz x 2 + x-5 \u003d a, a następnie / a / + / a-4 /=10. Znajdźmy takie punkty na osi x, że dla każdego z nich suma odległości do punktów o współrzędnych 0 i 4 jest równa 10. Warunek ten jest spełniony przez -4 i 7.

3 0 4 7

Więc x 2 + x-5 \u003d 4 x 2 + x-5 \u003d 7

X 2 + x-2 \u003d 0 x 2 + x-12 \u003d 0

X 1 \u003d 1, x 2 \u003d -2 x 1 \u003d -4, x 2 \u003d 3 Odpowiedź: -4; -2; jeden; 3.

ROZWIĄZANIE RÓWNAŃ | f(x)| = | g(x)|.

1. Ponieważ | a |=|b |, jeśli a=b, to równanie postaci | f(x)| = | g(x )| jest równoznaczne z agregatem

Przykład 1.

Rozwiąż równanie | x–2| = |3 - x |.

Rozwiązanie.

To równanie jest równoważne dwóm równaniom:

x - 2 \u003d 3 - x (1) i x - 2 \u003d -3 + x (2)

2x = 5 -2 = -3 - niepoprawnie

X = 2,5 równanie nie ma rozwiązań.

Odpowiedź: 2.5.

Przykład 2

Rozwiąż równanie |x 2 + 3x-20|= |x 2 -3x+ 2|.

Rozwiązanie.

Ponieważ obie strony równania są nieujemne, tokwadrat jest równoważną transformacją:

(x 2 + 3x-20) 2 \u003d (x 2 -3x + 2) 2

(x 2 + 3x-20) 2 - (x 2 -3x + 2) 2 \u003d 0,

(x 2 + 3x-20-x 2 + 3x-2) (x 2 + 3x-20 + x 2 -3x + 2) \u003d 0,

(6x-22) (2x 2 -18)=0,

6x-22=0 lub 2x 2 -18=0;

X=22/6, x=3, x=-3.

X=11/3

Odpowiedź: -3; 3; 11/3.

ROZWIĄZANIE RÓWNAŃ WIDOKU | f(x)| = g(x).

Różnica między tymi równaniami i| f(x)| = a w tym, że prawa strona jest również zmienną. I może być zarówno pozytywny, jak i negatywny. Dlatego musisz upewnić się, że jest nieujemny, ponieważ moduł nie może być równy liczbie ujemnej (właściwość№1 )

1 sposób

Rozwiązanie równania | f(x)| = g(x ) sprowadza się do zbioru rozwiązań równańi sprawdzanie zasadności nierówności g(x )>0 dla znalezionych wartości nieznanego.

Dwustronny (zgodnie z definicją modułu)

Ponieważ | f(x)| = g (x) jeśli f (x) = 0; | f(x)| = - f(x) jeśli f(x)

Przykład.

Rozwiąż równanie |3 x –10| = x - 2.

Rozwiązanie.

To równanie jest równoważne połączeniu dwóch systemów:

Ot e t: 3; cztery.

ROZWIĄZANIE RÓWNAŃ FORMY |f 1 (x)|+|f 2 (x)|+…+|f n (x)|=g(x)

Rozwiązanie równań tego typu opiera się na definicji modułu. Dla każdej funkcji f 1 (x), f 2 (x), …, f n (x) trzeba znaleźć dziedzinę definicji, jej zera i punkty nieciągłości, które się łamią obszar ogólny definicje na przedziały, w każdym z których funkcje f 1 (x), f 2 (x), …, f n (x) zachować swój znak. Dalej, korzystając z definicji modułu, dla każdego ze znalezionych obszarów otrzymujemy równanie, które należy rozwiązać na danym przedziale. Ta metoda nazywa się „metoda interwałowa»

Przykład.

Rozwiąż równanie |x-2|-3|x+4|=1.

Rozwiązanie.

Znajdźmy punkty, w których wyrażenia podmodułów są równe zero

x-2=0, x+4=0,

x=2; x=-4.

Podzielmy linię liczbową na przedziały x

Rozwiązanie równania sprowadza się do rozwiązania trzech układów:

Odpowiedź: -15, -1,8.

GRAFICZNA METODA ROZWIĄZYWANIA RÓWNAŃ ZAWIERAJĄCYCH ZNAK MODUŁU.

Graficzny sposób rozwiązywania równań jest przybliżony, ponieważ dokładność zależy od wybranego segmentu jednostki, grubości ołówka, kątów przecinania się linii itp. Ale ta metoda pozwala oszacować, ile rozwiązań ma dane równanie.

Przykład. Rozwiąż graficznie równanie |x - 2| + |x - 3| + |2x - 8| = 9

Rozwiązanie. Skonstruujmy wykresy funkcji w jednym układzie współrzędnych

y=|x - 2| + |x - 3| + |2x - 8| i y=9.

Aby zbudować wykres, rozważ ta funkcja na każdym przedziale (-∞; 2); [ 3/2 ; )

Odpowiedź: (- ∞ ; 4/3] [ 3/2 ; ∞ )

Zastosowaliśmy również metodę przekształceń równoważnych w rozwiązywaniu równań | f(x)| = | g(x)|.

RÓWNANIA Z „MODUŁEM KOMPLEKSOWYM”

Innym rodzajem równań są równania o „złożonym” module. Takie równania obejmują równania, które mają „moduły w module”. Równania tego typu można rozwiązywać różnymi metodami.

Przykład 1

Rozwiąż równanie ||||x| – |–2| –1| –2| = 2.

Rozwiązanie.

Z definicji modułu mamy:

Rozwiążmy pierwsze równanie.

1. ||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

x = 7.

Rozwiążmy drugie równanie.

1. ||| x | –2| –1| = 0,

|| x | –2| = 1,

| x | -2 = 1,

| x | = 3 i | x | = 1,

x = 3; x = 1.

W dniu: 1; 3; 7.

Przykład 2

Rozwiąż równanie |2 – |x + 1|| = 3.

Rozwiązanie.

Rozwiążmy równanie, wprowadzając nową zmienną.

Niech | x + 1| = y , to |2 – y | = 3, stąd

Zróbmy odwrotne podstawienie:

(1) | x + 1| = -1 - brak rozwiązań.

(2) | x + 1| = 5

A n e t: -6; cztery.

Przykład3 .

Ile pierwiastków ma równanie | 2 | x | -6 | = 5 - x?

Rozwiązanie. Rozwiążmy równanie za pomocą schematów równoważności.

Równanie | 2 | x | -6 | = 5 -x jest odpowiednikiem systemu:

Wartość bezwzględna liczby a to odległość od początku do punktu ALE(a).

Aby zrozumieć tę definicję, podstawiamy zamiast zmiennej a dowolna liczba, na przykład 3 i spróbuj ją przeczytać ponownie:

Wartość bezwzględna liczby 3 to odległość od początku do punktu ALE(3 ).

Staje się jasne, że moduł to nic innego jak zwykła odległość. Spróbujmy zobaczyć odległość od początku do punktu A( 3 )

Odległość od początku współrzędnych do punktu A( 3 ) jest równe 3 (trzy jednostki lub trzy kroki).

Moduł liczby wskazują dwie pionowe linie, na przykład:

Moduł liczby 3 oznaczamy następująco: |3|

Moduł liczby 4 oznaczamy następująco: |4|

Moduł liczby 5 oznaczamy następująco: |5|

Szukaliśmy modułu liczby 3 i okazało się, że jest on równy 3. Więc piszemy:

Czyta jak: „Moduł trzech to trzy”

Spróbujmy teraz znaleźć moduł liczby -3. Ponownie wracamy do definicji i podstawiamy do niej liczbę -3. Tylko zamiast kropki A posługiwać się nowy punkt B. Punkt A wykorzystaliśmy już w pierwszym przykładzie.

Moduł liczby to 3 nazwij odległość od początku do punktu B(—3 ).

Odległość od jednego punktu do drugiego nie może być ujemna. Dlatego moduł dowolnej liczby ujemnej, będącej odległością, również nie będzie ujemny. Modułem liczby -3 będzie liczba 3. Odległość od początku do punktu B(-3) jest również równa trzem jednostkom:

Czyta jak: „Moduł liczby minus trzy to trzy”

Moduł liczby 0 wynosi 0, ponieważ punkt o współrzędnej 0 pokrywa się z początkiem, tj. odległość od początku do punktu O(0) równa się zero:

„Moduł zera to zero”

Wyciągamy wnioski:

• Moduł liczby nie może być ujemny;
• W przypadku liczby dodatniej i zera moduł jest równy samej liczbie, a w przypadku ujemnej liczbie przeciwnej;
• Liczby przeciwne mają równe moduły.

Liczby przeciwne

Liczby różniące się tylko znakami nazywa się naprzeciwko. Na przykład liczby -2 i 2 są przeciwieństwami. Różnią się tylko znakami. Liczba -2 ma znak minus, a 2 ma znak plus, ale tego nie widzimy, ponieważ plus, jak powiedzieliśmy wcześniej, tradycyjnie nie jest pisany.

Więcej przykładów liczb przeciwnych:

Liczby przeciwne mają równe moduły. Na przykład znajdźmy moduły dla −2 i 2

Rysunek pokazuje, że odległość od początku do punktów A(−2) oraz B(2) równa się dwóm krokom.

Podobała Ci się lekcja?
Dołączć do naszego Nowa grupa Vkontakte i zacznij otrzymywać powiadomienia o nowych lekcjach

Moduł to wartość bezwzględna wyrażenia. Aby przynajmniej w jakiś sposób oznaczyć moduł, zwyczajowo używa się nawiasów prostych. Wartość zawarta w nawiasach parzystych jest wartością przyjmowaną modulo. Proces rozwiązywania dowolnego modułu polega na otwarciu tych samych nawiasów bezpośrednich, które w języku matematycznym nazywamy nawiasami modułowymi. Ich ujawnienie odbywa się zgodnie z pewną liczbą zasad. Ponadto w kolejności rozwiązywania modułów istnieją również zestawy wartości tych wyrażeń, które znajdowały się w nawiasach modułów. W większości przypadków moduł jest rozwijany w taki sposób, że wyrażenie będące submodułem otrzymuje zarówno wartości dodatnie, jak i ujemne, w tym wartość zero. Jeśli zaczniemy od ustalonych właściwości modułu, to w procesie zestawiane są różne równania lub nierówności z pierwotnego wyrażenia, które następnie należy rozwiązać. Zastanówmy się, jak rozwiązywać moduły.

Proces rozwiązania

Rozwiązanie modułu zaczyna się od napisania oryginalnego równania z modułem. Aby odpowiedzieć na pytanie, jak rozwiązywać równania z modułem, musisz je całkowicie otworzyć. Aby rozwiązać takie równanie, moduł jest rozwijany. Należy wziąć pod uwagę wszystkie wyrażenia modułowe. Konieczne jest ustalenie, przy jakich wartościach nieznanych wielkości zawartych w jego składzie znika wyrażenie modułowe w nawiasach. W tym celu wystarczy przyrównać wyrażenie w nawiasach modularnych do zera, a następnie obliczyć rozwiązanie otrzymanego równania. Znalezione wartości muszą zostać zarejestrowane. W ten sam sposób konieczne jest również wyznaczenie wartości wszystkich nieznanych zmiennych dla wszystkich modułów w tym równaniu. Następnie należy zająć się definicją i rozważeniem wszystkich przypadków istnienia zmiennych w wyrażeniach, gdy różnią się one od wartości zero. Aby to zrobić, musisz wypisać jakiś system nierówności odpowiadający wszystkim modułom w pierwotnej nierówności. Nierówności muszą być skomponowane w taki sposób, aby obejmowały wszystkie dostępne i możliwe wartości zmiennej, które znajdują się na osi liczbowej. Następnie musisz narysować do wizualizacji tę samą oś liczbową, na której w przyszłości umieścisz wszystkie uzyskane wartości.

Prawie wszystko można teraz zrobić online. Moduł nie jest wyjątkiem od zasad. Możesz rozwiązać go online na jednym z wielu nowoczesne zasoby. Wszystkie te wartości zmiennej, które znajdują się w module zerowym, będą specjalnym ograniczeniem, które zostanie użyte w procesie rozwiązywania równania modularnego. W pierwotnym równaniu wymagane jest rozwinięcie wszystkich dostępnych nawiasów modularnych, zmieniając znak wyrażenia tak, aby wartości żądanej zmiennej pokrywały się z wartościami widocznymi na osi liczbowej. Otrzymane równanie musi zostać rozwiązane. Wartość zmiennej, która zostanie uzyskana w trakcie rozwiązywania równania, musi być skonfrontowana z ograniczeniem ustawionym przez sam moduł. Jeżeli wartość zmiennej w pełni spełnia warunek, to jest poprawna. Wszystkie pierwiastki, które zostaną uzyskane w trakcie rozwiązywania równania, ale nie będą pasować do ograniczeń, należy odrzucić.