Liczby wymierne i operacje na nich. Działania na liczbach wymiernych: zasady, przykłady, rozwiązania
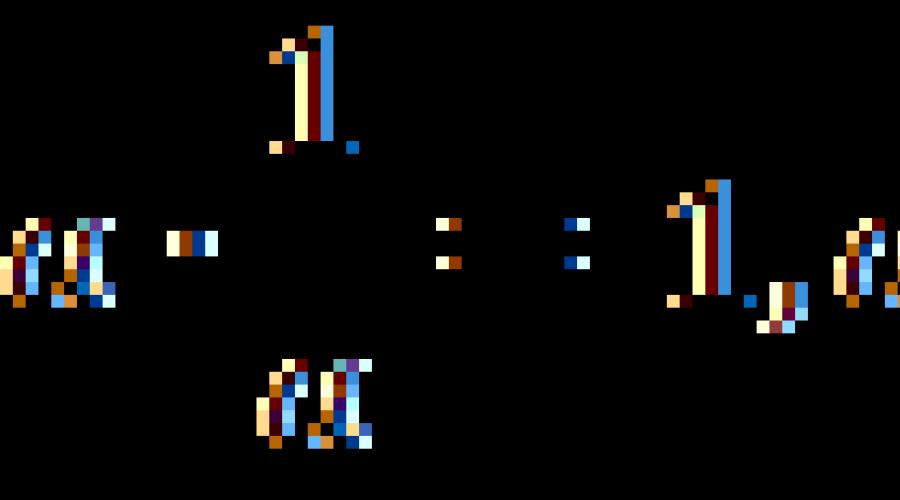
Na tej lekcji przypomnimy sobie podstawowe właściwości operacji na liczbach. Nie tylko przejrzymy podstawowe właściwości, ale także dowiemy się, jak zastosować je do liczb wymiernych. Całą zdobytą wiedzę utrwalimy rozwiązując przykłady.
Podstawowe właściwości operacji na liczbach:
Pierwsze dwie właściwości to właściwości dodawania, kolejne dwie to właściwości mnożenia. Piąta właściwość dotyczy obu operacji.
Nie ma w tych obiektach nic nowego. Obowiązywały one zarówno dla liczb naturalnych, jak i całkowitych. Są one również prawdziwe w przypadku liczb wymiernych i będą prawdziwe w przypadku liczb, które będziemy badać dalej (na przykład liczb niewymiernych).
Właściwości permutacyjne:
Zmiana układu terminów lub czynników nie zmienia wyniku.
Właściwości kombinacji:, .
Dodawanie lub mnożenie wielu liczb można wykonać w dowolnej kolejności.
Właściwość dystrybucji:.
Właściwość łączy obie operacje - dodawanie i mnożenie. Ponadto, jeśli czyta się to od lewej do prawej, nazywa się to regułą otwierania nawiasów, a jeśli czyta się w przeciwnym kierunku, nazywa się to zasadą umieszczania wspólnego czynnika poza nawiasami.
Poniższe dwie właściwości opisują elementy neutralne dla dodawania i mnożenia: dodanie zera i pomnożenie przez jeden nie powoduje zmiany pierwotnej liczby.
Dwie kolejne właściwości, które opisują elementy symetryczne w przypadku dodawania i mnożenia suma liczb przeciwnych wynosi zero; iloczyn liczb odwrotnych jest równy jeden.
![]()
Następna nieruchomość: . Jeśli liczbę pomnożymy przez zero, wynikiem zawsze będzie zero.
Ostatnią właściwością, której się przyjrzymy, jest: .
Mnożąc liczbę przez , otrzymujemy liczbę przeciwną. Ta właściwość ma szczególną cechę. Wszystkie inne rozważane właściwości nie mogły zostać udowodnione przy użyciu pozostałych. Tę samą właściwość można udowodnić, korzystając z poprzednich.
Mnożenie przez
Udowodnijmy, że jeśli pomnożymy liczbę przez , otrzymamy liczbę przeciwną. W tym celu używamy własności dystrybucji: .
Dotyczy to dowolnych liczb. Zastąpmy i zamiast liczby:
Po lewej stronie w nawiasach znajduje się suma wzajemnie przeciwnych liczb. Ich suma wynosi zero (mamy taką własność). Teraz po lewej stronie. Po prawej stronie otrzymujemy: ![]() .
.
Teraz mamy zero po lewej stronie i sumę dwóch liczb po prawej. Ale jeśli suma dwóch liczb wynosi zero, to liczby te są wzajemnie przeciwne. Ale liczba ma tylko jedną przeciwną liczbę: . A więc tak: .
Właściwość została udowodniona.
Taka właściwość, którą można udowodnić na podstawie poprzednich właściwości, nazywa się twierdzenie
Dlaczego nie ma tutaj właściwości odejmowania i dzielenia? Na przykład można napisać właściwość rozdzielności dla odejmowania: .
Lecz odkąd:
- Odejmowanie dowolnej liczby można równoważnie zapisać jako dodawanie, zastępując liczbę jej przeciwieństwem:
![]()
- Dzielenie można zapisać jako mnożenie przez jego odwrotność:
![]()
Oznacza to, że właściwości dodawania i mnożenia można zastosować do odejmowania i dzielenia. W rezultacie lista właściwości, o których należy pamiętać, jest krótsza.
Wszystkie własności, które rozważaliśmy, nie są wyłącznie własnościami liczb wymiernych. Inne liczby, na przykład niewymierne, również podlegają tym wszystkim zasadom. Na przykład suma liczby przeciwnej wynosi zero: .
Teraz przejdziemy do części praktycznej, rozwiązując kilka przykładów.
Liczby wymierne w życiu
Nazywa się te właściwości obiektów, które możemy opisać ilościowo, oznaczyć jakąś liczbą wartości: długość, waga, temperatura, ilość.
Tę samą wielkość można oznaczyć zarówno liczbą całkowitą, jak i ułamkową, dodatnią lub ujemną.
Na przykład twój wzrost to m - liczba ułamkowa. Ale możemy powiedzieć, że jest równy cm - to już liczba całkowita (ryc. 1).

Ryż. 1. Ilustracja na przykład
Jeszcze jeden przykład. Ujemna temperatura w skali Celsjusza będzie dodatnia w skali Kelvina (ryc. 2).

Ryż. 2. Ilustracja na przykład
Budując ścianę domu, jedna osoba może zmierzyć szerokość i wysokość w metrach. Wytwarza ilości ułamkowe. Wszystkie dalsze obliczenia przeprowadzi na liczbach ułamkowych (wymiernych). Inna osoba może zmierzyć wszystko w liczbie cegieł na szerokość i wysokość. Otrzymawszy jedynie wartości całkowite, przeprowadzi obliczenia na liczbach całkowitych.
Same wielkości nie są ani całkowite, ani ułamkowe, ani ujemne, ani dodatnie. Ale liczba, za pomocą której opisujemy wartość wielkości, jest już dość specyficzna (na przykład ujemna i ułamkowa). To zależy od skali pomiaru. A kiedy przechodzimy od ilości rzeczywistych do modelu matematycznego, pracujemy z określonym typem liczb
Zacznijmy od dodawania. Terminy można układać w dowolny dogodny dla nas sposób, a czynności wykonywać w dowolnej kolejności. Jeśli terminy różnych znaków kończą się tą samą cyfrą, wygodnie jest najpierw wykonać na nich operacje. Aby to zrobić, zamieńmy warunki. Na przykład:
Ułamki zwykłe o podobnych mianownikach można łatwo dodać.
Liczby przeciwne sumują się do zera. Liczby z tymi samymi końcami dziesiętnymi można łatwo odjąć. Wykorzystując te właściwości, a także prawo przemienności dodawania, można ułatwić obliczenie wartości na przykład następującego wyrażenia:
![]()
Liczby z dopełniającymi końcami dziesiętnymi są łatwe do dodania. Z częściami pełnymi i ułamkowymi liczby mieszane wygodna praca osobno. Korzystamy z tych właściwości przy obliczaniu wartości następującego wyrażenia:
![]()
Przejdźmy do mnożenia. Istnieją pary liczb, które można łatwo pomnożyć. Korzystając z właściwości przemienności, możesz zmienić kolejność czynników tak, aby sąsiadowały ze sobą. Można od razu policzyć minusy w produkcie i wyciągnąć wniosek na temat znaku wyniku.
Rozważmy ten przykład:
Jeśli jeden z czynników jest równy zero, to iloczyn jest równy zero, na przykład: .
Iloczyn liczb odwrotnych jest równy jeden, a pomnożenie przez jeden nie zmienia wartości iloczynu. Rozważmy ten przykład:
Spójrzmy na przykład wykorzystujący właściwość rozdzielności. Jeśli otworzysz nawiasy, każde mnożenie będzie łatwe.
Badamszyńska Liceum №2
Rozwój metodologiczny
matematyka
w 6 klasie
„Działania z liczbami wymiernymi”
przygotowany
nauczyciel matematyki
Babenko Larisa Grigoriewna
Z. Badamsza
2014
Temat lekcji:« Działania na liczbach wymiernych».
Typ lekcji :
Lekcja uogólniania i systematyzacji wiedzy.
Cele Lekcji:
edukacyjny:
Podsumować i usystematyzować wiedzę uczniów na temat zasad działania na liczbach dodatnich i ujemnych;
Wzmocnić umiejętność stosowania zasad podczas ćwiczeń;
Rozwijaj umiejętności niezależnej pracy;
rozwijanie:
Rozwijać logiczne myślenie, mowa matematyczna, umiejętności obliczeniowe; - rozwijać umiejętność stosowania zdobytej wiedzy do rozwiązywania stosowanych problemów; - poszerzanie horyzontów;
wychowywanie:
Wychowanie zainteresowanie poznawcze do tematu.
Sprzęt:
Arkusze z tekstami zadań, zadaniami dla każdego ucznia;
Matematyka. Podręcznik dla klasy 6 instytucje edukacyjne/
N.Ya. Vilenkin, V.I. Żochow, A.S. Chesnokov, S. I. Shvartsburd. – M., 2010.
Plan lekcji:
Organizowanie czasu.
Pracuj ustnie
Przegląd zasad dodawania i odejmowania liczb za pomocą różne znaki. Aktualizowanie wiedzy.
Rozwiązywanie zadań zgodnie z podręcznikiem
Uruchamianie testu
Podsumowanie lekcji. Zadawanie zadań domowych
Odbicie
Podczas zajęć
Organizowanie czasu.
Pozdrowienia od nauczyciela i uczniów.
Zgłoś temat lekcji, plan pracy na lekcję.
Dziś mamy nietypową lekcję. Na tej lekcji przypomnimy sobie wszystkie zasady działania na liczbach wymiernych oraz umiejętność wykonywania operacji dodawania, odejmowania, mnożenia i dzielenia.
Mottem naszej lekcji będzie chińska przypowieść:
„Powiedz mi, a zapomnę;
Pokaż mi, a zapamiętam;
Pozwól mi to zrobić, a zrozumiem.
Chcę Cię zaprosić w podróż.
Pośrodku przestrzeni, gdzie wyraźnie widać było wschód słońca, rozciągała się wąska, niezamieszkana kraina – oś liczbowa. Nie wiadomo, gdzie się zaczęło i nie wiadomo, gdzie się skończyło. A pierwszymi, które zaludniły ten kraj, były liczby naturalne. Jakie liczby nazywamy liczbami naturalnymi i jak je oznaczamy?
Odpowiedź:
Liczby 1, 2, 3, 4,….. używane do liczenia obiektów lub do wskazania numeru seryjnego obiektu wśród obiektów jednorodnych nazywane są naturalnymi (N ).
Liczenie werbalne
88-19 72:8 200-60
Odpowiedzi: 134; 61; 2180.
Było ich nieskończona liczba, ale kraj, choć niewielki w szerokości, miał nieskończoną długość, tak że wszystko od jednego do nieskończoności mieściło się i tworzyło pierwszy stan, zbiór liczb naturalnych.
Praca nad zadaniem.
Kraj był wyjątkowo piękny. Na całym jego terytorium znajdowały się wspaniałe ogrody. Są to wiśnia, jabłko, brzoskwinia. Przyjrzymy się teraz jednemu z nich.
Co trzy dni jest o 20 procent więcej dojrzałych wiśni. Ile dojrzałych owoców będzie miała ta wiśnia po 9 dniach, jeśli na początku obserwacji było na niej 250 dojrzałych wiśni?
Odpowiedź: za 9 dni na tej wiśni będą 432 dojrzałe owoce (300; 360; 432).
Na terytorium pierwszego stanu zaczęły osiedlać się nowe liczby i te liczby wraz z naturalnymi utworzyły nowy stan, dowiemy się który, rozwiązując zadanie.
Uczniowie mają na biurkach dwie kartki papieru:
1. Oblicz:
1)-48+53 2)45-(-23) 3)-7,5:(-0,5) 4)-4x(-15)
1)56:(-8) 2)-3,3-4,7 3)-5,6:(-0,1) 4)9-12
1)48-54 2)37-(-37) 3)-52,7+42,7 4)-6x1/3
1)-12x(-6) 2)-90:(-15) 3)-25+45 4)6-(-10)
Ćwiczenia: Połącz po kolei wszystkie liczby naturalne, nie podnosząc ręki, i nazwij powstałą literę.
Odpowiedzi do testu:
5 68 15 60
72 6 20 16
Pytanie: Co oznacza ten symbol? Jakie liczby nazywamy liczbami całkowitymi?
Odpowiedzi: 1) Na lewo, od terytorium pierwszego stanu, osiedliła się liczba 0, na lewo od niej -1, jeszcze dalej na lewo -2, itd. do nieskończoności. Liczby te wraz z liczbami naturalnymi utworzyły nowy stan rozszerzony, zbiór liczb całkowitych.
2) Liczby naturalne, ich przeciwieństwa i zero nazywane są liczbami całkowitymi ( Z ).
Powtarzanie tego, czego się nauczyłeś.
1) Kolejna strona naszej bajki jest zaczarowana. Odczarujmy to, poprawiajmy błędy.
27 · 4 0 -27 = 27 0 · (-27) = 0
63 3 0 · 40 (-6) · (-6) -625 124
50 · 8 27 -18: (-2)
Odpowiedzi:
-27 4 27 0 (-27) = 0
-50 8 4 -36: 6
2) Słuchajmy dalej tej historii.
NA wolne miejsca do osi liczbowej dodano ułamki 2/5; −4/5; 3,6; −2,2;... Ułamki wraz z pierwszymi osadnikami utworzyły kolejny stan rozwinięty – zbiór liczb wymiernych. ( Q)
1) Jakie liczby nazywamy wymiernymi?
2) Czy dowolna liczba całkowita, ułamek dziesiętny jest liczbą wymierną?
3) Pokaż, że dowolna liczba całkowita lub ułamek dziesiętny jest liczbą wymierną.
Zadanie na tablicy: 8; 3 ; -6; - ; - 4,2; – 7,36; 0; .
Odpowiedzi:
1) Liczba, którą można zapisać w postaci stosunku , gdzie a jest liczbą całkowitą, a n jest liczbą naturalną, nazywa się liczbą wymierną .
2) Tak.
3) .
Znasz teraz liczby całkowite i ułamkowe, dodatnie i ujemne, a nawet liczbę zero. Wszystkie te liczby nazywane są racjonalnymi, co w języku rosyjskim oznacza „ podlega umysłowi.”
Liczby wymierne
dodatnie zero ujemne
cały ułamek cały ułamek
Aby w przyszłości z powodzeniem studiować matematykę (i nie tylko matematykę), trzeba dobrze znać zasady działań arytmetycznych na liczbach wymiernych, w tym zasady znaków. A są tak różne! Nie trzeba długo czekać, aby się pomylić.
Minuta wychowania fizycznego.
Dynamiczna pauza.
Nauczyciel: Każda praca wymaga przerwy. Odpocznijmy!
Zróbmy ćwiczenia regeneracyjne:
1) Raz, dwa, trzy, cztery, pięć -
Raz! Wstań, podciągnij się,
Dwa! Pochyl się, wyprostuj,
Trzy! Trzy klaśnięcia w dłonie,
Trzy skinienia głową.
Cztery oznacza szersze ręce.
Pięć - machaj rękami. Sześć - usiądź cicho przy biurku.
(Dzieci wykonują ruchy podążając za nauczycielem zgodnie z treścią tekstu.)
2) Mrugnij szybko, zamknij oczy i siedź tak, licząc do pięciu. Powtórz 5 razy.
3) Zamknij mocno oczy, policz do trzech, otwórz je i spójrz w dal, licząc do pięciu. Powtórz 5 razy.
Strona historyczna.
W życiu, jak w bajkach, ludzie „odkrywali” liczby wymierne stopniowo. Początkowo przy liczeniu obiektów pojawiały się liczby naturalne. Na początku było ich niewielu. Początkowo powstały tylko cyfry 1 i 2. Słowa „solista”, „słońce”, „solidarność” pochodzą od łacińskiego „solus” (jeden). Wiele plemion nie miało innych cyfr. Zamiast „3” powiedzieli „raz-dwa”, zamiast „4” powiedzieli „dwa-dwa”. I tak dalej, aż do szóstej. A potem przyszło „dużo”. Ludzie spotykali się z ułamkami przy podziale łupów i mierzeniu ilości. Aby ułatwić pracę z ułamkami, zostały wymyślone miejsca dziesiętne. W Europie zostały wprowadzone w 1585 roku przez holenderskiego matematyka.
Praca nad równaniami
Nazwisko matematyka poznasz rozwiązując równania i wykorzystując linię współrzędnych do znalezienia litery odpowiadającej danej współrzędnej.
1) -2,5 + x = 3,5 2) -0,3 x = 0,6 3) y – 3,4 = -7,4
4) – 0,8: x = -0,4 5)a · (-8) =0 6)M + (- )=
JEŚĆ M I O W R N U S
-4 -3 -2 -1 0 1 2 3 4 5 6
Odpowiedzi:
6 (C) 4)2 (B)
-2 (T) 5) 0 (I)
-4(E) 6)4(H)
STEVIN – holenderski matematyk i inżynier (Simon Stevin)
Strona historyczna.
Nauczyciel:
Bez poznania przeszłości w rozwoju nauki nie da się zrozumieć jej teraźniejszości. Ludzie nauczyli się wykonywać operacje na liczbach ujemnych jeszcze przed naszą erą. Indyjscy matematycy uważali liczby dodatnie za „właściwości”, a liczby ujemne za „długi”. Oto jak indyjski matematyk Brahmagupta (VII w.) określił pewne zasady wykonywania operacji na liczbach dodatnich i ujemnych:
„Suma dwóch właściwości jest własnością”
„Suma dwóch długów to dług”
„Suma majątku i długu jest równa ich różnicy”
„Produktem dwóch aktywów lub dwóch długów jest własność”, „Produktem aktywów i długu jest dług”.
Chłopaki, przetłumaczcie starożytne indyjskie zasady na współczesny język.
Wiadomość nauczyciela:
Jak nie ma życia bez ciepło słońca,
Bez zimowego śniegu i bez liście kwiatów,
W matematyce nie ma działań bez znaków!
Dzieci proszone są o odgadnięcie, jakiego znaku akcji brakuje.
Ćwiczenia. Uzupełnij brakujący znak.
− 1,2 1,4 = − 2,6
3,2 (− 8) = − 0,4
1 (− 1,7) = 2,7
− 4,5 (− 0,5) = 9
− 1,3 2,8 = 1,5
Odpowiedzi: 1) + 2) ∙ 3) − 4) : 5) − 6) :
Niezależna praca(zapisz odpowiedzi do zadań na kartce):
Porównaj liczby
znajdź ich moduły
porównać z zerem
znajdź ich sumę
znajdź ich różnicę
znaleźć pracę
znajdź iloraz
napisz liczby przeciwne
znajdź odległość między tymi liczbami
10) ile liczb całkowitych znajduje się między nimi
11) znajdź sumę wszystkich liczb całkowitych znajdujących się między nimi.
Kryteria oceny: wszystko zostało rozwiązane poprawnie – „5”
1-2 błędy - „4”
3-4 błędy - „3”
więcej niż 4 błędy - „2”
Praca indywidualna przez karty(Dodatkowo).
Karta 1. Rozwiąż równanie: 8,4 – (x – 3,6) = 18
Karta 2. Rozwiąż równanie: -0,2x · (-4) = -0,8
Karta 3. Rozwiąż równanie: =
Odpowiedzi na karty :
1) 6; 2) -1; 3) 4/15.
Gra „Egzamin”.
Mieszkańcy kraju żyli szczęśliwie, grali w gry, rozwiązywali problemy, równania i zapraszali nas do zabawy w celu podsumowania wyników.
Uczniowie podchodzą do tablicy, biorą kartkę i odpowiadają na zapisane pytanie Odwrotna strona.
Pytania:
1. Którą z dwóch liczb ujemnych uważa się za większą?
2. Sformułuj zasadę dzielenia liczb ujemnych.
3. Sformułuj zasadę mnożenia liczb ujemnych.
4. Sformułuj zasadę mnożenia liczb o różnych znakach.
5. Sformułuj zasadę dzielenia liczb o różnych znakach.
6. Sformułuj zasadę dodawania liczb ujemnych.
7. Sformułuj zasadę dodawania liczb o różnych znakach.
8.Jak znaleźć długość odcinka na linii współrzędnych?
9.Jakie liczby nazywane są liczbami całkowitymi?
10. Jakie liczby nazywamy wymiernymi?
Zreasumowanie.
Nauczyciel: Dzisiaj Praca domowa będzie kreatywny:
Przygotuj wiadomość „Liczby dodatnie i ujemne wokół nas” lub ułóż bajkę.
« Dziękuję za lekcję!!!"
Powrót do przodu
Uwaga! Podglądy slajdów służą wyłącznie celom informacyjnym i mogą nie odzwierciedlać wszystkich funkcji prezentacji. Jeśli jesteś zainteresowany ta praca, pobierz pełną wersję.
Typ lekcji: lekcja uogólniania i systematyzowania wiedzy z wykorzystaniem technologii komputerowej.
Cele Lekcji:
- Edukacyjny:
- doskonalić umiejętności rozwiązywania przykładów i równań na temat „Właściwości operacji na liczbach wymiernych”;
- utrwalić umiejętność wykonywania operacji arytmetycznych na liczbach wymiernych;
- sprawdzić umiejętność wykorzystania właściwości operacji arytmetycznych do uproszczenia wyrażeń na liczbach wymiernych;
- uogólniać i systematyzować materiał teoretyczny.
- Rozwojowy:
- rozwijanie umiejętności liczenie mentalne;
- rozwijać logiczne myślenie;
- rozwinąć umiejętność jasnego i jasnego wyrażania swoich myśli;
- rozwijać mowę matematyczną uczniów w procesie wykonywania pracy ustnej w celu odtworzenia materiału teoretycznego;
- poszerzać horyzonty uczniów.
- Edukacyjny:
- rozwinąć umiejętność pracy z dostępnymi informacjami;
- rozwijać szacunek do tematu;
- kultywuj umiejętność słuchania przyjaciela, poczucie wzajemnej pomocy i wzajemnego wsparcia;
- przyczyniać się do rozwoju samokontroli i wzajemnej kontroli wśród uczniów.
Wyposażenie i widoczność: komputer, rzutnik multimedialny, ekran, prezentacja interaktywna, fiszki do liczenia w pamięci, kredki .
Struktura lekcji:
PODCZAS ZAJĘĆ
I. Moment organizacyjny
II. Komunikowanie tematu i celów lekcji
Sprawdzanie gotowości uczniów do zajęć. Przekazywanie uczniom celów i planu lekcji.
– Temat naszej lekcji: „Własności działań na liczbach wymiernych” i proszę o refrenem przeczytanie motto lekcji:
Tak, ścieżka wiedzy nie jest gładka.
Ale wiemy z lat szkolnych,
Więcej jest tajemnic niż odpowiedzi,
I nie ma ograniczeń w poszukiwaniach!
A dzisiaj na zajęciach będziemy polubownie i aktywnie tworzyć gazetkę matematyczną. Ja będę redaktorem naczelnym, a wy korektorami. Jak rozumiesz znaczenie tego słowa?
Aby przetestować innych, musimy usystematyzować naszą wiedzę na temat „Właściwości operacji na liczbach wymiernych”.
A nasza gazeta nazywa się „Liczby wymierne”. A przetłumaczone na tatarski?
Słyszałem, że dobrze znasz angielski, ale jak Anglicy będą nazywać tę gazetę?
Przedstawiam Państwu układ gazety, który składa się z następujących działów: czytanie chórem: „ Pytają – my odpowiadamy», « codzienne wiadomości», « Aukcja projektów», « Raport bieżący»,
« Czy wiesz...?".
III. Aktualizacja wiedzy referencyjnej
Praca ustna:
W pierwszej części „Pytają – my odpowiadamy” musimy sprawdzić prawdziwość informacji, które nasi korespondenci przesyłali nam listami. Przyjrzyj się uważnie i powiedz nam, o jakich zasadach musimy pamiętać, aby sprawdzić te informacje.
1. Zasada dodawania liczb ujemnych:
„Aby dodać dwie liczby ujemne, należy: 1) dodać ich moduły, 2) postawić znak minus przed otrzymaną liczbą.”
2. Zasada dzielenia liczb różnymi znakami:
„Przy dzieleniu liczb o różnych znakach należy: 1) podzielić moduł dzielnej przez moduł dzielnika, 2) postawić znak minus przed otrzymaną liczbą”.
3. Zasada mnożenia dwóch liczb ujemnych:
„Aby pomnożyć dwie liczby ujemne, należy pomnożyć ich wartości bezwzględne”.
4. Zasada mnożenia liczb o różnych znakach:
„Aby pomnożyć dwie liczby o różnych znakach, należy pomnożyć wartości bezwzględne tych liczb i umieścić znak minus przed otrzymaną liczbą”.
5. Zasada dzielenia liczby ujemnej przez liczba ujemna:
„Aby podzielić liczbę ujemną przez liczbę ujemną, należy podzielić moduł dzielnej przez moduł dzielnika”.
6. Zasada dodawania liczb o różnych znakach:
„Aby dodać dwie liczby o różnych znakach, należy 1) odjąć mniejszą od większego modułu wyrazów, 2) umieścić przed otrzymaną liczbą znak wyrazu, którego moduł jest większy.
1) – 8,4 + (– 8,4) = 0; (– 16,8)
2) (– 6,7) . (– 10) = – 67; (67)
3) (– 2,2) + 3,5 = 1,3;
4) – 13 – 8 = – 5; (– 21)
5) 15 – 18 = – 13; (– 3)
6) 7,4 – (– 3,2) = – 10,6; (10,6)
7) – 9 . 6 = – 54;
8) – 3,6 . 1 = –1; (– 3,6)
9) – 18: (– 0,3) = 60;
10) – 3,7 . 0 = – 3,7. (0)
- Dobra robota, wykonałeś dobrą robotę.
IV. Wzmocnienie pokrywanego materiału
– A teraz przechodzimy do sekcji "Codzienne wiadomości" Aby ukończyć tę sekcję, musimy usystematyzować naszą wiedzę o liczbach.
– Jakie znasz liczby? (Naturalne, ułamkowe, racjonalne)
– Jakie liczby uważa się za wymierne? (Dodatnie, ujemne i 0)
– Jakie znasz własności liczb wymiernych? (Przemienne, łączne i rozdzielne, mnożenie przez 1, mnożenie przez 0)
– Przejdźmy teraz do pracy pisemnej. Otworzyliśmy nasze zeszyty, zapisaliśmy numer, Praca klasowa, temat „Właściwości operacji na liczbach wymiernych”.
Korzystając z tych właściwości, upraszczamy wyrażenia:
A) x + 32 – 16 = x + 16
B) – x – 18 – 23 = – x – 41
B) – 1,5 + x – 20 = – 21,5 + x
D) 12 – 26 + x = x – 14
D) 1,7 + 3,6 – x = 5,3 – x
E) – x + a + 6,1 – a + 2,8 – 8,8 = – x + 0,1
- A poniższe przykłady wymagać od nas jeszcze więcej racjonalna decyzja z wyjaśnieniem.
– 98 + 85 + 45 – 55 – 28 + 63 = 12
– 6,56 + 2,4 – 3,2 + 6,56 + 4 + 3,2 – 2,4 = 4
– 19,61 * 20 + 19,61 * 120 = 1961
12.04.1961 – Czy odpowiedzi, które otrzymałeś, mówią Ci coś?
50 lat temu, 12 kwietnia 1961 roku, Jurij Gagarin poleciał w kosmos. Miasto Zainsk ma również swoją historię kosmiczną: 9 marca 1961 r., moduł zejścia nr 1 statek kosmiczny WOSTOK-4 ukończony miękkie lądowanie w pobliżu wsi Stary Tokmak, rejon Zainsky, z manekinem ludzkim, psem i innymi małymi zwierzętami na pokładzie. Na cześć tego wydarzenia na naszym terenie zostanie wzniesiony pomnik. Teraz w mieście działa komisja konkursowa. W konkursie biorą udział 3 projekty, są one przed Tobą na ekranie. A teraz przeprowadzimy aukcję projektów.
Proszę o oddanie głosu na swój ulubiony projekt. Twój głos może być decydujący.
V. Minuta wychowania fizycznego
– Wyrażasz swoją opinię oklaskami i tupaniem. Zróbmy próbę! Trzy klaśnięcia i trzy pieczątki.
- Spróbujmy jeszcze raz. Zatem rozpoczynamy głosowanie:
– Oddajemy głosy na Układ nr 1
– Oddajemy głosy na Układ nr 2
– Oddajemy głosy na Układ nr 3
- A teraz wszystkie układy razem.
– Układ nr wygrał... Dziękuję, nagrałem Wasze głosy (podbicia telefon komórkowy i pokazuje dzieciom) i przekazuje komisji liczącej.
- Dobra robota, dziękuję. A przyszłość jest nie mniej ważna - Raport bieżący.
VI. Przygotowanie do egzaminu państwowego
W kategorii „Raport bieżący” Otrzymałem list, w którym uczeń prosi o pomoc w rozwiązaniu zadań na egzamin końcowy w klasie IX. Potrzebujemy, aby każdy samodzielnie rozwiązywał zadania i testy.<Aneks 1 > na Twoich stołach:
1. Rozwiąż równania:
a) (x + 3)(x – 6) = 0
1) x = 3, x = – 6
2) x = – 3, x = – 6
3) x = – 3, x = 6