Jak rozumieć parzystość i nieparzystość funkcji. Wykres funkcji parzystych i nieparzystych

Konwersja wykresów.

Słowny opis funkcji.

Metoda graficzna.

Graficzna metoda określania funkcji jest najbardziej wizualna i często stosowana w technologii. W Analiza matematyczna Jako ilustracja wykorzystano graficzną metodę określania funkcji.

Wykres funkcji f jest zbiorem wszystkich punktów (x;y) płaszczyzny współrzędnych, gdzie y=f(x), a x „przebiega” przez całą dziedzinę definicji tej funkcji.

Podzbiór płaszczyzny współrzędnych jest wykresem funkcji, jeśli ma ona nie więcej niż jeden punkt wspólny z dowolną prostą równoległą do osi Oy.

Przykład. Czy liczby pokazane poniżej są wykresami funkcji?

Korzyść zadanie graficzne jest jego widoczność. Od razu widać jak funkcja się zachowuje, gdzie rośnie, a gdzie maleje. Z wykresu można od razu rozpoznać niektóre ważne cechy Funkcje.

Ogólnie rzecz biorąc, analityczne i graficzne metody definiowania funkcji idą ze sobą w parze. Praca z formułą pomaga w zbudowaniu wykresu. A wykres często sugeruje rozwiązania, których nawet nie zauważysz we wzorze.

Prawie każdy uczeń zna trzy sposoby definiowania funkcji, które właśnie omówiliśmy.

Spróbujmy odpowiedzieć na pytanie: „Czy istnieją inne sposoby określenia funkcji?”

Jest taki sposób.

Funkcję można dość jednoznacznie określić słownie.

Na przykład funkcję y=2x można określić za pomocą następującego opisu słownego: każda rzeczywista wartość argumentu x jest powiązana z jej podwójną wartością. Reguła jest ustalona, ​​​​funkcja jest określona.

Co więcej, można werbalnie określić funkcję, która jest niezwykle trudna, jeśli nie niemożliwa do zdefiniowania za pomocą wzoru.

Na przykład: każda wartość argumentu naturalnego x jest powiązana z sumą cyfr tworzących wartość x. Na przykład, jeśli x=3, to y=3. Jeśli x=257, to y=2+5+7=14. I tak dalej. Zapisanie tego we wzorze jest problematyczne. Ale znak jest łatwy do wykonania.

Metoda opisu werbalnego jest metodą dość rzadko stosowaną. Ale czasami tak się dzieje.

Jeśli istnieje prawo zgodności jeden do jednego między x i y, to istnieje funkcja. Jakie prawo, w jakiej formie jest wyrażone – formuła, tablica, wykres, słowa – nie zmienia istoty rzeczy.

Rozważmy funkcje, których dziedziny definicji są symetryczne względem początku, tj. dla kazdego X z dziedziny liczby definicyjnej (- X) również należy do domeny definicji. Wśród tych funkcji znajdują się parzyste i nieparzyste.

Definicja. Nazywa się funkcję f nawet, jeśli w ogóle X z jego dziedziny definicji

Przykład. Rozważ funkcję

Jest równo. Sprawdźmy to.

Dla kazdego X równości są spełnione

Zatem oba warunki są spełnione, co oznacza, że ​​funkcja jest parzysta. Poniżej znajduje się wykres tej funkcji.

Definicja. Nazywa się funkcję f dziwne, jeśli w ogóle X z jego dziedziny definicji

Przykład. Rozważ funkcję

To jest dziwne. Sprawdźmy to.

Dziedziną definicji jest cała oś liczbowa, czyli jest ona symetryczna względem punktu (0;0).

Dla kazdego X równości są spełnione

Zatem oba warunki są spełnione, co oznacza, że ​​funkcja jest nieparzysta. Poniżej znajduje się wykres tej funkcji.

Wykresy pokazane na pierwszej i trzeciej figurze są symetryczne względem osi rzędnych, natomiast wykresy pokazane na drugiej i czwartej figurze są symetryczne względem początku układu współrzędnych.

Które z funkcji, których wykresy są pokazane na rysunkach, są parzyste, a które nieparzyste?

Badanie funkcji.

1) D(y) – Dziedzina definicji: zbiór wszystkich tych wartości zmiennej x. dla których wyrażenia algebraiczne f(x) i g(x) mają sens.

Jeśli funkcja jest dana wzorem, wówczas dziedziną definicji są wszystkie wartości zmiennej niezależnej, dla których wzór ma sens.

2) Własności funkcji: parzysty/nieparzysty, okresowość:

Dziwne I nawet wywoływane są funkcje, których wykresy są symetryczne względem zmian znaku argumentu.

Dziwna funkcja- funkcja, która zmienia swoją wartość na przeciwną, gdy zmienia się znak zmiennej niezależnej (symetrycznie względem środka współrzędnych).

Nawet funkcjonować- funkcja, która nie zmienia swojej wartości przy zmianie znaku zmiennej niezależnej (symetrycznie względem rzędnej).

Ani funkcja parzysta, ani nieparzysta (funkcjonować ogólna perspektywa) - funkcja, która nie ma symetrii. Ta kategoria obejmuje funkcje, które nie mieszczą się w poprzednich 2 kategoriach.

Funkcje, które nie należą do żadnej z powyższych kategorii, są wywoływane ani parzyste, ani dziwne(lub funkcje ogólne).

Dziwne funkcje

Potęga nieparzysta gdzie jest dowolną liczbą całkowitą.

Nawet funkcje

Nawet potęga, gdzie jest dowolną liczbą całkowitą.

Funkcja okresowa- funkcja, która powtarza swoje wartości w pewnym regularnym odstępie argumentu, czyli nie zmienia swojej wartości po dodaniu do argumentu jakiejś stałej, niezerowej liczby ( okres funkcje) w całej dziedzinie definicji.

3) Zera (pierwiastki) funkcji to punkty, w których osiąga ona zero.

Znalezienie punktu przecięcia wykresu z osią Oj. Aby to zrobić, musisz obliczyć wartość F(0). Znajdź także punkty przecięcia wykresu z osią Wół, po co szukać pierwiastków równania F(X) = 0 (lub upewnij się, że nie ma pierwiastków).

Punkty, w których wykres przecina oś, nazywane są funkcje zerowe. Aby znaleźć zera funkcji, musisz rozwiązać równanie, czyli znaleźć te wartości „x”, w którym funkcja staje się zerowa.

4) Przedziały stałości znaków, znaki w nich zawarte.

Przedziały, w których funkcja f(x) zachowuje znak.

Przedział stałości znaku jest przedziałem w każdym jego punkcie funkcja jest dodatnia lub ujemna.

POWYŻEJ osi x.

PONIŻEJ osi.

5) Ciągłość (punkty nieciągłości, charakter nieciągłości, asymptoty).

Funkcja ciągła- funkcja bez „skoków”, czyli taka, w której małe zmiany argumentu prowadzą do małych zmian wartości funkcji.

Usuwalne punkty przerwania

Jeżeli granica funkcji istnieje, ale funkcja w tym punkcie nie jest zdefiniowana lub granica nie pokrywa się z wartością funkcji w tym punkcie:

,

wtedy nazywa się ten punkt usuwalny punkt przerwania funkcje (w analizie złożonej usuwalny punkt osobliwy).

Jeśli „poprawimy” funkcję w miejscu usuwalnej nieciągłości i wstawimy , to otrzymujemy funkcję ciągłą w danym punkcie. Ta operacja na funkcji nazywa się rozszerzenie funkcji na ciągłą Lub przedefiniowanie funkcji przez ciągłość, co uzasadnia nazwę punktu jako punktu usuwany pęknięcie.

Punkty nieciągłości pierwszego i drugiego rodzaju

Jeżeli funkcja ma w danym punkcie nieciągłość (tzn. granica funkcji w danym punkcie jest nieobecna lub nie pokrywa się z wartością funkcji w danym punkcie), to dla funkcji numerycznych możliwe są dwie opcje związane z istnieniem funkcji numerycznych jednostronne granice:

jeżeli obie granice jednostronne istnieją i są skończone, to taki punkt nazywa się punkt nieciągłości pierwszego rodzaju. Usuwalne punkty nieciągłości są punktami nieciągłości pierwszego rodzaju;

jeżeli przynajmniej jedna z jednostronnych granic nie istnieje lub nie jest wartością skończoną, to taki punkt nazywa się punkt nieciągłości drugiego rodzaju.

Asymptota - prosty, który ma tę właściwość, że odległość od punktu na krzywej do tego prosty dąży do zera w miarę oddalania się punktu wzdłuż gałęzi do nieskończoności.

Pionowy

Asymptota pionowa - linia graniczna .

Z reguły przy wyznaczaniu asymptoty pionowej szukają nie jednej granicy, ale dwóch jednostronnych (lewej i prawej). Ma to na celu określenie, jak funkcja zachowuje się, gdy zbliża się do asymptoty pionowej z różnych kierunków. Na przykład:

Poziomy

Asymptota pozioma - prosty gatunek, pod warunkiem istnienia limit

.

Skłonny

Asymptota ukośna - prosty gatunek, pod warunkiem istnienia limity

Uwaga: funkcja nie może mieć więcej niż dwie asymptoty ukośne (poziome).

Uwaga: jeśli przynajmniej jedna z dwóch powyższych granic nie istnieje (lub jest równa ), to asymptota ukośna w (lub ) nie istnieje.

jeśli w pkt. 2.), to , a granicę wyznacza się za pomocą wzoru na asymptotę poziomą, .

6) Znajdowanie przedziałów monotoniczności. Znajdź przedziały monotoniczności funkcji F(X) (to znaczy przedziały wzrostu i spadku). Dokonuje się tego poprzez sprawdzenie znaku pochodnej F(X). Aby to zrobić, znajdź pochodną F(X) i rozwiązuję nierówność F(X)0. W przedziałach, w których zachodzi ta nierówność, funkcja F(X) wzrasta. Gdzie zachodzi odwrotna nierówność F(X)0, funkcja F(X) maleje.

Znalezienie ekstremum lokalnego. Znaleźwszy przedziały monotoniczności, możemy od razu wyznaczyć lokalne ekstrema, w których wzrost zastępuje się spadkiem, znajdują się lokalne maksima, a tam, gdzie spadek zastępuje się wzrostem, znajdują się lokalne minima. Oblicz wartość funkcji w tych punktach. Jeśli funkcja ma punkty krytyczne, które nie są lokalnymi ekstremami, warto obliczyć wartość funkcji również w tych punktach.

Znajdowanie największych i najmniejszych wartości funkcji y = f(x) na segmencie(kontynuacja)

Funkcjonować jest jednym z najważniejszych pojęć matematycznych. Funkcja - zależność zmiennej Na ze zmiennej X, jeśli każda wartość X pasuje do jednej wartości Na. Zmienny X nazywaną zmienną niezależną lub argumentem. Zmienny Na zwaną zmienną zależną. Wszystkie wartości zmiennej niezależnej (zmienna X) tworzą dziedzinę definicji funkcji. Wszystkie wartości, jakie przyjmuje zmienna zależna (variable y), tworzą zakres wartości funkcji.

Wykres funkcji wywołaj zbiór wszystkich punktów płaszczyzny współrzędnych, których odcięte są równe wartościom argumentu, a rzędne są równe odpowiednim wartościom funkcji, to znaczy wartościom zmienne są wykreślane wzdłuż osi odciętych X, a wartości zmiennej są wykreślane wzdłuż osi rzędnych y. Aby narysować wykres funkcji, musisz znać jej właściwości. Główne właściwości funkcji zostaną omówione poniżej!

Do zbudowania wykresu funkcji polecamy skorzystać z naszego programu - Grafowanie funkcji online. Jeśli podczas studiowania materiałów na tej stronie będziesz miał jakieś pytania, zawsze możesz je zadać na naszym forum. Również na forum pomogą Ci rozwiązać problemy z matematyki, chemii, geometrii, teorii prawdopodobieństwa i wielu innych przedmiotów!

Podstawowe własności funkcji.

1) Dziedzina funkcji i zakres funkcji.

Dziedziną funkcji jest zbiór wszystkich prawidłowych wartości argumentów X(zmienny X), dla której funkcja y = f(x) określony.
Zakres funkcji to zbiór wszystkich wartości rzeczywistych y, co funkcja akceptuje.

W elementarna matematyka funkcje bada się tylko na zbiorze liczb rzeczywistych.

2) Zera funkcji.

Wartości X, w którym y=0, zwany funkcje zerowe. Są to odcięte punktów przecięcia wykresu funkcji z osią Wół.

3) Przedziały stałego znaku funkcji.

Takimi przedziałami wartości są przedziały znaku stałego funkcji X, na którym znajdują się wartości funkcji y wywoływane są albo tylko dodatnie, albo tylko ujemne przedziały stałego znaku funkcji.

4) Monotoniczność funkcji.

Funkcja rosnąca (w pewnym przedziale) to funkcja, dla której wyższa wartość argument z tego przedziału odpowiada większej wartości funkcji.

Funkcja malejąca (w pewnym przedziale) to funkcja, w której większa wartość argumentu z tego przedziału odpowiada mniejszej wartości funkcji.

5) Funkcja parzysta (nieparzysta)..

Funkcja parzysta to funkcja, której dziedzina definicji jest symetryczna względem początku i dla dowolnego X f(-x) = f(x). Wykres funkcji parzystej jest symetryczny względem rzędnej.

Funkcja nieparzysta to funkcja, której dziedzina definicji jest symetryczna względem początku i dla dowolnego X z dziedziny definicji równość jest prawdziwa f(-x) = - f(x). Wykres funkcji nieparzystej jest symetryczny względem początku.

Nawet funkcjonować
1) Dziedzina definicji jest symetryczna względem punktu (0; 0), to znaczy, jeśli punkt A należy do dziedziny definicji, a następnie do punktu -A również należy do domeny definicji.
2) Dla dowolnej wartości X f(-x)=f(x)
3) Wykres funkcji parzystej jest symetryczny względem osi Oy.

Dziwna funkcja ma następujące właściwości:
1) Dziedzina definicji jest symetryczna względem punktu (0; 0).
2) dla dowolnej wartości X, należący do dziedziny definicji, równość f(-x)=-f(x)
3) Wykres funkcji nieparzystej jest symetryczny względem początku (0; 0).

Nie każda funkcja jest parzysta lub nieparzysta. Funkcje ogólna perspektywa nie są ani parzyste, ani nieparzyste.

6) Ograniczone i nieograniczone funkcje.

Funkcję nazywamy ograniczoną, jeśli istnieje liczba dodatnia M taka, że ​​|f(x)| ≤ M dla wszystkich wartości x. Jeżeli taka liczba nie istnieje, to funkcja jest nieograniczona.

7) Okresowość funkcji.

Funkcja f(x) jest okresowa, jeśli istnieje niezerowa liczba T taka, że ​​dla dowolnego x z dziedziny definicji funkcji zachodzi: f(x+T) = f(x). Ten najmniejsza liczba nazywa się okresem funkcji. Wszystko funkcje trygonometryczne są okresowe. (Wzory trygonometryczne).

Funkcjonować F nazywa się okresowym, jeśli istnieje taka liczba, że ​​dla dowolnego X z dziedziny definicji równość f(x)=f(x-T)=f(x+T). T jest okresem funkcji.

Każda funkcja okresowa ma nieskończony zbiór okresy. W praktyce zwykle bierze się pod uwagę najmniejszy okres dodatni.

Wartości funkcji okresowej powtarzają się po odstępie równym okresowi. Jest to wykorzystywane podczas konstruowania wykresów.

Hide Show

Metody określania funkcji

Niech funkcję będzie dana wzorem: y=2x^(2)-3. Przypisując dowolne wartości zmiennej niezależnej x, można za pomocą tego wzoru obliczyć odpowiadające wartości zmiennej zależnej y. Na przykład, jeśli x=-0,5, to korzystając ze wzoru stwierdzamy, że odpowiadająca wartość y wynosi y=2 \cdot (-0,5)^(2)-3=-2,5.

Biorąc dowolną wartość przyjmowaną przez argument x we ​​wzorze y=2x^(2)-3, można obliczyć tylko jedną wartość funkcji, która jej odpowiada. Funkcję można przedstawić w postaci tabeli:

Korzystając z tej tabeli, możesz zobaczyć, że wartości argumentu -1 odpowiada wartość funkcji -3; a wartość x=2 będzie odpowiadać y=0 itd. Ważne jest również, aby wiedzieć, że każda wartość argumentu w tabeli odpowiada tylko jednej wartości funkcji.

Więcej funkcji można określić za pomocą wykresów. Za pomocą wykresu ustala się, która wartość funkcji koreluje z określoną wartością x. Najczęściej będzie to przybliżona wartość funkcji.

Funkcja parzysta i nieparzysta

Funkcja jest nawet funkcjonować, gdy f(-x)=f(x) dla dowolnego x z dziedziny definicji. Taka funkcja będzie symetryczna względem osi Oy.

Funkcja jest dziwna funkcja, gdy f(-x)=-f(x) dla dowolnego x z dziedziny definicji. Taka funkcja będzie symetryczna względem początku O (0;0).

Funkcja jest nawet nie, ani dziwne i nazywa się funkcja ogólna, gdy nie ma symetrii względem osi lub początku.

Przeanalizujmy następującą funkcję parzystości:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) z symetryczną dziedziną definicji względem początku. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Oznacza to, że funkcja f(x)=3x^(3)-7x^(7) jest nieparzysta.

Funkcja okresowa

Funkcja y=f(x) , w dziedzinie której zachodzi równość f(x+T)=f(x-T)=f(x) dla dowolnego x, nazywa się funkcja okresowa z okresem T \neq 0 .

Powtórzenie wykresu funkcji na dowolnym odcinku osi x o długości T.

Przedziały, w których funkcja jest dodatnia, czyli f(x) > 0, są odcinkami osi odciętych odpowiadającymi punktom wykresu funkcji leżącym nad osią odciętych.

f(x) > 0 włączone (x_(1); x_(2)) \cup (x_(3); +\infty)

Przedziały, w których funkcja jest ujemna, czyli f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

k(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Ograniczona funkcja

Ograniczone od dołu Zwyczajowo wywołuje się funkcję y=f(x), x \in X, gdy istnieje liczba A, dla której nierówność f(x) \geq A zachodzi dla dowolnego x \in X .

Przykład funkcji ograniczonej od dołu: y=\sqrt(1+x^(2)) ponieważ y=\sqrt(1+x^(2)) \geq 1 dla dowolnego x .

Ograniczone od góry funkcja y=f(x), x \in X jest wywoływana, gdy istnieje liczba B, dla której nierówność f(x) \neq B zachodzi dla dowolnego x \in X .

Przykład funkcji ograniczonej poniżej: y=\sqrt(1-x^(2)), x \in [-1;1] ponieważ y=\sqrt(1+x^(2)) \neq 1 dla dowolnego x \in [-1;1] .

Ograniczony Zwyczajowo wywołuje się funkcję y=f(x), x \in X, gdy istnieje liczba K > 0, dla której nierówność \left | f(x)\prawo | \neq K dla dowolnego x \in X .

Przykład ograniczona funkcja: y=\sin x jest ograniczone na całej osi liczbowej, ponieważ \w lewo | \sin x \right | \neq 1.

Funkcja rosnąca i malejąca

Zwyczajowo mówi się o funkcji, która rośnie w rozpatrywanym przedziale jako funkcja rosnąca wtedy, gdy większa wartość x odpowiada większej wartości funkcji y=f(x) . Wynika z tego, że biorąc dwie dowolne wartości argumentu x_(1) i x_(2) z rozważanego przedziału, gdzie x_(1) > x_(2) , wynikiem będzie y(x_(1)) > y(x_(2)).

Nazywa się funkcję, która maleje w rozpatrywanym przedziale funkcja malejąca gdy większa wartość x odpowiada mniejszej wartości funkcji y(x) . Wynika z tego, że biorąc dwie dowolne wartości argumentu x_(1) i x_(2) z rozważanego przedziału, przy x_(1) > x_(2) , wynikiem będzie y(x_(1))< y(x_{2}) .

Korzenie funkcji Zwyczajowo nazywa się punkty, w których funkcja F=y(x) przecina oś odciętych (uzyskuje się je rozwiązując równanie y(x)=0).

a) Jeżeli dla x > 0 funkcja parzysta rośnie, to dla x maleje< 0

b) Gdy funkcja parzysta maleje dla x > 0, to wzrasta dla x< 0

c) Gdy funkcja nieparzysta rośnie przy x > 0, to również rośnie przy x< 0

d) Gdy funkcja nieparzysta maleje dla x > 0, to zmniejsza się również dla x< 0

Ekstrema funkcji

Minimalny punkt funkcji y=f(x) nazywa się zwykle punktem x=x_(0), którego sąsiedztwo będzie miało inne punkty (z wyjątkiem punktu x=x_(0)), i dla nich nierówność f(x) > f będzie wówczas wynosić zadowolony (x_(0)) . y_(min) - oznaczenie funkcji w punkcie min.

Maksymalny punkt funkcji y=f(x) nazywa się zwykle punktem x=x_(0), którego sąsiedztwo będzie miało inne punkty (z wyjątkiem punktu x=x_(0)), i dla nich nierówność f(x) będzie wtedy spełniona< f(x^{0}) . y_{max} - обозначение функции в точке max.

Warunek wstępny

Zgodnie z twierdzeniem Fermata: f”(x)=0, gdy funkcja f(x) różniczkowalna w punkcie x_(0) będzie miała w tym punkcie ekstremum.

Stan wystarczający

1. Gdy pochodna zmieni znak z plusa na minus, wówczas x_(0) będzie punktem minimalnym;
2. x_(0) - będzie punktem maksymalnym tylko wtedy, gdy pochodna zmieni znak z minus na plus przy przejściu przez punkt stacjonarny x_(0) .

Największa i najmniejsza wartość funkcji w przedziale

Kroki obliczeniowe:

1. Poszukuje się pochodnej f”(x);
2. Znaleziono punkty stacjonarne i krytyczne funkcji oraz wybrano te należące do odcinka;
3. Wartości funkcji f(x) znajdują się w punktach stacjonarnych i krytycznych oraz na końcach odcinka. Mniejszy z uzyskanych wyników będzie najniższa wartość Funkcje, i więcej - największy.

Parzystość i nieparzystość funkcji to jedne z jej głównych właściwości, a parzystość zajmuje imponującą część kurs szkolny matematyka. W dużej mierze determinuje zachowanie funkcji i znacznie ułatwia konstrukcję odpowiedniego wykresu.

Określmy parzystość funkcji. Ogólnie rzecz biorąc, badaną funkcję rozważa się nawet wtedy, gdy dla przeciwnych wartości zmiennej niezależnej (x) znajdującej się w jej dziedzinie definicji odpowiadające wartości y (funkcji) okazują się równe.

Podajmy bardziej ścisłą definicję. Rozważmy pewną funkcję f(x), która jest zdefiniowana w dziedzinie D. Będzie tak nawet, jeśli dla dowolnego punktu x znajdującego się w dziedzinie definicji:

• -x (punkt przeciwny) również leży w tym zakresie,

• f(-x) = f(x).

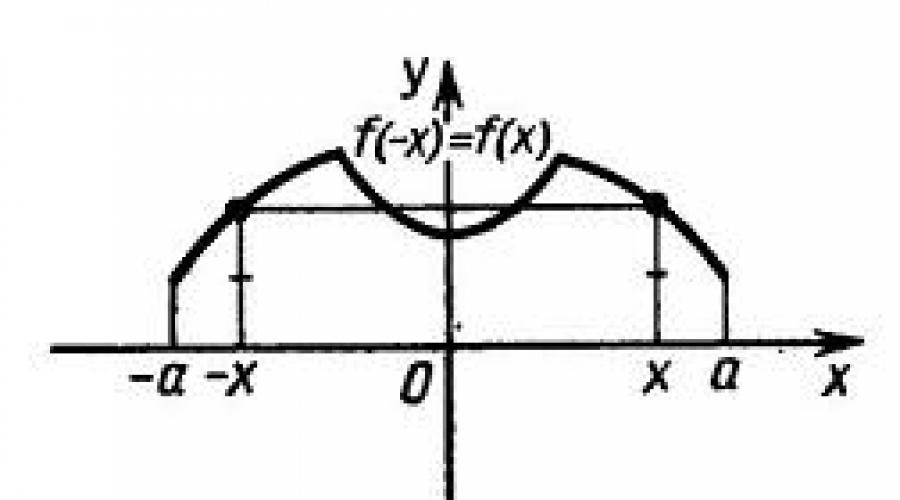
Z powyższej definicji wynika warunek niezbędny dla dziedziny definicji takiej funkcji, a mianowicie symetria względem punktu O, który jest początkiem współrzędnych, gdyż jeśli jakiś punkt b mieści się w dziedzinie definicji parzystej funkcji, to odpowiedni punkt b również należy do tej dziedziny. Z powyższego wynika więc wniosek: funkcja parzysta ma postać symetryczną względem osi rzędnych (Oy).

Jak w praktyce wyznaczyć parzystość funkcji?

Określmy to wzorem h(x)=11^x+11^(-x). Kierując się algorytmem wynikającym bezpośrednio z definicji, w pierwszej kolejności zbadamy jej dziedzinę definicyjną. Oczywiście jest on zdefiniowany dla wszystkich wartości argumentu, czyli spełniony jest pierwszy warunek.

Następnym krokiem jest zastąpienie argumentu (x) wartością przeciwną (-x).
Otrzymujemy:
h(-x) = 11^(-x) + 11^x.
Ponieważ dodawanie spełnia prawo przemienności (przemienności), oczywiste jest, że h(-x) = h(x) i dane zależność funkcjonalna- nawet.

Sprawdźmy parzystość funkcji h(x)=11^x-11^(-x). Postępując zgodnie z tym samym algorytmem, otrzymujemy, że h(-x) = 11^(-x) -11^x. Po odjęciu minusa ostatecznie mamy
h(-x)=-(11^x-11^(-x))=- h(x). Dlatego h(x) jest nieparzyste.

Nawiasem mówiąc, należy przypomnieć, że istnieją funkcje, których nie można sklasyfikować według tych kryteriów, nie nazywa się ich ani parzystymi, ani nieparzystymi.

Nawet funkcje mają wiele interesujących właściwości:

• w wyniku dodania podobnych funkcji otrzymują parzystą;
• w wyniku odjęcia takich funkcji otrzymuje się parzystą;
• nawet, także;
• w wyniku pomnożenia dwóch takich funkcji otrzymuje się parzystą;
• w wyniku pomnożenia funkcji nieparzystych i parzystych otrzymujemy funkcję nieparzystą;
• w wyniku podzielenia funkcji nieparzystych i parzystych otrzymuje się nieparzystą;
• pochodna takiej funkcji jest nieparzysta;
• jeśli nie budujesz nawet funkcjonować do kwadratu, mamy równość.

Parzystość funkcji można wykorzystać do rozwiązywania równań.

Aby rozwiązać równanie takie jak g(x) = 0, gdzie lewa strona równanie jest funkcją parzystą, wystarczy znaleźć jej rozwiązania dla nieujemnych wartości zmiennej. Powstałe pierwiastki równania należy połączyć z liczbami przeciwnymi. Jeden z nich podlega weryfikacji.

Jest to również z powodzeniem stosowane do rozwiązywania zadania niestandardowe z parametrem.

Na przykład, czy istnieje taka wartość parametru a, dla której równanie 2x^6-x^4-ax^2=1 będzie miało trzy pierwiastki?

Jeśli weźmiemy pod uwagę, że zmienna wchodzi do równania w potęgach parzystych, to jasne jest, że zastąpienie x przez - x dane równanie nie zmieni się. Wynika z tego, że jeśli pewna liczba jest jej pierwiastkiem, to liczba przeciwna również jest pierwiastkiem. Wniosek jest oczywisty: pierwiastki równania różne od zera zaliczamy do zbioru jego rozwiązań „parami”.

Oczywiste jest, że sama liczba nie wynosi 0, to znaczy liczba pierwiastków takiego równania może być tylko parzysta i oczywiście dla dowolnej wartości parametru nie może mieć trzech pierwiastków.

Ale liczba pierwiastków równania 2^x+ 2^(-x)=ax^4+2x^2+2 może być nieparzysta i to dla dowolnej wartości parametru. Rzeczywiście łatwo sprawdzić, że zbiór pierwiastków danego równania zawiera rozwiązania „parami”. Sprawdźmy, czy 0 jest pierwiastkiem. Kiedy podstawimy to do równania, otrzymamy 2 = 2. Zatem oprócz „sparowanych” 0 jest także pierwiastkiem, co dowodzi ich nieparzystej liczby.