Transformacja logarytmiczna. Wyrażenia logarytmiczne. przykłady

22.09.2019

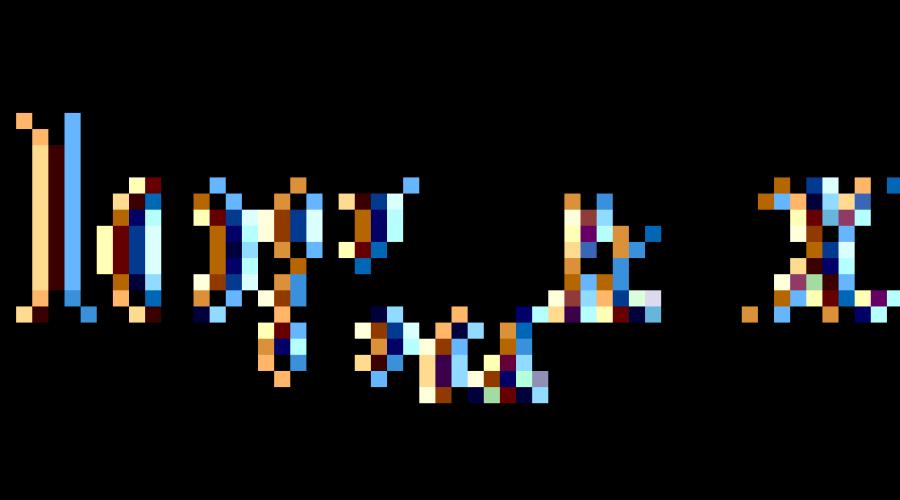
Przeczytaj także

Rozszerzenie nowego programu pomocy hipotecznej

Ceny jednostek terytorialnych robót budowlanych

Standard zawodowy „Specjalista ds. bezpieczeństwa i higieny pracy”: na co zwrócić uwagę?

Instrukcje ochrony pracy: wymagania podstawowe Zaktualizowano instrukcje ochrony pracy

Logarytmy, jak każdą liczbę, można dodawać, odejmować i przekształcać na różne sposoby. Ale ponieważ logarytmy nie są dokładnie zwykłe liczby, istnieją tu zasady, które są tzw główne właściwości.

Zdecydowanie musisz znać te zasady - bez nich nie da się rozwiązać ani jednego poważnego problemu logarytmicznego. W dodatku jest ich bardzo mało – wszystkiego można się nauczyć w jeden dzień. Więc zacznijmy.

Dodawanie i odejmowanie logarytmów

Rozważmy dwa logarytmy o tych samych podstawach: log A X i zaloguj się A y. Następnie można je dodawać i odejmować oraz:

dziennik A X+ log A y=log A (X · y);
dziennik A X− log A y=log A (X : y).

Zatem suma logarytmów jest równa logarytmowi iloczynu, a różnica jest równa logarytmowi ilorazu. Notatka: kluczowy moment Tutaj - identyczne podstawy. Jeśli przyczyny są inne, zasady te nie działają!

Te formuły pomogą ci obliczyć wyrażenie logarytmiczne, nawet jeśli nie uwzględnisz jego poszczególnych części (patrz lekcja „Co to jest logarytm”). Spójrz na przykłady i zobacz:

Dziennik 6 4 + dziennik 6 9.

Ponieważ logarytmy mają tę samą podstawę, stosujemy wzór na sumę:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Zadanie. Znajdź wartość wyrażenia: log 2 48 − log 2 3.

Podstawy są takie same, używamy wzoru na różnicę:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Zadanie. Znajdź wartość wyrażenia: log 3 135 − log 3 5.

Ponownie podstawy są takie same, więc mamy:
log 3 135 - log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Jak widać, oryginalne wyrażenia składają się ze „złych” logarytmów, których nie oblicza się osobno. Ale po przekształceniach otrzymuje się liczby całkowicie normalne. Wiele z nich opiera się na tym fakcie papiery testowe. Tak, wyrażenia przypominające test są oferowane z całą powagą (czasami praktycznie bez zmian) w ramach ujednoliconego egzaminu państwowego.

Wyodrębnianie wykładnika z logarytmu

Teraz skomplikujmy trochę zadanie. A co jeśli podstawą lub argumentem logarytmu jest potęga? Następnie wykładnik tego stopnia można odjąć od znaku logarytmu według następujących zasad:

Łatwo to zauważyć ostatnia zasada podąża za pierwszymi dwoma. Ale i tak lepiej o tym pamiętać - w niektórych przypadkach znacznie zmniejszy to ilość obliczeń.

Oczywiście wszystkie te zasady mają sens, jeśli przestrzega się ODZ logarytmu: A > 0, A ≠ 1, X> 0. I jeszcze jedno: naucz się stosować wszystkie formuły nie tylko od lewej do prawej, ale także odwrotnie, tj. Liczby przed znakiem logarytmu można wprowadzić do samego logarytmu. To jest to, czego najczęściej potrzeba.

Zadanie. Znajdź wartość wyrażenia: log 7 49 6 .

Pozbądźmy się stopnia w argumencie, korzystając z pierwszej formuły:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Zadanie. Znajdź znaczenie wyrażenia:
[Podpis do zdjęcia]

Zauważ, że w mianowniku znajduje się logarytm, którego podstawą i argumentem są dokładne potęgi: 16 = 2 4 ; 49 = 7 2. Mamy:

[Podpis do zdjęcia]

Myślę, że ostatni przykład wymaga pewnego wyjaśnienia. Gdzie się podziały logarytmy? Do ostatniej chwili pracujemy tylko z mianownikiem. Przedstawiliśmy podstawę i argument stojącego tam logarytmu w postaci potęg i wyciągnęliśmy wykładniki - otrzymaliśmy ułamek „trzypiętrowy”.

Teraz spójrzmy na ułamek główny. Licznik i mianownik zawierają tę samą liczbę: log 2 7. Ponieważ log 2 7 ≠ 0, możemy ułamek skrócić - w mianowniku pozostanie 2/4. Zgodnie z zasadami arytmetyki czwórkę można przenieść do licznika, co też uczyniono. W rezultacie otrzymaliśmy odpowiedź: 2.

Przejście na nowy fundament

Mówiąc o zasadach dodawania i odejmowania logarytmów, szczególnie podkreśliłem, że działają one tylko na tych samych podstawach. A co jeśli przyczyny są inne? A co jeśli nie są to dokładne potęgi tej samej liczby?

Na ratunek przychodzą formuły przejścia na nowy fundament. Sformułujmy je w formie twierdzenia:

Niech zostanie podany logarytm A X. Następnie dla dowolnej liczby C takie, że C> 0 i C≠ 1, prawdziwa jest równość:
[Podpis do zdjęcia]
W szczególności, jeśli umieścimy C = X, otrzymujemy:
[Podpis do zdjęcia]

Z drugiego wzoru wynika, że podstawę i argument logarytmu można zamienić, ale w tym przypadku całe wyrażenie zostaje „odwrócone”, tj. logarytm pojawia się w mianowniku.

Formuły te rzadko można znaleźć w konwencjonalnych wyrażenia numeryczne. Tylko podejmując decyzję, można ocenić, jak wygodne są równania logarytmiczne i nierówności.

Istnieją jednak problemy, których w ogóle nie można rozwiązać, chyba że przeprowadzka do nowego fundamentu. Przyjrzyjmy się kilku z nich:

Zadanie. Znajdź wartość wyrażenia: log 5 16 log 2 25.

Należy zauważyć, że argumenty obu logarytmów zawierają dokładne potęgi. Wyjmijmy wskaźniki: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Teraz „odwróćmy” drugi logarytm:

[Podpis do zdjęcia]

Ponieważ iloczyn nie zmienia się przy przestawianiu czynników, spokojnie pomnożyliśmy cztery przez dwa, a potem zajęliśmy się logarytmami.

Zadanie. Znajdź wartość wyrażenia: log 9 100 lg 3.

Podstawą i argumentem pierwszego logarytmu są potęgi dokładne. Zapiszmy to i pozbądźmy się wskaźników:

[Podpis do zdjęcia]

Teraz pozbądźmy się logarytmu dziesiętnego, przechodząc do nowej podstawy:

[Podpis do zdjęcia]

Podstawowa tożsamość logarytmiczna

Często w procesie rozwiązywania konieczne jest przedstawienie liczby jako logarytm o danej podstawie. W takim przypadku pomocne będą nam następujące formuły:

W pierwszym przypadku liczba N staje się wyznacznikiem stopnia stojącego w argumentacji. Numer N może być absolutnie dowolna, ponieważ jest to tylko wartość logarytmiczna.

Druga formuła jest właściwie sparafrazowaną definicją. Tak to się nazywa: podstawowa tożsamość logarytmiczna.

W rzeczywistości, co się stanie, jeśli numer B podnieść do takiej potęgi, że liczba B do tej potęgi daje liczbę A? Zgadza się: otrzymujesz ten sam numer A. Przeczytaj uważnie ten akapit jeszcze raz – wiele osób utknie na nim.

Podobnie jak wzory na przejście do nowej bazy, podstawowa tożsamość logarytmiczna jest czasami jedynym możliwym rozwiązaniem.

Zadanie. Znajdź znaczenie wyrażenia:
[Podpis do zdjęcia]

Zauważ, że log 25 64 = log 5 8 - po prostu wzięliśmy kwadrat z podstawy i argumentu logarytmu. Rozważając zasady mnożenia potęg przez ta sama podstawa, otrzymujemy:

[Podpis do zdjęcia]

Jeśli ktoś nie wie, to było prawdziwe zadanie z Egzaminu Państwowego Unified :)

Jednostka logarytmiczna i zero logarytmiczne

Podsumowując, podam dwie tożsamości, które trudno nazwać właściwościami - są one raczej konsekwencjami definicji logarytmu. Ciągle pojawiają się w problemach i, co zaskakujące, stwarzają problemy nawet dla „zaawansowanych” uczniów.

dziennik A A= 1 jest jednostką logarytmiczną. Zapamiętaj raz na zawsze: logarytm do dowolnej podstawy A od tej podstawy jest równa jeden.
dziennik A 1 = 0 to zero logarytmiczne. Baza A może być dowolna, ale jeśli argument zawiera jeden, logarytm jest równy zeru! Ponieważ A 0 = 1 jest bezpośrednią konsekwencją definicji.

To wszystkie właściwości. Pamiętaj, aby przećwiczyć ich wdrażanie! Pobierz ściągawkę znajdującą się na początku lekcji, wydrukuj ją i rozwiąż zadania.

Jak wiadomo, przy mnożeniu wyrażeń przez potęgi ich wykładniki zawsze się sumują (a b *a c = a b+c). Ten prawo matematyczne został wyprowadzony przez Archimedesa, a później, w VIII wieku, matematyk Virasen stworzył tabelę wykładników całkowitych. To oni posłużyli do dalszego odkrycia logarytmów. Przykłady wykorzystania tej funkcji można znaleźć niemal wszędzie tam, gdzie konieczne jest uproszczenie uciążliwego mnożenia poprzez proste dodawanie. Jeśli poświęcisz 10 minut na przeczytanie tego artykułu, wyjaśnimy Ci, czym są logarytmy i jak z nimi pracować. Prostym i przystępnym językiem.

Definicja w matematyce

Logarytm jest wyrażeniem w następującej postaci: log a b=c, to znaczy logarytm dowolnej liczby nieujemnej (czyli dowolnej liczby dodatniej) „b” do jej podstawy „a” jest uważany za potęgę „c” ”, do którego należy podnieść podstawę „a”, aby ostatecznie uzyskać wartość „b”. Przeanalizujmy logarytm na przykładach, powiedzmy, że istnieje wyrażenie log 2 8. Jak znaleźć odpowiedź? To bardzo proste, trzeba znaleźć taką potęgę, aby od 2 do wymaganej potęgi otrzymać 8. Po wykonaniu kilku obliczeń w głowie otrzymamy liczbę 3! I to prawda, ponieważ 2 do potęgi 3 daje odpowiedź 8.

Rodzaje logarytmów

Dla wielu uczniów i studentów ten temat wydaje się skomplikowany i niezrozumiały, ale w rzeczywistości logarytmy nie są takie straszne, najważniejsze jest zrozumienie ich ogólnego znaczenia i zapamiętanie ich właściwości i niektórych zasad. Są trzy poszczególne gatunki wyrażenia logarytmiczne:

Logarytm naturalny ln a, gdzie podstawą jest liczba Eulera (e = 2,7).
Dziesiętne a, gdzie podstawa wynosi 10.
Logarytm dowolnej liczby b o podstawie a>1.

Każdy z nich jest zdecydowany w standardowy sposób, co obejmuje uproszczenie, redukcję i późniejszą redukcję do jednego logarytmu za pomocą twierdzeń logarytmicznych. Za zdobycie prawidłowe wartości logarytmy, przy ich rozwiązywaniu należy pamiętać o ich właściwościach i kolejności działań.

Zasady i pewne ograniczenia

W matematyce istnieje kilka reguł-ograniczeń, które są akceptowane jako aksjomat, to znaczy nie podlegają dyskusji i są prawdą. Na przykład nie da się podzielić liczb przez zero, nie da się też z nich wydobyć pierwiastka parzystego liczby ujemne. Logarytmy również mają swoje własne zasady, zgodnie z którymi można łatwo nauczyć się pracy nawet z długimi i pojemnymi wyrażeniami logarytmicznymi:

Podstawa „a” musi być zawsze większa od zera, a nie równa 1, w przeciwnym razie wyrażenie straci sens, ponieważ „1” i „0” w dowolnym stopniu są zawsze równe swoim wartościom;
jeśli a > 0, to a b > 0, to okazuje się, że „c” również musi być większe od zera.

Jak rozwiązywać logarytmy?

Na przykład podano zadanie znalezienia odpowiedzi na równanie 10 x = 100. Jest to bardzo proste, trzeba wybrać potęgę, podnosząc liczbę dziesięć do uzyskania 100. To oczywiście jest 10 2 = 100.

Przedstawmy teraz to wyrażenie w formie logarytmicznej. Otrzymujemy log 10 100 = 2. Przy rozwiązywaniu logarytmów wszystkie działania praktycznie zbiegają się, aby znaleźć potęgę, do której należy wprowadzić podstawę logarytmu, aby otrzymać daną liczbę.

Aby dokładnie określić wartość nieznanego stopnia, musisz nauczyć się pracować z tabelą stopni. To wygląda tak:

Jak widać, niektóre wykładniki można odgadnąć intuicyjnie, jeśli masz techniczny umysł i wiedzę o tabliczce mnożenia. Jednak dla duże wartości będziesz potrzebować tabeli stopni. Mogą z niego korzystać nawet ci, którzy nie mają zielonego pojęcia o skomplikowanych zagadnieniach matematycznych. W lewej kolumnie znajdują się liczby (podstawa a), górny rząd liczb to wartość potęgi c, do której podnoszona jest liczba a. Na przecięciu komórki zawierają wartości liczbowe będące odpowiedzią (a c =b). Weźmy na przykład pierwszą komórkę z liczbą 10 i podnieś ją do kwadratu, otrzymamy wartość 100, która jest wskazana na przecięciu naszych dwóch komórek. Wszystko jest tak proste i łatwe, że nawet najbardziej prawdziwy humanista zrozumie!

Równania i nierówności

Okazuje się, że w pewnych warunkach wykładnikiem jest logarytm. Dlatego dowolne matematyczne wyrażenia liczbowe można zapisać jako równość logarytmiczną. Na przykład 3 4 = 81 można zapisać jako logarytm o podstawie 3 z 81 równy cztery (log 3 81 = 4). Dla potęg ujemnych zasady są takie same: 2 -5 = 1/32 zapisujemy jako logarytm, otrzymujemy log 2 (1/32) = -5. Jednym z najbardziej fascynujących działów matematyki jest temat „logarytmów”. Przyjrzymy się przykładom i rozwiązaniom równań poniżej, zaraz po przestudiowaniu ich właściwości. Przyjrzyjmy się teraz, jak wyglądają nierówności i jak odróżnić je od równań.

Biorąc pod uwagę wyrażenie w postaci: log 2 (x-1) > 3 - tak nierówność logarytmiczna, ponieważ nieznana wartość „x” znajduje się pod znakiem logarytmu. A także w wyrażeniu porównywane są dwie wielkości: logarytm żądanej liczby do podstawy dwa jest większy niż liczba trzy.

Najważniejsza różnica między równaniami logarytmicznymi a nierównością polega na tym, że równania z logarytmami (przykład - logarytm 2 x = √9) implikują w odpowiedzi jedną lub więcej określonych wartości liczbowych, natomiast przy rozwiązywaniu nierówności definiuje się je jako obszar dopuszczalne wartości i punkty przerwania tej funkcji. W rezultacie odpowiedź nie jest prostym zbiorem pojedynczych liczb, jak w przypadku odpowiedzi na równanie, ale ciągłą serią lub zbiorem liczb.

Podstawowe twierdzenia o logarytmach

Podczas rozwiązywania prymitywnych zadań znajdowania wartości logarytmu jego właściwości mogą nie być znane. Jeśli jednak chodzi o równania czy nierówności logarytmiczne, to przede wszystkim należy jasno zrozumieć i zastosować w praktyce wszystkie podstawowe właściwości logarytmów. Przyjrzymy się przykładom równań później; najpierw przyjrzyjmy się każdej właściwości bardziej szczegółowo.

Główna tożsamość wygląda następująco: a logaB =B. Ma zastosowanie tylko wtedy, gdy a jest większe niż 0, a nie równe jedności, a B jest większe niż zero.
Logarytm iloczynu można przedstawić za pomocą następującego wzoru: log d (s 1 * s 2) = log d s 1 + log d s 2. W tym przypadku warunkiem obowiązkowym jest: d, s 1 i s 2 > 0; a≠1. Możesz przedstawić dowód tej formuły logarytmicznej wraz z przykładami i rozwiązaniem. Zapiszmy a s 1 = f 1 i zalogujmy a s 2 = f 2, następnie a f1 = s 1, a f2 = s 2. Otrzymujemy, że s 1 * s 2 = a f1 *a f2 = a f1+f2 (własności stopnie ), a następnie z definicji: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log as 2, co należało udowodnić.
Logarytm ilorazu wygląda następująco: log a (s 1/ s 2) = log a s 1 - log a s 2.
Twierdzenie w formie wzoru przyjmuje się następny widok: log a q b n = n/q log a b.

Wzór ten nazywany jest „właściwością stopnia logarytmu”. Przypomina to właściwości zwykłych stopni i nie jest w tym nic dziwnego, gdyż cała matematyka opiera się na naturalnych postulatach. Spójrzmy na dowód.

Niech log a b = t, okaże się, że a t = b. Jeśli podniesiemy obie części do potęgi m: a tn = b n ;

ale ponieważ a tn = (a q) nt/q = b n, zatem log a q b n = (n*t)/t, to log a q b n = n/q log a b. Twierdzenie zostało udowodnione.

Przykłady problemów i nierówności

Najczęstszym typem problemów logarytmicznych są przykłady równań i nierówności. Można je znaleźć w prawie wszystkich podręcznikach problemowych, a także są wymaganą częścią egzaminów z matematyki. O przyjęcie na uniwersytet lub zaliczenie Egzaminy wstępne na matematyce trzeba wiedzieć, jak poprawnie rozwiązywać takie problemy.

Niestety nie ma jednego planu ani schematu rozwiązywania i wyznaczania nieznanej wartości logarytmu, ale do każdej nierówności matematycznej lub równania logarytmicznego można zastosować pewne zasady. Przede wszystkim powinieneś dowiedzieć się, czy wyrażenie można uprościć, czy też do niego doprowadzić Ogólny wygląd. Możesz uprościć długie wyrażenia logarytmiczne, jeśli poprawnie użyjesz ich właściwości. Poznajmy je szybko.

Rozwiązując równania logarytmiczne, musimy określić, jaki rodzaj logarytmu mamy: przykładowe wyrażenie może zawierać logarytm naturalny lub dziesiętny.

Oto przykłady ln100, ln1026. Ich rozwiązanie sprowadza się do tego, że muszą wyznaczyć potęgę, do której podstawa 10 będzie równa odpowiednio 100 i 1026. Aby rozwiązać logarytmy naturalne, należy zastosować tożsamości logarytmiczne lub ich właściwości. Spójrzmy na przykłady rozwiązywania problemów logarytmicznych różnego typu.

Jak korzystać ze wzorów logarytmicznych: z przykładami i rozwiązaniami

Przyjrzyjmy się więc przykładom użycia podstawowych twierdzeń o logarytmach.

Właściwość logarytmu iloczynu można wykorzystać w zadaniach, w których konieczne jest rozwinięcie bardzo ważne liczby b na prostsze czynniki. Na przykład log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odpowiedź brzmi 9.
log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - jak widać, korzystając z czwartej własności potęgi logarytmu, udało nam się rozwiązać pozornie złożone i nierozwiązywalne wyrażenie. Wystarczy rozłożyć podstawę, a następnie wyjąć wartości wykładników ze znaku logarytmu.

Zadania z jednolitego egzaminu państwowego

Często spotyka się logarytmy egzaminy wstępne, zwłaszcza wiele problemów logarytmicznych na egzaminie Unified State Exam ( Egzamin państwowy dla wszystkich absolwentów). Zazwyczaj zadania te występują nie tylko w części A (najłatwiejsza część testowa egzaminu), ale także w części C (zadania najbardziej złożone i obszerne). Egzamin wymaga dokładności i doskonała wiedza tematy „Logarity naturalne”.

Przykłady i rozwiązania problemów pochodzą z oficjalnych źródeł Opcje ujednoliconego egzaminu stanowego. Zobaczmy, jak rozwiązuje się takie zadania.

Biorąc pod uwagę log 2 (2x-1) = 4. Rozwiązanie:
przepiszmy wyrażenie, nieco je upraszczając log 2 (2x-1) = 2 2, z definicji logarytmu otrzymujemy, że 2x-1 = 2 4, zatem 2x = 17; x = 8,5.

Najlepiej jest sprowadzić wszystkie logarytmy do tej samej podstawy, aby rozwiązanie nie było kłopotliwe i mylące.
Wszystkie wyrażenia pod znakiem logarytmu są oznaczone jako dodatnie, dlatego też, gdy wykładnik wyrażenia znajdującego się pod znakiem logarytmu i jako jego podstawa zostanie wyjęty jako mnożnik, wyrażenie pozostające pod logarytmem musi być dodatnie.

Zadania, których rozwiązaniem jest konwertowanie wyrażeń logarytmicznych, dość często spotykany na egzaminie Unified State Exam.

Aby skutecznie sobie z nimi poradzić minimalny koszt czas z wyjątkiem głównych tożsamości logarytmiczne, musisz znać i poprawnie używać więcej formuł.

To jest: a log a b = b, gdzie a, b > 0, a ≠ 1 (wynika to wprost z definicji logarytmu).

log a b = log c b / log c a lub log a b = 1/log b a
gdzie a, b, c > 0; a, c ≠ 1.

log a m b n = (m/n) log |a| |b|
gdzie a, b > 0, a ≠ 1, m, n Є R, n ≠ 0.

a log do b = b log do a
gdzie a, b, c > 0 i a, b, c ≠ 1

Aby wykazać ważność czwartej równości, weźmy logarytm lewej i prawej strony o podstawę a. Otrzymujemy log a (log z b) = log a (b log z a) lub log z b = log z a · log a b; log c b = log c a · (log c b / log c a); log z b = log z b.

Udowodniliśmy równość logarytmów, co oznacza, że wyrażenia pod logarytmami są również równe. Formuła 4 została udowodniona.

Przykład 1.

Oblicz 81 log 27 5 log 5 4 .

Rozwiązanie.

81 = 3 4 , 27 = 3 3 .

log 27 5 = 1/3 log 3 5, log 5 4 = log 3 4 / log 3 5. Zatem

log 27 5 log 5 4 = 1/3 log 3 5 (log 3 4 / log 3 5) = 1/3 log 3 4.

Następnie 81 log 27 5 log 5 4 = (3 4) 1/3 log 3 4 = (3 log 3 4) 4/3 = (4) 4/3 = 4 3 √4.

Poniższe zadanie możesz wykonać samodzielnie.

Oblicz (8 log 2 3 + 3 1/ log 2 3) - log 0,2 5.

Jako wskazówka: 0,2 = 1/5 = 5 -1 ; log 0,2 5 = -1.

Odpowiedź: 5.

Przykład 2.

Oblicz (√11) dziennik √3 9- log 121 81 .

Rozwiązanie.

Zamieńmy wyrażenia: 9 = 3 2, √3 = 3 1/2, log √3 9 = 4,

121 = 11 2, 81 = 3 4, log 121 81 = 2 log 11 3 (użyto wzoru 3).

Następnie (√11) log √3 9- log 121 81 = (11 1/2) 4-2 log 11 3 = (11) 2- log 11 3 = 11 2 / (11) log 11 3 = 11 2 / ( 11 log 11 3) = 121/3.

Przykład 3.

Oblicz log 2 24 / log 96 2 - log 2 192 / log 12 2.

Rozwiązanie.

Zastępujemy logarytmy zawarte w przykładzie logarytmami o podstawie 2.

log 96 2 = 1/log 2 96 = 1/log 2 (2 5 3) = 1/(log 2 2 5 + log 2 3) = 1/(5 + log 2 3);

log 2 192 = log 2 (2 6 3) = (log 2 2 6 + log 2 3) = (6 + log 2 3);

log 2 24 = log 2 (2 3 3) = (log 2 2 3 + log 2 3) = (3 + log 2 3);

log 12 2 = 1/log 2 12 = 1/log 2 (2 2 3) = 1/(log 2 2 2 + log 2 3) = 1/(2 + log 2 3).

Następnie log 2 24 / log 96 2 – log 2 192 / log 12 2 = (3 + log 2 3) / (1/(5 + log 2 3)) – ((6 + log 2 3) / (1/( 2 + log 2 3)) =

= (3 + log 2 3) · (5 + log 2 3) – (6 + log 2 3)(2 + log 2 3).

Po otwarciu nawiasów i wprowadzeniu podobnych terminów otrzymujemy liczbę 3. (Uproszczając wyrażenie, możemy oznaczyć log 2 3 przez n i uprościć wyrażenie

(3 + n) · (5 + n) – (6 + n)(2 + n)).

Odpowiedź: 3.

Możesz samodzielnie wykonać następujące zadanie:

Oblicz (log 3 4 + log 4 3 + 2) log 3 16 log 2 144 3.

Tutaj konieczne jest przejście do logarytmów podstawowych 3 i rozłożenie na czynniki pierwsze duże liczby.

Odpowiedź: 1/2

Przykład 4.

Mając trzy liczby A = 1/(log 3 0,5), B = 1/(log 0,5 3), C = log 0,5 12 – log 0,5 3. Ułóż je w kolejności rosnącej.

Rozwiązanie.

Przekształćmy liczby A = 1/(log 3 0,5) = log 0,5 3; C = log 0,5 12 – log 0,5 3 = log 0,5 12/3 = log 0,5 4 = -2.

Porównajmy je

log 0,5 3 > log 0,5 4 = -2 i log 0,5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.

Lub 2< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.

Odpowiedź. Zatem kolejność umieszczania liczb jest następująca: C; A; W.

Przykład 5.

Ile liczb całkowitych znajduje się w przedziale (log 3 1/16; log 2 6 48).

Rozwiązanie.

Ustalmy, pomiędzy którymi potęgami liczby 3 mieści się liczba 1/16. Dostajemy 1/27< 1 / 16 < 1 / 9 .

Ponieważ funkcja y = log 3 x rośnie, to log 3 (1 / 27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.

log 6 48 = log 6 (36 4 / 3) = log 6 36 + log 6 (4 / 3) = 2 + log 6 (4 / 3). Porównajmy log 6 (4/3) i 1/5. I w tym celu porównujemy liczby 4/3 i 6 1/5. Podnieśmy obie liczby do potęgi 5. Otrzymujemy (4/3) 5 = 1024/243 = 4 52/243< 6. Следовательно,

log 6 (4 / 3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.

Dlatego przedział (log 3 1/16; log 6 48) obejmuje przedział [-2; 4] i umieszcza się na nim liczby całkowite -2; -1; 0; 1; 2; 3; 4.

Odpowiedź: 7 liczb całkowitych.

Przykład 6.

Oblicz 3 lglg 2/ lg 3 - lg20.

Rozwiązanie.

3 lg lg 2/ lg 3 = (3 1/ lg3) lg lg 2 = (3 lо g 3 10) lg lg 2 = 10 lg lg 2 = lg2.

Następnie 3 lglg2/lg3 - lg 20 = lg 2 – lg 20 = lg 0,1 = -1.

Odpowiedź 1.

Przykład 7.

Wiadomo, że log 2 (√3 + 1) + log 2 (√6 – 2) = A. Znajdź log 2 (√3 –1) + log 2 (√6 + 2).

Rozwiązanie.

Liczby (√3 + 1) i (√3 – 1); (√6 – 2) i (√6 + 2) są sprzężone.

Przeprowadźmy następującą transformację wyrażeń

√3 – 1 = (√3 – 1) · (√3 + 1)) / (√3 + 1) = 2/(√3 + 1);

√6 + 2 = (√6 + 2) · (√6 – 2)) / (√6 – 2) = 2/(√6 – 2).

Następnie log 2 (√3 – 1) + log 2 (√6 + 2) = log 2 (2/(√3 + 1)) + log 2 (2/(√6 – 2)) =

Log 2 2 – log 2 (√3 + 1) + log 2 2 – log 2 (√6 – 2) = 1 – log 2 (√3 + 1) + 1 – log 2 (√6 – 2) =

2 – log 2 (√3 + 1) – log 2 (√6 – 2) = 2 – A.

Odpowiedź: 2 – A.

Przykład 8.

Uprość i znajdź przybliżoną wartość wyrażenia (log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9.

Rozwiązanie.

Sprowadźmy wszystkie logarytmy do wspólnej podstawy 10.

(log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9 = (lg 2 / lg 3) (lg 3 / lg 4) (lg 4 / lg 5) (lg 5 / lg 6) · … · (lg 8 / lg 9) · lg 9 = lg 2 ≈ 0,3010. (Przybliżoną wartość lg 2 można znaleźć za pomocą tabeli, suwaka logarytmicznego lub kalkulatora).

Odpowiedź: 0,3010.

Przykład 9.

Oblicz log a 2 b 3 √(a 11 b -3), jeśli log √ a b 3 = 1. (W tym przykładzie a 2 b 3 jest podstawą logarytmu).

Rozwiązanie.

Jeśli log √ a b 3 = 1, to 3/(0,5 log a b = 1. I log a b = 1/6.

Następnie log a 2 b 3√(a 11 b -3) = 1/2 log a 2 b 3 (a 11 b -3) = log a (a 11 b -3) / (2log a (a 2 b 3) ) = (log a a 11 + log a b -3) / (2(log a a 2 + log a b 3)) = (11 – 3log a b) / (2(2 + 3log a b)) Biorąc pod uwagę, że log a b = 1/ 6 otrzymujemy (11 – 3 1 / 6) / (2(2 + 3 1 / 6)) = 10,5/5 = 2,1.

Odpowiedź: 2.1.

Możesz samodzielnie wykonać następujące zadanie:

Oblicz log √3 6 √2,1 jeśli log 0,7 27 = a.

Odpowiedź: (3 + a) / (3a).

Przykład 10.

Oblicz 6,5 4/ log 3 169 · 3 1/ log 4 13 + log125.

Rozwiązanie.

6,5 4/ log 3 169 · 3 1/ log 4 13 + log 125 = (13/2) 4/2 log 3 13 · 3 2/ log 2 13 + 2log 5 5 3 = (13/2) 2 log 13 3 3 2 log 13 2 + 6 = (13 log 13 3 / 2 log 13 3) 2 (3 log 13 2) 2 + 6 = (3/2 log 13 3) 2 (3 log 13 2) 2 + 6 = ( 3 2 /(2 log 13 3) 2) · (2 log 13 3) 2 + 6.

(2 log 13 3 = 3 log 13 2 (wzór 4))

Otrzymujemy 9 + 6 = 15.

Odpowiedź: 15.

Nadal masz pytania? Nie wiesz, jak znaleźć wartość wyrażenia logarytmicznego?
Aby skorzystać z pomocy korepetytora zarejestruj się.
Pierwsza lekcja jest bezpłatna!

stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do oryginalnego źródła.

Zadania, których rozwiązaniem jest konwertowanie wyrażeń logarytmicznych, dość często spotykany na egzaminie Unified State Exam.

Aby skutecznie sobie z nimi poradzić w minimalnym czasie, oprócz podstawowych tożsamości logarytmicznych, musisz znać i poprawnie używać jeszcze kilku formuł.