Która funkcja nazywa się parzystą i nieparzystą. Badanie funkcji

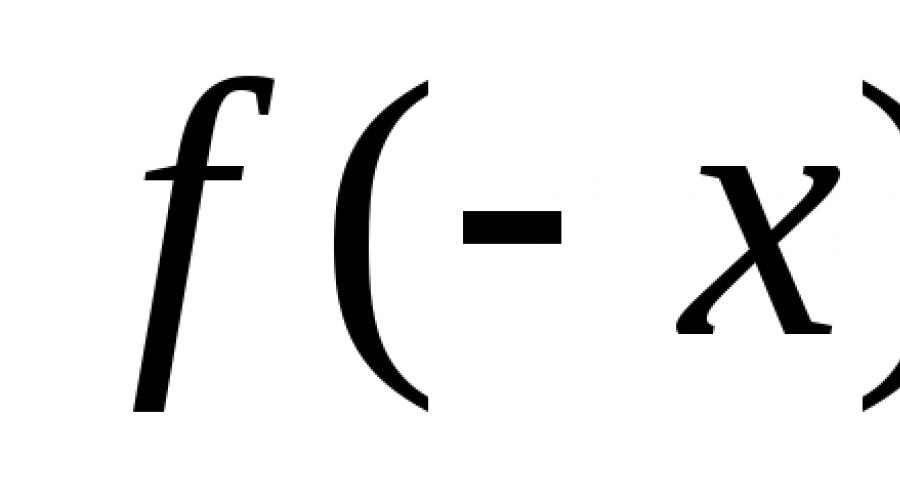
Równość i nieparzystość funkcji to jedne z jej głównych właściwości, a parzystość zajmuje imponującą część kurs szkolny matematyka. W dużej mierze determinuje zachowanie funkcji i znacznie ułatwia konstrukcję odpowiedniego wykresu.

Określmy parzystość funkcji. Ogólnie rzecz biorąc, badaną funkcję rozważa się nawet wtedy, gdy dla przeciwnych wartości zmiennej niezależnej (x) znajdującej się w jej dziedzinie definicji odpowiadające wartości y (funkcji) okazują się równe.

Podajmy bardziej ścisłą definicję. Rozważmy pewną funkcję f(x), która jest zdefiniowana w dziedzinie D. Będzie tak nawet, jeśli dla dowolnego punktu x znajdującego się w dziedzinie definicji:

• -x (punkt przeciwny) również leży w tym zakresie,

• f(-x) = f(x).

Z powyższej definicji wynika warunek niezbędny dla dziedziny definicji takiej funkcji, a mianowicie symetria względem punktu O, który jest początkiem współrzędnych, gdyż jeśli jakiś punkt b mieści się w dziedzinie definicji parzystej funkcji, to odpowiedni punkt b również należy do tej dziedziny. Z powyższego wynika zatem następujący wniosek: nawet funkcjonować ma wygląd symetryczny względem osi rzędnych (Oy).

Jak w praktyce wyznaczyć parzystość funkcji?

Określmy to wzorem h(x)=11^x+11^(-x). Kierując się algorytmem wynikającym bezpośrednio z definicji, w pierwszej kolejności zbadamy jej dziedzinę definicyjną. Oczywiście jest on zdefiniowany dla wszystkich wartości argumentu, czyli spełniony jest pierwszy warunek.

Następnym krokiem jest podstawienie argumentu (x) wartości przeciwnej (-x).
Otrzymujemy:
h(-x) = 11^(-x) + 11^x.
Ponieważ dodawanie spełnia prawo przemienności (przemienności), oczywiste jest, że h(-x) = h(x) i dane zależność funkcjonalna- nawet.

Sprawdźmy parzystość funkcji h(x)=11^x-11^(-x). Postępując zgodnie z tym samym algorytmem, otrzymujemy, że h(-x) = 11^(-x) -11^x. Po odjęciu minusa ostatecznie mamy
h(-x)=-(11^x-11^(-x))=- h(x). Dlatego h(x) jest nieparzyste.

Nawiasem mówiąc, należy przypomnieć, że istnieją funkcje, których nie można sklasyfikować według tych kryteriów, nie nazywa się ich ani parzystymi, ani nieparzystymi.

Nawet funkcje mają wiele interesujących właściwości:

• w wyniku dodania podobnych funkcji otrzymują parzystą;
• w wyniku odjęcia takich funkcji otrzymuje się parzystą;
• nawet, także;
• w wyniku pomnożenia dwóch takich funkcji otrzymuje się parzystą;
• w wyniku pomnożenia funkcji nieparzystych i parzystych otrzymujemy funkcję nieparzystą;
• w wyniku podzielenia funkcji nieparzystej i parzystej otrzymuje się nieparzystą;
• pochodna takiej funkcji jest nieparzysta;
• Jeśli podniesiesz funkcję nieparzystą do kwadratu, otrzymasz parzystą.

Parzystość funkcji można wykorzystać do rozwiązywania równań.

Aby rozwiązać równanie takie jak g(x) = 0, gdzie lewa strona równanie jest funkcją parzystą, wystarczy znaleźć jej rozwiązania dla nieujemnych wartości zmiennej. Powstałe pierwiastki równania należy połączyć z liczbami przeciwnymi. Jeden z nich podlega weryfikacji.

Jest to również z powodzeniem stosowane do rozwiązywania zadania niestandardowe z parametrem.

Na przykład, czy istnieje taka wartość parametru a, dla której równanie 2x^6-x^4-ax^2=1 będzie miało trzy pierwiastki?

Jeśli weźmiemy pod uwagę, że zmienna wchodzi do równania w potęgach parzystych, to jasne jest, że zastąpienie x przez - x dane równanie nie zmieni się. Wynika z tego, że jeśli pewna liczba jest jej pierwiastkiem, to liczba przeciwna również jest pierwiastkiem. Wniosek jest oczywisty: pierwiastki równania różne od zera włączamy do zbioru jego rozwiązań „parami”.

Oczywiste jest, że sama liczba nie wynosi 0, to znaczy liczba pierwiastków takiego równania może być tylko parzysta i oczywiście dla dowolnej wartości parametru nie może mieć trzech pierwiastków.

Ale liczba pierwiastków równania 2^x+ 2^(-x)=ax^4+2x^2+2 może być nieparzysta i to dla dowolnej wartości parametru. Rzeczywiście łatwo sprawdzić, że zbiór pierwiastków tego równania zawiera rozwiązania „parami”. Sprawdźmy, czy 0 jest pierwiastkiem. Kiedy podstawimy to do równania, otrzymamy 2=2. Zatem oprócz „sparowanych” 0 jest także pierwiastkiem, co dowodzi ich nieparzystej liczby.

Nawet funkcjonować.

Nawet jest funkcją, której znak nie zmienia się wraz ze zmianą znaku X.

X obowiązuje równość F(–X) = F(X). Podpisać X nie ma wpływu na znak y.

Wykres funkcji parzystej jest symetryczny względem osi współrzędnych (ryc. 1).

Przykłady funkcji parzystych:

y=co X

y = X 2

y = –X 2

y = X 4

y = X 6

y = X 2 + X

Wyjaśnienie:
Weźmy funkcję y = X 2 lub y = –X 2 .
Za dowolną wartość X funkcja jest dodatnia. Podpisać X nie ma wpływu na znak y. Wykres jest symetryczny względem osi współrzędnych. To jest funkcja parzysta.

Dziwna funkcja.

Dziwne jest funkcją, której znak zmienia się wraz ze zmianą znaku X.

Innymi słowy, dla dowolnej wartości X obowiązuje równość F(–X) = –F(X).

Wykres funkcji nieparzystej jest symetryczny względem początku (ryc. 2).

Przykłady funkcji nieparzystej:

y= grzech X

y = X 3

y = –X 3

Wyjaśnienie:

Weźmy funkcję y = – X 3 .
Wszystkie znaczenia Na będzie miał znak minus. To jest znak X wpływa na znak y. Jeśli zmienna niezależna jest liczbą dodatnią, to funkcja jest dodatnia, jeśli zmienna niezależna jest dodatnia liczba ujemna, to funkcja jest ujemna: F(–X) = –F(X).
Wykres funkcji jest symetryczny względem początku. To dziwna funkcja.

Własności funkcji parzystych i nieparzystych:

NOTATKA:

Nie wszystkie funkcje są parzyste lub nieparzyste. Istnieją funkcje, które nie podlegają takiej gradacji. Na przykład funkcja root Na = √X nie dotyczy ani funkcji parzystych, ani nieparzystych (ryc. 3). Przy wymienianiu właściwości takich funkcji należy podać odpowiedni opis: ani parzysty, ani nieparzysty.

Funkcje okresowe.

Jak wiadomo, okresowość to powtarzanie pewnych procesów w określonych odstępach czasu. Funkcje opisujące te procesy nazywane są funkcje okresowe. Oznacza to, że są to funkcje, na których wykresach znajdują się elementy powtarzające się w określonych odstępach liczbowych.

Funkcja nazywa się parzystą (nieparzystą), jeśli dla dowolnego i równości

.

Wykres funkcji parzystej jest symetryczny względem osi
.

Wykres funkcji nieparzystej jest symetryczny względem początku.

Przykład 6.2. Zbadaj, czy funkcja jest parzysta czy nieparzysta

1)
; 2)
; 3)
.

Rozwiązanie.

1) Funkcja jest zdefiniowana, gdy
. Znajdziemy
.

Te.
. Oznacza, tę funkcję jest równa.

2) Funkcja jest zdefiniowana, gdy

Te.
. Zatem ta funkcja jest nieparzysta.

3) funkcja jest zdefiniowana dla , tj. Dla

,
. Zatem funkcja nie jest ani parzysta, ani nieparzysta. Nazwijmy to funkcją postaci ogólnej.

3. Badanie funkcji monotoniczności.

Funkcjonować
nazywa się wzrostem (maleniem) w pewnym przedziale, jeśli w tym przedziale każdy wyższa wartość argument odpowiada większej (mniejszej) wartości funkcji.

Funkcje rosnące (malejące) w pewnym przedziale nazywane są monotonicznymi.

Jeśli funkcja
różniczkowalna na przedziale
i ma dodatnią (ujemną) pochodną
, a następnie funkcja
wzrasta (maleje) w tym przedziale.

Przykład 6.3. Znaleźć przedziały monotoniczności funkcji

1)
; 3)
.

Rozwiązanie.

1) Funkcja ta jest zdefiniowana na całej osi liczbowej. Znajdźmy pochodną.

Pochodna jest równa zeru, jeśli
I
. Dziedziną definicji jest oś liczbowa podzielona kropkami
,
w przerwach. Wyznaczmy znak pochodnej w każdym przedziale.

W przerwie
pochodna jest ujemna, funkcja maleje w tym przedziale.

W przerwie
pochodna jest dodatnia, zatem funkcja rośnie w tym przedziale.

2) Ta funkcja jest zdefiniowana jeśli
Lub

.

W każdym przedziale wyznaczamy znak trójmianu kwadratowego.

Zatem dziedzina definicji funkcji

Znajdźmy pochodną
,
, Jeśli
, tj.
, Ale
. Wyznaczmy znak pochodnej w przedziałach
.

W przerwie
pochodna jest ujemna, zatem funkcja maleje na przedziale
. W przerwie
pochodna jest dodatnia, funkcja rośnie w przedziale
.

4. Badanie funkcji ekstremum.

Kropka
nazywany maksymalnym (minimalnym) punktem funkcji
, jeżeli istnieje takie sąsiedztwo punktu to dla wszystkich
z tego sąsiedztwa zachodzi nierówność

.

Maksymalne i minimalne punkty funkcji nazywane są ekstremami.

Jeśli funkcja
w tym punkcie ma ekstremum, to pochodna funkcji w tym punkcie jest równa zero lub nie istnieje (warunek konieczny istnienia ekstremum).

Punkty, w których pochodna wynosi zero lub nie istnieje, nazywane są krytycznymi.

5. Warunki wystarczające na istnienie ekstremum.

Zasada nr 1. Jeśli podczas przejścia (od lewej do prawej) przez punkt krytyczny pochodna
zmienia znak z „+” na „–”, a następnie w punkcie funkcjonować
ma maksimum; jeśli od „–” do „+”, to minimum; Jeśli
nie zmienia znaku, to nie ma ekstremum.

Zasada 2. Niech w punkt
pierwsza pochodna funkcji
równy zeru
, a druga pochodna istnieje i jest różna od zera. Jeśli
, To – maksymalny punkt, jeśli
, To – minimalny punkt funkcji.

Przykład 6.4 . Poznaj funkcje maksymalne i minimalne:

1)
; 2)
; 3)
;

4)
.

Rozwiązanie.

1) Funkcja jest zdefiniowana i ciągła na przedziale
.

Znajdźmy pochodną
i rozwiązać równanie
, tj.
.Stąd
- punkt krytyczny.

Wyznaczmy znak pochodnej w przedziałach,
.

Podczas przechodzenia przez punkty
I
pochodna zmienia znak z „–” na „+”, zatem zgodnie z zasadą 1
– minimalna liczba punktów.

Podczas przechodzenia przez punkt
pochodna zmienia znak z „+” na „–”, tj
– maksymalny punkt.

,
.

2) Funkcja jest określona i ciągła w przedziale
. Znajdźmy pochodną
.

Po rozwiązaniu równania
, znajdziemy
I
- punkt krytyczny. Jeśli mianownik
, tj.
, to pochodna nie istnieje. Więc,
– trzeci punkt krytyczny. Wyznaczmy znak pochodnej w przedziałach.

Zatem funkcja ma w tym punkcie minimum
, maksimum w punktach
I
.

3) Funkcja jest zdefiniowana i ciągła jeśli
, tj. Na
.

Znajdźmy pochodną

.

Znajdźmy punkty krytyczne:

Sąsiedztwa punktów
nie należą do dziedziny definicji, zatem nie są ekstremami. Przeanalizujmy zatem punkty krytyczne
I
.

4) Funkcja jest określona i ciągła na przedziale
. Skorzystajmy z reguły 2. Znajdź pochodną
.

Znajdźmy punkty krytyczne:

Znajdźmy drugą pochodną
i określ jego znak w punktach

W punktach
funkcja ma minimum.

W punktach
funkcja ma maksimum.

Wykresy funkcji parzystych i nieparzystych mają następujące cechy:

Jeżeli funkcja jest parzysta, to jej wykres jest symetryczny względem rzędnej. Jeśli funkcja jest nieparzysta, to jej wykres jest symetryczny względem początku.

Rozwiązanie. Rozważmy funkcję: \(f\left(x \right)=\left|x \right|\) i zamieńmy odwrotnie \(-x \) zamiast \(x \). W wyniku prostych przekształceń otrzymujemy: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ In other słów, jeśli zastąpimy argument przeciwnym znakiem, funkcja się nie zmieni.

Oznacza to, że funkcja ta jest parzysta, a jej wykres będzie symetryczny względem osi rzędnych ( Oś pionowa). Wykres tej funkcji pokazano na rysunku po lewej stronie. Oznacza to, że konstruując wykres, można narysować tylko połowę, a drugą część (na lewo od osi pionowej narysować symetrycznie do prawej części). Określając symetrię funkcji przed rozpoczęciem rysowania jej wykresu, możesz znacznie uprościć proces konstruowania lub badania funkcji. Jeśli trudno jest przeprowadzić ogólną kontrolę, możesz to zrobić prościej: podstaw do równania te same wartości różnych znaków. Na przykład -5 i 5. Jeśli wartości funkcji okażą się takie same, to możemy mieć nadzieję, że funkcja będzie parzysta. Z matematycznego punktu widzenia podejście to nie jest całkowicie poprawne, ale z praktycznego punktu widzenia jest wygodne. Aby zwiększyć wiarygodność wyniku, możesz zastąpić kilka par takich przeciwnych wartości.

Rozwiązanie. Sprawdźmy to samo co w poprzednim przykładzie: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right ) $$ Oznacza to, że pierwotna funkcja jest nieparzysta (znak funkcji zmienił się na przeciwny).

Wniosek: funkcja jest symetryczna względem początku. Możesz zbudować tylko jedną połowę i narysować drugą symetrycznie. Ten rodzaj symetrii jest trudniejszy do narysowania. Oznacza to, że patrzysz na wykres z drugiej strony arkusza, a nawet do góry nogami. Możesz też to zrobić: weź narysowaną część i obróć ją wokół początku o 180 stopni w kierunku przeciwnym do ruchu wskazówek zegara.

Rozwiązanie. Przeprowadźmy tę samą kontrolę zmiany znaku, co w poprzednich dwóch przykładach. $$f\left(-x \right)=\left(-x \right)^3+\left(-x \right)^2=-x^2+x^2$$ W rezultacie otrzymujemy że: $$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$ I to oznacza, że ​​funkcja nie jest ani parzysta, ani nieparzysta.

Wniosek: funkcja nie jest symetryczna ani względem początku, ani środka układu współrzędnych. Stało się tak, ponieważ jest to suma dwóch funkcji: parzystej i nieparzystej. Ta sama sytuacja będzie miała miejsce, jeśli odejmiemy dwie różne funkcje. Ale mnożenie lub dzielenie doprowadzi do innego wyniku. Na przykład iloczyn funkcji parzystej i nieparzystej daje funkcję nieparzystą. Lub iloraz dwóch liczb nieparzystych prowadzi do funkcji parzystej.

Hide Show

Metody określania funkcji

Niech funkcję będzie dana wzorem: y=2x^(2)-3. Przypisując dowolne wartości zmiennej niezależnej x, można za pomocą tego wzoru obliczyć odpowiadające wartości zmiennej zależnej y. Na przykład, jeśli x=-0,5, to korzystając ze wzoru stwierdzamy, że odpowiadająca wartość y wynosi y=2 \cdot (-0,5)^(2)-3=-2,5.

Biorąc dowolną wartość przyjmowaną przez argument x we ​​wzorze y=2x^(2)-3, można obliczyć tylko jedną wartość funkcji, która jej odpowiada. Funkcję można przedstawić w postaci tabeli:

Korzystając z tej tabeli, możesz zobaczyć, że wartości argumentu -1 odpowiada wartość funkcji -3; a wartość x=2 będzie odpowiadać y=0 itd. Ważne jest również, aby wiedzieć, że każda wartość argumentu w tabeli odpowiada tylko jednej wartości funkcji.

Więcej funkcji można określić za pomocą wykresów. Za pomocą wykresu ustala się, która wartość funkcji koreluje z określoną wartością x. Najczęściej będzie to przybliżona wartość funkcji.

Funkcja parzysta i nieparzysta

Funkcja jest nawet funkcjonować, gdy f(-x)=f(x) dla dowolnego x z dziedziny definicji. Taka funkcja będzie symetryczna względem osi Oy.

Funkcja jest dziwna funkcja, gdy f(-x)=-f(x) dla dowolnego x z dziedziny definicji. Taka funkcja będzie symetryczna względem początku O (0;0).

Funkcja jest nawet nie, ani dziwne i nazywa się funkcjonować ogólna perspektywa , gdy nie ma symetrii względem osi lub początku.

Przeanalizujmy następującą funkcję parzystości:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) z symetryczną dziedziną definicji względem początku. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Oznacza to, że funkcja f(x)=3x^(3)-7x^(7) jest nieparzysta.

Funkcja okresowa

Funkcja y=f(x) , w dziedzinie której zachodzi równość f(x+T)=f(x-T)=f(x) dla dowolnego x, nazywa się funkcja okresowa z okresem T \neq 0 .

Powtórzenie wykresu funkcji na dowolnym odcinku osi x o długości T.

Przedziały, w których funkcja jest dodatnia, czyli f(x) > 0, są odcinkami osi odciętych odpowiadającymi punktom wykresu funkcji leżącym nad osią odciętych.

f(x) > 0 włączone (x_(1); x_(2)) \cup (x_(3); +\infty)

Przedziały, w których funkcja jest ujemna, czyli f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

k(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Ograniczona funkcja

Ograniczone od dołu Zwyczajowo wywołuje się funkcję y=f(x), x \in X, gdy istnieje liczba A, dla której nierówność f(x) \geq A zachodzi dla dowolnego x \in X .

Przykład funkcji ograniczonej od dołu: y=\sqrt(1+x^(2)) ponieważ y=\sqrt(1+x^(2)) \geq 1 dla dowolnego x .

Ograniczone od góry funkcja y=f(x), x \in X jest wywoływana, gdy istnieje liczba B, dla której nierówność f(x) \neq B zachodzi dla dowolnego x \in X .

Przykład funkcji ograniczonej poniżej: y=\sqrt(1-x^(2)), x \in [-1;1] ponieważ y=\sqrt(1+x^(2)) \neq 1 dla dowolnego x \in [-1;1] .

Ograniczony Zwyczajowo wywołuje się funkcję y=f(x), x \in X, gdy istnieje liczba K > 0, dla której nierówność \left | f(x)\prawo | \neq K dla dowolnego x \in X .

Przykład ograniczona funkcja: y=\sin x jest ograniczone na całej osi liczbowej, ponieważ \w lewo | \sin x \right | \neq 1.

Funkcja rosnąca i malejąca

Zwyczajowo mówi się o funkcji, która rośnie w rozpatrywanym przedziale jako funkcja rosnąca wtedy, gdy większa wartość x odpowiada większej wartości funkcji y=f(x) . Wynika z tego, że biorąc dwie dowolne wartości argumentu x_(1) i x_(2) z rozważanego przedziału, przy x_(1) > x_(2) , wynikiem będzie y(x_(1)) > y(x_(2)).

Nazywa się funkcję, która maleje w rozpatrywanym przedziale funkcja malejąca gdy większa wartość x odpowiada mniejszej wartości funkcji y(x) . Wynika z tego, że biorąc z rozpatrywanego przedziału dwie dowolne wartości argumentu x_(1) i x_(2) oraz x_(1) > x_(2) , wynikiem będzie y(x_(1))< y(x_{2}) .

Korzenie funkcji Zwyczajowo nazywa się punkty, w których funkcja F=y(x) przecina oś odciętych (uzyskuje się je rozwiązując równanie y(x)=0).

a) Jeżeli dla x > 0 funkcja parzysta rośnie, to dla x maleje< 0

b) Gdy funkcja parzysta maleje przy x > 0, to rośnie przy x< 0

c) Gdy funkcja nieparzysta rośnie przy x > 0, to również rośnie przy x< 0

d) Gdy funkcja nieparzysta maleje dla x > 0, to zmniejsza się również dla x< 0

Ekstrema funkcji

Minimalny punkt funkcji y=f(x) nazywa się zwykle punktem x=x_(0), którego sąsiedztwo będzie miało inne punkty (z wyjątkiem punktu x=x_(0)), i dla nich nierówność f(x) > f będzie wówczas wynosić zadowolony (x_(0)) . y_(min) - oznaczenie funkcji w punkcie min.

Maksymalny punkt funkcji y=f(x) nazywa się zwykle punktem x=x_(0), którego sąsiedztwo będzie miało inne punkty (z wyjątkiem punktu x=x_(0)), i dla nich nierówność f(x) będzie wówczas spełniona< f(x^{0}) . y_{max} - обозначение функции в точке max.

Warunek wstępny

Zgodnie z twierdzeniem Fermata: f”(x)=0, gdy funkcja f(x) różniczkowalna w punkcie x_(0) będzie miała w tym punkcie ekstremum.

Stan wystarczający

1. Gdy pochodna zmieni znak z plusa na minus, wówczas x_(0) będzie punktem minimalnym;
2. x_(0) - będzie punktem maksymalnym tylko wtedy, gdy pochodna zmieni znak z minus na plus przy przejściu przez punkt stacjonarny x_(0) .

Największa i najmniejsza wartość funkcji w przedziale

Kroki obliczeniowe:

1. Poszukuje się pochodnej f”(x);
2. Znaleziono punkty stacjonarne i krytyczne funkcji oraz wybrano te, które należą do odcinka;
3. Wartości funkcji f(x) znajdują się w punktach stacjonarnych i krytycznych oraz na końcach odcinka. Mniejszy z uzyskanych wyników będzie najniższa wartość Funkcje, i więcej - największy.