Określ najkrótszą odległość między dwiema przecinającymi się liniami. Odległość pomiędzy przecinającymi się liniami - definicja i przykłady znalezienia
Przeczytaj także
Cele i zadania:
- edukacyjne - kształtowanie i rozwój koncepcji przestrzennych u uczniów; rozwijanie umiejętności rozwiązywania problemów w celu znalezienia odległości między przecinającymi się liniami
- edukacyjne – kształtowanie woli i wytrwałości w osiąganiu końcowych rezultatów przy odnajdywaniu odległości pomiędzy przecinającymi się liniami; Rozwijaj miłość i zainteresowanie nauką matematyki.
- rozwojowy – rozwój logicznego myślenia uczniów, koncepcji przestrzennych, rozwój umiejętności samokontroli.
Projekt odpowiada następującym punktom tematycznym program przedmiot szkolny.
- Przekraczanie linii prostych.
- Znak równoległości linii i płaszczyzny
- Rzut ortogonalny w przestrzeni.
- Objętość wielościanów.
Wstęp.
Przekraczanie granic jest niesamowite!
Gdyby ich nie było, życie byłoby sto razy mniej interesujące. Chciałoby się powiedzieć, że jeśli warto studiować stereometrię, to dlatego, że zawiera ona przecinające się linie proste. Mają tak wiele globalnych, interesujących właściwości: w architekturze, budownictwie, medycynie, przyrodzie.
Bardzo chcę, żeby nasze zdziwienie niepowtarzalnością przecinających się linii zostało Państwu przekazane. Ale jak to zrobić?
Może nasz projekt będzie odpowiedzią na to pytanie?
Wiadomo, że długość wspólnej prostopadłej przecinających się linii jest równa odległości między tymi liniami.
Twierdzenie: Odległość między dwiema przecinającymi się liniami jest równa odległości między równoległymi płaszczyznami przechodzącymi przez te linie.
Poniższe twierdzenie podaje jeden ze sposobów znalezienia odległości i kąta między liniami ukośnymi.
Odległość pomiędzy przecinającymi się liniami jest równa odległości od punktu będącego rzutem jednej z tych linii na płaszczyznę do niej prostopadłą, do rzutu drugiej linii na tę samą płaszczyznę.
Podstawowe pytanie:
Czy można znaleźć odległość między przecinającymi się liniami bez konstruowania ich wspólnej prostopadłej?
Rozważmy problem z sześcianem.
Dlaczego z kostką? Tak, ponieważ w sześcianie ukryta jest cała geometria, łącznie z geometrią przecinających się linii.
Zadanie.
Krawędź sześcianu jest równa A. Znajdź odległość między liniami, na których leżą przecinające się przekątne dwóch sąsiednich ścian sześcianu.
Odpowiedni różne metody badania tego problemu.
- a-przeor;
- metoda projekcji;
- metoda objętościowa;
- metoda współrzędnych.
Badania.
Klasa jest podzielona na grupy zgodnie ze sposobem studiowania problemu. Każda grupa staje przed zadaniem pokazania i udowodnienia zastosowania tej metody do wyznaczania odległości pomiędzy przecinającymi się liniami. Ostatnim etapem badania problemu jest zabezpieczenie projektów w postaci prezentacji, publikacji czy stron internetowych. Dzieci i nauczyciel mają możliwość oceny projektu każdej grupy według kryteriów opracowanych na potrzeby publikacji i prezentacji.
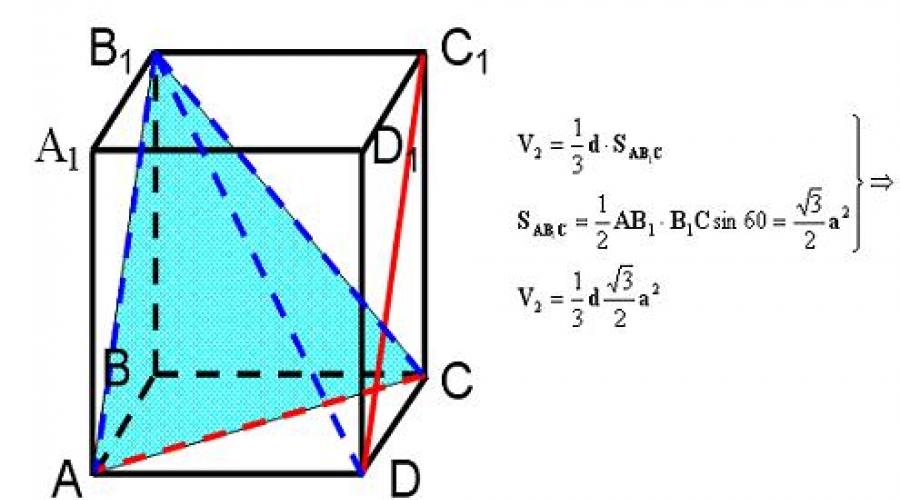
Metoda objętościowa.
- zbuduj piramidę, w której wysokość obniżona ze szczytu tej piramidy do płaszczyzny podstawy jest wymaganą odległością między dwiema przecinającymi się liniami prostymi;
- udowodnić, że ta wysokość jest wymaganą odległością;
- znajdź objętość tej piramidy za pomocą dwóch;
- sposoby wyrażania tej wysokości;
Metoda ta jest bardzo interesująca ze względu na swoją oryginalność, piękno i indywidualność. Metoda objętościowa sprzyja rozwojowi wyobraźni przestrzennej i umiejętności mentalnego tworzenia pomysłów na temat kształtu figur.
W wyniku dodatkowych konstrukcji otrzymaliśmy piramidę DAB 1 C.
W piramidzie DAB 1 C wysokość obniżona z wierzchołka D do płaszczyzny podstawy AB 1 C będzie wymaganą odległością pomiędzy przecinającymi się prostymi AC i DC 1.
Rozważmy piramidę. Wniosek: Rozważmy tę samą piramidę, ale z wierzchołkiem w punkcie D:
Biorąc pod uwagę, że V1 = V2, otrzymujemy d=
Wymagana odległość.
Metoda projekcji.
- Wybieramy płaszczyznę prostopadłą do jednej z przecinających się linii.
- Rzutujemy każdą linię prostą na tę płaszczyznę.
- Odległość między rzutami będzie odległością między przecinającymi się liniami.
Odległość pomiędzy przecinającymi się liniami można zdefiniować jako odległość pomiędzy ortogonalnymi rzutami tych linii na płaszczyznę projekcji.
Korzystanie z definicji linii skośnych.
Formacje dodatkowe: A1B, BD, AK.
A1O BD, OS BD
BD przecinając proste A 1 O i OS
Z tym kalkulator internetowy możesz znaleźć odległość między liniami prostymi w przestrzeni. Dany szczegółowe rozwiązanie z wyjaśnieniami. Aby obliczyć odległość między prostymi w przestrzeni, należy ustawić typ równania prostych („kanoniczne” lub „parametryczne”), wprowadzić współczynniki równań prostych w komórkach i kliknąć przycisk „Rozwiąż”.
×
Ostrzeżenie
Wyczyścić wszystkie komórki?
Zamknij Wyczyść
Instrukcje wprowadzania danych. Liczby wprowadza się jako liczby całkowite (przykłady: 487, 5, -7623 itd.), ułamki dziesiętne (np. 67., 102,54 itd.) lub ułamki zwykłe. Ułamek należy wpisać w formie a/b, gdzie a i b (b>0) są liczbami całkowitymi lub liczby dziesiętne. Przykłady 45/5, 6,6/76,4, -7/6,7 itd.
Odległość między liniami w przestrzeni - teoria, przykłady i rozwiązania
Niech będzie dany kartezjański prostokątny układ współrzędnych Oksyz L 1 i L 2:
| . | (1) |
 , ,
| (2) |
Gdzie M 1 (X 1 , y 1 , z 1) i M 2 (X 2 , y 2 , z 2) − punkty leżące na liniach prostych L 1 i L 2, za Q 1 ={M 1 , P 1 , l 1) i Q 2 ={M 2 , P 2 , l 2 ) – wektory kierunkowe linii prostych L 1 i L 2, odpowiednio.
Linie (1) i (2) w przestrzeni mogą się pokrywać, być równoległe, przecinać się lub przecinać. Jeśli linie w przestrzeni przecinają się lub pokrywają, wówczas odległość między nimi wynosi zero. Rozważymy dwa przypadki. Po pierwsze, linie są równoległe, a po drugie, linie się przecinają. Reszta to zwykłe przypadki. Jeżeli przy obliczaniu odległości między równoległymi liniami otrzymamy odległość równą zeru, oznacza to, że te linie się pokrywają. Jeśli odległość między przecinającymi się liniami wynosi zero, wówczas linie te przecinają się.
1. Odległość między równoległymi liniami w przestrzeni
Przyjrzyjmy się dwóm metodom obliczania odległości między liniami.
Metoda 1. Z punktu M 1 prosto L 1 narysuj samolot α , prostopadle do linii L 2. Znalezienie punktu M 3 (X 3 , y 3 , y 3) przecięcia płaszczyzn α i proste L 3. Zasadniczo znajdujemy rzut punktu M 1 prosto L 2. Jak znaleźć rzut punktu na linię, spójrz. Następnie obliczamy odległość pomiędzy punktami M 1 (X 1 , y 1 , z 1) i M 3 (X 3 , y 3 , z 3):
Przykład 1. Znajdź odległość między liniami L 1 i L 2:Prosty L 2 przechodzi przez ten punkt M 2 (X 2 , y 2 , z 2)=M
Podstawianie wartości M 2 , P 2 , l 2 , X 1 , y 1 , z 1 w (5) otrzymujemy:
Znajdźmy punkt przecięcia linii L 2 i samolot α , w tym celu konstruujemy równanie parametryczne linii prostej L 2 .
Aby znaleźć punkt przecięcia linii L 2 i samolot α , zamień wartości zmiennych X, y, z od (7) do (6):
Podstawianie otrzymanej wartości T w (7) otrzymujemy punkt przecięcia prostej L 2 i samolot α :
Pozostaje znaleźć odległość między punktami M 1 i M 3:
  |
L 1 i L 2 równa się D=7.2506.
Metoda 2. Znajdź odległość między liniami L 1 i L 2 (równania (1) i (2)). Najpierw sprawdzamy równoległość linii L 1 i L 2. Jeśli wektory kierunkowe linii prostych L 1 i L 2 są współliniowe, tj. jeśli istnieje liczba λ taka, że równość Q 1 =λ Q 2, potem prosto L 1 i L 2 są równoległe.
Ta metoda obliczania odległości między równoległymi wektorami opiera się na koncepcji iloczynu wektorów. Wiadomo, że norma iloczynu wektorów wektorów i Q 1 podaje obszar równoległoboku utworzonego przez te wektory (ryc. 2). Gdy znasz obszar równoległoboku, możesz znaleźć wierzchołek równoległoboku D, dzieląc obszar przez podstawę Q 1 równoległobok.
Q 1:
Odległość między liniami L 1 i L 2 równa się:
| , |
Przykład 2. Rozwiąż przykład 1, stosując metodę 2. Znajdź odległość między liniami
Prosty L 2 przechodzi przez ten punkt M 2 (X 2 , y 2 , z 2)=M 2 (8, 4, 1) i ma wektor kierunkowy
| Q 2 ={M 2 , P 2 , l 2 }={2, −4, 8} |
Wektory Q 1 i Q 2 są współliniowe. Dlatego prosto L 1 i L 2 są równoległe. Aby obliczyć odległość między liniami równoległymi, używamy iloczynu wektorów.
Skonstruujmy wektor =( X 2 −X 1 , y 2 −y 1 , z 2 −z 1 }={7, 2, 0}.
Obliczmy iloczyn wektorowy wektorów i Q 1. W tym celu tworzymy macierz 3×3, której pierwszy rząd to wektory bazowe ja, j, k, a pozostałe linie są wypełnione elementami wektorów i Q 1:
Zatem wynik iloczynu wektorów wektorów i Q 1 będzie wektorem:
Odpowiedź: Odległość między liniami L 1 i L 2 równa się D=7.25061.
2. Odległość pomiędzy przecinającymi się liniami w przestrzeni
Niech będzie dany kartezjański prostokątny układ współrzędnych Oksyz i niech w tym układzie współrzędnych zostaną podane linie proste L 1 i L 2 (równania (1) i (2)).
Niech prosto L 1 i L 2 nie są równoległe (proste równoległe omówiliśmy w poprzednim akapicie). Aby znaleźć odległość między liniami L 1 i L Trzeba zbudować 2 płaszczyzny równoległe α 1 i α 2 tak, aby było prosto L 1 leżałem w samolocie α 1 prosta L 2 - w samolocie α 2. Następnie odległość między liniami L 1 i L 2 jest równe odległości między płaszczyznami L 1 i L 2 (ryc. 3).
Gdzie N 1 ={A 1 , B 1 , C 1 ) − wektor normalny płaszczyzny α 1. Aby samolot α 1 przeszedł przez linię prostą L 1, wektor normalny N 1 musi być prostopadłe do wektora kierunku Q 1 prosto L 1, tj. iloczyn skalarny tych wektorów musi być równy zero:
Rozwiązywanie układu równań liniowych (27)−(29), z trzema równaniami i czterema niewiadomymi A 1 , B 1 , C 1 , D 1 i podstawiając do równania
Samoloty α 1 i α 2 są równoległe, stąd powstałe wektory normalne N 1 ={A 1 , B 1 , C 1) i N 2 ={A 2 , B 2 , C 2) te płaszczyzny są współliniowe. Jeżeli te wektory nie są równe, to możemy pomnożyć (31) przez pewną liczbę tak, aby powstały wektor normalny N 2 pokrywało się z wektorem normalnym równania (30).
Następnie odległość między równoległymi płaszczyznami oblicza się ze wzoru:
| (33) |
Rozwiązanie. Prosty L 1 przechodzi przez ten punkt M 1 (X 1 , y 1 , z 1)=M 1 (2, 1, 4) i ma wektor kierunkowy Q 1 ={M 1 , P 1 , l 1 }={1, 3, −2}.
Prosty L 2 przechodzi przez ten punkt M 2 (X 2 , y 2 , z 2)=M 2 (6, −1, 2) i ma wektor kierunkowy Q 2 ={M 2 , P 2 , l 2 }={2, −3, 7}.
Zbudujmy samolot α 1 przechodzący przez linię L 1, równolegle do linii prostej L 2 .
Od samolotu α 1 przechodzi przez linię L 1, to również przechodzi przez ten punkt M 1 (X 1 , y 1 , z 1)=M 1 (2, 1, 4) i wektor normalny N 1 ={M 1 , P 1 , l 1) samolot α 1 prostopadle do wektora kierunku Q 1 prosto L 1. Wtedy równanie płaszczyzny musi spełniać warunek:
Od samolotu α 1 musi być równoległa do linii L 2, wówczas musi być spełniony warunek:
Przedstawmy te równania w postaci macierzowej:
 | (40) |
Rozwiążmy układ równań liniowych (40) względem A 1 , B 1 , C 1 , D 1.
W artykule na przykładzie rozwiązania zadania C2 z Unified State Examination przeanalizowano metodę znajdowania metodą współrzędnych. Przypomnijmy, że linie proste są skośne, jeśli nie leżą w tej samej płaszczyźnie. W szczególności, jeśli jedna prosta leży na płaszczyźnie, a druga prosta przecina tę płaszczyznę w punkcie, który nie leży na pierwszej linii, to takie proste przecinają się (patrz rysunek).
Znaleźć odległości pomiędzy przecinającymi się liniami niezbędny:
- Narysuj płaszczyznę przechodzącą przez jedną z przecinających się linii, która jest równoległa do drugiej przecinającej się linii.
- Rzuć prostopadłą z dowolnego punktu drugiej linii na powstałą płaszczyznę. Długość tej prostopadłej będzie wymaganą odległością między liniami.
Przeanalizujmy ten algorytm bardziej szczegółowo na przykładzie rozwiązania problemu C2 z Unified State Examination z matematyki.
Odległość między liniami w przestrzeni
Zadanie. W sześcianie jednostkowym ABCDA 1 B 1 C 1 D 1 znajdź odległość między liniami licencjat 1 i D.B. 1 .

Ryż. 1. Rysunek do zadania
Rozwiązanie. Przez środek przekątnej sześcianu D.B. 1 (pkt O) narysuj linię równoległą do linii A 1 B. Punkty przecięcia tej linii z krawędziami PNE. I A 1 D 1 oznacza się odpowiednio N I M. Prosty MN leży w samolocie MNB 1 i równolegle do linii A 1 B, która nie leży w tej płaszczyźnie. Oznacza to, że linia prosta A 1 B równolegle do płaszczyzny MNB 1 w oparciu o równoległość prostej i płaszczyzny (ryc. 2).

Ryż. 2. Wymagana odległość pomiędzy przecinającymi się liniami jest równa odległości dowolnego punktu wybranej linii od przedstawianej płaszczyzny
Teraz szukamy odległości od jakiegoś punktu na linii A 1 B do samolotu MNB 1. Odległość ta z definicji będzie wymaganą odległością pomiędzy liniami przecinającymi się.
Aby znaleźć tę odległość, użyjemy metody współrzędnych. Wprowadźmy prostokątny kartezjański układ współrzędnych, tak aby jego początek pokrywał się z punktem B, osią X skierowany był wzdłuż krawędzi licencjat, oś Y- wzdłuż żebra PNE., oś Z- wzdłuż żebra nocleg ze śniadaniem 1 (ryc. 3).

Ryż. 3. Wybieramy prostokątny kartezjański układ współrzędnych, jak pokazano na rysunku
Znalezienie równania płaszczyzny MNB 1 w tym układzie współrzędnych. Aby to zrobić, najpierw określamy współrzędne punktów M, N I B 1: ![]() Otrzymane współrzędne podstawiamy do ogólnego równania prostej i otrzymujemy następujący układ równań:
Otrzymane współrzędne podstawiamy do ogólnego równania prostej i otrzymujemy następujący układ równań:

Z drugiego równania układu otrzymujemy z trzeciego, po czym z pierwszego otrzymujemy. Podstaw otrzymane wartości do ogólnego równania prostej:
Zauważmy, że w przeciwnym razie samolot MNB 1 przejdzie przez początek. Podziel obie strony tego równania przez i otrzymamy:
Odległość punktu od płaszczyzny określa się ze wzoru.
Geometria. Klasa 11
Temat lekcji: Odległość pomiędzy przecinającymi się liniami
Ter-Ovanesyan G.L., nauczyciel najwyższej kategorii, laureat Nagrody Fundacji Sorosa
Moskwa
Rozważmy problem znalezienia odległości pomiędzy przecinającymi się liniami. Odległość między przecinającymi się liniami to długość wspólnej prostopadłej do tych linii.
Dajmy sobie sześcian ABCDA 1 B 1 C 1 D 1, którego krawędź jest równa jednostce AB = 1. Musisz znaleźć odległość między liniami prostymi AB i DC 1: ρ(AB;DC 1) -?
Te dwie proste leżą w równoległych płaszczyznach: AB leży w płaszczyźnie AA 1 B 1 B, DC 1 leży w płaszczyźnie D 1 DC 1 C. Znajdźmy najpierw prostopadłą do tych dwóch płaszczyzn. Na rysunku jest wiele takich prostopadłych. To jest odcinek BC, B 1 C 1, A 1 D 1 i AD. Spośród nich sensowne jest wybranie odcinka, który jest nie tylko prostopadły do tych płaszczyzn, a zatem prostopadły do naszych prostych AB i DC 1, ale także przechodzi przez te proste. Takim segmentem jest AD. Jest jednocześnie prostopadła do prostej AB, ponieważ jest prostopadła do płaszczyzny AA 1 B 1 B i do prostej DC 1, ponieważ jest prostopadła do płaszczyzny D 1 DC 1 C. Oznacza to, że AD jest wspólnym prostopadle do przecinających się prostych AB i DC 1. Odległość między tymi prostymi to długość tej prostopadłej, czyli długość odcinka AD. Ale AD jest krawędzią sześcianu. Zatem odległość wynosi 1:
ρ(AB;DC 1)=AD=1
Rozważmy inny problem, nieco bardziej złożony, dotyczący wyznaczania odległości między przecinającymi się liniami.
Znowu otrzymamy sześcian, którego krawędź jest równa jeden. Musisz znaleźć odległość między przekątnymi przeciwległych ścian. Oznacza to, że biorąc pod uwagę sześcian ABCDA 1 B 1 C 1 D 1. Krawędź AB=1. Musisz znaleźć odległość między liniami prostymi BA 1 i DC 1: ρ(A 1 B; DC 1) -?
Te dwie linie przecinają się, co oznacza, że odległość jest długością wspólnej prostopadłej. Nie możesz narysować ogólnej prostopadłej, ale sformułuj ją w następujący sposób: jest to długość prostopadłej między równoległymi płaszczyznami, w których leżą te linie. Prosta BA 1 leży w płaszczyźnie АВВ 1 А 1 , a prosta DC 1 leży w płaszczyźnie D 1 DCC 1 . Są równoległe, co oznacza, że odległość między nimi jest odległością między tymi prostymi. A odległość między ścianami sześcianu to długość krawędzi. Na przykład długość żebra BC. Ponieważ BC jest prostopadła zarówno do płaszczyzny АВВ 1 А 1, jak i płaszczyzny DСС 1 D 1. Oznacza to, że odległość między prostymi podana w warunku jest równa odległości między płaszczyznami równoległymi i wynosi 1:
ρ(A 1 B; DC 1) = BC = 1
Rozważmy inny problem dotyczący wyznaczania odległości pomiędzy przecinającymi się liniami.
Otrzymamy regularny trójkątny pryzmat, w którym znane są wszystkie krawędzie. Musisz znaleźć odległość między krawędziami górnej i dolnej podstawy. Oznacza to, że mamy pryzmat ABCA 1 B 1 C 1. Ponadto AB=3=AA 1. Musisz znaleźć odległość między prostymi BC i A 1 C 1: ρ(BC;A 1 C 1) - ?
Ponieważ te linie przecinają się, odległość między nimi jest długością wspólnej prostopadłej lub długością prostopadłej do równoległych płaszczyzn, w których leżą. Znajdźmy te równoległe płaszczyzny.
Prosta BC leży w płaszczyźnie ABC, a prosta A 1 C 1 leży w płaszczyźnie A 1 B 1 C 1. Te dwie płaszczyzny są równoległe, ponieważ stanowią górną i dolną podstawę pryzmatu. Oznacza to, że odległość między naszymi prostymi jest odległością między tymi równoległymi płaszczyznami. A odległość między nimi jest dokładnie równa długości bocznej krawędzi AA 1, czyli równa 3:
ρ(BC;A 1 do 1)=AA 1 =3
W tym Szczególnym zadaniem możesz znaleźć nie tylko długość wspólnej prostopadłej, ale także ją skonstruować. Aby to zrobić, ze wszystkich krawędzi bocznych wybieramy tę, która ma wspólne punkty z linią prostą BC i A 1 C 1. Na naszym rysunku jest to krawędź CC 1. Będzie prostopadła do prostej A 1 C 1, ponieważ jest prostopadła do płaszczyzny górnej podstawy i do prostej BC, ponieważ jest prostopadła do płaszczyzny dolnej podstawy. W ten sposób możemy znaleźć nie tylko odległość, ale także skonstruować tę ogólną prostopadłą.
Dzisiaj na lekcji przypomnieliśmy sobie, jak znaleźć długość wspólnej prostopadłej między przecinającymi się prostymi.
Nie minęła nawet minuta, a utworzyłem nowy akt Verdova i kontynuowałem tak fascynujący temat. Musisz uchwycić chwile ducha pracy, tzw wprowadzenie liryczne nie będzie. Będzie prozaiczne klapsy =)
Dwie proste przestrzenie mogą:
1) krzyżować się;
2) przecinają się w punkcie ;
3) być równoległe;
4) mecz.
Sprawa nr 1 różni się zasadniczo od pozostałych spraw. Dwie linie proste przecinają się, jeśli nie leżą w tej samej płaszczyźnie. Podnieś jedno ramię do góry, a drugie wyciągnij do przodu – oto przykład przecinania się linii. W punktach nr 2-4 muszą leżeć linie proste w jednej płaszczyźnie.
Jak znaleźć względne położenie linii w przestrzeni?
Rozważmy dwie bezpośrednie przestrzenie:
- prosty, podane przez punkt oraz wektor kierunkowy;
– linia prosta wyznaczona przez punkt i wektor kierunkowy.
Dla lepszego zrozumienia zróbmy schematyczny rysunek: 
Na rysunku jako przykład przedstawiono przecinające się linie proste.
Jak sobie poradzić z tymi prostymi liniami?
Znając punkty, łatwo jest znaleźć wektor.
Jeśli prosto krzyżować, następnie wektory nie współpłaszczyznowe(patrz lekcja Liniowa (nie)zależność wektorów. Baza wektorów), a zatem wyznacznik złożony z ich współrzędnych jest niezerowy. Lub, co w rzeczywistości oznacza to samo, będzie niezerowe: ![]() .
.
W przypadkach nr 2-4 nasza struktura „wpada” w jedną płaszczyznę, natomiast wektory współpłaszczyznowy, a mieszany produkt jest liniowy wektory zależne równa się zeru: ![]() .
.
Rozwińmy algorytm dalej. Udawajmy, że ![]() Dlatego linie albo przecinają się, są równoległe, albo pokrywają się.
Dlatego linie albo przecinają się, są równoległe, albo pokrywają się.
Jeżeli wektory kierunkowe współliniowy, to linie są albo równoległe, albo pokrywające się. W przypadku ostatniego gwoździa proponuję następującą technikę: weź dowolny punkt na jednej linii i podstaw jego współrzędne do równania drugiej linii; jeśli współrzędne „pasują”, to linie się pokrywają; jeśli „nie pasują”, to linie są równoległe.
Algorytm jest prosty, ale praktyczne przykłady nadal nie zaszkodzi:
Przykład 11
Znajdź względne położenie dwóch linii
Rozwiązanie: jak w przypadku wielu problemów geometrycznych, wygodnie jest sformułować rozwiązanie punkt po punkcie:
1) Z równań wyciągamy punkty i wektory kierunkowe:

2) Znajdź wektor:

Zatem wektory są współpłaszczyznowe, co oznacza, że linie leżą w tej samej płaszczyźnie i mogą się przecinać, być równoległe lub pokrywać się.
4) Sprawdźmy kolinearność wektorów kierunkowych.
Stwórzmy układ z odpowiednich współrzędnych tych wektorów:
Z wszyscy z równań wynika, że zatem układ jest spójny, odpowiednie współrzędne wektorów są proporcjonalne, a wektory są współliniowe.
Wniosek: linie są równoległe lub pokrywają się.
5) Sprawdź, czy proste mają punkty wspólne. Weźmy punkt należący do pierwszej prostej i podstawmy jego współrzędne do równań prostej: 
Zatem, punkty wspólne linie proste tego nie robią i nie mają innego wyjścia, jak tylko być równoległe.
Odpowiedź:
Ciekawy przykład Dla niezależna decyzja:
Przykład 12
Znajdź względne położenie linii

To jest przykład, który możesz rozwiązać samodzielnie. Należy pamiętać, że druga linia zawiera literę jako parametr. Logiczny. W ogólnym przypadku są to dwie różne linie, więc każda linia ma swój własny parametr.
I jeszcze raz apeluję, aby nie pomijać przykładów, zadania, które proponuję, nie są przypadkowe ;-)
Problemy z linią w przestrzeni
W końcowej części lekcji postaram się to rozważyć maksymalna ilość różne zadania z liniami przestrzennymi. W tym przypadku zachowany zostanie pierwotny porządek historii: najpierw rozważymy problemy z przecinającymi się liniami, potem z przecinającymi się liniami, a na koniec porozmawiamy o liniach równoległych w przestrzeni. Muszę jednak powiedzieć, że niektóre zadania tej lekcji można sformułować dla kilku przypadków lokalizacji linii jednocześnie i pod tym względem podział sekcji na akapity jest nieco arbitralny. Jest ich więcej proste przykłady, jest ich więcej złożone przykłady i mam nadzieję, że każdy znajdzie to, czego potrzebuje.
Przekraczanie linii
Przypomnę, że linie proste przecinają się, jeśli nie ma płaszczyzny, w której obie leżą. Kiedy zastanawiałem się nad praktyką, przyszedł mi do głowy problem z potworem i teraz cieszę się, że mogę przedstawić wam smoka z czterema głowami:
Przykład 13
Biorąc pod uwagę linie proste. Wymagany:
a) udowodnić, że proste się przecinają;
b) znaleźć równania prostej przechodzącej przez punkt prostopadły do danych prostych;
c) ułożyć równania prostej zawierającej wspólna prostopadła przekraczanie linii;
d) znajdź odległość między liniami.
Rozwiązanie: Ten, kto idzie, opanuje drogę:
a) Udowodnijmy, że proste się przecinają. Znajdźmy punkty i wektory kierunkowe tych linii: 
Znajdźmy wektor:
Obliczmy mieszany produkt wektorów:
Zatem wektory nie współpłaszczyznowe, co oznacza, że linie się przecinają i właśnie to należało udowodnić.
Chyba każdy już dawno zauważył, że przy przekroczeniu linii algorytm weryfikacji jest najkrótszy.
b) Znajdź równania prostej przechodzącej przez punkt i prostopadłej do prostych. Zróbmy schematyczny rysunek: 
Dla odmiany zamieściłem direct ZA prosto, spójrz, jak jest trochę wymazany na skrzyżowaniach. Krzyżowanie? Tak, ogólnie rzecz biorąc, linia prosta „de” zostanie skrzyżowana z pierwotnymi liniami prostymi. Chociaż ten moment jeszcze nas to nie interesuje, wystarczy zbudować prostą prostopadłą i tyle.
Co wiadomo o bezpośrednim „de”? Punkt do niego należący jest znany. Nie ma wystarczającej liczby wektorów prowadzących.
Zgodnie z warunkiem linia prosta musi być prostopadła do prostych, co oznacza, że jej wektor kierunkowy będzie prostopadły do wektorów kierunkowych. Znane już z przykładu nr 9, znajdźmy iloczyn wektorowy:

Ułóżmy równania prostej „de” za pomocą punktu i wektora kierunkowego:
![]()
Gotowy. Zasadniczo możesz zmienić znaki w mianownikach i wpisać odpowiedź w formularzu ![]() , ale nie ma takiej potrzeby.
, ale nie ma takiej potrzeby.
Aby to sprawdzić, należy podstawić współrzędne punktu do otrzymanych równań prostych, a następnie użyć Iloczyn skalarny wektorów upewnij się, że wektor jest rzeczywiście ortogonalny do wektorów kierunkowych „pe jeden” i „pe dwa”.
Jak znaleźć równania prostej zawierającej wspólną prostopadłą?
c) To zadanie będzie trudniejsze. Manekinom radzę pominąć ten punkt, nie chcę studzić Waszej szczerej sympatii do geometrii analitycznej =) Swoją drogą, może dla bardziej przygotowanych czytelników też będzie lepiej się wstrzymać, faktem jest, że pod względem złożoności przykład powinien być umieszczony na końcu artykułu, ale zgodnie z logiką prezentacji powinien się on znaleźć tutaj.
Musisz więc znaleźć równania linii, która zawiera wspólną prostopadłą do linii skośnych.
- jest to odcinek łączący te proste i prostopadły do tych prostych: 
Oto nasz przystojniak: - wspólna prostopadła przecinających się linii. On jest jedyny. Nie ma drugiego takiego. Musimy utworzyć równania dla prostej zawierającej ten odcinek.
Co wiadomo o bezpośrednim „um”? Znany jest jego wektor kierunkowy, podany w poprzednim akapicie. Ale niestety nie znamy ani jednego punktu należącego do prostej „em”, ani nie znamy końców prostopadłych – punktów. W którym miejscu ta prostopadła linia przecina dwie pierwotne linie? W Afryce, na Antarktydzie? Ze wstępnego przeglądu i analizy stanu nie wynika wcale, jak rozwiązać problem... Istnieje jednak pewien skomplikowany trik związany z użyciem równań parametrycznych linii prostej.
Sformułujemy decyzję punkt po punkcie:
1) Przepiszmy równania pierwszej linii w postaci parametrycznej: 
Rozważmy tę kwestię. Nie znamy współrzędnych. ALE. Jeżeli punkt należy do danej prostej, to jego współrzędne odpowiadają , oznaczmy go przez . Następnie współrzędne punktu zostaną zapisane w postaci:
Życie staje się coraz lepsze, jedna niewiadoma to wciąż nie trzy niewiadome.
2) To samo oburzenie należy powtórzyć w drugim punkcie. Przepiszmy równania drugiej prostej w postaci parametrycznej: 
Jeżeli punkt należy do danej prostej, to z bardzo konkretnym znaczeniem jego współrzędne muszą spełniać równania parametryczne:
Lub: ![]()
3) Wektor, podobnie jak poprzednio znaleziony wektor, będzie wektorem kierującym linii prostej. Jak skonstruować wektor z dwóch punktów, omówiono w odwieczny czas na lekcji Wektory dla manekinów. Różnica polega na tym, że współrzędne wektorów są zapisywane z nieznanymi wartościami parametrów. Więc co? Nikt nie zabrania odejmowania odpowiednich współrzędnych początku wektora od współrzędnych końca wektora.
Istnieją dwa punkty: ![]() .
.
Znajdowanie wektora:
4) Ponieważ wektory kierunkowe są współliniowe, jeden wektor wyraża się liniowo przez drugi z pewnym współczynnikiem proporcjonalności „lambda”:
Lub współrzędna po współrzędnej: 
Okazało się, że jest to najzwyklejsze układ równań liniowych z trzema niewiadomymi, które są standardowo rozwiązywalne, na przykład Metoda Cramera. Ale jest szansa, żeby stąd uciec mało krwi, z trzeciego równania wyrażamy „lambda” i podstawiamy go do pierwszego i drugiego równania:

Zatem: ![]() i nie potrzebujemy „lambdy”. To, że wartości parametrów okazały się takie same, jest czystym przypadkiem.
i nie potrzebujemy „lambdy”. To, że wartości parametrów okazały się takie same, jest czystym przypadkiem.
5) Niebo całkowicie się przejaśnia, podmieńmy znalezione wartości ![]() do naszych punktów:
do naszych punktów:
Wektor kierunkowy nie jest szczególnie potrzebny, ponieważ znaleziono już jego odpowiednik.
Zawsze ciekawie jest sprawdzić po długiej podróży.
![]() :
:
Otrzymuje się prawidłowe równości.
Podstawmy współrzędne punktu do równań ![]() :
:
Otrzymuje się prawidłowe równości.
6) Końcowy akord: utwórzmy równania linii prostej za pomocą punktu (możesz go wziąć) i wektora kierunku:

Zasadniczo można wybrać „dobry” punkt z nienaruszonymi współrzędnymi, ale jest to kwestia kosmetyczna.
Jak znaleźć odległość między przecinającymi się liniami?
d) Odcięliśmy czwartą głowę smoka.
Metoda pierwsza. Nawet nie sposób, ale mały szczególny przypadek. Odległość pomiędzy przecinającymi się liniami jest równa długości ich wspólnej prostopadłej: ![]() .
.
Skrajne punkty wspólna prostopadła ![]() znalezione w poprzednim akapicie, a zadanie jest elementarne:
znalezione w poprzednim akapicie, a zadanie jest elementarne:
Metoda druga. W praktyce najczęściej końce wspólnej prostopadłej są nieznane, dlatego stosuje się inne podejście. Przez dwie przecinające się linie można poprowadzić płaszczyzny równoległe, a odległość między tymi płaszczyznami jest równa odległości między tymi liniami. W szczególności pomiędzy tymi płaszczyznami wystaje wspólna prostopadła.
W toku geometrii analitycznej z powyższych rozważań wyprowadza się wzór na znalezienie odległości pomiędzy przecinającymi się prostymi:  (zamiast naszych punktów „um jeden, dwa” możesz wziąć dowolne punkty linii).
(zamiast naszych punktów „um jeden, dwa” możesz wziąć dowolne punkty linii).
Mieszany iloczyn wektorów już znaleziony w punkcie „a”: ![]() .
.
Iloczyn wektorowy wektorów znaleziony w akapicie „być”: ![]() , obliczmy jego długość:
, obliczmy jego długość:
Zatem:
Z dumą eksponujmy trofea w jednym rzędzie:
Odpowiedź:
A) ![]() , co oznacza, że proste przecinają się, co należało udowodnić;
, co oznacza, że proste przecinają się, co należało udowodnić;
B) ![]() ;
;
V)  ;
;
G) ![]()
Co jeszcze możesz powiedzieć o przekraczaniu granic? Pomiędzy nimi istnieje określony kąt. Ale uniwersalna formuła Rozważymy kąt w następnym akapicie:
Przecinające się przestrzenie proste koniecznie leżą w tej samej płaszczyźnie: 
Pierwszą myślą jest pchnięcie z całych sił w punkt przecięcia. I od razu pomyślałam: po co odmawiać sobie właściwych pragnień?! Zajmijmy się nią teraz!
Jak znaleźć punkt przecięcia linii przestrzennych?
Przykład 14
Znajdź punkt przecięcia linii
Rozwiązanie: Przepiszmy równania prostych w postaci parametrycznej: 
To zadanie zostało szczegółowo omówione w przykładzie nr 7 tej lekcji (patrz. Równania prostej w przestrzeni). A tak przy okazji, same proste wziąłem z przykładu nr 12. Nie będę kłamać, jestem zbyt leniwy, żeby wymyślać nowe.
Rozwiązanie jest standardowe i spotykaliśmy się już, gdy próbowaliśmy znaleźć równania na wspólną prostopadłą przecinających się prostych.
Punkt przecięcia prostych należy do prostej, zatem jego współrzędne spełniają równania parametryczne tej prostej i odpowiadają bardzo specyficzną wartość parametru:
Ale ten sam punkt należy również do drugiej linii, zatem: 
Przyrównujemy odpowiednie równania i przeprowadzamy uproszczenia: 
Otrzymane system trzech równania liniowe z dwiema niewiadomymi. Jeżeli linie się przecinają (co udowodniono w przykładzie nr 12), to układ jest z konieczności spójny i ma unikalne rozwiązanie. Można to rozwiązać Metoda Gaussa, ale nie grzeszmy takim przedszkolnym fetyszyzmem, zróbmy to prościej: z pierwszego równania wyrażamy „te zero” i podstawiamy je do równania drugiego i trzeciego: 
Dwa ostatnie równania okazały się w zasadzie takie same i wynika z nich, że . Następnie:
Podstawiamy znalezioną wartość parametru do równań: 
Odpowiedź:
Aby to sprawdzić, podstawiamy znalezioną wartość parametru do równań: 
Uzyskano te same współrzędne, jakie były potrzebne do sprawdzenia. Skrupulatni czytelnicy mogą zastąpić współrzędne punktu oryginalnymi równaniami kanonicznymi prostych.
Nawiasem mówiąc, można było zrobić odwrotnie: znaleźć punkt przez „es zero” i sprawdzić go przez „te zero”.
Znany matematyczny przesąd głosi: tam, gdzie mówi się o przecięciu prostych, zawsze unosi się zapach prostopadłych.
Jak skonstruować linię przestrzeni prostopadłą do danej?
(linie przecinają się)
Przykład 15
a) Zapisz równania prostej przechodzącej przez punkt prostopadły do tej prostej ![]() (linie przecinają się).
(linie przecinają się).
b) Znajdź odległość punktu od prostej.
Notatka
: klauzula „linie przecinają się” – istotne. Przez punkt
możesz narysować nieskończoną liczbę linii prostopadłych, które przetną się z linią prostą „el”. Jedyne rozwiązanie występuje w przypadku, gdy przez ten punkt linia prosta jest rysowana prostopadle dwa dany linią prostą (patrz przykład nr 13, punkt „b”).
A) Rozwiązanie: Nieznaną linię oznaczamy przez . Zróbmy schematyczny rysunek:

Co wiadomo o linii prostej? Zgodnie z warunkiem przyznawany jest punkt. Aby ułożyć równania prostej, należy znaleźć wektor kierunkowy. Wektor jest całkiem odpowiedni jako taki wektor, więc sobie z nim poradzimy. Dokładniej, weźmy nieznany koniec wektora za kark.
1) Wyciągnijmy jego wektor kierunkowy z równań prostej „el” i przepiszmy same równania w postaci parametrycznej: 
Wielu domyślało się, że teraz po raz trzeci podczas lekcji mag wyciągnie białego łabędzia z kapelusza. Rozważmy punkt o nieznanych współrzędnych. Ponieważ punkt jest , jego współrzędne spełniają równania parametryczne prostej „el” i odpowiadają określonej wartości parametru:
Lub w jednej linii:
2) Zgodnie z warunkiem linie muszą być prostopadłe, dlatego ich wektory kierunkowe są ortogonalne. A jeśli wektory są ortogonalne, to ich produkt skalarny równa się zeru: ![]()
Co się stało? Najprostszy równanie liniowe z jedną niewiadomą: 
3) Znana jest wartość parametru, znajdźmy punkt:
I wektor kierunkowy:
.
4) Równania prostej ułożymy za pomocą punktu i wektora kierunkowego ![]() :
:

Mianowniki proporcji okazały się ułamkowe i dokładnie tak jest, gdy należy pozbyć się ułamków. Pomnożę je przez -2: 
Odpowiedź: ![]()
Notatka
: bardziej rygorystyczne zakończenie rozwiązania sformalizujemy w następujący sposób: ułóżmy równania prostej za pomocą punktu i wektora kierunku ![]() . Rzeczywiście, jeśli wektor jest wektorem prowadzącym linii prostej, to wektor współliniowy będzie oczywiście również wektorem prowadzącym tej prostej.
. Rzeczywiście, jeśli wektor jest wektorem prowadzącym linii prostej, to wektor współliniowy będzie oczywiście również wektorem prowadzącym tej prostej.
Weryfikacja składa się z dwóch etapów:
1) sprawdź wektory kierunkowe linii pod kątem ortogonalności;
2) podstawiamy współrzędne punktu do równań każdej prostej, powinny one „pasować” zarówno tam, jak i tam.
O typowe działania Było wiele powiedziane, więc sprawdziłem projekt.
Nawiasem mówiąc, zapomniałem o innym punkcie - skonstruować punkt „zyu” symetryczny do punktu „en” względem prostej „el”. Istnieje jednak dobry „płaski analog”, który można znaleźć w artykule Najprostsze zadania z linią prostą na płaszczyźnie. W tym przypadku jedyną różnicą będzie dodatkowa współrzędna „Z”.
Jak znaleźć odległość punktu od linii w przestrzeni?
B) Rozwiązanie: Znajdźmy odległość punktu od linii.
Metoda pierwsza. Ta odległość dokładnie równa długości prostopadłej: . Rozwiązanie jest oczywiste: jeśli znane są punkty ![]() , To:
, To:
Metoda druga. W praktycznych problemach podstawa prostopadłej jest często zapieczętowaną tajemnicą, dlatego bardziej racjonalne jest skorzystanie z gotowego wzoru.
Odległość punktu od prostej wyraża się wzorem:  , gdzie jest wektorem kierunkowym prostej „el” oraz – bezpłatny punkt należący do danej prostej.
, gdzie jest wektorem kierunkowym prostej „el” oraz – bezpłatny punkt należący do danej prostej.
1) Z równań linii ![]() wyciągamy wektor kierunkowy i najbardziej dostępny punkt.
wyciągamy wektor kierunkowy i najbardziej dostępny punkt.
2) Punkt jest znany z warunku, wyostrz wektor:
3) Znajdźmy produkt wektorowy i oblicz jego długość: 
4) Oblicz długość wektora prowadzącego:
5) Zatem odległość punktu od linii: