Zbadaj liniową zależność układu wektorów online. Zależność liniowa układu wektorów. Wektory współliniowe
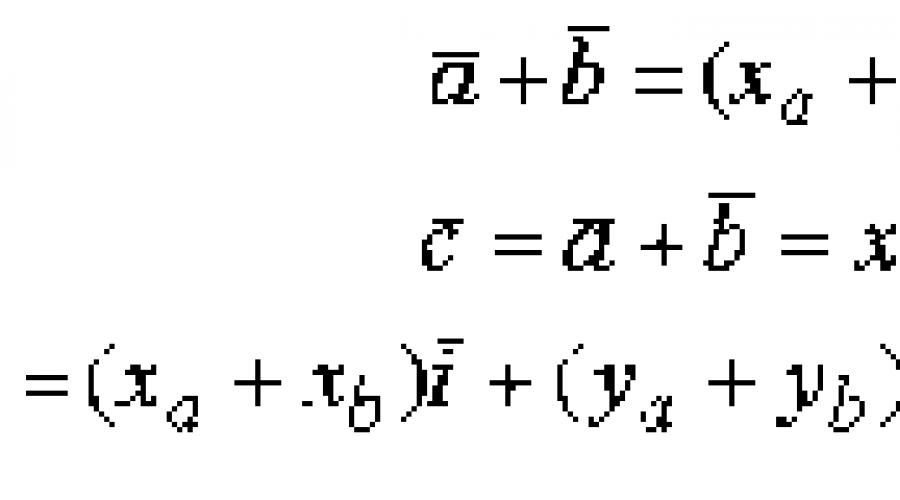
Przeczytaj także
Wektory, ich właściwości i działania z nimi
Wektory, działania z wektorami, liniowa przestrzeń wektorowa.
Wektory są uporządkowanym zbiorem skończonej liczby liczb rzeczywistych.
Działania: 1.Mnożenie wektora przez liczbę: lambda*wektor x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3,4, 0, 7)*3=(9, 12,0,21)
2. Dodawanie wektorów (należących do tej samej przestrzeni wektorowej) wektor x + wektor y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)
3. Wektor 0=(0,0…0)---n E n – n-wymiarowy (przestrzeń liniowa) wektor x + wektor 0 = wektor x
Twierdzenie. Aby układ n wektorów, n-wymiarowa przestrzeń liniowa, był liniowo zależny, konieczne i wystarczające jest, aby jeden z wektorów był liniową kombinacją pozostałych.
Twierdzenie. Dowolny zbiór n+ pierwszych wektorów n-wymiarowej przestrzeni liniowej zjawisk. liniowo zależne.
Dodawanie wektorów, mnożenie wektorów przez liczby. Odejmowanie wektorów.
Suma dwóch wektorów jest wektorem skierowanym od początku wektora do końca wektora, pod warunkiem, że początek pokrywa się z końcem wektora. Jeżeli wektory są dane przez ich rozwinięcia w wektorach jednostek bazowych, to przy dodawaniu wektorów dodawane są odpowiadające im współrzędne.
Rozważmy to na przykładzie kartezjańskiego układu współrzędnych. Pozwalać
Pokażmy to

Z rysunku 3 jasno wynika, że ![]()

Sumę dowolnej skończonej liczby wektorów można obliczyć korzystając z reguły wielokąta (ryc. 4): aby skonstruować sumę skończonej liczby wektorów, wystarczy połączyć początek każdego kolejnego wektora z końcem poprzedniego i skonstruuj wektor łączący początek pierwszego wektora z końcem ostatniego.

Właściwości operacji dodawania wektorów:
W tych wyrażeniach m, n są liczbami.
Różnica między wektorami nazywana jest wektorem. Drugi człon jest wektorem przeciwnym do kierunku wektora, ale o równej długości.

Zatem operację odejmowania wektorów zastępuje się operacją dodawania
Wektor, którego początek znajduje się w początku, a kończy w punkcie A (x1, y1, z1) nazywany jest wektorem promienia punktu A i jest po prostu oznaczany. Ponieważ jego współrzędne pokrywają się ze współrzędnymi punktu A, jego rozwinięcie w wektory jednostkowe ma postać

Wektor rozpoczynający się w punkcie A(x1, y1, z1) i kończący się w punkcie B(x2, y2, z2) można zapisać jako ![]()
gdzie r 2 jest wektorem promienia punktu B; r 1 - wektor promienia punktu A.
Dlatego rozwinięcie wektora w wektorach jednostkowych ma postać
Jego długość jest równa odległości między punktami A i B
MNOŻENIE
Tak w tym przypadku problem z samolotem iloczyn wektora przez a = (ax; ay) przez liczbę b można znaleźć za pomocą wzoru
a b = (ax b; ay b)
Przykład 1. Znajdź iloczyn wektora a = (1; 2) przez 3.
3 za = (3 1; 3 2) = (3; 6)
Zatem w przypadku problemu przestrzennego iloczyn wektora a = (ax; ay; az) przez liczbę b można znaleźć według wzoru
a b = (ax b; ay b; az b)
Przykład 1. Znajdź iloczyn wektora a = (1; 2; -5) przez 2.
2 za = (2 1; 2 2; 2 (-5)) = (2; 4; -10)
Iloczyn skalarny wektorów i ![]() gdzie jest kątem między wektorami i ; jeśli jedno, to
gdzie jest kątem między wektorami i ; jeśli jedno, to
Z definicji iloczynu skalarnego wynika, że ![]()
gdzie, na przykład, jest wielkością rzutu wektora na kierunek wektora.
Skalarny kwadrat wektora:
Właściwości iloczynu skalarnego:
![]()
![]()
![]()
![]()
Iloczyn skalarny we współrzędnych
Jeśli ![]()
![]() To
To ![]()
Kąt między wektorami
Kąt między wektorami - kąt między kierunkami tych wektorów (najmniejszy kąt).
Iloczyn krzyżowy (Iloczyn krzyżowy dwóch wektorów.) - jest to pseudowektor prostopadły do płaszczyzny zbudowanej z dwóch czynników, będący wynikiem operacji binarnej „mnożenia wektorów” po wektorach w trójwymiarowej przestrzeni euklidesowej. Iloczyn nie jest ani przemienny, ani łączny (jest antyprzemienny) i różni się od iloczynu skalarnego wektorów. W wielu zadaniach inżynierskich i fizycznych trzeba umieć skonstruować wektor prostopadły do dwóch istniejących - iloczyn wektorowy zapewnia taką możliwość. Iloczyn krzyżowy jest przydatny do „pomiaru” prostopadłości wektorów - długość iloczynu krzyżowego dwóch wektorów jest równa iloczynowi ich długości, jeśli są one prostopadłe i maleje do zera, jeśli wektory są równoległe lub antyrównoległe.
Iloczyn krzyżowy definiuje się tylko w przestrzeniach trójwymiarowych i siedmiwymiarowych. Wynik iloczynu wektorowego, podobnie jak iloczynu skalarnego, zależy od metryki przestrzeni euklidesowej.
W przeciwieństwie do wzoru na obliczanie wektorów iloczynu skalarnego ze współrzędnych w trójwymiarowym prostokątnym układzie współrzędnych, wzór na iloczyn poprzeczny zależy od orientacji prostokątnego układu współrzędnych, czyli innymi słowy od jego „chiralności”
Kolinearność wektorów.
Dwa niezerowe (nierówne 0) wektory nazywane są współliniowymi, jeśli leżą na prostych równoległych lub na tej samej prostej. Dopuszczalnym, ale nie zalecanym synonimem są wektory „równoległe”. Wektory współliniowe mogą być skierowane identycznie („współkierunkowo”) lub przeciwnie (w tym drugim przypadku są czasami nazywane „antywspółliniowymi” lub „antyrównoległymi”).
Mieszany iloczyn wektorów ( a, b, c)- iloczyn skalarny wektora a oraz iloczyn wektorowy wektorów b i c:
(a,b,c)=a ⋅(b ×c)
czasami nazywa się to iloczynem potrójnej kropki wektorów, najwyraźniej dlatego, że wynikiem jest skalar (a dokładniej pseudoskalar).
Znaczenie geometryczne: Moduł zmieszanego produktu jest liczbowo równy objętości równoległościanu utworzonego przez wektory (ABC) .
Nieruchomości
Mieszany kawałek skośno-symetryczny w odniesieniu do wszystkich swoich argumentów: tj. e. przestawienie dowolnych dwóch czynników zmienia znak iloczynu. Wynika z tego, że iloczyn mieszany w prawym kartezjańskim układzie współrzędnych (w bazie ortonormalnej) jest równy wyznacznikowi macierzy złożonej z wektorów i:
Iloczyn mieszany w lewym kartezjańskim układzie współrzędnych (w bazie ortonormalnej) jest równy wyznacznikowi macierzy złożonej z wektorów i wzięty ze znakiem minus:
W szczególności,
Jeśli dowolne dwa wektory są równoległe, to z dowolnym trzecim wektorem tworzą iloczyn mieszany równy zero.
Jeśli trzy wektory są liniowo zależne (to znaczy współpłaszczyznowe, leżące w tej samej płaszczyźnie), to ich iloczyn mieszany jest równy zero.
Zmysł geometryczny - Produkt mieszany wg całkowita wartość równa objętości równoległościanu (patrz rysunek) utworzonej przez wektory i; znak zależy od tego, czy ta trójka wektorów jest prawoskrętna, czy lewoskrętna.
Współpłaszczyznowość wektorów.
Trzy wektory (lub więcej) nazywane są współpłaszczyznowymi, jeśli po sprowadzeniu ich do wspólnego początku leżą w tej samej płaszczyźnie
Własności współpłaszczyznowości
Jeśli chociaż jeden z trzy wektory- zero, wówczas trzy wektory są również uważane za współpłaszczyznowe.
Trójka wektorów zawierających parę współliniowych wektorów jest współpłaszczyznowa.
Iloczyn mieszany wektorów współpłaszczyznowych. Jest to kryterium współpłaszczyznowości trzech wektorów.
Wektory współpłaszczyznowe są liniowo zależne. Jest to również kryterium współpłaszczyznowości.
W przestrzeni trójwymiarowej podstawą są 3 niewspółpłaszczyznowe wektory
Wektory liniowo zależne i liniowo niezależne.
Liniowo zależne i niezależne układy wektorowe.Definicja. Nazywa się system wektorowy liniowo zależne, jeśli istnieje co najmniej jedna nietrywialna kombinacja liniowa tych wektorów równa wektorowi zerowemu. W przeciwnym razie, tj. jeśli tylko trywialna kombinacja liniowa danych wektorów jest równa wektorowi zerowemu, wektory są wywoływane liniowo niezależny.
Twierdzenie (kryterium zależności liniowej). Aby układ wektorów w przestrzeni liniowej był liniowo zależny, konieczne i wystarczające jest, aby przynajmniej jeden z tych wektorów był liniową kombinacją pozostałych.
1) Jeżeli wśród wektorów znajduje się co najmniej jeden wektor zerowy, to cały układ wektorów jest liniowo zależny.
Faktycznie, jeśli np. , to zakładając , mamy nietrywialną kombinację liniową .▲
2) Jeżeli wśród wektorów niektóre tworzą układ liniowo zależny, to cały układ jest liniowo zależny.
Rzeczywiście, niech wektory , , będą liniowo zależne. Oznacza to, że istnieje nietrywialna kombinacja liniowa równa wektorowi zerowemu. Ale wtedy, zakładając ![]() , otrzymujemy także nietrywialną kombinację liniową równą wektorowi zerowemu.
, otrzymujemy także nietrywialną kombinację liniową równą wektorowi zerowemu.
2. Podstawa i wymiar. Definicja. Układ wektorów liniowo niezależnych ![]() nazywa się przestrzeń wektorową podstawa tej przestrzeni, jeśli dowolny wektor z można przedstawić jako kombinację liniową wektorów tego układu, tj. dla każdego wektora istnieją liczby rzeczywiste
nazywa się przestrzeń wektorową podstawa tej przestrzeni, jeśli dowolny wektor z można przedstawić jako kombinację liniową wektorów tego układu, tj. dla każdego wektora istnieją liczby rzeczywiste ![]() tak, że zachodzi równość. Ta równość nazywa się rozkład wektorowy według podstawy i liczb
tak, że zachodzi równość. Ta równość nazywa się rozkład wektorowy według podstawy i liczb ![]() są nazywane współrzędne wektora względem podstawy(Lub w podstawie) .
są nazywane współrzędne wektora względem podstawy(Lub w podstawie) .
Twierdzenie (o jednoznaczności rozwinięcia względem bazy). Każdy wektor w przestrzeni można rozwinąć w bazę w jedyny sposób, tj. współrzędne każdego wektora w bazie są określone jednoznacznie.
Zadanie 1. Sprawdź, czy układ wektorów jest liniowo niezależny. Układ wektorów będzie określony przez macierz układu, której kolumny składają się ze współrzędnych wektorów.
 .
.
Rozwiązanie. Niech kombinacja liniowa  równy zeru. Po zapisaniu tej równości we współrzędnych otrzymujemy następujący układ równań:
równy zeru. Po zapisaniu tej równości we współrzędnych otrzymujemy następujący układ równań:
 .
.
Taki układ równań nazywa się trójkątnym. Ona ma tylko jedno rozwiązanie  . Dlatego wektory
. Dlatego wektory  liniowo niezależny.
liniowo niezależny.
Zadanie 2. Dowiedz się, czy jest to liniowe niezależny system wektory.
 .
.
Rozwiązanie. Wektory  są liniowo niezależne (patrz Problem 1). Udowodnijmy, że wektor jest liniową kombinacją wektorów
są liniowo niezależne (patrz Problem 1). Udowodnijmy, że wektor jest liniową kombinacją wektorów  . Współczynniki rozszerzalności wektora
. Współczynniki rozszerzalności wektora  wyznaczane są z układu równań
wyznaczane są z układu równań
 .
.
System ten, podobnie jak trójkątny, posiada unikalne rozwiązanie.
Dlatego układ wektorów  liniowo zależne.
liniowo zależne.
Komentarz. Nazywa się macierze tego samego typu co w Zadaniu 1 trójkątny , a w zadaniu 2 – schodkowy trójkątny . Zagadnienie liniowej zależności układu wektorów można łatwo rozwiązać, jeśli macierz złożona ze współrzędnych tych wektorów jest trójkątna. Jeśli matryca nie ma specjalny typ, a następnie za pomocą konwersje ciągów elementarnych , zachowując liniowe zależności między kolumnami, można je sprowadzić do postaci trójkąta schodkowego.
Transformacje elementarne linie macierze (EPS) nazywane są następującymi operacjami na macierzy:
1) przegrupowanie linii;
2) pomnożenie ciągu przez liczbę niezerową;
3) dodanie kolejnego ciągu do ciągu pomnożonego przez dowolną liczbę.
Zadanie 3. Znajdź maksymalny liniowo niezależny podsystem i oblicz rząd układu wektorów
 .
.
Rozwiązanie. Zredukujmy macierz układu za pomocą EPS do postaci trójkąta schodkowego. Aby wyjaśnić procedurę, oznaczamy linię z numerem macierzy, która ma zostać przekształcona przez symbol . Kolumna za strzałką wskazuje działania na wierszach konwertowanej macierzy, które należy wykonać, aby otrzymać wiersze nowej macierzy.

 .
.
Oczywiście dwie pierwsze kolumny wynikowej macierzy są liniowo niezależne, trzecia kolumna jest ich liniową kombinacją, a czwarta nie zależy od pierwszych dwóch. Wektory  nazywane są podstawowymi. Tworzą maksymalnie liniowo niezależny podsystem systemu
nazywane są podstawowymi. Tworzą maksymalnie liniowo niezależny podsystem systemu  , a ranga systemu wynosi trzy.
, a ranga systemu wynosi trzy.
Podstawa, współrzędne
Zadanie 4. Znajdź bazę i współrzędne wektorów z tej bazy na zbiorze wektorów geometrycznych, których współrzędne spełniają warunek  .
.
Rozwiązanie. Zbiór jest płaszczyzną przechodzącą przez początek układu współrzędnych. Dowolna baza na płaszczyźnie składa się z dwóch niewspółliniowych wektorów. Współrzędne wektorów w wybranej bazie są określone przez rozwiązanie odpowiedniego układu równania liniowe.
Istnieje inny sposób rozwiązania tego problemu, polegający na znalezieniu podstawy za pomocą współrzędnych.
Współrzędne  przestrzenie nie są współrzędnymi na płaszczyźnie, ponieważ są ze sobą powiązane relacją
przestrzenie nie są współrzędnymi na płaszczyźnie, ponieważ są ze sobą powiązane relacją  , to znaczy, że nie są niezależne. Zmienne niezależne i (nazywane są wolnymi) jednoznacznie definiują wektor na płaszczyźnie i dlatego można je wybrać jako współrzędne w . Potem podstawa
, to znaczy, że nie są niezależne. Zmienne niezależne i (nazywane są wolnymi) jednoznacznie definiują wektor na płaszczyźnie i dlatego można je wybrać jako współrzędne w . Potem podstawa  składa się z wektorów leżących w zbiorach wolnych zmiennych i odpowiadających im
składa się z wektorów leżących w zbiorach wolnych zmiennych i odpowiadających im  I
I  , to jest .
, to jest .
Zadanie 5. Znajdź bazę i współrzędne wektorów na tej podstawie na zbiorze wszystkich wektorów w przestrzeni, których współrzędne nieparzyste są sobie równe.
Rozwiązanie. Wybierzmy, podobnie jak w poprzednim zadaniu, współrzędne w przestrzeni.
Ponieważ  , a następnie wolne zmienne
, a następnie wolne zmienne  jednoznacznie określają wektor z i dlatego są współrzędnymi. Odpowiednia baza składa się z wektorów.
jednoznacznie określają wektor z i dlatego są współrzędnymi. Odpowiednia baza składa się z wektorów.
Zadanie 6. Znajdź bazę i współrzędne wektorów na tej podstawie na zbiorze wszystkich macierzy postaci  , Gdzie
, Gdzie  – liczby dowolne.
– liczby dowolne.
Rozwiązanie. Każda macierz jest jednoznacznie reprezentowana w postaci:
Relacja ta jest rozwinięciem wektora względem podstawy  ze współrzędnymi
ze współrzędnymi  .
.
Zadanie 7. Znajdź wymiar i podstawę liniowego kadłuba układu wektorów
 .
.
Rozwiązanie. Korzystając z EPS, przekształcamy macierz ze współrzędnych wektorów układu do postaci trójkąta schodkowego.


 .
.
Kolumny  ostatnie macierze są liniowo niezależne, a kolumny
ostatnie macierze są liniowo niezależne, a kolumny  wyrażane poprzez nie liniowo. Dlatego wektory
wyrażane poprzez nie liniowo. Dlatego wektory  stanowić podstawę
stanowić podstawę  , I
, I  .
.
Komentarz. Podstawa w  jest wybrany niejednoznacznie. Na przykład wektory
jest wybrany niejednoznacznie. Na przykład wektory  stanowią również podstawę
stanowią również podstawę  .
.
A 1 = { 3, 5, 1 , 4 }, A 2 = { –2, 1, -5 , -7 }, A 3 = { -1, –2, 0, –1 }.
Rozwiązanie. Szuka wspólna decyzja układy równań
A 1 X 1 + A 2 X 2 + A 3 X 3 = Θ
Metoda Gaussa. Aby to zrobić, zapisujemy ten jednorodny układ we współrzędnych:
Matryca systemu
Dozwolony system ma postać: ![]() (r A = 2, N= 3). System jest kooperatywny i niepewny. Jego rozwiązanie ogólne ( X 2 – zmienna wolna): X 3 = 13X 2 ; 3X 1 – 2X 2 – 13X 2 = 0 => X 1 = 5X 2 => X o = . Na przykład obecność niezerowego rozwiązania konkretnego wskazuje, że wektory A
1 , A
2 , A
3
liniowo zależne.
(r A = 2, N= 3). System jest kooperatywny i niepewny. Jego rozwiązanie ogólne ( X 2 – zmienna wolna): X 3 = 13X 2 ; 3X 1 – 2X 2 – 13X 2 = 0 => X 1 = 5X 2 => X o = . Na przykład obecność niezerowego rozwiązania konkretnego wskazuje, że wektory A
1 , A
2 , A
3
liniowo zależne.
Przykład 2.
Dowiedz się czy ten system wektory liniowo zależne lub liniowo niezależne:
1. A 1 = { -20, -15, - 4 }, A 2 = { –7, -2, -4 }, A 3 = { 3, –1, –2 }.
Rozwiązanie. Rozważmy jednorodny układ równań A 1 X 1 + A 2 X 2 + A 3 X 3 = Θ
lub w formie rozwiniętej (według współrzędnych)

System jest jednorodny. Jeśli nie jest zdegenerowany, to ma unikalne rozwiązanie. W przypadku układu jednorodnego istnieje rozwiązanie zerowe (trywialne). Oznacza to, że w tym przypadku układ wektorów jest niezależny. Jeśli układ jest zdegenerowany, to ma rozwiązania niezerowe i dlatego jest zależny.
Sprawdzamy system pod kątem degeneracji:
 = –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
Układ jest niezdegenerowany, a co za tym idzie i wektory A 1 , A 2 , A 3 liniowo niezależny.
Zadania. Dowiedz się, czy dany układ wektorów jest liniowo zależny czy liniowo niezależny:
1. A 1 = { -4, 2, 8 }, A 2 = { 14, -7, -28 }.
2. A 1 = { 2, -1, 3, 5 }, A 2 = { 6, -3, 3, 15 }.
3. A 1 = { -7, 5, 19 }, A 2 = { -5, 7 , -7 }, A 3 = { -8, 7, 14 }.
4. A 1 = { 1, 2, -2 }, A 2 = { 0, -1, 4 }, A 3 = { 2, -3, 3 }.
5. A 1 = { 1, 8 , -1 }, A 2 = { -2, 3, 3 }, A 3 = { 4, -11, 9 }.
6. A 1 = { 1, 2 , 3 }, A 2 = { 2, -1 , 1 }, A 3 = { 1, 3, 4 }.
7. A 1 = {0, 1, 1 , 0}, A 2 = {1, 1 , 3, 1}, A 3 = {1, 3, 5, 1}, A 4 = {0, 1, 1, -2}.
8. A 1 = {-1, 7, 1 , -2}, A 2 = {2, 3 , 2, 1}, A 3 = {4, 4, 4, -3}, A 4 = {1, 6, -11, 1}.
9. Udowodnij, że układ wektorów będzie liniowo zależny, jeżeli zawiera:
a) dwa równe wektory;
b) dwa wektory proporcjonalne.
Definicja. Liniowa kombinacja wektorów a 1 , ..., an o współczynnikach x 1 , ..., x n nazywa się wektorem
x 1 za 1 + ... + x n za n .
trywialny, jeśli wszystkie współczynniki x 1 , ..., x n są równe zero.
Definicja. Nazywa się kombinację liniową x 1 a 1 + ... + x n a n nietrywialne, jeśli przynajmniej jeden ze współczynników x 1, ..., x n nie jest równy zero.
liniowo niezależny, jeśli nie ma nietrywialnej kombinacji tych wektorów równej wektorowi zerowemu.
Oznacza to, że wektory a 1, ..., a n są liniowo niezależne, jeśli x 1 a 1 + ... + x n a n = 0 wtedy i tylko wtedy, gdy x 1 = 0, ..., x n = 0.
Definicja. Nazywa się wektory a 1, ..., an liniowo zależne, jeśli istnieje nietrywialna kombinacja tych wektorów równa wektorowi zerowemu.
Własności wektorów liniowo zależnych:
Dla wektorów n-wymiarowych.
wektory n + 1 są zawsze liniowo zależne.
Dla wektorów 2 i 3 wymiarowych.
Dwa liniowe wektory zależne- współliniowy. (Wektory współliniowe są liniowo zależne.)
Dla wektorów trójwymiarowych.
Trzy liniowo zależne wektory są współpłaszczyznowe. (Trzy współpłaszczyznowe wektory są liniowo zależne.)
Przykładowe problemy liniowej zależności i liniowej niezależności wektorów:
Przykład 1. Sprawdź, czy wektory a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) są liniowo niezależne .
Rozwiązanie:
Wektory będą liniowo zależne, ponieważ wymiar wektorów jest mniejszy niż liczba wektorów.
Przykład 2. Sprawdź, czy wektory a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) są liniowo niezależne.
Rozwiązanie:
| x 1 + x 2 = 0 | |
| x 1 + 2 x 2 - x 3 = 0 | |
| x 1 + x 3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
odejmij drugą od pierwszej linii; dodaj drugą linię do trzeciej linii:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
Rozwiązanie to pokazuje, że układ ma wiele rozwiązań, czyli istnieje niezerowa kombinacja wartości liczb x 1, x 2, x 3 taka, że kombinacja liniowa wektorów a, b, c jest równa wektor zerowy, na przykład:
A + b + do = 0
co oznacza, że wektory a, b, c są liniowo zależne.
Odpowiedź: wektory a, b, c są liniowo zależne.
Przykład 3. Sprawdź, czy wektory a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) są liniowo niezależne.
Rozwiązanie: Znajdźmy wartości współczynników, przy których kombinacja liniowa tych wektorów będzie równa wektorowi zerowemu.
x 1 za + x 2 b + x 3 do 1 = 0To równanie wektorowe można zapisać jako układ równań liniowych
| x 1 + x 2 = 0 | |
| x 1 + 2 x 2 - x 3 = 0 | |
| x 1 + 2 x 3 = 0 |
Rozwiążmy ten układ metodą Gaussa
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
odejmij pierwszą od drugiej linii; odejmij pierwszą od trzeciej linii:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
odejmij drugą od pierwszej linii; dodaj drugą do trzeciej linii.