U mnogim slučajevima zadatak dobivanja (izračunavanja) spektra signala izgleda ovako. Postoji ADC koji, sa frekvencijom uzorkovanja Fd, pretvara kontinuirani signal koji stiže na njegov ulaz tokom vremena T u digitalne uzorke - N komada. Zatim se niz uzoraka unosi u određeni program koji proizvodi N/2 nekih numeričkih vrijednosti (programer koji ukrao sa interneta napisao program, uvjerava da radi Fourierovu transformaciju).

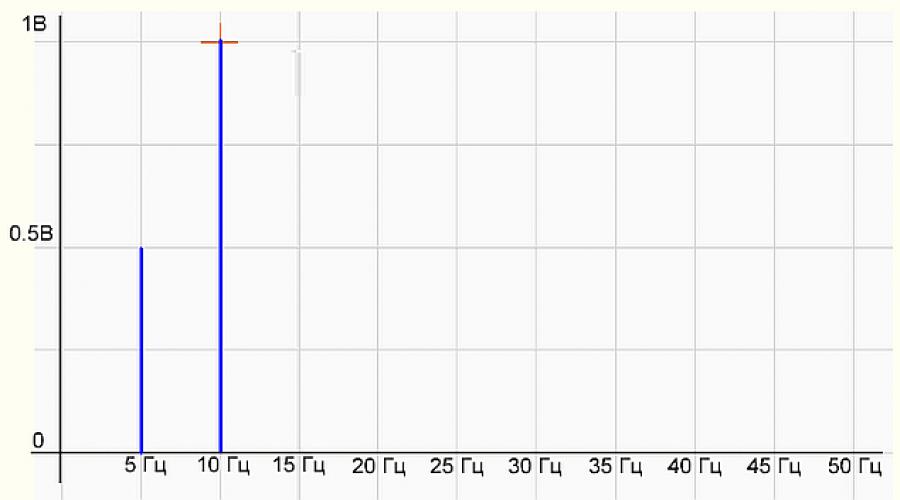
Da bismo provjerili da li program radi ispravno, formirat ćemo niz uzoraka kao zbir dvije sinusoide sin(10*2*pi*x)+0,5*sin(5*2*pi*x) i ubaciti ga u program . Program je nacrtao sljedeće:

Slika 1 Grafikon funkcije vremena signala

Slika 2. Grafikon spektra signala

Na grafu spektra nalaze se dva štapa (harmonika) 5 Hz sa amplitudom od 0,5 V i 10 Hz sa amplitudom od 1 V, sve je isto kao u formuli originalnog signala. Sve je u redu, bravo programer! Program radi ispravno.

To znači da ako na ulaz ADC primijenimo pravi signal iz mješavine dvije sinusoide, dobićemo sličan spektar koji se sastoji od dva harmonika.

Ukupno, naš pravi izmereni signal u trajanju od 5 sekundi, digitaliziran ADC-om, odnosno predstavljen diskretno broji, ima diskretni neperiodični domet.

Sa matematičke tačke gledišta, koliko grešaka ima u ovoj frazi?

Sada su nadležni odlučili, odlučili smo da je 5 sekundi predugo, hajde da izmjerimo signal za 0,5 sekundi.



Slika 3 Grafikon funkcije sin(10*2*pi*x)+0,5*sin(5*2*pi*x) za period mjerenja od 0,5 sek.

Slika 4 Spektar funkcija

Nešto ne izgleda u redu! Harmonik od 10 Hz se iscrtava normalno, ali umjesto štapića od 5 Hz pojavljuje se nekoliko čudnih harmonika. Gledamo na internetu da vidimo šta se dešava...

Pa, kažu da morate dodati nule na kraj uzorka i spektar će biti iscrtan normalno.

Sl.5 Dodane nule do 5 sekundi

Slika 6 Primljeni spektar

Još uvijek nije isto kao što je bilo na 5 sekundi. Moraćemo da se pozabavimo teorijom. Idemo na Wikipedia- izvor znanja.

2. Kontinuirana funkcija i njen Fourierov red prikaz

Matematički, naš signal u trajanju od T sekundi je neka funkcija f(x) definirana na segmentu (0, T) (X u u ovom slučaju- vrijeme). Takva funkcija se uvijek može predstaviti kao zbir harmonijskih funkcija (sinus ili kosinus) oblika:

(1), gdje:

K - broj trigonometrijske funkcije (broj harmonijske komponente, harmonijski broj)
T - segment u kojem je funkcija definirana (trajanje signala)
Ak je amplituda k-te harmonijske komponente,
θk- početna faza k-te harmonijske komponente

Šta znači “predstaviti funkciju kao zbir niza”? To znači da dodavanjem vrijednosti harmonijskih komponenti Fourierovog reda u svakoj tački, dobijamo vrijednost naše funkcije u ovoj tački.

(Strogije rečeno, srednja kvadratna devijacija niza od funkcije f(x) težit će nuli, ali uprkos konvergenciji srednjeg kvadrata, Fourierov red funkcije, općenito govoreći, nije potreban da konvergiraju u tačkama na njega. Vidi https://ru.wikipedia.org/wiki/Fourier_Series.)

Ova serija se takođe može napisati kao:

(2),
gdje, k-ti kompleks amplituda.

Odnos između koeficijenata (1) i (3) izražava se sljedećim formulama:

Imajte na umu da su sva ova tri prikaza Fourierovog reda potpuno ekvivalentna. Ponekad je pri radu s Fourierovim redovima prikladnije koristiti eksponente imaginarnog argumenta umjesto sinusa i kosinusa, odnosno koristiti Fourierovu transformaciju u složenom obliku. Ali nam je zgodno koristiti formulu (1), gdje je Fourierov niz predstavljen kao zbir kosinusa sa odgovarajućim amplitudama i fazama. U svakom slučaju, pogrešno je reći da će Fourierova transformacija realnog signala rezultirati složenim harmonijskim amplitudama. Kao što Wiki ispravno kaže, “Furierova transformacija (ℱ) je operacija koja povezuje jednu funkciju realne varijable s drugom funkcijom, također realnom varijablom.”

Ukupno:
Matematička osnova za spektralnu analizu signala je Fourierova transformacija.

Fourierova transformacija vam omogućava da predstavite kontinuiranu funkciju f(x) (signal) definiranu na segmentu (0, T) kao zbir beskonačnog broja (beskonačni niz) trigonometrijske funkcije(sinus i/ili kosinus) sa određenim amplitudama i fazama, takođe uzeti u obzir na segmentu (0, T). Takav niz se naziva Fourierov red.

Napomenimo još neke tačke čije je razumijevanje potrebno ispravnu primjenu Fourierove transformacije za analizu signala. Ako uzmemo u obzir Fourierov niz (zbir sinusoida) na cijeloj X-osi, možemo vidjeti da će izvan segmenta (0, T) funkcija predstavljena Fourierovim redom povremeno ponavljati našu funkciju.

Na primjer, na grafu na slici 7, originalna funkcija je definirana na segmentu (-T\2, +T\2), a Fourierov red predstavlja periodičnu funkciju definiranu na cijeloj x-osi.

To se događa zato što su same sinusoide periodične funkcije, pa će prema tome njihov zbir biti periodična funkcija.

Slika 7. Predstavljanje neperiodične originalne funkcije Fourierovim redom

ovako:

Naša izvorna funkcija je kontinuirana, neperiodična, definirana na određenom segmentu dužine T.
Spektar ove funkcije je diskretan, odnosno predstavljen je u obliku beskonačnog niza harmonijskih komponenti - Fourierovog reda.
U stvari, Fourierov niz definira neke periodična funkcija, koji se poklapa sa našim na segmentu (0, T), ali za nas ova periodičnost nije značajna.

Periodi harmonijskih komponenti su višekratnici vrijednosti segmenta (0, T) na kojem je definirana originalna funkcija f(x). Drugim riječima, periodi harmonika su višekratnici trajanja mjerenja signala. Na primjer, period prvog harmonika Fourierovog reda jednak je intervalu T na kojem je definirana funkcija f(x). Period drugog harmonika Fourierovog reda jednak je intervalu T/2. I tako dalje (vidi sliku 8).

Slika 8 Periodi (frekvencije) harmonijskih komponenti Fourierovog reda (ovdje T = 2π)

Shodno tome, frekvencije harmonijskih komponenti su višekratne od 1/T. Odnosno, frekvencije harmonijskih komponenti Fk jednake su Fk= k\T, gdje se k kreće od 0 do ∞, na primjer k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (na nultoj frekvenciji - konstantna komponenta).

Neka naša originalna funkcija bude signal snimljen tokom T=1 sek. Tada će period prvog harmonika biti jednak trajanju našeg signala T1=T=1 sek, a frekvencija harmonika će biti 1 Hz. Period drugog harmonika će biti jednak trajanju signala podeljenom sa 2 (T2=T/2=0,5 sek), a frekvencija će biti 2 Hz. Za treći harmonik T3=T/3 sec i frekvencija je 3 Hz. I tako dalje.

Korak između harmonika u ovom slučaju je 1 Hz.

Tako se signal u trajanju od 1 sekunde može razložiti na harmonijske komponente (dobijajući spektar) sa frekvencijskom rezolucijom od 1 Hz.
Da biste povećali rezoluciju za 2 puta na 0,5 Hz, potrebno je povećati trajanje mjerenja za 2 puta - do 2 sekunde. Signal u trajanju od 10 sekundi može se razložiti na harmonijske komponente (da bi se dobio spektar) sa frekvencijskom rezolucijom od 0,1 Hz. Ne postoje drugi načini za povećanje rezolucije frekvencije.

Postoji način da se umjetno poveća trajanje signala dodavanjem nula nizu uzoraka. Ali to ne povećava stvarnu rezoluciju frekvencije.

3. Diskretni signali i diskretna Fourierova transformacija

Sa razvojem digitalna tehnologija Promijenjene su i metode pohranjivanja mjernih podataka (signala). Ako se ranije signal mogao snimiti na magnetofon i pohraniti na traku u analognom obliku, sada se signali digitaliziraju i pohranjuju u datoteke u memoriji računala kao skup brojeva (uzoraka).

Uobičajena shema za mjerenje i digitalizaciju signala je sljedeća.

Sl.9 Dijagram mjernog kanala

Signal iz mjernog pretvarača stiže do ADC-a tokom vremenskog perioda T. Uzorci signala (uzorkovanje) dobijeni tokom vremena T se prenose u računar i pohranjuju u memoriju.

Slika 10 Digitalizovani signal - N uzoraka primljenih tokom vremena T

Koji su zahtjevi za parametre digitalizacije signala? Uređaj koji pretvara ulaz analogni signal na diskretni kod ( digitalni signal) naziva se analogno-digitalni pretvarač (ADC, engleski analogno-digitalni pretvarač, ADC) (Wiki).

Jedan od glavnih parametara ADC-a je maksimalna frekvencija uzorkovanja (ili brzina uzorkovanja, engleska brzina uzorkovanja) - brzina uzorkovanja vremenski neprekidnog signala prilikom uzorkovanja. Mjeri se u hercima. ((Wiki))

Prema Kotelnikovovoj teoremi, ako kontinuirani signal ima spektar ograničen frekvencijom Fmax, tada se može potpuno i nedvosmisleno rekonstruirati iz njegovih diskretnih uzoraka uzetih u vremenskim intervalima , tj. sa frekvencijom Fd ≥ 2*Fmax, gdje je Fd frekvencija uzorkovanja; Fmax - maksimalna frekvencija spektra signala. Drugim riječima, frekvencija digitalizacije signala (ADC frekvencija uzorkovanja) mora biti najmanje 2 puta veća od maksimalne frekvencije signala koju želimo izmjeriti.

Šta će se dogoditi ako uzmemo uzorke s nižom frekvencijom nego što to zahtijeva Kotelnikova teorema?

U ovom slučaju dolazi do “aliasing” efekta (poznatog i kao stroboskopski efekat, moiré efekat), u kojem se visokofrekventni signal nakon digitalizacije pretvara u niskofrekventni signal, koji zapravo ne postoji. Na sl. 11 crveni visokofrekventni sinusni val je pravi signal. Plava sinusoida niže frekvencije je fiktivni signal koji nastaje zbog činjenice da tokom vremena uzorkovanja više od pola perioda visokofrekventnog signala ima vremena da prođe.

Rice. 11. Pojava lažnog niskofrekventnog signala pri nedovoljno visokoj stopi uzorkovanja

Da bi se izbjegao efekat aliasinga, ispred ADC-a se postavlja poseban filter za snižavanje – niskopropusni filter (LPF), koji propušta frekvencije ispod polovine frekvencije uzorkovanja ADC-a, i odsijeca više frekvencije.

Da bi se izračunao spektar signala iz njegovih diskretnih uzoraka, koristi se diskretna Fourierova transformacija (DFT). Napomenimo još jednom da je spektar diskretnog signala „po definiciji“ ograničen frekvencijom Fmax, koja je manja od polovine frekvencije uzorkovanja Fd. Stoga se spektar diskretnog signala može predstaviti zbirom konačnog broja harmonika, za razliku od beskonačne sume za Fourierov niz kontinuiranog signala, čiji spektar može biti neograničen. Prema Kotelnikovovoj teoremi, maksimalna frekvencija harmonika mora biti takva da obuhvata najmanje dva uzorka, stoga je broj harmonika jednak polovini broja uzoraka diskretnog signala. Odnosno, ako u uzorku ima N uzoraka, tada će broj harmonika u spektru biti jednak N/2.

Razmotrimo sada diskretnu Fourierovu transformaciju (DFT).

Poređenje sa Fourierovim redom

Vidimo da se poklapaju, osim što je vrijeme u DFT-u diskretne prirode i broj harmonika je ograničen sa N/2 - polovinom broja uzoraka.

DFT formule su zapisane u bezdimenzionalnim cjelobrojnim varijablama k, s, gdje su k brojevi uzoraka signala, s brojevi spektralnih komponenti.
Vrijednost s pokazuje broj potpunih harmonijskih oscilacija u periodu T (trajanje mjerenja signala). Diskretna Fourierova transformacija se koristi za pronalaženje amplituda i faza harmonika pomoću numeričke metode, tj. "na kompjuteru"

Da se vratimo na rezultate dobijene na početku. Kao što je već spomenuto, kada se proširi neperiodična funkcija (naš signal) u Fourierov niz, rezultirajući Fourierov red zapravo odgovara periodičnoj funkciji s periodom T (slika 12).

Slika 12 Periodična funkcija f(x) sa periodom T0, sa periodom merenja T>T0

Kao što se može vidjeti na slici 12, funkcija f(x) je periodična sa periodom T0. Međutim, zbog činjenice da se trajanje mjernog uzorka T ne poklapa s periodom funkcije T0, funkcija dobijena kao Fourierov red ima diskontinuitet u tački T. Kao rezultat toga, spektar ove funkcije će sadržavati veliki broj visokofrekventnih harmonika. Ako bi se trajanje mjernog uzorka T poklopilo s periodom funkcije T0, tada bi spektar dobiven nakon Fourierove transformacije sadržavao samo prvi harmonik (sinusoid s periodom jednakim trajanju uzorkovanja), budući da funkcija f(x) je sinusoida.

Drugim riječima, DFT program “ne zna” da je naš signal “komad sinusoida”, ali pokušava da predstavi periodičnu funkciju u obliku serije, koja ima diskontinuitet zbog nekonzistentnosti pojedinih dijelova sinusoida.

Kao rezultat, u spektru se pojavljuju harmonici, koji bi trebali sumirati oblik funkcije, uključujući i ovaj diskontinuitet.

Dakle, da bi se dobio "tačan" spektar signala koji je zbir nekoliko sinusoida sa različiti periodi, potrebno je da period mjerenja signala sadrži cijeli broj perioda svake sinusoide. U praksi, ovaj uslov se može ispuniti za dovoljno dugo trajanje mjerenja signala.

Slika 13 Primjer funkcije i spektra signala kinematičke greške mjenjača

Sa kraćim trajanjem, slika će izgledati "gore":

Slika 14 Primjer funkcije i spektra vibracijskog signala rotora

U praksi može biti teško razumjeti gdje su "prave komponente", a gdje "artefakti" uzrokovani nevišestrukim periodima komponenti i trajanjem uzorkovanja signala ili "skokova i prekida" u obliku signala. . Naravno, riječi “stvarne komponente” i “artefakti” su s razlogom stavljene pod navodnike. Prisustvo mnogih harmonika na grafu spektra ne znači da se naš signal zapravo „sastoji“ od njih. Ovo je isto kao da mislite da se broj 7 „sastoji“ od brojeva 3 i 4. Broj 7 se može predstaviti kao zbir brojeva 3 i 4 – to je tačno.

Dakle, naš signal... ili bolje rečeno, čak i ne "naš signal", već periodična funkcija sastavljena od ponavljanja našeg signala (uzorkovanje) može se predstaviti kao zbir harmonika (sinusnih valova) s određenim amplitudama i fazama. Ali u mnogim slučajevima koji su važni za praksu (vidi gornje slike), zaista je moguće povezati harmonike dobijene u spektru sa stvarni procesi, koji su ciklične prirode i daju značajan doprinos obliku signala.

Neki rezultati

1. Realno izmjereni signal u trajanju od T sekundi, digitaliziran ADC-om, odnosno predstavljen skupom diskretnih uzoraka (N komada), ima diskretni neperiodični spektar, predstavljen skupom harmonika (N/ 2 komada).

2. Signal je predstavljen skupom realnih vrijednosti, a njegov spektar je predstavljen skupom realnih vrijednosti. Harmoničke frekvencije su pozitivne. Činjenica da je matematičarima zgodnije predstaviti spektar u složenom obliku koristeći negativne frekvencije ne znači da je “ovo ispravno” i “ovo uvijek treba raditi”.

3. Signal mjeren u vremenskom intervalu T određen je samo u vremenskom intervalu T. Šta se dešavalo prije nego što smo počeli mjeriti signal, a šta će se dogoditi nakon toga, nauci je nepoznato. A u našem slučaju to nije zanimljivo. DFT vremenski ograničenog signala daje njegov "pravi" spektar, u smislu da, pod određenim uslovima, omogućava izračunavanje amplitude i frekvencije njegovih komponenti.

Korišteni materijali i drugi korisni materijali.

Iznad vidimo da nam proširenje funkcija u nizove stepena omogućava da izračunamo približne vrijednosti ovih funkcija sa potrebnom preciznošću. Ali postoje mnoge funkcije koje se ne mogu proširiti u nizove snage (Taylor ili Maclaurin niz), jer zahtjevi za funkcije su prilično strogi (funkcija mora biti beskonačno diferencibilna, itd.). Stoga se koriste i druge vrste funkcionalnih nizova čiji su uslovi za razlaganje manje opterećujući. Ovi redovi uključuju trigonometrijske serije.

Definicija: Trigonometrijski niz funkcionalni nizovi oblika:, (1)

gdje postoje konstantni brojevi koji se nazivaju:

Koeficijenti trigonometrijskog niza.

Svi članovi serije (1) su funkcionalni neperiodični i imaju zajednički minimalni period od 2p. Slijedi: ako se funkcija f(x) proširi u trigonometrijski niz (1), tj. to je zbir ovog niza, onda ova funkcija sama po sebi mora biti zbir niza (1) samo u određenom intervalu dužine 2p.

Osnovna svojstva trigonometrijskog niza proizlaze iz osnovnih svojstava sistema trigonometrijskih funkcija. Došao sam do jedne definicije.

Definicija: Beskonačan sistem funkcija j1(x),j2(x),...,j3(x)... definisano na segmentu se zove ortogonalno na ovom segmentu, ako su ispunjeni sljedeći uslovi:
za m¹n;

za bilo koji n.

Teorema: Sistem trigonometrijskih funkcija je ortogonan na segmentu [-p,p].

dokaz: Potrebno je provjeriti uslove 1) i 2) prethodne definicije.

1) Razmotrimo integrale:

Primijenimo trigonometrijske formule:

Očigledno, uz njihovu pomoć, svi prethodni integrali se svode na integrale oblika:
I

Hajde da ih izračunamo.

;

Dakle, prvi uslov ortogonalnosti će biti zadovoljen.

2)
;

a drugi uslov je ispunjen itd.

1. Trigonometrijska Fourierova serija.

Neka periodična funkcija f(x) sa periodom 2p bude predstavljena kao zbir trigonometrijskog niza
(1).

za sve x iz nekog intervala dužine 2p. Ali zbir niza S(x) je periodična funkcija s periodom od 2p. Stoga se vrijednosti f(x) i S(x) poklapaju na cijeloj brojevnoj pravoj (-¥, +¥). Stoga je dovoljno proučiti jednakost (1) na nekom intervalu dužine 2p, obično [-p,p] .

Dakle, neka je f(x) zbir serije (1) na [-p,p] i, pored toga, pretpostavimo da se može integrirati pojam po član s intervalom. To je, na primjer, moguće ako numerički niz koeficijenata serije (1) apsolutno konvergira, tj. serija konvergira

(2).

U ovom slučaju, članovi funkcionalnog niza (1) u apsolutnoj vrijednosti ne prelaze odgovarajuće članove niza (2), što implicira uniformnu konvergenciju niza (1), a samim tim i mogućnost njegovog neusklađenosti. -term integracija preko [-p,p].

Koristimo ovo za izračunavanje koeficijenta a 0 . Integrirajmo obje strane nejednakosti (1) polovično preko [-p,p]:

Svi integrali s desne strane, prema svojstvu ortogonalnosti trigonometrijskih funkcija, jednaki su nuli osim prvog. Zbog toga:
, gdje
(3).

Za izračunavanje k /k¹0/ množimo obje strane (1) sa coskx. Rezultirajući niz će se također ravnomjerno konvergirati na [-p,p], jer ½coskx½£1 i može se integrirati pojam po član preko [-p,p].

Po istom svojstvu ortogonalnosti, svi integrali na desnoj strani jednaki su nuli osim onog koji sadrži k.

Onda
. Gdje

(4).

Pomnoživši obje strane (1) sa sin kx i integrirajući rezultirajuću jednakost sa , dobivamo
. Gdje

(5).

Pozivaju se koeficijenti izračunati pomoću formula (3)-(5).

Fourierovi koeficijenti za funkciju f(x), a trigonometrijski niz (1) sa ovim koeficijentima je Fourierov red funkcije (x).

Treba napomenuti da nije uvijek moguće integrirati niz (1) pojam po član. Stoga je formalno moguće izračunati Fourierove koeficijente i kompilirati Fourierov red (1), ali se ne može garantirati da će ovaj niz uopće konvergirati; a ako konvergira, tada je njegov zbir funkcija f(x). U takvim slučajevima, umjesto jednakosti (1) dogovorili smo se o “prepisci”:

funkcije. Ova transformacija ima veliki značaj, jer se može koristiti za rješavanje mnogih praktičnih problema. Fourierove redove koriste ne samo matematičari, već i stručnjaci iz drugih nauka.

Proširenje funkcija u Fourierov niz je matematička tehnika koja se može promatrati u prirodi ako koristite uređaj koji osjeća sinusne funkcije.

Ovaj proces nastaje kada osoba čuje zvuk. Ljudsko uho je dizajnirano na način da može osjetiti pojedinačne sinusne fluktuacije u vazdušnom pritisku različitih frekvencija, što zauzvrat omogućava osobi da prepozna govor i sluša muziku.

Ljudsko uho ne percipira zvuk u cjelini, već kroz njegove komponente Fourierove serije. Strings muzički instrument proizvodi zvukove koji su sinusoidne vibracije različitih frekvencija. Realnost širenja svjetlosti iz Fourierove serije predstavljena je dugom. Ljudski vid opaža svjetlost kroz neke od njenih komponenti različitih frekvencija elektromagnetnih oscilacija.

Fourierova transformacija je funkcija koja opisuje fazu i amplitudu sinusoida određene frekvencije. Ova transformacija se koristi za rješavanje jednadžbi koje opisuju dinamičke procese koji nastaju pod utjecajem energije. Fourierovi redovi rješavaju problem identifikacije konstantnih komponenti u složenim oscilatornim signalima, što je omogućilo ispravnu interpretaciju podataka dobijenih iz eksperimenata, opservacija u medicini, hemiji i astronomiji.

Otkriće ove transformacije pripada francuskom matematičaru Jean Baptiste Joseph Fourieru. U čast koga je Fourierova serija kasnije dobila ime. U početku je naučnik pronašao primenu svoje metode u proučavanju i objašnjavanju mehanizama toplotne provodljivosti. Predloženo je da se početna nepravilna raspodjela topline može predstaviti u obliku jednostavnih sinusoida. Za svaki od kojih će biti određeni temperaturni minimum, maksimum i faza. Funkcija koja opisuje gornji i donji vrh krivulje, faza svakog harmonika naziva se Fourierova transformacija iz izraza raspodjele temperature. Autor transformacije je predložio metodu dekompozicije složena funkcija kao zbir periodičnih funkcija kosinus, sinus.

Svrha rad na kursu je proučavanje Fourierovog reda i važnost praktične primjene ove transformacije.

Za postizanje ovog cilja formulirani su sljedeći zadaci:

1) dati pojam trigonometrijskog Furijeovog reda;

2) odrediti uslove za dekompozibilnost funkcije u Fourierovom redu;

3) razmotriti proširenje u Fourierov red parnih i neparnih funkcija;

4) razmotriti proširenje Furijeovog reda neperiodične funkcije;

5) otkriti praktičnu primjenu Fourierovog reda.

Predmet proučavanja: proširenje funkcija u Fourierove redove.

Predmet proučavanja: Fourierov red.

Metode istraživanja: analiza, sinteza, poređenje, aksiomatska metoda.

1.5. Fourierov red za parne i neparne funkcije

Razmotrimo simetrični integral

gdje je kontinuirano ili po komadu kontinuirano na. Napravimo promjenu u prvom integralu. Mi vjerujemo. Onda

Stoga, ako je funkcija parna, onda (tj. graf parne funkcije je simetričan u odnosu na os i

Ako je neparna funkcija, onda (tj. graf neparne funkcije je simetričan u odnosu na ishodište) i

One. simetrični integral parne funkcije jednak je dvostrukom integralu preko polovine intervala integracije, a simetrični integral neparne funkcije jednak je nuli.

Obratite pažnju na sljedeća dva svojstva parnih i neparnih funkcija:

1) proizvod parne funkcije i neparne je neparna funkcija;

2) proizvod dvije parne (neparne) funkcije je parna funkcija.

Neka je parna funkcija definirana i proširiva na ovom segmentu u trigonometrijski Fourierov red. Koristeći rezultate dobivene gore, nalazimo da će koeficijenti ove serije imati oblik:

Ako je neparna funkcija definirana na segmentu i proširuje se na ovaj segment u trigonometrijski Fourierov red, tada će koeficijenti ovog niza imati oblik:

Shodno tome, trigonometrijski Fourierov red na segmentu će imati oblik

za parnu funkciju:

(16)

za neparnu funkciju:

Niz (16) ne sadrži sinuse više uglova, odnosno Fourierov red parne funkcije uključuje samo parne funkcije i nezavisni član. Niz (17) ne sadrži kosinuse više uglova, odnosno Fourierov red neparne funkcije uključuje samo neparne funkcije.

Definicija. Redovi
su dijelovi puni opseg Fourier i nazivaju se nepotpunitrigonometrijski Fourierov red.

Ako se funkcija proširi u nepotpun trigonometrijski niz (16) (ili (17)), onda se kaže da ješiri u trigonometrijski Fourierov red u kosinusima (ili sinusima).

1.6. Proširenje neperiodične funkcije u Fourierov red

1.6.1. Proširenje funkcija u Fourierov red

Neka je funkcija data na intervalu i da zadovoljava uslove Dirichletove teoreme na tom intervalu. Izvršimo promjenu varijable. Neka gdje odabiremo tako da je rezultujuća funkcija argumenta definirana na. Stoga vjerujemo u to

Rezultirajuća funkcija može se proširiti u Fourierov niz:

Gdje

Napravimo obrnutu zamjenu⇒ Dobijamo

Gdje

(19)

Niz (18) – Fourierov red u osnovnom trigonometrijskom sistemu funkcija

Tako smo otkrili da ako je funkcija data na intervalu i zadovoljava uslove Dirichletove teoreme na tom intervalu, onda se može proširiti u trigonometrijski Fourierov red (18) prema trigonometrijskom sistemu funkcija (20).

Trigonometrijski Fourierov red za parnu funkciju definiranu na imat će oblik

Gdje

za neparnu funkciju

Gdje

Komentiraj! U nekim problemima je potrebno proširiti funkciju u trigonometrijski Fourierov red prema sistemu funkcija (20) ne na segmentu, već na segmentu. U ovom slučaju, trebate samo promijeniti granice integracije u formulama (19) ((15), ako, tj. u ovom slučaju

(23)

ili ako

(24)

Zbir trigonometrijskog Fourierovog reda je periodična funkcija s periodom, koja je periodični nastavak datu funkciju. A za periodičnu funkciju vrijedi jednakost (4).

1.6.2. Proširenje funkcija u Fourierov red

Neka je funkcija data na i zadovoljava uvjete Dirichletove teoreme na ovom intervalu. Takva funkcija se također može proširiti u Fourierov red. Da biste to učinili, funkcija mora biti proširena na interval, a rezultirajuća funkcija proširena u Fourierov niz na intervalu. U ovom slučaju, rezultirajuću seriju treba uzeti u obzir samo na segmentu na kojem je funkcija specificirana. Radi lakšeg izračunavanja, funkciju ćemo definirati na paran i neparan način.

1) Proširimo funkciju u interval na paran način, odnosno konstruiraćemo novu ravnomjerna funkcija, koji se poklapa na segmentu sa funkcijom. Prema tome, graf ove funkcije je simetričan u odnosu na os i poklapa se sa grafikom na segmentu. Koristeći formule (21), nalazimo koeficijente Fourierovog reda za funkciju i zapisujemo sam Fourierov red. Zbir Fourierovog reda za je periodična funkcija s tačkom. Poklapaće se sa funkcijom na svim tačkama kontinuiteta.

2) Proširimo funkciju na interval na neparan način, odnosno konstruiraćemo novu neparna funkcija, što se podudara s funkcijom. Graf takve funkcije je simetričan u odnosu na ishodište koordinata i poklapa se sa grafikom na segmentu. Koristeći formule (22), nalazimo koeficijente Fourierovog reda za funkciju i zapisujemo sam Fourierov red. Zbir Fourierovog reda za je periodična funkcija s tačkom. Poklapaće se sa funkcijom na svim tačkama kontinuiteta.

Notes!

1) Slično, možete proširiti funkciju definiranu na intervalu u Fourierov red

2) Budući da proširenje funkcije na segment pretpostavlja njen nastavak na segment na proizvoljan način, Fourierov red za funkciju neće biti jedinstven.

1.6.3. Proširenje funkcija u Fourierov red

Neka je funkcija data na proizvoljnom segmentu dužine i neka na njemu zadovoljava uslove Dirichletove teoreme.

Tada se ova funkcija može proširiti u Fourierov niz. Da bi se to postiglo, funkcija se mora periodično (sa tačkom) nastaviti duž cijele brojevne prave, a rezultirajuća funkcija se mora proširiti u Fourierov niz, koji treba uzeti u obzir samo na segmentu. Zbog svojstva (3) periodičnih funkcija imamo

Stoga se Fourierovi koeficijenti za rezultirajući nastavak funkcije mogu pronaći pomoću formula

(25)

2. Praktična upotreba Fourierova serija

2.1. Problemi koji uključuju proširenje funkcija u Fourierove redove i njihovo rješavanje

Potrebno je proširiti u trigonometrijski Fourierov niz funkciju koja je periodični nastavak funkcije specificirane u intervalu. Da biste to učinili, potrebno je koristiti algoritam za proširenje periodične funkcije u Fourierov red.

Algoritam za proširenje periodične funkcije u Fourierov red:

1) Konstruisati graf date funkcije i njen periodični nastavak;

2) Podesite period date funkcije;

3) Odredite da li je funkcija parna, neparna ili opšti pogled;

4) Proveriti izvodljivost uslova Dirihletove teoreme;

5) Kreirati formalni prikaz Fourierovog reda generisan ovom funkcijom;

6) Izračunati Furijeove koeficijente;

7) Zapišite Fourierov red za datu funkciju, koristeći koeficijente Fourierovog reda (stavka 4).

Primjer 1. Proširite funkciju u Fourierov niz na intervalu.

Rješenje:

1) Napravimo graf date funkcije i njenog periodičnog nastavka.

2) Period proširenja funkcije.

3) Funkcija je neparna.

4) Funkcija je kontinuirana i monotona uključena, tj. funkcija zadovoljava Dirichletove uslove.

5) Izračunajmo koeficijente Furijeovog reda.

6) Napišite Fourierov red zamjenom Fourierovih koeficijenata u formulu

odgovor:

Primjer 2. Proširimo funkciju sa proizvoljnim periodom u Fourierov red.

Rješenje: funkcija je definirana na poluintervalu (-3;3). Period proširenja funkcije, poluperiod. Proširimo funkciju u Fourierov red

U početku, funkcija je diskontinuirana, pa ćemo svaki Fourierov koeficijent predstaviti kao zbir dva integrala.

Zapišimo Fourierov red zamjenom pronađenih koeficijenata Fourierovog reda u formulu.

Primjer 3. Proširite funkcijuizmeđuu Fourierovom nizu u kosinusima. Konstruirajte graf zbira niza.

Rješenje: proširimo funkciju u interval na paran način, odnosno konstruiramo novu parnu funkciju koja se poklapa sa funkcijom na intervalu. Nađimo koeficijente Fourierovog reda za funkciju i napišemo Fourierov red. Zbir Fourierovog reda za je periodična funkcija s tačkom. Poklapaće se sa funkcijom na svim tačkama kontinuiteta.

Trigonometrijski Fourierov red za funkciju će imati oblik

Nađimo koeficijente Fourierovog reda

Dakle, kada se pronađu koeficijenti, možemo napisati Fourierov red

Nacrtajmo zbir serije

Primjer 4. Zadana funkcija definirana na segmentu. Saznajte može li se funkcija proširiti u Fourierov niz. Napišite proširenje funkcije u Fourierov red.

Rješenje:

1) konstruirati graf funkcije na .

2) funkcija je neprekidna i monotona na , odnosno, prema Dirichletovom teoremu, može se proširiti u trigonometrijski Fourierov red.

3) izračunati Furijeove koeficijente koristeći formule (1.19).

4) napišite Fourierov red koristeći pronađene koeficijente.

2.2. Primjeri primjene Fourierovih redova u različitim područjima ljudske djelatnosti

Matematika je jedna od nauka koje ima široka primena na praksi. Svaki proizvodni i tehnološki proces zasnovan je na matematičkim zakonima. Aplikacija razni instrumenti matematički aparat vam omogućava da dizajnirate uređaje i automatizirane jedinice sposobne za obavljanje operacija, složene proračune i proračuni u projektovanju zgrada i objekata.

Fourierove redove koriste matematičari u geometriji kadarješavanje problema iz sferne geometrije; u matematska fizika urješavanje problema o malim vibracijama elastičnih medija. No, osim matematike, Fourierovi redovi su svoju primjenu našli i u drugim oblastima nauke.

Svaki dan ljudi koriste razni uređaji. I često ovi uređaji ne rade kako treba. Na primjer, zvuk je teško čuti zbog velike buke ili je slika primljena faksom nejasna. Osoba može utvrditi uzrok kvara zvukom. Računar također može dijagnosticirati da li je uređaj oštećen. Višak buke se može ukloniti korištenjem kompjuterske obrade signala. Signal se predstavlja kao niz digitalnih vrijednosti, koje se zatim unose u kompjuter. Nakon završetka određene kalkulacije, dobiti koeficijente Fourierovog reda.

Promjenom spektra signala možete očistiti snimak od šuma, kompenzirati izobličenje signala raznim uređajima za snimanje, promijeniti tembre instrumenata i usmjeriti pažnju slušatelja na pojedine dijelove.

U digitalnoj obradi slike, upotreba Fourierove serije omogućava sljedeće efekte: zamućenje, naglašavanje rubova, restauracija slike, umjetnički efekti (utiskivanje)

Ekspanzija Fourierovog reda se koristi u arhitekturi u proučavanju oscilatornih procesa. Na primjer, prilikom kreiranja projekta razne vrste konstrukcije izračunavaju snagu, krutost i stabilnost konstruktivnih elemenata.

U medicini, za provođenje medicinskog pregleda uz pomoć kardiograma i ultrazvučnog aparata, koristi se matematički aparat koji se temelji na teoriji Fourierove serije.

Veliki računski problemi procjene statističkih karakteristika signala i filtriranja šuma javljaju se prilikom snimanja i obrade kontinuiranih podataka o morskom dnu. Prilikom izvođenja mjerenja i njihovog snimanja obećavajuće holografske metode koje koriste Fourierov niz. To jest, Fourierove serije se također koriste u nauci kao što je oceanologija.

Elementi matematike se nalaze u proizvodnji gotovo na svakom koraku, pa je važno da stručnjaci poznaju i budu dobro orijentisani u oblasti primene određenih alata za analizu i proračun.

Zaključak

Tema nastavnog rada je posvećena proučavanju Fourierovog reda. Proizvoljna funkcija se može proširiti u jednostavnije, odnosno može se proširiti u Fourierov red. Opseg rada na predmetu ne dozvoljava nam da detaljno otkrijemo sve aspekte proširenja funkcije u niz. Međutim, iz postavljenih zadataka činilo se mogućim otkriti osnovnu teoriju o Fourierovim redovima.

Predmetni rad otkriva koncept trigonometrijskog Fourierovog reda. Utvrđeni su uvjeti za razgradljivost funkcije u Fourierovom redu. Razmatraju se proširenja parnih i neparnih funkcija u Fourierov red; neperiodične funkcije.

Drugo poglavlje daje samo neke primjere proširenja funkcija datih na različitim intervalima u Fourierove redove. Opisane su oblasti nauke u kojima se ova transformacija koristi.

Postoji i složen oblik predstavljanja Fourierovog reda, koji se ne bi mogao uzeti u obzir jer obim nastavnog rada to ne dozvoljava. Složena forma niz je algebarski jednostavan. Stoga se često koristi u fizici i primijenjenim proračunima.

Važnost teme nastavnog rada je zbog činjenice da se ona široko koristi ne samo u matematici, već iu drugim naukama: fizici, mehanici, medicini, hemiji i mnogim drugim.

Bibliografija

1. Bari, N.K. Trigonometrijski niz. [tekst]/ N.K. Bari. - Moskva, 1961. - 936 s.

2. Bermant, A.F. Kratki kurs matematička analiza: udžbenik za univerzitete[tekst]/ A.F. Bermant, I.G. Aramanović. – 11. izd., izbrisano. – Sankt Peterburg: Izdavačka kuća “Lan”, 2005. – 736 str.

3. Bugrov, Ya. S. Viša matematika: Udžbenik za univerzitete: U 3 toma.[tekst]/ Ya. S. Bugrov, S. M. Nikolsky; Ed. V. A. Sadovnichy. - 6. izd., stereotip. - M.: Drfa, 2004. -512 str.

4. Vinogradova, I. A. Problemi i vježbe iz matematičke analize: priručnik za univerzitete, pedagoški. univerziteti: U 2 sata.[tekst]/ I. A. Vinogradova, S. N. Olehnik, V. A. Sadovnichy; uređeno od V.A. Sadovnichigo. – 3. izd., rev. – M.: Drfa, 2001. – 712 str.

5. Gusak, A.A. Viša matematika. U 2 toma T. 2. Udžbenik za studente.[tekst]/ A. A. Gusak.– 5. izd. – Minsk: TetraSystems, 2004.

6. Danko, P.E. Viša matematika u vježbama i zadacima: udžbenik za fakultete: 2 sata.[tekst]/ P.E. Danko, A.G. Popov, T.Ya. Kozhevnikova. Moskva: ONIX: Mir i obrazovanje, 2003. – 306 str.

7. Lukin, A. Uvod u digitalna obrada signali (matematičke osnove) [tekst]/ A. Lukin. - M., 2007. - 54 str.

8. Piskunov, N. S. Diferencijalni i integralni račun za studente, vol. 2: Tutorial za fakultete i univerzitete.[tekst]/ N. S. Piskunov. - 13. izd. - M.: Nauka, 1985. - 432 str.

9. Rudin, U. Osnove matematičke analize.[tekst]/ U. Rudin. - 2. izd., Trans. sa engleskog .- M.: Mir, 1976.- 206 str.

10. Fikhtengolts, G. M. Osnove matematičke analize. Dio 2.[tekst]/ G. M. Fikhtengolts. -6. izdanje, izbrisano. - Sankt Peterburg: Izdavačka kuća Lan, 2005. – 464 str.

Orenburg, 2015

1

Mogućnost aproksimacije Fourierovog reda u slučaju linearnog signala može biti neophodna za konstruisanje funkcija u slučaju diskontinuiranih signala. periodični elementi. Mogućnost korištenja ovu metodu da ih konstruiše i razloži koristeći konačni iznosi Fourierovi redovi se koriste u rješavanju mnogih problema raznih nauka, kao što su fizika, seizmologija i tako dalje. Metodom dekompozicije oscilatornih procesa i funkcija opisanih ovim transformacijama razmatraju se procesi okeanske plime i sunčeve aktivnosti. Sa razvojem kompjuterska tehnologija Fourierovi redovi su počeli da se koriste sve više i više složeni zadaci, a zahvaljujući tome, postalo je moguće koristiti ove transformacije u indirektnim naukama, kao što su medicina i hemija. Fourierova transformacija je opisana u stvarnom i kompleksnom obliku, druga distribucija je omogućila napredak u istraživanju vanjski prostor. Rezultat ovog rada je primjena Fourierovog reda na linearizaciju diskontinuirana funkcija i izbor broja koeficijenata serije za preciznije nametanje serije na funkciju. Štaviše, kada se koristi proširenje Fourierove serije, ovu funkciju prestaje biti diskontinuiran i već pri dovoljno malim vrijednostima postiže se dobra aproksimacija korištene funkcije.

Fourierova serija

Fourierova transformacija

fazni spektar.

1. Alašejeva E.A., Rogova N.V. Numerička metoda za rješavanje problema elektrodinamike u aproksimaciji tanke žice. Nauka i mir. International Science Magazine, br. 8(12), 2014. Tom 1. Volgograd. P.17-19.

2. Vorobyov N.N. Teorija serija. Ed. Nauka, Glavna redakcija fizičke i matematičke literature, M., 1979, -408 S.

3. Kalinina V.N., Pankin V.F. Math statistics. - M.: postdiplomske škole, 2001.

4. R. Edwards Fourier serijal u modernoj prezentaciji. Ed. Svijet. U 2 toma. Tom 1. 1985. 362 pp.

5. Sigorsky V.P. Inženjerski matematički aparat. Ed. 2. stereotipno. "Tehnika", 1997. – 768 str.

Reprezentacija proizvoljne funkcije sa određenim periodom u obliku niza naziva se Fourierov red. Ekspanzija u ortogonalnoj bazi se naziva ovu odluku Uglavnom. Proširenje funkcija Fourierovom nizom je prilično moćan alat za rješavanje raznih problema. Jer Osobine ove transformacije tokom integracije, diferencijacije, kao i pomeranja izraza argumentom i konvolucijom su dobro poznate i proučavane. Osoba nepoznata višu matematiku, kao i sa radovima francuskog naučnika Furijea, najverovatnije neće razumeti šta su ove „serije“ i čemu su potrebne. Ova Fourierova transformacija postala je sastavni dio naših života. Koriste ga ne samo matematičari, već i fizičari, hemičari, doktori, astronomi, seizmolozi, okeanografi i mnogi drugi.

Fourierovi redovi se koriste za rješavanje mnogih primijenjenih problema. Fourierova transformacija se može izvesti analitičkim, numeričkim i drugim metodama. Procesi kao što su okeanske plime i oseke i svetlosni talasi ciklusi solarne aktivnosti se odnose na numeričku metodu dekompozicije bilo kojeg oscilatornog procesa u Fourierov niz. Koristeći ove matematičke tehnike, možete analizirati funkcije, predstavljajući sve oscilatorne procese kao niz sinusnih komponenti koje se kreću od minimuma do maksimuma i nazad. Fourierova transformacija je funkcija koja opisuje fazu i amplitudu sinusoida koje odgovaraju određenoj frekvenciji. Ova transformacija se koristi za rješavanje vrlo složene jednačine, koji opisuju dinamičke procese koji nastaju pod utjecajem topline, svjetlosti ili električna energija. Takođe, Fourierovi nizovi omogućavaju izolaciju konstantnih komponenti u složenim oscilatornim signalima, što omogućava ispravnu interpretaciju eksperimentalnih zapažanja dobijenih u medicini, hemiji i astronomiji.

Sa razvojem tehnologije, tj. Pojava i razvoj kompjutera doveli su do Fourierove transformacije novi nivo. Ova tehnikačvrsto uspostavljena u gotovo svim oblastima nauke i tehnologije. Primjer je digitalni audio i video. Što je postalo jasno ostvarenje rasta naučni proces i primjene Fourierovih redova. Dakle, Fourierov niz u složenom obliku omogućio je iskorak u proučavanju svemira. Osim toga, to je uticalo na proučavanje fizike poluprovodnički materijali i plazma, mikrotalasna akustika, okeanografija, radar, seizmologija.

Razmotrimo fazni spektar periodičnog signala određen iz sljedećeg izraza:

gdje simboli i označavaju imaginarni i realni dio količine u uglastim zagradama.

Ako se pomnoži sa realnom konstantnom vrijednošću K, tada proširenje Fourierovog reda ima sljedeći oblik:

Iz izraza (1) proizilazi da fazni Fourierov spektar ima sljedeća svojstva:

1) je funkcija , tj. za razliku od spektra snage, koji ne zavisi od , mijenja se kako se signal pomjera duž vremenske ose;

2) ne zavisi od K, odnosno invarijantan je na pojačanje ili slabljenje signala, dok je spektar snage funkcija K.

3) tj. to je neparna funkcija od n.

Bilješka. Uzimajući u obzir geometrijsku interpretaciju gornjih razmatranja, može se izraziti u smislu spektra snage i spektra faza na sljedeći način:

Zbog

onda iz (2) i (3) proizilazi da se može nedvosmisleno rekonstruisati ako su poznati amplituda (ili spektar snage) i fazni spektri.

Pogledajmo primjer. Dobili smo funkciju između

Opšti pogled na Fourierov niz:

Zamijenimo naše vrijednosti i dobijemo:

Zamenimo naše vrednosti i dobijemo.

funkcije. Ova transformacija je od velike važnosti jer se može koristiti za rješavanje mnogih praktičnih problema. Fourierove redove koriste ne samo matematičari, već i stručnjaci iz drugih nauka.

Proširenje funkcija u Fourierov niz je matematička tehnika koja se može promatrati u prirodi ako koristite uređaj koji osjeća sinusne funkcije.

Ovaj proces se dešava kada osoba čuje zvuk. Ljudsko uho je dizajnirano na način da može osjetiti pojedinačne sinusne fluktuacije u vazdušnom pritisku različitih frekvencija, što zauzvrat omogućava osobi da prepozna govor i sluša muziku.

Ljudsko uho ne percipira zvuk u cjelini, već kroz njegove komponente Fourierove serije. Žice muzičkog instrumenta proizvode zvukove koji su sinusoidne vibracije različitih frekvencija. Realnost širenja svjetlosti iz Fourierove serije predstavljena je dugom. Ljudski vid opaža svjetlost kroz neke od njenih komponenti različitih frekvencija elektromagnetnih oscilacija.

Fourierova transformacija je funkcija koja opisuje fazu i amplitudu sinusoida određene frekvencije. Ova transformacija se koristi za rješavanje jednadžbi koje opisuju dinamičke procese koji nastaju pod utjecajem energije. Fourierovi redovi rješavaju problem identifikacije konstantnih komponenti u složenim oscilatornim signalima, što je omogućilo ispravnu interpretaciju podataka dobijenih iz eksperimenata, opservacija u medicini, hemiji i astronomiji.

Otkriće ove transformacije pripada francuskom matematičaru Jean Baptiste Joseph Fourieru. U čast koga je Fourierova serija kasnije dobila ime. U početku je naučnik pronašao primenu svoje metode u proučavanju i objašnjavanju mehanizama toplotne provodljivosti. Predloženo je da se početna nepravilna raspodjela topline može predstaviti u obliku jednostavnih sinusoida. Za svaki od kojih će biti određeni temperaturni minimum, maksimum i faza. Funkcija koja opisuje gornji i donji vrh krivulje, faza svakog harmonika naziva se Fourierova transformacija iz izraza raspodjele temperature. Autor transformacije je predložio metodu za dekomponovanje kompleksne funkcije kao sume periodičnih funkcija kosinus, sinus.

Svrha predmeta je proučavanje Fourierovog reda i važnosti praktične primjene ove transformacije.

Za postizanje ovog cilja formulirani su sljedeći zadaci:

1) dati pojam trigonometrijskog Furijeovog reda;

2) odrediti uslove za dekompozibilnost funkcije u Fourierovom redu;

3) razmotriti proširenje u Fourierov red parnih i neparnih funkcija;

4) razmotriti proširenje Furijeovog reda neperiodične funkcije;

5) otkriti praktičnu primjenu Fourierovog reda.

Predmet proučavanja: proširenje funkcija u Fourierove redove.

Predmet proučavanja: Fourierov red.

Metode istraživanja: analiza, sinteza, poređenje, aksiomatska metoda.

1.5. Fourierov red za parne i neparne funkcije

Razmotrimo simetrični integral

gdje je kontinuirano ili po komadu kontinuirano na. Napravimo promjenu u prvom integralu. Mi vjerujemo. Onda

Stoga, ako je funkcija parna, onda (tj. graf parne funkcije je simetričan u odnosu na os i

Ako je neparna funkcija, onda (tj. graf neparne funkcije je simetričan u odnosu na ishodište) i

One. simetrični integral parne funkcije jednak je dvostrukom integralu preko polovine intervala integracije, a simetrični integral neparne funkcije jednak je nuli.

Obratite pažnju na sljedeća dva svojstva parnih i neparnih funkcija:

1) proizvod parne funkcije i neparne je neparna funkcija;

2) proizvod dvije parne (neparne) funkcije je parna funkcija.

Neka je parna funkcija definirana i proširiva na ovom segmentu u trigonometrijski Fourierov red. Koristeći rezultate dobivene gore, nalazimo da će koeficijenti ove serije imati oblik:

Ako je neparna funkcija definirana na segmentu i proširuje se na ovaj segment u trigonometrijski Fourierov red, tada će koeficijenti ovog niza imati oblik:

Shodno tome, trigonometrijski Fourierov red na segmentu će imati oblik

za parnu funkciju:

(16)

za neparnu funkciju:

Niz (16) ne sadrži sinuse više uglova, odnosno Fourierov red parne funkcije uključuje samo parne funkcije i nezavisni član. Niz (17) ne sadrži kosinuse više uglova, odnosno Fourierov red neparne funkcije uključuje samo neparne funkcije.

Definicija. Redovi
su dijelovi potpunog Fourierovog reda i nazivaju se nepotpunimtrigonometrijski Fourierov red.

Ako se funkcija proširi u nepotpun trigonometrijski niz (16) (ili (17)), onda se kaže da ješiri u trigonometrijski Fourierov red u kosinusima (ili sinusima).

1.6. Proširenje neperiodične funkcije u Fourierov red

1.6.1. Proširenje funkcija u Fourierov red

Neka je funkcija data na intervalu i da zadovoljava uslove Dirichletove teoreme na tom intervalu. Izvršimo promjenu varijable. Neka gdje odabiremo tako da je rezultujuća funkcija argumenta definirana na. Stoga vjerujemo u to

Rezultirajuća funkcija može se proširiti u Fourierov niz:

Gdje

Napravimo obrnutu zamjenu⇒ Dobijamo

Gdje

(19)

Niz (18) – Fourierov red u osnovnom trigonometrijskom sistemu funkcija

Tako smo otkrili da ako je funkcija data na intervalu i zadovoljava uslove Dirichletove teoreme na tom intervalu, onda se može proširiti u trigonometrijski Fourierov red (18) prema trigonometrijskom sistemu funkcija (20).

Trigonometrijski Fourierov red za parnu funkciju definiranu na imat će oblik

Gdje

za neparnu funkciju

Gdje

Komentiraj! U nekim problemima je potrebno proširiti funkciju u trigonometrijski Fourierov red prema sistemu funkcija (20) ne na segmentu, već na segmentu. U ovom slučaju, trebate samo promijeniti granice integracije u formulama (19) ((15), ako, tj. u ovom slučaju

(23)

ili ako

(24)

Zbir trigonometrijskog Fourierovog reda je periodična funkcija s periodom, koja je periodični nastavak date funkcije. A za periodičnu funkciju vrijedi jednakost (4).

1.6.2. Proširenje funkcija u Fourierov red

Neka je funkcija data na i zadovoljava uvjete Dirichletove teoreme na ovom intervalu. Takva funkcija se također može proširiti u Fourierov red. Da biste to učinili, funkcija mora biti proširena na interval, a rezultirajuća funkcija proširena u Fourierov niz na intervalu. U ovom slučaju, rezultirajuću seriju treba uzeti u obzir samo na segmentu na kojem je funkcija specificirana. Radi lakšeg izračunavanja, funkciju ćemo definirati na paran i neparan način.

1) Proširimo funkciju u interval na paran način, odnosno konstruiraćemo novu parnu funkciju koja se poklapa sa funkcijom na intervalu. Prema tome, graf ove funkcije je simetričan u odnosu na os i poklapa se sa grafikom na segmentu. Koristeći formule (21), nalazimo koeficijente Fourierovog reda za funkciju i zapisujemo sam Fourierov red. Zbir Fourierovog reda za je periodična funkcija s tačkom. Poklapaće se sa funkcijom na svim tačkama kontinuiteta.

2) Proširimo funkciju na interval na neparan način, odnosno konstruiraćemo novu neparnu funkciju koja se poklapa sa funkcijom. Graf takve funkcije je simetričan u odnosu na ishodište koordinata i poklapa se sa grafikom na segmentu. Koristeći formule (22), nalazimo koeficijente Fourierovog reda za funkciju i zapisujemo sam Fourierov red. Zbir Fourierovog reda za je periodična funkcija s tačkom. Poklapaće se sa funkcijom na svim tačkama kontinuiteta.

Notes!

1) Slično, možete proširiti funkciju definiranu na intervalu u Fourierov red

2) Budući da proširenje funkcije na segment pretpostavlja njen nastavak na segment na proizvoljan način, Fourierov red za funkciju neće biti jedinstven.

1.6.3. Proširenje funkcija u Fourierov red

Neka je funkcija data na proizvoljnom segmentu dužine i neka na njemu zadovoljava uslove Dirichletove teoreme.

Tada se ova funkcija može proširiti u Fourierov niz. Da bi se to postiglo, funkcija se mora periodično (sa tačkom) nastaviti duž cijele brojevne prave, a rezultirajuća funkcija se mora proširiti u Fourierov niz, koji treba uzeti u obzir samo na segmentu. Zbog svojstva (3) periodičnih funkcija imamo

Stoga se Fourierovi koeficijenti za rezultirajući nastavak funkcije mogu pronaći pomoću formula

(25)

2. Praktična primjena Fourierovih redova

2.1. Problemi koji uključuju proširenje funkcija u Fourierove redove i njihovo rješavanje

Potrebno je proširiti u trigonometrijski Fourierov niz funkciju koja je periodični nastavak funkcije specificirane u intervalu. Da biste to učinili, potrebno je koristiti algoritam za proširenje periodične funkcije u Fourierov red.

Algoritam za proširenje periodične funkcije u Fourierov red:

1) Konstruisati graf date funkcije i njen periodični nastavak;

2) Podesite period date funkcije;

3) Odrediti da li je funkcija parna, neparna ili opšta;

4) Proveriti izvodljivost uslova Dirihletove teoreme;

5) Kreirati formalni prikaz Fourierovog reda generisan ovom funkcijom;

6) Izračunati Furijeove koeficijente;

7) Zapišite Fourierov red za datu funkciju, koristeći koeficijente Fourierovog reda (stavka 4).

Primjer 1. Proširite funkciju u Fourierov niz na intervalu.

Rješenje:

1) Napravimo graf date funkcije i njenog periodičnog nastavka.

2) Period proširenja funkcije.

3) Funkcija je neparna.

4) Funkcija je kontinuirana i monotona uključena, tj. funkcija zadovoljava Dirichletove uslove.

5) Izračunajmo koeficijente Furijeovog reda.

6) Napišite Fourierov red zamjenom Fourierovih koeficijenata u formulu

odgovor:

Primjer 2. Proširimo funkciju sa proizvoljnim periodom u Fourierov red.

Rješenje: funkcija je definirana na poluintervalu (-3;3). Period proširenja funkcije, poluperiod. Proširimo funkciju u Fourierov red

U početku, funkcija je diskontinuirana, pa ćemo svaki Fourierov koeficijent predstaviti kao zbir dva integrala.

Zapišimo Fourierov red zamjenom pronađenih koeficijenata Fourierovog reda u formulu.

Primjer 3. Proširite funkcijuizmeđuu Fourierovom nizu u kosinusima. Konstruirajte graf zbira niza.

Rješenje: proširimo funkciju u interval na paran način, odnosno konstruiramo novu parnu funkciju koja se poklapa sa funkcijom na intervalu. Nađimo koeficijente Fourierovog reda za funkciju i napišemo Fourierov red. Zbir Fourierovog reda za je periodična funkcija s tačkom. Poklapaće se sa funkcijom na svim tačkama kontinuiteta.

Trigonometrijski Fourierov red za funkciju će imati oblik

Nađimo koeficijente Fourierovog reda

Dakle, kada se pronađu koeficijenti, možemo napisati Fourierov red

Nacrtajmo zbir serije

Primjer 4. Zadana funkcija definirana na segmentu. Saznajte može li se funkcija proširiti u Fourierov niz. Napišite proširenje funkcije u Fourierov red.

Rješenje:

1) konstruirati graf funkcije na .

2) funkcija je neprekidna i monotona na , odnosno, prema Dirichletovom teoremu, može se proširiti u trigonometrijski Fourierov red.

3) izračunati Furijeove koeficijente koristeći formule (1.19).

4) napišite Fourierov red koristeći pronađene koeficijente.

2.2. Primjeri primjene Fourierovih redova u različitim područjima ljudske djelatnosti

Matematika je jedna od nauka koja ima široku primenu u praksi. Svaki proizvodni i tehnološki proces zasnovan je na matematičkim zakonima. Upotreba različitih matematičkih alata omogućava projektovanje uređaja i automatizovanih jedinica sposobnih za izvođenje operacija, složenih proračuna i proračuna u projektovanju zgrada i objekata.

Fourierove redove koriste matematičari u geometriji kadarješavanje problema iz sferne geometrije; u matematska fizika urješavanje problema o malim vibracijama elastičnih medija. No, osim matematike, Fourierovi redovi su svoju primjenu našli i u drugim oblastima nauke.

Ljudi svakodnevno koriste razne uređaje. I često ovi uređaji ne rade kako treba. Na primjer, zvuk je teško čuti zbog velike buke ili je slika primljena faksom nejasna. Osoba može utvrditi uzrok kvara zvukom. Računar također može dijagnosticirati da li je uređaj oštećen. Višak buke se može ukloniti korištenjem kompjuterske obrade signala. Signal se predstavlja kao niz digitalnih vrijednosti, koje se zatim unose u kompjuter. Nakon izvođenja određenih proračuna dobijaju se koeficijenti Fourierovog reda.

Promjenom spektra signala možete očistiti snimak od šuma, kompenzirati izobličenje signala raznim uređajima za snimanje, promijeniti tembre instrumenata i usmjeriti pažnju slušatelja na pojedine dijelove.

U digitalnoj obradi slike, upotreba Fourierove serije omogućava sljedeće efekte: zamućenje, naglašavanje rubova, restauracija slike, umjetnički efekti (utiskivanje)

Ekspanzija Fourierovog reda se koristi u arhitekturi u proučavanju oscilatornih procesa. Na primjer, prilikom izrade projekta za različite vrste konstrukcija izračunava se čvrstoća, krutost i stabilnost konstrukcijskih elemenata.

U medicini, za provođenje medicinskog pregleda uz pomoć kardiograma i ultrazvučnog aparata, koristi se matematički aparat koji se temelji na teoriji Fourierove serije.

Veliki računski problemi procjene statističkih karakteristika signala i filtriranja šuma javljaju se prilikom snimanja i obrade kontinuiranih podataka o morskom dnu. Prilikom izvođenja mjerenja i njihovog snimanja obećavajuće holografske metode koje koriste Fourierov niz. To jest, Fourierove serije se također koriste u nauci kao što je oceanologija.

Elementi matematike se nalaze u proizvodnji gotovo na svakom koraku, pa je važno da stručnjaci poznaju i budu dobro orijentisani u oblasti primene određenih alata za analizu i proračun.

Zaključak

Tema nastavnog rada je posvećena proučavanju Fourierovog reda. Proizvoljna funkcija se može proširiti u jednostavnije, odnosno može se proširiti u Fourierov red. Opseg rada na predmetu ne dozvoljava nam da detaljno otkrijemo sve aspekte proširenja funkcije u niz. Međutim, iz postavljenih zadataka činilo se mogućim otkriti osnovnu teoriju o Fourierovim redovima.

Predmetni rad otkriva koncept trigonometrijskog Fourierovog reda. Utvrđeni su uvjeti za razgradljivost funkcije u Fourierovom redu. Razmatraju se proširenja parnih i neparnih funkcija u Fourierov red; neperiodične funkcije.

Drugo poglavlje daje samo neke primjere proširenja funkcija datih na različitim intervalima u Fourierove redove. Opisane su oblasti nauke u kojima se ova transformacija koristi.

Postoji i složen oblik predstavljanja Fourierovog reda, koji se ne bi mogao uzeti u obzir jer obim nastavnog rada to ne dozvoljava. Složeni oblik niza je algebarski jednostavan. Stoga se često koristi u fizici i primijenjenim proračunima.

Važnost teme nastavnog rada je zbog činjenice da se ona široko koristi ne samo u matematici, već iu drugim naukama: fizici, mehanici, medicini, hemiji i mnogim drugim.

Bibliografija

1. Bari, N.K. Trigonometrijski niz. [tekst]/ N.K. Bari. - Moskva, 1961. - 936 s.

2. Bermant, A.F. Kratki kurs matematičke analize: udžbenik za univerzitete[tekst]/ A.F. Bermant, I.G. Aramanović. – 11. izd., izbrisano. – Sankt Peterburg: Izdavačka kuća “Lan”, 2005. – 736 str.

3. Bugrov, Ya. S. Viša matematika: Udžbenik za univerzitete: U 3 toma.[tekst]/ Ya. S. Bugrov, S. M. Nikolsky; Ed. V. A. Sadovnichy. - 6. izd., stereotip. - M.: Drfa, 2004. -512 str.

4. Vinogradova, I. A. Problemi i vježbe iz matematičke analize: priručnik za univerzitete, pedagoški. univerziteti: U 2 sata.[tekst]/ I. A. Vinogradova, S. N. Olehnik, V. A. Sadovnichy; uređeno od V.A. Sadovnichigo. – 3. izd., rev. – M.: Drfa, 2001. – 712 str.

5. Gusak, A.A. Viša matematika. U 2 toma T. 2. Udžbenik za studente.[tekst]/ A. A. Gusak.– 5. izd. – Minsk: TetraSystems, 2004.

6. Danko, P.E. Viša matematika u vježbama i zadacima: udžbenik za fakultete: 2 sata.[tekst]/ P.E. Danko, A.G. Popov, T.Ya. Kozhevnikova. Moskva: ONIX: Mir i obrazovanje, 2003. – 306 str.

7. Lukin, A. Uvod u digitalnu obradu signala (matematičke osnove) [tekst]/ A. Lukin. - M., 2007. - 54 str.

8. Piskunov, N. S. Diferencijalni i integralni račun za fakultete, tom 2: Udžbenik za fakultete.[tekst]/ N. S. Piskunov. - 13. izd. - M.: Nauka, 1985. - 432 str.

9. Rudin, U. Osnove matematičke analize.[tekst]/ U. Rudin. - 2. izd., Trans. sa engleskog .- M.: Mir, 1976.- 206 str.

10. Fikhtengolts, G. M. Osnove matematičke analize. Dio 2.[tekst]/ G. M. Fikhtengolts. -6. izdanje, izbrisano. - Sankt Peterburg: Izdavačka kuća Lan, 2005. – 464 str.

Orenburg, 2015