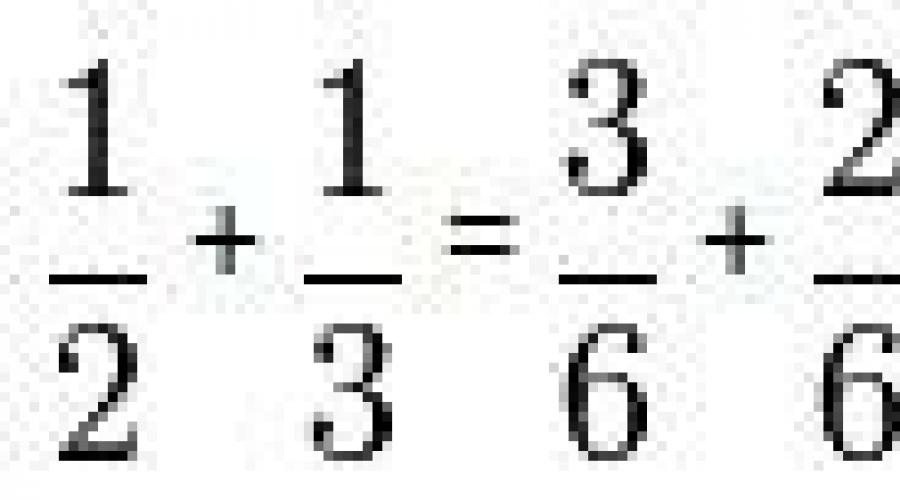
U članku ćemo pokazati kako riješiti razlomke na jednostavnom razumljivi primjeri. Hajde da shvatimo šta je razlomak i razmotrimo rješavanje razlomaka!

koncept razlomci uvodi se u predmet matematike počev od 6. razreda srednje škole.

Razlomci izgledaju ovako: ±X / Y, gdje je Y imenilac, govori na koliko je dijelova podijeljena cjelina, a X je brojilac, govori koliko je takvih dijelova uzeto. Radi jasnoće, uzmimo primjer s tortom:

U prvom slučaju se kolač jednako seče i uzima se jedna polovina, tj. 1/2. U drugom slučaju, torta je isječena na 7 dijelova, od kojih su uzeta 4 dijela, tj. 4/7.

Ako dio dijeljenja jednog broja drugim nije cijeli broj, zapisuje se kao razlomak.

Na primjer, izraz 4:2 \u003d 2 daje cijeli broj, ali 4:7 nije potpuno djeljiv, pa se ovaj izraz zapisuje kao razlomak 4/7.

Drugim riječima frakcija je izraz koji označava podjelu dva broja ili izraza i koji se piše kosom crtom.

Ako je brojilac manji od imenioca- razlomak je tačan, ako je obrnuto - netačan. Razlomak može sadržavati cijeli broj.

Na primjer, 5 cijelih 3/4.

Ovaj unos znači da za dobijanje celih 6 jedan deo od četiri nije dovoljan.

Ako želite da zapamtite kako riješiti razlomke za 6. razred morate to shvatiti rješavanje razlomaka u osnovi se svodi na razumijevanje nekoliko jednostavnih stvari.

• Razlomak je u suštini izraz za razlomak. tj numerički izraz koliki je dio date vrijednosti iz jedne cjeline. Na primjer, razlomak 3/5 izražava da ako podijelimo nešto cijelo na 5 dijelova i broj dijelova ili dijelova ove cjeline je tri.
• Razlomak može biti manji od 1, na primjer 1/2 (ili u suštini polovina), tada je ispravan. Ako je razlomak veći od 1, na primjer 3/2 (tri polovine ili jedan i po), onda je netačno i da pojednostavimo rješenje, bolje je da odaberemo cijeli dio 3/2= 1 cijeli 1 /2.
• Razlomci su isti brojevi kao 1, 3, 10, pa čak i 100, samo brojevi nisu cijeli, već razlomci. S njima možete izvršiti sve iste operacije kao i s brojevima. Brojanje razlomaka nije teže, i dalje konkretnim primjerima pokazaćemo to.

Kako riješiti razlomke. Primjeri.

Na razlomke su primjenjive razne aritmetičke operacije.

Dovođenje razlomka na zajednički nazivnik

Na primjer, trebate uporediti razlomke 3/4 i 4/5.

Da bismo riješili problem, prvo nađemo najmanji zajednički imenilac, tj. najmanji broj, koji je bez ostatka djeljiv sa svakim od nazivnika razlomaka

Najmanji zajednički imenilac (4.5) = 20

Tada se imenilac oba razlomka svodi na najmanji zajednički imenilac

Odgovor: 15/20

Sabiranje i oduzimanje razlomaka

Ako je potrebno izračunati zbir dva razlomka, oni se prvo dovode do zajedničkog imenioca, zatim se sabiraju brojnici, a imenilac ostaje nepromijenjen. Razlika razlomaka se razmatra na sličan način, jedina razlika je u tome što se brojioci oduzimaju.

Na primjer, trebate pronaći zbir razlomaka 1/2 i 1/3

Sada pronađite razliku između razlomaka 1/2 i 1/4

Množenje i dijeljenje razlomaka

Ovdje je rješenje razlomaka jednostavno, ovdje je sve prilično jednostavno:

• Množenje - brojnici i imenioci razlomaka se međusobno množe;
• Dijeljenje - prvo dobijemo razlomak, recipročnu vrijednost drugog razlomka, tj. zamijenite njegov brojnik i nazivnik, nakon čega množimo rezultirajuće razlomke.

Na primjer:

O ovome o kako riješiti razlomke, sve. Ako imate bilo kakvih pitanja o rješavanje razlomaka, nešto nije jasno, onda pišite u komentarima pa ćemo vam odgovoriti.

Ako ste nastavnik, prezentaciju je moguće preuzeti osnovna škola(http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) dobro će doći.

Aritmetičke operacije s običnim razlomcima

1. Dodatak.

Da biste sabrali razlomke sa istim nazivnicima, dodajte njihove brojioce i ostavite nazivnik istim.

Primjer. .

Za dodavanje razlomaka sa različiti imenioci, potrebno ih je dovesti na najmanji zajednički imenilac, a zatim dodati dobijene brojioce i potpisati zajednički imenilac ispod zbroja.

Primjer.

Ukratko napisano ovako:

Da biste dodali mješovite brojeve, morate zasebno pronaći zbir cijelih brojeva i zbir razlomaka. Akcija je napisana ovako:

2. Oduzimanje.

Da biste oduzeli razlomke sa istim nazivnicima, potrebno je da oduzmete brojnik oduzetog od brojnika minusa i ostavite isti imenilac. Akcija je napisana ovako:

Da biste oduzeli razlomke sa različitim nazivnicima, prvo ih morate dovesti do najmanjeg zajedničkog imenioca, zatim od brojnika minusa oduzeti brojnik oduzetog i potpisati zajednički imenilac ispod njihove razlike. Akcija je napisana ovako:

Ako trebate oduzeti jedan mješoviti broj od drugog mješovitog broja, onda, ako je moguće, oduzmite razlomak od razlomka, a cijeli od cjeline. Akcija je napisana ovako:

Ako je razlomak odbitka veći od razlomka minuenda, tada se od cijelog broja minuenda uzima jedna jedinica, dijeli se na odgovarajuće udjele i dodaje razlomku minuenda, nakon čega se nastavlja kako je opisano. iznad. Akcija je napisana ovako:

Uradite isto kada trebate oduzeti razlomak od cijelog broja.

Primjer. .

3. Proširenje svojstava sabiranja i oduzimanja na razlomke.Svi zakoni i svojstva sabiranja i oduzimanja prirodni brojevi važi i za razlomke. Njihova upotreba u mnogim slučajevima uvelike pojednostavljuje proces izračunavanja.

4. Množenje.

Da biste pomnožili razlomak razlomkom, potrebno je pomnožiti brojilac sa brojicom, a nazivnik sa imeniocem i prvi proizvod učiniti brojnikom, a drugi proizvod nazivnikom.

Prilikom množenja treba izvršiti (ako je moguće) redukciju.

Primjer. .

Ako uzmemo u obzir da je cijeli broj razlomak s nazivnikom 1, tada se množenje razlomka cijelim brojem i cijelog broja razlomkom može izvesti po istom pravilu.

Primjeri.

5. Množenje mešoviti brojevi.

Da biste pomnožili mješovite brojeve, prvo ih morate pretvoriti u nepravilni razlomci a zatim pomnožite po pravilu množenja razlomaka.

Primjer. .

6. Podjela razlomka razlomkom.

Da biste razlomak podijelili razlomkom, trebate pomnožiti brojilac prvog razlomka sa nazivnikom drugog, a nazivnik prvog s brojnikom drugog i prvi proizvod napisati kao brojilac, a drugi kao imenilac.

Primjer. .

Po istom pravilu, možete podijeliti razlomak cijelim brojem, a cijeli broj razlomkom, ako cijeli broj predstavite kao razlomak s nazivnikom 1.

Primjeri.

7. Podjela mješovitih brojeva.

Da bi se izvršilo dijeljenje mješovitih brojeva, oni se prvo pretvaraju u nepravilne razlomke, a zatim dijele prema pravilu za dijeljenje razlomaka.

Primjer. .

8. Zamjena dijeljenja množenjem.

Ako zamenite brojilac i imenilac u bilo kom razlomku, dobićete novi razlomak, obrnuto od ovog. Na primjer, za razlomakrecipročno će biti.

Očigledno, proizvod dvije recipročne vrijednosti je 1.

1. Pronalaženje razlomka broja.

Postoji mnogo zadataka u kojima morate pronaći dio ili dio datog broja. Takvi se problemi rješavaju množenjem.

Zadatak. Domaćica je imala 20 rubalja;koristila ih je za kupovinu. Koliko koštaju kupovine?

Ovdje morate pronaćibroj 20. Možete to učiniti ovako:

Odgovori. Domaćica je potrošila 8 rubalja.

Primjeri. Pronađite od 30. Rješenje. .

Pronađite od . Odluka. .

1. Pronalaženje broja po poznatoj vrijednosti njegovog razlomka.

Ponekad je potrebno odrediti cijeli broj iz poznatog dijela broja i razlomka koji izražava ovaj dio. Takvi zadaci se rješavaju podjelom.

Zadatak. U razredu ima 12 komsomolaca, tjdeo svih učenika u razredu. Koliko učenika ima u razredu?

Odluka. .

Odgovori. 20 studenata.

Primjer. Nađi brojšto je 34.

Odluka. .

Odgovori. Željeni broj je.

1. Pronalaženje omjera dva broja.

Hajde da razmotrimo problem: Radnik je napravio 40 delova za jedan dan. Koji dio mjesečnog zadatka je izvršio radnik ako je mjesečni plan 400 dijelova?

Odluka. .

Odgovori. Radnik završendio mjesečnog plana.

AT ovaj slučaj dio (40 dijelova) izražava se u razlomcima cjeline (400 dijelova). Kažu i da je pronađen omjer broja dnevno proizvedenih dijelova prema mjesečnom planu.

1. Pretvaranje decimale u običan razlomak.

Za pretvaranje decimalni u običan, piše se sa nazivnikom i, ako je moguće, redukuje:

Primjeri.

1. Pretvaranje razlomka u decimalu.

Postoji nekoliko načina da se obični razlomak pretvori u decimalu.

Prvi način. Da biste razlomak pretvorili u decimalu, trebate podijeliti brojilac sa nazivnikom.

Primjeri. .

Drugi način. Da biste obični razlomak pretvorili u decimalu, trebate pomnožiti brojilac i nazivnik ovog razlomka s takvim brojem da nazivnik bude jedan sa nulama (ako je moguće).

Primjer.

1. Uporedite decimale po veličini. Da biste saznali koji je od dva decimalna razlomka veći, potrebno je uporediti njihove cijele dijelove, desetine, stotinke itd. Ako su cijeli dijelovi jednaki, razlomak sa više desetina je veći; ako su cijeli brojevi i decimali jednaki, veći je onaj s više stotinki, itd.

Primjer. Od tri razlomka 2,432; 2,41 i 2,4098 je najveći prvi, jer ima najviše stotinki, a cijeli i deseti dio su isti u svim razlomcima.

Operacije sa decimalama

1. Množenje i dijeljenje decimale sa 10, 100, 1000, itd.

Da pomnožite decimalu sa 10, 100, 1000, itd. morate pomjeriti zarez na jedan, dva, tri, itd. znak desno. Ako u isto vrijeme nema dovoljno znakova za broj, tada se dodjeljuju nule.

Primjer. 15,45 10 = 154,5; 32,3 100 = 3230.

Da biste decimalu podijelili sa 10, 100, 1000, itd., trebate pomjeriti zarez na jedan, dva, tri, itd. znak lijevo. Ako nema dovoljno znakova za pomicanje zareza, njihov broj se dopunjava odgovarajućim brojem nula na lijevoj strani.

Primjeri. 184,35: 100 = 1,8435; 3,5: 100 = 0,035.

1. Zbrajanje i oduzimanje decimalnih razlomaka.

Decimale se sabiraju i oduzimaju na isti način kao što se sabiraju i oduzimaju prirodni brojevi. Cifra se upisuje ispod cifre, a zarez se piše ispod zareza

Primjeri.

1. Množenje decimala.

Za množenje dva decimalna razlomka dovoljno je, ne obraćajući pažnju na zareze, pomnožiti ih kao cijele brojeve i u proizvodu odvojiti zarezom na desnoj strani onoliko decimalnih mjesta koliko ih je bilo u množeniku i činiti zajedno.

Primjer 1. 2,064 0,05.

Množimo cijele brojeve 2064 5 = 10320. Prvi faktor je imao tri decimale, drugi - dva. Proizvod mora imati pet decimalnih mjesta. Odvajamo ih na desnoj strani i dobijamo 0,10320. Nula na kraju se može odbaciti: 2,064 0,05 = 0,1032.

Primjer 2. 1,125 0,08; 1125 8 = 9000.

Broj decimalnih mjesta bi trebao biti 3 + 2 = 5. Dodjeljujemo nule lijevo od 9000 (009000) i odvajamo pet znakova sa desne strane. Dobijamo 1,125 0,08 = 0,09000 = 0,09.

1. Podjela decimala.

Razmatraju se dva slučaja deljenja decimalnih razlomaka bez ostatka: 1) deljenje decimalnog razlomka celim brojem; 2) dijeljenje broja (cjelog ili razlomka) sa decimalnim razlomkom.

Dijeljenje decimale cijelim brojem je isto kao i dijeljenje cijelih brojeva; rezultujući ostaci se dijele uzastopno na manje decimalne dijelove i dijeljenje se nastavlja sve dok ostatak ne bude nula.

Primjeri.

Dijeljenje broja (cijelog ili razlomka) decimalom u svim slučajevima dovodi do dijeljenja cijelim brojem. Da biste to učinili, povećajte djelitelj za 10, 100, 1000 itd. puta, a kako se količnik ne bi promijenio, dividenda se povećava za isti broj puta, nakon čega se dijeli cijelim brojem (kao u prvom slučaju).

Primjer. 47,04: 0,0084 = 470400: 84 = 5600;

1. Primjeri na saradnja sa običnim i decimalnim razlomcima.

Razmotrimo prvo primjer za sve radnje s decimalnim razlomcima.

Primjer 1 Izračunajte:

Ovdje koriste redukciju dividende i djelitelja na cijeli broj, uzimajući u obzir činjenicu da se količnik ne mijenja. tada imamo:

Prilikom rješavanja primjera za zajedničke radnje s običnim i decimalnim razlomcima neke od radnji se mogu izvesti u decimalnim razlomcima, a neke u običnim. Mora se imati na umu da nije uvijek običan razlomak može se pretvoriti u konačnu decimalu. Stoga je zapisivanje kao decimalni razlomak moguće samo kada je potvrđeno da je takva konverzija moguća.

Primjer 2 Izračunajte:

Interes

Koncept interesa.Procenat broja je stoti dio tog broja. Na primjer, umjesto da kažete "54 posto svih stanovnika naše zemlje su žene", možete reći "54 posto svih stanovnika naše zemlje su žene". Umjesto riječi "postotak" pišu i znak %, na primjer, 35% znači 35 posto.

Kako je postotak stoti dio, slijedi da je taj postotak razlomak sa nazivnikom 100. Dakle, razlomak je 0,49, odnosno, može se čitati kao 49 posto i pisati bez nazivnika kao 49%. Općenito, nakon utvrđivanja koliko stotinki je u datom decimalnom razlomku, lako ga je zapisati kao postotak. Da biste to učinili, koristite pravilo: da biste zapisali decimalni razlomak kao postotak, morate pomaknuti zarez u ovom razlomku dvije znamenke udesno.

Primjeri. 0,33 = 33%; 1,25 = 125%; 0,002 = 0,2%; 21 = 2100%.

I obrnuto: 7% = 0,07; 24,5% = 0,245; 0,1% = 0,001; 200% = 2.

1. Pronalaženje postotaka datog broja

Zadatak. Prema planu, ekipa traktorista mora da potroši 9 tona goriva. Traktoristi su preuzeli socijalnu obavezu da uštede 20% goriva. Odredite uštedu goriva u tonama.

Ako u ovom zadatku umjesto 20% zapišemo njemu jednak broj 0,2, dobićemo problem da pronađemo razlomak broja. A takvi problemi se rješavaju množenjem. Odavde dolazi rješenje:

20% = 0,2; 9 0,2 = 1,8 (m).

Izračuni se mogu napisati i ovako:

(m)

Da biste pronašli nekoliko procenata datog broja, dovoljno je dati broj podijeliti sa 100 i rezultat pomnožiti sa brojem postotaka.

Zadatak. Radnik je 1963. primao 90 rubalja mjesečno, a 1964. počeo je primati 30% više. Koliko je zaradio 1964. godine?

Rješenje (prva metoda).

1) Koliko je još rubalja dobio radnik?

(rub.)

90 + 27 = 117 (rub).

Drugi način.

1) Koliki je procenat prethodne zarade radnik primao 1964. godine?

100% + 30% = 130%.

2) Kolika je bila mjesečna plata radnika 1964. godine?

(rub.)

2. Pronalaženje broja iz date vrijednosti njegovog procenta.

Zadatak. Na kolskom imanju kukuruz je zasejan na površini od 280 hektara, što je 14% od ukupne zasejane površine. Odrediti zasejanu površinu kolektivne farme.

Ako u ovom zadatku umjesto 14% upišemo 0,14 ili, tada dobijamo problem pronalaženja broja po poznatoj vrijednosti njegovog razlomka. A takvi problemi se rješavaju podjelom.

Odluka. 14% = 0,14; 280: 0,14 = 2000 (ha). Ovu odluku možete donijeti na sljedeći način:

(ha)

Da biste pronašli broj za datu vrijednost od nekoliko postotaka, dovoljno je ovu vrijednost podijeliti brojem postotaka i rezultat pomnožiti sa 100.

Zadatak. U martu je fabrika istopila 125,4 t metala, premašivši plan za 4,5%. Koliko je tona metala fabrika prema planu trebala da istopi u martu?

Odluka.

1) U kom procentu je fabrika ispunila plan u martu?

100% + 4,5% = 104,5%.

2) Koliko je tona metala fabrika morala da istopi?

(ha)

1. Određivanje procenta dva broja.

Zadatak. Potrebno je preorati 300 hektara zemlje. Prvog dana je poorano 120 hektara. Koliki je postotak zadatka obavljen prvog dana?

Odluka.

Prvi način. 300 ha je 100%, što znači da 1% otpada na 3 ha. Nakon što smo utvrdili koliko puta 3 hektara, što je 1%, sadržano u 120 hektara, saznaćemo koliko je posto zadatka zemljište bilo preorano prvog dana

120: 3 = 40(%).

Drugi način. Nakon što smo utvrdili koji je dio zemlje izoran prvog dana, ovaj dio izražavamo u postocima.

Napišimo računicu:

Za izračunavanje procenta broja a do broja b , morate pronaći omjer a do b i pomnožite ga sa 100.

Ovaj članak je o obični razlomci. Ovdje ćemo se upoznati s pojmom razlomka cjeline, što će nas dovesti do definicije običnog razlomka. Zatim ćemo se zadržati na prihvaćenom zapisu za obične razlomke i dati primjere razlomaka, recimo o brojniku i nazivniku razlomka. Nakon toga daćemo definicije tačnih i nepravilnih, pozitivnih i negativnih razlomaka, a takođe ćemo razmotriti položaj razlomaka na koordinatni snop. U zaključku navodimo glavne radnje sa razlomcima.

Navigacija po stranici.

Dionice cjeline

Prvo predstavljamo dijele koncept.

Pretpostavimo da imamo neki objekat sastavljen od nekoliko apsolutno identičnih (odnosno jednakih) delova. Radi jasnoće, možete zamisliti, na primjer, jabuku izrezanu na nekoliko dijelova jednaki dijelovi, ili narandža, koja se sastoji od nekoliko jednakih kriški. Svaki od ovih jednakih dijelova koji čine cijeli objekt naziva se udeo u celini ili jednostavno dionice.

Imajte na umu da su udjeli različiti. Hajde da objasnimo ovo. Recimo da imamo dvije jabuke. Prvu jabuku prerežemo na dva jednaka dijela, a drugu na 6 jednakih dijelova. Jasno je da će se udio prve jabuke razlikovati od udjela druge jabuke.

Ovisno o broju dionica koje čine cijeli objekt, ove dionice imaju vlastita imena. Hajde da analiziramo dijeliti imena. Ako se predmet sastoji od dva dijela, bilo koji od njih se naziva jednim drugim dijelom cijelog objekta; ako se objekt sastoji od tri dijela, onda se bilo koji od njih naziva jednim trećim dijelom, i tako dalje.

Jedan drugi ritam ima posebno ime - pola. Jedna trećina se zove treći, i jedan četvorostruki - kvartal.

Radi kratkoće, sledeće oznake udjela. Jedna druga akcija označava se kao ili 1/2, jedna trećina akcija - kao ili 1/3; jedna četvrtina dionica - lajk ili 1/4 i tako dalje. Imajte na umu da se zapis s horizontalnom trakom češće koristi. Da bismo konsolidirali gradivo, navedimo još jedan primjer: upis označava sto šezdeset sedmu cjelinu.

Koncept udjela prirodno se proteže od objekata do veličina. Na primjer, jedna od mjera za dužinu je metar. Za mjerenje dužina manjih od metra mogu se koristiti razlomci metra. Dakle, možete koristiti, na primjer, pola metra ili deseti dio ili hiljaditi dio metra. Slično se primjenjuju udjeli ostalih količina.

Obični razlomci, definicija i primjeri razlomaka

Za opisivanje se koristi broj dionica obični razlomci. Navedimo primjer koji će nam omogućiti da pristupimo definiciji običnih razlomaka.

Neka se narandža sastoji od 12 dijelova. Svaka dionica u ovom slučaju predstavlja jednu dvanaestinu cijele narandže, odnosno . Označimo dva otkucaja kao , tri otkucaja kao , I tako dalje, 12 otkucaja kao . Svaki od ovih unosa naziva se običan razlomak.

Sada dajmo generala definicija običnih razlomaka.

Izražena definicija običnih razlomaka nam omogućava da donesemo primjeri običnih razlomaka: 5/10 , , 21/1 , 9/4 , . A evo i zapisa ne uklapaju se u izraženu definiciju običnih razlomaka, odnosno nisu obični razlomci.

Brojač i nazivnik

Radi praktičnosti razlikujemo u običnim razlomcima brojilac i imenilac.

Definicija.

Brojač obični razlomak (m/n) je prirodan broj m.

Definicija.

Nazivnik obični razlomak (m/n) je prirodan broj n.

Dakle, brojilac se nalazi iznad linije razlomaka (lijevo od kose crte), a imenilac ispod linije razlomka (desno od kose crte). Na primjer, uzmimo običan razlomak 17/29, brojilac ovog razlomka je broj 17, a nazivnik je broj 29.

Ostaje raspraviti značenje sadržano u brojniku i nazivniku običnog razlomka. Imenitelj razlomka pokazuje od koliko se dionica sastoji jedna stavka, brojnik, zauzvrat, označava broj takvih dionica. Na primjer, nazivnik 5 razlomka 12/5 znači da se jedna stavka sastoji od pet dijelova, a brojnik 12 znači da je uzeto 12 takvih dijelova.

Prirodni broj kao razlomak sa nazivnikom 1

Imenilac običnog razlomka može biti jednak jedan. U ovom slučaju možemo pretpostaviti da je predmet nedjeljiv, drugim riječima, da je nešto cjelovito. Brojač takvog razlomka pokazuje koliko je cijelih predmeta uzeto. Dakle, običan razlomak oblika m/1 ima značenje prirodnog broja m. Ovako smo potkrijepili jednakost m/1=m .

Zapišimo posljednju jednakost ovako: m=m/1 . Ova jednakost nam omogućava da bilo koji prirodni broj m predstavimo kao običan razlomak. Na primjer, broj 4 je razlomak 4/1, a broj 103498 je razlomak 103498/1.

dakle, svaki prirodni broj m može se predstaviti kao običan razlomak sa nazivnikom 1 kao m/1, a svaki obični razlomak oblika m/1 može se zamijeniti prirodnim brojem m.

Razlomak kao znak dijeljenja

Predstavljanje originalnog objekta u obliku n dionica nije ništa drugo do podjela na n jednakih dijelova. Nakon što se stavka podijeli na n dionica, možemo je podijeliti na n ljudi - svaki će dobiti po jednu dionicu.

Ako u početku imamo m identičnih objekata, od kojih je svaki podijeljen na n dionica, onda možemo jednako podijeliti ovih m objekata na n ljudi, dajući svakoj osobi po jedan dio od svakog od m objekata. U ovom slučaju, svaka osoba će imati m dionica 1/n, a m dionica 1/n daje običan razlomak m/n. Dakle, zajednički razlomak m/n može se koristiti za predstavljanje podjele m stavki između n ljudi.

Tako smo dobili eksplicitnu vezu između običnih razlomaka i dijeljenja (pogledajte opću ideju dijeljenja prirodnih brojeva). Ovaj odnos se izražava na sljedeći način: Šipka razlomka se može shvatiti kao znak dijeljenja, odnosno m/n=m:n.

Uz pomoć običnog razlomka možete napisati rezultat dijeljenja dva prirodna broja za koja se dijeljenje ne vrši cijelim brojem. Na primjer, rezultat dijeljenja 5 jabuka sa 8 ljudi može se zapisati kao 5/8, odnosno svaki će dobiti pet osminki jabuke: 5:8=5/8.

Jednaki i nejednaki obični razlomci, poređenje razlomaka

Prilično prirodna akcija je poređenje običnih razlomaka, jer je jasno da se 1/12 narandže razlikuje od 5/12, a 1/6 jabuke je isto kao i druga 1/6 ove jabuke.

Kao rezultat poređenja dva obična razlomka, dobije se jedan od rezultata: razlomci su ili jednaki ili nisu jednaki. U prvom slučaju imamo jednaki obični razlomci, au drugom nejednaki obični razlomci. Hajde da damo definiciju jednakih i nejednakih običnih razlomaka.

Definicija.

jednaka, ako je jednakost a d=b c tačna.

Definicija.

Dva obična razlomka a/b i c/d nije jednako, ako jednakost a d=b c nije zadovoljena.

Evo nekoliko primjera jednakih razlomaka. Na primjer, obični razlomak 1/2 jednak je razlomku 2/4, jer je 1 4=2 2 (ako je potrebno, pogledajte pravila i primjere množenja prirodnih brojeva). Radi jasnoće, možete zamisliti dvije identične jabuke, prva je prepolovljena, a druga - na 4 dijela. Očigledno je da je dvije četvrtine jabuke 1/2 dionice. Drugi primjeri jednakih običnih razlomaka su razlomci 4/7 i 36/63, te par razlomaka 81/50 i 1620/1000.

A obični razlomci 4/13 i 5/14 nisu jednaki, jer je 4 14=56 i 13 5=65, odnosno 4 14≠13 5. Drugi primjer nejednakih običnih razlomaka su razlomci 17/7 i 6/4.

Ako se pri usporedbi dva obična razlomka pokaže da nisu jednaki, možda ćete morati saznati koji od ovih običnih razlomaka manji drugi, i koji više. Da bismo saznali, koristi se pravilo za poređenje običnih razlomaka, čija je suština da se uspoređeni razlomci dovedu do zajedničkog nazivnika, a zatim uporede brojioce. Detaljne informacije o ovoj temi prikupljene su u članku usporedba razlomaka: pravila, primjeri, rješenja.

Razlomci brojeva

Svaki razlomak je zapis razlomak broj. To jest, razlomak je samo „ljuska“ razlomka, njegov izgled, a cjelokupno semantičko opterećenje sadržano je upravo u razlomku. Međutim, radi sažetosti i praktičnosti, koncept razlomka i razlomka se kombiniraju i jednostavno nazivaju razlomak. Ovdje je prikladno preformulisati poznata izreka: kažemo razlomak - mislimo razlomak broj, kažemo razlomak - mislimo na razlomak.

Razlomci na koordinatnoj gredi

Svi frakcijski brojevi koji odgovaraju običnim razlomcima imaju svoje jedinstveno mjesto na , odnosno postoji korespondencija jedan prema jedan između razlomaka i tačaka koordinatnog zraka.

Da bi se došlo do tačke koja odgovara razlomku m/n na koordinatnoj zraci, potrebno je odložiti m segmenata od početka u pozitivnom pravcu, čija je dužina 1/n jediničnog segmenta. Takvi segmenti se mogu dobiti dijeljenjem jednog segmenta na n jednakih dijelova, što se uvijek može učiniti pomoću šestara i ravnala.

Na primjer, pokažimo tačku M na koordinatnoj zraci, koja odgovara razlomku 14/10. Dužina segmenta čiji su krajevi u tački O i tački najbliže njoj, označene malom crticom, iznosi 1/10 jediničnog segmenta. Tačka sa koordinatom 14/10 udaljena je od početka za 14 takvih segmenata.

Jednaki razlomci odgovaraju istom razlomku, tj. jednakih razlomaka su koordinate iste tačke na koordinatnoj zraci. Na primjer, jedna tačka odgovara koordinatama 1/2, 2/4, 16/32, 55/110 na koordinatnoj zraci, pošto su svi napisani razlomci jednaki (nalazi se na udaljenosti od polovine jediničnog segmenta, odloženo od ishodište u pozitivnom smjeru).

Na horizontalnoj i desno usmjerenoj koordinatnoj zraci, tačka čija je koordinata veliki razlomak nalazi se desno od tačke čija je koordinata manji razlomak. Slično, tačka sa manjom koordinatom leži levo od tačke sa većom koordinatom.

Pravi i nepravilni razlomci, definicije, primjeri

Među običnim razlomcima ima ih pravilni i nepravilni razlomci. Ova podjela u osnovi ima poređenje brojnika i nazivnika.

Hajde da damo definiciju pravih i nepravilnih običnih razlomaka.

Definicija.

Pravilan razlomak je običan razlomak čiji je brojilac manji od nazivnika, odnosno ako je m

Definicija.

Nepravilan razlomak je običan razlomak u kojem je brojilac veći ili jednak nazivniku, odnosno, ako je m≥n, tada je obični razlomak nepravilan.

Evo nekoliko primjera pravih razlomaka: 1/4 , , 32 765/909 003 . Zaista, u svakom od napisanih običnih razlomaka, brojilac je manji od nazivnika (ako je potrebno, pogledajte članak poređenje prirodnih brojeva), tako da su oni tačni po definiciji.

A evo primjera nepravilnih razlomaka: 9/9, 23/4,. Zaista, brojilac prvog od napisanih običnih razlomaka jednak je nazivniku, a u preostalim razlomcima brojilac je veći od nazivnika.

Postoje i definicije pravih i nepravilnih razlomaka zasnovanih na upoređivanju razlomaka sa jedan.

Definicija.

ispravan ako je manji od jedan.

Definicija.

Običan razlomak se zove pogrešno, ako je ili jednako jedan ili veće od 1 .

Dakle, obični razlomak 7/11 je tačan, budući da je 7/11<1 , а обыкновенные дроби 14/3 и 27/27 – неправильные, так как 14/3>1 i 27/27=1.

Razmislimo o tome kako obični razlomci s brojnikom većim ili jednakim nazivniku zaslužuju takvo ime - "pogrešno".

Uzmimo nepravilan razlomak 9/9 kao primjer. Ovaj razlomak znači da se uzima devet dijelova objekta koji se sastoji od devet dijelova. Odnosno, od raspoloživih devet dionica možemo sastaviti cijeli predmet. To jest, nepravilan razlomak 9/9 u suštini daje cijeli objekt, to jest, 9/9=1. Općenito, nepravilni razlomci sa brojicom jednakim nazivniku označavaju jedan cijeli objekt, a takav razlomak se može zamijeniti prirodnim brojem 1.

Sada razmotrite nepravilne razlomke 7/3 i 12/4. Sasvim je očito da od ovih sedam trećina možemo napraviti dva cijela objekta (jedan cijeli objekt je 3 udjela, a za sastavljanje dva cijela objekta treba nam 3 + 3 = 6 dionica) i još će biti jedna trećina udjela. Odnosno, nepravilan razlomak 7/3 u suštini znači 2 stavke, pa čak i 1/3 udjela takve stavke. A od dvanaest četvrtina možemo napraviti tri cijela objekta (tri objekta sa po četiri dijela). To jest, razlomak 12/4 u suštini znači 3 cijela objekta.

Razmatrani primjeri dovode nas do sljedećeg zaključka: nepravilni razlomci se mogu zamijeniti ili prirodnim brojevima, kada se brojilac u potpunosti podijeli sa nazivnikom (na primjer, 9/9=1 i 12/4=3), ili zbirom prirodni broj i pravi razlomak, kada brojilac nije jednako djeljiv sa nazivnikom (na primjer, 7/3=2+1/3). Možda je to upravo ono što nepravilni razlomci zaslužuju takvo ime - "pogrešno".

Posebno je zanimljivo predstavljanje nepravilnog razlomka kao zbira prirodnog broja i pravog razlomka (7/3=2+1/3). Ovaj proces se zove ekstrakcija cijelog broja iz nepravilnog razlomka i zaslužuje posebno i pažljivije razmatranje.

Također je vrijedno napomenuti da postoji vrlo bliska veza između nepravilnih razlomaka i mješovitih brojeva.

Pozitivni i negativni razlomci

Svaki obični razlomak odgovara pozitivnom razlomku (pogledajte članak pozitivni i negativni brojevi). To jest, obični razlomci jesu pozitivni razlomci. Na primjer, obični razlomci 1/5, 56/18, 35/144 su pozitivni razlomci. Kada je potrebno naglasiti pozitivnost razlomka, tada se ispred njega stavlja znak plus, na primjer, +3/4, +72/34.

Ako stavite znak minus ispred običnog razlomka, tada će ovaj unos odgovarati negativnom razlomku. U ovom slučaju se može govoriti o negativni razlomci. Evo nekoliko primjera negativnih razlomaka: −6/10 , −65/13 , −1/18 .

Pozitivni i negativni razlomci m/n i −m/n su suprotni brojevi. Na primjer, razlomci 5/7 i −5/7 su suprotni razlomci.

Pozitivni razlomci, kao i pozitivni brojevi općenito, označavaju povećanje, prihod, promjenu neke vrijednosti naviše, itd. Negativni razlomci odgovaraju trošku, dugu, promjeni bilo koje vrijednosti u smjeru smanjenja. Na primjer, negativan razlomak -3/4 može se tumačiti kao dug čija je vrijednost 3/4.

Na horizontalnoj i desnoj strani negativni razlomci nalaze se lijevo od referentne točke. Tačke koordinatne linije čije su koordinate pozitivni razlomak m/n i negativni razlomak −m/n nalaze se na istoj udaljenosti od početka, ali na suprotnim stranama tačke O.

Ovdje je vrijedno spomenuti razlomke oblika 0/n. Ovi razlomci su jednaki broju nula, odnosno 0/n=0.

Pozitivni razlomci, negativni razlomci i 0/n razlomci se kombinuju da formiraju racionalne brojeve.

Radnje sa razlomcima

Jednu radnju s običnim razlomcima - upoređivanje razlomaka - već smo razmotrili gore. Definirane su još četiri aritmetike operacije sa razlomcima- sabiranje, oduzimanje, množenje i dijeljenje razlomaka. Hajde da se zadržimo na svakom od njih.

Opća suština radnji s razlomcima slična je suštini odgovarajućih radnji s prirodnim brojevima. Hajde da povučemo analogiju.

Množenje razlomaka može se smatrati radnjom u kojoj se iz razlomka nalazi razlomak. Da pojasnimo, uzmimo primjer. Pretpostavimo da imamo 1/6 jabuke i da moramo uzeti 2/3 od nje. Dio koji nam treba je rezultat množenja razlomaka 1/6 i 2/3. Rezultat množenja dva obična razlomka je običan razlomak (koji je u određenom slučaju jednak prirodnom broju). Dalje preporučujemo da proučite informacije članka množenje razlomaka - pravila, primjere i rješenja.

Bibliografija.

• Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S., Shvartsburd S.I. Matematika: udžbenik za 5 ćelija. obrazovne institucije.
• Vilenkin N.Ya. itd. Matematika. 6. razred: udžbenik za obrazovne ustanove.
• Gusev V.A., Mordkovich A.G. Matematika (priručnik za polaznike tehničkih škola).

Online kalkulator.
Evaluacija izraza s brojčanim razlomcima.
Množenje, oduzimanje, dijeljenje, sabiranje i smanjenje razlomaka sa različitim nazivnicima.

Pomoću ovog online kalkulatora možete množe, oduzimaju, dijele, sabiraju i smanjuju brojčane razlomke s različitim nazivnicima.

Program radi s tačnim, nepravilnim i mješovitim brojčanim razlomcima.

Ovaj program (online kalkulator) može:
- sabirati mješovite razlomke s različitim nazivnicima
- Oduzmite mješovite razlomke s različitim nazivnicima
- podijeliti mješovite razlomke s različitim nazivnicima
- Pomnožite mješovite razlomke s različitim nazivnicima
- dovesti razlomke na zajednički imenilac
- Pretvorite mješovite razlomke u nepravilne
- smanjiti razlomke

Također možete unijeti ne izraz s razlomcima, već jedan jedini razlomak.
U ovom slučaju, razlomak će se smanjiti, a cijeli broj će biti odabran iz rezultata.

Online kalkulator za izračunavanje izraza s brojčanim razlomcima ne daje samo odgovor na problem, on pruža detaljno rješenje sa objašnjenjima, tj. prikazuje proces pronalaženja rješenja.

Ovaj program može biti od koristi srednjoškolcima u pripremi za testove i ispite, prilikom provjere znanja prije Jedinstvenog državnog ispita, roditeljima za kontrolu rješavanja mnogih zadataka iz matematike i algebre. Ili vam je možda preskupo unajmiti nastavnika ili kupiti nove udžbenike? Ili samo želite da svoj domaći zadatak iz matematike ili algebre uradite što je brže moguće? U tom slučaju možete koristiti i naše programe sa detaljnim rješenjem.

Na taj način možete sami provoditi obuku i/ili obuku vaše mlađe braće ili sestara, dok se nivo obrazovanja u oblasti zadataka koji se rješavaju povećava.

Ako niste upoznati s pravilima za unos izraza s brojčanim razlomcima, preporučujemo da se upoznate s njima.

Pravila za unos izraza sa brojčanim razlomcima

Samo cijeli broj može biti brojnik, nazivnik i cijeli broj razlomka.

Imenilac ne može biti negativan.

Prilikom unosa brojčanog razlomka, brojilac je odvojen od nazivnika znakom dijeljenja: /
Ulaz: -2/3 + 7/5
Rezultat: \(-\frac(2)(3) + \frac(7)(5) \)

Cjelobrojni dio je odvojen od razlomka ampersandom: &
Ulaz: -1&2/3 * 5&8/3
Rezultat: \(-1\frac(2)(3) \cdot 5\frac(8)(3) \)

Podjela razlomaka se uvodi dvotočkom: :
Ulaz: -9&37/12: -3&5/14
Rezultat: \(-9\frac(37)(12) : \left(-3\frac(5)(14) \right) \)
Zapamtite da ne možete dijeliti sa nulom!

Zagrade se mogu koristiti prilikom unosa izraza s brojčanim razlomcima.
Unos: -2/3 * (6&1/2-5/9) : 2&1/4 + 1/3
Rezultat: \(-\frac(2)(3) \cdot \left(6 \frac(1)(2) - \frac(5)(9) \right) : 2\frac(1)(4) + \frac(1)(3) \)

Utvrđeno je da neke skripte potrebne za rješavanje ovog zadatka nisu učitane i program možda neće raditi.
Možda imate omogućen AdBlock.
U tom slučaju, onemogućite ga i osvježite stranicu.

Jer Ima puno ljudi koji žele riješiti problem, vaš zahtjev je u redu.
Nakon nekoliko sekundi, rješenje će se pojaviti ispod.
Sačekaj molim te sec...

Ako ti uočio grešku u rješenju, onda o tome možete pisati u Obrascu za povratne informacije.
Nemoj zaboraviti naznačiti koji zadatak ti odluči šta unesite u polja.

Naše igre, zagonetke, emulatori:

Malo teorije.

Obični razlomci. Podjela s ostatkom

Ako trebamo 497 podijeliti sa 4, onda ćemo prilikom dijeljenja vidjeti da 497 nije djeljivo sa 4, tj. ostaje ostatak divizije. U takvim slučajevima se kaže da podjela sa ostatkom, a rješenje se piše na sljedeći način:
497: 4 = 124 (1 ostatak).

Komponente dijeljenja na lijevoj strani jednakosti nazivaju se isto kao i kod dijeljenja bez ostatka: 497 - dividenda, 4 - razdjelnik. Rezultat dijeljenja pri dijeljenju s ostatkom se zove nepotpuno privatno. U našem slučaju, ovaj broj je 124. I na kraju, posljednja komponenta, koja nije u uobičajenoj podjeli, je ostatak. Kada nema ostatka, kaže se da je jedan broj podijeljen drugim. bez traga ili potpuno. Vjeruje se da je s takvom podjelom ostatak jednak nuli. U našem slučaju, ostatak je 1.

Ostatak je uvijek manji od djelitelja.

Prilikom dijeljenja možete provjeriti množenjem. Ako, na primjer, postoji jednakost 64: 32 = 2, onda se provjera može izvršiti ovako: 64 = 32 * 2.

Često u slučajevima kada se vrši dijeljenje s ostatkom, zgodno je koristiti jednakost
a \u003d b * n + r,
gdje je a dividenda, b je djelitelj, n je parcijalni količnik, r je ostatak.

Količnik dijeljenja prirodnih brojeva može se napisati kao razlomak.

Brojnik razlomka je dividenda, a nazivnik je djelitelj.

Pošto je brojnik razlomka dividenda, a imenilac djelitelj, vjeruju da linija razlomka znači akciju dijeljenja. Ponekad je zgodno napisati deljenje kao razlomak bez upotrebe znaka ":".

Kvocijent dijeljenja prirodnih brojeva m i n može se zapisati kao razlomak \(\frac(m)(n) \), gdje je brojnik m dividenda, a nazivnik n djelitelj:
\(m:n = \frac(m)(n) \)

Tačna su sljedeća pravila:

Da biste dobili razlomak \(\frac(m)(n) \), trebate podijeliti jedinicu na n jednakih dijelova (udjela) i uzeti m takvih dijelova.

Da biste dobili razlomak \(\frac(m)(n) \), trebate broj m podijeliti brojem n.

Da biste pronašli dio cjeline, trebate podijeliti broj koji odgovara cjelini sa nazivnikom i rezultat pomnožiti s brojnikom razlomka koji izražava ovaj dio.

Da biste pronašli cjelinu po njenom dijelu, trebate podijeliti broj koji odgovara ovom dijelu brojicom i rezultat pomnožiti sa nazivnikom razlomka koji izražava ovaj dio.

Ako se i brojnik i nazivnik razlomka pomnože istim brojem (osim nule), vrijednost razlomka se neće promijeniti:
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

Ako su i brojnik i nazivnik razlomka podijeljeni istim brojem (osim nule), vrijednost razlomka se neće promijeniti:
\(\veliki \frac(a)(b) = \frac(a: m)(b: m) \)
Ovo svojstvo se zove osnovno svojstvo razlomka.

Posljednje dvije transformacije se zovu smanjenje frakcije.

Ako razlomke treba predstaviti kao razlomke sa istim nazivnikom, onda se takva radnja naziva svođenje razlomaka na zajednički nazivnik.

Pravilni i nepravilni razlomci. mešoviti brojevi

Već znate da se razlomak može dobiti ako se cjelina podijeli na jednake dijelove i uzme nekoliko takvih dijelova. Na primjer, razlomak \(\frac(3)(4) \) znači tri četvrtine jedan. U mnogim problemima u prethodnom dijelu, razlomci su korišteni za označavanje dijela cjeline. Zdrav razum nalaže da dio uvijek treba biti manji od cjeline, ali šta je sa razlomcima kao što su \(\frac(5)(5) \) ili \(\frac(8)(5) \)? Jasno je da ovo više nije dio jedinice. Vjerovatno se zbog toga nazivaju razlomci kod kojih je brojilac veći ili jednak nazivniku nepravilni razlomci. Preostali razlomci, odnosno razlomci kod kojih je brojilac manji od nazivnika, nazivaju se pravilni razlomci.

Kao što znate, svaki obični razlomak, i pravilan i nepravilan, može se smatrati rezultatom dijeljenja brojnika sa nazivnikom. Dakle, u matematici, za razliku od običnog jezika, izraz "nepravilan razlomak" ne znači da smo nešto pogriješili, već samo da taj razlomak ima brojnik veći ili jednak nazivniku.

Ako se broj sastoji od cijelog broja i razlomka, onda je takav razlomci se nazivaju mješoviti.

Na primjer:
\(5:3 = 1\frac(2)(3) \) : 1 je cijeli broj, a \(\frac(2)(3) \) je razlomak.

Ako je brojilac razlomka \(\frac(a)(b) \) djeljiv prirodnim brojem n, tada da bi se ovaj razlomak podijelio s n, njegov brojnik mora biti podijeljen ovim brojem:
\(\veliki \frac(a)(b) : n = \frac(a:n)(b) \)

Ako brojilac razlomka \(\frac(a)(b) \) nije djeljiv prirodnim brojem n, tada da biste podijelili ovaj razlomak sa n, trebate pomnožiti njegov nazivnik s ovim brojem:
\(\veliki \frac(a)(b) : n = \frac(a)(bn) \)

Imajte na umu da drugo pravilo vrijedi i kada je brojilac djeljiv sa n. Stoga ga možemo koristiti kada je na prvi pogled teško odrediti da li je brojnik razlomka djeljiv sa n ili ne.

Radnje sa razlomcima. Sabiranje razlomaka.

Sa razlomcima, kao i sa prirodnim brojevima, možete izvoditi aritmetičke operacije. Pogledajmo prvo sabiranje razlomaka. Lako je sabirati razlomke sa istim nazivnicima. Pronađite, na primjer, zbir \(\frac(2)(7) \) i \(\frac(3)(7) \). Lako je vidjeti da je \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

Da biste sabrali razlomke sa istim nazivnicima, morate sabrati njihove brojnike, a nazivnik ostaviti istim.

Koristeći slova, pravilo za sabiranje razlomaka sa istim nazivnicima može se napisati na sljedeći način:
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

Ako želite da saberete razlomke sa različitim nazivnicima, prvo ih morate svesti na zajednički imenilac. Na primjer:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

Za razlomke, kao i za prirodne brojeve, vrijede komutativna i asocijativna svojstva sabiranja.

Dodavanje miješanih frakcija

Snimci kao što je \(2\frac(2)(3) \) se pozivaju miješane frakcije. Zove se broj 2 cijeli dio mješoviti razlomak, a broj \(\frac(2)(3) \) je njegov frakcijski dio. Unos \(2\frac(2)(3) \) se čita ovako: "dvije i dvije trećine".

Dijeljenjem broja 8 sa brojem 3 dobijamo dva odgovora: \(\frac(8)(3) \) i \(2\frac(2)(3) \). Oni izražavaju isti razlomak, tj. \(\frac(8)(3) = 2 \frac(2)(3) \)

Dakle, nepravilni razlomak \(\frac(8)(3) \) je predstavljen kao mješoviti razlomak \(2\frac(2)(3) \). U takvim slučajevima to kažu iz nepravilnog razlomka izdvojio celinu.

Oduzimanje razlomaka (razlomački brojevi)

Oduzimanje razlomaka, kao i prirodnih, određuje se na osnovu radnje sabiranja: oduzimanje drugog od jednog broja znači pronalaženje broja koji, kada se doda drugom, daje prvi. Na primjer:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) jer \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9) \)

Pravilo za oduzimanje razlomaka sa sličnim nazivnicima je slično pravilu za sabiranje takvih razlomaka:
Da biste pronašli razliku između razlomaka sa istim nazivnicima, oduzmite brojilac drugog razlomka od brojnika prvog razlomka, a imenilac ostavite isti.

Koristeći slova, ovo pravilo se piše na sljedeći način:
\(\veliki \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Množenje razlomaka

Da biste razlomak pomnožili razlomkom, trebate pomnožiti njihove brojnike i nazivnike i prvi proizvod napisati kao brojilac, a drugi kao nazivnik.

Koristeći slova, pravilo za množenje razlomaka može se napisati na sljedeći način:
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

Koristeći formulirano pravilo, moguće je množiti razlomak prirodnim brojem, mješovitim razlomkom, a također i množenje mješovitih razlomaka. Da biste to učinili, trebate napisati prirodni broj kao razlomak s nazivnikom 1, mješoviti razlomak kao nepravilan razlomak.

Rezultat množenja treba pojednostaviti (ako je moguće) smanjenjem razlomka i isticanjem cijelog broja nepravilnog razlomka.

Za razlomke, kao i za prirodne brojeve, vrijede komutativna i asocijativna svojstva množenja, kao i distributivna svojstva množenja u odnosu na sabiranje.

Podjela razlomaka

Uzmite razlomak \(\frac(2)(3) \) i "okrenite" ga zamjenom brojnika i nazivnika. Dobijamo razlomak \(\frac(3)(2) \). Ovaj razlomak se zove obrnuto razlomci \(\frac(2)(3) \).

Ako sada "obrnemo" razlomak \(\frac(3)(2) \), onda ćemo dobiti originalni razlomak \(\frac(2)(3) \). Stoga se razlomci kao što su \(\frac(2)(3) \) i \(\frac(3)(2) \) nazivaju međusobno inverzno.

Na primjer, razlomci \(\frac(6)(5) \) i \(\frac(5)(6) \), \(\frac(7)(18) \) i \(\frac (18) )(7) \).

Koristeći slova, međusobno inverzni razlomci se mogu napisati na sljedeći način: \(\frac(a)(b) \) i \(\frac(b)(a) \)

To je jasno proizvod recipročnih razlomaka je 1. Na primjer: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

Koristeći recipročne razlomke, dijeljenje razlomaka se može svesti na množenje.

Pravilo za dijeljenje razlomka sa razlomkom:
Da biste podijelili jedan razlomak drugim, trebate pomnožiti dividendu recipročnom vrijednosti djelitelja.

Razlomak- broj koji se sastoji od cijelog broja razlomaka od jedan i predstavljen je kao: a / b

Brojilac razlomaka (a)- broj iznad linije razlomka i koji pokazuje broj dionica na koje je jedinica podijeljena.

Imenilac razlomka (b)- broj ispod linije razlomka i koji pokazuje na koliko je udjela jedinica podijeljena.

2. Dovođenje razlomaka na zajednički nazivnik

3. Aritmetičke operacije nad običnim razlomcima

3.1. Sabiranje običnih razlomaka

3.2. Oduzimanje običnih razlomaka

3.3. Množenje običnih razlomaka

3.4. Podjela običnih razlomaka

4. Recipročni brojevi

5. Decimale

6. Aritmetičke operacije nad decimalnim razlomcima

6.1. Sabiranje decimala

6.2. Oduzimanje decimala

6.3. Decimalno množenje

6.4. Decimalna podjela

#jedan. Osnovno svojstvo razlomka

Ako se brojnik i imenilac razlomka pomnože ili podijele sa istim brojem koji nije jednak nuli, onda će se dobiti razlomak jednak datom jedinici.

3/7=3*3/7*3=9/21 tj. 3/7=9/21

a/b=a*m/b*m - ovako izgleda glavno svojstvo razlomka.

Drugim riječima, razlomak jednak datom dobivamo množenjem ili dijeljenjem brojnika i nazivnika originalnog razlomka istim prirodnim brojem.

Ako a ad=bc, zatim dva razlomka a/b =c /d se smatraju jednakim.

Na primjer, razlomci 3/5 i 9/15 će biti jednaki, jer je 3*15=5*9, odnosno 45=45

Smanjenje frakcije je proces zamjene razlomka, u kojem je novi razlomak jednak originalnom, ali sa manjim brojnikom i nazivnikom.

Uobičajeno je reducirati razlomke na osnovu glavnog svojstva razlomka.

Na primjer, 45/60=15/ ​ ​20 =9/12=3/4 ​ ​ ​ (brojilac i imenilac su djeljivi sa 3, sa 5 i sa 15).

nesmanjivi razlomak je djelić forme 3/4 ​ ​ , gdje su brojilac i imenilac relativno prosti brojevi. Glavna svrha redukcije razlomaka je da razlomak učini nesvodljivim.

2. Svođenje razlomaka na zajednički imenilac

Da dva razlomka dovedemo do zajedničkog nazivnika:

1) razložiti imenilac svakog razlomka na proste faktore;

2) pomnožimo brojilac i imenilac prvog razlomka onima koji nedostaju

faktori iz ekspanzije drugog imenioca;

3) pomnožimo brojilac i imenilac drugog razlomka faktorima koji nedostaju iz prvog proširenja.

Primjeri: Svedite razlomke na zajednički nazivnik.

Razložimo nazivnike na proste činioce: 18=3∙3∙2, 15=3∙5

Pomnožili smo brojilac i imenilac razlomka sa faktorom koji nedostaje 5 iz drugog proširenja.

brojnik i imenilac razlomka faktorima koji nedostaju 3 i 2 iz prvog proširenja.

= , 90 je zajednički nazivnik razlomaka .

3. Aritmetičke operacije nad običnim razlomcima

3.1. Sabiranje običnih razlomaka

a) Sa istim nazivnicima, brojilac prvog razlomka se dodaje brojiocu drugog razlomka, a imenilac ostaje isti. Kao što se vidi u primjeru:

a/b+c/b=(a+c)/b ​ ​ ;

b) Kod različitih nazivnika razlomci se prvo svode na zajednički imenilac, a zatim se sabiraju brojnici prema pravilu a):

7/3+1/4=7*4/12+1*3/12=(28+3)/12=31/12

3.2. Oduzimanje običnih razlomaka

a) Sa istim nazivnicima oduzmi brojilac drugog razlomka od brojnika prvog razlomka, a imenilac ostane isti:

a/b-c/b=(a-c)/b ​ ​ ;

b) Ako su imenioci razlomaka različiti, onda se prvo razlomci svode na zajednički imenilac, a zatim se ponavljaju koraci kao u paragrafu a).

3.3. Množenje običnih razlomaka

Množenje razlomaka poštuje sljedeće pravilo:

a/b*c/d=a*c/b*d,

odnosno pomnožite brojnike i nazivnike odvojeno.

Na primjer:

3/5*4/8=3*4/5*8=12/40.

3.4. Podjela običnih razlomaka

Razlomci se dijele na sljedeći način:

a/b:c/d=a*d/b*c,

to jest, razlomak a / b množi se recipročnim iznosom datog, odnosno množi se sa d / c.

Primjer: 7/2:1/8=7/2*8/1=56/2=28

4. Recipročni brojevi

Ako a a*b=1, tada je broj b obrnuti broj za broj a.

Primjer: za broj 9, obrnuto je 1/9 ​ ​ , od 9*1/9 = 1 , za broj 5 - recipročna vrijednost 1/5 ​ ​ , as 5* ​ 1/5 ​ ​ = 1 .

5. Decimale

Decimala je pravi razlomak čiji je imenilac 10, 1000, 10000, …, 10^n 1 0 , 1 0 0 0 , 1 0 0 0 0 , . . . , 1 0 ​ n​ ​ .

Na primjer: 6/10 =0,6; 44/1000=0,044 ​ .

Na isti način, netačni se pišu sa nazivnikom 10^n ili mešoviti brojevi.

Na primjer: 51/10= 5,1; 763/100=7,63

U obliku decimalnog razlomka predstavljen je svaki obični razlomak sa nazivnikom koji je djelitelj određenog stepena broja 10.

imenilac, koji je djelitelj određenog stepena broja 10.

Primjer: 5 je djelitelj 100, dakle razlomak 1/5=1 *20/5*20=20/100=0,2 ​ 0 = 0 , 2 .

6. Aritmetičke operacije nad decimalnim razlomcima

6.1. Sabiranje decimala

Da biste dodali dva decimalna razlomka, trebate ih rasporediti tako da se iste cifre i zarez ispod zareza pojavljuju jedan ispod drugog, a zatim razlomke sabrati kao obične brojeve.

6.2. Oduzimanje decimala

Djeluje na isti način kao i dodavanje.

6.3. Decimalno množenje

Prilikom množenja decimalnih brojeva dovoljno je pomnožiti date brojeve, zanemarujući zareze (kao prirodne brojeve), a u dobijenom odgovoru zarezom desno odvaja onoliko cifara koliko ih ima iza decimalne zapete u oba faktora ukupno. .

Uradimo množenje 2,7 sa 1,3. Imamo 27\cdot 13=351 2 7 ⋅ 1 3 = 3 5 1 . Dvije cifre odvajamo zarezom na desnoj strani (prvi i drugi broj imaju jednu cifru iza decimalne zareze; 1+1=2 1 + 1 = 2 ). Kao rezultat, dobijamo 2,7\cdot 1,3=3,51 2 , 7 ⋅ 1 , 3 = 3 , 5 1 .

Ako je rezultat manje znamenki nego što je potrebno odvojiti zarezom, tada se nule koje nedostaju upisuju ispred, na primjer:

Za množenje sa 10, 100, 1000, u decimalnom razlomku, pomaknite zarez za 1, 2, 3 cifre udesno (ako je potrebno, određeni broj nula se dodjeljuje udesno).

Na primjer: 1,47 \cdot 10.000 = 14.700 1 , 4 7 ⋅ 1 0 0 0 0 = 1 4 7 0 0 .

6.4. Decimalna podjela

Dijeljenje decimalnog razlomka prirodnim brojem vrši se na isti način kao i dijeljenje prirodnog broja prirodnim brojem. Zarez u privatnom se stavlja nakon što je dijeljenje cijelog broja završeno.

Ako je cijeli broj dividende manji od djelitelja, tada je odgovor nula cijelih brojeva, na primjer:

Razmislite o dijeljenju decimale sa decimalom. Recimo da trebamo podijeliti 2,576 sa 1,12. Prije svega, pomnožimo dividendu i djelitelj razlomka sa 100, odnosno pomaknemo zarez udesno u dividendi i djelitelju za onoliko znakova koliko ima u djelitelju nakon decimalnog zareza (u ovom primjeru , dva). Zatim morate podijeliti razlomak 257,6 prirodnim brojem 112, odnosno problem se svodi na već razmatrani slučaj:

Dešava se da se konačni decimalni razlomak ne dobije uvijek kada se jedan broj dijeli s drugim. Rezultat je beskonačna decimala. U takvim slučajevima idite na obične razlomke.

Na primjer, 2,8: 0,09= 28/10: 9/100= 28*100/10*9=2800/90=280/9= ​ 31 1/9 ​ ​ .