Jak rozwiązywać nierówności wymierne za pomocą modułu. Nierówności z modułem. Nowe spojrzenie na rozwiązanie

Moduł liczb ta liczba jest wywoływana, jeśli jest nieujemna lub jest tą samą liczbą przeciwny znak, jeśli jest ona ujemna.

Na przykład moduł liczby 6 wynosi 6, a moduł liczby -6 również wynosi 6.

To znaczy, przez moduł liczby mamy na myśli całkowita wartość, całkowita wartość tę liczbę bez uwzględnienia jej znaku.

Oznacza się go następująco: |6|, | X|, |A| itp.

(Więcej szczegółów w dziale „Moduł numeryczny”).

Równania z modułem.

Przykład 1 . Rozwiązać równanie|10 X - 5| = 15.

Rozwiązanie.

Zgodnie z regułą równanie jest równoważne kombinacji dwóch równań:

10X - 5 = 15
10X - 5 = -15

My decydujemy:

10X = 15 + 5 = 20
10X = -15 + 5 = -10

X = 20: 10
X = -10: 10

X = 2
X = -1

Odpowiedź: X 1 = 2, X 2 = -1.

Przykład 2 . Rozwiązać równanie|2 X + 1| = X + 2.

Rozwiązanie.

Zatem moduł jest liczbą nieujemną X+ 2 ≥ 0. Odpowiednio:

X ≥ -2.

Zróbmy dwa równania:

2X + 1 = X + 2
2X + 1 = -(X + 2)

My decydujemy:

2X + 1 = X + 2
2X + 1 = -X - 2

2X - X = 2 - 1
2X + X = -2 - 1

X = 1
X = -1

Obie liczby są większe od -2. Zatem oba są pierwiastkami równania.

Odpowiedź: X 1 = -1, X 2 = 1.

Przykład 3 . Rozwiązać równanie

|X + 3| - 1
————— = 4
X - 1

Rozwiązanie.

Równanie ma sens, jeśli mianownik nie jest zerem - to znaczy, jeśli X≠ 1. Weźmy ten warunek pod uwagę. Nasza pierwsza akcja jest prosta – nie tylko pozbywamy się ułamka, ale go przekształcamy tak, aby otrzymać moduł w czystej postaci:

|X+ 3| - 1 = 4 · ( X - 1),

|X + 3| - 1 = 4X - 4,

|X + 3| = 4X - 4 + 1,

|X + 3| = 4X - 3.

Teraz mamy tylko wyrażenie pod modułem po lewej stronie równania. Zacząć robić.
Moduł liczby jest liczbą nieujemną — to znaczy musi być większy od zera lub równy zero. W związku z tym rozwiązujemy nierówność:

4X - 3 ≥ 0

4X ≥ 3

X ≥ 3/4

Mamy zatem drugi warunek: pierwiastek równania musi wynosić co najmniej 3/4.

Zgodnie z regułą układamy układ dwóch równań i rozwiązujemy je:

X + 3 = 4X - 3
X + 3 = -(4X - 3)

X + 3 = 4X - 3
X + 3 = -4X + 3

X - 4X = -3 - 3
X + 4X = 3 - 3

X = 2
X = 0

Otrzymaliśmy dwie odpowiedzi. Sprawdźmy, czy są one pierwiastkami pierwotnego równania.

Mieliśmy dwa warunki: pierwiastek równania nie może być równy 1 i musi wynosić co najmniej 3/4. To jest X ≠ 1, X≥ 3/4. Obydwa te warunki odpowiadają tylko jednej z dwóch otrzymanych odpowiedzi - liczbie 2. Oznacza to, że tylko to jest pierwiastkiem pierwotnego równania.

Odpowiedź: X = 2.

Nierówności z modułem.

Przykład 1 . Rozwiąż nierówność| X - 3| < 4

Rozwiązanie.

Reguła modułu stwierdza:

|A| = A, Jeśli A ≥ 0.

|A| = -A, Jeśli A < 0.

Moduł może mieć zarówno liczby nieujemne, jak i ujemne. Musimy więc rozważyć oba przypadki: X- 3 ≥ 0 i X - 3 < 0.

1) Kiedy X- 3 ≥ 0 nasza pierwotna nierówność pozostaje taka, jaka jest, tylko bez znaku modułu:
X - 3 < 4.

2) Kiedy X - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

-(X - 3) < 4.

Otwierając nawiasy otrzymujemy:

-X + 3 < 4.

Zatem z tych dwóch warunków doszliśmy do unifikacji dwóch systemów nierówności:

X - 3 ≥ 0
X - 3 < 4

X - 3 < 0
-X + 3 < 4

Rozwiążmy je:

X ≥ 3
X < 7

X < 3
X > -1

Zatem naszą odpowiedzią jest suma dwóch zbiorów:

3 ≤ X < 7 U -1 < X < 3.

Określ najmniejszy i najwyższa wartość. Są to -1 i 7. Co więcej X większa niż -1, ale mniejsza niż 7.
Oprócz, X≥ 3. Oznacza to, że rozwiązaniem nierówności jest cały zbiór liczb od -1 do 7, z wyłączeniem tych liczb skrajnych.

Odpowiedź: -1 < X < 7.

Lub: X ∈ (-1; 7).

Dodatki.

1) Istnieje prostszy i krótka droga rozwiązania naszej nierówności - graficzne. Aby to zrobić, musisz narysować oś poziomą (ryc. 1).

Wyrażenie | X - 3| < 4 означает, что расстояние от точки X do punktu 3 jest mniejsza niż cztery jednostki. Na osi zaznaczamy cyfrę 3 i liczymy 4 podziały na lewo i na prawo od niej. Po lewej stronie dojdziemy do punktu -1, po prawej - do punktu 7. Tym samym punkty X po prostu je widzieliśmy, bez obliczenia.

Ponadto, zgodnie z warunkiem nierówności, same liczby -1 i 7 nie są uwzględniane w zbiorze rozwiązań. W ten sposób otrzymujemy odpowiedź:

1 < X < 7.

2) Istnieje jednak inne rozwiązanie, prostsze nawet niż metoda graficzna. Aby to zrobić, naszą nierówność należy przedstawić w następującej postaci:

4 < X - 3 < 4.

Przecież tak to jest zgodnie z regułą modułu. Nieujemna liczba 4 i podobna liczba ujemna -4 stanowią granice rozwiązania nierówności.

4 + 3 < X < 4 + 3

1 < X < 7.

Przykład 2 . Rozwiąż nierówność| X - 2| ≥ 5

Rozwiązanie.

Ten przykład znacznie różni się od poprzedniego. Lewa strona większa niż 5 lub równa 5. Z geometrycznego punktu widzenia rozwiązaniem nierówności są wszystkie liczby, które znajdują się w odległości 5 jednostek lub większej od punktu 2 (ryc. 2). Z wykresu wynika, że ​​są to wszystkie liczby mniejsze lub równe -3 i większe lub równe 7. Oznacza to, że otrzymaliśmy już odpowiedź.

Odpowiedź: -3 ≥ X ≥ 7.

Po drodze rozwiązujemy tę samą nierówność, przestawiając wolny wyraz w lewo i w prawo za pomocą przeciwnego znaku:

5 ≥ X - 2 ≥ 5

5 + 2 ≥ X ≥ 5 + 2

Odpowiedź jest taka sama: -3 ≥ X ≥ 7.

Lub: X ∈ [-3; 7]

Przykład został rozwiązany.

Przykład 3 . Rozwiąż nierówność 6 X 2 - | X| - 2 ≤ 0

Rozwiązanie.

Numer X może być liczbą dodatnią, liczbą ujemną lub zerem. Dlatego musimy wziąć pod uwagę wszystkie trzy okoliczności. Jak wiadomo, uwzględnia się je w dwóch nierównościach: X≥ 0 i X < 0. При X≥ 0 po prostu przepisujemy naszą pierwotną nierówność w niezmienionej postaci, tylko bez znaku modułu:

6x 2 - X - 2 ≤ 0.

Teraz o drugim przypadku: jeśli X < 0. Модулем Liczba ujemna to ta sama liczba z przeciwnym znakiem. Oznacza to, że zapisujemy liczbę pod modułem o przeciwnym znaku i ponownie uwalniamy się od znaku modułu:

6X 2 - (-X) - 2 ≤ 0.

Rozszerzanie nawiasów:

6X 2 + X - 2 ≤ 0.

Otrzymaliśmy zatem dwa układy równań:

6X 2 - X - 2 ≤ 0
X ≥ 0

6X 2 + X - 2 ≤ 0
X < 0

Musimy rozwiązać nierówności w układach - a to oznacza, że ​​musimy znaleźć pierwiastki dwóch równań kwadratowych. Aby to zrobić, przyrównujemy lewą stronę nierówności do zera.

Zacznijmy od pierwszego:

6X 2 - X - 2 = 0.

Jak rozwiązać równanie kwadratowe - patrz sekcja „Równanie kwadratowe”. Natychmiast nazwiemy odpowiedź:

X 1 = -1/2, x 2 = 2/3.

Z pierwszego układu nierówności dowiadujemy się, że rozwiązaniem pierwotnej nierówności jest cały zbiór liczb od -1/2 do 2/3. Sumę rozwiązań piszemy pod adresem X ≥ 0:
[-1/2; 2/3].

Rozwiążmy teraz drugie równanie kwadratowe:

6X 2 + X - 2 = 0.

Jego korzenie:

X 1 = -2/3, X 2 = 1/2.

Wniosek: kiedy X < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.

Połączmy dwie odpowiedzi i uzyskajmy ostateczną odpowiedź: rozwiązaniem jest cały zbiór liczb od -2/3 do 2/3, łącznie z tymi liczbami skrajnymi.

Odpowiedź: -2/3 ≤ X ≤ 2/3.

Lub: X ∈ [-2/3; 2/3].

Metody (reguły) ujawniania nierówności modułami polegają na sekwencyjnym odkrywaniu modułów, wykorzystując przedziały stałego znaku funkcji submodułowych. W ostatecznej wersji uzyskuje się kilka nierówności, z których znajdują się przedziały lub przedziały spełniające warunki problemu.

Przejdźmy do rozwiązywania typowych przykładów w praktyce.

Nierówności liniowe z modułami

Przez liniowe rozumiemy równania, w których zmienna wchodzi do równania liniowo.

Przykład 1. Znajdź rozwiązanie nierówności

Rozwiązanie:
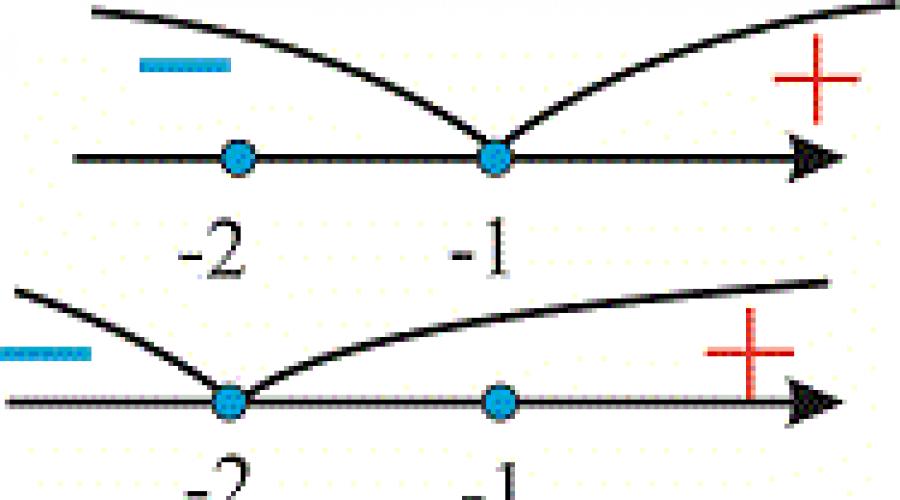
Z warunków zadania wynika, że ​​moduły zwracają się do zera przy x=-1 i x=-2. Punkty te dzielą oś liczbową na przedziały

W każdym z tych przedziałów rozwiązujemy zadaną nierówność. W tym celu najpierw sporządzamy rysunki graficzne obszarów stałego znaku funkcji submodularnych. Są one przedstawiane jako obszary ze znakami każdej z funkcji

lub przedziały ze znakami wszystkich funkcji.

W pierwszej przerwie rozbudowujemy moduły

Mnożymy obie strony przez minus jeden, a znak nierówności zmieni się na przeciwny. Jeśli trudno Ci się przyzwyczaić do tej zasady, możesz przesunąć każdą część za znak, aby pozbyć się minusa. Na koniec otrzymasz

Przecięcie zbioru x>-3 z obszarem, na którym rozwiązano równania, będzie przedziałem (-3;-2). Dla tych, którym łatwiej jest znaleźć rozwiązania, można graficznie narysować przecięcie tych obszarów

Rozwiązaniem będzie wspólne przecięcie obszarów. Jeśli są bardzo nierówne, krawędzie nie są uwzględniane. Jeśli nie jest to rygorystyczne, sprawdź przez podstawienie.

W drugim przedziale otrzymujemy

Przekrój będzie przedziałem (-2;-5/3). Graficznie rozwiązanie będzie wyglądać

W trzecim przedziale otrzymujemy

Ten stan nie daje rozwiązań w żądanej dziedzinie.

Ponieważ oba znalezione rozwiązania (-3;-2) i (-2;-5/3) graniczą z punktem x=-2, również to sprawdzamy.

Rozwiązaniem jest więc punkt x=-2. Wspólna decyzja biorąc to pod uwagę, będzie to wyglądać (-3;5/3).

Przykład 2. Znajdź rozwiązanie nierówności
|x-2|-|x-3|>=|x-4|

Rozwiązanie:
Zerami funkcji submodularnych będą punkty x=2, x=3, x=4. Dla wartości argumentów mniejszych niż te punkty funkcje submodularne są ujemne, a dla większych wartości są dodatnie.

Punkty dzielą rzeczywistą oś na cztery przedziały. Rozbudowujemy moduły według przedziałów znaku stałego i rozwiązujemy nierówności.

1) W pierwszym przedziale wszystkie funkcje submodularne są ujemne, więc rozszerzając moduły, zmieniamy znak na przeciwny.

Przecięcie znalezionych wartości x z rozważanym przedziałem będzie zbiorem punktów

2) W przedziale pomiędzy punktami x=2 i x=3 pierwsza funkcja submodułowa jest dodatnia, druga i trzecia są ujemne. Rozbudowując moduły otrzymujemy

nierówność, która po przecięciu przez przedział, który rozwiązujemy daje jedno rozwiązanie – x=3.

3) W przedziale pomiędzy punktami x=3 i x=4 pierwsza i druga funkcja submodułowa są dodatnie, a trzecia ujemna. Na tej podstawie otrzymujemy

Warunek ten pokazuje, że cały przedział będzie spełniał nierówność modułami.

4) Dla wartości x>4 wszystkie funkcje mają znaki dodatnie. Rozbudowując moduły nie zmieniamy ich znaku.

Znaleziony warunek na przecięciu z przedziałem daje następujący zestaw rozwiązań

Ponieważ nierówność została rozwiązana we wszystkich przedziałach, pozostaje znaleźć wspólną wartość wszystkich znalezionych wartości x. Rozwiązaniem będą dwa przedziały

Na tym kończy się przykład.

Przykład 3. Znajdź rozwiązanie nierówności
||x-1|-5|>3-2x

Rozwiązanie:
Mamy nierówność z modułem od modułu. Nierówności te ujawniają się w miarę zagnieżdżania modułów, zaczynając od tych, które znajdują się głębiej.

Funkcja submodularna x-1 jest konwertowana na zero przy x=1. Dla mniejszych wartości powyżej 1 jest to wartość ujemna i dodatnia dla x>1. Na tej podstawie rozwijamy moduł wewnętrzny i uwzględniamy nierówność na każdym z przedziałów.

Najpierw rozważ przedział od minus nieskończoności do jedności

Funkcja submodularna wynosi zero przy x=-4. Przy mniejszych wartościach jest dodatni, przy większych wartościach jest ujemny. Rozwińmy moduł dla x<-4:

Na przecięciu z obszarem, który rozważamy, otrzymujemy zbiór rozwiązań

Kolejnym krokiem jest rozwinięcie modułu o przedział (-4;1)

Biorąc pod uwagę obszar rozbudowy modułu, otrzymujemy przedział rozwiązania

PAMIĘTAJ: jeśli w takich nieprawidłowościach z modułami otrzymasz dwa przedziały graniczące ze wspólnym punktem, to z reguły jest to również rozwiązanie.

Aby to zrobić, wystarczy sprawdzić.

W tym przypadku zastępujemy punkt x=-4.

Zatem x=-4 jest rozwiązaniem.
Rozwińmy moduł wewnętrzny dla x>1

Funkcja submodularna ujemna dla x<6.
Rozbudowując moduł otrzymamy

Ten warunek w sekcji z przedziałem (1;6) daje pusty zbiór rozwiązań.

Dla x>6 otrzymujemy nierówność

Rozwiązując również, otrzymaliśmy pusty zestaw.
Biorąc wszystko pod uwagę, jedynym rozwiązaniem nierówności z modułami będzie następujący przedział.

Nierówności o modułach zawierających równania kwadratowe

Przykład 4. Znajdź rozwiązanie nierówności
|x^2+3x|>=2-x^2

Rozwiązanie:
Funkcja submodularna zanika w punktach x=0, x=-3. Proste podstawienie minus jeden

ustalamy, że w przedziale (-3;0) jest on mniejszy od zera, a poza nim dodatni.
Rozbudujmy moduł w obszarach, w których funkcja submodularna jest dodatnia

Pozostaje określić obszary, w których funkcja kwadratowa jest dodatnia. Aby to zrobić, definiujemy korzenie równanie kwadratowe

Dla wygody podstawimy punkt x=0, który należy do przedziału (-2;1/2). Funkcja w tym przedziale jest ujemna, co oznacza, że ​​rozwiązaniem będą zbiory x

Tutaj krawędzie obszarów z rozwiązaniami oznaczono nawiasami; zrobiono to celowo, biorąc pod uwagę następującą zasadę.

PAMIĘTAJ: Jeśli nierówność z modułami lub nierówność prosta jest ścisła, to krawędzie znalezionych obszarów nie są rozwiązaniami, natomiast jeśli nierówności nie są ścisłe (), to krawędzie są rozwiązaniami (oznaczone nawiasami kwadratowymi).

Zasada ta jest stosowana przez wielu nauczycieli: jeśli jest podana ścisła nierówność, a podczas obliczeń wpiszesz w rozwiązaniu nawias kwadratowy ([,]) - automatycznie uznają to za niepoprawną odpowiedź. Ponadto, jeśli podczas testowania podana jest nieścisła nierówność z modułami, należy wśród rozwiązań szukać obszarów z nawiasami kwadratowymi.

Na przedziale (-3;0) rozwijając moduł zmieniamy znak funkcji na przeciwny

Uwzględniając obszar ujawnienia nierówności, rozwiązanie będzie miało postać

Razem z poprzednim obszarem da to dwa półprzedziały

Przykład 5. Znajdź rozwiązanie nierówności
9x^2-|x-3|>=9x-2

Rozwiązanie:
Podana jest nieścisła nierówność, której funkcja submodularna jest równa zeru w punkcie x=3. Dla mniejszych wartości jest to wartość ujemna, dla większych wartości jest ona dodatnia. Rozwiń moduł na przedziale x<3.

Znalezienie dyskryminatora równania

i korzenie

Podstawiając punkt zero dowiadujemy się, że na przedziale [-1/9;1] funkcja kwadratowa jest ujemna, zatem przedział jest rozwiązaniem. Następnie rozwijamy moduł w x>3

Matematyka jest symbolem mądrości nauki,

model naukowej dyscypliny i prostoty,

standard doskonałości i piękna w nauce.

Rosyjski filozof, profesor A.V. Wołoszynow

Nierówności z modułem

Najtrudniejszymi problemami do rozwiązania w matematyce szkolnej są nierówności, zawierające zmienne pod znakiem modułu. Aby skutecznie rozwiązać takie nierówności, trzeba mieć dobrą wiedzę na temat właściwości modułu i umieć je wykorzystać.

Podstawowe pojęcia i właściwości

Moduł (wartość bezwzględna) liczby rzeczywistej oznaczony przez i jest zdefiniowany w następujący sposób:

Do prostych właściwości modułu zaliczają się następujące zależności:

I .

Notatka, że dwie ostatnie właściwości obowiązują dla dowolnego parzystego stopnia.

Co więcej, jeśli, gdzie, to i

Bardziej złożone właściwości modułu, które można skutecznie wykorzystać przy rozwiązywaniu równań i nierówności za pomocą modułów, formułuje się za pomocą następujących twierdzeń:

Twierdzenie 1.Dla dowolnych funkcji analitycznych I nierówność jest prawdziwa.

Twierdzenie 2. Równość równoznaczne z nierównością.

Twierdzenie 3. Równość równoznaczne z nierównością.

Najczęstsze nierówności w matematyce szkolnej, zawierające nieznane zmienne pod znakiem modułu, są nierównościami postaci i gdzie jakąś dodatnią stałą.

Twierdzenie 4. Nierówność jest równoważne podwójnej nierówności, i rozwiązanie nierównościsprowadza się do rozwiązania zbioru nierówności I .

Twierdzenie to jest szczególnym przypadkiem twierdzeń 6 i 7.

Bardziej złożone nierówności, zawierające moduł są nierównościami postaci, I .

Metody rozwiązywania takich nierówności można sformułować, korzystając z trzech poniższych twierdzeń.

Twierdzenie 5. Nierówność jest równoważne połączeniu dwóch systemów nierówności

ja (1)

Dowód. Od tego czasu

Oznacza to ważność (1).

Twierdzenie 6. Nierówność jest równoważny układowi nierówności

Dowód. Ponieważ , następnie z nierówności wynika z tego . Pod tym warunkiem nierównośćiw tym przypadku drugi układ nierówności (1) okaże się niespójny.

Twierdzenie zostało udowodnione.

Twierdzenie 7. Nierówność jest równoważne połączeniu jednej nierówności i dwóch systemów nierówności

ja (3)

Dowód. Ponieważ , to nierówność zawsze wykonywane, Jeśli .

Pozwalać , następnie nierównośćbędzie równoważne nierówności, z czego wynika zbiór dwóch nierówności I .

Twierdzenie zostało udowodnione.

Rozważmy typowe przykłady rozwiązywanie problemów na temat „Nierówności, zawierające zmienne pod znakiem modułu.”

Rozwiązywanie nierówności za pomocą modułu

Bardzo prosta metoda Metodą jest rozwiązywanie nierówności za pomocą modułu, w oparciu o rozbudowę modułów. Ta metoda jest uniwersalna, jednakże w ogólnym przypadku jego użycie może prowadzić do bardzo uciążliwych obliczeń. Dlatego też uczniowie powinni znać inne (bardziej skuteczne) metody i techniki rozwiązywania takich nierówności. W szczególności, konieczna jest umiejętność stosowania twierdzeń, podane w tym artykule.

Przykład 1.Rozwiąż nierówność

. (4)

Rozwiązanie.Nierówność (4) rozwiążemy metodą „klasyczną” – metodą odkrywania modułów. W tym celu dzielimy oś liczbową kropki i na przedziały i rozważ trzy przypadki.

1. Jeśli , to , , i nierówność (4) przyjmuje postać Lub .

Ponieważ przypadek ten jest tutaj rozpatrywany, jest to rozwiązanie nierówności (4).

2. Jeśli następnie z nierówności (4) otrzymujemy Lub . Od przecięcia przedziałów I jest pusty, wówczas na rozważanym przedziale rozwiązań nie ma nierówności (4).

3. Jeśli wówczas nierówność (4) przyjmuje postać Lub . To oczywiste jest również rozwiązaniem nierówności (4).

Odpowiedź: , .

Przykład 2. Rozwiąż nierówność.

Rozwiązanie. Załóżmy, że. Ponieważ , wówczas dana nierówność przyjmuje postać Lub . Od tego czasu i stąd wynika Lub .

Jednak zatem lub.

Przykład 3. Rozwiąż nierówność

. (5)

Rozwiązanie. Ponieważ , wówczas nierówność (5) jest równoważna nierównościom Lub . Stąd, zgodnie z Twierdzeniem 4, mamy zbiór nierówności I .

Odpowiedź: , .

Przykład 4.Rozwiąż nierówność

. (6)

Rozwiązanie. Oznaczmy . Następnie z nierówności (6) otrzymujemy nierówności , lub .

Stąd, stosując metodę interwałową, otrzymujemy. Ponieważ , wtedy mamy tutaj system nierówności

Rozwiązaniem pierwszej nierówności układu (7) jest suma dwóch przedziałów I , a rozwiązaniem drugiej nierówności jest nierówność podwójna. Oznacza to, że rozwiązaniem układu nierówności (7) jest suma dwóch przedziałów I .

Odpowiedź: ,

Przykład 5.Rozwiąż nierówność

. (8)

Rozwiązanie. Przekształćmy nierówność (8) w następujący sposób:

Lub .

Stosowanie metody interwałowej, otrzymujemy rozwiązanie nierówności (8).

Odpowiedź: .

Notatka. Jeśli wstawimy i w warunkach Twierdzenia 5, otrzymamy .

Przykład 6. Rozwiąż nierówność

. (9)

Rozwiązanie. Z nierówności (9) wynika. Przekształćmy nierówność (9) w następujący sposób:

Lub

Ponieważ , wtedy lub .

Odpowiedź: .

Przykład 7.Rozwiąż nierówność

. (10)

Rozwiązanie. Od i , następnie lub .

Pod tym względem oraz nierówność (10) przyjmuje postać

Lub

. (11)

Wynika z tego, że lub . Ponieważ , to nierówność (11) implikuje również lub .

Odpowiedź: .

Notatka. Jeśli zastosujemy Twierdzenie 1 do lewej strony nierówności (10), wtedy otrzymamy . Z tego i nierówności (10) wynika, co lub . Ponieważ , wówczas nierówność (10) przyjmuje postać Lub .

Przykład 8. Rozwiąż nierówność

. (12)

Rozwiązanie. Od tego czasu i z nierówności (12) wynika Lub . Jednak zatem lub. Stąd otrzymujemy lub .

Odpowiedź: .

Przykład 9. Rozwiąż nierówność

. (13)

Rozwiązanie. Zgodnie z Twierdzeniem 7 rozwiązaniem nierówności (13) jest lub .

Niech tak będzie teraz. W tym przypadku oraz nierówność (13) przyjmuje postać Lub .

Jeśli połączysz interwały I , wówczas otrzymujemy rozwiązanie nierówności (13) postaci.

Przykład 10. Rozwiąż nierówność

. (14)

Rozwiązanie. Zapiszmy nierówność (14) w równoważnej postaci: . Jeśli zastosujemy Twierdzenie 1 do lewej strony tej nierówności, otrzymamy nierówność .

Z tego i z twierdzenia 1 wynika, że nierówność (14) jest spełniona dla dowolnych wartości.

Odpowiedź: dowolna liczba.

Przykład 11. Rozwiąż nierówność

. (15)

Rozwiązanie. Zastosowanie twierdzenia 1 do lewej strony nierówności (15), otrzymujemy . To i nierówność (15) dają równanie, który ma formę.

Zgodnie z twierdzeniem 3, równanie równoznaczne z nierównością. Stąd dostajemy.

Przykład 12.Rozwiąż nierówność

. (16)

Rozwiązanie. Z nierówności (16) zgodnie z Twierdzeniem 4 otrzymujemy układ nierówności

Podczas rozwiązywania nierównościSkorzystajmy z Twierdzenia 6 i otrzymajmy układ nierównościz czego wynika.

Rozważ nierówność. Zgodnie z twierdzeniem 7, otrzymujemy zbiór nierówności I . Druga nierówność populacji jest ważna dla dowolnej liczby rzeczywistej.

Stąd , rozwiązaniem nierówności (16) jest.

Przykład 13.Rozwiąż nierówność

. (17)

Rozwiązanie. Zgodnie z Twierdzeniem 1 możemy pisać

(18)

Uwzględniając nierówność (17) wnioskujemy, że obie nierówności (18) przekształcają się w równość, tj. istnieje układ równań

Według twierdzenia 3 ten system równania są równoważne układowi nierówności

Lub

Przykład 14.Rozwiąż nierówność

. (19)

Rozwiązanie. Od tego czasu. Pomnóżmy obie strony nierówności (19) przez wyrażenie , które dla dowolnych wartości przyjmuje tylko wartości dodatnie. Otrzymujemy wówczas nierówność równoważną nierówności (19) postaci

Stąd dostajemy lub, gdzie. Od i wówczas rozwiązaniem nierówności (19) jest: I .

Odpowiedź: , .

Aby uzyskać bardziej szczegółowe przestudiowanie metod rozwiązywania nierówności za pomocą modułu, zalecamy skorzystanie z podręczników, podane w wykazie zalecanej literatury.

1. Zbiór problemów z matematyki dla kandydatów na studia / wyd. MI. Scanavi. – M.: Pokój i edukacja, 2013. – 608 s.

2. Suprun V.P. Matematyka dla uczniów szkół średnich: metody rozwiązywania i udowadniania nierówności. – M.: Lenand / URSS, 2018. – 264 s.

3. Suprun V.P. Matematyka dla uczniów szkół średnich: metody niestandardowe rozwiązywanie problemów. – M.: CD „Librocom” / URSS, 2017. – 296 s.

Nadal masz pytania?

Aby skorzystać z pomocy korepetytora zarejestruj się.

stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do oryginalnego źródła.