1 x parzysty lub nieparzysty. Funkcje parzyste i nieparzyste. Funkcje okresowe

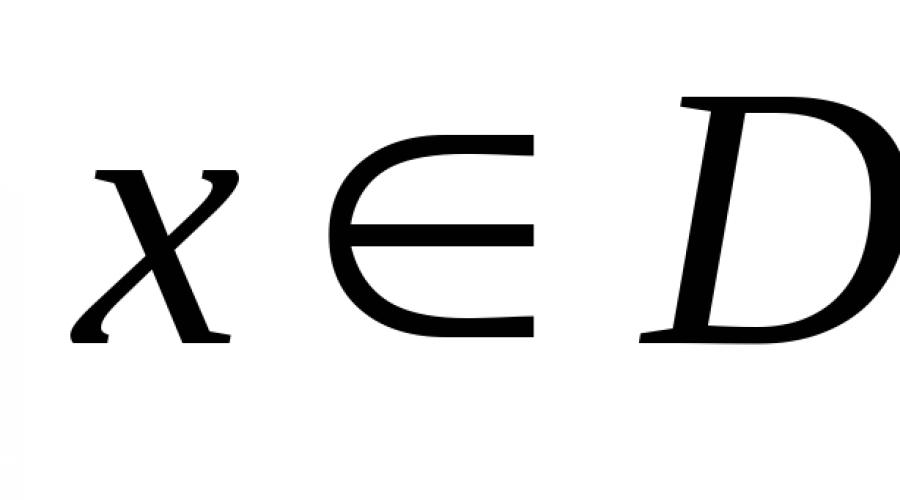
Wykresy parzystych i nie nawet funkcjonować mają następujące cechy:

Jeżeli funkcja jest parzysta, to jej wykres jest symetryczny względem rzędnej. Jeśli funkcja jest nieparzysta, to jej wykres jest symetryczny względem początku.

Rozwiązanie. Rozważmy funkcję: \(f\left(x \right)=\left|x \right|\) i zamieńmy odwrotnie \(-x \) zamiast \(x \). W wyniku prostych przekształceń otrzymujemy: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ In other słów, jeśli zastąpimy argument przeciwnym znakiem, funkcja się nie zmieni.

Oznacza to, że funkcja ta jest parzysta, a jej wykres będzie symetryczny względem osi rzędnych ( Oś pionowa). Wykres tej funkcji pokazano na rysunku po lewej stronie. Oznacza to, że konstruując wykres, można narysować tylko połowę, a drugą część (na lewo od osi pionowej narysować symetrycznie do prawej części). Określając symetrię funkcji przed rozpoczęciem rysowania jej wykresu, możesz znacznie uprościć proces konstruowania lub badania funkcji. Jeśli trudno jest przeprowadzić ogólną kontrolę, możesz to zrobić prościej: podstaw do równania te same wartości różnych znaków. Na przykład -5 i 5. Jeśli wartości funkcji okażą się takie same, to możemy mieć nadzieję, że funkcja będzie parzysta. Z matematycznego punktu widzenia podejście to nie jest całkowicie poprawne, ale z praktycznego punktu widzenia jest wygodne. Aby zwiększyć wiarygodność wyniku, możesz zastąpić kilka par takich przeciwnych wartości.

Rozwiązanie. Sprawdźmy to samo co w poprzednim przykładzie: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right ) $$ Oznacza to, że pierwotna funkcja jest nieparzysta (znak funkcji zmienił się na przeciwny).

Wniosek: funkcja jest symetryczna względem początku. Możesz zbudować tylko jedną połowę i narysować drugą symetrycznie. Ten rodzaj symetrii jest trudniejszy do narysowania. Oznacza to, że patrzysz na wykres z drugiej strony arkusza, a nawet do góry nogami. Możesz też to zrobić: weź narysowaną część i obróć ją wokół początku o 180 stopni w kierunku przeciwnym do ruchu wskazówek zegara.

Rozwiązanie. Przeprowadźmy tę samą kontrolę zmiany znaku, co w poprzednich dwóch przykładach. $$f\left(-x \right)=\left(-x \right)^3+\left(-x \right)^2=-x^2+x^2$$ W rezultacie otrzymujemy że: $$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$ A to oznacza, że ​​funkcja nie jest ani parzysta, ani nieparzysta.

Wniosek: funkcja nie jest symetryczna ani względem początku, ani środka układu współrzędnych. Stało się tak, ponieważ jest to suma dwóch funkcji: parzystej i nieparzystej. Ta sama sytuacja będzie miała miejsce, jeśli odejmiemy dwie różne funkcje. Ale mnożenie lub dzielenie doprowadzi do innego wyniku. Na przykład iloczyn funkcji parzystej i nieparzystej daje funkcję nieparzystą. Lub iloraz dwóch liczb nieparzystych prowadzi do funkcji parzystej.

Parzystość i nieparzystość funkcji to jedne z jej głównych właściwości, a parzystość zajmuje imponującą część kurs szkolny matematyka. W dużej mierze determinuje zachowanie funkcji i znacznie ułatwia konstrukcję odpowiedniego wykresu.

Określmy parzystość funkcji. Ogólnie rzecz biorąc, badaną funkcję rozważa się nawet wtedy, gdy dla przeciwnych wartości zmiennej niezależnej (x) znajdującej się w jej dziedzinie definicji odpowiadające wartości y (funkcji) okazują się równe.

Podajmy bardziej ścisłą definicję. Rozważmy pewną funkcję f(x), która jest zdefiniowana w dziedzinie D. Będzie tak nawet, jeśli dla dowolnego punktu x znajdującego się w dziedzinie definicji:

• -x (punkt przeciwny) również leży w tym zakresie,

• f(-x) = f(x).

Z powyższej definicji wynika warunek niezbędny dla dziedziny definicji takiej funkcji, a mianowicie symetria względem punktu O, który jest początkiem współrzędnych, gdyż jeśli jakiś punkt b mieści się w dziedzinie definicji parzystej funkcji, to odpowiedni punkt b również należy do tej dziedziny. Z powyższego wynika więc wniosek: funkcja parzysta ma postać symetryczną względem osi rzędnych (Oy).

Jak w praktyce wyznaczyć parzystość funkcji?

Określmy to wzorem h(x)=11^x+11^(-x). Kierując się algorytmem wynikającym bezpośrednio z definicji, w pierwszej kolejności zbadamy jej dziedzinę definicyjną. Oczywiście jest on zdefiniowany dla wszystkich wartości argumentu, czyli spełniony jest pierwszy warunek.

Następnym krokiem jest zastąpienie argumentu (x) wartością przeciwną (-x).
Otrzymujemy:
h(-x) = 11^(-x) + 11^x.
Ponieważ dodawanie spełnia prawo przemienności (przemienności), oczywiste jest, że h(-x) = h(x) i dane zależność funkcjonalna- nawet.

Sprawdźmy parzystość funkcji h(x)=11^x-11^(-x). Postępując zgodnie z tym samym algorytmem, otrzymujemy, że h(-x) = 11^(-x) -11^x. Po odjęciu minusa ostatecznie mamy
h(-x)=-(11^x-11^(-x))=- h(x). Dlatego h(x) jest nieparzyste.

Nawiasem mówiąc, należy przypomnieć, że istnieją funkcje, których nie można sklasyfikować według tych kryteriów, nie nazywa się ich ani parzystymi, ani nieparzystymi.

Nawet funkcje mają wiele interesujących właściwości:

• w wyniku dodania podobnych funkcji otrzymują parzystą;
• w wyniku odjęcia takich funkcji otrzymuje się parzystą;
• nawet, także;
• w wyniku pomnożenia dwóch takich funkcji otrzymuje się parzystą;
• w wyniku pomnożenia funkcji nieparzystych i parzystych otrzymujemy funkcję nieparzystą;
• w wyniku podzielenia funkcji nieparzystych i parzystych otrzymuje się nieparzystą;
• pochodna takiej funkcji jest nieparzysta;
• Jeśli podniesiesz funkcję nieparzystą do kwadratu, otrzymasz parzystą.

Parzystość funkcji można wykorzystać do rozwiązywania równań.

Aby rozwiązać równanie takie jak g(x) = 0, gdzie lewa strona równanie jest funkcją parzystą, wystarczy znaleźć jej rozwiązania dla nieujemnych wartości zmiennej. Powstałe pierwiastki równania należy połączyć z liczbami przeciwnymi. Jeden z nich podlega weryfikacji.

Jest to również z powodzeniem stosowane do rozwiązywania zadania niestandardowe z parametrem.

Na przykład, czy istnieje taka wartość parametru a, dla której równanie 2x^6-x^4-ax^2=1 będzie miało trzy pierwiastki?

Jeśli weźmiemy pod uwagę, że zmienna wchodzi do równania w potęgach parzystych, to jasne jest, że zastąpienie x przez - x dane równanie nie zmieni się. Wynika z tego, że jeśli pewna liczba jest jej pierwiastkiem, to liczba przeciwna również jest pierwiastkiem. Wniosek jest oczywisty: pierwiastki równania różne od zera zaliczamy do zbioru jego rozwiązań „parami”.

Oczywiste jest, że sama liczba nie wynosi 0, to znaczy liczba pierwiastków takiego równania może być tylko parzysta i oczywiście dla dowolnej wartości parametru nie może mieć trzech pierwiastków.

Ale liczba pierwiastków równania 2^x+ 2^(-x)=ax^4+2x^2+2 może być nieparzysta i to dla dowolnej wartości parametru. Rzeczywiście łatwo sprawdzić, że zbiór pierwiastków danego równania zawiera rozwiązania „parami”. Sprawdźmy, czy 0 jest pierwiastkiem. Kiedy podstawimy to do równania, otrzymamy 2 = 2. Zatem oprócz „sparowanych” 0 jest także pierwiastkiem, co dowodzi ich nieparzystej liczby.

Definicja 1. Funkcja zostaje wywołana nawet (dziwne ), jeśli razem z każdą wartością zmiennej
oznaczający - X również należy
i zachodzi równość

Zatem funkcja może być parzysta lub nieparzysta tylko wtedy, gdy jej dziedzina definicji jest symetryczna względem początku współrzędnych na osi liczbowej (liczba X I - X należeć jednocześnie
). Na przykład funkcja
nie jest ani parzysty, ani nieparzysty, ponieważ jest to dziedzina definicji
nie symetryczny względem początku.

Funkcjonować
nawet, ponieważ
symetryczny względem początku i.

Funkcjonować
dziwne, ponieważ
I
.

Funkcjonować
nie jest parzyste i nieparzyste, ponieważ chociaż
i jest symetryczny względem początku, równości (11.1) nie są spełnione. Na przykład,.

Wykres funkcji parzystej jest symetryczny względem osi Jednostka organizacyjna, bo jeśli o to chodzi

również należy do harmonogramu. Wykres funkcji nieparzystej jest symetryczny względem początku, ponieważ jeśli
należy do wykresu, a następnie do punktu
również należy do harmonogramu.

Przy dowodzie, czy funkcja jest parzysta czy nieparzysta, przydatne są następujące stwierdzenia.

Twierdzenie 1. a) Suma dwóch funkcji parzystych (nieparzystych) jest funkcją parzystą (nieparzystą).

b) Iloczyn dwóch parzystych (nieparzystych) funkcji jest funkcją parzystą.

c) Iloczyn funkcji parzystej i nieparzystej jest funkcją nieparzystą.

d) Jeśli F– nawet działa na planie X i funkcja G zdefiniowany na planie
, a następnie funkcja
- nawet.

d) Jeśli F– dziwna funkcja na zestawie X i funkcja G zdefiniowany na planie
i parzysty (nieparzysty), to funkcja
- nawet dziwne).

Dowód. Udowodnimy na przykład b) i d).

b) Niech
I
– nawet funkcje. Zatem zatem. Przypadek funkcji nieparzystych jest traktowany podobnie
I
.

d) Niech F jest funkcją parzystą. Następnie.

Pozostałe twierdzenia twierdzenia można udowodnić w podobny sposób. Twierdzenie zostało udowodnione.

Twierdzenie 2. Dowolna funkcja
, zdefiniowany na planie X, symetryczny względem początku, można przedstawić jako sumę funkcji parzystych i nieparzystych.

Dowód. Funkcjonować
można zapisać w postaci

.

Funkcjonować
– nawet, ponieważ
i funkcja
– dziwne, ponieważ. Zatem,
, Gdzie
– nawet i
– dziwne funkcje. Twierdzenie zostało udowodnione.

Definicja 2. Funkcja
zwany okresowy , jeśli istnieje liczba
, tak że dla dowolnego
liczby
I
również należą do domeny definicji
i równości są spełnione

Taki numer T zwany okres Funkcje
.

Z definicji 1 wynika, że ​​jeśli T– okres funkcji
, następnie liczba – T To samo jest okresem funkcji
(od czasu wymiany T NA - T zachowana jest równość). Korzystając z metody indukcji matematycznej można wykazać, że jeśli T– okres funkcji F, Następnie
, to także kropka. Wynika z tego, że jeśli funkcja ma okres, to ma nieskończenie wiele okresów.

Definicja 3. Najmniejszy z dodatnich okresów funkcji nazywa się jej główny okres.

Twierdzenie 3. Jeśli T– główny okres funkcji F, to pozostałe okresy są jego wielokrotnościami.

Dowód. Załóżmy odwrotnie, to znaczy, że istnieje kropka Funkcje F (> 0), a nie wielokrotność T. Potem dzielenie NA T z resztą otrzymujemy
, Gdzie
. Dlatego

to jest – okres funkcji F, I
, a to jest sprzeczne z faktem, że T– główny okres funkcji F. Stwierdzenie twierdzenia wynika z powstałej sprzeczności. Twierdzenie zostało udowodnione.

Powszechnie wiadomo, że funkcje trygonometryczne są okresowe. Główny okres
I
równa się
,
I
. Znajdźmy okres funkcji
. Pozwalać
- okres tej funkcji. Następnie

(ponieważ
.

albo albo
.

Oznaczający T, wyznaczone z pierwszej równości, nie może być okresem, gdyż zależy od X, tj. jest funkcją X, a nie liczba stała. Okres wyznacza się z drugiej równości:
. Jest nieskończenie wiele okresów, z
najmniejszy dodatni okres uzyskuje się przy
:
. Jest to główny okres funkcji
.

Przykładem bardziej złożonej funkcji okresowej jest funkcja Dirichleta

Zauważ, że jeśli T jest zatem liczbą wymierną
I
są liczbami wymiernymi dla wymiernych X i irracjonalne, gdy irracjonalne X. Dlatego

dla dowolnej liczby wymiernej T. Zatem dowolna liczba wymierna T jest okresem funkcji Dirichleta. Oczywiste jest, że ta funkcja nie ma głównego okresu, ponieważ jest dodatnia liczby wymierne, dowolnie blisko zera (na przykład można dokonać wyboru liczby wymiernej N arbitralnie bliskie zeru).

Twierdzenie 4. Jeśli funkcja F zdefiniowany na planie X i ma okres T i funkcja G zdefiniowany na planie
, to funkcja złożona
też ma okres T.

Dowód. Mamy zatem

to znaczy, stwierdzenie twierdzenia zostało udowodnione.

Na przykład od sałata X ma okres
, a następnie funkcje
mieć okres
.

Definicja 4. Wywołuje się funkcje, które nie są okresowe nieokresowe .

Funkcjonować jest jednym z najważniejszych pojęć matematycznych. Funkcja - zależność zmiennej Na ze zmiennej X, jeśli każda wartość X pasuje do jednej wartości Na. Zmienny X nazywaną zmienną niezależną lub argumentem. Zmienny Na zwaną zmienną zależną. Wszystkie wartości zmiennej niezależnej (zmienna X) tworzą dziedzinę definicji funkcji. Wszystkie wartości, jakie przyjmuje zmienna zależna (variable y), tworzą zakres wartości funkcji.

Wykres funkcji wywołaj zbiór wszystkich punktów płaszczyzny współrzędnych, których odcięte są równe wartościom argumentu, a rzędne są równe odpowiednim wartościom funkcji, to znaczy wartościom zmienne są wykreślane wzdłuż osi odciętych X, a wartości zmiennej są wykreślane wzdłuż osi rzędnych y. Aby narysować wykres funkcji, musisz znać jej właściwości. Główne właściwości funkcji zostaną omówione poniżej!

Do zbudowania wykresu funkcji polecamy skorzystać z naszego programu - Grafowanie funkcji online. Jeśli podczas studiowania materiałów na tej stronie będziesz miał jakieś pytania, zawsze możesz je zadać na naszym forum. Również na forum pomogą Ci rozwiązać problemy z matematyki, chemii, geometrii, teorii prawdopodobieństwa i wielu innych przedmiotów!

Podstawowe własności funkcji.

1) Dziedzina funkcji i zakres funkcji.

Dziedziną funkcji jest zbiór wszystkich prawidłowych wartości argumentów X(zmienny X), dla której funkcja y = f(x) określony.
Zakres funkcji to zbiór wszystkich wartości rzeczywistych y, co funkcja akceptuje.

W elementarna matematyka funkcje bada się tylko na zbiorze liczb rzeczywistych.

2) Zera funkcji.

Wartości X, w którym y=0, zwany funkcje zerowe. Są to odcięte punktów przecięcia wykresu funkcji z osią Wół.

3) Przedziały stałego znaku funkcji.

Takimi przedziałami wartości są przedziały znaku stałego funkcji X, na którym znajdują się wartości funkcji y wywoływane są albo tylko dodatnie, albo tylko ujemne przedziały stałego znaku funkcji.

4) Monotoniczność funkcji.

Funkcja rosnąca (w pewnym przedziale) to funkcja, dla której wyższa wartość argument z tego przedziału odpowiada większej wartości funkcji.

Funkcja malejąca (w pewnym przedziale) to funkcja, w której większa wartość argumentu z tego przedziału odpowiada mniejszej wartości funkcji.

5) Funkcja parzysta (nieparzysta)..

Funkcja parzysta to funkcja, której dziedzina definicji jest symetryczna względem początku i dla dowolnego X f(-x) = f(x). Wykres funkcji parzystej jest symetryczny względem rzędnej.

Funkcja nieparzysta to funkcja, której dziedzina definicji jest symetryczna względem początku i dla dowolnego X z dziedziny definicji równość jest prawdziwa f(-x) = - f(x). Wykres funkcji nieparzystej jest symetryczny względem początku.

Nawet funkcjonować
1) Dziedzina definicji jest symetryczna względem punktu (0; 0), to znaczy, jeśli punkt A należy do dziedziny definicji, a następnie do punktu -A również należy do domeny definicji.
2) Dla dowolnej wartości X f(-x)=f(x)
3) Wykres funkcji parzystej jest symetryczny względem osi Oy.

Dziwna funkcja ma następujące właściwości:
1) Dziedzina definicji jest symetryczna względem punktu (0; 0).
2) dla dowolnej wartości X, należący do dziedziny definicji, równość f(-x)=-f(x)
3) Wykres funkcji nieparzystej jest symetryczny względem początku (0; 0).

Nie każda funkcja jest parzysta lub nieparzysta. Funkcje ogólna perspektywa nie są ani parzyste, ani nieparzyste.

6) Ograniczone i nieograniczone funkcje.

Funkcję nazywamy ograniczoną, jeśli istnieje liczba dodatnia M taka, że ​​|f(x)| ≤ M dla wszystkich wartości x. Jeżeli taka liczba nie istnieje, to funkcja jest nieograniczona.

7) Okresowość funkcji.

Funkcja f(x) jest okresowa, jeśli istnieje niezerowa liczba T taka, że ​​dla dowolnego x z dziedziny definicji funkcji zachodzi: f(x+T) = f(x). Ten najmniejsza liczba nazywa się okresem funkcji. Wszystko funkcje trygonometryczne są okresowe. (Wzory trygonometryczne).

Funkcjonować F nazywa się okresowym, jeśli istnieje taka liczba, że ​​dla dowolnego X z dziedziny definicji równość f(x)=f(x-T)=f(x+T). T jest okresem funkcji.

Każda funkcja okresowa ma nieskończony zbiór okresy. W praktyce zwykle bierze się pod uwagę najmniejszy okres dodatni.

Wartości funkcji okresowej powtarzają się po odstępie równym okresowi. Jest to wykorzystywane podczas konstruowania wykresów.

Zależność zmiennej y od zmiennej x, w której każda wartość x odpowiada pojedynczej wartości y, nazywana jest funkcją. Do oznaczenia należy stosować zapis y=f(x). Każda funkcja ma szereg podstawowych właściwości, takich jak monotoniczność, parzystość, okresowość i inne.

Przyjrzyj się bliżej właściwości parzystości.

Funkcja y=f(x) wywoływana jest nawet wtedy, gdy spełnia dwa warunki:

2. Wartość funkcji w punkcie x, należąca do dziedziny definicji funkcji, musi być równa wartości funkcji w punkcie -x. Czyli dla dowolnego punktu x z dziedziny definicji funkcji musi być spełniona równość: f(x) = f(-x).

Wykres funkcji parzystej

Jeśli narysujesz wykres funkcji parzystej, będzie on symetryczny względem osi Oy.

Na przykład funkcja y=x^2 jest parzysta. Sprawdźmy to. Dziedziną definicji jest cała oś liczbowa, czyli jest ona symetryczna względem punktu O.

Weźmy dowolne x=3. f(x)=3^2=9.

f(-x)=(-3)^2=9. Zatem f(x) = f(-x). Zatem oba warunki są spełnione, co oznacza, że ​​funkcja jest parzysta. Poniżej znajduje się wykres funkcji y=x^2.

Rysunek pokazuje, że wykres jest symetryczny względem osi Oy.

Wykres funkcji nieparzystej

Funkcję y=f(x) nazywamy nieparzystą, jeżeli spełnia dwa warunki:

1. Dziedzina definicji danej funkcji musi być symetryczna względem punktu O. To znaczy, jeśli jakiś punkt a należy do dziedziny definicji funkcji, to odpowiadający mu punkt -a także musi należeć do dziedziny definicji funkcji danej funkcji.

2. Dla dowolnego punktu x musi być spełniona równość z dziedziny definicji funkcji: f(x) = -f(x).

Wykres funkcji nieparzystej jest symetryczny względem punktu O – początku współrzędnych. Na przykład funkcja y=x^3 jest nieparzysta. Sprawdźmy to. Dziedziną definicji jest cała oś liczbowa, czyli jest ona symetryczna względem punktu O.

Weźmy dowolne x=2. f(x)=2^3=8.

f(-x)=(-2)^3=-8. Zatem f(x) = -f(x). Zatem oba warunki są spełnione, co oznacza, że ​​funkcja jest nieparzysta. Poniżej znajduje się wykres funkcji y=x^3.

Rysunek wyraźnie pokazuje, że funkcja nieparzysta y=x^3 jest symetryczna względem początku.