بولتن علمی دانشجویی بین المللی. مسائل مربوط به بسط توابع در یک سری فوریه و حل آنها. نقاط صفر سینوس را پیدا کنید

20.09.2019

همچنین بخوانید

تبریک سال نو گذشته - شعر، نثر، اس ام اس تبریک سال نو و کریسمس گذشته

کارت پستال با اولین روز بهار - زیبا و خنده دار با کتیبه: اس ام اس کوتاه تبریک اولین روز بهار

می توانید با یک کارت پستال زیبا به عزیزان خود تبریک بگویید

عکس خنده دار تبریک روز مادر برای کودکان - تبریک به مادر از دانش آموزان مهد کودک

در بسیاری از موارد، وظیفه به دست آوردن (محاسبه) طیف سیگنال به شرح زیر است. یک ADC وجود دارد که با فرکانس نمونه برداری Fd سیگنال پیوسته ای را که در زمان T به ورودی خود می رسد، به قرائت های دیجیتال - N قطعه تبدیل می کند. در مرحله بعد، آرایه خوانش ها به برنامه خاصی وارد می شود که N/2 مقداری عددی را ارائه می دهد (برنامه نویسی که از اینترنت کشیده شدهبرنامه ای نوشت و ادعا کرد که تبدیل فوریه را انجام می دهد).

برای بررسی اینکه آیا برنامه به درستی کار می کند، آرایه ای از قرائت ها را به عنوان مجموع دو سینوسی sin(10*2*pi*x)+0.5*sin(5*2*pi*x) تشکیل می دهیم و آن را به داخل میل می کنیم. برنامه این برنامه موارد زیر را ترسیم کرد:

شکل 1 نمودار تابع زمان سیگنال

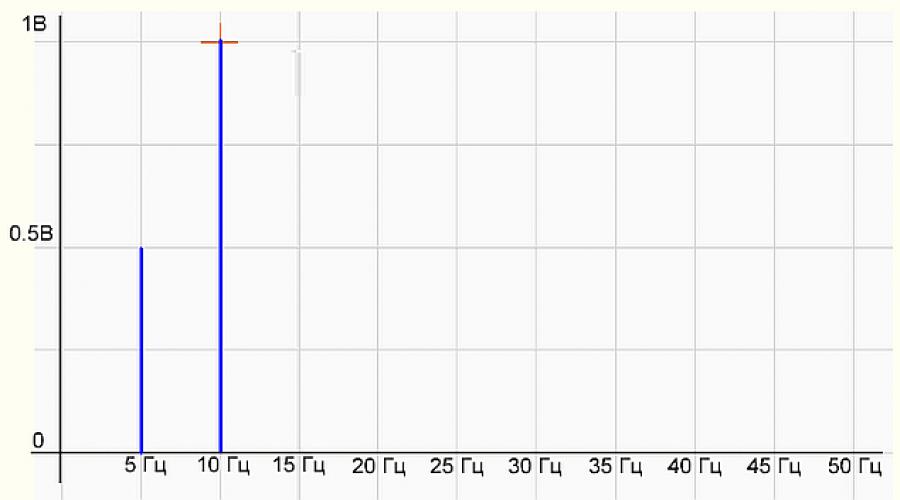
Fig.2 نمودار طیف سیگنال

روی نمودار طیف دو میله (هارمونیک) 5 هرتز با دامنه 0.5 ولت و 10 هرتز وجود دارد - با دامنه 1 ولت، همه مانند فرمول سیگنال اصلی. همه چیز خوب است، آفرین برنامه نویس! برنامه به درستی کار می کند.

این بدان معناست که اگر یک سیگنال واقعی از مخلوط دو سینوسی به ورودی ADC اعمال کنیم، طیف مشابهی متشکل از دو هارمونیک به دست خواهیم آورد.

مجموع، ما واقعیسیگنال اندازه گیری شده مدت زمان 5 ثانیه، دیجیتالی شده توسط ADC، یعنی نشان داده شده است گسستهشمارش، دارد گسسته غیر تناوبیدامنه.

از نظر ریاضی چه تعداد اشتباه در این عبارت وجود دارد؟

اکنون مقامات تصمیم گرفته اند که ما تصمیم گرفته ایم که 5 ثانیه خیلی طولانی است، بیایید سیگنال را در 0.5 ثانیه اندازه گیری کنیم.

شکل 3 نمودار تابع sin(10*2*pi*x)+0.5*sin(5*2*pi*x) برای دوره اندازه گیری 0.5 ثانیه

Fig.4 طیف تابع

یک چیزی درست نیست! هارمونیک 10 هرتز به طور معمول رسم می شود، اما به جای یک چوب 5 هرتز، چندین هارمونیک نامفهوم ظاهر شد. ما در اینترنت نگاه می کنیم، چه چیزی و چگونه ...

در می گویند باید به انتهای نمونه صفر اضافه شود و طیف نرمال رسم شود.

fig.5 صفرهای تمام شده تا 5 ثانیه

Fig.6 ما طیف را دریافت کردیم

هنوز آن چیزی که در 5 ثانیه بود نیست. شما باید با تئوری برخورد کنید. بریم به ویکیپدیا- منبع دانش

2. یک تابع پیوسته و نمایش آن توسط یک سری فوریه

از نظر ریاضی، سیگنال ما با مدت زمان T ثانیه تابعی از f(x) است که بر روی قطعه (0، T) (X در) تعریف شده است. این مورد- زمان). چنین تابعی را همیشه می توان به صورت مجموع توابع هارمونیک (سینوس یا کسینوس) به شکل زیر نشان داد:

(1)، جایی که:

K - تعداد تابع مثلثاتی (تعداد جزء هارمونیک، عدد هارمونیک)
T - قسمتی که تابع در آن تعریف شده است (مدت زمان سیگنال)
Ak - دامنه مولفه هارمونیک k-امین،
θk - فاز اولیه مولفه هارمونیک k-امین

"نمایش یک تابع به عنوان مجموع یک سری" به چه معناست؟ به این معنی که با اضافه کردن مقادیر مولفه های هارمونیک سری فوریه در هر نقطه، مقدار تابع خود را در این نقطه به دست می آوریم.

(به طور دقیق تر، انحراف استاندارد سری از تابع f(x) به سمت صفر میل خواهد کرد، اما با وجود همگرایی استاندارد، سری فوریه تابع، به طور کلی، نیازی به همگرایی نقطه ای با آن ندارد. https: //ru.wikipedia.org/ wiki/Fourier_Series.)

این سریال را می توان به صورت زیر نیز نوشت:

(2),
جایی که ، مجموعه k-امدامنه

رابطه بین ضرایب (1) و (3) با فرمول های زیر بیان می شود:

توجه داشته باشید که هر سه نمایش سری فوریه کاملاً معادل هستند. گاهی اوقات هنگام کار با سری فوریه، به جای استفاده از سینوس و کسینوس، استفاده از تبدیل فوریه به شکل مختلط، راحت تر است. اما استفاده از فرمول (1) برای ما راحت است، که در آن سری فوریه به صورت مجموع امواج کسینوس با دامنه ها و فازهای مربوطه نشان داده می شود. در هر صورت، این نادرست است که بگوییم نتیجه تبدیل فوریه سیگنال واقعی، دامنه های پیچیده هارمونیک ها خواهد بود. همانطور که ویکی به درستی بیان می کند، "تبدیل فوریه (ℱ) عملیاتی است که یک تابع از یک متغیر واقعی را به یک تابع دیگر، همچنین از یک متغیر واقعی، نگاشت می کند."

جمع:
مبنای ریاضی تحلیل طیفی سیگنال ها تبدیل فوریه است.

تبدیل فوریه به ما امکان می دهد یک تابع پیوسته f(x) (سیگنال) را که در بازه (0, T) به عنوان مجموع یک عدد نامتناهی (یک سری نامتناهی) تعریف شده است، نشان دهیم. توابع مثلثاتی(سینوسی و/یا امواج کسینوس) با دامنه ها و فازهای معین، که روی قطعه (0، T) نیز در نظر گرفته شده است. به چنین سریالی سری فوریه می گویند.

چند نکته دیگر وجود دارد که برای درک آنها باید درک شود کاربرد صحیحتبدیل فوریه به تجزیه و تحلیل سیگنال. اگر سری فوریه (مجموع سینوسی ها) را در کل محور X در نظر بگیریم، می بینیم که خارج از قطعه (0, T)، تابعی که توسط سری فوریه نمایش داده می شود، به صورت دوره ای تابع ما را تکرار می کند.

به عنوان مثال، در نمودار در شکل 7، تابع اصلی بر روی قطعه (-T \ 2، + T \ 2) تعریف شده است، و سری فوریه نشان دهنده یک تابع تناوبی است که در کل محور x تعریف شده است.

این به این دلیل است که خود سینوسی ها به ترتیب توابع تناوبی هستند و مجموع آنها تابع تناوبی خواهد بود.

شکل 7 نمایش یک تابع اصلی غیر تناوبی توسط یک سری فوریه

بدین ترتیب:

تابع اصلی ما پیوسته و غیر تناوبی است که در بازه ای از طول T تعریف شده است.
طیف این تابع گسسته است، یعنی به عنوان یک سری نامتناهی از اجزای هارمونیک - سری فوریه - ارائه می شود.
در واقع سری فوریه برخی را تعریف می کند تابع دوره ای، همزمان با بخش ما در بخش (0، T)، اما برای ما این تناوب ضروری نیست.

دوره های اجزای هارمونیک مضربی از قطعه (0, T) است که تابع اصلی f(x) بر روی آن تعریف شده است. به عبارت دیگر، دوره های هارمونیک مضربی از مدت زمان اندازه گیری سیگنال هستند. به عنوان مثال، دوره اولین هارمونیک سری فوریه برابر با بازه T است که تابع f(x) بر روی آن تعریف شده است. دوره هارمونیک دوم سری فوریه برابر با بازه T/2 است. و به همین ترتیب (شکل 8 را ببینید).

شکل 8 دوره‌ها (فرکانس‌های) مولفه‌های هارمونیک سری فوریه (در اینجا T=2π)

بر این اساس، فرکانس اجزای هارمونیک مضرب 1/T است. یعنی فرکانس اجزای هارمونیک Fk برابر است با Fk= k\T، جایی که k از 0 تا ∞ متغیر است، برای مثال k=0 F0=0. k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (در فرکانس صفر - جزء ثابت).

اجازه دهید تابع اصلی ما یک سیگنال ثبت شده برای T=1 ثانیه باشد. سپس دوره هارمونیک اول برابر با مدت زمان سیگنال ما T1=T=1 ثانیه خواهد بود و فرکانس هارمونیک 1 هرتز است. دوره هارمونیک دوم برابر است با مدت زمان سیگنال تقسیم بر 2 (T2=T/2=0.5 ثانیه) و فرکانس آن 2 هرتز است. برای هارمونیک سوم T3=T/3 ثانیه و فرکانس 3 هرتز است. و غیره.

گام بین هارمونیک ها در این مورد 1 هرتز است.

بنابراین، یک سیگنال با مدت زمان 1 ثانیه را می توان به اجزای هارمونیک (برای به دست آوردن یک طیف) با وضوح فرکانس 1 هرتز تجزیه کرد.
برای افزایش وضوح 2 برابر به 0.5 هرتز، لازم است مدت زمان اندازه گیری را 2 برابر - حداکثر تا 2 ثانیه افزایش دهید. یک سیگنال با مدت زمان 10 ثانیه را می توان به اجزای هارمونیک (برای بدست آوردن یک طیف) با وضوح فرکانس 0.1 هرتز تجزیه کرد. هیچ راه دیگری برای افزایش وضوح فرکانس وجود ندارد.

راهی برای افزایش مصنوعی مدت زمان سیگنال با افزودن صفر به آرایه نمونه ها وجود دارد. اما وضوح فرکانس واقعی را افزایش نمی دهد.

3. سیگنال های گسسته و تبدیل فوریه گسسته

با توسعه تکنولوژی دیجیتالیروش های ذخیره سازی داده های اندازه گیری (سیگنال ها) نیز تغییر کرده است. اگر قبلاً سیگنال را می‌توان بر روی ضبط صوت ضبط کرد و روی نوار به شکل آنالوگ ذخیره کرد، اکنون سیگنال‌ها دیجیتالی شده و در فایل‌هایی در حافظه رایانه به عنوان مجموعه‌ای از اعداد (شمارش) ذخیره می‌شوند.

طرح معمول برای اندازه گیری و دیجیتالی کردن سیگنال به شرح زیر است.

شکل 9 طرح کانال اندازه گیری

سیگنال از مبدل اندازه گیری در یک دوره زمانی T به ADC می رسد. نمونه سیگنال (نمونه) به دست آمده در طول زمان T به کامپیوتر منتقل شده و در حافظه ذخیره می شود.

شکل 10 سیگنال دیجیتالی - N قرائت دریافت شده در زمان T

الزامات پارامترهای دیجیتالی شدن سیگنال چیست؟ دستگاهی که ورودی را تبدیل می کند سیگنال آنالوگبه یک کد گسسته ( سیگنال دیجیتال) مبدل آنالوگ به دیجیتال (ADC) (ویکی) نامیده می شود.

یکی از پارامترهای اصلی ADC حداکثر نرخ نمونه برداری (یا نرخ نمونه برداری، نرخ نمونه انگلیسی) است - فرکانس نمونه برداری از یک سیگنال مداوم در زمان در طول نمونه برداری آن. بر حسب هرتز اندازه گیری می شود. ((ویکی))

طبق قضیه کوتلنیکوف، اگر یک سیگنال پیوسته دارای طیف محدود شده با فرکانس Fmax باشد، می توان آن را به طور کامل و منحصر به فرد از نمونه های گسسته آن که در فواصل زمانی گرفته شده است، بازیابی کرد. ، یعنی با فرکانس Fd ≥ 2*Fmax، که در آن Fd - فرکانس نمونه برداری. Fmax - حداکثر فرکانس طیف سیگنال. به عبارت دیگر، نرخ نمونه برداری سیگنال (نرخ نمونه برداری ADC) باید حداقل 2 برابر حداکثر فرکانس سیگنالی باشد که می خواهیم اندازه گیری کنیم.

و چه اتفاقی می‌افتد اگر خوانش‌هایی را با فرکانس پایین‌تر از آنچه قضیه کوتلنیکف لازم است انجام دهیم؟

در این مورد، اثر "Aliasing" (معروف به اثر استروبوسکوپی، اثر moiré) رخ می دهد، که در آن سیگنال فرکانس بالا پس از دیجیتالی شدن به سیگنال فرکانس پایین تبدیل می شود که در واقع وجود ندارد. روی انجیر 11 موج سینوسی قرمز فرکانس بالا سیگنال واقعی است. موج سینوسی آبی فرکانس پایین یک سیگنال ساختگی است که از این واقعیت ناشی می شود که بیش از نیمی از یک دوره سیگنال فرکانس بالا در طول زمان نمونه برداری زمان دارد.

برنج. 11. ظهور یک سیگنال فرکانس پایین کاذب زمانی که نرخ نمونه برداری به اندازه کافی بالا نیست

برای جلوگیری از تاثیر آلیاسینگ، یک فیلتر ضد آلیاسینگ مخصوص در جلوی ADC - LPF (فیلتر پایین گذر) قرار می گیرد که فرکانس های زیر نصف فرکانس نمونه برداری ADC را عبور داده و فرکانس های بالاتر را قطع می کند.

برای محاسبه طیف یک سیگنال از نمونه های گسسته آن، تبدیل فوریه گسسته (DFT) استفاده می شود. ما یک بار دیگر متذکر می شویم که طیف یک سیگنال گسسته "طبق تعریف" توسط فرکانس Fmax محدود می شود که کمتر از نصف فرکانس نمونه برداری Fd است. بنابراین، طیف یک سیگنال گسسته را می توان با مجموع تعداد محدودی از هارمونیک ها نشان داد، برخلاف مجموع نامتناهی سری فوریه یک سیگنال پیوسته، که طیف آن می تواند نامحدود باشد. طبق قضیه کوتلنیکف، حداکثر فرکانس هارمونیک باید به گونه ای باشد که حداقل دو نمونه را به خود اختصاص دهد، بنابراین تعداد هارمونیک ها برابر با نصف تعداد نمونه های سیگنال گسسته است. یعنی اگر N نمونه در نمونه وجود داشته باشد، تعداد هارمونیک های طیف برابر N/2 خواهد بود.

اکنون تبدیل فوریه گسسته (DFT) را در نظر بگیرید.

مقایسه با سری فوریه

می بینیم که آنها بر هم منطبق هستند، با این تفاوت که زمان در DFT گسسته است و تعداد هارمونیک ها به N/2 محدود می شود - نصف تعداد نمونه ها.

فرمول‌های DFT در متغیرهای عدد صحیح بدون بعد k، s نوشته می‌شوند، که k تعداد نمونه‌های سیگنال، s تعداد اجزای طیفی است.
مقدار s تعداد نوسانات کامل هارمونیک را در دوره T (مدت زمان اندازه گیری سیگنال) نشان می دهد. تبدیل فوریه گسسته برای یافتن دامنه ها و فازهای هارمونیک ها به صورت عددی استفاده می شود. "روی کامپیوتر"

بازگشت به نتایج به دست آمده در ابتدا. همانطور که در بالا ذکر شد، هنگام گسترش یک تابع غیر تناوبی (سیگنال ما) به یک سری فوریه، سری فوریه حاصل در واقع با یک تابع تناوبی با دوره T مطابقت دارد (شکل 12).

شکل 12 تابع تناوبی f(x) با دوره Т0، با دوره اندازه گیری Т>T0

همانطور که در شکل 12 مشاهده می شود، تابع f(x) تناوبی با دوره Т0 است. اما با توجه به اینکه مدت زمان نمونه اندازه گیری T با دوره تابع T0 منطبق نیست، تابع به دست آمده به عنوان سری فوریه در نقطه T دارای ناپیوستگی است. در نتیجه طیف این تابع خواهد بود. حاوی تعداد زیادی هارمونیک با فرکانس بالا اگر مدت زمان نمونه اندازه گیری T با دوره تابع T0 منطبق باشد، آنگاه تنها هارمونیک اول (یک سینوسی با دوره ای برابر با مدت زمان نمونه) در طیف به دست آمده پس از تبدیل فوریه وجود خواهد داشت، زیرا تابع f (x) یک سینوسی است.

به عبارت دیگر، برنامه DFT "نمی داند" که سیگنال ما "قطعه ای از یک موج سینوسی" است، اما سعی می کند یک تابع تناوبی را به صورت یک سری نشان دهد که به دلیل ناهماهنگی تک تک قطعات دارای شکاف است. موج سینوسی

در نتیجه هارمونیک هایی در طیف ظاهر می شوند که در مجموع باید شکل تابع را نشان دهند که شامل این ناپیوستگی نیز می شود.

بنابراین، برای به دست آوردن طیف "صحیح" سیگنال، که مجموع چندین سینوسی با دوره های مختلف، لازم است که یک عدد صحیح از دوره های هر سینوسی بر روی دوره اندازه گیری سیگنال قرار گیرد. در عمل، این شرط را می توان برای مدت زمان کافی طولانی اندازه گیری سیگنال برآورده کرد.

شکل 13 نمونه ای از عملکرد و طیف سیگنال خطای سینماتیکی گیربکس

با مدت زمان کوتاه تر، تصویر "بدتر" به نظر می رسد:

شکل 14 نمونه ای از عملکرد و طیف سیگنال ارتعاش روتور

در عمل، درک این که «مولفه‌های واقعی» کجا هستند و «مصنوعات» کجا هستند ناشی از عدم تعدد دوره‌های اجزا و مدت زمان نمونه سیگنال یا «پرش‌ها و شکستن‌ها» در کجا هستند. شکل موج البته نقل قول های «مؤلفه های واقعی» و «مصنوعات» بیهوده نیست. وجود هارمونیک‌های زیاد در نمودار طیف به این معنا نیست که سیگنال ما واقعاً از آنها تشکیل شده است. مثل این است که فکر کنید عدد 7 "شامل" اعداد 3 و 4 است. عدد 7 را می توان به عنوان مجموع اعداد 3 و 4 نشان داد - این درست است.

سیگنال ما نیز همینطور است... یا بهتر است بگوییم، نه حتی "سیگنال ما"، بلکه یک تابع تناوبی که با تکرار سیگنال ما (نمونه برداری) کامپایل شده است را می توان به صورت مجموع هارمونیک ها (سینوسوئیدها) با دامنه ها و فازهای معین نشان داد. اما در بسیاری از موارد مهم برای تمرین (شکل های بالا را ببینید)، واقعاً می توان هارمونیک های به دست آمده در طیف را به فرآیندهای واقعیکه ماهیت چرخه ای دارند و سهم بسزایی در شکل سیگنال دارند.

برخی از نتایج

1. سیگنال واقعی اندازه گیری شده، مدت زمان T ثانیه، دیجیتالی شده توسط ADC، یعنی با مجموعه ای از نمونه های گسسته (تکه N) نشان داده شده است، دارای یک طیف غیر تناوبی گسسته است که با مجموعه ای از هارمونیک ها (N/2 قطعه نشان داده شده است). ).

2. سیگنال با مجموعه ای از مقادیر واقعی و طیف آن با مجموعه ای از مقادیر واقعی نمایش داده می شود. فرکانس های هارمونیک مثبت هستند. این واقعیت که برای ریاضیدانان راحت‌تر است که طیف را به شکل پیچیده با استفاده از فرکانس‌های منفی نشان دهند، به این معنی نیست که "درست است" و "همیشه باید اینطور انجام شود".

3. سیگنال اندازه گیری شده در بازه زمانی T فقط در بازه زمانی T تعیین می شود. آنچه قبل از شروع اندازه گیری سیگنال اتفاق افتاده است و بعد از آن چه اتفاقی خواهد افتاد - این برای علم ناشناخته است. و در مورد ما - جالب نیست. DFT یک سیگنال محدود به زمان، طیف "واقعی" خود را می دهد، به این معنا که، تحت شرایط خاص، به شما امکان می دهد دامنه و فرکانس اجزای آن را محاسبه کنید.

مواد استفاده شده و سایر مواد مفید.

در بالا می بینیم که گسترش توابع به سری های توانی امکان محاسبه مقادیر تقریبی این توابع را با دقت لازم فراهم می کند. اما بسیاری از توابع وجود دارند که به سری های قدرتی (سری تیلور یا مکلارین) گسترش نمی یابند، زیرا الزامات توابع نسبتاً سختگیرانه هستند (تابع باید بی نهایت قابل تمایز باشد و غیره). بنابراین از انواع دیگری از سری های کاربردی نیز استفاده می شود که شرایط انبساط در آنها فشار کمتری دارد. این ردیف ها شامل سری مثلثاتی

تعریف: سری مثلثاتی سری عملکردی به شکل:، (1)

جایی که اعداد ثابتی وجود دارد که به آنها گفته می شود:

ضرایب سری مثلثاتی.

تمام عبارات سری (1) عملکردی غیر تناوبی هستند و دارای حداقل دوره مشترک 2p هستند. این بدان معناست که اگر تابع f(x) به یک سری مثلثاتی (1) بسط داده شود، یعنی. این مجموع این سری است، پس این تابع باید خود مجموع سری (1) فقط در فاصله ای به طول 2p باشد.

ویژگی های اصلی سری مثلثاتی از ویژگی اصلی سیستم توابع مثلثاتی پیروی می کند. Stochala یک تعریف.

تعریف: یک سیستم نامتناهی از توابع j1(x),j2(x),...,j3(x)... تعریف شده بر روی قطعه نامیده می شود متعامد در این بخشدر صورت احراز شرایط زیر:
برای m¹n

برای هر n.

قضیه: سیستم توابع مثلثاتی بر روی بازه [-p,p] متعامد است.

اثبات:باید شرایط 1) و 2) تعریف قبلی را بررسی کنیم.

1) انتگرال ها را در نظر بگیرید:

بیایید فرمول های مثلثاتی را اعمال کنیم:

بدیهی است که با کمک آنها، تمام انتگرال های قبلی به انتگرال های شکل کاهش می یابد:
و

بیایید آنها را محاسبه کنیم.

;

بنابراین، اولین شرط قائم بودن برآورده خواهد شد.

2)
;

و شرط دوم h و غیره برآورده می شود.

سری فوریه مثلثاتی.

اجازه دهید یک تابع f(x) تناوبی با دوره 2p به عنوان مجموع یک سری مثلثاتی نمایش داده شود.
(1).

برای همه x از بازه ای به طول 2p. اما مجموع سری S(x) یک تابع تناوبی با دوره 2p است. بنابراین، مقدار f(x) و S(x) در کل خط عددی (-¥، +¥) منطبق هستند. بنابراین، مطالعه تساوی (1) در بازه ای به طول 2p، معمولاً [-p,p] کافی است.

بنابراین، اجازه دهید f(x) مجموع سری (1) در [-p,p] باشد و، علاوه بر این، فرض کنید که می‌توان آن را ترم به ترم، بنابراین، یک قطعه ادغام کرد. به عنوان مثال، این امکان وجود دارد که سری عددی ضرایب سری (1) به طور مطلق همگرا شوند، یعنی. سری همگرا می شود

(2).

در این حالت، عبارات سری تابعی (1) در مقدار مطلق از شرایط متناظر سری (2) تجاوز نمی‌کند، که این امر دلالت بر همگرایی یکنواخت سری (1) و از این رو، امکان عدم آن را دارد. ادغام مدت بر روی [-p,p].

از این برای محاسبه ضریب a 0 استفاده می کنیم. ما هر دو بخش نابرابری (1) را بر روی [-p,p] یکپارچه می کنیم:

تمام انتگرال های سمت راست، با توجه به خاصیت متعامد بودن توابع مثلثاتی، به جز انتگرال اول برابر با صفر هستند. بنابراین:
، جایی که
(3).

برای محاسبه a به /k¹0/ هر دو طرف (1) را در coskx ضرب می کنیم. سری حاصل نیز به طور یکنواخت روی [-p,p] همگرا خواهند شد، زیرا ½coskx1£ 1 و می تواند ترم به ترم بر روی [-p,p] ادغام شود.

با همان ویژگی متعامد، همه انتگرال های سمت راست برابر با صفر هستند، به جز انتگرال حاوی k.

سپس
. جایی که

(4).

با ضرب هر دو طرف (1) در sin kx و ادغام برابری حاصل در .
. جایی که

(5).

ضرایب محاسبه شده با فرمول (3)-(5) نامیده می شوند

ضرایب فوریهبرای تابع f(x) و سری مثلثاتی (1) با این ضرایب - در کنار تابع فوریه (x).

لازم به ذکر است که ادغام سری (1) ترم به ترم همیشه امکان پذیر نیست. بنابراین، محاسبه ضرایب فوریه و تشکیل سری فوریه (1) به طور رسمی امکان پذیر است، اما نمی توان تضمین کرد که این سری اصلاً همگرا می شود. و اگر همگرا شود، مجموع آن تابعی از f(x) است. در چنین مواردی، ما به جای برابری (1) "مطابقات" موافقت کردیم:

کارکرد. این تحول دارد پراهمیتزیرا می توان از آن برای حل بسیاری از مسائل عملی استفاده کرد. سری فوریه نه تنها توسط ریاضیدانان، بلکه توسط متخصصان علوم دیگر نیز استفاده می شود.

بسط توابع به یک سری فوریه یک تکنیک ریاضی است که اگر از ابزاری استفاده کنید که توابع سینوسی را حس می کند، می توان آن را در طبیعت مشاهده کرد.

این فرآیندزمانی اتفاق می افتد که شخص صدایی را می شنود. گوش انسان به گونه ای طراحی شده است که می تواند نوسانات سینوسی فردی را در فشار هوا با فرکانس های مختلف احساس کند، که به نوبه خود به فرد اجازه می دهد گفتار را تشخیص دهد و به موسیقی گوش دهد.

گوش انسان صدا را به عنوان یک کل درک نمی کند، بلکه از طریق اجزای سری فوریه آن را درک می کند. رشته های ساز موسیقیصداهایی تولید می کند که نوسانات سینوسی با فرکانس های مختلف هستند. واقعیت تجزیه نور به سری فوریه توسط یک رنگین کمان نشان داده می شود. بینایی انسان نور را از طریق برخی از اجزای آن در فرکانس های مختلف نوسانات الکترومغناطیسی درک می کند.

تبدیل فوریه تابعی است که فاز و دامنه سینوسی ها را با فرکانس معین توصیف می کند. این تبدیل برای حل معادلات استفاده می شود که فرآیندهای دینامیکی را که تحت تأثیر انرژی رخ می دهند، توصیف می کنند. سری فوریه مشکل استخراج مولفه های ثابت در سیگنال های نوسانی پیچیده را حل می کند، که امکان تفسیر صحیح داده های به دست آمده از آزمایش ها، مشاهدات در پزشکی، شیمی و نجوم را فراهم می کند.

کشف این تبدیل متعلق به ژان باپتیست ژوزف فوریه، ریاضیدان فرانسوی است. به افتخار کسی که بعداً در نزدیکی فوریه نامگذاری شد. در ابتدا، دانشمند کاربرد روش خود را در مطالعه و توضیح مکانیسم های هدایت گرما یافت. فرض بر این بود که توزیع نامنظم اولیه گرما را می توان به شکل ساده ترین سینوسی ها نشان داد. برای هر یک از آنها حداقل، حداکثر و فاز دما تعیین خواهد شد. تابعی که پیک های بالایی و پایینی منحنی را توصیف می کند، فاز هر هارمونیک تبدیل فوریه بیان توزیع دما نامیده می شود. نویسنده تبدیل یک روش تجزیه را پیشنهاد کرد تابع پیچیدهبه عنوان مجموع توابع کسینوس تناوبی، سینوس.

هدف مقاله ترممطالعه سری فوریه و ارتباط کاربرد عملی این تبدیل است.

برای دستیابی به این هدف، وظایف زیر تدوین شد:

1) مفهوم سری فوریه مثلثاتی را ارائه دهید.

2) تعیین شرایط برای بسط یک تابع به یک سری فوریه.

3) بسط سری فوریه توابع زوج و فرد را در نظر بگیرید.

4) بسط یک تابع غیر تناوبی را در یک سری فوریه در نظر بگیرید.

5) کاربرد عملی سری فوریه را آشکار کنید.

موضوع مطالعه: بسط توابع در یک سری فوریه.

موضوع مطالعه: سری فوریه.

روش تحقیق: تحلیل، سنتز، مقایسه، روش بدیهی.

1.5. سری فوریه برای توابع زوج و فرد

انتگرال متقارن را در نظر بگیرید

که در آن پیوسته یا تکه ای پیوسته روشن است. در انتگرال اول تغییر ایجاد می کنیم. ما معتقدیم. سپس

بنابراین، اگر یک تابع زوج باشد، پس (یعنی نمودار یک تابع زوج متقارن با محور و

اگر یک تابع فرد است، پس (یعنی نمودار یک تابع فرد نسبت به مبدا متقارن است) و

آن ها انتگرال متقارن یک تابع زوج برابر با دو برابر انتگرال بیش از نیمی از فاصله انتگرال گیری است و انتگرال متقارن یک تابع فرد برابر با صفر است.

به دو ویژگی زیر توابع زوج و فرد توجه کنید:

1) حاصل ضرب یک تابع زوج با یک فرد، یک تابع فرد است.

2) حاصل ضرب دو تابع زوج (فرد) یک تابع زوج است.

اجازه دهید یک تابع زوج داده شود و در این بخش به یک سری فوریه مثلثاتی بسط داده شود. با استفاده از نتایج به دست آمده در بالا، به این نتیجه می رسیم که ضرایب این سری به صورت زیر خواهد بود:

اگر یک تابع فرد بر روی یک قطعه داده شود و در این قطعه به یک سری فوریه مثلثاتی بسط داده شود، ضرایب این سری به شکل زیر خواهد بود:

بنابراین، سری فوریه مثلثاتی روی پاره، شکل خواهد داشت

برای عملکرد یکنواخت:

(16)

برای یک تابع فرد:

سری (16) شامل سینوس چندین زاویه نیست، یعنی سری فوریه یک تابع زوج فقط شامل توابع زوج و یک جمله آزاد است. سری (17) شامل کسینوس های چند زاویه نیست، یعنی سری فوریه یک تابع فرد فقط شامل توابع فرد است.

تعریف. رتبه ها
قطعات هستند محدوده کاملفوریه و ناقص نامیده می شوندسری فوریه مثلثاتی

اگر تابعی به یک سری مثلثاتی ناقص (16) (یا (17) بسط داده شود، می گویند کهبه یک سری فوریه مثلثاتی در کسینوس (یا سینوس) گسترش می یابد.

1.6. بسط فوریه یک تابع غیر تناوبی

1.6.1. بسط توابع سری فوریه در

اجازه دهید یک تابع در یک بازه داده شود و شرایط قضیه دیریکله در این بازه را برآورده کند. بیایید متغیر را تغییر دهیم. اجازه دهید جایی که ما انتخاب می کنیم تا تابع آرگومان حاصل در آن تعریف شود. بنابراین، ما آن را در نظر می گیریم

تابع حاصل را می توان به یک سری فوریه گسترش داد:

جایی که

بیایید یک تعویض معکوس انجام دهیم⇒ گرفتن

جایی که

(19)

سری (18) - سری فوریه در سیستم مثلثاتی اصلی توابع

بنابراین، به این نتیجه رسیدیم که اگر تابعی بر روی یک قطعه داده شود و شرایط قضیه دیریکله در این قطعه را برآورده کند، می توان آن را به یک سری فوریه مثلثاتی (18) با توجه به سیستم مثلثاتی توابع (20) گسترش داد.

سری فوریه مثلثاتی برای تابع زوجی که در آن داده شده است شکل خواهد داشت

جایی که

برای یک تابع فرد

جایی که

اظهار نظر! در برخی مسائل، لازم است که یک تابع به یک سری فوریه مثلثاتی بر حسب سیستم توابع (20) نه بر روی یک قطعه، بلکه در یک قطعه بسط داده شود. در این مورد، شما فقط باید محدودیت های ادغام را در فرمول (19) ((15) تغییر دهید، اگر، یعنی در این مورد

(23)

یا اگر

(24)

مجموع سری فوریه مثلثاتی یک تابع تناوبی با نقطه است که ادامه تناوبی است. عملکرد داده شده. و برای یک تابع تناوبی، برابری (4) معتبر است.

1.6.2. بسط توابع سری فوریه در

اجازه دهید یک تابع داده شود و شرایط قضیه دیریکله در این بازه را برآورده کند. چنین تابعی را می توان در سری فوریه نیز گسترش داد. برای انجام این کار، تابع باید به بازه گسترش داده شود و تابع حاصل به یک سری فوریه در قطعه گسترش یابد. در این مورد، سری به دست آمده باید فقط در قسمتی که تابع در آن داده شده است در نظر گرفته شود. برای راحتی محاسبات، تعریف تابع را به صورت زوج و فرد گسترش می دهیم.

1) تابع روی بازه را به صورت زوج ادامه می دهیم، یعنی یک تابع جدید می سازیم حتی عملکرد، منطبق بر بخش با تابع. بنابراین نمودار این تابع نسبت به محور متقارن بوده و با نمودار روی پاره منطبق است. با استفاده از فرمول (21) ضرایب سری فوریه تابع را پیدا کرده و خود سری فوریه را می نویسیم. مجموع سری فوریه برای یک تابع تناوبی با نقطه است. در تمام نقاط تداوم با عملکرد روشن منطبق خواهد شد.

2) اجازه دهید تابع روی بازه را به روشی عجیب بسط دهیم، یعنی یک تابع جدید بسازیم تابع فرد، همزمان با تابع. نمودار چنین تابعی با توجه به مبدأ مختصات متقارن است و با نمودار روی قطعه منطبق است. با استفاده از فرمول (22) ضرایب سری فوریه تابع را پیدا کرده و خود سری فوریه را می نویسیم. مجموع سری فوریه برای یک تابع تناوبی با نقطه است. در تمام نقاط تداوم با عملکرد روشن منطبق خواهد شد.

ملاحظات!

1) به طور مشابه، ما می توانیم در یک سری فوریه یک تابع تعریف شده در بازه را گسترش دهیم

2) از آنجایی که بسط یک تابع در یک قطعه به معنای گسترش آن به قطعه به روش دلخواه است، پس سری فوریه برای تابع منحصر به فرد نخواهد بود.

1.6.3. بسط توابع سری فوریه در

اجازه دهید تابع بر روی یک قطعه دلخواه از طول داده شود و شرایط قضیه دیریکله روی آن را برآورده کند.

سپس این تابع را می توان در یک سری فوریه گسترش داد. برای انجام این کار، تابع باید به صورت دوره ای (با نقطه) به کل خط اعداد گسترش یابد و تابع حاصل به یک سری فوریه گسترش یابد، که فقط باید در یک قطعه در نظر گرفته شود. به دلیل خاصیت (3) توابع تناوبی، داریم

بنابراین، ضرایب فوریه برای ادامه تابع به دست آمده را می توان با فرمول ها پیدا کرد.

(25)

2. استفاده عملیسری فوریه

2.1. مسائل مربوط به بسط توابع در یک سری فوریه و حل آنها

در سری فوریه مثلثاتی، باید تابعی را که ادامه متناوب تابعی است که روی یک قطعه داده شده است، بسط دهیم. برای این کار، استفاده از الگوریتمی برای بسط یک تابع تناوبی در سری فوریه ضروری است.

الگوریتم بسط تابع تناوبی در سری فوریه:

1) یک نمودار از یک تابع معین و ادامه دوره ای آن بسازید.

2) دوره تابع داده شده را تنظیم کنید.

3) تابع زوج، فرد یا را تعیین کنید نمای کلی;

4) امکان سنجی شرایط قضیه دیریکله را بررسی کنید.

5) یک رکورد رسمی از سری فوریه تولید شده توسط این تابع ایجاد کنید.

6) ضرایب فوریه را محاسبه کنید.

7) سری فوریه را برای تابع داده شده با استفاده از ضرایب سری فوریه بنویسید (مورد 4).

مثال 1 تابع را در یک سری فوریه در بازه گسترش دهید.

تصمیم:

1) بیایید یک نمودار از یک تابع داده شده و ادامه دوره ای آن بسازیم.

2) دوره گسترش تابع.

3) تابع فرد است.

4) تابع پیوسته و یکنواخت است، یعنی. تابع شرایط دیریکله را برآورده می کند.

5) ضرایب سری فوریه را محاسبه کنید.

6) سری فوریه را با جایگزینی ضرایب فوریه در فرمول می نویسیم

پاسخ:

مثال 2 ما یک تابع را با یک دوره دلخواه در یک سری فوریه گسترش می دهیم.

راه حل: تابع بر روی نیم بازه تعریف می شود (-3; 3). دوره بسط تابع، نیم دوره. اجازه دهید تابع را به یک سری فوریه بسط دهیم.

در مبدأ، تابع ناپیوسته است، بنابراین هر ضریب فوریه به عنوان مجموع دو انتگرال نشان داده می شود.

سری فوریه را با جایگزین کردن ضرایب پیدا شده سری فوریه در فرمول می نویسیم.

مثال 3 گسترش تابعدر بیندر یک سری فوریه در کسینوس. مجموع سریال را ترسیم کنید.

راه حل: تابع روی بازه را به صورت زوج ادامه می دهیم، یعنی یک تابع زوج جدید می سازیم که منطبق بر تابع روی قطعه باشد. ضرایب سری فوریه تابع را بیابید و سری فوریه را یادداشت کنید. مجموع سری فوریه برای یک تابع تناوبی با نقطه است. در تمام نقاط تداوم با عملکرد روشن منطبق خواهد شد.

سری فوریه مثلثاتی برای تابع شبیه خواهد بود

ضرایب سری فوریه را بیابید

بنابراین، هنگامی که ضرایب یافت می شوند، می توان سری فوریه را نوشت

بیایید مجموع سریال را ترسیم کنیم

مثال 4 با توجه به یک تابع تعریف شده در بخش. دریابید که آیا تابع را می توان به یک سری فوریه گسترش داد یا خیر. بسط تابع را در یک سری فوریه بنویسید.

تصمیم:

1) نمودار تابع را بر روی رسم کنید.

2) تابع پیوسته و یکنواخت است، یعنی طبق قضیه دیریکله به یک سری فوریه مثلثاتی منبسط می شود.

3) ضرایب فوریه را با استفاده از فرمول (1.19) محاسبه کنید.

4) سری فوریه را با استفاده از ضرایب پیدا شده بنویسید.

2.2. نمونه هایی از کاربرد سری فوریه در زمینه های مختلف فعالیت انسانی

ریاضیات یکی از علومی است که دارد کاربرد گستردهدر تمرین هر فرآیند تولید و فناوری مبتنی بر قوانین ریاضی است. کاربرد ابزارهای مختلفدستگاه ریاضی به شما امکان می دهد دستگاه ها و واحدهای خودکاری که قادر به انجام عملیات هستند طراحی کنید. محاسبات پیچیدهو محاسبات در طراحی ساختمان ها، سازه ها.

سری فوریه توسط ریاضیدانان در هندسه برایحل مسائل در هندسه کروی؛ در مترفیزیک ریاضی درحل مشکلات نوسانات کوچک محیط الاستیک. اما علاوه بر ریاضیات، سری های فوریه کاربرد خود را در سایر حوزه های علوم نیز یافته اند.

هر روز مردم استفاده می کنند دستگاه های مختلف. و اغلب این دستگاه ها به درستی کار نمی کنند. به عنوان مثال، تشخیص صدا به دلیل نویز زیاد دشوار است یا تصویر فکس شده واضح نیست. فرد می تواند علت نقص را با صدا تعیین کند. رایانه همچنین می تواند آسیب وارده به دستگاه را تشخیص دهد. نویز بیش از حد را می توان با استفاده از پردازش سیگنال کامپیوتری حذف کرد. سیگنال به صورت دنباله ای از مقادیر دیجیتالی نمایش داده می شود که سپس وارد کامپیوتر می شود. پس از تکمیل محاسبات خاص، ضرایب سری فوریه را بدست آورید.

تغییر طیف سیگنال به شما امکان می دهد ضبط نویز را پاک کنید، اعوجاج سیگنال را توسط دستگاه های مختلف ضبط صدا جبران کنید، صدای سازها را تغییر دهید و توجه شنوندگان را بر روی قسمت های جداگانه متمرکز کنید.

در پردازش تصویر دیجیتال، استفاده از سری فوریه امکان ایجاد افکت‌های زیر را فراهم می‌کند: محو کردن، بهبود لبه، بازسازی تصویر، جلوه‌های هنری (نقوش برجسته)

بسط سری فوریه در معماری در مطالعه فرآیندهای نوسانی استفاده می شود. به عنوان مثال، هنگام ایجاد یک پروژه نوع متفاوتسازه ها استحکام، سختی و پایداری عناصر سازه را محاسبه می کنند.

در پزشکی برای انجام معاینه پزشکی با استفاده از کاردیوگرام، دستگاه سونوگرافی، از دستگاه ریاضی استفاده می شود که بر اساس نظریه سری فوریه است.

مشکلات محاسباتی حجمی تخمین ویژگی‌های آماری سیگنال‌ها و فیلتر نویز در طول ثبت و پردازش داده‌های پیوسته کف دریا بوجود می‌آیند. هنگام انجام اندازه گیری ها و ثبت آنها، روش های هولوگرافیک با استفاده از سری فوریه امیدوار کننده است. یعنی سری های فوریه در علمی مانند اقیانوس شناسی نیز استفاده می شود.

عناصر ریاضی تقریباً در هر مرحله در تولید یافت می شوند، بنابراین برای متخصصان مهم است که بدانند و در زمینه استفاده از ابزارهای تحلیل و محاسبات خاص به خوبی حرکت کنند..

نتیجه

موضوع کار درسی به مطالعه سری فوریه اختصاص دارد. یک تابع دلخواه را می توان به تابع های ساده تر، یعنی می توان آن را به یک سری فوریه تجزیه کرد. حجم کار دوره اجازه نمی دهد تمام جنبه های گسترش عملکرد در یک سری با جزئیات افشا شود. با این حال، از مجموعه وظایف، می توان نظریه اولیه سری فوریه را آشکار کرد.

مقاله اصطلاح مفهوم یک سری فوریه مثلثاتی را آشکار می کند. شرایط برای بسط یک تابع به یک سری فوریه تعیین می شود. بسط سری فوریه توابع زوج و فرد در نظر گرفته می شود. توابع غیر تناوبی

در فصل دوم، تنها چند نمونه از بسط توابع داده شده در فواصل مختلف به یک سری فوریه آورده شده است. زمینه های علمی که در آن از این تحول استفاده می شود، توضیح داده شده است.

همچنین شکل پیچیده ای از نمایش سری فوریه وجود دارد که نمی توان آن را در نظر گرفت، زیرا حجم کار دوره اجازه نمی دهد. فرم پیچیدهسری از نظر جبری ساده است. بنابراین، اغلب در فیزیک و محاسبات کاربردی استفاده می شود.

اهمیت موضوع کار درسی به این دلیل است که نه تنها در ریاضیات، بلکه در سایر علوم نیز به طور گسترده استفاده می شود: فیزیک، مکانیک، پزشکی، شیمی و بسیاری دیگر.

کتابشناسی - فهرست کتب

1. باری، ن.ک. سری مثلثاتی. [متن] / N.K. باری. - مسکو، 1961. - 936 s.

2. برمانت، A.F. دوره کوتاه تجزیه و تحلیل ریاضی: کتاب درسی برای دانشگاه ها[متن]/ ع.ف. برمانت، آی.جی. آرامانوویچ. - ویرایش یازدهم، Sr. - سن پترزبورگ: انتشارات "لان"، 2005. - 736 ص.

3. Bugrov, Ya. S. ریاضیات عالی: کتاب درسی برای دانشگاه ها: در 3 جلد.[متن]/ Ya. S. Bugrov, S. M. Nikolsky; اد. V. A. Sadovnichy. - ویرایش ششم، کلیشه. - م.: بوستارد، 2004. -512 ص.

4. وینوگرادوا، I. A. مسائل و تمرینات در تجزیه و تحلیل ریاضی: راهنمای دانشگاه ها، Ped. دانشگاه ها: ساعت 2[متن]/ I. A. Vinogradova، S. N. Olehnik، V.A. سادوونیچی; ویرایش V.A. سادوونیچی - چاپ سوم، کشیش. – M.: Bustard, 2001. – 712 p.

5. گوسک، ع.الف. ریاضیات عالی در 2 جلد T. 2. کتاب درسی برای دانشجویان.[متن]/ A. A. Gusak.– ویرایش پنجم – مینسک: TetraSystems، 2004.

6. دانکو، پی.ای. ریاضیات عالی در تمرین ها و تکالیف: کتاب درسی دانشگاه ها: 2 ساعت.[متن]/ پلی اتیلن. دانکو، A.G. پوپوف، تی.یا. کوژونیکوف. مسکو: ONIKS: جهان و آموزش، 2003. - 306 ص.

7. لوکین، الف. مقدمه بر پردازش دیجیتالسیگنال ها (مبانی ریاضی) [متن] / A. Lukin. - م.، 2007. - 54 ص.

8. پیسکونوف، N. S. حساب دیفرانسیل و انتگرال برای مؤسسات آموزش عالی، جلد 2: آموزشبرای دانشگاه ها[متن]/ N. S. Piskunov. - چاپ سیزدهم - م.: ناوکا، 1985. - 432 ص.

9. رودین، U. مبانی آنالیز ریاضی.[متن]/ دبلیو رودین. - چاپ دوم، پر. از انگلیسی. .- م.: میر، 1355 .- 206 ص.

10. فیختنگولتس، G. M. مبانی آنالیز ریاضی. قسمت 2.[متن]/ جی ام فیختنگولت. -ویرایش ششم، ster. - سن پترزبورگ: انتشارات "لان"، 2005. - 464 ص.

اورنبورگ، 2015

امکان تقریب سری فوریه در مورد سیگنال خطی ممکن است برای ساخت توابع در حالت ناپیوسته ضروری باشد. عناصر دوره ای. امکانات استفاده این روشبرای ساخت و تجزیه آنها با استفاده از جمع های متناهیسری فوریه در حل بسیاری از مسائل علوم مختلف مانند فیزیک، زلزله شناسی و غیره استفاده می شود. فرآیندهای جزر و مد اقیانوس، فعالیت خورشیدی از طریق گسترش فرآیندهای نوسانی در نظر گرفته می شوند، توابع توصیف شده توسط این تحولات. با توسعه فناوری رایانهسری فوریه شروع به استفاده بیشتر و بیشتر کرد کارهای چالش برانگیزو همچنین به لطف این امر امکان استفاده از این تحولات در علوم غیرمستقیم مانند پزشکی، شیمی فراهم شد. تبدیل فوریه به دو شکل واقعی و پیچیده توصیف می‌شود، توزیع دوم امکان دستیابی به موفقیت در مطالعه را فراهم کرد. فضای بیرونی. نتیجه این کار استفاده از سری فوریه در خطی سازی است عملکرد ناپیوستهو انتخاب تعداد ضرایب سری برای تحمیل دقیق تر سری بر روی تابع. علاوه بر این، هنگام استفاده از بسط در یک سری فوریه، عملکرد داده شدهناپیوسته بودن متوقف می شود و در حال حاضر به اندازه کافی کوچک است، یک تقریب خوب از تابع استفاده شده محقق می شود.

سری فوریه

تبدیل فوریه

طیف فاز

1. Alasheeva E.A., Rogova N.V. روش عددی برای حل مسئله الکترودینامیک در تقریب سیم نازک. علم و صلح. بین المللی مجله علم، شماره 8(12)، 2014. جلد 1. ولگوگراد. صص 17-19.

2. Vorobyov N.N. نظریه ردیف. اد. Nauka، ویرایش اصلی ادبیات فیزیکی و ریاضی، M.، 1979، -408 ص.

3. Kalinina V.N., Pankin V.F. آمار ریاضی - م.: دانشکده تحصیلات تکمیلی, 2001.

4. سری R. Edwards Fourier در ارائه مدرن. اد. جهان در 2 جلد. جلد 1. 1985. 362 صفحه

5. Sigorsky V.P. دستگاه ریاضی یک مهندس. اد. 2 کلیشه ای "تکنیک"، 1997. - 768 ص.

نمایش یک تابع دلخواه با یک دوره خاص به عنوان یک سری، سری فوریه نامیده می شود. بسط در یک پایه متعامد نامیده می شود این تصمیمبه طور کلی بسط توابع در سری فوریه ابزار نسبتاً قدرتمندی برای حل مسائل مختلف است. زیرا ویژگی‌های این تبدیل هنگام ادغام، تمایز، و همچنین تغییر بیان با توجه به استدلال و پیچیدگی به خوبی شناخته شده و مورد مطالعه قرار گرفته است. فردی که با آن آشنا نیست ریاضیات بالاتر، و همچنین با کارهای دانشمند فرانسوی فوریه ، به احتمال زیاد متوجه نخواهد شد که این "سریال ها" چیست و برای چه هستند. این تبدیل فوریه به بخش بسیار متراکمی از زندگی ما تبدیل شده است. این نه تنها توسط ریاضیدانان، بلکه توسط فیزیکدانان، شیمیدانان، پزشکان، ستاره شناسان، زلزله شناسان، اقیانوس شناسان و بسیاری دیگر استفاده می شود.

سری فوریه در حل بسیاری از مسائل کاربردی استفاده می شود. تبدیل فوریه را می توان با روش های تحلیلی، عددی و غیره انجام داد. فرآیندهایی مانند جزر و مد اقیانوس و امواج نورتا چرخه فعالیت خورشیدی به روش عددی بسط هر فرآیند نوسانی در یک سری فوریه اشاره دارد. با استفاده از این تکنیک های ریاضی، می توان توابع را تجزیه و تحلیل کرد، که هر فرآیند نوسانی را به عنوان یک سری اجزای سینوسی که از حداقل به حداکثر و بالعکس می روند، نشان می دهد. تبدیل فوریه تابعی است که فاز و دامنه سینوسی مربوط به یک فرکانس خاص را توصیف می کند. این تبدیل برای حل یک خیلی استفاده می شود معادلات پیچیده، که فرآیندهای دینامیکی را که تحت تأثیر حرارتی، نوری یا انرژی الکتریکی. همچنین سری های فوریه امکان جداسازی اجزای ثابت در سیگنال های نوسانی پیچیده را فراهم می کند که امکان تفسیر صحیح مشاهدات تجربی به دست آمده در پزشکی، شیمی و نجوم را فراهم می کند.

با رشد تکنولوژی، یعنی. ظهور و توسعه کامپیوتر، تبدیل فوریه را به ارمغان آورد سطح جدید. این تکنیکتقریباً در تمام زمینه های علم و فناوری جا افتاده است. یک مثال سیگنال دیجیتال صوتی و تصویری است. که به تحقق روشنی از رشد تبدیل شده است فرآیند علمیو کاربرد سری فوریه بنابراین، سری فوریه در شکل پیچیده ای امکان دستیابی به موفقیت در مطالعه فضای بیرونی را فراهم کرد. علاوه بر این، مطالعه فیزیک را تحت تأثیر قرار داد مواد نیمه هادیو پلاسما، آکوستیک مایکروویو، اقیانوس شناسی، رادار، زلزله شناسی.

در نظر بگیرید که طیف فاز یک سیگنال دوره ای از عبارت زیر تعیین می شود:

که در آن نمادها و به ترتیب قسمت های خیالی و واقعی مقدار محصور در پرانتز را نشان می دهند.

اگر در یک مقدار ثابت واقعی K ضرب شود، بسط در یک سری فوریه به شکل زیر است:

از عبارت (1) برمی‌آید که طیف فوریه فاز دارای ویژگی‌های زیر است:

1) یک تابع است، یعنی بر خلاف طیف توان، که به , وابسته نیست، هنگامی که سیگنال در امتداد محور زمان جابجا می شود، تغییر می کند.

2) به K بستگی ندارد، یعنی نسبت به تقویت یا تضعیف سیگنال ثابت است، در حالی که طیف توان تابعی از K است.

3) یعنی تابعی از n است.

توجه داشته باشید. با توجه به تفسیر هندسی استدلال فوق، می توان آن را بر حسب طیف توان و طیف فاز به صورت زیر بیان کرد:

تا جایی که

سپس از (2) و (3) نتیجه می‌شود که اگر دامنه (یا طیف توان) و طیف فاز مشخص باشد، می‌توان آن را به‌طور منحصربه‌فرد بازیابی کرد.

یک مثال را در نظر بگیرید. به ما یک تابع داده می شود در بین

نمای کلی سری فوریه:

ارزش های ما را جایگزین کنید و دریافت کنید:

ارزش های خود را جایگزین کنید و بدست آورید.

کارکرد. این تحول از اهمیت زیادی برخوردار است، زیرا می توان از آن برای حل بسیاری از مشکلات عملی استفاده کرد. سری فوریه نه تنها توسط ریاضیدانان، بلکه توسط متخصصان علوم دیگر نیز استفاده می شود.

این فرآیند زمانی اتفاق می افتد که فرد صدایی را می شنود. گوش انسان به گونه ای طراحی شده است که می تواند نوسانات سینوسی فردی را در فشار هوا با فرکانس های مختلف احساس کند، که به نوبه خود به فرد اجازه می دهد گفتار را تشخیص دهد و به موسیقی گوش دهد.

گوش انسان صدا را به عنوان یک کل درک نمی کند، بلکه از طریق اجزای سری فوریه آن را درک می کند. سیم های یک آلات موسیقی صداهایی تولید می کنند که ارتعاشات سینوسی با فرکانس های مختلف هستند. واقعیت تجزیه نور به سری فوریه توسط یک رنگین کمان نشان داده می شود. بینایی انسان نور را از طریق برخی از اجزای آن در فرکانس های مختلف نوسانات الکترومغناطیسی درک می کند.

کشف این تبدیل متعلق به ژان باپتیست ژوزف فوریه، ریاضیدان فرانسوی است. به افتخار کسی که بعداً در نزدیکی فوریه نامگذاری شد. در ابتدا، دانشمند کاربرد روش خود را در مطالعه و توضیح مکانیسم های هدایت گرما یافت. فرض بر این بود که توزیع نامنظم اولیه گرما را می توان به شکل ساده ترین سینوسی ها نشان داد. برای هر یک از آنها حداقل، حداکثر و فاز دما تعیین خواهد شد. تابعی که پیک های بالایی و پایینی منحنی را توصیف می کند، فاز هر هارمونیک تبدیل فوریه بیان توزیع دما نامیده می شود. نویسنده تبدیل روشی را برای بسط یک تابع پیچیده به عنوان مجموع توابع تناوبی کسینوس، سینوس پیشنهاد کرد.

هدف از کار درسی مطالعه سری فوریه و ارتباط کاربرد عملی این تبدیل است.

برای دستیابی به این هدف، وظایف زیر تدوین شد:

1) مفهوم سری فوریه مثلثاتی را ارائه دهید.

2) تعیین شرایط برای بسط یک تابع به یک سری فوریه.

3) بسط سری فوریه توابع زوج و فرد را در نظر بگیرید.

4) بسط یک تابع غیر تناوبی را در یک سری فوریه در نظر بگیرید.

5) کاربرد عملی سری فوریه را آشکار کنید.

موضوع مطالعه: بسط توابع در یک سری فوریه.

موضوع مطالعه: سری فوریه.

روش تحقیق: تحلیل، سنتز، مقایسه، روش بدیهی.

1.5. سری فوریه برای توابع زوج و فرد

انتگرال متقارن را در نظر بگیرید

که در آن پیوسته یا تکه ای پیوسته روشن است. در انتگرال اول تغییر ایجاد می کنیم. ما معتقدیم. سپس

بنابراین، اگر یک تابع زوج باشد، پس (یعنی نمودار یک تابع زوج متقارن با محور و

اگر یک تابع فرد است، پس (یعنی نمودار یک تابع فرد نسبت به مبدا متقارن است) و

به دو ویژگی زیر توابع زوج و فرد توجه کنید:

1) حاصل ضرب یک تابع زوج با یک فرد، یک تابع فرد است.

2) حاصل ضرب دو تابع زوج (فرد) یک تابع زوج است.

بنابراین، سری فوریه مثلثاتی روی پاره، شکل خواهد داشت

برای عملکرد یکنواخت:

(16)

برای یک تابع فرد:

تعریف. رتبه ها
بخشی از سری کامل فوریه هستند و ناقص نامیده می شوندسری فوریه مثلثاتی