حل بزرگترین و کوچکترین بخش را بررسی کنید. بزرگترین و کوچکترین مقدار تابع. وظیفه B15 (2014)

بیایید ببینیم چگونه یک تابع را با استفاده از نمودار کاوش کنیم. به نظر می رسد که با نگاه کردن به نمودار، می توانید همه چیزهایی را که به ما علاقه مند است، پیدا کنید، یعنی:

• محدوده عملکرد
• محدوده عملکرد
• تابع صفر
• دوره های افزایش و کاهش
• نقاط بالا و پایین
• بزرگترین و کوچکترین مقدار تابع در بازه.

بیایید اصطلاحات را روشن کنیم:

اوکیسامختصات افقی نقطه است.
ترتیب دهید- مختصات عمودی
اوکیسا- محور افقی که اغلب محور نامیده می شود.
محور Y - محور عمودی, یا محور .

بحث و جدلیک متغیر مستقل است که مقادیر تابع به آن بستگی دارد. اغلب نشان داده شده است.
به عبارت دیگر، ما خودمان انتخاب می کنیم، در فرمول تابع جایگزین می کنیم و می گیریم.

دامنهتوابع - مجموعه ای از آن (و فقط آن) مقادیر آرگومان که تابع برای آن وجود دارد.
نشان داده شده است: یا .

در شکل ما دامنه تابع یک قطعه است. روی این قطعه است که نمودار تابع رسم می شود. فقط اینجا عملکرد داده شدهوجود داشته باشد.

محدوده عملکردمجموعه مقادیری است که متغیر می گیرد. در شکل ما، این یک بخش است - از کمترین تا بالاترین مقدار.

تابع صفرها- نقاطی که مقدار تابع برابر با صفر است، یعنی . در شکل ما اینها نکات و .

مقادیر تابع مثبت هستندجایی که . در شکل ما، این فواصل و .
مقادیر تابع منفی استجایی که . ما این بازه (یا بازه) را از تا داریم.

مهمترین مفاهیم - توابع افزایش و کاهشدر برخی از مجموعه ها به عنوان یک مجموعه، می توانید یک قطعه، یک بازه، یک اتحادیه از بازه ها، یا کل خط اعداد را بگیرید.

عملکرد افزایش

به عبارت دیگر، هر چه بیشتر، بیشتر باشد، یعنی نمودار به سمت راست و بالا می رود.

عملکرد در حال کاهشدر مجموعه اگر برای هر و متعلق به مجموعه نابرابری دلالت بر نابرابری دارد.

برای یک تابع کاهشی، مقدار بزرگتر با مقدار کوچکتر مطابقت دارد. نمودار به سمت راست و پایین می رود.

در شکل ما، تابع در بازه افزایش می یابد و در بازه ها کاهش می یابد.

بیایید تعریف کنیم که چیست حداکثر و حداقل امتیاز تابع.

حداکثر امتیاز- این یک نقطه داخلی از دامنه تعریف است، به طوری که مقدار تابع در آن بیشتر از همه نقاط به اندازه کافی نزدیک به آن است.
به عبارت دیگر، حداکثر نقطه چنین نقطه ای است، مقدار تابعی که در آن بیشترنسبت به همسایگان این یک "تپه" محلی در نمودار است.

در شکل ما - حداکثر امتیاز.

نقطه پایین- یک نقطه داخلی از دامنه تعریف، به طوری که مقدار تابع در آن کمتر از همه نقاط به اندازه کافی نزدیک به آن باشد.
یعنی حداقل نقطه به گونه ای است که مقدار تابع در آن کمتر از تابع های همسایه باشد. در نمودار، این یک "سوراخ" محلی است.

در شکل ما - حداقل امتیاز.

نقطه مرز است. این یک نقطه داخلی حوزه تعریف نیست و بنابراین با تعریف یک نقطه حداکثر مطابقت ندارد. از این گذشته ، او هیچ همسایه ای در سمت چپ ندارد. به همین ترتیب، هیچ نقطه حداقلی در نمودار ما وجود ندارد.

حداکثر و حداقل امتیاز در مجموع نامیده می شوند نقاط انتهایی تابع. در مورد ما، این است و.

اما اگر لازم باشد مثلاً پیدا کنید، حداقل عملکردروی برش؟ AT این موردپاسخ: . زیرا حداقل عملکردمقدار آن در حداقل نقطه است.

به طور مشابه، حداکثر تابع ما است. به آن نقطه رسیده است.

می توانیم بگوییم که منتهی الیه تابع برابر و است.

گاهی اوقات در وظایف باید پیدا کنید بزرگترین و کوچکترین مقادیر تابعدر یک بخش داده شده آنها لزوماً با افراط منطبق نیستند.

در مورد ما کوچکترین مقدار تابعبر روی بازه برابر و منطبق بر حداقل تابع است. اما بزرگترین مقدار آن در این بخش برابر است با . در انتهای سمت چپ بخش به آن رسیده است.

در هر صورت، بزرگترین و کوچکترین مقادیر یک تابع پیوسته در یک بخش یا در نقاط منتهی یا در انتهای قطعه به دست می آید.

ریزه و زیبا کار سادهاز دسته آنهایی که به عنوان راه نجات برای یک دانش آموز شناور عمل می کنند. در طبیعت، قلمرو خواب آلود اواسط ژوئیه، پس وقت آن است که با یک لپ تاپ در ساحل آرام بگیرید. اوایل صبح، یک پرتو خورشیدی از نظریه شروع به پخش کرد تا به زودی روی تمرین متمرکز شود، که با وجود سبکی اعلام شده، حاوی قطعات شیشه ای در شن است. در این راستا، توصیه می کنم وجداناً چند نمونه از این صفحه را در نظر بگیرید. برای حل تکالیف عملی باید بتوانید مشتقات را پیدا کنیدو مطالب مقاله را درک کنید فواصل یکنواختی و افراطی یک تابع.

ابتدا به طور خلاصه در مورد موضوع اصلی. در یک درس در مورد تداوم عملکردمن تعریف تداوم در یک نقطه و تداوم در یک فاصله را ارائه کردم. رفتار مثالی یک تابع در یک قطعه به روشی مشابه فرموله می شود. یک تابع در یک قطعه پیوسته است اگر:

1) در بازه پیوسته است.
2) پیوسته در یک نقطه سمت راستو در نقطه ترک کرد.

پاراگراف دوم به اصطلاح می پردازد تداوم یک طرفهدر یک نقطه عمل می کند. چندین رویکرد برای تعریف آن وجود دارد، اما من به خطی که قبلاً شروع شده است پایبند می‌مانم:

تابع در یک نقطه پیوسته است سمت راست، اگر در یک نقطه معین تعریف شده باشد و حد سمت راست آن با مقدار تابع در یک نقطه معین منطبق باشد: . در نقطه پیوسته است ترک کرد، اگر در یک نقطه معین تعریف شده باشد و حد سمت چپ آن برابر با مقدار آن نقطه باشد:

تصور کنید که نقاط سبز میخ هایی هستند که نوار لاستیکی جادویی روی آن ها وصل شده است:

خط قرمز را ذهنی در دستان خود بگیرید. بدیهی است، مهم نیست که چقدر نمودار را به سمت بالا و پایین بکشیم (در امتداد محور)، تابع همچنان باقی خواهد ماند. محدود- یک پرچین در بالا، یک پرچین در پایین، و محصول ما در یک پادوک چرا می کند. بدین ترتیب، یک تابع پیوسته روی یک قطعه روی آن محدود شده است. در جریان تجزیه و تحلیل ریاضی، این واقعیت به ظاهر ساده بیان شده و به طور دقیق ثابت می شود قضیه اول وایرشتراس... بسیاری از اینکه گزاره های ابتدایی به طور خسته کننده ای در ریاضیات اثبات می شوند، آزرده می شوند، اما این معنای مهمی دارد. فرض کنید یک ساکن خاص در قرون وسطی ترسناک نمودار را فراتر از محدوده دید به آسمان کشید و این درج شد. قبل از اختراع تلسکوپ، عملکرد محدود در فضا اصلاً مشخص نبود! به راستی، از کجا می دانی چه چیزی فراتر از افق در انتظار ماست؟ از این گذشته ، زمانی زمین مسطح در نظر گرفته می شد ، بنابراین امروزه حتی حمل و نقل از راه دور معمولی نیاز به اثبات دارد =)

مطابق با قضیه دوم وایرشتراس, پیوسته در بخشتابع به آن می رسد لبه بالایی دقیقو او لبه پایینی دقیق .

شماره نیز نامیده می شود حداکثر مقدار تابع در بخشو نشان داده شده با، و عدد - حداقل مقدار تابع در بخشمشخص شده .

در مورد ما:

توجه داشته باشید : در تئوری، رکوردها رایج هستند .

به طور کلی، بالاترین ارزشجایی است که بالاترین نقطه نمودار، و کوچکترین - جایی که پایین ترین نقطه قرار دارد.

مهم!همانطور که قبلاً در مقاله در مورد اشاره شد حداکثر عملکرد, بزرگترین مقدار تابعو کوچکترین مقدار تابع – یکسان نیست، چی حداکثر عملکردو حداقل عملکرد. بنابراین، در این مثال، عدد حداقل تابع است، اما مقدار حداقل نیست.

به هر حال، در خارج از بخش چه اتفاقی می افتد؟ بله، حتی سیل، در چارچوب مشکل مورد بررسی، این اصلاً برای ما جالب نیست. این کار فقط شامل یافتن دو عدد است و بس!

علاوه بر این، راه حل صرفاً تحلیلی است، بنابراین، نیازی به کشیدن نیست!

الگوریتم روی سطح قرار دارد و خود را از شکل بالا نشان می دهد:

1) مقادیر تابع را در آن بیابید نقاط بحرانی, که متعلق به این بخش هستند.

یک چیز دیگر را بگیرید: نیازی به بررسی شرایط کافی برای اکستریم نیست، زیرا، همانطور که نشان داده شد، وجود حداقل یا حداکثر وجود دارد. هنوز تضمین نشده استحداقل یا حداکثر مقدار چقدر است. تابع نمایش به حداکثر خود می رسد و به خواست سرنوشت، همان عدد بزرگترین مقدار تابع در بازه است. اما، البته، چنین تصادفی همیشه اتفاق نمی افتد.

بنابراین، در مرحله اول، محاسبه مقادیر تابع در نقاط بحرانی متعلق به بخش، سریعتر و آسانتر است، بدون اینکه مزاحمتی برای داشتن یا نبودن آنها ایجاد شود.

2) مقادیر تابع را در انتهای بخش محاسبه می کنیم.

3) از بین مقادیر تابع موجود در پاراگراف 1 و 2، کوچکترین و بیشترین را انتخاب می کنیم. عدد بزرگ، پاسخ را یادداشت کنید.

در ساحل دریای آبی می نشینیم و پاشنه پاها را در آب کم عمق می زنیم:

مثال 1

بزرگترین و کوچکترین مقادیر یک تابع را در یک بخش پیدا کنید

تصمیم گیری:
1) مقادیر تابع را در نقاط بحرانی متعلق به این بخش محاسبه کنید:

اجازه دهید مقدار تابع را در نقطه بحرانی دوم محاسبه کنیم:

2) مقادیر تابع را در انتهای بخش محاسبه کنید:

3) نتایج "پررنگ" با نمایی و لگاریتم به دست آمد که به طور قابل توجهی مقایسه آنها را پیچیده می کند. به همین دلیل، ما خود را با یک ماشین حساب یا اکسل مسلح می کنیم و مقادیر تقریبی را محاسبه می کنیم، فراموش نکنیم که:

حالا همه چیز مشخص است.

پاسخ:

مثال کسری-عقلانی برای راه حل مستقل:

مثال 6

حداکثر و حداقل مقدارتوابع در بازه

فرآیند یافتن کوچکترین و بزرگترین مقادیر یک تابع در یک بخش، یادآور یک پرواز جذاب حول یک جسم (نمودار یک تابع) در هلیکوپتر با شلیک از یک توپ دوربرد در نقاط خاص و انتخاب از بین است. این نقاط نقاط بسیار ویژه ای برای ضربات کنترلی هستند. امتیازها به روشی خاص و طبق قوانین خاصی انتخاب می شوند. با چه قوانینی؟ در ادامه در این مورد صحبت خواهیم کرد.

اگر تابع y = f(ایکس) پیوسته در بخش [ آ, ب]، سپس به این بخش می رسد کمترین و بالاترین ارزش ها . این می تواند در هر دو اتفاق بیفتد نقاط افراطییا در انتهای بخش بنابراین، برای پیدا کردن کمترین و بزرگترین مقادیر تابع ، پیوسته در بازه [ آ, ب]، باید مقادیر آن را در کل محاسبه کنید نقاط بحرانیو در انتهای بخش، و سپس کوچکترین و بزرگترین آنها را انتخاب کنید.

اجازه دهید، برای مثال، برای تعیین حداکثر مقدار تابع مورد نیاز است f(ایکس) در بخش [ آ, ب] . برای انجام این کار، تمام نقاط مهم آن را در [ آ, ب] .

نقطه بحرانی نقطه ای نامیده می شود که در آن تابع تعریف شده است، و او مشتقیا صفر است یا وجود ندارد. سپس باید مقادیر تابع را در نقاط بحرانی محاسبه کنید. و در نهایت، باید مقادیر تابع را در نقاط بحرانی و در انتهای بخش مقایسه کرد ( f(آ) و f(ب) ). بزرگترین این اعداد خواهد بود بزرگترین مقدار تابع در بازه [آ, ب] .

مشکل پیدا کردن کوچکترین مقادیر تابع .

ما با هم به دنبال کوچکترین و بزرگترین مقادیر تابع هستیم

مثال 1. کوچکترین و بزرگترین مقادیر یک تابع را بیابید در بخش [-1, 2] .

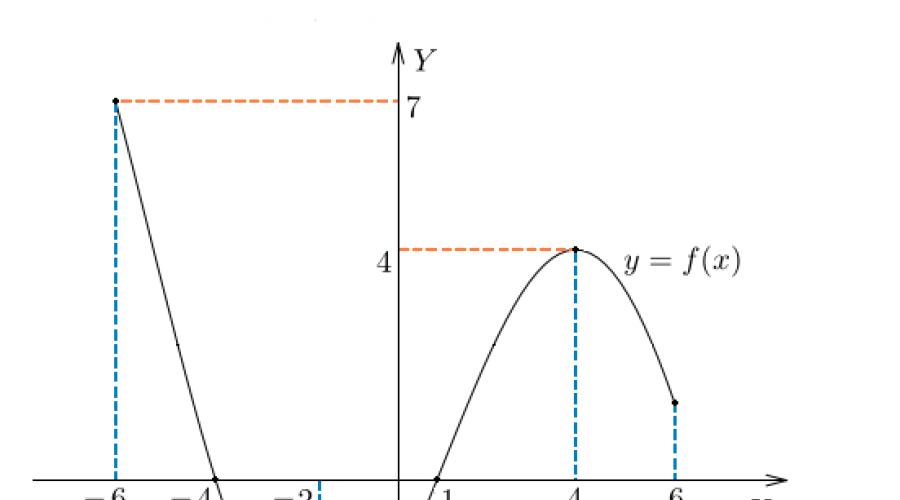
تصمیم گیری مشتق این تابع را پیدا می کنیم. مشتق را با صفر () برابر کنید و دو نقطه بحرانی بدست آورید: و. برای یافتن کوچکترین و بزرگترین مقادیر یک تابع در یک بخش داده شده، کافی است مقادیر آن را در انتهای بخش و در نقطه محاسبه کنید، زیرا نقطه به بخش تعلق ندارد [-1، 2]. این مقادیر تابع به شرح زیر است: , , . نتیجه می شود که کوچکترین مقدار تابع(در نمودار زیر با رنگ قرمز مشخص شده است)، برابر با 7-، در انتهای سمت راست بخش - در نقطه، و بزرگترین(همچنین روی نمودار قرمز است)، برابر با 9 است - در نقطه بحرانی.

اگر تابع در یک بازه معین پیوسته باشد و این بازه یک قطعه نباشد (اما مثلاً یک بازه باشد؛ تفاوت بین بازه و پاره: نقاط مرزی بازه در بازه گنجانده نشده است، اما نقاط مرزی بخش در بخش گنجانده شده است)، سپس در بین مقادیر تابع ممکن است کوچکترین و بزرگترین وجود نداشته باشد. بنابراین، برای مثال، تابع نشان داده شده در شکل زیر در ]-∞، +∞[ پیوسته است و بزرگترین مقدار را ندارد.

با این حال، برای هر بازه ای (بسته، باز یا بی نهایت)، ویژگی زیر از توابع پیوسته برقرار است.

مثال 4. کوچکترین و بزرگترین مقادیر یک تابع را بیابید در بخش [-1, 3] .

تصمیم گیری مشتق این تابع را به عنوان مشتق ضریب می یابیم:

.

مشتق را با صفر برابر می کنیم که یک نقطه بحرانی به ما می دهد: . به بازه [-1، 3] تعلق دارد. برای یافتن کوچکترین و بزرگترین مقادیر یک تابع در یک بخش داده شده، مقادیر آن را در انتهای بخش و در نقطه بحرانی پیدا می کنیم:

بیایید این مقادیر را با هم مقایسه کنیم. نتیجه گیری: برابر با -5/13، در نقطه و بزرگترین ارزشبرابر 1 در نقطه .

ما به جستجوی کوچکترین و بزرگترین مقادیر تابع با هم ادامه می دهیم

معلمانی هستند که در مبحث یافتن کوچکترین و بزرگ ترین مقادیر یک تابع، مثال هایی پیچیده تر از نمونه هایی که اکنون در نظر گرفته شده است، به دانش آموزان نمی گویند، یعنی نمونه هایی که در آنها تابع چند جمله ای یا کسری است، شمارنده. و مخرج آن چند جمله ای هستند. اما ما خود را به چنین نمونه هایی محدود نمی کنیم ، زیرا در بین معلمان دوستداران تفکر کامل دانش آموزان وجود دارد (جدول مشتقات). بنابراین از لگاریتم و تابع مثلثاتی استفاده خواهد شد.

مثال 6. کوچکترین و بزرگترین مقادیر یک تابع را بیابید در بخش .

تصمیم گیری مشتق این تابع را به صورت می یابیم مشتق محصول :

مشتق را با صفر برابر می کنیم که یک نقطه بحرانی به دست می دهد: . متعلق به بخش است. برای یافتن کوچکترین و بزرگترین مقادیر یک تابع در یک بخش داده شده، مقادیر آن را در انتهای بخش و در نقطه بحرانی پیدا می‌کنیم:

نتیجه همه اقدامات: تابع به حداقل مقدار خود می رسد، برابر 0، در یک نقطه و در یک نقطه و بزرگترین ارزشمساوی با ه²، در نقطه .

مثال 7. کوچکترین و بزرگترین مقادیر یک تابع را بیابید در بخش .

تصمیم گیری مشتق این تابع را پیدا می کنیم:

مشتق را با صفر برابر کنید:

تنها نقطه بحرانی متعلق به بخش است. برای یافتن کوچکترین و بزرگترین مقادیر یک تابع در یک بخش داده شده، مقادیر آن را در انتهای بخش و در نقطه بحرانی پیدا می‌کنیم:

نتیجه: تابع به حداقل مقدار خود می رسد، برابر با ، در نقطه و بزرگترین ارزش, برابر با , در نقطه .

در مسائل Extremal اعمال شده، یافتن کوچکترین (بزرگترین) مقادیر تابع، به عنوان یک قاعده، به یافتن حداقل (حداکثر) کاهش می یابد. اما این حداقلها یا حداکثرها نیستند که مورد توجه عملی بیشتری هستند، بلکه ارزشهای استدلالی هستند که در آنها به دست می آیند. هنگام حل مسائل کاربردی، یک مشکل اضافی ایجاد می شود - تلفیقی توابعی که پدیده یا فرآیند مورد بررسی را توصیف می کند.

مثال 8مخزن با ظرفیت 4 که به شکل موازی شکل با پایه مربع و در قسمت بالایی باز است، باید قلع بندی شود. ابعاد مخزن چقدر باید باشد تا با کمترین مواد پوشش داده شود؟

تصمیم گیری بگذار باشد ایکس- سمت پایه ساعت- ارتفاع مخزن، اس- سطح آن بدون پوشش، V- حجم آن مساحت سطح مخزن با فرمول بیان می شود. تابعی از دو متغیر است. عنوان کردن اسبه عنوان تابعی از یک متغیر، از این واقعیت استفاده می کنیم که , Wherece . جایگزینی عبارت یافت شده ساعتبه فرمول برای اس:

اجازه دهید این تابع را برای یک اکستروم بررسی کنیم. در همه جا در ]0، +∞[ و قابل تمایز است

.

مشتق را با صفر () برابر می کنیم و نقطه بحرانی را پیدا می کنیم. علاوه بر این، در، مشتق وجود ندارد، اما این مقدار در حوزه تعریف گنجانده نشده است و بنابراین نمی تواند یک نقطه افراطی باشد. بنابراین، - تنها نقطه بحرانی. بیایید آن را برای وجود یک اکستروم با استفاده از دوم بررسی کنیم علامت کافی. بیایید مشتق دوم را پیدا کنیم. وقتی مشتق دوم بزرگتر از صفر باشد (). این بدان معنی است که وقتی تابع به حداقل می رسد . چون این حداقل - تنها منتهی این تابع، کوچکترین مقدار آن است. بنابراین، ضلع پایه مخزن باید برابر با 2 متر و ارتفاع آن باشد.

مثال 9از پاراگراف آ، واقع در خط راه آهن، به نقطه با، در فاصله ای از آن ل، کالا باید حمل شود. هزینه حمل یک واحد وزن در واحد مسافت با راه آهن برابر است و از طریق بزرگراه برابر است. به چه نقطه ای مخطوط راه آهنبزرگراه باید ساخته شود تا حمل و نقل کالا از ولیکه در بابه صرفه ترین بود ABخط آهن مستقیم فرض می شود)؟

در عمل، استفاده از مشتق برای محاسبه بزرگترین و کوچکترین مقدار یک تابع کاملاً رایج است. ما این عمل را زمانی انجام می دهیم که بفهمیم چگونه هزینه ها را به حداقل برسانیم، سود را افزایش دهیم، محاسبه کنیم بار بهینهبرای تولید و غیره، یعنی در مواردی که لازم است تعیین شود مقدار بهینههر پارامتر برای حل صحیح چنین مسائلی، باید درک خوبی از بزرگترین و کوچکترین مقادیر یک تابع داشته باشید.

Yandex.RTB R-A-339285-1

معمولاً این مقادیر را در بازه ای x تعریف می کنیم که به نوبه خود می تواند با کل محدوده تابع یا بخشی از آن مطابقت داشته باشد. می تواند یک قطعه [a; b ]، و بازه باز (a ; b) , (a ; b ] , [ a ; b) , بازه بی نهایت (a ; b) , (a ; b ] , [ a ; b) یا بازه بی نهایت - ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .

در این مقاله نحوه محاسبه صریح بزرگترین و کوچکترین مقادیر را توضیح خواهیم داد. عملکرد داده شدهبا یک متغیر y=f(x) y = f (x) .

تعاریف اساسی

ما مثل همیشه با تدوین تعاریف اصلی شروع می کنیم.

تعریف 1

بزرگترین مقدار تابع y = f (x) در بازه ای x مقدار m a x y = f (x 0) x ∈ X است که برای هر مقدار x x ∈ X , x ≠ x 0، نابرابری f (x را ایجاد می کند. ) ≤ f (x 0) .

تعریف 2

کوچکترین مقدار تابع y = f (x) در یک بازه x مقدار m i n x ∈ X y = f (x 0) است که برای هر مقدار x ∈ X , x ≠ x 0، نابرابری f(X را ایجاد می کند. f (x) ≥ f(x0) .

این تعاریف نسبتاً واضح هستند. حتی ساده تر، می توانید این را بگویید: بزرگترین مقدار یک تابع، بیشترین مقدار آن است پراهمیتدر یک بازه شناخته شده در آبسیسا x 0، و کوچکترین، کوچکترین مقدار پذیرفته شده در همان بازه در x 0 است.

تعریف 3

نقاط ثابت، مقادیری از آرگومان تابع هستند که در آن مشتق آن 0 می شود.

چرا باید بدانیم نقاط ثابت چیست؟ برای پاسخ به این سوال، باید قضیه فرما را به خاطر بسپاریم. از آن نتیجه می‌شود که یک نقطه ثابت نقطه‌ای است که انتها یک تابع متمایز در آن قرار دارد (یعنی حداقل یا حداکثر محلی آن). در نتیجه، تابع کوچکترین یا بزرگترین مقدار را در یک بازه زمانی مشخص دقیقاً در یکی از نقاط ثابت خواهد گرفت.

تابع دیگری می تواند بزرگترین یا کوچکترین مقدار را در نقاطی که خود تابع معین است و اولین مشتق آن وجود ندارد به خود بگیرد.

اولین سوالی که هنگام مطالعه این مبحث مطرح می شود این است: آیا در همه موارد، آیا می توانیم حداکثر یا حداقل مقدار یک تابع را در یک بازه معین تعیین کنیم؟ خیر، زمانی که مرزهای بازه داده شده با مرزهای حوزه تعریف منطبق باشد، یا اگر با یک بازه نامتناهی سروکار داشته باشیم، نمی توانیم این کار را انجام دهیم. همچنین اتفاق می افتد که یک تابع در یک بازه معین یا در بینهایت بی نهایت کوچک یا بی نهایت می شود. ارزش های بزرگ. در این موارد، تعیین بزرگترین و/یا کوچکترین مقدار ممکن نیست.

این لحظات بعد از تصویر روی نمودارها واضح تر می شوند:

شکل اول تابعی را به ما نشان می دهد که بزرگترین و کوچکترین مقادیر (m a x y و m i n y) را در نقاط ثابت واقع در قطعه [-6; 6].

اجازه دهید به طور مفصل مورد نشان داده شده در نمودار دوم را بررسی کنیم. بیایید مقدار بخش را به [ 1 ; 6] و دریافت می کنیم که بیشترین مقدار تابع در نقطه ای با آبسیسا در مرز سمت راست بازه و کوچکترین آن در نقطه ثابت به دست می آید.

در شکل سوم، ابسیساهای نقاط نشان دهنده نقاط مرزی قطعه هستند [-3; 2]. آنها با بزرگترین و کوچکترین مقدار تابع داده شده مطابقت دارند.

حالا بیایید به تصویر چهارم نگاه کنیم. در آن، تابع m a x y (بزرگترین مقدار) و m i n y (کوچکترین مقدار) را در نقاط ثابت در بازه باز (- 6 ; 6) می گیرد.

اگر فاصله [ 1 ; 6) ، پس می توان گفت که کوچکترین مقدار تابع روی آن در یک نقطه ثابت به دست خواهد آمد. ما حداکثر مقدار را نمی دانیم. اگر x = 6 متعلق به بازه باشد، تابع می تواند بزرگترین مقدار را در x برابر با 6 بگیرد. این مورد است که در شکل 5 نشان داده شده است.

در نمودار 6، این تابع کوچکترین مقدار را در مرز سمت راست بازه به دست می آورد (- 3 ؛ 2 ]، و ما نمی توانیم نتیجه گیری قطعی در مورد بزرگترین مقدار بگیریم.

در شکل 7 می بینیم که تابع m a x y در نقطه ثابت خواهد داشت که دارای آبسیسا برابر با 1 است. تابع در مرز بازه سمت راست به حداقل مقدار خود می رسد. در منهای بی نهایت، مقادیر تابع به طور مجانبی به y = 3 نزدیک می شود.

اگر بازه x ∈ 2 را در نظر بگیریم. + ∞، سپس خواهیم دید که تابع داده شده کوچکترین یا بزرگترین مقدار را نخواهد گرفت. اگر x به 2 متمایل شود، مقادیر تابع به منهای بی‌نهایت گرایش پیدا می‌کند، زیرا خط مستقیم x = 2 مجانبی عمودی است. اگر آبسیسا به اضافه بی نهایت تمایل داشته باشد، مقادیر تابع به طور مجانبی به y = 3 نزدیک می شود. این موردی است که در شکل 8 نشان داده شده است.

در این پاراگراف، دنباله ای از اقداماتی را ارائه می دهیم که باید انجام شوند تا بزرگترین یا کوچکترین مقدار یک تابع در یک بازه مشخص را پیدا کنیم.

1. ابتدا دامنه تابع را پیدا می کنیم. بیایید بررسی کنیم که آیا بخش مشخص شده در شرط در آن گنجانده شده است یا خیر.
2. حال بیایید نقاط موجود در این بخش را محاسبه کنیم که مشتق اول در آنها وجود ندارد. اغلب آنها را می توان در توابعی یافت که آرگومان آنها در زیر علامت ماژول یا در نوشته شده است توابع قدرت، که توان آن یک عدد گویا کسری است.
3. در مرحله بعد، متوجه می شویم که کدام نقاط ثابت در یک بخش معین قرار می گیرند. برای این کار باید مشتق تابع را محاسبه کنید، سپس آن را برابر 0 قرار دهید و معادله حاصل را حل کنید و سپس ریشه های مناسب را انتخاب کنید. اگر یک نقطه ثابت به دست نیاوردیم یا در یک بخش مشخص قرار نگرفتیم، به مرحله بعدی می رویم.
4. اجازه دهید تعیین کنیم که تابع در نقاط ثابت داده شده (در صورت وجود)، یا در آن نقاطی که اولین مشتق وجود ندارد (در صورت وجود) چه مقادیری می گیرد، یا مقادیر x = a و x را محاسبه می کنیم. = ب
5. 5. ما یک سری مقادیر تابع داریم که اکنون باید بزرگترین و کوچکترین را از بین آنها انتخاب کنیم. این بزرگترین و کوچکترین مقادیر تابعی است که باید پیدا کنیم.

بیایید ببینیم که چگونه این الگوریتم را در هنگام حل مسائل به درستی اعمال کنیم.

مثال 1

شرایط. شرط:تابع y = x 3 + 4 x 2 داده شده است. بزرگترین و کوچکترین مقدار آن را در بخش ها تعیین کنید [1; 4 ] و [ - 4 ; - یک ] .

تصمیم:

بیایید با پیدا کردن دامنه این تابع شروع کنیم. در این حالت، مجموعه تمام اعداد حقیقی به جز 0 خواهد بود. به عبارت دیگر، D (y): x ∈ (- ∞ ; 0) ∪ 0 ; +∞ . هر دو بخش مشخص شده در شرط در داخل ناحیه تعریف خواهند بود.

اکنون مشتق تابع را با توجه به قانون تمایز کسری محاسبه می کنیم:

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x 4 = x 3 - 8 x 3

ما آموختیم که مشتق تابع در تمام نقاط بخش وجود خواهد داشت [1; 4 ] و [ - 4 ; - یک ] .

حال باید نقاط ثابت تابع را مشخص کنیم. بیایید این کار را با معادله x 3 - 8 x 3 = 0 انجام دهیم. فقط یک ریشه واقعی دارد که 2 است. این یک نقطه ثابت تابع خواهد بود و در بخش اول قرار می گیرد [1; 4 ] .

اجازه دهید مقادیر تابع را در انتهای اولین بخش و در نقطه داده شده محاسبه کنیم. برای x = 1، x = 2 و x = 4:

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

ما دریافتیم که بزرگترین مقدار تابع m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 در x = 1 و کوچکترین m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 - در x = 2.

بخش دوم هیچ نقطه ثابتی را شامل نمی شود، بنابراین باید مقادیر تابع را فقط در انتهای بخش داده شده محاسبه کنیم:

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

بنابراین، m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3، m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

پاسخ:برای بخش [1; 4 ] - m a x y x ∈ [ 1 ; 4 ] = y (2) = 3، m i n y x ∈ [ 1 ; 4 ] = y (2) = 3، برای بخش [ - 4 ; - 1 ] - m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3، m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

تصویر را ببینید:

قبل از مطالعه این روش، به شما توصیه می کنیم نحوه محاسبه صحیح حد یک طرفه و حد در بی نهایت را تکرار کنید و همچنین روش های اساسی برای یافتن آنها را بیاموزید. برای یافتن بزرگترین و/یا کوچکترین مقدار یک تابع در بازه باز یا بی نهایت، مراحل زیر را به ترتیب انجام می دهیم.

1. ابتدا باید بررسی کنید که آیا بازه داده شده زیر مجموعه ای از دامنه تابع داده شده خواهد بود یا خیر.
2. اجازه دهید تمام نقاطی را که در بازه مورد نیاز وجود دارد و اولین مشتق در آنها وجود ندارد را تعیین کنیم. معمولاً آنها برای توابعی هستند که آرگومان در علامت مدول محصور شده است، و برای توابع توان با کسری شاخص منطقی. اگر این نکات از دست رفته است، می توانید به مرحله بعدی بروید.
3. حال تعیین می کنیم که کدام نقاط ثابت در یک بازه معین قرار می گیرند. ابتدا مشتق را معادل 0 می کنیم و معادله را حل می کنیم و ریشه های مناسب را پیدا می کنیم. اگر یک نقطه ثابت نداشته باشیم یا آنها در یک بازه مشخص قرار نگیرند، بلافاصله به آن می رویم اقدامات بیشتر. آنها بر اساس نوع فاصله تعیین می شوند.

• اگر بازه مانند [ a ; b) ، سپس باید مقدار تابع را در نقطه x = a و حد یک طرفه lim x → b - 0 f (x) محاسبه کنیم.
• اگر بازه دارای شکل (a ; b ] باشد، باید مقدار تابع را در نقطه x = b و حد یک طرفه lim x → a + 0 f (x) محاسبه کنیم.
• اگر بازه دارای شکل (a ; b) باشد، پس باید حدهای یک طرفه lim x → b - 0 f (x) , lim x → a + 0 f (x) را محاسبه کنیم.
• اگر بازه مانند [ a ; + ∞) ، سپس باید مقدار را در نقطه x = a و حد را به اضافه بی نهایت lim x → + ∞ f (x) محاسبه کرد.
• اگر بازه مانند (-∞ ؛ b ] باشد، مقدار را در نقطه x = b و حد را در منهای بی نهایت lim x → - ∞ f (x) محاسبه می کنیم.
• اگر - ∞ ; b ، سپس حد یک طرفه lim x → b - 0 f (x) و حد را در منهای بی نهایت lim x → - ∞ f (x) در نظر می گیریم.
• اگر - ∞ ; + ∞، سپس حدود منهای و به اضافه بی نهایت lim x → + ∞ f (x) , lim x → - ∞ f (x) را در نظر می گیریم.

1. در پایان باید بر اساس مقادیر به دست آمده از تابع و حدود نتیجه گیری کنید. در اینجا گزینه های زیادی وجود دارد. بنابراین، اگر حد یک طرفه برابر با منهای بی‌نهایت یا به اضافه بی‌نهایت باشد، بلافاصله مشخص می‌شود که در مورد کوچک‌ترین و بزرگ‌ترین مقدار تابع چیزی نمی‌توان گفت. در زیر یک مثال معمولی را در نظر خواهیم گرفت. توضیحات مفصلبه شما کمک می کند بفهمید چیست در صورت لزوم، می توانید به شکل های 4 - 8 در قسمت اول مطالب بازگردید.

شرط: تابع y = 3 e 1 x 2 + x - 6 - 4 داده می شود. بزرگترین و کوچکترین مقدار آن را در فواصل محاسبه کنید - ∞ ; - 4 , - ∞ ; - 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2 ) , 2 ; + ∞ , [ 4 ; +∞).

تصمیم گیری

اول از همه، دامنه تابع را پیدا می کنیم. مخرج کسر است مثلث مربع، که نباید به 0 تبدیل شود:

x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ؛ - 3) ∪ (- 3 ؛ 2) ∪ (2 ; + ∞)

دامنه تابع را به دست آورده ایم که تمام بازه های مشخص شده در شرط به آن تعلق دارد.

حالا بیایید تابع را متمایز کنیم و دریافت کنیم:

y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

در نتیجه، مشتقات یک تابع در کل دامنه تعریف آن وجود دارد.

بیایید به سراغ یافتن نقاط ثابت برویم. مشتق تابع در x = - 1 2 0 می شود. این یک نقطه ثابت است که در فواصل (- 3 ; 1 ] و (- 3 ; 2) است.

بیایید مقدار تابع را در x = - 4 برای بازه (- ∞ ; - 4 ] و همچنین حد در منهای بی نهایت محاسبه کنیم:

y (- 4) \u003d 3 e 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 e 1 6 - 4 ≈ - 0. 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1

از آنجایی که 3 e 1 6 - 4 > - 1 , سپس m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4 . این به ما اجازه نمی دهد که کوچکترین مقدار تابع را به طور منحصر به فرد تعیین کنیم. ما فقط می توانیم نتیجه بگیریم که یک حد زیر - 1 وجود دارد، زیرا به این مقدار است که تابع به صورت مجانبی در منهای بی نهایت نزدیک می شود.

یکی از ویژگی های بازه دوم این است که یک نقطه ثابت و یک مرز دقیق ندارد. بنابراین، ما نمی توانیم بزرگترین یا کوچکترین مقدار تابع را محاسبه کنیم. با تعریف حد در منهای بی نهایت و با تمایل آرگومان به - 3 در سمت چپ، فقط محدوده مقادیر را دریافت می کنیم:

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

این بدان معنی است که مقادیر تابع در بازه - 1 قرار خواهند گرفت. +∞

برای یافتن حداکثر مقدار تابع در بازه سوم، مقدار آن را در نقطه ثابت x = - 1 2 اگر x = 1 تعیین می کنیم. همچنین باید حد یک طرفه را برای مواردی که آرگومان تمایل به - 3 در سمت راست دارد بدانیم:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

معلوم شد که تابع بزرگترین مقدار را در یک نقطه ثابت m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4 خواهد گرفت. در مورد کوچکترین مقدار، ما نمی توانیم آن را تعیین کنیم. دانستن وجود یک حد پایین تر به 4 است.

برای بازه (- 3 ؛ 2)، بیایید نتایج محاسبه قبلی را در نظر بگیریم و یک بار دیگر محاسبه کنیم که حد یک طرفه در هنگام تمایل به 2 از سمت چپ برابر است:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

بنابراین، m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4، و کوچکترین مقدار را نمی توان تعیین کرد و مقادیر تابع از زیر با عدد - 4 محدود می شود.

بر اساس آنچه در دو محاسبات قبلی انجام دادیم، می‌توانیم ادعا کنیم که در بازه [1; 2) تابع بیشترین مقدار را در x = 1 خواهد گرفت و یافتن کوچکترین آن غیرممکن است.

در بازه (2 ; + ∞)، تابع به بزرگترین یا کوچکترین مقدار نمی رسد، یعنی. مقادیر را از بازه - 1 می گیرد. +∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

پس از محاسبه مقدار تابع در x = 4 , متوجه می شویم که m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4، و تابع داده شده به اضافه بی نهایت به طور مجانبی به خط y = - 1 نزدیک می شود.

بیایید آنچه را که در هر محاسبه به دست آوردیم با نمودار تابع داده شده مقایسه کنیم. در شکل مجانب ها با خطوط نقطه چین نشان داده شده اند.

این تمام چیزی است که می خواستیم در مورد یافتن بزرگترین و کوچکترین مقدار یک تابع صحبت کنیم. آن دسته از اقداماتی که ارائه کرده ایم به شما کمک می کند تا محاسبات لازم را با بیشترین سرعت و سادگی انجام دهید. اما به یاد داشته باشید که اغلب مفید است ابتدا دریابید که تابع در چه بازه هایی کاهش می یابد و در چه بازه هایی افزایش می یابد و پس از آن می توان نتیجه گیری های بیشتری کرد. بنابراین می توانید با دقت بیشتری بزرگترین و کوچکترین مقدار تابع را تعیین کرده و نتایج را توجیه کنید.

اگر متوجه اشتباهی در متن شدید، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید