Especifique os intervalos de aumento e diminuição da função. "funções ascendentes e decrescentes"

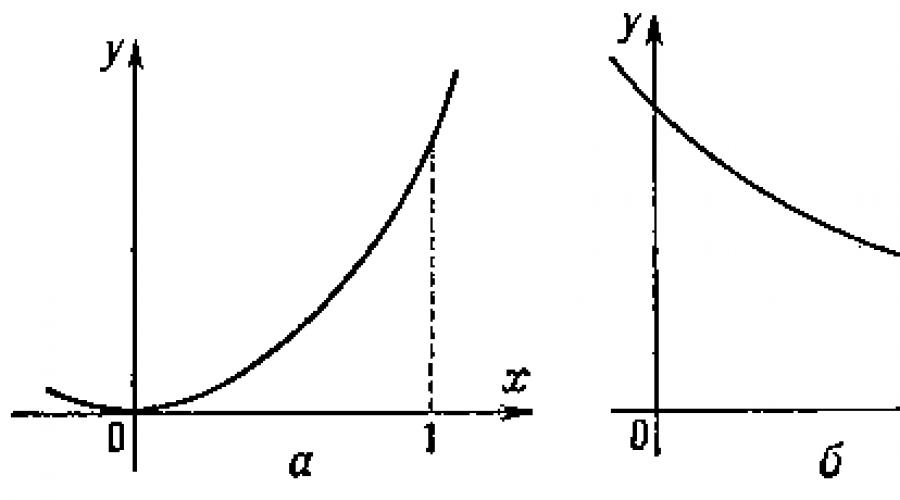
Função crescente e decrescente

função y = f(x) é chamado crescente no intervalo [ uma, b], se para qualquer par de pontos X e X", a ≤ x, a desigualdade f(x) ≤ f (x"), e estritamente crescente - se a desigualdade f (x) f(x"). A diminuição e a diminuição estrita de uma função são definidas de forma semelhante. Por exemplo, a função no = X 2 (arroz. , a) é estritamente crescente no segmento , e

(arroz. , b) diminui estritamente neste intervalo. As funções crescentes são indicadas f (x), e diminuindo f (x)↓. Para uma função diferenciável f (x) foi aumentando no segmento [ uma, b], é necessário e suficiente que sua derivada f"(x) foi não negativo em [ uma, b].

Juntamente com o aumento e a diminuição de uma função em um segmento, o aumento e a diminuição de uma função em um ponto são considerados. Função no = f (x) é chamado crescente no ponto x 0 se existe tal intervalo (α, β) contendo o ponto x 0 , que para qualquer ponto X de (α, β), x> x 0 , a desigualdade f (x 0) ≤ f (x), e para qualquer ponto X de (α, β), x 0 , a desigualdade f (x) ≤ f (x 0). O aumento estrito de uma função em um ponto é definido de forma semelhante x 0. Se um f"(x 0) > 0, então a função f(x) é estritamente crescente no ponto x 0. Se um f (x) aumenta em cada ponto do intervalo ( uma, b), então ela aumenta nesse intervalo.

S.B.Stechkin.

Grande Enciclopédia Soviética. - M.: Enciclopédia Soviética. 1969-1978 .

Veja o que é "função crescente e decrescente" em outros dicionários:

Conceitos analise matemática. A função f(x) é chamada aumentando no intervalo POPULATION AGE STRUCTURE a razão entre o número de diferentes faixas etárias população. Depende das taxas de natalidade e mortalidade, expectativa de vida das pessoas... Grande Dicionário Enciclopédico

Conceitos de análise matemática. A função f(x) é chamada crescente no intervalo se para qualquer par de pontos x1 e x2, a≤x1 ... dicionário enciclopédico

Os conceitos de matemática. análise. Função f(x) chamada. crescente no segmento [a, b], se para qualquer par de pontos x1 e x2, e<или=х1 <х<или=b, выполняется неравенство f(x1)Ciência natural. dicionário enciclopédico

Um ramo da matemática que estuda derivadas e diferenciais de funções e suas aplicações ao estudo de funções. registro de D. e. em uma disciplina matemática independente está associada aos nomes de I. Newton e G. Leibniz (a segunda metade de 17 ... Grande Enciclopédia Soviética

Um ramo da matemática em que os conceitos de derivada e diferencial são estudados e como eles são aplicados ao estudo de funções. desenvolvimento de D. e. intimamente relacionado com o desenvolvimento do cálculo integral. Inextricavelmente e seu conteúdo. Juntos, eles formam a base... Enciclopédia Matemática

Este termo tem outros significados, veja função. A solicitação "Exibir" é redirecionada aqui; veja também outros significados... Wikipedia

Aristóteles e os peripatéticos- A Questão Aristotélica Vida de Aristóteles Aristóteles nasceu em 384/383. BC e. em Estagira, na fronteira com a Macedônia. Seu pai, chamado Nicômaco, era médico a serviço do rei macedônio Amintas, pai de Filipe. Juntamente com sua família, o jovem Aristóteles ... ... A filosofia ocidental desde suas origens até os dias atuais

- (QCD), a teoria quântica de campos do forte impacto de quarks e glúons, construída à imagem do quantum. eletrodinâmica (QED) baseada na simetria de calibre de "cor". Ao contrário do QED, os férmions no QCD têm um complemento. grau de liberdade quântico. número,… … Enciclopédia Física

I Coração O coração (latim cor, grego cárdia) é um órgão fibromuscular oco que, funcionando como uma bomba, assegura o movimento do sangue no sistema circulatório. Anatomia O coração está localizado no mediastino anterior (mediastino) no pericárdio entre ... ... Enciclopédia Médica

A vida de uma planta, como a de qualquer outro organismo vivo, é um conjunto complexo de processos inter-relacionados; o mais significativo deles, como se sabe, é a troca de substâncias com o meio ambiente. O meio ambiente é a fonte de onde ... ... Enciclopédia Biológica

Definição de uma função crescente.

Função y=f(x) aumenta no intervalo X, se para qualquer e a desigualdade é satisfeita. Em outras palavras - maior valor argumento corresponde ao maior valor da função.

Definição de função decrescente.

Função y=f(x) diminui no intervalo X, se para qualquer e a desigualdade . Em outras palavras, um valor maior do argumento corresponde a um valor menor da função.

NOTA: se a função for definida e for contínua nas extremidades do intervalo de aumento ou diminuição (a; b), ou seja, quando x=a e x=b, então esses pontos são incluídos no intervalo de aumento ou diminuição. Isso não contradiz as definições de uma função crescente e decrescente no intervalo X.

Por exemplo, pelas propriedades das funções elementares básicas, sabemos que y=sinxé definido e contínuo para todos os valores reais do argumento. Portanto, a partir do aumento da função seno no intervalo, podemos afirmar o aumento no intervalo .

Pontos extremos, função extrema.

O ponto é chamado ponto máximo funções y=f(x) se para todos x de sua vizinhança, a desigualdade é verdadeira. O valor da função no ponto de máximo é chamado função máxima e denotar.

O ponto é chamado ponto mínimo funções y=f(x) se para todos x de sua vizinhança, a desigualdade é verdadeira. O valor da função no ponto mínimo é chamado função mínima e denotar.

A vizinhança de um ponto é entendida como o intervalo , onde é um número positivo suficientemente pequeno.

Os pontos mínimo e máximo são chamados pontos extremos, e os valores da função correspondentes aos pontos extremos são chamados função extrema.

Não confunda os extremos de uma função com o maior e o menor valor funções.

Na primeira foto valor mais alto funções no intervalo é atingido no ponto de máximo e é igual ao máximo da função, e na segunda figura, o valor máximo da função é atingido no ponto x=b, que não é um ponto máximo.

Condições suficientes para funções crescentes e decrescentes.

Com base em condições suficientes (sinais) para o aumento e diminuição da função, os intervalos de aumento e diminuição da função são encontrados.

Aqui estão as formulações dos sinais de funções crescentes e decrescentes no intervalo:

se a derivada da função y=f(x) positivo para qualquer x do intervalo X, então a função aumenta em X;

se a derivada da função y=f(x) negativo para qualquer x do intervalo X, então a função diminui em X.

Assim, para determinar os intervalos de aumento e diminuição de uma função, é necessário:

Considere um exemplo de encontrar os intervalos de funções crescentes e decrescentes para esclarecer o algoritmo.

Exemplo.

Encontre os intervalos de aumento e diminuição da função .

Decisão.

O primeiro passo é encontrar o escopo da definição da função. Em nosso exemplo, a expressão no denominador não deve desaparecer, portanto, .

Vamos passar para encontrar a derivada da função:

Para determinar os intervalos de aumento e diminuição de uma função por um critério suficiente, resolvemos as desigualdades e no domínio de definição. Vamos usar uma generalização do método intervalar. A única raiz real do numerador é x=2, e o denominador desaparece em x=0. Esses pontos dividem o domínio de definição em intervalos nos quais a derivada da função mantém seu sinal. Vamos marcar esses pontos na reta numérica. Por mais e menos, denotamos condicionalmente os intervalos nos quais a derivada é positiva ou negativa. As setas abaixo mostram esquematicamente o aumento ou diminuição da função no intervalo correspondente.

1. Encontre o domínio da função

2. Encontre a derivada da função

3. Iguale a derivada a zero e encontre os pontos críticos da função

4. Marcar pontos críticos no domínio de definição

5. Calcule o sinal da derivada em cada um dos intervalos obtidos

6. Descubra o comportamento da função em cada intervalo.

Exemplo: Encontre os intervalos de aumento e diminuição de uma funçãof(x) = e o número de zeros desta função no intervalo .

Decisão:

1.D( f) = R

2. f"(x) =

D( f") = D( f) = R

3. Encontre os pontos críticos da função resolvendo a equação f"(x) = 0.

x(x – 10) = 0

pontos críticos da função x= 0 e x = 10.

4. Vamos determinar o sinal da derivada.

f"(x) + – +

f(x) 0 10x

nos intervalos (-∞; 0) e (10; +∞) a derivada da função é positiva e nos pontos x= 0 e x = 10 função f(x) é contínua, portanto, esta função aumenta nos intervalos: (-∞; 0]; .

Vamos determinar o sinal dos valores da função nas extremidades do segmento.

f(0) = 3, f(0) > 0

f(10) = , f(10) < 0.

Como a função diminui no segmento e o sinal dos valores da função muda, há um zero da função neste segmento.

Resposta: a função f(x) aumenta nos intervalos: (-∞; 0]; ;

no intervalo, a função tem um zero da função.

2. Pontos extremos da função: pontos máximos e pontos mínimos. Condições necessárias e suficientes para a existência de um extremo de uma função. A regra para examinar uma função para um extremo .

Definição 1:Os pontos em que a derivada é igual a zero são chamados críticos ou estacionários.

Definição 2. Um ponto é chamado de ponto mínimo (máximo) da função se o valor da função neste ponto for menor (maior) que os valores mais próximos da função.

Note-se que o máximo e o mínimo em este caso são locais.

Na fig. 1. descreve máximos e mínimos locais.

Teorema 1.(um critério necessário para a existência de um extremo da função). Se uma função diferenciável em um ponto tem um máximo ou mínimo neste ponto, então sua derivada se anula em , .

Teorema 2. (sinal suficiente a existência de um extremo da função). Se uma função contínua tem uma derivada em todos os pontos de algum intervalo contendo um ponto crítico (com a possível exceção deste próprio ponto), e se a derivada, quando o argumento passa da esquerda para a direita através do ponto crítico, muda de sinal de mais para menos, então a função neste ponto tem um máximo, e quando o sinal muda de menos para mais, tem um mínimo.

Para determinar a natureza de uma função e falar sobre seu comportamento, é necessário encontrar intervalos de aumento e diminuição. Esse processo é chamado de exploração e plotagem de funções. O ponto extremo é usado ao encontrar os maiores e menores valores da função, pois eles aumentam ou diminuem a função a partir do intervalo.

Este artigo revela as definições, formulamos um sinal suficiente de aumento e diminuição no intervalo e a condição para a existência de um extremo. Isso se aplica à resolução de exemplos e problemas. A seção sobre derivação de funções deve ser repetida, pois ao resolvê-la será necessário usar a descoberta da derivada.

Yandex.RTB R-A-339285-1 Definição 1

A função y = f (x) aumentará no intervalo x quando para qualquer x 1 ∈ X ex 2 ∈ X , x 2 > x 1 a desigualdade f (x 2) > f (x 1) for viável. Em outras palavras, um valor maior do argumento corresponde a um valor maior da função.

Definição 2

A função y = f (x) é considerada decrescente no intervalo x quando para qualquer x 1 ∈ X , x 2 ∈ X , x 2 > x 1 a igualdade f (x 2) > f (x 1) é considerada factível. Em outras palavras, um valor de função maior corresponde a um valor de argumento menor. Considere a figura abaixo.

Comente: Quando a função é definida e contínua nas extremidades do intervalo ascendente e descendente, ou seja, (a; b) onde x = a, x = b, os pontos são incluídos no intervalo ascendente e descendente. Isso não contradiz a definição, o que significa que ocorre no intervalo x.

Propriedades básicas funções elementares do tipo y = sin x – definitividade e continuidade para valores reais dos argumentos. Daqui temos que o aumento do seno ocorre no intervalo - π 2; π 2, então o aumento no segmento tem a forma - π 2; π 2 .

O ponto x 0 é chamado ponto máximo para uma função y = f (x) quando para todos os valores de x a desigualdade f (x 0) ≥ f (x) é verdadeira. Máximo do recursoé o valor da função no ponto, e é denotado por y m a x .

O ponto x 0 é chamado de ponto mínimo para a função y \u003d f (x) quando para todos os valores de x a desigualdade f (x 0) ≤ f (x) é verdadeira. Mínimo do recursoé o valor da função no ponto, e tem a notação da forma y m i n .

As vizinhanças do ponto x 0 são consideradas pontos extremos, e o valor da função que corresponde aos pontos extremos. Considere a figura abaixo.

Extrema da função com o maior e menor valor da função. Considere a figura abaixo.

A primeira figura diz que é necessário encontrar o maior valor da função do segmento [ a ; b] . É encontrado usando pontos máximos e é igual ao valor máximo da função, e a segunda figura é mais como encontrar um ponto máximo em x = b.

Condições suficientes para aumentar e diminuir funções

Para encontrar os máximos e mínimos de uma função, é necessário aplicar os sinais de um extremo no caso em que a função satisfaça essas condições. O primeiro recurso é o mais utilizado.

A primeira condição suficiente para um extremo

Seja dada uma função y = f (x), que é diferenciável na vizinhança ε do ponto x 0 , e tem continuidade no ponto x 0 dado. Daí obtemos que

• quando f "(x) > 0 com x ∈ (x 0 - ε; x 0) ef" (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• quando f"(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 para x ∈ (x 0 ; x 0 + ε) , então x 0 é o ponto mínimo.

Em outras palavras, obtemos suas condições de ajuste de sinal:

• quando a função é contínua no ponto x 0, então ela tem uma derivada com sinal variável, ou seja, de + para -, o que significa que o ponto é chamado de máximo;
• quando a função é contínua no ponto x 0, então ela tem uma derivada com um sinal que muda de - para +, o que significa que o ponto é chamado de mínimo.

Para determinar corretamente os pontos máximo e mínimo da função, você deve seguir o algoritmo para encontrá-los:

• encontre o domínio de definição;
• encontre a derivada da função nesta área;
• identificar zeros e pontos onde a função não existe;
• determinar o sinal da derivada em intervalos;
• selecione os pontos onde a função muda de sinal.

Considere o algoritmo no exemplo de resolver vários exemplos de encontrar os extremos da função.

Exemplo 1

Encontre pontos altos e baixos determinada função y = 2 (x + 1) 2 x - 2 .

Decisão

O domínio desta função são todos os números reais, exceto x = 2. Primeiro, encontramos a derivada da função e obtemos:

y "= 2 x + 1 2 x - 2" = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2) ) - (x + 2) 2 (x - 2) 2 = = 2 (x + 1) (x - 5) (x - 2) 2

A partir daqui, vemos que os zeros da função são x \u003d - 1, x \u003d 5, x \u003d 2, ou seja, cada colchete deve ser igualado a zero. Marque na reta numérica e obtenha:

Agora determinamos os sinais da derivada de cada intervalo. É necessário selecionar um ponto incluído no intervalo, substituí-lo na expressão. Por exemplo, pontos x = - 2, x = 0, x = 3, x = 6.

Nós entendemos isso

y "(- 2) \u003d 2 (x + 1) (x - 5) (x - 2) 2 x \u003d - 2 \u003d 2 (- 2 + 1) (- 2 - 5) (- 2 - 2 ) 2 \u003d 2 7 16 \u003d 7 8 > 0, portanto, o intervalo - ∞; - 1 tem uma derivada positiva. Da mesma forma, obtemos que

y "(0) = 2 (0 + 1) 0 - 5 0 - 2 2 = 2 - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Como o segundo intervalo acabou sendo menor que zero, isso significa que a derivada no segmento será negativa. O terceiro com menos, o quarto com mais. Para determinar a continuidade, é necessário prestar atenção ao sinal da derivada, se mudar, então este é um ponto extremo.

Obtemos que no ponto x = - 1 a função será contínua, o que significa que a derivada mudará de sinal de + para -. De acordo com o primeiro sinal, temos que x = - 1 é o ponto de máximo, o que significa que temos

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

O ponto x = 5 indica que a função é contínua e a derivada mudará de sinal de - para +. Portanto, x=-1 é o ponto mínimo, e sua descoberta tem a forma

y m in = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

Imagem gráfica

Responda: y m a x = y (- 1) = 0 , y m i n = y (5) = 24 .

Vale a pena atentar para o fato de que o uso do primeiro sinal suficiente de um extremo não exige que a função seja diferenciável do ponto x 0 , e isso simplifica o cálculo.

Exemplo 2

Encontre os pontos de máximo e mínimo da função y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 .

Decisão.

O domínio de uma função são todos os números reais. Isso pode ser escrito como um sistema de equações da forma:

1 6 x 3 - 2 x 2 - 22 3 x - 8, x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Então você precisa encontrar a derivada:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 ", x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

O ponto x = 0 não tem derivada, pois os valores dos limites laterais são diferentes. Obtemos isso:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y "x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

Segue que a função é contínua no ponto x = 0, então calculamos

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 (0 - 0) 3 - 2 (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 ( 0 + 0) 2 + 22 3 (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

É necessário realizar cálculos para encontrar o valor do argumento quando a derivada se tornar zero:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

Todos os pontos obtidos devem ser marcados na linha para determinar o sinal de cada intervalo. Portanto, é necessário calcular a derivada em pontos arbitrários para cada intervalo. Por exemplo, podemos tirar pontos com valores x = - 6 , x = - 4 , x = - 1 , x = 1 , x = 4 , x = 6 . Nós entendemos isso

y " (- 6) \u003d - 1 2 x 2 - 4 x - 22 3 x \u003d - 6 \u003d - 1 2 - 6 2 - 4 (- 6) - 22 3 \u003d - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

A imagem em linha reta tem a forma

Assim, chegamos ao ponto em que é necessário recorrer ao primeiro sinal de um extremo. Calculamos e obtemos isso

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , então daqui os pontos máximos têm os valores x = - 4 + 2 3 3 , x = 4 - 2 3 3

Vamos para o cálculo dos mínimos:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Vamos calcular o máximo da função. Nós entendemos isso

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Imagem gráfica

Responda:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 8 27 3

Se a função f "(x 0) = 0 é dada, então com seu f "" (x 0) > 0 obtemos que x 0 é o ponto mínimo se f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Exemplo 3

Encontre os máximos e mínimos da função y = 8 x x + 1 .

Decisão

Primeiro, encontramos o domínio de definição. Nós entendemos isso

D (y): x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

É necessário derivar a função, após o que obtemos

y "= 8 x x + 1" = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

Quando x = 1, a derivada torna-se igual a zero, o que significa que o ponto é um possível extremo. Para esclarecimento, é necessário encontrar a segunda derivada e calcular o valor em x \u003d 1. Nós temos:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x "(x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2" x + (x + 1) 2 x "(x + 1) 4 x == 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1)" x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 - 4 8 = - 1< 0

Assim, usando a condição 2 suficiente para o extremo, obtemos que x = 1 é o ponto de máximo. Caso contrário, a entrada é y m a x = y (1) = 8 1 1 + 1 = 4 .

Imagem gráfica

Responda: y m a x = y (1) = 4 ..

A função y = f(x) tem sua derivada até a n-ésima ordem na vizinhança ε dado ponto x 0 e a derivada até n + 1ª ordem no ponto x 0 . Então f "(x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

Segue-se que quando n é um número par, então x 0 é considerado um ponto de inflexão, quando n é um número ímpar, então x 0 é um ponto extremo, e f (n + 1) (x 0) > 0, então x 0 é um ponto mínimo, f(n+1)(x0)< 0 , тогда x 0 является точкой максимума.

Exemplo 4

Encontre os pontos de máximo e mínimo da função y y = 1 16 (x + 1) 3 (x - 3) 4 .

Decisão

A função original é uma função racional inteira, daí segue-se que o domínio de definição são todos os números reais. A função precisa ser diferenciada. Nós entendemos isso

y "= 1 16 x + 1 3" (x - 3) 4 + (x + 1) 3 x - 3 4 " == 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Esta derivada irá para zero em x 1 = - 1, x 2 = 5 7, x 3 = 3. Ou seja, os pontos podem ser pontos de um possível extremo. É necessário aplicar a terceira condição extrema suficiente. Encontrar a segunda derivada permite determinar com precisão a presença de um máximo e um mínimo de uma função. A segunda derivada é calculada nos pontos de seu possível extremo. Nós entendemos isso

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

Isso significa que x 2 \u003d 5 7 é o ponto máximo. Aplicando 3 critérios suficientes, obtemos que para n = 1 ef (n + 1) 5 7< 0 .

É necessário determinar a natureza dos pontos x 1 = - 1, x 3 = 3. Para fazer isso, você precisa encontrar a terceira derivada, calcular os valores nesses pontos. Nós entendemos isso

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " == 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Portanto, x 1 = - 1 é o ponto de inflexão da função, pois para n = 2 e f (n + 1) (- 1) ≠ 0. É necessário investigar o ponto x 3 = 3 . Para fazer isso, encontramos a 4ª derivada e realizamos cálculos neste ponto:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " == 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

Do exposto, concluímos que x 3 \u003d 3 é o ponto mínimo da função.

Imagem gráfica

Responda: x 2 \u003d 5 7 é o ponto máximo, x 3 \u003d 3 - o ponto mínimo da função fornecida.

Se você notar um erro no texto, destaque-o e pressione Ctrl+Enter

derivado. Se a derivada de uma função é positiva para qualquer ponto do intervalo, então a função é crescente; se for negativa, é decrescente.

Para encontrar os intervalos de aumento e diminuição de uma função, você precisa encontrar o domínio de sua definição, a derivada, resolver desigualdades da forma F'(x) > 0 e F'(x)

Decisão.

3. Resolva as desigualdades y' > 0 e y' 0;
(4 - x)/x³

Decisão.
1. Encontre o domínio da função. Obviamente, a expressão no denominador deve ser sempre diferente de zero. Portanto, 0 é excluído do domínio de definição: a função é definida para x ∈ (-∞; 0)∪(0; +∞).

2. Calcule a derivada da função:
y'(x) = ((3 x² + 2 x - 4)' x² – (3 x² + 2 x - 4) (x²)')/x^4 = ((6 x + 2) x² - (3 x² + 2 x - 4) 2 x) / x^4 = (6 x³ + 2 x² - 6 x³ - 4 x² + 8 x) / x^ 4 \u003d (8 x - 2 x²) / x ^ 4 \u003d 2 (4 - x) / x³.

3. Resolva as desigualdades y' > 0 e y' 0;
(4 - x)/x³

4. Lado esquerdo a desigualdade tem um real x = 4 e se transforma em x = 0. Portanto, o valor x = 4 está incluído tanto no intervalo quanto no intervalo decrescente, e o ponto 0 não está incluído.
Assim, a função requerida aumenta no intervalo x ∈ (-∞; 0) ∪ .

4. O lado esquerdo da desigualdade tem um real x = 4 e se transforma em x = 0. Portanto, o valor x = 4 está incluído no intervalo e no intervalo decrescente, e o ponto 0 não está incluído.
Assim, a função requerida aumenta no intervalo x ∈ (-∞; 0) ∪ .

Origens:

• como encontrar intervalos decrescentes em uma função

A função é uma dependência estrita de um número em outro, ou o valor da função (y) no argumento (x). Cada processo (não apenas em matemática) pode ser descrito por sua própria função, que terá características: intervalos de diminuição e aumento, pontos de mínimos e máximos, e assim por diante.

Você vai precisar

• - papel;
• - caneta.

Instrução

Exemplo 2
Encontre os intervalos de f(x)=senx +x decrescentes.
A derivada desta função será igual a: f'(x)=cosx+1.
Resolvendo a desigualdade cosx+1

intervalo monotonia Uma função pode ser chamada de intervalo em que a função só aumenta ou só diminui. Várias ações específicas ajudarão a encontrar esses intervalos para uma função, o que geralmente é necessário em problemas algébricos desse tipo.

Instrução

O primeiro passo para resolver o problema de determinar os intervalos em que a função aumenta ou diminui monotonicamente é o cálculo dessa função. Para fazer isso, descubra todos os valores dos argumentos (valores no eixo x) para os quais você pode encontrar o valor da função. Marque os pontos onde as lacunas são observadas. Encontre a derivada da função. Depois de definir uma expressão que representa uma derivada, defina-a igual a zero. Depois disso, você deve encontrar as raízes do arquivo . Não sobre a área de inadmissível.

Os pontos em que a função ou em que sua derivada é igual a zero são os limites dos intervalos monotonia. Esses intervalos, bem como os pontos que os separam, devem ser inseridos sequencialmente na tabela. Encontre o sinal da derivada da função nos intervalos resultantes. Para fazer isso, substitua qualquer argumento do intervalo na expressão correspondente à derivada. Se o resultado for positivo, a função neste intervalo aumenta, caso contrário, diminui. Os resultados são inseridos em uma tabela.

A linha que denota a derivada da função f'(x) é escrita correspondente aos valores dos argumentos: "+" - se a derivada for positiva, "-" - negativa ou "0" - igual a zero. Na próxima linha, observe a monotonicidade da própria expressão original. A seta para cima corresponde ao aumento, a seta para baixo corresponde à diminuição. Verifique as características. Estes são os pontos onde a derivada é zero. Um extremo pode ser um ponto alto ou um ponto baixo. Se a seção anterior da função estava aumentando e a atual está diminuindo, este é o ponto máximo. No caso em que a função estava diminuindo até um determinado ponto, e agora está aumentando, este é o ponto mínimo. Insira na tabela os valores da função nos pontos extremos.

Origens:

• qual é a definição de monotonicidade

O estudo do comportamento de uma função que tem uma dependência complexa do argumento é feito usando a derivada. Pela natureza da mudança na derivada, pode-se encontrar pontos críticos e áreas de crescimento ou diminuição da função.