Solução Nok 34 e 2. Como encontrar o mínimo múltiplo comum de dois números

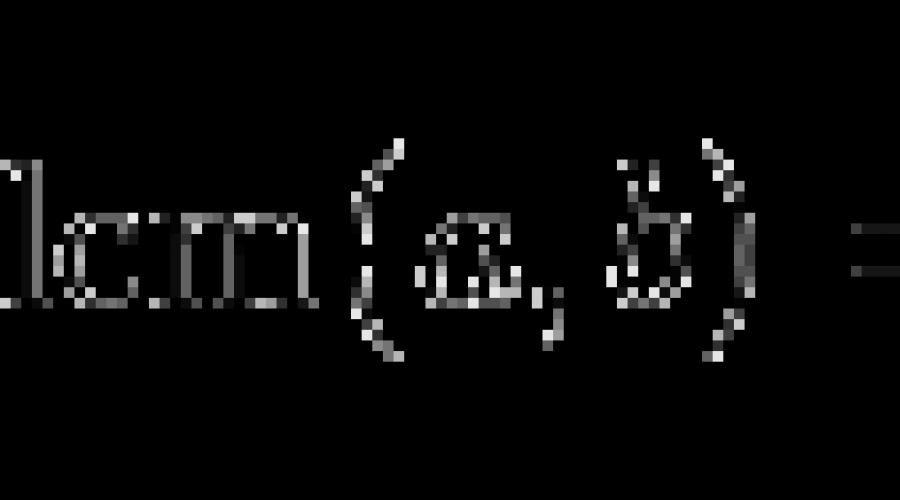
O máximo divisor comum e o mínimo múltiplo comum são conceitos aritméticos importantes que permitem operar sem esforço frações ordinárias. LCM e são mais frequentemente usados ​​para encontrar o denominador comum de várias frações.

Conceitos Básicos

O divisor de um inteiro X é outro inteiro Y pelo qual X é dividido sem deixar resto. Por exemplo, o divisor de 4 é 2 e 36 é 4, 6, 9. Um múltiplo de um inteiro X é um número Y que é divisível por X sem resto. Por exemplo, 3 é múltiplo de 15 e 6 é múltiplo de 12.

Para qualquer par de números podemos encontrar seus divisores comuns e múltiplos. Por exemplo, para 6 e 9, o múltiplo comum é 18 e o divisor comum é 3. Obviamente, os pares podem ter vários divisores e múltiplos, portanto os cálculos usam o maior divisor GCD e o menor múltiplo LCM.

O mínimo divisor não tem sentido, pois para qualquer número é sempre um. O maior múltiplo também não tem sentido, pois a sequência de múltiplos vai até o infinito.

Encontrando o MDC

Existem muitos métodos para encontrar o máximo divisor comum, sendo os mais famosos:

• busca sequencial de divisores, seleção dos comuns para um par e busca do maior deles;
• decomposição de números em fatores indivisíveis;
• Algoritmo euclidiano;
• algoritmo binário.

Hoje às instituições educacionais os mais populares são os métodos de decomposição em fatores primos e o algoritmo euclidiano. Este último, por sua vez, é utilizado na resolução de equações diofantinas: a busca pelo GCD é necessária para verificar a possibilidade de resolução da equação em números inteiros.

Encontrando o NOC

O mínimo múltiplo comum também é determinado por busca sequencial ou decomposição em fatores indivisíveis. Além disso, é fácil encontrar o MMC se o maior divisor já estiver determinado. Para os números X e Y, o MMC e o GCD estão relacionados pela seguinte relação:

LCD(X,Y) = X × Y / MDC(X,Y).

Por exemplo, se GCM(15,18) = 3, então LCM(15,18) = 15 × 18/3 = 90. O exemplo mais óbvio de uso de LCM é encontrar o denominador comum, que é o mínimo múltiplo comum de dadas frações.

Números coprimos

Se um par de números não tiver divisores comuns, esse par é chamado de coprimo. O mdc para tais pares é sempre igual a um e, com base na conexão entre divisores e múltiplos, o mdc para pares coprimos é igual ao seu produto. Por exemplo, os números 25 e 28 são relativamente primos, porque não têm divisores comuns, e MMC(25, 28) = 700, que corresponde ao seu produto. Quaisquer dois números indivisíveis serão sempre relativamente primos.

Divisor comum e calculadora múltipla

Usando nossa calculadora, você pode calcular GCD e LCM para um número arbitrário de números para escolher. As tarefas de cálculo de divisores comuns e múltiplos são encontradas na aritmética do 5º e 6º ano, mas GCD e LCM são conceitos-chave em matemática e são usados ​​​​na teoria dos números, planimetria e álgebra comunicativa.

Exemplos da vida real

Denominador comum de frações

O mínimo múltiplo comum é usado para encontrar o denominador comum de várias frações. Digamos que em um problema aritmético você precise somar 5 frações:

1/8 + 1/9 + 1/12 + 1/15 + 1/18.

Para adicionar frações, a expressão deve ser reduzida a denominador comum, o que se reduz ao problema de encontrar o MMC. Para fazer isso, selecione 5 números na calculadora e insira os valores dos denominadores nas células correspondentes. O programa irá calcular o MMC (8, 9, 12, 15, 18) = 360. Agora você precisa calcular fatores adicionais para cada fração, que são definidos como a razão entre o MMC e o denominador. Portanto, os multiplicadores adicionais seriam assim:

• 360/8 = 45
• 360/9 = 40
• 360/12 = 30
• 360/15 = 24
• 360/18 = 20.

Depois disso, multiplicamos todas as frações pelo fator adicional correspondente e obtemos:

45/360 + 40/360 + 30/360 + 24/360 + 20/360.

Podemos facilmente somar essas frações e obter o resultado de 159/360. Reduzimos a fração em 3 e vemos a resposta final - 53/120.

Resolvendo equações diofantinas lineares

As equações diofantinas lineares são expressões da forma ax + by = d. Se a razão d / mdc(a, b) for um número inteiro, então a equação pode ser resolvida em números inteiros. Vamos verificar algumas equações para ver se elas têm uma solução inteira. Primeiro, vamos verificar a equação 150x + 8y = 37. Usando uma calculadora, encontramos MDC (150,8) = 2. Divida 37/2 = 18,5. O número não é um número inteiro, portanto a equação não possui raízes inteiras.

Vamos verificar a equação 1320x + 1760y = 10120. Use uma calculadora para encontrar GCD(1320, 1760) = 440. Divida 10120/440 = 23. Como resultado, obtemos um número inteiro, portanto, a equação Diofantina pode ser resolvida em coeficientes inteiros .

Conclusão

GCD e LCM desempenham um grande papel na teoria dos números, e os próprios conceitos são amplamente utilizados na maioria Áreas diferentes matemática. Use nossa calculadora para calcular os maiores divisores e os menores múltiplos de qualquer número de números.

Mas muitos números naturais também são divisíveis por outros números naturais.

Por exemplo:

O número 12 é divisível por 1, por 2, por 3, por 4, por 6, por 12;

O número 36 é divisível por 1, por 2, por 3, por 4, por 6, por 12, por 18, por 36.

Os números pelos quais o número é divisível por um inteiro (para 12 são 1, 2, 3, 4, 6 e 12) são chamados divisores de números. Divisor de um número natural a- é um número natural que divide um determinado número a sem deixar vestígios. Um número natural que possui mais de dois divisores é chamado composto .

Observe que os números 12 e 36 têm fatores comuns. Esses números são: 1, 2, 3, 4, 6, 12. O maior divisor desses números é 12. O divisor comum desses dois números a E b- este é o número pelo qual ambos os números dados são divididos sem resto a E b.

Múltiplos comuns vários números é um número que é divisível por cada um desses números. Por exemplo, os números 9, 18 e 45 têm um múltiplo comum de 180. Mas 90 e 360 ​​também são seus múltiplos comuns. Entre todos os múltiplos comuns há sempre um menor, em nesse caso este é 90. Este número é chamado o menormúltiplo comum (CMM).

O MMC é sempre um número natural que deve ser maior que o maior dos números para os quais está definido.

Mínimo múltiplo comum (LCM). Propriedades.

Comutatividade:

Associatividade:

Em particular, se e são números primos, então:

Mínimo múltiplo comum de dois inteiros eu E né um divisor de todos os outros múltiplos comuns eu E n. Além disso, o conjunto de múltiplos comuns m, n coincide com o conjunto de múltiplos para LCM( m, n).

Os assintóticos para podem ser expressos em termos de algumas funções da teoria dos números.

Então, Função Chebyshev. E:

Isto decorre da definição e propriedades da função Landau g(n).

O que se segue da lei de distribuição dos números primos.

Encontrando o mínimo múltiplo comum (LCM).

NOC( um, b) pode ser calculado de várias maneiras:

1. Se o máximo divisor comum for conhecido, você pode usar sua conexão com o LCM:

2. Seja conhecida a decomposição canônica de ambos os números em fatores primos:

Onde p 1 ,...,p k- vários números primos, A d 1 ,...,d k E e 1 ,...,e k— inteiros não negativos (podem ser zeros se o primo correspondente não estiver na expansão).

Então NOC ( a,b) é calculado pela fórmula:

Em outras palavras, a decomposição LCM contém todos os fatores primos incluídos em pelo menos uma das decomposições de números um, b, e o maior dos dois expoentes deste multiplicador é considerado.

Exemplo:

O cálculo do mínimo múltiplo comum de vários números pode ser reduzido a vários cálculos sequenciais do MMC de dois números:

Regra. Para encontrar o MMC de uma série de números, você precisa:

- decompor números em fatores primos;

- transferir a maior expansão (o produto dos fatores do produto desejado) para os fatores do produto desejado número grande dos dados) e depois somar fatores da expansão de outros números que não aparecem no primeiro número ou aparecem nele menos vezes;

— o produto resultante de fatores primos será o MMC dos números fornecidos.

Quaisquer dois ou mais números naturais têm seu próprio NOC. Se os números não forem múltiplos entre si ou não tiverem os mesmos fatores na expansão, então seu MMC será igual ao produto desses números.

Os fatores primos do número 28 (2, 2, 7) são complementados com o fator 3 (o número 21), o produto resultante (84) será o menor número, que é divisível por 21 e 28.

Os fatores primos do maior número 30 são complementados pelo fator 5 do número 25, o produto resultante 150 é maior que o maior número 30 e é divisível por todos os números dados sem deixar resto. Este é o menor produto possível (150, 250, 300...) que é um múltiplo de todos os números dados.

Os números 2,3,11,37 são números primos, então seu MMC é igual ao produto dos números fornecidos.

Regra. Para calcular o MMC de números primos, você precisa multiplicar todos esses números.

Outra opção:

Para encontrar o mínimo múltiplo comum (MCC) de vários números, você precisa:

1) representar cada número como um produto de seus fatores primos, por exemplo:

504 = 2 2 2 3 3 7,

2) anote as potências de todos os fatores primos:

504 = 2 2 2 3 3 7 = 2 3 3 2 7 1,

3) anote todos os divisores primos (multiplicadores) de cada um desses números;

4) escolher a maior potência de cada um deles, encontrada em todas as expansões desses números;

5) multiplique esses poderes.

Exemplo. Encontre o MMC dos números: 168, 180 e 3024.

Solução. 168 = 2 2 2 3 7 = 2 3 3 1 7 1,

180 = 2 2 3 3 5 = 2 2 3 2 5 1,

3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1.

Escrevemos as maiores potências de todos os divisores primos e as multiplicamos:

NOC = 2 4 3 3 5 1 7 1 = 15120.

Um múltiplo é um número que é divisível por um determinado número sem deixar resto. O mínimo múltiplo comum (MCM) de um grupo de números é o menor número divisível por cada número do grupo sem deixar resto. Para encontrar o mínimo múltiplo comum, você precisa encontrar os fatores primos de determinados números. O MMC também pode ser calculado usando vários outros métodos que se aplicam a grupos de dois ou mais números.

Passos

Série de múltiplos

Veja esses números. O método descrito aqui é melhor usado quando são fornecidos dois números, cada um deles menor que 10. Se forem fornecidos números maiores, use um método diferente.

• Por exemplo, encontre o mínimo múltiplo comum de 5 e 8. Esses números são pequenos, então você pode usar este método.

1. Um múltiplo é um número que é divisível por um determinado número sem deixar resto. Os múltiplos podem ser encontrados na tabuada.

   • Por exemplo, os números múltiplos de 5 são: 5, 10, 15, 20, 25, 30, 35, 40.

2. Escreva uma série de números que sejam múltiplos do primeiro número. Faça isso sob múltiplos do primeiro número para comparar dois conjuntos de números.

   • Por exemplo, os números múltiplos de 8 são: 8, 16, 24, 32, 40, 48, 56 e 64.

3. Encontre o menor número presente em ambos os conjuntos de múltiplos. Você pode ter que escrever longas séries de múltiplos para encontrar número total. O menor número presente em ambos os conjuntos de múltiplos é o mínimo múltiplo comum.

   • Por exemplo, o menor número que aparece na série de múltiplos de 5 e 8 é o número 40. Portanto, 40 é o mínimo múltiplo comum de 5 e 8.

   Fatoração principal

   1. Veja esses números. O método descrito aqui é melhor usado quando são fornecidos dois números, cada um deles maior que 10. Se forem fornecidos números menores, use um método diferente.

      • Por exemplo, encontre o mínimo múltiplo comum dos números 20 e 84. Cada um dos números é maior que 10, então você pode usar este método.

   2. Fatore o primeiro número em fatores primos. Ou seja, você precisa encontrar os números primos que, quando multiplicados, resultarão em um determinado número. Depois de encontrar os fatores primos, escreva-os como igualdades.

      • Por exemplo, 2 × 10 = 20 (\ displaystyle (\ mathbf (2) )\ vezes 10=20) E 2 × 5 = 10 (\ displaystyle (\ mathbf (2) )\times (\mathbf (5) )=10). Assim, os fatores primos do número 20 são os números 2, 2 e 5. Escreva-os como uma expressão: .

   3. Fatore o segundo número em fatores primos. Faça isso da mesma forma que fatorou o primeiro número, ou seja, encontre os números primos que, quando multiplicados, resultarão no número fornecido.

      • Por exemplo, 2 × 42 = 84 (\ displaystyle (\ mathbf (2) )\ vezes 42=84), 7 × 6 = 42 (\displaystyle (\mathbf (7) )\vezes 6=42) E 3 × 2 = 6 (\ displaystyle (\ mathbf (3) )\times (\mathbf (2) )=6). Assim, os fatores primos do número 84 são os números 2, 7, 3 e 2. Escreva-os como uma expressão: .

   4. Anote os fatores comuns a ambos os números. Escreva esses fatores como uma operação de multiplicação. Ao escrever cada fator, risque-o em ambas as expressões (expressões que descrevem a fatoração de números em fatores primos).

      • Por exemplo, ambos os números têm um fator comum de 2, então escreva 2 × (\estilo de exibição 2\vezes) e risque o 2 em ambas as expressões.
      • O que ambos os números têm em comum é outro fator de 2, então escreva 2 × 2 (\estilo de exibição 2\vezes 2) e risque o segundo 2 em ambas as expressões.

   5. Adicione os fatores restantes à operação de multiplicação. São fatores que não estão riscados em ambas as expressões, ou seja, fatores que não são comuns aos dois números.

      • Por exemplo, na expressão 20 = 2 × 2 × 5 (\estilo de exibição 20=2\vezes 2\vezes 5) Ambos os dois (2) estão riscados porque são fatores comuns. O fator 5 não está riscado, então escreva a operação de multiplicação assim: 2 × 2 × 5 (\estilo de exibição 2\vezes 2\vezes 5)
      • Em expressão 84 = 2 × 7 × 3 × 2 (\displaystyle 84=2\vezes 7\vezes 3\vezes 2) ambos os dois (2) também estão riscados. Os fatores 7 e 3 não estão riscados, então escreva a operação de multiplicação assim: 2 × 2 × 5 × 7 × 3 (\displaystyle 2\vezes 2\vezes 5\vezes 7\vezes 3).

   6. Calcule o mínimo múltiplo comum. Para fazer isso, multiplique os números na operação de multiplicação escrita.

      • Por exemplo, 2 × 2 × 5 × 7 × 3 = 420 (\estilo de exibição 2\vezes 2\vezes 5\vezes 7\vezes 3=420). Portanto, o mínimo múltiplo comum de 20 e 84 é 420.

   Encontrando fatores comuns

   1. Desenhe uma grade como se fosse um jogo da velha. Tal grade consiste em duas linhas paralelas que se cruzam (em ângulos retos) com outras duas linhas paralelas. Isso lhe dará três linhas e três colunas (a grade se parece muito com o ícone #). Escreva o primeiro número na primeira linha e na segunda coluna. Escreva o segundo número na primeira linha e na terceira coluna.

      • Por exemplo, encontre o mínimo múltiplo comum dos números 18 e 30. Escreva o número 18 na primeira linha e na segunda coluna e escreva o número 30 na primeira linha e na terceira coluna.

   2. Encontre o divisor comum a ambos os números. Escreva na primeira linha e na primeira coluna. É melhor procurar fatores primos, mas isso não é obrigatório.

      • Por exemplo, 18 e 30 são números pares, então seu fator comum é 2. Portanto, escreva 2 na primeira linha e na primeira coluna.

   3. Divida cada número pelo primeiro divisor. Escreva cada quociente sob o número apropriado. Um quociente é o resultado da divisão de dois números.

      • Por exemplo, 18 ÷ 2 = 9 (\estilo de exibição 18\div 2=9), então escreva 9 menores de 18 anos.
      • 30 ÷ 2 = 15 (\estilo de exibição 30\div 2=15), então anote 15 abaixo de 30.

   4. Encontre o divisor comum a ambos os quocientes. Se não existir tal divisor, pule as próximas duas etapas. Caso contrário, escreva o divisor na segunda linha e na primeira coluna.

      • Por exemplo, 9 e 15 são divisíveis por 3, então escreva 3 na segunda linha e na primeira coluna.

   5. Divida cada quociente por seu segundo divisor. Escreva cada resultado de divisão sob o quociente correspondente.

      • Por exemplo, 9 ÷ 3 = 3 (\estilo de exibição 9\div 3=3), então escreva 3 abaixo de 9.
      • 15 ÷ 3 = 5 (\estilo de exibição 15\div 3=5), então escreva 5 com menos de 15 anos.

   6. Se necessário, adicione células adicionais à grade. Repita as etapas descritas até que os quocientes tenham um divisor comum.

   7. Circule os números na primeira coluna e na última linha da grade. Em seguida, escreva os números selecionados como uma operação de multiplicação.

      • Por exemplo, os números 2 e 3 estão na primeira coluna e os números 3 e 5 estão na última linha, então escreva a operação de multiplicação assim: 2 × 3 × 3 × 5 (\estilo de exibição 2\vezes 3\vezes 3\vezes 5).

   8. Encontre o resultado da multiplicação de números. Isso calculará o mínimo múltiplo comum de dois números fornecidos.

      • Por exemplo, 2 × 3 × 3 × 5 = 90 (\estilo de exibição 2\vezes 3\vezes 3\vezes 5=90). Portanto, o mínimo múltiplo comum de 18 e 30 é 90.

   Algoritmo de Euclides

   1. Lembre-se da terminologia associada à operação de divisão. O dividendo é o número que está sendo dividido. O divisor é o número pelo qual está sendo dividido. Um quociente é o resultado da divisão de dois números. Um resto é o número que resta quando dois números são divididos.

      • Por exemplo, na expressão 15 ÷ 6 = 2 (\estilo de exibição 15\div 6=2) ost. 3:
        15 é o dividendo
        6 é um divisor
        2 é quociente
        3 é o resto.

O material apresentado abaixo é continuação lógica teorias do artigo intitulado LCM - mínimo múltiplo comum, definição, exemplos, conexão entre LCM e GCD. Aqui falaremos sobre encontrar o mínimo múltiplo comum (LCM), E Atenção especial Vamos nos concentrar na resolução de exemplos. Primeiro, mostraremos como o MMC de dois números é calculado usando o MDC desses números. A seguir, veremos como encontrar o mínimo múltiplo comum fatorando números em fatores primos. Depois disso, vamos nos concentrar em encontrar o MMC de três e mais números, e também preste atenção ao cálculo do MMC de números negativos.

Navegação na página.

Cálculo do mínimo múltiplo comum (LCM) via GCD

Uma maneira de encontrar o mínimo múltiplo comum é baseada na relação entre LCM e GCD. A conexão existente entre LCM e GCD nos permite calcular o mínimo múltiplo comum de dois inteiros positivos através de um máximo divisor comum conhecido. A fórmula correspondente é MMC(a, b)=a b:MDC(a, b) . Vejamos exemplos de como encontrar o MMC usando a fórmula fornecida.

Exemplo.

Encontre o mínimo múltiplo comum de dois números 126 e 70.

Solução.

Neste exemplo a=126 , b=70 . Vamos usar a conexão entre LCM e GCD, expressa pela fórmula MMC(a, b)=a b:MDC(a, b). Ou seja, primeiro temos que encontrar o máximo divisor comum dos números 70 e 126, após o qual podemos calcular o MMC desses números usando a fórmula escrita.

Vamos encontrar MDC(126, 70) usando o algoritmo euclidiano: 126=70·1+56, 70=56·1+14, 56=14·4, portanto, MDC(126, 70)=14.

Agora encontramos o mínimo múltiplo comum necessário: MDC(126, 70)=126·70:MDC(126, 70)= 126·70:14=630.

Responder:

MMC(126, 70)=630 .

Exemplo.

A que LCM (68, 34) é igual?

Solução.

Porque 68 é divisível por 34, então GCD(68, 34)=34. Agora calculamos o mínimo múltiplo comum: MDC(68, 34)=68·34:MDC(68, 34)= 68·34:34=68.

Responder:

MMC(68, 34)=68 .

Observe que o exemplo anterior se ajusta à seguinte regra para encontrar o MMC para inteiros positivos a e b: se o número a é divisível por b, então o mínimo múltiplo comum desses números é a.

Encontrando o MMC fatorando números em fatores primos

Outra maneira de encontrar o mínimo múltiplo comum é fatorar números em fatores primos. Se você compor um produto de todos os fatores primos de determinados números e, em seguida, excluir deste produto todos os fatores primos comuns presentes nas decomposições dos números fornecidos, então o produto resultante será igual ao mínimo múltiplo comum dos números fornecidos .

A regra declarada para encontrar o MMC segue da igualdade MMC(a, b)=a b:MDC(a, b). Na verdade, o produto dos números aeb é igual ao produto de todos os fatores envolvidos na expansão dos números aeb. Por sua vez, MDC(a, b) é igual ao produto de todos os fatores primos presentes simultaneamente nas expansões dos números aeb (conforme descrito na seção sobre como encontrar o MDC usando a expansão de números em fatores primos).

Vamos dar um exemplo. Deixe-nos saber que 75=3·5·5 e 210=2·3·5·7. Vamos compor o produto de todos os fatores dessas expansões: 2·3·3·5·5·5·7 . Agora deste produto excluímos todos os fatores presentes tanto na expansão do número 75 quanto na expansão do número 210 (esses fatores são 3 e 5), então o produto assumirá a forma 2·3·5·5·7 . O valor deste produto é igual ao mínimo múltiplo comum de 75 e 210, ou seja, NOC(75, 210)= 2·3·5·5·7=1.050.

Exemplo.

Fatore os números 441 e 700 em fatores primos e encontre o mínimo múltiplo comum desses números.

Solução.

Vamos fatorar os números 441 e 700 em fatores primos:

Obtemos 441=3·3·7·7 e 700=2·2·5·5·7.

Agora vamos criar um produto de todos os fatores envolvidos na expansão desses números: 2·2·3·3·5·5·7·7·7. Excluamos deste produto todos os fatores que estão presentes simultaneamente em ambas as expansões (só existe um desses fatores - este é o número 7): 2·2·3·3·5·5·7·7. Por isso, MMC(441, 700)=2·2·3·3·5·5·7·7=44 100.

Responder:

NOC(441, 700)= 44 100 .

A regra para encontrar o MMC usando a fatoração de números em fatores primos pode ser formulada de maneira um pouco diferente. Se os fatores que faltam na expansão do número b forem somados aos fatores da expansão do número a, então o valor do produto resultante será igual ao mínimo múltiplo comum dos números a e b.

Por exemplo, tomemos os mesmos números 75 e 210, suas decomposições em fatores primos são as seguintes: 75=3·5·5 e 210=2·3·5·7. Aos fatores 3, 5 e 5 da expansão do número 75 somamos os fatores que faltam 2 e 7 da expansão do número 210, obtemos o produto 2·3·5·5·7, cujo valor é igual a LCM(75, 210).

Exemplo.

Encontre o mínimo múltiplo comum de 84 e 648.

Solução.

Primeiro obtemos as decomposições dos números 84 e 648 em fatores primos. Eles se parecem com 84=2·2·3·7 e 648=2·2·2·3·3·3·3. Aos fatores 2, 2, 3 e 7 da expansão do número 84 adicionamos os fatores que faltam 2, 3, 3 e 3 da expansão do número 648, obtemos o produto 2 2 2 3 3 3 3 7, que é igual a 4 536 . Assim, o mínimo múltiplo comum desejado de 84 e 648 é 4.536.

Responder:

MMC(84, 648)=4.536 .

Encontrando o MMC de três ou mais números

O mínimo múltiplo comum de três ou mais números pode ser encontrado encontrando sequencialmente o MMC de dois números. Lembremos o teorema correspondente, que fornece uma maneira de encontrar o MMC de três ou mais números.

Teorema.

Sejam dados números inteiros positivos a 1 , a 2 , …, a k, o mínimo múltiplo comum m k desses números é encontrado calculando sequencialmente m 2 = LCM(a 1 , a 2) , m 3 = LCM(m 2 , a 3) , … , m k = LCM(m k−1 , a k) .

Vamos considerar a aplicação deste teorema usando o exemplo de como encontrar o mínimo múltiplo comum de quatro números.

Exemplo.

Encontre o MMC de quatro números 140, 9, 54 e 250.

Solução.

Neste exemplo, a 1 =140, a 2 =9, a 3 =54, a 4 =250.

Primeiro encontramos m 2 = LOC(a 1, a 2) = LOC(140, 9). Para fazer isso, usando o algoritmo euclidiano, determinamos GCD(140, 9), temos 140=9·15+5, 9=5·1+4, 5=4·1+1, 4=1·4, portanto, GCD(140, 9)=1 , de onde MDC(140, 9)=140 9:MDC(140, 9)= 140·9:1=1.260. Ou seja, m 2 =1 260.

Agora encontramos m 3 = LOC (m 2 , a 3) = LOC (1 260, 54). Vamos calculá-lo através do MDC(1 260, 54), que também determinamos usando o algoritmo euclidiano: 1 260=54·23+18, 54=18·3. Então mdc(1.260, 54)=18, do qual mdc(1.260, 54)= 1.260·54:mdc(1.260, 54)= 1.260·54:18=3.780. Ou seja, m 3 =3 780.

Tudo o que resta é encontrar m 4 = LOC(m 3, a 4) = LOC(3 780, 250). Para fazer isso, encontramos o MDC(3.780, 250) usando o algoritmo euclidiano: 3.780=250·15+30, 250=30·8+10, 30=10·3. Portanto, GCM(3.780, 250)=10, de onde GCM(3.780, 250)= 3 780 250: MDC(3 780, 250)= 3.780·250:10=94.500. Ou seja, m 4 =94 500.

Portanto, o mínimo múltiplo comum dos quatro números originais é 94.500.

Responder:

MMC(140, 9, 54, 250)=94.500.

Em muitos casos, é conveniente encontrar o mínimo múltiplo comum de três ou mais números usando fatorações primárias dos números fornecidos. Neste caso, você deve seguir a seguinte regra. O mínimo múltiplo comum de vários números é igual ao produto, que é composto da seguinte forma: os fatores que faltam na expansão do segundo número são somados a todos os fatores da expansão do primeiro número, os fatores que faltam na expansão de o terceiro número é adicionado aos fatores resultantes e assim por diante.

Vejamos um exemplo de como encontrar o mínimo múltiplo comum usando a fatoração primária.

Exemplo.

Encontre o mínimo múltiplo comum dos cinco números 84, 6, 48, 7, 143.

Solução.

Primeiro, obtemos decomposições desses números em fatores primos: 84=2·2·3·7, 6=2·3, 48=2·2·2·2·3, 7 (7 é um número primo, coincide com sua decomposição em fatores primos) e 143=11·13.

Para encontrar o MMC desses números, aos fatores do primeiro número 84 (são 2, 2, 3 e 7), você precisa adicionar os fatores que faltam na expansão do segundo número 6. A decomposição do número 6 não contém fatores faltantes, pois tanto 2 quanto 3 já estão presentes na decomposição do primeiro número 84. A seguir, aos fatores 2, 2, 3 e 7 adicionamos os fatores que faltam 2 e 2 da expansão do terceiro número 48, obtemos um conjunto de fatores 2, 2, 2, 2, 3 e 7. Não haverá necessidade de adicionar multiplicadores a este conjunto na próxima etapa, pois ele já contém 7. Finalmente, aos fatores 2, 2, 2, 2, 3 e 7 adicionamos os fatores que faltam 11 e 13 da expansão do número 143. Obtemos o produto 2·2·2·2·3·7·11·13, que é igual a 48.048.

Maior divisor comum

Definição 2

Se um número natural a é divisível por um número natural $b$, então $b$ é chamado de divisor de $a$, e $a$ é chamado de múltiplo de $b$.

Sejam $a$ e $b$ números naturais. O número $c$ é chamado de divisor comum de $a$ e $b$.

O conjunto de divisores comuns dos números $a$ e $b$ é finito, pois nenhum desses divisores pode ser maior que $a$. Isso significa que entre esses divisores existe um maior, que é chamado de máximo divisor comum dos números $a$ e $b$ e é denotado pela seguinte notação:

$MDC\(a;b)\ ou \D\(a;b)$

Para encontrar o máximo divisor comum de dois números você precisa:

1. Encontre o produto dos números encontrados na etapa 2. O número resultante será o máximo divisor comum desejado.

Exemplo 1

Encontre o mdc dos números $121$ e $132.$

$242=2\cponto 11\cponto 11$

$132=2\cponto 2\cponto 3\cponto 11$

Escolha os números incluídos na expansão desses números

$242=2\cponto 11\cponto 11$

$132=2\cponto 2\cponto 3\cponto 11$

Encontre o produto dos números encontrados na etapa 2. O número resultante será o máximo divisor comum desejado.

$MDC=2\cponto 11=22$

Exemplo 2

Encontre o mdc dos monômios $63$ e $81$.

Encontraremos de acordo com o algoritmo apresentado. Por esta:

Vamos fatorar os números em fatores primos

$63=3\cponto 3\cponto 7$

$81=3\cponto 3\cponto 3\cponto 3$

Selecionamos os números que estão incluídos na expansão desses números

$63=3\cponto 3\cponto 7$

$81=3\cponto 3\cponto 3\cponto 3$

Vamos encontrar o produto dos números encontrados na etapa 2. O número resultante será o máximo divisor comum desejado.

$MDC=3\cponto 3=9$

Você pode encontrar o MDC de dois números de outra maneira, usando um conjunto de divisores de números.

Exemplo 3

Encontre o mdc dos números $48$ e $60$.

Solução:

Vamos encontrar o conjunto de divisores do número $48$: $\left\((\rm 1,2,3.4.6,8,12,16,24,48)\right\)$

Agora vamos encontrar o conjunto de divisores do número $60$:$\ \left\((\rm 1,2,3,4,5,6,10,12,15,20,30,60)\right\) $

Vamos encontrar a interseção desses conjuntos: $\left\((\rm 1,2,3,4,6,12)\right\)$ - este conjunto determinará o conjunto de divisores comuns dos números $48$ e $60 $. Maior elemento em dado conjunto o número será $ 12$. Isso significa que o máximo divisor comum dos números $48$ e $60$ é $12$.

Definição de NPL

Definição 3

Múltiplos comuns de números naturais$a$ e $b$ são números naturais múltiplos de $a$ e $b$.

Múltiplos comuns de números são números que são divisíveis pelos números originais sem resto. Por exemplo, para os números $25$ e $50$, os múltiplos comuns serão os números $50.100.150.200$, etc.

O menor múltiplo comum será chamado de mínimo múltiplo comum e será denotado LCM$(a;b)$ ou K$(a;b).$

Para encontrar o MMC de dois números, você precisa:

1. Fatore números em fatores primos
2. Anote os fatores que fazem parte do primeiro número e some a eles os fatores que fazem parte do segundo e não fazem parte do primeiro

Exemplo 4

Encontre o MMC dos números $99$ e $77$.

Encontraremos de acordo com o algoritmo apresentado. Por esta

Fatore números em fatores primos

$99=3\cponto 3\cponto 11$

Anote os fatores incluídos no primeiro

adicione a eles multiplicadores que fazem parte do segundo e não fazem parte do primeiro

Encontre o produto dos números encontrados na etapa 2. O número resultante será o mínimo múltiplo comum desejado

$NOK=3\cponto 3\cponto 11\cponto 7=693$

Compilar listas de divisores de números costuma ser uma tarefa muito trabalhosa. Existe uma maneira de encontrar o GCD chamada algoritmo euclidiano.

Declarações nas quais o algoritmo euclidiano se baseia:

Se $a$ e $b$ são números naturais, e $a\vdots b$, então $D(a;b)=b$

Se $a$ e $b$ são números naturais tais que $b

Usando $D(a;b)= D(a-b;b)$, podemos reduzir sucessivamente os números em consideração até chegarmos a um par de números tal que um deles seja divisível pelo outro. Então o menor desses números será o máximo divisor comum desejado para os números $a$ e $b$.

Propriedades de GCD e LCM

1. Qualquer múltiplo comum de $a$ e $b$ é divisível por K$(a;b)$
2. Se $a\vdots b$ , então К$(a;b)=a$

Se K$(a;b)=k$ e $m$ for um número natural, então K$(am;bm)=km$

Se $d$ é um divisor comum para $a$ e $b$, então K($\frac(a)(d);\frac(b)(d)$)=$\ \frac(k)(d )$

Se $a\vdots c$ e $b\vdots c$ , então $\frac(ab)(c)$ é o múltiplo comum de $a$ e $b$

Para quaisquer números naturais $a$ e $b$ a igualdade é válida

$D(a;b)\cdot К(a;b)=ab$

Qualquer divisor comum dos números $a$ e $b$ é um divisor do número $D(a;b)$