فرمول های تانژانت تانژانت سینوسی کسینوس. سینوس، کسینوس، مماس، کتانژانت زاویه حاد. توابع مثلثاتی
مثلثات شاخه ای از ریاضیات است که به مطالعه توابع مثلثاتی و کاربرد آنها در هندسه می پردازد. توسعه مثلثات در آن زمان آغاز شد یونان باستان. در طول قرون وسطی، دانشمندان خاورمیانه و هند سهم مهمی در توسعه این علم داشتند.
این مقاله در مورد مفاهیم اساسیو تعاریف مثلثات این تعاریف توابع مثلثاتی اصلی را مورد بحث قرار می دهد: سینوس، کسینوس، مماس و کوتانژانت. معنای آنها در زمینه هندسه توضیح و تشریح شده است.
Yandex.RTB R-A-339285-1
در ابتدا، تعاریف توابع مثلثاتی که استدلال آنها یک زاویه است، از طریق نسبت اضلاع یک مثلث قائم الزاویه بیان شد.
تعاریف توابع مثلثاتی
سینوس یک زاویه (sin α) نسبت پای مقابل این زاویه به هیپوتنوز است.
کسینوس زاویه (cos α) نسبت پای مجاور به هیپوتنوز است.
مماس زاویه (t g α) نسبت پای مقابل به مجاور است.
کوتانژانت زاویه (c t g α) نسبت پایه مجاور به سمت مقابل است.
این تعاریف برای زاویه حادراست گوشه!
بیایید یک تصویر ارائه دهیم.
در مثلث ABC با زاویه قائم C، سینوس زاویه A است برابر با نسبت استپای BC به هیپوتانوز AB.
تعاریف سینوس، کسینوس، مماس و کتانژانت امکان محاسبه مقادیر این توابع را از طول های شناخته شده اضلاع یک مثلث فراهم می کند.
مهم به یاد داشته باشید!
محدوده مقادیر سینوس و کسینوس: از 1- تا 1. به عبارت دیگر سینوس و کسینوس مقادیری از 1- تا 1 می گیرند. محدوده مقادیر مماس و کتانژانت کل خط اعداد است، یعنی اینها توابع می توانند هر مقداری را بگیرند.
تعاریف ارائه شده در بالا به زوایای حاد اشاره دارد. در مثلثات مفهوم زاویه چرخش مطرح می شود که مقدار آن بر خلاف زاویه حاد با فریم هایی از 0 تا 90 درجه محدود نمی شود.زاویه چرخش بر حسب درجه یا رادیان با هر عدد واقعی از - بیان می شود. ∞ به + ∞.
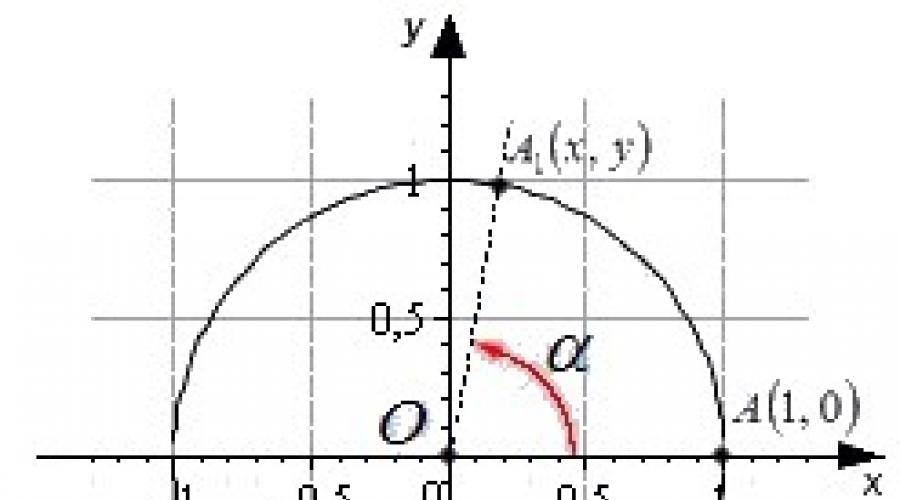
در این زمینه، می توان سینوس، کسینوس، مماس و کوتانژانت یک زاویه با قدر دلخواه را تعریف کرد. دایره واحدی را تصور کنید که در مرکز مبدأ سیستم مختصات دکارتی قرار دارد.

نقطه شروع A با مختصات (1، 0) در اطراف مرکز دایره واحد با مقداری زاویه α می چرخد و به نقطه A 1 می رود. تعریف از طریق مختصات نقطه A 1 (x, y) ارائه شده است.
سینوس (سین) زاویه چرخش
سینوس زاویه چرخش α، مختص نقطه A 1 (x,y) است. sinα = y
کسینوس (cos) زاویه چرخش
کسینوس زاویه چرخش α آبسیسا نقطه A 1 (x,y) است. cos α = x
مماس (tg) زاویه چرخش
مماس زاویه چرخش α نسبت مختصات نقطه A 1 (x, y) به آبسیسا آن است. t g α = y x
کوتانژانت (ctg) زاویه چرخش
کوتانژانت زاویه چرخش α نسبت آبسیسا نقطه A 1 (x, y) به مختص آن است. c t g α = x y
سینوس و کسینوس برای هر زاویه چرخش تعریف می شوند. این منطقی است، زیرا ابسیسا و مختصات نقطه بعد از چرخش را می توان در هر زاویه ای تعیین کرد. وضعیت با مماس و کوتانژانت متفاوت است. مماس زمانی تعریف نمی شود که نقطه بعد از چرخش به نقطه صفر (0، 1) و (0، - 1) برود. در چنین مواردی، بیان مماس t g α = y x به سادگی معنی ندارد، زیرا شامل تقسیم بر صفر است. وضعیت مشابه با کوتانژانت است. با این تفاوت که کوتانژانت در مواردی که ترتیب نقطه ناپدید می شود، تعریف نمی شود.
مهم به یاد داشته باشید!
سینوس و کسینوس برای هر زاویه α تعریف می شوند.
مماس برای همه زوایا تعریف می شود به جز α = 90 درجه + 180 درجه k , k ∈ Z (α = π 2 + π k , k ∈ Z)
کوتانژانت برای همه زوایا به جز α = 180 درجه k، k ∈ Z (α = π k، k ∈ Z) تعریف می شود.
هنگام تصمیم گیری نمونه های عملینگویید "سینوس زاویه چرخش α". واژههای "زاویه چرخش" به سادگی حذف شدهاند، به این معنی که از پیش زمینه مشخص است که چه چیزی در خطر است.
شماره
تعریف سینوس، کسینوس، مماس و کتانژانت یک عدد و نه زاویه چرخش چیست؟
سینوس، کسینوس، مماس، کتانژانت یک عدد
سینوس، کسینوس، مماس و کتانژانت یک عدد تیعددی نامیده می شود که به ترتیب برابر با سینوس، کسینوس، مماس و کوتانژانت در تیرادیان
به عنوان مثال، سینوس 10 π برابر با سینوسزاویه چرخش 10 π راد.
رویکرد دیگری برای تعریف سینوس، کسینوس، مماس و کوتانژانت یک عدد وجود دارد. بیایید آن را با جزئیات بیشتر در نظر بگیریم.
هر عدد واقعی تییک نقطه روی دایره واحد مطابق با مرکز در مبدأ سیستم مختصات دکارتی مستطیلی قرار می گیرد. سینوس، کسینوس، مماس و کوتانژانت بر حسب مختصات این نقطه تعریف می شوند.
نقطه شروع روی دایره نقطه A با مختصات (1، 0) است.
عدد مثبت تی
عدد منفی تیمربوط به نقطه ای است که اگر نقطه شروع در خلاف جهت عقربه های ساعت در امتداد دایره حرکت کند به سمت آن حرکت می کند و راه را طی خواهد کردتی .
اکنون که ارتباط بین عدد و نقطه روی دایره برقرار شد، به تعریف سینوس، کسینوس، مماس و کوتانژانت میپردازیم.
سینوس (سین) عدد t
سینوس یک عدد تی- ترتیب نقطه دایره واحد مربوط به عدد تی sin t = y
کسینوس (cos) از t
کسینوس یک عدد تی- آبسیسا نقطه دایره واحد مربوط به عدد تی cos t = x
مماس (tg) t
مماس یک عدد تی- نسبت مجمل به آبسیسا نقطه دایره واحد مربوط به عدد تی t g t = y x = گناه t cos t
تعاریف اخیر با تعریف ارائه شده در ابتدای این بخش مطابقت دارد و در تضاد نیست. روی یک دایره مربوط به یک عدد اشاره کنید تی، منطبق بر نقطه ای است که نقطه شروع پس از چرخش از زاویه به آن می گذرد تیرادیان
توابع مثلثاتی آرگومان زاویه ای و عددی
هر مقدار از زاویه α مربوط به مقدار مشخصی از سینوس و کسینوس این زاویه است. درست مانند تمام زوایای α غیر از α = 90 ° + 180 ° · k ، k ∈ Z (α = π 2 + π · k , k ∈ Z) به مقدار معینی از مماس مطابقت دارد. کوتانژانت، همانطور که در بالا ذکر شد، برای همه α تعریف شده است، به جز α = 180 درجه k , k ∈ Z (α = π k , k ∈ Z).
میتوان گفت sin α، cos α، tg α، c tg α توابعی از زاویه آلفا یا توابعی از آرگومان زاویهای هستند.
به طور مشابه، می توان از سینوس، کسینوس، مماس و کوتانژانت به عنوان توابعی از یک استدلال عددی صحبت کرد. هر عدد واقعی تیمربوط به مقدار خاصی از سینوس یا کسینوس یک عدد است تی. همه اعداد غیر از π 2 + π · k , k ∈ Z با مقدار مماس مطابقت دارند. کوتانژانت به طور مشابه برای همه اعداد به جز π · k , k ∈ Z تعریف شده است.
توابع اصلی مثلثات
سینوس، کسینوس، مماس و کوتانژانت توابع اصلی مثلثاتی هستند.
از زمینه، معمولاً مشخص می شود که با کدام آرگومان تابع مثلثاتی ( استدلال زاویه اییا یک استدلال عددی) که با آن سروکار داریم.
بیایید به داده های همان ابتدای تعاریف و زاویه آلفا که در محدوده 0 تا 90 درجه قرار دارد بازگردیم. تعاریف مثلثاتیسینوس، کسینوس، مماس و کوتانژانت کاملاً مطابقت دارند تعاریف هندسی، با نسبت اضلاع یک مثلث قائم الزاویه به دست می آید. بیایید آن را نشان دهیم.

یک دایره واحد در مرکز یک سیستم مختصات دکارتی مستطیلی شکل بگیرید. نقطه شروع A (1, 0) را تا 90 درجه بچرخانیم و از نقطه A 1 (x, y) عمود بر محور x بکشیم. در مثلث قائم الزاویه حاصل، زاویه A 1 O H برابر با زاویهچرخش α، طول ساق O H برابر است با آبسیسا نقطه A 1 (x, y) . طول پای مقابل گوشه برابر با مختص نقطه A 1 (x, y) و طول هیپوتانوس برابر با یک است، زیرا شعاع دایره واحد است.
مطابق با تعریف هندسه، سینوس زاویه α برابر است با نسبت پای مقابل به هیپوتنوز.
sin α \u003d A 1 H O A 1 \u003d y 1 \u003d y
این بدان معنی است که تعریف سینوس یک زاویه حاد در یک مثلث قائم الزاویه از طریق نسبت ابعاد معادل تعریف سینوس زاویه چرخش α است که آلفا در محدوده 0 تا 90 درجه قرار دارد.
به طور مشابه، مطابقت تعاریف را می توان برای کسینوس، مماس و کوتانژانت نشان داد.

اگر متوجه اشتباهی در متن شدید، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید
در جایی که تکالیف حل مثلث قائم الزاویه در نظر گرفته شد، قول دادم تکنیکی برای حفظ تعاریف سینوس و کسینوس ارائه کنم. با استفاده از آن، همیشه به سرعت به یاد خواهید آورد که کدام پا متعلق به هیپوتنوز (مجاور یا مقابل) است. تصمیم گرفتم آن را برای مدت نامحدود به تعویق ندهم، مواد لازمدر زیر، لطفا ببینید
واقعیت این است که من بارها مشاهده کرده ام که چگونه دانش آموزان کلاس های 10-11 در به خاطر سپردن این تعاریف مشکل دارند. آنها به خوبی به یاد دارند که پا به هیپوتونوس اشاره دارد، اما کدام یک- فراموش کن و سردرگم. بهای یک اشتباه همانطور که می دانید در امتحان یک نمره از دست رفته است.
اطلاعاتی که من مستقیماً به ریاضیات ارائه خواهم کرد هیچ ربطی ندارد. او با تفکر مجازی، و با روش های ارتباط کلامی-منطقی. درسته من خودم یه بار برای همیشه یادم اومدداده های تعریف اگر هنوز آنها را فراموش کرده اید، با کمک تکنیک های ارائه شده همیشه به راحتی می توانید به خاطر بسپارید.
بگذارید تعاریف سینوس و کسینوس را در مثلث قائم الزاویه به شما یادآوری کنم:
کسینوسزاویه حاد در مثلث قائم الزاویه نسبت ساق مجاور به هیپوتنوز است:

سینوسیزاویه حاد در یک مثلث قائم الزاویه، نسبت پای مقابل به هیپوتنوز است:

بنابراین، کلمه کسینوس چه تداعی هایی را در شما برمی انگیزد؟
احتمالاً هرکسی خود را داردلینک را به خاطر بسپار:
بنابراین، شما بلافاصله یک بیان در حافظه خود خواهید داشت -
«… نسبت پای مجاور به هیپوتنوز».
مشکل تعریف کسینوس حل شد.
اگر لازم است تعریف سینوس در یک مثلث قائم الزاویه را به خاطر بسپارید، سپس با یادآوری تعریف کسینوس، به راحتی می توانید ثابت کنید که سینوس یک زاویه حاد در یک مثلث قائم الزاویه، نسبت سمت مقابل به هیپوتانوس است. از این گذشته ، فقط دو پا وجود دارد ، اگر پای مجاور توسط کسینوس "اشغال" شود ، فقط طرف مقابل برای سینوس باقی می ماند.
مماس و کوتانژانت چطور؟ همان سردرگمی دانشآموزان میدانند که این نسبت پاها است، اما مشکل این است که به یاد داشته باشیم که کدام یک به کدام اشاره دارد - یا مخالف مجاور یا برعکس.
تعاریف:
مماسیک زاویه حاد در یک مثلث قائم الزاویه، نسبت سمت مقابل به سمت مجاور است:

کوتانژانتزاویه حاد در مثلث قائم الزاویه نسبت ساق مجاور به مخالف است:

چگونه به خاطر بسپاریم؟ دو راه وجود دارد. یکی همچنین از یک ارتباط کلامی-منطقی استفاده می کند، دیگری - یک ارتباط ریاضی.
روش ریاضی
چنین تعریفی وجود دارد - مماس یک زاویه حاد نسبت سینوس یک زاویه به کسینوس آن است:

* با به خاطر سپردن فرمول، همیشه می توانید تعیین کنید که مماس یک زاویه حاد در یک مثلث قائم الزاویه، نسبت پای مقابل به سمت مجاور است.
به همین ترتیب.کوتانژانت یک زاویه تند نسبت کسینوس یک زاویه به سینوس آن است:

بنابراین! با یادآوری این فرمول ها، همیشه می توانید تعیین کنید که:
- مماس یک زاویه تند در یک مثلث قائم الزاویه، نسبت پای مقابل به مجاور است.
- کتانژانت یک زاویه حاد در یک مثلث قائم الزاویه، نسبت ساق مجاور به سمت مقابل است.
روش کلامی-منطقی
در مورد مماس لینک را به خاطر بسپار:

یعنی اگر لازم است تعریف مماس را به خاطر بسپارید، با استفاده از این ارتباط منطقی، می توانید به راحتی آن را به خاطر بسپارید.
"... نسبت پای مقابل به مجاور"
اگر صحبت از کوتانژانت به میان می آید، پس با یادآوری تعریف مماس، می توانید به راحتی تعریف کوتانژانت را بیان کنید -
«... نسبت پای مجاور به مخالف»
یک تکنیک جالب برای به خاطر سپردن مماس و کوتانژانت در سایت وجود دارد " پشت سر هم ریاضی " ، نگاه کن
روش جهانی
شما فقط می توانید آسیاب کنید.اما همانطور که تمرین نشان می دهد، به لطف ارتباطات کلامی-منطقی، فرد اطلاعات را برای مدت طولانی و نه تنها ریاضی به یاد می آورد.
امیدوارم مطالب برای شما مفید بوده باشد.
با احترام، الکساندر کروتیتسکیخ
P.S: اگر در مورد سایت در شبکه های اجتماعی بگویید ممنون می شوم.
چگونه سینوس را پیدا کنیم؟



مطالعه هندسه به رشد تفکر کمک می کند. این موضوع در برنامه درسی گنجانده شده است. در زندگی، دانش این موضوع می تواند مفید باشد - به عنوان مثال، هنگام برنامه ریزی یک آپارتمان.
از تاریخ
به عنوان بخشی از درس هندسه، مثلثات نیز مورد مطالعه قرار می گیرد که توابع مثلثاتی را بررسی می کند. در مثلثات، سینوس ها، کسینوس ها، مماس ها و کوتانژانت های یک زاویه را مطالعه می کنیم.
اما در این لحظهبیایید با ساده ترین - سینوس شروع کنیم. بیایید نگاهی دقیق تر به اولین مفهوم - سینوس یک زاویه در هندسه بیندازیم. سینوس چیست و چگونه آن را پیدا کنیم؟
مفهوم "سینوس زاویه" و سینوسی
سینوس یک زاویه نسبت مقادیر پای مقابل و هیپوتنوز یک مثلث قائم الزاویه است. این یک تابع مثلثاتی مستقیم است که به صورت "سین (x)" نوشته می شود، جایی که (x) زاویه مثلث است.
در نمودار، سینوس یک زاویه با یک سینوسی با ویژگی های خاص خود نشان داده می شود. یک سینوسی شبیه یک خط موجی پیوسته است که در محدوده خاصی در صفحه مختصات قرار دارد. تابع فرد است، بنابراین با توجه به 0 در صفحه مختصات متقارن است (از مبدا مختصات خارج می شود).
دامنه این تابع در محدوده 1- تا 1+ در سیستم مختصات دکارتی قرار دارد. دوره تابع زاویه سینوسی 2 Pi است. این بدان معنی است که هر 2 Pi الگوی تکرار می شود و موج سینوسی یک چرخه کامل را طی می کند.
معادله سینوسی
- گناه x = a / c
- جایی که a سمت مقابل زاویه مثلث است
- ج - هیپوتنوز مثلث قائم الزاویه
ویژگی های سینوس یک زاویه
- sin(x) = - sin(x). این ویژگی نشان می دهد که تابع متقارن است و اگر مقادیر x و (-x) در هر دو جهت روی سیستم مختصات کنار گذاشته شوند، آنگاه مختصات این نقاط مخالف خواهند بود. آنها در فاصله مساوی از یکدیگر خواهند بود.
- یکی دیگر از ویژگی های این تابع این است که نمودار تابع در بخش [- P / 2 + 2 Pn] افزایش می یابد. [P/2 + 2Pn]، که در آن n هر عدد صحیحی است. کاهش در نمودار سینوس زاویه در بخش مشاهده می شود: [P / 2 + 2 Pn]. [ 3P/2 + 2Pn].
- sin (x) > 0 وقتی x در محدوده (2Pn، P + 2Pn) است
- (ایکس)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)
مقادیر سینوس های زاویه توسط جداول ویژه تعیین می شود. چنین جداول برای تسهیل روند شمارش ایجاد شده است. فرمول های پیچیدهو معادلات استفاده از آن آسان است و نه تنها حاوی مقادیر است توابع گناه(x) و همچنین مقادیر سایر توابع.
علاوه بر این، جدولی از مقادیر استاندارد برای این توابع در آن گنجانده شده است مطالعه اجباریبرای حافظه، مانند جدول ضرب. این امر به ویژه برای کلاس هایی که دارای سوگیری فیزیکی و ریاضی هستند صادق است. در جدول می توانید مقادیر زوایای اصلی مورد استفاده در مثلثات را مشاهده کنید: 0، 15، 30، 45، 60، 75، 90، 120، 135، 150، 180، 270 و 360 درجه.
همچنین جدولی وجود دارد که مقادیر توابع مثلثاتی زوایای غیر استاندارد را مشخص می کند. استفاده از فرصت جداول مختلف، می توانید به راحتی سینوس، کسینوس، مماس و کوتانژانت برخی از زوایا را محاسبه کنید.
معادلات با توابع مثلثاتی ساخته می شوند. حل این معادلات آسان است اگر ساده بدانید هویت های مثلثاتیو کاهش توابع، به عنوان مثال، مانند گناه (P/2 + x) = cos (x) و دیگران. جدول جداگانه ای نیز برای این گونه بازیگران تهیه شده است.
نحوه پیدا کردن سینوس یک زاویه
وقتی وظیفه یافتن سینوس یک زاویه است و بر اساس شرط فقط کسینوس، مماس یا کوتانژانت زاویه را داریم، میتوانیم به راحتی با استفاده از هویتهای مثلثاتی آنچه را که نیاز داریم محاسبه کنیم.
- sin 2 x + cos 2 x = 1
از این معادله، بسته به اینکه کدام مقدار ناشناخته است، می توانیم هر دو سینوس و کسینوس را پیدا کنیم. ما موفق خواهیم شد معادله مثلثاتیبا یک ناشناخته:
- sin 2 x = 1 - cos 2 x
- sin x = ± √ 1 - cos 2 x
- ctg 2 x + 1 = 1 / sin 2 x
از این معادله، با دانستن مقدار کوتانژانت زاویه، می توانید مقدار سینوس را پیدا کنید. برای ساده کردن، جایگزین sin 2 x = y کنید و سپس یک معادله ساده خواهید داشت. به عنوان مثال، مقدار کوتانژانت 1 است، سپس:
- 1 + 1 = 1/سال
- 2 = 1 / سال
- 2y = 1
- y = 1/2
اکنون تعویض معکوس پخش کننده را انجام می دهیم:
- گناه 2 x = ½
- sin x = 1 / √2
از آنجایی که ما مقدار کوتانژانت را برای زاویه استاندارد (45 0) گرفتیم، مقادیر به دست آمده را می توان در جدول بررسی کرد.
اگر مقدار مماس دارید، اما باید سینوس را پیدا کنید، هویت مثلثاتی دیگری به شما کمک می کند:
- tg x * ctg x = 1
نتیجه می شود که:
- ctg x = 1 / tg x
برای پیدا کردن سینوس یک زاویه غیر استاندارد، به عنوان مثال، 240 0، باید از فرمول های کاهش زاویه استفاده کنید. می دانیم که π برای ما برابر با 180 0 است. بنابراین، برابری خود را با استفاده از زوایای استاندارد با بسط بیان خواهیم کرد.
- 240 0 = 180 0 + 60 0
ما باید موارد زیر را پیدا کنیم: گناه (180 0 + 60 0). در مثلثات، فرمول های کاهشی وجود دارد که در این موردبه کار بیاید این فرمول است:
- گناه (π + x) = - گناه (x)
بنابراین، سینوس زاویه 240 درجه است:
- گناه (180 0 + 60 0) = - گناه (60 0) = - √3/2
در مورد ما، x = 60، و P، به ترتیب، 180 درجه. ما مقدار (-√3/2) را از جدول مقادیر توابع زوایای استاندارد پیدا کردیم.
بنابراین امکان تجزیه وجود دارد زوایای غیر استانداردبه عنوان مثال: 210 = 180 + 30.
مفاهیم سینوس ()، کسینوس ()، مماس ()، کوتانژانت () با مفهوم زاویه پیوند ناگسستنی دارند. برای اینکه در نگاه اول این مفاهیم پیچیده (که باعث ایجاد حالت وحشت در بسیاری از دانش آموزان مدرسه می شود) به خوبی درک شود و مطمئن شویم که "شیطان آنقدر ترسناک نیست که نقاشی می کند"، از همان ابتدا شروع کنیم و درک کنیم. مفهوم زاویه
مفهوم زاویه: رادیان، درجه
بیایید به تصویر نگاه کنیم. بردار نسبت به نقطه با مقدار مشخصی "چرخش" شد. بنابراین اندازه گیری این چرخش نسبت به موقعیت اولیه خواهد بود تزریق.
چه چیز دیگری در مورد مفهوم زاویه باید بدانید؟ خب، واحدهای زاویه، البته!
زاویه، هم در هندسه و هم در مثلثات، می تواند بر حسب درجه و رادیان اندازه گیری شود.
زاویه (یک درجه) را زاویه مرکزی در دایره می گویند که بر اساس یک قوس دایره ای برابر با قسمت دایره است. بنابراین، کل دایره از "قطعات" کمان های دایره ای تشکیل شده است، یا زاویه توصیف شده توسط دایره برابر است.

یعنی شکل بالا زاویه ای را نشان می دهد که مساوی است، یعنی این زاویه بر اساس یک قوس دایره ای به اندازه محیط است.
زاویه بر حسب رادیان یک زاویه مرکزی در یک دایره است که بر اساس یک کمان دایره ای شکل است که طول آن برابر با شعاع دایره است. خوب فهمیدی؟ اگر نه، پس بیایید به تصویر نگاه کنیم.

بنابراین، شکل زاویه ای برابر با رادیان را نشان می دهد، یعنی این زاویه بر اساس یک قوس دایره ای است که طول آن برابر با شعاع دایره است (طول برابر با طول یا شعاع است. برابر طولقوس ها). بنابراین، طول قوس با فرمول محاسبه می شود:
زاویه مرکزی بر حسب رادیان کجاست.
خوب، با دانستن این موضوع، می توانید پاسخ دهید که چند رادیان دارای زاویه توصیف شده توسط یک دایره است؟ بله، برای این باید فرمول محیط دایره را به خاطر بسپارید. او اینجاست:
خوب، حالا بیایید این دو فرمول را به هم مرتبط کنیم و دریافت کنیم که زاویه توصیف شده توسط دایره برابر است. یعنی با همبستگی مقدار بر حسب درجه و رادیان، آن را دریافت می کنیم. به ترتیب، . همانطور که می بینید، بر خلاف "درجه"، کلمه "رادیان" حذف شده است، زیرا واحد اندازه گیری معمولاً از متن مشخص است.
رادیان چند است؟ درست است!
فهمیدم؟ سپس به جلو ببندید:
هیچ مشکلی؟ سپس نگاه کنید پاسخ می دهد:
مثلث قائم الزاویه: سینوس، کسینوس، مماس، کتانژانت یک زاویه
بنابراین، با مفهوم زاویه مشخص شد. اما سینوس، کسینوس، مماس، کتانژانت یک زاویه چیست؟ بیایید آن را بفهمیم. برای این کار، مثلث قائم الزاویه به ما کمک می کند.

اضلاع مثلث قائم الزاویه چه نام دارند؟ درست است، هیپوتنوز و پاها: هیپوتنوز سمتی است که در مقابل قرار دارد زاویه راست(در مثال ما، این طرف است)؛ ساق ها دو ضلع باقی مانده و (آنهایی که مجاور زاویه قائمه هستند) هستند، به علاوه اگر ساق ها را نسبت به زاویه در نظر بگیریم، ساق پای مجاور و ساق طرف مقابل است. خب حالا بیایید به این سوال پاسخ دهیم: سینوس، کسینوس، مماس و کتانژانت یک زاویه چیست؟
سینوس یک زاویهنسبت پای مخالف (دور) به هیپوتنوز است.
در مثلث ما
کسینوس یک زاویه- این نسبت پای مجاور (نزدیک) به هیپوتنوز است.
در مثلث ما
مماس زاویه- این نسبت پای مخالف (دور) به مجاور (نزدیک) است.
در مثلث ما
کوتانژانت یک زاویه- این نسبت پای مجاور (نزدیک) به مخالف (دور) است.
در مثلث ما
این تعاریف لازم است یاد آوردن! برای اینکه راحتتر به خاطر بسپارید کدام پا را به چه چیزی تقسیم کنید، باید آن را به وضوح درک کنید مماسو کتانژانتفقط پاها می نشینند و هیپوتنوز فقط در داخل ظاهر می شود سینوسیو کسینوس. و سپس می توانید با زنجیره ای از انجمن ها بیایید. مثلا این یکی:
کسینوس← لمس← لمس← مجاور;
کوتانژانت← لمس← لمس← مجاور.
اول از همه، لازم به یادآوری است که سینوس، کسینوس، مماس و کوتانژانت به عنوان نسبت اضلاع یک مثلث به طول این ضلع ها (در یک زاویه) بستگی ندارد. باور نکن؟ سپس با دیدن عکس مطمئن شوید:

برای مثال کسینوس یک زاویه را در نظر بگیرید. طبق تعریف، از مثلث: ، اما ما می توانیم کسینوس یک زاویه را از مثلث محاسبه کنیم: . ببینید طول اضلاع متفاوت است، اما مقدار کسینوس یک زاویه یکسان است. بنابراین، مقادیر سینوس، کسینوس، مماس و کوتانژانت تنها به بزرگی زاویه بستگی دارد.
اگر تعاریف را فهمیدید، پس ادامه دهید و آنها را اصلاح کنید!
برای مثلثی که در شکل زیر نشان داده شده است، پیدا می کنیم.

خوب متوجه شدی؟ سپس خودتان آن را امتحان کنید: همان را برای گوشه محاسبه کنید.
دایره واحد (مثلثی).
با درک مفاهیم درجه و رادیان دایره ای با شعاع برابر در نظر گرفتیم. چنین دایره ای نامیده می شود تنها. در مطالعه مثلثات بسیار مفید است. بنابراین، ما کمی بیشتر در مورد آن صحبت می کنیم.

همانطور که می بینید، این دایره در سیستم مختصات دکارتی ساخته شده است. شعاع دایره برابر با یک است، در حالی که مرکز دایره در مبدا قرار دارد، موقعیت اولیه بردار شعاع در امتداد جهت مثبت محور ثابت است (در مثال ما، این شعاع است).
هر نقطه از دایره مربوط به دو عدد است: مختصات در امتداد محور و مختصات در امتداد محور. این اعداد مختصات چیست؟ و در کل چه ربطی به موضوع مورد بحث دارن؟ برای انجام این کار، مثلث قائم الزاویه در نظر گرفته شده را به خاطر بسپارید. در شکل بالا دو مثلث کامل قائم الزاویه را مشاهده می کنید. مثلثی را در نظر بگیرید. مستطیل شکل است زیرا بر محور عمود است.
از یک مثلث برابر با چه چیزی است؟ درست است. علاوه بر این، می دانیم که شعاع دایره واحد است، و بنابراین، . این مقدار را با فرمول کسینوس ما جایگزین کنید. در اینجا چیزی است که اتفاق می افتد:
و مساوی از مثلث چیست؟ خوب البته، ! مقدار شعاع را با این فرمول جایگزین کنید و بدست آورید:
بنابراین، آیا می توانید بگویید یک نقطه چه مختصاتی دارد، متعلق به دایره? خوب، هیچ راهی؟ و اگر متوجه شوید که فقط اعداد هستند؟ با چه مختصاتی مطابقت دارد؟ خوب، البته، مختصات! با چه مختصاتی مطابقت دارد؟ درست است، هماهنگ کنید! بنابراین، نکته.

و پس چه چیزی برابر است و؟ درست است، بیایید از تعاریف مناسب مماس و کوتانژانت استفاده کنیم و دریافت کنیم که، الف.
اگر زاویه بزرگتر باشد چه؟ برای مثال، مانند این تصویر:

چه چیزی در این مثال تغییر کرده است؟ بیایید آن را بفهمیم. برای انجام این کار، دوباره به یک مثلث قائم الزاویه می رویم. مثلث قائم الزاویه را در نظر بگیرید: یک زاویه (به عنوان مجاور یک زاویه). مقدار سینوس، کسینوس، مماس و کوتانژانت یک زاویه چقدر است؟ درست است، ما به تعاریف مربوط به توابع مثلثاتی پایبند هستیم:
خوب، همانطور که می بینید، مقدار سینوس زاویه همچنان با مختصات مطابقت دارد. مقدار کسینوس زاویه - مختصات؛ و مقادیر مماس و کتانژانت به نسبت های مربوطه. بنابراین، این روابط برای هر چرخش بردار شعاع قابل اعمال هستند.
قبلاً ذکر شد که موقعیت اولیه بردار شعاع در امتداد جهت مثبت محور است. تاکنون این بردار را در خلاف جهت عقربه های ساعت چرخانده ایم، اما اگر آن را در جهت عقربه های ساعت بچرخانیم چه اتفاقی می افتد؟ هیچ چیز خارقالعادهای نیست، شما همچنین زاویهای با اندازه خاصی دریافت خواهید کرد، اما فقط منفی خواهد بود. بنابراین، هنگام چرخش بردار شعاع در خلاف جهت عقربه های ساعت، به دست می آوریم زوایای مثبتو هنگام چرخش در جهت عقربه های ساعت - منفی.
بنابراین، می دانیم که یک چرخش کامل از بردار شعاع در اطراف دایره یا است. آیا می توان بردار شعاع را با یا برحسب چرخش کرد؟ خوب، البته که می توانید! بنابراین، در حالت اول، بردار شعاع یک دور کامل میکند و در موقعیت یا توقف میکند.
در حالت دوم، یعنی بردار شعاع سه دور کامل میکند و در موقعیت یا توقف میکند.
بنابراین، از مثالهای بالا، میتوان نتیجه گرفت که زوایایی که با یا (جایی که هر عدد صحیحی است) متفاوت هستند، با موقعیت یکسان بردار شعاع مطابقت دارند.
شکل زیر یک زاویه را نشان می دهد. همان تصویر مربوط به گوشه و غیره است. این لیست را می توان به طور نامحدود ادامه داد. همه این زوایا را می توان با فرمول کلی یا (هر عدد صحیح کجاست) نوشت.

اکنون، با دانستن تعاریف توابع مثلثاتی اساسی و با استفاده از دایره واحد، سعی کنید پاسخ دهید که مقادیر برابر است:
در اینجا یک حلقه واحد برای کمک به شما وجود دارد:

هیچ مشکلی؟ سپس بیایید آن را بفهمیم. پس می دانیم که:
از اینجا مختصات نقاط مربوط به معیارهای خاصی از زاویه را تعیین می کنیم. خوب، بیایید به ترتیب شروع کنیم: گوشه در با یک نقطه با مختصات مطابقت دارد، بنابراین:
وجود ندارد؛
علاوه بر این، با رعایت همین منطق، متوجه می شویم که گوشه ها به ترتیب با نقاط دارای مختصات مطابقت دارند. با دانستن این موضوع، تعیین مقادیر توابع مثلثاتی در نقاط مربوطه آسان است. ابتدا خودتان آن را امتحان کنید، سپس پاسخ ها را بررسی کنید.
پاسخ ها:
وجود ندارد
وجود ندارد
وجود ندارد
وجود ندارد
بنابراین می توانیم جدول زیر را تهیه کنیم:

نیازی به یادآوری تمام این ارزش ها نیست. کافی است مطابقت بین مختصات نقاط روی دایره واحد و مقادیر توابع مثلثاتی را به خاطر بسپارید:
اما مقادیر توابع مثلثاتی زوایای در و، داده شده در جدول زیر، باید به یاد آورد:

نترسید، اکنون یکی از نمونه ها را نشان خواهیم داد حفظ نسبتاً ساده مقادیر مربوطه:
برای استفاده از این روش، به خاطر سپردن مقادیر سینوس برای هر سه اندازه زاویه () و همچنین مقدار مماس زاویه در بسیار مهم است. با دانستن این مقادیر، بازیابی کل جدول بسیار آسان است - مقادیر کسینوس مطابق با فلش ها منتقل می شوند، یعنی:
با دانستن این موضوع، می توانید مقادیر مربوط به آن را بازیابی کنید. صورت " " مطابقت دارد و مخرج " " مطابقت دارد. مقادیر کوتانژانت مطابق با فلش های نشان داده شده در شکل منتقل می شوند. اگر این را فهمیدید و نمودار را با فلش به خاطر بسپارید، کافی است کل مقدار را از جدول به خاطر بسپارید.
مختصات یک نقطه روی یک دایره
آیا می توان نقطه ای (مختصات آن) را روی یک دایره پیدا کرد؟ دانستن مختصات مرکز دایره، شعاع و زاویه چرخش آن?
خوب، البته که می توانید! بیایید بیرون بیاوریم فرمول کلیبرای یافتن مختصات یک نقطه.
در اینجا، برای مثال، ما چنین دایره ای داریم:

به ما داده می شود که نقطه مرکز دایره است. شعاع دایره برابر است. لازم است مختصات نقطه به دست آمده از چرخش نقطه به درجه را پیدا کنید.
همانطور که از شکل مشخص است، مختصات نقطه مطابق با طول قطعه است. طول قطعه مطابق با مختصات مرکز دایره است، یعنی برابر است با. طول یک قطعه را می توان با استفاده از تعریف کسینوس بیان کرد:
سپس ما آن را برای نقطه مختصات داریم.
با همین منطق، مقدار مختصات y را برای نقطه پیدا می کنیم. بدین ترتیب،
بنابراین در نمای کلیمختصات نقطه با فرمول تعیین می شود:
مختصات مرکز دایره،
شعاع دایره،
زاویه چرخش بردار شعاع.
همانطور که می بینید، برای دایره واحدی که در نظر می گیریم، این فرمول ها به طور قابل توجهی کاهش می یابد، زیرا مختصات مرکز صفر است و شعاع برابر با یک است:
خوب، بیایید این فرمول ها را برای طعم دادن، تمرین یافتن نقاط روی یک دایره امتحان کنیم؟
1. مختصات یک نقطه را در یک دایره واحد که با روشن کردن یک نقطه به دست می آید، پیدا کنید.
2. مختصات یک نقطه را در یک دایره واحد که با چرخش یک نقطه روی آن به دست می آید، پیدا کنید.
3. مختصات یک نقطه را در یک دایره واحد که با روشن کردن یک نقطه به دست می آید، پیدا کنید.
4. نقطه - مرکز دایره. شعاع دایره برابر است. لازم است مختصات نقطه ای را که با چرخش بردار شعاع اولیه به دست می آید، پیدا کنیم.
5. نقطه - مرکز دایره. شعاع دایره برابر است. لازم است مختصات نقطه ای را که با چرخش بردار شعاع اولیه به دست می آید، پیدا کنیم.
آیا در یافتن مختصات یک نقطه روی یک دایره مشکل دارید؟
این پنج مثال را حل کنید (یا راه حل را خوب درک کنید) و یاد خواهید گرفت که چگونه آنها را پیدا کنید!
1.
دیده می شود که. و ما می دانیم که چه چیزی مربوط به چرخش کامل نقطه شروع است. بنابراین، نقطه مورد نظر در همان موقعیتی قرار می گیرد که هنگام چرخش به. با دانستن این موضوع، مختصات مورد نظر نقطه را پیدا می کنیم:
2. دایره واحدی با مرکز در یک نقطه است، به این معنی که می توانیم از فرمول های ساده شده استفاده کنیم:
دیده می شود که. ما می دانیم که چه چیزی مربوط به دو چرخش کامل نقطه شروع است. بنابراین، نقطه مورد نظر در همان موقعیتی قرار می گیرد که هنگام چرخش به. با دانستن این موضوع، مختصات مورد نظر نقطه را پیدا می کنیم:
سینوس و کسینوس هستند مقادیر جدول. ما ارزش های آنها را به خاطر می آوریم و دریافت می کنیم:
بنابراین نقطه مورد نظر دارای مختصاتی است.
3. دایره واحدی با مرکز در یک نقطه است، به این معنی که می توانیم از فرمول های ساده شده استفاده کنیم:
دیده می شود که. بیایید مثال در نظر گرفته شده را در شکل به تصویر بکشیم:

شعاع زاویه هایی با محور برابر با و می سازد. با دانستن اینکه مقادیر جدولی کسینوس و سینوس برابر هستند و با تعیین اینکه کسینوس در اینجا مقدار منفی می گیرد و سینوس مثبت است، داریم:
هنگام مطالعه فرمول های کاهش توابع مثلثاتی در مبحث، نمونه های مشابه با جزئیات بیشتری تحلیل می شوند.
بنابراین نقطه مورد نظر دارای مختصاتی است.
4.
زاویه چرخش بردار شعاع (بر اساس شرایط)
برای تعیین علائم مربوط به سینوس و کسینوس، یک دایره و یک زاویه می سازیم:

همانطور که می بینید، مقدار، یعنی مثبت است و مقدار، یعنی منفی. با دانستن مقادیر جدولی توابع مثلثاتی مربوطه، به دست می آوریم که:
بیایید مقادیر به دست آمده را در فرمول خود جایگزین کنیم و مختصات را پیدا کنیم:
بنابراین نقطه مورد نظر دارای مختصاتی است.
5. برای حل این مشکل از فرمول هایی به صورت کلی استفاده می کنیم که کجا
مختصات مرکز دایره (در مثال ما،
شعاع دایره (بر اساس شرایط)
زاویه چرخش بردار شعاع (بر اساس شرایط).
همه مقادیر را در فرمول جایگزین کنید و دریافت کنید:
و - مقادیر جدول. آنها را به خاطر می آوریم و در فرمول جایگزین می کنیم:
بنابراین نقطه مورد نظر دارای مختصاتی است.
خلاصه و فرمول اساسی
سینوس یک زاویه نسبت پای مقابل (دور) به هیپوتنوز است.
کسینوس یک زاویه نسبت ساق مجاور (نزدیک) به هیپوتنوز است.
مماس یک زاویه نسبت پای مقابل (دور) به مجاور (نزدیک) است.
کتانژانت یک زاویه، نسبت ساق مجاور (نزدیک) به طرف مقابل (دور) است.
دستورالعمل
اگر مقدار آن زاویه را می دانید، از تابع آرکسین برای محاسبه مقدار یک زاویه بر حسب درجه استفاده کنید. اگر یک تزریقکه با حرف α نشان داده می شود، به طور کلی، راه حل را می توان به صورت زیر نوشت: α = arcsin(sin(a)).
اگر فرصت استفاده از رایانه را دارید، ساده ترین کار استفاده از سیستم عامل داخلی برای محاسبات عملی است. در دو نسخه اخیر ویندوز، می توانید آن را به این صورت شروع کنید: کلید Win را فشار دهید، "ka" را تایپ کنید و Enter را فشار دهید. در نسخه های قبلی این سیستم عامل، پیوند "ماشین حساب" را در زیربخش "استاندارد" از بخش "همه برنامه ها" منوی اصلی سیستم جستجو کنید.
پس از راه اندازی برنامه، آن را به حالتی تغییر دهید که به شما امکان می دهد با توابع مثلثاتی کار کنید. این کار را می توان با انتخاب خط "مهندسی" در بخش "مشاهده" منوی ماشین حساب یا با فشار دادن Alt + 2 انجام داد.
یک مقدار سینوسی وارد کنید. به طور پیش فرض، رابط ماشین حساب دکمه ای برای محاسبه آرکسین ندارد. برای اینکه بتوانید از این تابع استفاده کنید، باید مقادیر پیش فرض دکمه ها را معکوس کنید - روی دکمه Inv در پنجره برنامه کلیک کنید. در بیشتر نسخه های اولیهاین دکمه با یک کادر انتخاب با همان علامت جایگزین می شود - آن را علامت بزنید.
شما می توانید در محاسبات و خدمات مختلف که در اینترنت بیش از حد کافی هستند استفاده کنید. برای مثال به صفحه http://planetcalc.com/326/ بروید، کمی به پایین اسکرول کنید و در قسمت Input مقدار سینوس را وارد کنید. برای شروع روش محاسبه، دکمه ای با عنوان Calculate وجود دارد - روی آن کلیک کنید. نتیجه محاسبات را در خط اول جدول زیر این دکمه خواهید دید. علاوه بر آرکسین، هم مقادیر و هم مماس قوس مقدار وارد شده را نمایش می دهد.
تابع مثلثاتی سینوس معکوس نامیده می شود آرکسین. می تواند مقادیری را بگیرد که در نصف عدد پی قرار دارند، هم مثبت و هم منفی. جنبه منفیهنگامی که در رادیان اندازه گیری می شود. هنگامی که بر حسب درجه اندازه گیری می شود، این مقادیر به ترتیب در محدوده -90 درجه تا +90 درجه خواهد بود.
دستورالعمل
برخی از مقادیر "گرد" لازم نیست محاسبه شوند، به خاطر سپردن آنها آسان تر است. به عنوان مثال: - اگر آرگومان تابع صفر باشد، مقدار آرکسین از آن نیز صفر است؛ - از 1/2 30 درجه یا 1/6 Pi است، اگر اندازه گیری شود؛ - کمان از 1/2- برابر است. تا 30- درجه یا 1/6- از پی در ؛- آرکسین 1 90 درجه یا 1/2 پی در رادیان است؛- آرکسین 1- 90- درجه یا 1/2- از پی در رادیان است.
برای اندازهگیری مقادیر این تابع از آرگومانهای دیگر، سادهترین راه استفاده از ماشینحساب استاندارد ویندوز است، اگر دارید. برای شروع، منوی اصلی را روی دکمه "شروع" باز کنید (یا با فشار دادن کلید WIN)، به بخش "همه برنامه ها" و سپس به بخش "لوازم جانبی" بروید و روی مورد "ماشین حساب" کلیک کنید.
رابط ماشین حساب را به حالت عملیاتی تغییر دهید که به شما امکان می دهد توابع مثلثاتی را محاسبه کنید. برای انجام این کار، بخش "View" را در منوی آن باز کرده و مورد "مهندسی" یا "علمی" (بسته به سیستم عامل مورد استفاده) را انتخاب کنید.
مقدار آرگومانی را که از آن تانژانت قوس محاسبه می شود وارد کنید. این کار را می توان با کلیک روی دکمه های رابط ماشین حساب با ماوس، یا با فشار دادن کلیدهای روی یا با کپی کردن مقدار (CTRL + C) و سپس چسباندن آن (CTRL + V) در قسمت ورودی ماشین حساب انجام داد.
واحدهایی را که می خواهید نتیجه محاسبه تابع را در آنها بدست آورید، انتخاب کنید. در زیر فیلد ورودی سه گزینه وجود دارد که باید از بین آنها (با کلیک روی آن با ماوس) یک - ، رادیان یا راد را انتخاب کنید.
کادر انتخابی را که عملکردهای نشان داده شده در دکمه های رابط ماشین حساب را معکوس می کند، علامت بزنید. در کنار آن یک کتیبه کوتاه Inv.
روی دکمه گناه کلیک کنید. ماشین حساب تابع متصل به آن را معکوس می کند، محاسبه را انجام می دهد و نتیجه را در واحدهای داده شده به شما ارائه می دهد.
ویدیو های مرتبط
در یک مثلث قائم الزاویه، به عنوان ساده ترین چند ضلعی، دانشمندان مختلف دانش خود را در زمینه مثلثات در آن روزها تقویت کردند، زمانی که هیچ کس حتی این حوزه از ریاضیات را با آن کلمه نمی نامید. بنابراین، نویسنده ای را که الگوهایی را در نسبت طول اضلاع و مقادیر زوایای این تخت مشخص کرده است، مشخص کنید. شکل هندسیامروز ممکن نیست چنین روابطی توابع مثلثاتی نامیده می شوند و به چندین گروه تقسیم می شوند که اصلی ترین آنها معمولاً توابع "مستقیم" در نظر گرفته می شوند. تنها دو تابع به این گروه اختصاص داده شده است که یکی از آنها سینوس است.

دستورالعمل
طبق تعریف، در مثلث قائم الزاویه یکی از زوایای آن 90 درجه است و با توجه به اینکه مجموع زوایای آن در هندسه اقلیدسی باید برابر با 180 درجه باشد، دو زاویه دیگر (یعنی 90 درجه) هستند. قاعده مندی نسبت های دقیقاً این زوایا و طول ضلع ها توابع مثلثاتی را توصیف می کند.
تابعی که سینوس زاویه تند نامیده می شود، نسبت بین طول دو ضلع یک مثلث قائم الزاویه را تعیین می کند که یکی از آنها در مقابل این زاویه تند قرار دارد و دیگری در مجاورت آن و در مقابل زاویه قائمه قرار دارد. از آنجایی که ضلع مقابل زاویه قائمه در چنین مثلثی هیپوتنوز نامیده می شود و دو ضلع دیگر پاها هستند، توابع سینوسی را می توان به عنوان نسبت بین طول ساق و هیپوتنوز فرموله کرد.
علاوه بر چنین تعریف ساده ای از این تابع مثلثاتی، موارد پیچیده تری نیز وجود دارد: از طریق دایره در مختصات دکارتی، از طریق سری، از طریق معادلات دیفرانسیل و تابعی. این تابع پیوسته است، یعنی آرگومان های آن ("حوزه تعاریف") می تواند هر عددی باشد - از بی نهایت منفی تا بی نهایت مثبت. و حداکثر مقادیر این تابع با محدوده -1 تا +1 محدود می شود - این "محدوده مقادیر آن" است. حداقل ارزشسینوس در زاویه 270 درجه است که مربوط به 3 / Pi است و حداکثر در 90 درجه (½ Pi) به دست می آید. مقادیر تابع در 0 درجه، 180 درجه، 360 درجه و غیره صفر می شود. از همه اینها نتیجه می شود که سینوس یک تابع تناوبی است و دوره آن برابر با 360 درجه یا دو برابر عدد Pi است.
برای محاسبات عملی مقادیر این تابع از یک آرگومان داده شده، می توانید از اکثریت قریب به اتفاق آنها (از جمله ماشین حساب نرم افزاری ساخته شده در) استفاده کنید. سیستم عاملکامپیوتر شما) گزینه مربوطه را دارد.
ویدیو های مرتبط
سینوسیو کسینوس- اینها توابع مثلثاتی مستقیم هستند که چندین تعاریف برای آنها وجود دارد - از طریق یک دایره در سیستم مختصات دکارتی، از طریق راه حل ها معادله دیفرانسیل، از طریق زوایای تند در یک مثلث قائم الزاویه. هر یک از این تعاریف به شما امکان می دهد تا رابطه بین این دو تابع را استنباط کنید. زیر شاید ساده ترین راه برای بیان باشد کسینوساز طریق سینوس - از طریق تعاریف آنها برای زوایای حاد مثلث قائم الزاویه.

دستورالعمل
سینوس زاویه تند مثلث قائم الزاویه را بر حسب طول اضلاع این شکل بیان کنید. طبق تعریف، سینوس زاویه (α) باید نسبت طول ضلع (الف) مقابل آن - ساق - به طول ضلع (ج) مقابل زاویه راست باشد - فرضیه: sin. (a) = a / c.
یک فرمول مشابه برای کسینوساما همان زاویه طبق تعریف، این مقدار باید به عنوان نسبت طول ضلع (b) مجاور این گوشه (پای دوم) به طول ضلع (c) که در مقابل زاویه راست قرار دارد بیان شود: cos (a) \u003d a/c
معادله حاصل از قضیه فیثاغورث را به گونه ای بازنویسی کنید که از روابط بین پاها و هیپوتانوس حاصل شده در دو مرحله قبل استفاده کند. برای انجام این کار، ابتدا هر دو قضیه اصلی (a² + b² = c²) را بر مربع فرضیه (a² / c² + b² / c² = 1) تقسیم کنید و سپس تساوی حاصل را به این شکل بازنویسی کنید: / c)² + (b / c)² = 1.
در عبارت حاصل، نسبت طول پاها و هیپوتانوس را با توابع مثلثاتی، بر اساس فرمول های مرحله اول و دوم جایگزین کنید: sin² (a) + cos² (a) \u003d 1. Express کسینوساز برابری حاصل: cos(a) = √(1 - sin²(a)). این مشکل به صورت کلی قابل حل است.
اگر علاوه بر نتیجه کلی، نیاز به یک نتیجه عددی دارید، برای مثال از یک ماشین حساب تعبیه شده در اتاق عمل استفاده کنید. سیستم ویندوز. پیوندی به راهاندازی آن در بخش «استاندارد» از بخش «همه برنامهها» از منوی سیستم عامل. این پیوند به طور خلاصه بیان شده است - "ماشین حساب". برای اینکه بتوانید توابع مثلثاتی را از این برنامه محاسبه کنید، رابط "مهندسی" آن را روشن کنید - کلید ترکیبی Alt + 2 را فشار دهید.
مقدار سینوس زاویه را در شرایط وارد کنید و روی دکمه رابط با نام x² کلیک کنید - این مقدار اصلی را مربع می کند. سپس روی صفحه کلید *-1 را تایپ کنید، Enter را فشار دهید، +1 را تایپ کنید و دوباره Enter را فشار دهید - به این ترتیب مربع سینوس را از واحد کم می کنید. روی کلید آیکون رادیکال کلیک کنید تا مربع را استخراج کنید و نتیجه نهایی را بگیرید.
مطالعه مثلث ها توسط ریاضیدانان برای چندین هزار سال انجام شده است. علم مثلث - مثلثات - از مقادیر خاصی استفاده می کند: سینوس و کسینوس.

راست گوشه
در ابتدا سینوس و کسینوس به دلیل نیاز به محاسبه کمیت ها در مثلث های قائم الزاویه به وجود آمدند. متوجه شدیم که اگر مقدار درجه اندازه گیری زوایای یک مثلث قائم الزاویه تغییر نکند، نسبت ابعاد، مهم نیست که این ضلع ها چقدر از نظر طول تغییر کنند، همیشه ثابت می ماند.
اینگونه بود که مفاهیم سینوس و کسینوس معرفی شدند. سینوس یک زاویه حاد در یک مثلث قائم الزاویه نسبت پای مقابل به هیپوتنوز و کسینوس نسبت ساق مجاور به هیپوتنوز است.
قضایای کسینوس و سینوس
اما کسینوس و سینوس نه تنها در مثلث قائم الزاویه قابل استفاده هستند. برای یافتن مقدار یک زاویه منفرد یا تند، ضلع هر مثلث، کافی است قضیه کسینوس و سینوس را اعمال کنیم.
قضیه کسینوس کاملاً ساده است: "مربع یک ضلع مثلث برابر است با مجموع مربع های دو ضلع دیگر منهای دو برابر حاصلضرب این ضلع ها به وسیله کسینوس زاویه بین آنها."
دو تفسیر از قضیه سینوس وجود دارد: کوچک و گسترده. به گزارش کوچک: «در مثلث، زاویه ها با اضلاع مقابل هم تناسب دارند». این قضیه اغلب به دلیل خاصیت دایره محصور در اطراف یک مثلث بسط مییابد: «در مثلث، زاویهها با اضلاع مقابل هم تناسب دارند و نسبت آنها برابر است با قطر دایره محصور شده».
مشتقات
مشتق یک ابزار ریاضی است که نشان می دهد یک تابع با توجه به تغییر در آرگومانش چقدر سریع تغییر می کند. مشتقات در هندسه و در تعدادی از رشته های فنی استفاده می شود.
هنگام حل مسائل، باید مقادیر جدولی مشتقات توابع مثلثاتی را بدانید: سینوس و کسینوس. مشتق سینوس کسینوس است و مشتق کسینوس سینوس است اما با علامت منفی.
کاربرد در ریاضیات
به خصوص اغلب از سینوس و کسینوس در حل استفاده می شود مثلث های قائم الزاویهو وظایف مرتبط با آنها
راحتی سینوس ها و کسینوس ها نیز در فناوری منعکس شده است. ارزیابی زوایا و اضلاع با استفاده از قضایای کسینوس و سینوسی، شکستن اشکال و اجسام پیچیده به مثلثهای "ساده" آسان بود. مهندسان و اغلب با محاسبات نسبت ابعاد و اندازه گیری درجه سر و کار دارند، زمان و تلاش زیادی را صرف محاسبه کسینوس ها و سینوس های زوایای غیر جدولی کردند.
سپس جداول بردیس به کمک آمدند که حاوی هزاران مقدار سینوس، کسینوس، مماس و کوتانژانت بود. زوایای مختلف. در زمان شوروی، برخی از معلمان بخش های خود را مجبور می کردند که صفحات جداول برادیس را حفظ کنند.
رادیان - قدر زاویه ایکمان، در طول برابر با شعاعیا 57.295779513 درجه.
درجه (در هندسه) - 1/360 دایره یا 1/90 زاویه راست.
π = 3.141592653589793238462… (مقدار تقریبی pi).
جدول کسینوس برای زوایای: 0 درجه، 30 درجه، 45 درجه، 60 درجه، 90 درجه، 120 درجه، 135 درجه، 150 درجه، 180 درجه، 210 درجه، 225 درجه، 240 درجه، 270 درجه، 300 درجه، 315 درجه، 330 درجه، 360 درجه.
| زاویه x (بر حسب درجه) | 0° | 30 درجه | 45 درجه | 60 درجه | 90 درجه | 120 درجه | 135 درجه | 150 درجه | 180 درجه | 210 درجه | 225 درجه | 240 درجه | 270 درجه | 300 درجه | 315 درجه | 330 درجه | 360 درجه |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| زاویه x (به رادیان) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3xπ/4 | 5xπ/6 | π | 7xπ/6 | 5xπ/4 | 4xπ/3 | 3xπ/2 | 5xπ/3 | 7xπ/4 | 11xπ/6 | 2xπ |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |