حل معادلات دیفرانسیل با استفاده از تبدیل لاپلاس. روش عملیاتی برای حل معادلات دیفرانسیل خطی و سیستم های آنها. §یک. اصل و تصاویر توابع طبق لاپلاس

07.10.2020

همچنین بخوانید

هدایای غیر معمول سال نو که می توانید با دستان خود درست کنید

بررسی نظرات در مورد آیین آرینا اودوکیمووا روانی برای تحقق آرزو

تاتیانا: روز فرشته، روز نام

مرلین کر - بیوگرافی و زندگی شخصی یک جادوگر استونیایی

تعبیر برای زنان دیدن سوسک در خواب چه تعبیری دارد

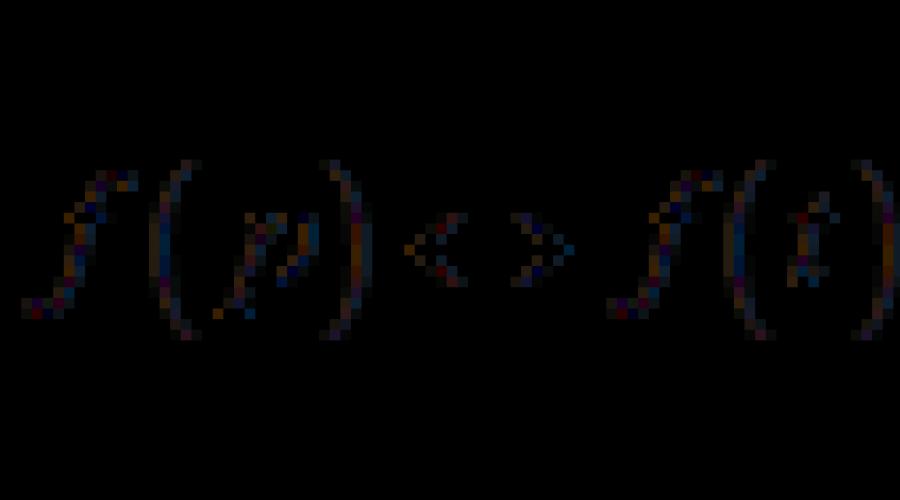
اندازه: px

شروع نمایش از صفحه:

رونوشت

1 حل معادلات دیفرانسیل با استفاده از تبدیل لاپلاس (روش عملیاتی) حساب عملیاتی یکی از مقرون به صرفه ترین روش ها برای ادغام معادلات دیفرانسیل خطی با ضرایب ثابت است و بسیار مورد علاقه مهندسان است. این روش توسط مهندس برق و فیزیکدان مشهور آمریکایی O. Heaviside (892) پیشنهاد شد. او قوانین رسمی برای برخورد با عملگر d dx و برخی از توابع از این عملگر پیشنهاد کرد که با استفاده از آنها تعدادی از مهمترین مسائل الکترودینامیک را حل کرد. با این حال، حساب عملیاتی در آثار O. Heaviside یک توجیه ریاضی دریافت نکرد ("ریاضیات او در زمینه فیزیکی بوجود آمد که جدا کردن از آن آسان نبود" [، ص 8]، بسیاری از نتایج او باقی ماندند. اثبات نشده تنها در سال دوم قرن بیستم، این روش در آثار برومویچ (T. J. I A. Bromwich) و Carson (J. R. Carson) 2 توجیه شد.. مفهوم اصلی و تصویر مطابق با تعریف لاپلاس. تابع اصلی هر تابع با ارزش مختلط f(x) از آرگومان واقعی x است که شرایط زیر را برآورده می‌کند: f(x) در x پیوسته است، به جز، شاید، تعداد محدودی از نقاط ناپیوستگی از نوع -ام. 2) برای همه x< f(x) = ; 3) существуют такие постоянные M >و a > که f(x) M e ax برای x. () معادلات دیفرانسیل و انتگرال: کتاب درسی برای دانشجویان دانشکده فیزیک و فناوری: در 3 ساعت قسمت 2 / کامپ. : N. Yu. Svetova، E. E. Semyonova. پتروزاوودسک: انتشارات PetrSU، تلاش برای توجیه دقیق و ارائه "از نظر ریاضی قابل قبول" حساب دیفرانسیل و انتگرال شبیه یک "حمله عمومی" ریاضیدان انگلیسی برومویچ (96)، مهندس آمریکایی کارسون (925)، مهندس برق هلندی وان در پل () نتایج را به خود جلب کردند. از نظریات مختلف، حساب Heaviside را با تبدیل لاپلاس، با نظریه توابع یک متغیر مختلط مرتبط کرد.

2 2 عدد a تمام اعداد a که نابرابری () برای آنها صادق است، نرخ رشد تابع f(x) نامیده می شود. توجه داشته باشید که برای هر تابع محدود، نرخ رشد a = است. ساده ترین اصلی تابع Heaviside است (, x ; χ(x) =, x<. Очевидно, для любой функции ϕ(x) { ϕ(x), x, ϕ(x) χ(x) =, x <. Если при x функция ϕ(x) удовлетворяет условиям и 3 определения, то функция ϕ(x)χ(x) является оригиналом. В дальнейшем для сокращения записи будем, как правило, записывать ϕ(x) вместо ϕ(x)χ(x), считая, что рассматриваемые нами функции продолжены нулем для отрицательных значений аргумента x. Определение 2. Функция F (p) комплексного переменного p (p C), определяемая интегралом F (p) = e px f(x) dx, () называется преобразованием Лапласа, или изображением по Лапласу 3, функции f(x). Для указания соответствия между оригиналом и изображением будем использовать следующую запись 4: f(x) F (p). 3 В мемуарах П. Лапласа (782 82) современные оригинал и изображение именуются fonction determinant и fonction generatrice «определяющая функция» и «производящая». Эти названия, хотя и признанные неудачными, сохранились до XX в. Хевисайд употреблял названия «подоператорная функция» (892). Оператор он обозначал буквой p, которая употребляется в современном исчислении . 4 Названия original и image и знак предложил Ван дер Поль в статьях гг. В русской литературе термин изображение и символ, по-видимому, впервые появились в книге харьковских математиков А. М. Эфроса и А. М. Данилевского «Операционное исчисление и контурные интегралы» (937), а термин оригинал только в 953 г. . Используются и другие варианты записи соответствия между оригиналами и изображениями. Например, f(x) F (p) или L{f(x)} = F (p).

3 برای هر f(x) اصلی، تصویر F (p) آن در نیم صفحه Re p > a تعریف می شود (a نرخ رشد تابع f(x) است)، جایی که انتگرال نامناسب () همگرا می شود. مثال. با استفاده از تعریف، تصویر تابع f(x) = sin 3x را پیدا کنید. تصمیم گیری برای تابع f(x) = sin 3x یک = داریم. بنابراین، تصویر F (p) در نیم صفحه Re p > تعریف می شود. اجازه دهید با استفاده از قانون ادغام توسط قطعات و محدودیت در مجموعه مقادیر متغیر p، فرمول () را برای تابع داده شده اعمال کنیم، که همگرایی انتگرال را تضمین می کند: F (p) = + e px sin 3x dx = = p e px sin 3x x= = 3 p p e px cos 3x = 3 p 2 9 p 2 ). F (p) = 3 p 2 9 p 2 F (p). F (p) = 3 p بنابراین، مطابقت زیر معتبر است: sin 3x 3 p 2، Re p >. + 9 e px sin 3x dx = 3

4 4 2. ویژگی های تبدیل لاپلاس در عمل، هنگام ساخت تصاویر، تکنیک های مختلفی بر اساس ویژگی های تبدیل لاپلاس استفاده می شود. ما ویژگی های اصلی را لیست می کنیم که اعتبار آنها با استفاده از تعاریف تصویر و اصل به راحتی قابل تشخیص است. ویژگی Linearity. اگر f(x) F (p)، g(x) G(p)، سپس برای هر α، β C αf(x) + βg(x) αf (p) + βg(p)، Re p > max( الف، ب). در اینجا و زیر، a و b به ترتیب نرخ رشد توابع f(x) و g(x) هستند. 2. قضیه تشابه. اگر f(x) F (p)، پس برای هر α > f(αx) α F (p α)، Re p > αa. 3. قضیه جابجایی. اگر f(x) F (p)، پس برای هر λ C e λx f(x) F (p λ)، Re p > a + Re λ. 4. تمایز اصلی. فرض کنید تابع f(x) n برابر متمایزپذیر باشد. سپس f (x) pf (p) f(+)، f (x) p 2 F (p) pf(+) f (+)، f (n) (x) p n F (p) p n f(+). .. pf (n 2) (+) f (n) (+)، که در آن f (k) (+) = lim x + f (k) (x)، k =، n. اظهار نظر. هنگام ساخت تصاویر مشتقات توابع پیوسته در صفر، علامت مثبت در علامت گذاری آرگومان تابع و مشتقات آن حذف می شود. 5. تمایز تصویر. اگر f(x) F (p)، به طور خاص، برای n = F (n) (p) (x) n f(x)، Re p > داریم. F(p)xf(x).

5 5 6. ادغام نسخه اصلی. اگر f(x) F (p)، آنگاه x f(ξ) dξ F (p) p، Re p > α. 7. یکپارچه سازی تصویر. اگر انتگرال و F (p) f(x)، سپس p F (p) dp f(x) x، Re p > α. p F (p) dp همگرا می شود 8. قضیه ضرب تصویر (قضیه کانولوشن) اگر f(x) F (p)، g(x) G(p)، سپس F (p)g(p) x f(t) g( x t) dt = x f(x t)g(t) dt زمانی که Re p > max(a, b). انتگرال های سمت راست تناظر را کانولوشن توابع f(x) و g(x) می نامند. 9. قضیه تاخیر. اگر f(x) F (p)، پس برای هر ξ > f(x ξ)χ(x ξ) e ξp F (p)، Re p > α. نسخه اصلی به روشی منحصر به فرد از تصویر بازیابی می شود، تا مقادیر در نقاط شکست. در عمل معمولاً از جداول آماده از اصل ها و تصاویر استفاده می شود. مثال 2. با استفاده از ویژگی های تبدیل لاپلاس و جدول اصلی و تصاویر اصلی، تصاویری از توابع زیر را بیابید:) f(x) = e 4x sin 3x cos 2x; 3) f(x) = x 2 e 3x; 2) f (x) \u003d e (x 2) sin (x 2)؛ 4) f(x) = sin2 x x. 5 Ditkin V. A., Prudnikov A. P. Handbook of Operational Calculus. م.، 965.

6 6 جدول. نسخه اصلی و تصاویر اصلی تصویر اصلی تصویر اصلی p cos ωx p p 2 + ω 2 x n n! p n+ e λx p + λ sin ωx x cos ωx x n e λx n! (p + λ) n+ x sin ωx ω p 2 + ω 2 p 2 ω 2 (p 2 + ω 2) 2 2pω (p 2 + ω 2) 2 راه حل.) ما عبارت تابع f (x) را تبدیل می کنیم. به صورت زیر: f(x) = e 4x sin 3x cos 2x = 2 e 4x (sin 5x + sin x) = = 2 e 4x sin 5x + 2 e 4x sin x. از آنجایی که sin x 5 p 2 و sin 5x + p , پس با استفاده از خاصیت خطی بودن و قضیه جابجایی، برای تصویر تابع f (x) خواهیم داشت: F (p) = () 5 2 (p + 4) ) (p + 4 )) از آنجایی که sin x p 2 +، ex sin x (p) 2 +، پس با استفاده از قضیه تاخیر، f (x) = e x 2 sin (x 2) F (p) = e خواهیم داشت. 2p (p)) بنابراین به عنوان x 2 2 p 3، سپس با قضیه جابجایی داریم: f(x) = x 2 e 3x F (p) = 2 (p 3) 3.

7 برای مقایسه، روشی را برای ساختن تصویری از تابع f(x) = x 2 e 3x با استفاده از ویژگی تمایز تصویر ارائه می‌کنیم: همین نتیجه را گرفتیم. 4) از آنجایی که e 3x p 3 ; xe 3x d () = dp p 3 (p 3) 2 ; x 2 e 3x d () 2 dp (p 3) 2 = (p 3) 3. sin 2 x = 2 2 cos 2x 2p 2 p p 2 + 4، سپس با استفاده از خاصیت ادغام تصویر، خواهیم داشت: sin 2 x ( x 2p) 2 p p 2 dp = + 4 p (= 4 ln p2) 4 ln(p2 + 4) = p 4 ln p 2 p p = 4 ln p2 + 4 p کسر منطقی مناسب (یک تابع گویا است). اگر کسری به مجموع ساده‌ترین کسرهای (بنیادی) تجزیه شود، برای هر یک از آنها می‌توان اصل متناظر را با استفاده از ویژگی‌های تبدیل لاپلاس و جدول کسرهای اصلی و تصاویر آنها پیدا کرد. در واقع، A p a A eax ; A (p a) n A (n)! xn e تبر.

8 8 پس از انجام تبدیل کسری Ap + B A(p a) + aa + B A(p a) (p a) 2 = + b2 (p a) 2 + b 2 = (p a) 2 + b 2 + aa + B (p a) 2 + b 2، Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sin bx را دریافت می کنیم. b برای ساختن اصلی مربوط به کسر Ap + B ((p a) 2 + b 2) n، می توانید از قضیه ضرب استفاده کنید. به عنوان مثال، برای n = 2 ما Ap + B ((p a) 2 + b 2) 2 = Ap + B (p a) 2 + b 2 (p a) 2 + b 2 داریم. از آن زمان برای n = 3: Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sin bx = h (x) b (p a) 2 + b 2 b eax sin bx = g(x)، Ap + B ((p a) 2 + b 2) 2 = x Ap + B ((p a) 2 + b 2) 2 (p a) 2 + b 2 g(x t) h (t) dt = h 2 (t). x g(x t) h 2 (t) dt اگر k صفرهای مختلف داشته باشد p i، i =، k، سپس، در حال گسترش است

9 مخرج توسط عوامل (p p i)، اصل مربوط به Y (p) را می توان با فرمول پیدا کرد: y(x) = k (Y (p) (p p i)e px) p=pi. (2) i= حاصلضرب Y (p)(p p i) تابع گویا را به دست می دهد که مخرج آن ضریب (p p i) را ندارد و با محاسبه p = p i ضریب ورود کسری به بسط p p i تابع را تعیین می کند. Y (p) به مجموع کسرهای ابتدایی. مثال 3. نسخه اصلی را پیدا کنید که با تصویر مطابقت دارد: Y (p) = p 3 p. تصمیم گیری با بزرگ کردن تصویر داده شده به مجموع کسرهای ابتدایی: p 3 p = p (p) (p +) = p + 2 (p) + 2 (p +)، پاسخ اصلی را پیدا می کنیم: y (x) = + ch ایکس. y(x) = + 2 ex + 2 e x = + ch x. مثال 4. تصویر اصلی را پیدا کنید: Y (p) = p (p 2 +). تصمیم گیری از آنجایی که p 2 sin x، پس با اعمال ویژگی یکپارچه سازی اصلی، + دریافت می کنیم: p(p 2 +) x پاسخ: y(x) = cos x. sin t dt = cos t x = cos x. مثال 5. نسخه اصلی را پیدا کنید که با تصویر مطابقت دارد: Y (p) = (p 2 + 4) 2. 9

10 تصمیم. با استفاده از ویژگی تصویر پیچیدگی، داریم: Y (p) = (p 2 + 4) 2 = p p x sin 2(x t) sin 2t dt. پس از محاسبه انتگرال، عبارت مورد نظر را برای اصل به دست می آوریم. پاسخ: y(x) = 6 sin 2x x cos 2x. 8 مثال 6. نسخه اصلی را پیدا کنید که با تصویر مطابقت دارد: Y (p) = p p 3 p 2 6p. تصمیم گیری از آنجایی که p 3 p 2 6p \u003d p (p 3) (p + 2) ، مخرج کسری Y (p) دارای سه ریشه ساده است: p \u003d ، p 2 \u003d 3 و p 3 \u003d 2. ما اصل مربوطه را با استفاده از فرمول (2) می سازیم: y(x) = (p2 + 2) e px (p 3) (p + 2) + (p2 + 2) e px p= p (p + 2) + (p2 + 2)e px p = 3 p(p 3) = p= 2 = e3x e 2x. مثال 7. نسخه اصلی را پیدا کنید که با تصویر مطابقت دارد: Y (p) = e p 2 p (p +) (p 2 + 4). تصمیم گیری بیایید کسر موجود در عبارت را به شکل کسرهای ساده نشان دهیم: p(p +) (p 2 + 4) = A p + B p + + Cp + D p با استفاده از روش ضرایب نامشخص برای بسط، به دست می‌آییم. : B=D=5; C \u003d 2. Y (p) \u003d e p 2 4 p 5 e p 2 p + pe p 2 2 p e p 2 5 p (a)

11 با استفاده از روابط: p χ(x)، p + e x χ(x)، p p cos 2x χ(x)، p sin 2x χ(x) 2 و با در نظر گرفتن قضیه تاخیر، اصل مورد نظر را برای تصویر (الف). پاسخ: y(x) = (4 5 e (x 2) cos (2x) sin (2x) 2) χ (x) حل مسئله کوشی برای یک معادله دیفرانسیل با ضرایب ثابت روش حل کلاس های مختلف معادلات با استفاده از تبدیل لاپلاس را روش عملیاتی می نامند. ویژگی تمایز تبدیل لاپلاس اصلی به شما امکان می دهد حل معادلات دیفرانسیل خطی را با ضرایب ثابت به حل معادلات جبری کاهش دهید. مسئله کوشی را برای یک معادله ناهمگن با شرایط اولیه y (n) + a y (n) a n y + a n y = f(x) (3) y() = y، y () = y،...، y (n) در نظر بگیرید. ) ( ) = yn. (4) اجازه دهید تابع f(x) و جواب مورد نظر شرایط وجود تبدیل لاپلاس را برآورده کنند. با Y (p) تصویر تابع مجهول (اصلی) y(x) و با F (p) تصویر سمت راست f(x) را نشان می دهیم: y(x) Y (p), f(x ) F (p). با قاعده تمایز اصلی، ما y (x) py (p) y، y (x) p 2 Y (p) py y، y (n) (x) p n Y (p) p n y p n 2 y داریم. . y n.

12 2 سپس به دلیل خطی بودن تبدیل لاپلاس، پس از اعمال آن بر روی قسمت های چپ و راست معادله (3)، معادله عملگر M(p)Y (p) N(p) = F (p) به دست می آید. ، (5) که در آن چند جمله ای مشخصه M(p) معادله (3): M(p) = pn + a p n a n p + a n y، N(p) چند جمله ای حاوی داده های اولیه مسئله کوشی (زمانی که داده اولیه صفر باشد ناپدید می شود. ): N(p) = y (p n + a p n a n) + + y (p n 2 + a p n a n 2) y n 2 (p + a) + y n، F (p) تصویر تابع f(x). با حل معادله عملگر (5)، تصویر لاپلاس Y (p) از راه حل مورد نظر y(x) را به شکل Y (p) = F (p) + N(p) بدست می آوریم. M(p) با بازیابی نسخه اصلی برای Y (p)، راه حلی برای معادله (3) پیدا می کنیم که شرایط اولیه (4) را برآورده می کند. مثال 8. یک راه حل برای معادله دیفرانسیل پیدا کنید: y (x) + y(x) = e x که شرط را برآورده می کند: y() =. تصمیم گیری فرض کنید y(x) Y (p). از آنجایی که y (x) py (p) y() = py (p)، e x p +، پس با اعمال تبدیل لاپلاس به معادله داده شده، با استفاده از خاصیت خطی، یک معادله جبری با توجه به Y (p) بدست می آوریم: py (p) + Y (p) = p +. جایی که عبارت Y (p) را پیدا می کنیم:

13 از آن زمان ما Y (p) = p + e x، (p +) 2 + p + داریم. (p +) 2 xe x، Y (p) y(x) = e x x + e x. تأیید: اجازه دهید نشان دهیم که تابع یافت شده در واقع راه حلی برای مسئله کوشی است. عبارت را برای تابع y(x) و مشتق آن در معادله داده شده جایگزین می کنیم: y (x) = e x x + e x e x = e x x e x x + e x x + e x = e x. پس از کاهش عبارت های مشابه در سمت چپ معادله، هویت صحیح را بدست می آوریم: e x e x. بنابراین، تابع ساخته شده یک راه حل برای معادله است. بیایید بررسی کنیم که آیا شرط اولیه y() = : y() = e + e = را برآورده می کند یا خیر. بنابراین، تابع یافت شده راه حلی برای مسئله کوشی است. پاسخ: y(x) = e x x + e x. مثال 9. حل مسئله کوشی y + y =، y() =، y () =. تصمیم گیری فرض کنید y(x) Y (p). از آنجایی که 3 y (x) p 2 Y (p) py() y ()، /p، پس با اعمال تبدیل لاپلاس به معادله، با در نظر گرفتن شرایط اولیه، (p 2 +)Y (p) را به دست می آوریم. = p = Y ( p) = p (p 2 +). بیایید کسر را به کسرهای ساده تجزیه کنیم: Y (p) = p طبق جدول، y(x) = cos x را پیدا می کنیم. p p 2 +.

14 4 همچنین می توانید با اعمال ویژگی ادغام اصلی، نسخه اصلی را از تصویر بازیابی کنید (به مثال 4 مراجعه کنید). پاسخ: y(x) = cosx. مثال. حل مسئله کوشی y +3y = e 3x، y() =، y () =. تصمیم گیری فرض کنید y(x) Y (p). از آنجایی که y py (p) y()، y (x) p 2 Y (p) py() y () و e 3x p + 3، پس با توجه به شرایط اولیه، معادله عملگر را بدست می آوریم (p 2 + 3p) Y (p) + = p + 2 = Y (p) = p + 3 (p + 3) 2 p. اجازه دهید تابع گویا را به کسرهای ساده بسط دهیم: p + 2 (p + 3) 2 p = A p + B p C (p + 3) 2 = A(p2 + 6p + 9) + B(p 2 + 3p) + Cp p (p + 3) 2. یک سیستم معادلات برای یافتن ضرایب A، B و C بسازید: A + B =، 6A + 3B + C =، 9A = 2، با حل آن A = 2/9 را پیدا می کنیم. ، B = 2/9، C = /3. بنابراین، Y (p) = 2 9 p p (p + 3) 2. با استفاده از جدول، پاسخ را دریافت می کنیم. پاسخ: y(x) = e 3x 3 x 3x. مثال. یک راه حل برای معادله دیفرانسیل پیدا کنید: y (x) + 2y (x) + 5y (x) = ارضای شرایط: y() =، y () = 2، y () =. تصمیم گیری فرض کنید y(x) Y (p). از آنجایی که، با توجه به شرایط داده شده، داریم y (x) p Y (p) y() = py (p) () = py (p) +, y (x) p 2 Y (p) p y() y ( ) = = p 2 Y (p) p () 2 = p 2 Y (p) + p 2, y (x) p 3 Y (p) p 2 y() p y () y () = = p 3 Y (p) p 2 () p 2 = p 3 Y (p) + p 2 2p,

15 سپس پس از اعمال تبدیل لاپلاس به معادله داده شده، معادله عملگر زیر را به دست می آوریم: p 3 Y (p) + p 2 2p + 2p 2 Y (p) + 2p 4 + 5pY (p) + 5 = یا بعد از تبدیل ها : Y (p) (p 3 + 2p 2 + 5p) = p 2. با حل این معادله برای Y (p)، Y (p) = p 2 p (p 2 + 2p + 5) بدست می آوریم. عبارت به دست آمده را به کسرهای ساده گسترش می دهیم: p 2 p (p 2 + 2p + 5) = A p + Bp + C p 2 + 2p + 5. با استفاده از روش ضرایب نامشخص، A, B, C را پیدا می کنیم. این کار را انجام دهید، کسرها را به یک مخرج مشترک کاهش می دهیم و ضرایب را با توان های مساوی p برابر می کنیم: p 2 p (p 2 + 2p + 5) = Ap2 + 2Ap + 5A + Bp 2 + Cp p (p p + 5) به دست می آوریم یک سیستم معادلات جبری برای A، B، C: با حل این معادلات: A + B =، 2A + C =، 5A =، A = 5، B = 4 5، C = 2 5. سپس Y(p) = 5p + 5 4p + 2p 2 + 2p + 5. برای پیدا کردن کسر دوم، مربع کامل را در مخرج آن انتخاب کنید: p 2 + 2p + 5 = (p +) 2 + 4، سپس عبارت p+ را انتخاب کنید. در صورت حساب: 4p+2 = 4(p+)+6 و کسر را به مجموع دو کسر بسط دهید: 5 4p + 2 p 2 + 2p + 5 = 4 5 p + (p +) (p +) پاسخ: y(x) = e x cos 2x e x sin 2x.

16 6 راه حل کلی معادله (3) را نیز می توان با روش عملیاتی ساخت. برای انجام این کار، مقادیر خاص y، y،...، y (n) شرایط اولیه باید با ثابت های دلخواه C، C 2،...، C n جایگزین شوند. کتابشناسی - فهرست کتب. Alexandrova N. V. تاریخچه اصطلاحات، مفاهیم، نامگذاری های ریاضی: کتاب دیکشنری-مرجع. م.: انتشارات LKI، ص. 2. Vasilyeva A. B.، Medvedev G. N.، Tikhonov N. A.، Urazgildina T. A. معادلات دیفرانسیل و انتگرال، حساب تغییرات در مثال ها و مسائل. M.: FIZ-MATLIT، ص. 3. Sidorov Yu. V. سخنرانی در مورد تئوری توابع یک متغیر مختلط / Yu. V. Sidorov، M. V. Fedoryuk، M. I. Shabunin. M.: Nauka، 989.

حساب عملیاتی حساب عملیاتی یک حساب نمادین است که بر اساس ساخت تحلیل ریاضی به عنوان سیستمی از عملیات رسمی بر روی

درس 18 اصل ها و تصاویر آنها حساب عملیاتی یکی از روش های آنالیز ریاضی است که در حل معادلات و سیستم های دیفرانسیل به کار می بریم. ماهیت این روش

معادلات فیزیک ریاضی مجموعه مثال ها و تمرین ها پتروزاوودسک 1 دانشگاه دولتی پتروزاوودسک دانشکده ریاضی معادلات فیزیک ریاضی مجموعه مثال ها و تمرین ها

عنوان مقدمه. مفاهیم پایه .... 4 1. معادلات انتگرال ولترا ... 5 گزینه تکلیف .... 8 2. حل کننده معادله انتگرال ولترا. 10 گزینه تکلیف .... 11

1 مبحث 4. روش عملگر برای حل معادلات و سیستم های دیفرانسیل خطی 4.1 تبدیل لاپلاس یک تابع اصلی هر تابع f(t) از یک متغیر واقعی t است که موارد زیر را برآورده کند.

عناصر محاسبات عملیاتی انتشارات خانه TGTU وزارت آموزش و پرورش و علوم فدراسیون روسیه GOU VPO "دانشگاه فنی دولتی تامبوف" عناصر محاسبه عملیاتی

تجزیه و تحلیل ریاضی بخش: حساب عملیاتی موضوع: تبدیل لاپلاس و خواص آن مدرس پاخوموا E.G. 2011 11. اصل و تصویر. قضیه وارونگی تعریف 1. اجازه دهید: R C. تابع

اعداد مختلط، توابع و عملیات روی آنها y ماژول R قسمت واقعی عدد واقعی، yim قسمت خیالی عدد واقعی iy نماد جبری عدد مختلط مقدار اصلی آرگومان

راه حل گزینه های استاندارد برای کار کنترل در موضوع انتگرال های یک تابع از یک متغیر دستورالعمل UDC 517.91 دستورالعمل حاوی راه حل های دقیق برای گزینه های استاندارد برای کار کنترل است.

فصل 1 حساب عملیاتی. 1. تعریف تبدیل لاپلاس. تبدیل لاپلاس تابع f(t) را با متغیر واقعی t با تابع F () از متغیر مختلط = x + iy مرتبط می کند.

وزارت حمل و نقل فدراسیون روسیه بودجه دولتی فدرال موسسه آموزش عالی "دانشگاه حمل و نقل روسیه (MIIT)"

مؤسسه آموزش عالی بودجه ایالتی فدرال "دانشگاه دولتی ارتباطات امپراتور نیکلاس دوم" گروه "ریاضیات عالی و محاسباتی"

82 4. بخش 4. سری عملکردی و توانی 4.2. درس 3 4.2. درس 3 4.2.. بسط تیلور یک تابع تعریف 4.2.. اجازه دهید تابع y = f(x) در برخی از همسایگی ها بی نهایت متمایز باشد.

سخنرانی ادغام کسرهای گویا کسرهای گویا ادغام کسرهای گویا ساده تجزیه یک کسر گویا به کسرهای ساده ادغام کسرهای گویا

موضوع 5 معادله خطی ولترا از نوع ام تعاریف و قضایای اساسی معادله y = λ K(,) y() d+ f()، [، یا به شکل عملگر y = λ By+ f، معادله ولترای هفتم نامیده می شود. مهربان اجازه دهید

سخنرانی 6 حساب عملیاتی تبدیل لاپلاس تصاویری از توابع ساده ویژگی های اساسی تبدیل لاپلاس تصویر مشتق از تبدیل لاپلاس حساب عملیاتی اصلی

درس 19 حل معادلات دیفرانسیل و سیستم ها با استفاده از روش عملیاتی 19.1 حل معادلات دیفرانسیل خطی با ضرایب ثابت.

2.2. روش اپراتور برای محاسبه فرآیندهای گذرا. اطلاعات نظری محاسبه فرآیندهای گذرا در مدارهای پیچیده با روش کلاسیک اغلب برای یافتن ثابت های یکپارچه سازی دشوار است.

DOROKHOV VM راهنمای حل مسائل در حساب عملیاتی مسکو، 4 پیشگفتار این کتاب درسی مبانی نظری حساب عملیاتی روش‌های حل مسائل را تشریح می‌کند.

وزارت آموزش و علوم فدراسیون روسیه موسسه آموزشی بودجه دولتی فدرال آموزش عالی حرفه ای "دانشگاه فناوری شیمیایی روسیه به نام DI Mendeleev" موسسه نووموسکوفسک (شعبه) تست 8 در ریاضیات (عملیاتی)

UDC 53.7 در مورد یک روش برای یافتن یک راه حل خاص معادلات دیفرانسیل خطی با ضرایب ثابت Zhanybekova A.A.، [ایمیل محافظت شده]دانشگاه فنی قزاقستان-بریتانیا،

حساب انتگرال انتگرال نامشخص تابع ضد مشتق و انتگرال نامعین لم ضد مشتق تابع F(برای تابع f(در بازه X، اگر F (=f(X تابع،

معادلات مرتبه اول با توجه به مشتق حل نشده اند ما معادلات مرتبه اولی را که نسبت به مشتق حل نشده اند در نظر می گیریم: F (x, y, y) = 0, (1)

معادلات دیفرانسیل دوم معادلات دیفرانسیل مرتبه اول تعریف معادلات دیفرانسیل به روابطی که در آنها متغیرهای مجهول و توابع آنها تحت علامت مشتق یا دیفرانسیل قرار دارند گفته می شود.

عناصر تئوری توابع یک حساب عملیاتی متغیر مختلط

وزارت آموزش و پرورش و علوم فدراسیون روسیه "MATI" دانشگاه دولتی فناوری روسیه. K.E. Tsiolkovsky گروه ریاضیات عالی اعداد مختلط و حساب عملیاتی

1 مبحث 3. معادلات دیفرانسیل خطی با ضرایب ثابت 3.1 معادله همگن خطی معادله دیفرانسیل به شکل y (n) + a n 1 y (n 1) +... + a 1 y + a 0 y = 0، (3.1) که در آن آ

انتگرال نامعین. ضد مشتق و انتگرال نامعین وظیفه اصلی حساب دیفرانسیل یافتن مشتق (یا دیفرانسیل) یک تابع معین است. حساب انتگرال

وزارت آموزش و پرورش و علوم فدراسیون روسیه شعبه آچینسک مؤسسه آموزشی مستقل دولتی فدرال آموزش عالی حرفه ای "دانشگاه فدرال سیبری" ریاضیات

محدودیت عملکرد ارتباط مطالعه موضوع نظریه حدود نقش اساسی در تجزیه و تحلیل ریاضی ایفا می کند، به شما امکان می دهد ماهیت رفتار یک تابع را برای یک تغییر معین در استدلال تعیین کنید. از طريق

انتگرال ضد مشتق و نامعین مفاهیم و فرمول های اساسی 1. تعریف انتگرال ضد مشتق و نامعین. تعریف. تابع F(x) برای تابع f(x) در بازه پاد مشتق نامیده می شود

فصل 1 معادلات دیفرانسیل 1.1 مفهوم معادله دیفرانسیل 1.1.1 مسائل منجر به معادلات دیفرانسیل. در فیزیک کلاسیک، به هر کمیت فیزیکی اختصاص داده می شود

معادلات دیفرانسیل مرتبه اول معمولی مفاهیم اساسی معادلات دیفرانسیل با متغیرهای قابل تفکیک بسیاری از مشکلات در علم و فناوری به معادلات دیفرانسیل کاهش می یابد.

توسعه روش شناسی حل مسائل در TFKP اعداد مختلط عملیات روی اعداد مختلط صفحه مختلط یک عدد مختلط را می توان به صورت نمایی جبری و مثلثاتی نشان داد.

سخنرانی 3 سری تیلور و مکلارین کاربرد سری توانی بسط توابع به سری های توانی تیلور و مکلارین برای کاربردها، مهم است که بتوان یک تابع معین را به یک سری توانی، آن توابع، گسترش داد.

نوع معمولی "اعداد مختلط چند جمله ای ها و کسرهای گویا" وظیفه با توجه به دو عدد مختلط و cos sn نتیجه را به شکل جبری بنویسید و نتیجه را به صورت مثلثاتی بنویسید.

آژانس فدرال آموزش موسسه آموزشی دولتی فدرال آموزش عالی حرفه ای دانشگاه فدرال جنوب R. M. Gavrilova, G. S. Kostetskaya Methodical

S P PREOBRAZHENSKY، SR TIKHOMIROV ادغام معادلات دیفرانسیل با استفاده از سری توان 987 مطالب

تجزیه و تحلیل ریاضی بخش: انتگرال نامعین موضوع: ادغام کسرهای گویا مدرس پاخوموا E.G. 0 5. ادغام کسرهای گویا تعریف. کسر گویا نامیده می شود

وزارت حمل و نقل فدراسیون روسیه موسسه آموزش عالی بودجه دولتی فدرال "دانشگاه حمل و نقل روسیه (MIIT)" موسسه اقتصاد و دارایی

حساب عملیاتی تبدیل لاپلاس و فرمول وارونگی اجازه دهید بازه دیریکله را وارد کنیم، یعنی: انتگرال فوریه (l l) a) در این بازه محدود است. تابع شرایط را برآورده می کند ب) به صورت تکه ای پیوسته است

وزارت آموزش و پرورش فدراسیون روسیه دانشگاه دولتی نفت و گاز گوبکین روسیه VI دستورالعمل های ایوانف برای مطالعه موضوع "معادلات دیفرانسیل" (برای دانش آموزان)

57 ادغام ساده ترین کسر گویا از نوع چهارم (M N) d () p q p را در نظر بگیرید بیایید با تنظیم d تغییری در متغیر ایجاد کنیم. جایی که یک p q. سپس انتگرال M N d p p p q q a، M p N Mp q d M (p q) p

معادله دیفرانسیل مرتبه n خطی نامیده می شود اگر نسبت به تابع y و مشتقات آن y..., y (n) درجه اول باشد، یعنی به شکل a y (n) + a باشد. 1 y (n 1) +. .. + a ny = f(x)، که در آن

تجزیه و تحلیل ریاضی بخش: انتگرال نامعین موضوع: ادغام کسرهای گویا مدرس Rozhkova S.V. 0 5. ادغام کسرهای گویا تعریف. کسر گویا نامیده می شود

وزارت مخابرات و ارتباطات جمعی موسسه آموزشی دولتی آموزش عالی حرفه ای فدراسیون روسیه دانشگاه دولتی ارتباطات راه دور ولگا

معادلات دیفرانسیل مرتبه اول حل شده با توجه به مشتق قضیه وجود و یکتایی برای یک راه حل در حالت کلی، یک معادله دیفرانسیل مرتبه اول به شکل F است ()

T A Matveeva V B vetlichnaya D K Agisheva A Zotova

حساب انتگرال INTEGRAL نامعین یک تابع ضد مشتق و یک انتگرال نامعین از یک پاد مشتق تابع F() برای تابع f() در بازه X، اگر F/() = f() X، پاد مشتق نامیده می شود.

5. 4 روش های اساسی یکپارچه سازی ادغام مستقیم. محاسبه انتگرال ها بر اساس آوردن انتگرال به شکل جدولی و استفاده از ویژگی های نامشخص

سخنرانی 3 شرح ریاضی سیستم های کنترل در تئوری کنترل در تحلیل و سنتز سیستم های کنترل به مدل ریاضی آنها می پردازند.مدل ریاضی ACS یک معادله است.

ادغام یک سیستم معادلات دیفرانسیل با حذف متغیرها یکی از روشهای اصلی ادغام یک سیستم معادلات دیفرانسیل به شرح زیر است: از معادلات نرمال

معادلات دیفرانسیل جزئی مرتبه اول برخی از مسائل مکانیک کلاسیک، مکانیک پیوسته، آکوستیک، اپتیک، هیدرودینامیک، انتقال تابش به معادلات دیفرانسیل جزئی تقلیل می‌یابند.

ساده ترین انتگرال های نامعین نمونه هایی از حل مسئله انتگرال های زیر با تبدیل یکسان انتگرال به انتگرال های جدولی کاهش می یابند. 1. dx = dx = 2x 2/3 /3 + 2x 1/2 + C. >2.

فعالیت عملی ادغام کسرهای گویا کسر گویا کسری است به شکل PQ، که در آن P و Q چند جمله ای هستند، اگر درجه چند جمله ای P کمتر از درجه باشد، کسر گویا مناسب نامیده می شود.

[F] Filippov AV مجموعه مسائل مربوط به معادلات دیفرانسیل مسکو-ایژفسک: مرکز تحقیقات "دینامیک منظم و آشوب" 00 URL: http://librarbsaz/kitablar/846pf [M] Matveev NM مجموعه مسائل و تمرینات در مورد

E شغل ردیف های تیلور مجموع سری قدرت مت. تجزیه و تحلیل، برنامه ریاضیات، ترم 3، بسط یک تابع را به یک سری توانی در توان ها پیدا کنید، شعاع همگرایی سری توانی را محاسبه کنید: A f()

وظیفه 1.1. راه حل های y = y(x) معادله دیفرانسیل را بیابید که در ناحیه نشان داده شده به طور یکسان صفر هستند و شرایط مرزی داده شده را برآورده می کنند (مسئله Sturm-Liouville) راه حل: در نظر بگیرید

9. ضد مشتق و انتگرال نامعین 9.. اجازه دهید تابع f() در بازه I R داده شود. تابع F () تابع ضد مشتق f() در بازه I نامیده می شود، اگر F () = f() برای هر I و ضد مشتق

~ ~ انتگرال نامعین و معین مفهوم انتگرال ضد مشتق و نامعین. تعریف: اگر این توابع به صورت زیر مرتبط باشند، تابع F با توجه به تابع f یک پاد مشتق نامیده می شود.

سخنرانی 5 7 قضیه هیلبرت اشمیت ما یک عملگر انتگرال A را در نظر خواهیم گرفت، هسته آن K(شرایط زیر را برآورده می کند: K(s) متقارن است، پیوسته در مجموعه متغیرهای [،]

وزارت آموزش و پرورش جمهوری بلاروس دانشگاه دولتی بلاروس دانشکده فیزیک گروه ریاضیات عالی و فیزیک ریاضی O A Kononova، N I Ilyinkova، N K Filippova Linear

مبحث 9 سری توانی یک سری توانی یک سری تابعی از فرم است در حالی که اعداد ... ضرایب سری هستند و نقطه انبساط سری.، ...، ... R ... نامیده می شود. the center Power series اصطلاح کلی سری power

سیستم های معادلات دیفرانسیل خطی با ضرایب ثابت کاهش به یک معادله منفرد مرتبه هفتم از نقطه نظر عملی، سیستم های خطی با ضرایب ثابت بسیار مهم هستند.

انتگرال ها و معادلات دیفرانسیل ماژول 1. انتگرال نامعین سخنرانی 1.2 کسری گویا انتزاعی. تجزیه یک کسر گویا مناسب به مجموع کسرهای ساده. ادغام تک یاخته ها

فرمول انبساط Heaviside

اجازه دهید تصویر تابع یک تابع گویا کسری باشد.

قضیه.اجازه دهید، کجا و باشد توابع متمایز. اجازه دهید هر دو قطب تابع را معرفی کنیم، i.e. ریشه (صفر) مخرج آن. سپس، اگر فرمول Heaviside را بدست آوریم:

ما برای حالتی که چندجمله ای درجه هستند، اثبات خواهیم کرد تیو پبر این اساس، در حالی که تی پ. سپس یک کسر منطقی مناسب است. بیایید آن را به صورت مجموع کسرهای ساده نشان دهیم:

از اینجا ما ضرایب هویت (17.2) را پیدا می کنیم و آن را در فرم بازنویسی می کنیم

هر دو طرف آخرین تساوی را در ضرب می کنیم و از حد در عبور می کنیم. با در نظر گرفتن آن و، دریافت می کنیم

از آنجا به شرح زیر است (17.1). قضیه ثابت شده است.

تبصره 1.اگر ضرایب چند جمله ای ها و واقعی باشند، ریشه های مختلط چند جمله ای به صورت زوجی مزدوج هستند. در نتیجه، در فرمول (17.1)، کمیت‌های مزدوج مختلط عبارت‌های مربوط به ریشه‌های مزدوج مختلط چند جمله‌ای خواهند بود و فرمول Heaviside شکل خواهد گرفت.

که در آن مجموع اول به تمام ریشه های واقعی چند جمله ای گسترش می یابد، دومی - به تمام ریشه های پیچیده آن با بخش های خیالی مثبت.

تبصره 2.هر عضو فرمول (17.1) یک نوسان است که به شکل مختلط نوشته شده است، که در آن. بنابراین، ریشه های واقعی () مربوط به نوسانات غیر پریودیک، ریشه های پیچیده با قسمت های واقعی منفی - نوسانات میرا، ریشه های کاملاً خیالی - نوسانات هارمونیک بدون میرایی است.

اگر مخرج هیچ ریشه ای با قسمت های واقعی مثبت نداشته باشد، برای مقادیر به اندازه کافی بزرگ یک حالت ثابت به دست می آوریم:

ریشه های کاملاً خیالی یک چند جمله ای با اجزای خیالی مثبت.

نوسانات مربوط به ریشه هایی با قسمت های واقعی منفی به صورت تصاعدی فرو می ریزند و بنابراین وارد حالت پایدار نمی شوند.

مثال 1تصویر اصلی را پیدا کنید

تصمیم گیری ما داریم. ریشه های چند جمله ای را می نویسیم: .

با فرمول (17.1)

در اینجا، از آنجایی که اعداد ریشه معادله هستند. از این رو،

مثال 2تصویر اصلی را پیدا کنید

جایی که آ 0; .

تصمیم گیری در اینجا تابع علاوه بر ریشه آشکار، بی نهایت ریشه دارد که صفرهای تابع هستند. با حل معادله به کجا می رسیم

بنابراین، ریشه های مخرج شکل و، کجا را دارند

با فرمول (17.3) ما اصل را پیدا می کنیم

روش عملگر برای حل معادلات دیفرانسیل

معادلات دیفرانسیل.مسئله کوشی را برای معادله دیفرانسیل خطی در نظر بگیرید

(اینجا) با شرایط اولیه

با عبور از تصاویر در (18.1)، به دلیل خطی بودن تبدیل لاپلاس، داریم

تصاویر مشتقات را با استفاده از قضیه 3 از § 16 و شرایط اولیه (18.2) به شکل می نویسیم.

با جایگزینی (18.4) به (18.3)، پس از تبدیل های ساده، معادله عملگر را به دست می آوریم.

کجا (چند جمله ای مشخص)؛ .

از معادله (18.5) جواب عملگر را پیدا می کنیم

راه حل مسئله کوشی (18.1)، (18.2) راه حل اصلی عملگر (18.6) است:

برای مسئله کوشی، در نماد پذیرفته شده، می توانیم بنویسیم

معادله عملگر شکل دارد

اجازه دهید حل عملگر را به کسرهای ساده تجزیه کنیم:

با استفاده از فرمول های به دست آمده در § 15، نسخه های اصلی را به دست می آوریم:

بنابراین، حل مسئله کوشی شکل خواهد داشت

مثال 1حل مسئله کوشی برای یک معادله دیفرانسیل با شرایط اولیه، که در آن.

تصمیم گیری

راه حل او به نظر می رسد

با استفاده از قضیه 2 از § 16، به طور متوالی در می یابیم:

مثال 2حل مشکل کوشی برای یک معادله دیفرانسیل با شرایط اولیه صفر، که در آن یک تابع ضربه گام است.

تصمیم گیری اجازه دهید معادله عملگر را بنویسیم

و راه حل او

قضیه 2 از § 16 دلالت دارد

مطابق با قضیه تاخیر (§ 15)

سرانجام،

مثال 3به یک نقطه جرم تیبا سفتی به فنر متصل می شود باو در یک صفحه افقی صاف قرار دارد، یک نیروی متناوب در حال تغییر عمل می کند. در لحظه‌ای از زمان، نقطه در معرض یک ضربه حمل‌کننده ضربه قرار گرفت. با غفلت از مقاومت، قانون حرکت یک نقطه را در صورتی پیدا کنید که در لحظه اولیه زمان در مبدأ در حالت سکون بوده است.

تصمیم گیری معادله حرکت را به شکل می نویسیم

نیروی الاستیک کجاست تابع دیراک است. بیایید معادله عملگر را حل کنیم

اگر (مورد رزونانس)، پس

با توجه به قضیه تاخیر

سرانجام،

انتگرال (فرمول) دوهامل. مسئله کوشی را برای معادله (18.1) در شرایط اولیه در نظر بگیرید. راه حل عملگر در این مورد دارای فرم است

اجازه دهید تابع وزن اصلی باشد. سپس با قضیه 1 از § 16 به دست می آوریم

رابطه (18.7) انتگرال دوهامل (فرمول) نامیده می شود.

اظهار نظر.در شرایط اولیه غیر صفر، فرمول Duhamel به طور مستقیم قابل اجرا نیست. در این صورت لازم است ابتدا مسئله اصلی به مسئله ای با شرایط اولیه همگن (صفر) تبدیل شود. برای انجام این کار، ما یک تابع جدید، تنظیمات را معرفی می کنیم

مقادیر اولیه راه حل مورد نظر کجا هستند.

همانطور که مشاهده آن آسان است، و بنابراین، .

بنابراین، تابع حل معادله (18.1) با سمت راست با جایگزینی (18.8) به (18.1)، با صفر داده اولیه است.

با استفاده از (18.7)، و.

مثال 4از انتگرال دوهامل برای یافتن راه حلی برای مشکل کوشی استفاده کنید

با شرایط اولیه

تصمیم گیری داده های اولیه غیر صفر است. ما مطابق با (18.8) فرض می کنیم. سپس و برای تعریف، معادله ای با شرایط اولیه همگن به دست می آوریم.

برای مسئله مورد بررسی، چند جمله ای مشخصه، تابع وزن. طبق فرمول دوهامل

سرانجام،

سیستم های معادلات دیفرانسیل خطی با ضرایب ثابت.مسئله کوشی برای سیستم معادلات دیفرانسیل خطی در نمادگذاری ماتریسی شکل دارد

بردار توابع مورد نظر کجاست. - بردار قطعات سمت راست؛ - ماتریس ضرایب؛ - بردار داده های اولیه

حساب عملیاتی اکنون به یکی از مهم ترین فصل های تحلیل عملی ریاضی تبدیل شده است. روش عملیاتی به طور مستقیم در حل معادلات دیفرانسیل معمولی و سیستم های چنین معادلات استفاده می شود. همچنین می توان از آن در حل معادلات دیفرانسیل جزئی استفاده کرد.

بنیانگذاران محاسبه نمادین (عملیاتی) دانشمندان روسی M. E. Vashchenko-Zakharchenko و A. V. Letnikov هستند.

حساب عملیاتی پس از آن که مهندس برق انگلیسی Heaviside، با استفاده از حساب نمادین، تعدادی نتایج مهم را به دست آورد، توجه را به خود جلب کرد. اما بی‌اعتمادی به حساب نمادین تا زمانی که جورجی، برومویچ، کارسون، A. M. Efros، A. I. Lurie، V. A. Ditkin و دیگران ارتباط بین حساب عملیاتی و دگرگونی‌های انتگرالی را برقرار کردند، ادامه یافت.

ایده حل معادله دیفرانسیل به روش عملیاتی این است که از معادله دیفرانسیل با توجه به تابع اصلی مورد نظر f ( تی ) برای یک تابع دیگر به معادله بروید اف ( پ ), یک تصویر نامیده می شود f ( تی ) . معادله (عملیاتی) حاصل معمولاً از قبل جبری است (به این معنی که ساده تر از معادله اصلی است). حل آن با توجه به تصویر اف ( پ ) و سپس به سمت اصل مربوطه، جواب مورد نظر این معادله دیفرانسیل را پیدا می کنند.

روش عملیاتی برای حل معادلات دیفرانسیل را می توان با محاسبه عبارات مختلف با استفاده از لگاریتم مقایسه کرد، زمانی که، برای مثال، هنگام ضرب، محاسبات نه بر روی خود اعداد، بلکه بر روی لگاریتم آنها انجام می شود، که منجر به جایگزینی ضرب با یک عدد می شود. عملیات ساده تر - اضافه کردن.

مانند لگاریتم، هنگام استفاده از روش عملیاتی، شما نیاز دارید:

1) جدولی از اصل و تصاویر مربوط به آنها؛

2) آگاهی از قوانین انجام عملیات روی تصویر، مطابق با اقدامات انجام شده بر روی تصویر اصلی.

§یک. اصل و تصاویر توابع طبق لاپلاس

تعریف 1ما تابع واقعی آرگومان واقعی خواهیم بود f (تی) صدا زدن اصلی، اگر سه شرط را برآورده کند:

1) f (تی) 0 , در تی 0

2) f ( تی ) سریعتر از برخی تابع های نمایی افزایش نمی یابد

، در تی0، جایی که م 0, s00 - چند ثابت واقعی، س 0 تماس گرفت نشانگر رشد تابع f(t) .

3) روی هر قطعه محدود  آ , بنیمه محور مثبت از جانبعملکرد f (تی) شرایط دیریکله را برآورده می کند، به عنوان مثال،

الف) محدود،

ب) یا پیوسته است یا فقط دارای تعداد محدودی از نقاط ناپیوستگی نوع اول است.

ج) دارای تعداد محدودی است

توابعی که این سه الزام را برآورده می کنند در حساب عملیاتی نامیده می شوند توسط لاپلاس به تصویر کشیده شده است یا اصل .

ساده ترین اصلی تابع هویت Heaviside است

اگر تابع

شرایط 2 را برآورده می کند و شرط 1 را برآورده نمی کند، سپس محصول شرایط 1 را نیز برآورده می کند، یعنی. اصلی خواهد بود برای ساده کردن نماد، به عنوان یک قاعده از ضرب کننده استفاده می کنیم اچ (تی) حذف شود، با این فرض که تمام توابع در نظر گرفته شده برابر با صفر برای مقادیر منفی هستند تی .

انتگرال لاپلاس برای اصلی f (تی) انتگرال نامناسب شکل نامیده می شود