Encuentra la distancia más corta entre dos líneas que se cruzan. Distancia entre líneas que se cruzan - definición y ejemplos de búsqueda

Metas y objetivos:

• educativo: la formación y el desarrollo de representaciones espaciales entre los estudiantes; desarrollar habilidades para resolver problemas para encontrar la distancia entre líneas que se cruzan
• educativo: educar la voluntad y la perseverancia para lograr resultados finales al encontrar la distancia entre las líneas que se cruzan; cultivar el amor y el interés por el estudio de las matemáticas.
• desarrollo: el desarrollo del pensamiento lógico de los estudiantes, las representaciones espaciales, el desarrollo de habilidades de autocontrol.

El proyecto corresponde a los siguientes puntos de la temática plan de estudios Asignatura escolar.

1. Cruce de líneas rectas.
2. Signo de paralelismo de una recta y un plano
3. Proyección ortogonal en el espacio.
4. El volumen de los poliedros.

Introducción.

Líneas cruzadas: ¡es increíble!

Sin ellos, la vida sería cien veces menos interesante. Uno quisiera decir que si vale la pena estudiar la estereometría, es porque tiene líneas que se cruzan. Cuántas propiedades globales e interesantes tienen: en la arquitectura, en la construcción, en la medicina, en la naturaleza.

Deseo que nuestra sorpresa por la singularidad de las líneas que se cruzan les sea transmitida. Pero, ¿cómo hacer eso?

¿Quizás la respuesta a esta pregunta será nuestro proyecto?

Se sabe que la longitud de la perpendicular común de las líneas oblicuas es igual a la distancia entre estas líneas.

Teorema: La distancia entre dos rectas que se cortan es igual a la distancia entre planos paralelos que pasan por estas rectas.

El siguiente teorema da una forma de encontrar la distancia y el ángulo entre las líneas oblicuas.

La distancia entre las líneas oblicuas es igual a la distancia del punto, que es la proyección de una de estas líneas sobre un plano perpendicular a él, a la proyección de la otra línea sobre el mismo plano.

Cuestión fundamental:

¿Es posible encontrar la distancia entre rectas que se cortan sin construir su perpendicular común?

Considere un problema con un cubo.

¿Por qué con un cubo? Sí, porque toda la geometría está oculta en el cubo, incluida la geometría de las líneas oblicuas.

Tarea.

La arista del cubo es un. Encuentre la distancia entre las líneas en las que se encuentran las diagonales que se cruzan de dos caras adyacentes de un cubo.

Aplicable varios métodos investigación para este tema.

• un priorato;
• método de proyección;
• método de volumen;
• método de coordenadas.

Investigar.

La clase se divide en grupos según el método de estudio del problema. Cada grupo se enfrenta a la tarea de mostrar y probar la aplicación de este método para encontrar la distancia entre líneas oblicuas. La etapa final del estudio del problema es la protección de proyectos en forma de presentaciones, publicaciones o sitios web. Los niños y el maestro tienen la oportunidad de evaluar el proyecto de cada grupo de acuerdo con los criterios desarrollados para publicaciones y presentaciones.

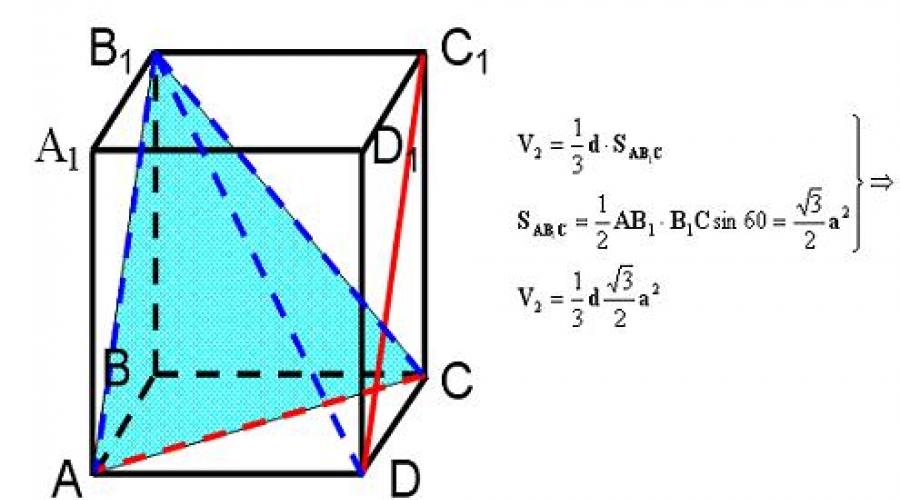
Método de volumen.

• construya una pirámide en la que la altura bajada desde la parte superior de esta pirámide hasta el plano de la base sea la distancia requerida entre dos líneas que se cruzan;
• probar que esta altura es la distancia requerida;
• encuentra el volumen de esta pirámide por dos;
• maneras y expresar esta altura;

Este método es muy interesante por su originalidad, belleza e individualidad. El método de los volúmenes contribuye al desarrollo de la imaginación espacial y la capacidad de crear mentalmente ideas sobre la forma de las figuras.

Como resultado de construcciones adicionales, obtuvimos la pirámide DAB 1 C.

En la pirámide DAB 1 C, la altura caída desde el vértice D hasta el plano de la base AB 1 C será la distancia requerida entre las líneas de cruce AC y DC 1 .

Considere la pirámide Conclusión: Considere la misma pirámide, pero con la parte superior en el punto D:

Considerando que V1 = V2 , obtenemos d=

distancia deseada.

método de proyección.

1. Seleccione un plano perpendicular a una de las líneas de intersección.
2. Proyectamos cada línea en este plano.
3. La distancia entre las proyecciones será la distancia entre las líneas oblicuas.

La distancia entre líneas oblicuas se puede definir como la distancia entre las proyecciones ortogonales de estas líneas sobre el plano de proyección.

Usando la definición de líneas oblicuas.

Formaciones adicionales: A1B, BD, AK.

A 1 O BD, OS BD

BD líneas de intersección A 1 O y OS

Con la ayuda de este calculadora online usted puede encontrar la distancia entre las líneas en el espacio. dado solución detallada con explicaciones. Para calcular la distancia entre líneas en el espacio, especifique el tipo de ecuación de líneas ("canónica" o "paramétrica"), ingrese los coeficientes de las ecuaciones de líneas en las celdas y haga clic en el botón "Resolver".

×

Una advertencia

¿Borrar todas las celdas?

Cerrar Limpiar

Instrucción de entrada de datos. Los números se ingresan como números enteros (ejemplos: 487, 5, -7623, etc.), números decimales (por ejemplo, 67, 102,54, etc.) o fracciones. La fracción debe escribirse en la forma a/b, donde a y b (b>0) son números enteros o numeros decimales. Ejemplos 45/5, 6.6/76.4, -7/6.7, etc.

Distancia entre líneas en el espacio - teoría, ejemplos y soluciones

Sea un sistema cartesiano de coordenadas rectangulares Oxyz L 1 y L 2:

.

(1)

,

(2)

donde METRO 1 (X 1 , y 1 , z 1) y METRO 2 (X 2 , y 2 , z 2) − puntos que se encuentran en líneas L 1 y L 2, y q 1 ={metro 1 , pag 1 , yo 1) y q 2 ={metro 2 , pag 2 , yo 2 ) − vectores directores de rectas L 1 y L 2, respectivamente.

Las líneas (1) y (2) en el espacio pueden coincidir, ser paralelas, intersecarse o estar sesgadas. Si las líneas en el espacio se cruzan o coinciden, entonces la distancia entre ellas es igual a cero. Consideraremos dos casos. La primera es que las rectas son paralelas y la segunda es que las rectas se cortan. El resto son hechos comunes. Si, al calcular la distancia entre líneas paralelas, obtenemos la distancia igual a cero, esto significa que estas líneas coinciden. Si la distancia entre las líneas que se intersecan es igual a cero, entonces estas líneas se intersecan.

1. Distancia entre líneas paralelas en el espacio

Considere dos métodos para calcular la distancia entre líneas.

Método 1. Desde un punto METRO 1 recto L 1 dibujar un avión α , perpendicular a la recta L 2. Encontrar un punto METRO 3 (X 3 , y 3 , y 3) intersecciones de planos α y directo L 3 . En esencia, encontramos la proyección de un punto METRO 1 recto L 2. Vea cómo encontrar la proyección de un punto en una línea. A continuación, calculamos la distancia entre los puntos. METRO 1 (X 1 , y 1 , z 1) y METRO 3 (X 3 , y 3 , z 3):

Ejemplo 1. Encuentra la distancia entre líneas L 1 y L 2:

Derecho L 2 pasa por el punto METRO 2 (X 2 , y 2 , z 2)=METRO

Sustituyendo valores metro 2 , pag 2 , yo 2 , X 1 , y 1 , z 1 en (5) obtenemos:

Encuentre el punto de intersección de la recta L 2 y avión α , para ello construimos una ecuación paramétrica de la recta L 2 .

Para encontrar el punto de intersección de una recta L 2 y avión α , sustituye los valores de las variables X, y, z de (7) a (6):

Sustituyendo el valor resultante t en (7), obtenemos el punto de intersección de la recta L 2 y avión α :

Queda por encontrar la distancia entre los puntos. METRO 1 y METRO 3:

L 1 y L 2 es igual d=7.2506.

Método 2. Encuentra la distancia entre las líneas L 1 y L 2 (ecuaciones (1) y (2)). Primero comprobamos el paralelismo de las rectas L 1 y L 2. Si los vectores directores de las rectas L 1 y L 2 son colineales, es decir si existe un número λ tal que la igualdad q 1 =λ q 2, luego líneas rectas L 1 y L 2 son paralelos.

Este método para calcular la distancia entre vectores paralelos se basa en el concepto del producto vectorial de vectores. Se sabe que la norma del producto vectorial de vectores y q 1 da el área del paralelogramo formado por estos vectores (Fig. 2). Conociendo el área de un paralelogramo, puedes encontrar el vértice del paralelogramo d dividiendo el area por la base q 1 paralelogramo.

q 1:

.

Distancia entre rectas L 1 y L 2 es igual a:

,

,

Ejemplo 2. Resuelve el ejemplo 1 usando el método 2. Encuentra la distancia entre las líneas

Derecho L 2 pasa por el punto METRO 2 (X 2 , y 2 , z 2)=METRO 2 (8, 4, 1) y tiene un vector de dirección

q 2 ={metro 2 , pag 2 , yo 2 }={2, −4, 8}

Vectores q 1 y q 2 son colineales. De ahí el directo L 1 y L 2 son paralelos. Para calcular la distancia entre rectas paralelas, usamos el producto vectorial de vectores.

Construyamos un vector =( X 2 −X 1 , y 2 −y 1 , z 2 −z 1 }={7, 2, 0}.

Calculemos el producto vectorial de vectores y q uno . Para ello, componemos una matriz de 3 × 3, cuya primera fila son los vectores base yo, j, k, y las filas restantes se rellenan con elementos de vectores y q 1:

Así, el resultado del producto vectorial de vectores y q 1 será un vector:

Respuesta: distancia entre lineas L 1 y L 2 es igual d=7.25061.

2. Distancia entre líneas que se cruzan en el espacio

Sea un sistema cartesiano de coordenadas rectangulares Oxyz y deje que las líneas se den en este sistema de coordenadas L 1 y L 2 (ecuaciones (1) y (2)).

dejar recto L 1 y L 2 no son paralelas (discutimos líneas paralelas en el párrafo anterior). Para hallar la distancia entre rectas L 1 y L 2 necesidad de construir planos paralelos α 1 y α 2 para que recto L 1 acostado α 1 una recta L 2 - en el avión α 2. Entonces la distancia entre las líneas L 1 y L 2 es igual a la distancia entre los planos L 1 y L 2 (figura 3).

donde norte 1 ={UN 1 , B 1 , C 1 ) − vector normal del plano α uno . Calle superior α 1 pasó por una línea recta L 1, vector normal norte 1 debe ser ortogonal al vector de dirección q 1 recto L 1, es decir el producto escalar de estos vectores debe ser igual a cero:

Resolviendo el sistema de ecuaciones lineales (27)−(29), con tres ecuaciones y cuatro incógnitas UN 1 , B 1 , C 1 , D 1, y reemplazando en la ecuación

aviones α 1 y α 2 son paralelos, por lo tanto, los vectores normales resultantes norte 1 ={UN 1 , B 1 , C 1) y norte 2 ={UN 2 , B 2 , C 2) de estos planos son colineales. Si estos vectores no son iguales, entonces podemos multiplicar (31) por algún número para que el vector normal resultante norte 2 coincidió con el vector normal de la ecuación (30).

Entonces la distancia entre planos paralelos se calcula mediante la fórmula:

(33)

Decisión. Derecho L 1 pasa por el punto METRO 1 (X 1 , y 1 , z 1)=METRO 1 (2, 1, 4) y tiene un vector de dirección q 1 ={metro 1 , pag 1 , yo 1 }={1, 3, −2}.

Derecho L 2 pasa por el punto METRO 2 (X 2 , y 2 , z 2)=METRO 2 (6, −1, 2) y tiene un vector de dirección q 2 ={metro 2 , pag 2 , yo 2 }={2, −3, 7}.

Construyamos un avión α 1 pasando por la línea L 1 , paralelo a la línea L 2 .

Desde el avión α 1 pasa por la línea L 1 , entonces también pasa por el punto METRO 1 (X 1 , y 1 , z 1)=METRO 1 (2, 1, 4) y vector normal norte 1 ={metro 1 , pag 1 , yo 1) avión α 1 es perpendicular al vector director q 1 recto L uno . Entonces la ecuación del plano debe satisfacer la condición:

Desde el avión α 1 debe ser paralelo a la línea L 2, entonces se debe cumplir la siguiente condición:

Representamos estas ecuaciones en forma matricial:

(40)

Resolvamos el sistema de ecuaciones lineales (40) con respecto a UN 1 , B 1 , C 1 , D 1.

En este artículo, utilizando el ejemplo de resolución del problema C2 del Examen de Estado Unificado, se analiza el método para encontrar coordenadas utilizando el método. Recuerda que las líneas están sesgadas si no están en el mismo plano. En particular, si una línea se encuentra en un plano y la segunda línea se cruza con este plano en un punto que no se encuentra en la primera línea, entonces dichas líneas están sesgadas (ver figura).

Para encontrar distancias entre lineas que se cortan necesario:

1. Dibuja un plano a través de una de las líneas oblicuas que sea paralela a la otra línea oblicua.
2. Coloque una perpendicular desde cualquier punto de la segunda línea recta al plano resultante. La longitud de esta perpendicular será la distancia deseada entre las líneas.

Analicemos este algoritmo con más detalle utilizando el ejemplo de resolución del problema C2 del Examen estatal unificado de matemáticas.

Distancia entre líneas en el espacio

Tarea. en un solo cubo ABCDA 1 B 1 C 1 D 1 hallar la distancia entre las rectas licenciado en Letras 1 y DB 1 .

Arroz. 1. Dibujar para la tarea

Decisión. Por el punto medio de la diagonal del cubo DB 1 (punto O) dibujar una línea paralela a la línea UN 1 B. Puntos de intersección de una recta dada con aristas antes de Cristo y UN 1 D 1 denota respectivamente norte y METRO. Derecho Minnesota se encuentra en el avión BMN 1 y paralela a la recta UN 1 B, que no está en este plano. Esto significa que el directo UN 1 B paralelo al plano BMN 1 sobre la base del paralelismo de una línea recta y un plano (Fig. 2).

Arroz. 2. La distancia deseada entre las líneas que se cruzan es igual a la distancia desde cualquier punto de la línea seleccionada al plano representado

Ahora estamos buscando la distancia desde algún punto en la línea recta UN 1 B hasta el avión BMN uno . Esta distancia, por definición, será la distancia deseada entre las líneas oblicuas.

Para encontrar esta distancia, usamos el método de las coordenadas. Introducimos un sistema de coordenadas cartesianas rectangulares de modo que su origen coincida con el punto B, el eje X fue dirigido a lo largo del borde licenciado en Letras, eje Y- a lo largo de la costilla antes de Cristo, eje Z- a lo largo de la costilla cama y desayuno 1 (figura 3).

Arroz. 3. Elegimos un sistema de coordenadas cartesianas rectangulares como se muestra en la figura

Hallamos la ecuación del plano BMN 1 en este sistema de coordenadas. Para ello, primero determinamos las coordenadas de los puntos METRO, norte y B 1: Sustituimos las coordenadas obtenidas en la ecuación general de una recta y obtenemos el siguiente sistema de ecuaciones:

De la segunda ecuación del sistema, obtenemos de la tercera, y luego de la primera obtenemos Sustituimos los valores obtenidos en la ecuación general de la recta:

Tenga en cuenta que, de lo contrario, el avión BMN 1 pasaría por el origen. Dividimos ambos lados de esta ecuación por y obtenemos:

La distancia de un punto a un plano está determinada por la fórmula.

Geometría. Grado 11

Tema de la lección: Distancia entre líneas que se cruzan

Ter-Ovanesyan G.L., docente de la máxima categoría, laureada del Premio Fundación Soros

Moscú

Considere el problema de encontrar la distancia entre líneas oblicuas. La distancia entre rectas que se cortan es la longitud de la perpendicular común a estas rectas.

Sea dado un cubo ABCDA 1 B 1 C 1 D 1 cuya arista es igual a uno AB=1. Es necesario encontrar la distancia entre las rectas AB y DC 1: ρ (AB; DC 1) - ?

Estas dos líneas se encuentran en planos paralelos: AB se encuentra en el plano AA 1 B 1 B, DC 1 se encuentra en el plano D 1 DC 1 C. Primero encontramos la perpendicular a estos dos planos. Hay muchas de esas perpendiculares en la figura. Este es el segmento BC, B 1 C 1, A 1 D 1 y AD. De estos, tiene sentido elegir el segmento que no solo es perpendicular a estos planos, y por lo tanto perpendicular a nuestras líneas AB y DC 1, sino que también pasa por estas líneas. Tal segmento es AD. Es simultáneamente perpendicular a la línea AB, porque es perpendicular al plano AA 1 B 1 B y a la línea DC 1, porque es perpendicular al plano D 1 DC 1 C. Y esto significa que AD es una perpendicular común a las líneas que se cruzan AB y DC 1. La distancia entre estas líneas es la longitud de esta perpendicular, es decir, la longitud del segmento AD. Pero AD es una arista de un cubo. Por lo tanto, la distancia es 1:

ρ(AB;CC 1)=AD=1

Considere otro problema, un poco más complicado, acerca de encontrar la distancia entre las líneas oblicuas.

Demos de nuevo un cubo cuya arista es igual a uno. Necesitas encontrar la distancia entre las diagonales de las caras opuestas. Es decir, dado el cubo ABCD 1 B 1 C 1 D 1 . Arista AB=1. Es necesario encontrar la distancia entre las rectas VA 1 y DC 1: ρ (A 1 B; DC 1) -?

Estas dos líneas se intersecan, lo que significa que la distancia es la longitud de la perpendicular común. No puede dibujar una perpendicular común, pero formule de la siguiente manera: esta es la longitud de la perpendicular entre los planos paralelos en los que se encuentran estas líneas. La línea BA 1 se encuentra en el plano ABB 1 A 1 y la línea DC 1 se encuentra en el plano D 1 DCC 1 . Son paralelos, por lo que la distancia entre ellos es la distancia entre estas líneas. Y la distancia entre las caras de un cubo es la longitud de la arista. Por ejemplo, la longitud de la arista BC. Porque BC es perpendicular tanto al plano ABB 1 A 1 como al plano DCC 1 D 1. Esto quiere decir que la distancia entre las rectas dada en la condición es igual a la distancia entre planos paralelos y es igual a 1:

ρ (A 1 B; DС 1) \u003d BC \u003d 1

Considere otro problema de encontrar la distancia entre las líneas oblicuas.

Tengamos un prisma triangular regular, en el que se conozcan todas las aristas. Necesita encontrar la distancia entre los bordes de las bases superior e inferior. Es decir, nos dan el prisma ABCA 1 B 1 C 1. Además, AB=3=AA 1 . Es necesario encontrar la distancia entre las rectas BC y A 1 C 1: ρ (BC; A 1 C 1) - ?

Dado que estas líneas se cortan, la distancia entre ellas es la longitud de la perpendicular común, o la longitud de la perpendicular a los planos paralelos en los que se encuentran. Encuentra estos planos paralelos.

La línea BC se encuentra en el plano ABC, y la línea A 1 C 1 se encuentra en el plano A 1 B 1 C 1 . Estos dos planos son paralelos porque son las bases superior e inferior del prisma. Entonces, la distancia entre nuestras líneas es la distancia entre estos planos paralelos. Y la distancia entre ellos es exactamente igual a la longitud del borde lateral AA 1, es decir, igual a 3:

ρ (BC; A 1 C 1) \u003d AA 1 \u003d 3

En esto tarea específica puede encontrar no solo la longitud de la perpendicular común, sino también construirla. Para ello, elegimos de todas las aristas laterales una que tenga puntos comunes con la recta BC y A 1 C 1 . En nuestra figura, este es el borde SS 1. Será perpendicular a la línea A 1 C 1, ya que es perpendicular al plano de la base superior, ya la línea BC, ya que es perpendicular al plano de la base inferior. Por lo tanto, podemos encontrar no solo la distancia, sino también construir esta perpendicular común.

Hoy en la lección recordamos cómo encontrar la longitud de la perpendicular común entre líneas oblicuas.

En menos de un minuto, creé un nuevo archivo Verdov y continué con un tema tan emocionante. Necesita captar los momentos del estado de ánimo de trabajo, por lo que introducción lírica no lo haré Habrá nalgadas prosaicas =)

Los dos espacios rectos pueden:

1) cruzarse;

2) se intersecan en el punto ;

3) ser paralelo;

4) partido.

El caso #1 es fundamentalmente diferente de los otros casos. Dos rectas se cortan si no están en el mismo plano.. Levante un brazo y estire el otro brazo hacia adelante; aquí hay un ejemplo de líneas que se cruzan. En los puntos 2-4, las líneas necesariamente se encuentran en un plano.

¿Cómo saber la posición relativa de las líneas en el espacio?

Considere dos espacios rectos:

- derecho, punto y vector de dirección;
es una línea recta definida por un punto y un vector de dirección.

Para una mejor comprensión, hagamos un dibujo esquemático:

El dibujo muestra líneas oblicuas como ejemplo.

¿Cómo lidiar con estas líneas?

Como se conocen los puntos, es fácil encontrar el vector.

si recto cruzarse, entonces los vectores no coplanario(ver lección (No) dependencia lineal de vectores. base vectorial), lo que significa que el determinante compuesto por sus coordenadas es distinto de cero. O, que en realidad es lo mismo, será diferente de cero: .

En los casos No. 2-4, nuestra construcción "cae" en un plano, mientras que los vectores coplanario, y el producto mixto es lineal Vectores dependientes es igual a cero: .

Ampliamos el algoritmo aún más. pretendamos que , por lo tanto, las rectas o se cortan, o son paralelas, o coinciden.

Si los vectores de dirección colineal, entonces las rectas son paralelas o coinciden. Como último clavo, propongo la siguiente técnica: tomamos cualquier punto de una recta y sustituimos sus coordenadas en la ecuación de la segunda recta; si las coordenadas "se acercaron", entonces las líneas coinciden, si "no se acercaron", entonces las líneas son paralelas.

El curso del algoritmo es simple, pero ejemplos prácticos todavía no dolerá:

Ejemplo 11

Averiguar la posición relativa de dos líneas

Decisión: como en muchos problemas de geometría, conviene ordenar la solución punto por punto:

1) Extraemos puntos y vectores de dirección de las ecuaciones:

2) Encuentra el vector:

Así, los vectores son coplanares, lo que significa que las rectas se encuentran en el mismo plano y pueden intersecarse, ser paralelas o coincidir.

4) Compruebe la colinealidad de los vectores de dirección.

Compongamos un sistema a partir de las coordenadas correspondientes de estos vectores:

Desde todo el mundo La ecuación implica que, por lo tanto, el sistema es consistente, las coordenadas correspondientes de los vectores son proporcionales y los vectores son colineales.

Conclusión: las rectas son paralelas o coinciden.

5) Averigüe si las rectas tienen puntos en común. Tomemos un punto perteneciente a la primera recta y sustituyamos sus coordenadas en las ecuaciones de la recta:

Por lo tanto, puntos comunes las líneas rectas no, y no tienen más remedio que ser paralelas.

Responder:

un ejemplo interesante por decisión independiente:

Ejemplo 12

Averiguar la posición relativa de las líneas.

Este es un ejemplo de bricolaje. Tenga en cuenta que la segunda línea tiene la letra como parámetro. Lógicamente. En el caso general, estas son dos líneas diferentes, por lo que cada línea tiene su propio parámetro.

Y de nuevo les insto a que no se salten los ejemplos, voy a abofetear las tareas que propongo están lejos de ser aleatorias ;-)

Problemas con una línea recta en el espacio

En la parte final de la lección, trataré de considerar cantidad máxima varias tareas con líneas espaciales. En este caso, se observará el orden de inicio de la narración: primero consideraremos problemas con líneas que se cruzan, luego con líneas que se cortan, y al final hablaremos sobre líneas paralelas en el espacio. Sin embargo, debo decir que algunas de las tareas de esta lección se pueden formular para varios casos de líneas rectas a la vez y, en este sentido, la división de la sección en párrafos es algo arbitraria. Hay mas ejemplos simples, hay mas ejemplos complejos y con suerte todos encontrarán lo que necesitan.

lineas cruzadas

Les recuerdo que las rectas se cortan si no existe un plano en el que ambas se encuentren. Cuando estaba pensando en la práctica, me vino a la mente una tarea monstruosa, y ahora me complace presentarles un dragón con cuatro cabezas:

Ejemplo 13

Se dan líneas rectas. Requerido:

a) probar que las rectas se cortan;

b) encontrar las ecuaciones de la recta que pasa por el punto perpendicular a las rectas dadas;

c) componer las ecuaciones de una recta que contiene perpendicular común líneas secantes;

d) hallar la distancia entre las rectas.

Decisión: El camino será dominado por el que camina:

a) Probemos que las rectas se cortan. Encontremos los puntos y los vectores directores de estas rectas:

Encontremos el vector:

Calcular producto mixto de vectores:

Entonces los vectores no coplanario, lo que significa que las rectas se cortan, lo cual se iba a demostrar.

Probablemente, todos hayan notado durante mucho tiempo que, para las líneas oblicuas, el algoritmo de verificación resulta ser el más corto.

b) Encontremos las ecuaciones de la recta que pasa por el punto y es perpendicular a las rectas. Hagamos un dibujo esquemático:

Para variar, publiqué un directo DETRÁS lineas rectas, ver como se borra un poco en los puntos de cruce. ¿Cruces? Sí, en el caso general, la línea "de" se cruzará con las líneas originales. Aunque este momento todavía no nos interesa, solo necesitamos construir una línea perpendicular y eso es todo.

¿Qué se sabe del directo "de"? El punto que le pertenece es conocido. Falta el vector de dirección.

Por condición, la recta debe ser perpendicular a las rectas, lo que significa que su vector director será ortogonal a los vectores directores. El motivo ya familiar del Ejemplo No. 9, encontremos el producto vectorial:

Compongamos las ecuaciones de la recta "de" por el punto y el vector director:

Listo. En principio, uno puede cambiar los signos en los denominadores y escribir la respuesta en la forma , pero no hay necesidad de esto.

Para verificar, es necesario sustituir las coordenadas del punto en las ecuaciones obtenidas de la línea recta, luego usando producto escalar de vectores asegúrese de que el vector sea realmente ortogonal a los vectores de dirección "pe one" y "pe two".

¿Cómo encontrar las ecuaciones de una línea que contiene una perpendicular común?

c) Este problema es más difícil. Recomiendo a los tontos que se salten este párrafo, no quiero enfriar su sincera simpatía por la geometría analítica =) Por cierto, probablemente sea mejor que los lectores más preparados también esperen, el hecho es que el ejemplo debería ponerse en último lugar. artículo en términos de complejidad, pero de acuerdo con la lógica de presentación debe ubicarse aquí.

Entonces, se requiere encontrar las ecuaciones de la línea recta, que contiene la perpendicular común de las líneas oblicuas.

es un segmento de línea que conecta las líneas dadas y es perpendicular a las líneas dadas:

Aquí está nuestro guapo: - perpendicular común de líneas que se cruzan. Él es el único. No hay otro como este. También necesitamos componer las ecuaciones de una línea recta que contiene un segmento dado.

¿Qué se sabe del "uh" directo? Su vector director es conocido, encontrado en el párrafo anterior. Pero, desafortunadamente, no conocemos un solo punto que pertenezca a la línea recta "em", no conocemos los extremos de los puntos perpendiculares. ¿Dónde se cruza esta línea perpendicular con las dos líneas originales? ¿África, la Antártida? Desde la revisión inicial y el análisis de la condición, no está nada claro cómo resolver el problema ... Pero hay un movimiento engañoso asociado con el uso de ecuaciones paramétricas de una línea recta.

Vamos a tomar una decisión punto por punto:

1) Reescribamos las ecuaciones de la primera recta en forma paramétrica:

Consideremos un punto. No sabemos las coordenadas. PERO. Si un punto pertenece a una línea dada, entonces sus coordenadas corresponden a , denótelo con . Entonces las coordenadas del punto se escribirán como:

La vida está mejorando, una incógnita, después de todo, no tres incógnitas.

2) El mismo ultraje debe realizarse sobre el segundo punto. Reescribamos las ecuaciones de la segunda recta en forma paramétrica:

Si un punto pertenece a una recta dada, entonces con un significado muy especifico sus coordenadas deben satisfacer las ecuaciones paramétricas:

O:

3) El vector, al igual que el vector encontrado anteriormente, será el vector director de la línea. Cómo componer un vector a partir de dos puntos se discutió en tiempos inmemoriales en la lección Vectores para tontos. Ahora la diferencia es que las coordenadas de los vectores se escriben con valores de parámetros desconocidos. ¿Así que lo que? Nadie prohíbe restar las coordenadas correspondientes del comienzo del vector de las coordenadas del final del vector.

Hay dos puntos: .

Encontrar un vector:

4) Dado que los vectores de dirección son colineales, entonces un vector se expresa linealmente a través del otro con algún coeficiente de proporcionalidad "lambda":

O coordinadamente:

Resultó ser el más común. sistema de ecuaciones lineales con tres incógnitas, que tiene solución estándar, por ejemplo, método de Cramer. Pero hay una oportunidad aquí poca sangre, de la tercera ecuación expresamos "lambda" y la sustituimos en la primera y segunda ecuaciones:

Por lo tanto: , y "lambda" no necesitamos. El hecho de que los valores de los parámetros resulten ser los mismos es pura casualidad.

5) El cielo se aclara completamente, sustituya los valores encontrados a nuestras ubicaciones:

El vector de dirección no es particularmente necesario, ya que ya se ha encontrado su contraparte.

Después de un largo viaje, siempre es interesante realizar una comprobación.

:

Se obtienen las igualdades correctas.

Sustituye las coordenadas del punto en las ecuaciones :

Se obtienen las igualdades correctas.

6) La cuerda final: compondremos las ecuaciones de una recta para un punto (puedes tomar) y un vector director:

En principio, puede seleccionar un punto "bueno" con coordenadas enteras, pero esto es cosmético.

¿Cómo hallar la distancia entre rectas que se cortan?

d) Cortamos la cuarta cabeza del dragón.

método uno. Ni siquiera un camino, sino uno pequeño caso especial. La distancia entre rectas que se cortan es igual a la longitud de su perpendicular común: .

puntos extremos perpendicular común encontrado en el párrafo anterior, y la tarea es elemental:

método dos. En la práctica, la mayoría de las veces se desconocen los extremos de la perpendicular común, por lo que se utiliza un enfoque diferente. A través de dos líneas que se cortan se pueden dibujar planos paralelos, y la distancia entre los planos dados es igual a la distancia entre las líneas dadas. En particular, una perpendicular común sobresale entre estos planos.

En el curso de la geometría analítica, a partir de las consideraciones anteriores, se derivó una fórmula para encontrar la distancia entre las líneas oblicuas:
(en lugar de nuestros puntos "em uno, dos" podemos tomar puntos arbitrarios de líneas).

Producto mixto de vectores ya se encuentra en el párrafo "a": .

producto cruz de vectores que se encuentra en el párrafo "ser": , calcula su longitud:

Por lo tanto:

Coloque con orgullo los trofeos en una fila:

Responder:
un) , por lo tanto, las líneas se cortan, lo que se requería probar;
b) ;
en) ;
GRAMO)

¿Qué más se puede decir acerca de las rectas que se cruzan? Se define un ángulo entre ellos. Pero fórmula universal El ángulo se discutirá en el siguiente párrafo:

Las líneas rectas que se cortan necesariamente se encuentran en el mismo plano:

El primer pensamiento es apoyarse en el punto de intersección con todas sus fuerzas. E inmediatamente pensé, ¿por qué negarte los deseos correctos? ¡Vamos a saltar sobre él ahora mismo!

¿Cómo encontrar el punto de intersección de líneas espaciales?

Ejemplo 14

Encuentra el punto de intersección de las rectas

Decisión: Reescribamos las ecuaciones de las rectas en forma paramétrica:

Esta tarea discutido en detalle en el Ejemplo No. 7 de esta lección (ver. Ecuaciones de una recta en el espacio). Y las líneas rectas en sí mismas, por cierto, las tomé del Ejemplo No. 12. No mentiré, soy demasiado perezoso para inventar nuevas.

La solución es estándar y ya se encontró cuando calculamos las ecuaciones de la perpendicular común de las líneas oblicuas.

El punto de intersección de las rectas pertenece a la recta, por lo tanto sus coordenadas satisfacen las ecuaciones paramétricas de esta recta, y corresponden a un valor de parámetro muy específico:

Pero el mismo punto pertenece a la segunda línea, por lo tanto:

Igualamos las ecuaciones correspondientes y hacemos simplificaciones:

Recibió sistema de tres ecuaciones lineales con dos incógnitas. Si las líneas se intersecan (como se demuestra en el Ejemplo 12), entonces el sistema es necesariamente consistente y tiene una solución única. se puede resolver método de Gauss, pero no pecaremos con ese fetichismo infantil, hagámoslo más fácil: de la primera ecuación expresamos “te cero” y lo sustituimos en la segunda y tercera ecuaciones:

Las últimas dos ecuaciones resultaron ser esencialmente las mismas, y de ellas se sigue que . Entonces:

Sustituyamos el valor encontrado del parámetro en las ecuaciones:

Responder:

Para verificar, sustituimos el valor encontrado del parámetro en las ecuaciones:
Se obtuvieron las mismas coordenadas requeridas para ser verificadas. Los lectores meticulosos pueden sustituir las coordenadas del punto en las ecuaciones canónicas originales de las líneas.

Por cierto, era posible hacer lo contrario: encontrar el punto a través de "es cero" y verificarlo a través de "te cero".

Un conocido cartel matemático dice: donde se habla de la intersección de rectas, siempre huele a perpendiculares.

¿Cómo construir una línea de espacio perpendicular a una dada?

(líneas se cruzan)

Ejemplo 15

a) Componer las ecuaciones de una recta que pasa por un punto perpendicular a la recta (las líneas se cruzan).

b) Hallar la distancia del punto a la recta.

Nota : cláusula "las líneas se cruzan" - significativo. a través del punto
es posible dibujar un número infinito de líneas perpendiculares que se cruzarán con la línea "el". La única solución es en el caso en que Punto dado dibujado recto, perpendicular dos líneas rectas dadas (ver Ejemplo No. 13, párrafo "b").

un) Decisión: Denote la línea desconocida por . Hagamos un dibujo esquemático:

¿Qué se sabe de la línea? Por condición, se da un punto. Para componer las ecuaciones de una línea recta, es necesario encontrar el vector director. Como tal vector, el vector es bastante adecuado, y nos ocuparemos de él. Más precisamente, tomemos el extremo desconocido del vector por el cogote.

1) Extraeremos su vector director de las ecuaciones de la recta "el", y reescribiremos las ecuaciones mismas en forma paramétrica:

Muchos adivinaron que ahora por tercera vez en una lección el mago sacará un cisne blanco de su sombrero. Considere un punto con coordenadas desconocidas. Dado que el punto , entonces sus coordenadas satisfacen las ecuaciones paramétricas de la recta "el" y corresponden a un valor de parámetro específico:

O en una línea:

2) Por condición, las rectas deben ser perpendiculares, por tanto, sus vectores directores son ortogonales. Y si los vectores son ortogonales, entonces sus producto escalar es igual a cero:

¿Qué sucedió? protozoos ecuación lineal con una incógnita:

3) Se conoce el valor del parámetro, encontremos el punto:

Y el vector director:
.

4) Compondremos las ecuaciones de la recta por el punto y el vector director :

Los denominadores de la proporción resultaron ser fraccionarios, y este es exactamente el caso cuando es apropiado deshacerse de las fracciones. Los multiplicaré por -2:

Responder:

Nota : un final más riguroso de la solución se elabora de la siguiente manera: componemos las ecuaciones de una línea recta por un punto y un vector de dirección . De hecho, si un vector es un vector director de una línea recta, entonces el vector colineal a él, por supuesto, también será un vector director de esta línea recta.

La verificación consta de dos etapas:

1) verificar la ortogonalidad de los vectores de dirección de las líneas;

2) sustituimos las coordenadas del punto en las ecuaciones de cada recta, deberían “encajar” tanto aquí como allá.

O acciones típicas Se habló mucho, así que revisé un borrador.

Por cierto, olvidé otra moda: construir un punto "sue" simétrico al punto "en" con respecto a la línea recta "el". Sin embargo, hay un buen "análogo plano", que se puede encontrar en el artículo Los problemas más simples con una línea recta en un plano.. Aquí, toda la diferencia estará en la coordenada "Z" adicional.

¿Cómo encontrar la distancia de un punto a una línea en el espacio?

b) Decisión: Encuentra la distancia de un punto a una línea.

método uno. distancia dada exactamente igual a la longitud de la perpendicular: . La solución es obvia: si se conocen los puntos , entonces:

método dos. En problemas prácticos, la base de la perpendicular suele ser un misterio, por lo que es más racional utilizar una fórmula preparada.

La distancia de un punto a una recta se expresa mediante la fórmula:
, donde es el vector director de la recta "el", y - arbitrario un punto en una línea dada.

1) De las ecuaciones de la recta obtenemos el vector de dirección y el punto más accesible.

2) El punto se conoce a partir de la condición, agudice el vector:

3) Vamos a encontrar producto vectorial y calcula su longitud:

4) Calcular la longitud del vector de dirección:

5) Así, la distancia de un punto a una línea: