Resolución de ecuaciones diferenciales mediante la transformada de Laplace. Método operacional para la resolución de ecuaciones diferenciales lineales y sus sistemas. §uno. Originales e imágenes de funciones según Laplace

07.10.2020

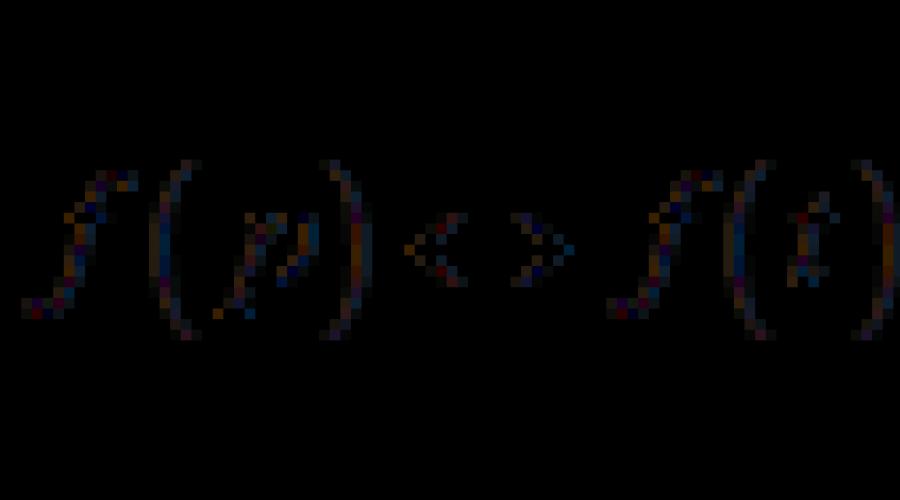
Leer también

Regalos inusuales de Año Nuevo que puedes hacer con tus propias manos.

Revisión de revisiones sobre el ritual psíquico Arina Evdokimova para el cumplimiento del deseo.

Tatyana: día del ángel, día del nombre

Marilyn Kerro - biografía y vida personal de una bruja estonia

Qué significa ver cucarachas en un sueño - interpretación para mujeres

Tamaño: píxeles

Iniciar impresión desde la página:

transcripción

1 Resolver ecuaciones diferenciales usando la transformada de Laplace (método operativo) El cálculo operativo es uno de los métodos más económicos para integrar ecuaciones diferenciales lineales con coeficientes constantes y es muy popular entre los ingenieros. El método fue propuesto por el famoso ingeniero eléctrico y físico estadounidense O. Heaviside (892). Propuso reglas formales para tratar con el operador d dx y algunas funciones de este operador, con las que resolvió varios de los problemas más importantes de la electrodinámica. Sin embargo, el cálculo operacional no recibió una justificación matemática en los trabajos de O. Heaviside (“sus matemáticas surgieron en un contexto físico del que no era fácil distinguirlas” [, p. 8]), muchos de sus resultados permanecieron no probado Recién en los 2 años del siglo XX se justifica el método en los trabajos de Bromwich (T. J. I A. Bromwich) y Carson (J. R. Carson) 2 .. El concepto de original y la imagen según la Definición de Laplace. Una función original es cualquier función de valores complejos f(x) de un argumento real x que satisface las siguientes condiciones: f(x) es continua en x, excepto, quizás, para un número finito de puntos de discontinuidad del tipo -ésimo; 2) para todo x< f(x) = ; 3) существуют такие постоянные M >y a > para lo cual f(x) M e ax para x. () Ecuaciones diferenciales e integrales: un libro de texto para estudiantes de la Facultad de Física y Tecnología: en 3 horas Parte 2 / comp. : N. Yu. Svetova, E. E. Semyonova. Petrozavodsk: PetrSU Publishing House, Los intentos de justificar rigurosamente y la presentación "matemáticamente aceptable" del cálculo se parecían a un "ataque general" El matemático inglés Bromwich (96), el ingeniero estadounidense Carson (925), el ingeniero eléctrico holandés Van der Pol () atrajeron los resultados de diversas teorías, vinculó el cálculo de Heaviside con la transformada de Laplace, con la teoría de funciones de variable compleja.

2 2 El mínimo a de todos los números a para los que la desigualdad () es cierta se llama tasa de crecimiento de la función f(x). Tenga en cuenta que para cualquier función acotada, la tasa de crecimiento a =. La original más simple es la función de Heaviside (, x ; χ(x) =, x<. Очевидно, для любой функции ϕ(x) { ϕ(x), x, ϕ(x) χ(x) =, x <. Если при x функция ϕ(x) удовлетворяет условиям и 3 определения, то функция ϕ(x)χ(x) является оригиналом. В дальнейшем для сокращения записи будем, как правило, записывать ϕ(x) вместо ϕ(x)χ(x), считая, что рассматриваемые нами функции продолжены нулем для отрицательных значений аргумента x. Определение 2. Функция F (p) комплексного переменного p (p C), определяемая интегралом F (p) = e px f(x) dx, () называется преобразованием Лапласа, или изображением по Лапласу 3, функции f(x). Для указания соответствия между оригиналом и изображением будем использовать следующую запись 4: f(x) F (p). 3 В мемуарах П. Лапласа (782 82) современные оригинал и изображение именуются fonction determinant и fonction generatrice «определяющая функция» и «производящая». Эти названия, хотя и признанные неудачными, сохранились до XX в. Хевисайд употреблял названия «подоператорная функция» (892). Оператор он обозначал буквой p, которая употребляется в современном исчислении . 4 Названия original и image и знак предложил Ван дер Поль в статьях гг. В русской литературе термин изображение и символ, по-видимому, впервые появились в книге харьковских математиков А. М. Эфроса и А. М. Данилевского «Операционное исчисление и контурные интегралы» (937), а термин оригинал только в 953 г. . Используются и другие варианты записи соответствия между оригиналами и изображениями. Например, f(x) F (p) или L{f(x)} = F (p).

3 Para cualquier f(x) original, su imagen F (p) está definida en el semiplano Re p > a (a es la tasa de crecimiento de la función f(x)), donde converge la integral impropia (). Ejemplo. Usando la definición, encuentra la imagen de la función f(x) = sen 3x. Decisión. Para la función f(x) = sen 3x tenemos a =. Por lo tanto, la imagen F (p) estará definida en el semiplano Re p >. Apliquemos la fórmula () a la función dada, usando la regla de integración por partes y la restricción en el conjunto de valores de la variable p para asegurar la convergencia de la integral: F (p) = + e px sin 3x dx = = p e px sen 3x x= = 3 p p e px cos 3x = 3 p 2 9 p 2 ). F (p) = 3 p 2 9 p 2 F (p). F (p) = 3 p Por tanto, es válida la siguiente correspondencia: sen 3x 3 p 2, Re p >. + 9 e px sen 3x dx = 3

4 4 2. Propiedades de la transformada de Laplace En la práctica, a la hora de construir imágenes se utilizan diversas técnicas basadas en las propiedades de la transformada de Laplace. Enumeramos las principales propiedades, cuya validez es fácil de establecer utilizando las definiciones de la imagen y el original.Propiedad de linealidad. Si f(x) F (p), g(x) G(p), entonces para cualquier α, β C αf(x) + βg(x) αf (p) + βg(p), Re p > max( a, b). Aquí ya continuación, a y b son las tasas de crecimiento de las funciones f(x) y g(x), respectivamente. 2. Teorema de la semejanza. Si f(x) F (p), entonces para cualquier α > f(αx) α F (p α), Re p > αa. 3. El teorema del desplazamiento. Si f(x) F (p), entonces para cualquier λ C e λx f(x) F (p λ), Re p > a + Re λ. 4. Diferenciación del original. Sea la función f(x) n veces diferenciable. Entonces f (x) pf (p) f(+), f (x) p 2 F (p) pf(+) f (+), f (n) (x) p n F (p) p n f(+). .. pf (n 2) (+) f (n) (+), donde f (k) (+) = lím x + f (k) (x), k =, n. Comentario. Al construir imágenes de derivadas de funciones continuas en cero, se omite el signo más en la notación del argumento de la función y sus derivadas. 5. Diferenciación de imágenes. Si f(x) F (p), entonces En particular, para n = tenemos F (n) (p) (x) n f(x), Re p >. F(p)xf(x).

5 5 6. Integración del original. Si f(x) F (p), entonces x f(ξ) dξ F (p) p, Re p > α. 7. Integración de imágenes. Si la integral y F (p) f(x), entonces p F (p) dp f(x) x, Re p > α. p F (p) dp converge 8. Teorema de multiplicación de imágenes (teorema de convolución) Si f(x) F (p), g(x) G(p), entonces F (p)g(p) x f(t) g( x t) dt = x f(x t)g(t) dt cuando Re p > max(a, b). Las integrales del lado derecho de la correspondencia se denominan convolución de las funciones f(x) y g(x). 9. Teorema del retardo. Si f(x) F (p), entonces para cualquier ξ > f(x ξ)χ(x ξ) e ξp F (p), Re p > α. Se restaura el original a partir de la imagen de forma única, hasta los valores en los puntos de ruptura. En la práctica, se suelen utilizar tablas preparadas de originales e imágenes 5. La tabla enumera los principales originales e imágenes que se encuentran a menudo en las aplicaciones. Ejemplo 2. Utilizando las propiedades de la transformada de Laplace y la tabla de originales e imágenes básicos, encuentre imágenes de las siguientes funciones:) f(x) = e 4x sen 3x cos 2x; 3) f(x) = x 2 e 3x; 2) f (x) \u003d e (x 2) sin (x 2); 4) f(x) = sen2 x x. 5 Ditkin V. A., Prudnikov A. P. Manual de cálculo operativo. M, 965.

6 6 Tabla. Principales originales e imágenes Imagen original Imagen original p cos ωx p p 2 + ω 2 x n n! pags norte+ mi λx pags + λ sen ωx x cos ωx x norte mi λx norte! (p + λ) n+ x sen ωx ω p 2 + ω 2 p 2 ω 2 (p 2 + ω 2) 2 2pω (p 2 + ω 2) 2 Solución.) Transformamos la expresión para la función f (x) como sigue: f(x) = e 4x sen 3x cos 2x = 2 e 4x (sen 5x + sen x) = = 2 e 4x sen 5x + 2 e 4x sen x. Como sen x 5 p 2 y sen 5x + p , entonces, usando la propiedad de linealidad y el teorema del desplazamiento, para la imagen de la función f (x) tendremos: F (p) = () 5 2 (p + 4 ) (p + 4 )) Como sen x p 2 +, ex sen x (p) 2 +, entonces, usando el teorema del retraso, tendremos f (x) = e x 2 sen (x 2) F (p) = e 2p (p)) Así como x 2 2 p 3, entonces por el teorema del desplazamiento tenemos: f(x) = x 2 e 3x F (p) = 2 (p 3) 3.

7 A modo de comparación, presentamos un método para construir una imagen de la función f(x) = x 2 e 3x usando la propiedad de diferenciación de imagen: Obtuvimos el mismo resultado. 4) Dado que e 3x p 3 ; xe 3x d () = dp p 3 (p 3) 2 ; x 2 e 3x d () 2 dp (p 3) 2 = (p 3) 3. sen 2 x = 2 2 cos 2x 2p 2 p p 2 + 4, entonces, usando la propiedad de integración de la imagen, tendremos: sen 2 x ( x 2p) 2 p p 2 dp = + 4 p (= 4 ln p2) 4 ln(p2 + 4) = p 4 ln p 2 p p = 4 ln p2 + 4 p fracción racional propia (es una función racional). Si la fracción se descompone en la suma de las fracciones más simples (elementales), entonces para cada una de ellas se puede encontrar el original correspondiente utilizando las propiedades de la transformada de Laplace y la tabla de originales y sus imágenes. De hecho, A p a A eax ; A (pa) n A (n)! xn e hacha.

8 8 Después de realizar transformaciones fraccionarias Ap + B A(p a) + aa + B A(p a) (p a) 2 = + b2 (p a) 2 + b 2 = (p a) 2 + b 2 + aa + B (p a) 2 + b 2, obtenemos Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sen bx. b Para construir el original correspondiente a la fracción Ap + B ((p a) 2 + b 2) n, puedes usar el teorema de la multiplicación. Por ejemplo, para n = 2 tenemos Ap + B ((p a) 2 + b 2) 2 = Ap + B (p a) 2 + b 2 (p a) 2 + b 2. Desde entonces Para n = 3: Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sen bx = h (x) b (p a) 2 + b 2 b eax sen bx = g(x), Ap + B ((p a) 2 + b 2) 2 = x Ap + B ((p a) 2 + b 2) 2 (p a) 2 + b 2 g(x t) h (t) dt = h 2 (t). x g(x t) h 2 (t) dt Si tiene k ceros diferentes p i, i =, k, entonces, expandiendo

9 el denominador por factores (p p i), el original correspondiente para Y (p) se puede encontrar mediante la fórmula: y(x) = k (Y (p)(p p i)e px) p=pi. (2) i= El producto de Y (p)(p p i) da una función racional cuyo denominador no contiene el factor (p p i), y calculado en p = p i determina el coeficiente con el que la fracción entra en la expansión p p i de la función Y (p) en la suma de fracciones elementales. Ejemplo 3. Encuentra el original que coincide con la imagen: Y (p) = p 3 p. Decisión. Expandiendo la imagen dada a la suma de fracciones elementales: p 3 p = p(p)(p +) = p + 2(p) + 2(p +), encontramos la respuesta original: y(x) = + ch X. y(x) = + 2 ex + 2 e x = + ch x. Ejemplo 4. Encuentra el original de la imagen: Y (p) = p(p 2 +). Decisión. Como p 2 sen x, entonces, aplicando la propiedad de integración del original, + obtenemos: p(p 2 +) x Respuesta: y(x) = cos x. sen t dt = cos t x = cos x. Ejemplo 5. Encuentra el original que coincide con la imagen: Y (p) = (p 2 + 4) 2. 9

10 Decisión. Usando la propiedad de imagen de convolución, tenemos: Y (p) = (p 2 + 4) 2 = p p x sen 2(x t) sen 2t dt. Habiendo calculado la integral, obtenemos la expresión deseada para el original. Respuesta: y(x) = 6 sen 2x x cos 2x. 8 Ejemplo 6. Encuentra el original que coincide con la imagen: Y (p) = p p 3 p 2 6p. Decisión. Como p 3 p 2 6p \u003d p (p 3) (p + 2), entonces el denominador de la fracción Y (p) tiene tres raíces simples: p \u003d, p 2 \u003d 3 y p 3 \u003d 2. Construimos el original correspondiente usando la fórmula (2): y(x) = (p2 + 2)e px (p 3)(p + 2) + (p2 + 2)e px p= p(p + 2) + (p2 + 2)e px p =3 p(p 3) = p= 2 = e3x e 2x. Ejemplo 7. Encuentra el original que coincide con la imagen: Y (p) = e p 2 p(p +)(p 2 + 4). Decisión. Representemos la fracción incluida en la expresión en forma de fracciones simples: p(p +)(p 2 + 4) = A p + B p + + Cp + D p Aplicando el método de coeficientes indefinidos a la expansión, obtenemos : ; B=D=5; C \u003d 2. Y (p) \u003d e p 2 4 p 5 e p 2 p + pe p 2 2 p e p 2 5 p (a)

11 Usando las relaciones: p χ(x), p + e x χ(x), p p cos 2x χ(x), p sen 2x χ(x) 2 y teniendo en cuenta el teorema del retraso, obtenemos el original deseado para el imagen (a). Respuesta: y(x) = (4 5 e (x 2) cos (2x) sen (2x) 2) χ (x) Solución del problema de Cauchy para una ecuación diferencial con coeficientes constantes El método para resolver varias clases de ecuaciones usando la transformada de Laplace se llama método operacional. La propiedad de diferenciación de la transformada de Laplace del original permite reducir la solución de ecuaciones diferenciales lineales con coeficientes constantes a la solución de ecuaciones algebraicas. Considere el problema de Cauchy para una ecuación no homogénea con condiciones iniciales y (n) + a y (n) a n y + a n y = f(x) (3) y() = y, y () = y,..., y (n ) ( ) = yn. (4) Deje que la función f(x) y la solución deseada satisfagan las condiciones para la existencia de la transformada de Laplace. Denotemos por Y (p) la imagen de la función desconocida (original) y(x), y por F (p) la imagen del lado derecho de f(x): y(x) Y (p), f(x) ) F (pag). Por la regla de diferenciación del original, tenemos y (x) py (p) y, y (x) p 2 Y (p) py y, y (n) (x) p n Y (p) p n y p n 2 y.. .y n.

12 2 Entonces, debido a la propiedad de linealidad de la transformada de Laplace, después de aplicarla a la parte izquierda y derecha de la ecuación (3), obtenemos la ecuación del operador M(p)Y (p) N(p) = F (p ), (5) donde M(p) polinomio característico de la ecuación (3): M(p) = p n + a p n a n p + a n y, N(p) polinomio que contiene los datos iniciales del problema de Cauchy (desaparece cuando los datos iniciales son cero ): N(p) = y (p n + a p n a n) + + y (p n 2 + a p n a n 2) y n 2 (p + a) + y n, F (p) imagen de la función f(x). Resolviendo la ecuación del operador (5), obtenemos la imagen de Laplace Y (p) de la solución deseada y(x) en la forma Y (p) = F (p) + N(p). M(p) Restaurando el original para Y (p), encontramos una solución a la ecuación (3) que satisface las condiciones iniciales (4). Ejemplo 8. Encontrar una solución a la ecuación diferencial: y (x) + y(x) = e x que satisfaga la condición: y() =. Decisión. Sea y(x) Y (p). Como y (x) py (p) y() = py (p), e x p +, entonces, aplicando la transformada de Laplace a la ecuación dada, usando la propiedad de linealidad, obtenemos una ecuación algebraica con respecto a Y (p): py (p) + Y (p) = p +. Donde encontramos la expresión para Y (p):

13 Desde entonces tenemos Y (p) = p + e x, (p +) 2 + p +. (p +) 2 xe x, Y (p) y(x) = e x x + e x. Verificación: Demostremos que la función encontrada es de hecho una solución al problema de Cauchy. Sustituimos la expresión de la función y(x) y su derivada en la ecuación dada: y (x) = e x x + e x e x = e x x e x x + e x x + e x = e x. Después de reducir términos similares en el lado izquierdo de la ecuación, obtenemos la identidad correcta: e x e x. Por lo tanto, la función construida es una solución a la ecuación. Comprobemos si cumple la condición inicial y() = : y() = e + e =. Por lo tanto, la función encontrada es una solución al problema de Cauchy. Respuesta: y(x) = e x x + e x. Ejemplo 9. Resolver el problema de Cauchy y + y =, y() =, y() =. Decisión. Sea y(x) Y (p). Como 3 y (x) p 2 Y (p) py() y (), /p, entonces, aplicando la transformada de Laplace a la ecuación, teniendo en cuenta las condiciones iniciales, obtenemos (p 2 +)Y (p) = p = Y (p) = p (p 2 +). Descompongamos la fracción en fracciones simples: Y (p) = p Según la tabla, encontramos y(x) = cos x. p p 2 +.

14 4 También puede restaurar el original a partir de la imagen aplicando la propiedad de integración original (ver ejemplo 4). Respuesta: y(x) = cosx. Ejemplo. Resolver el problema de Cauchy y +3y = e 3x, y() =, y () =. Decisión. Sea y(x) Y (p). Como y py (p) y(), y (x) p 2 Y (p) py() y (), y e 3x p + 3, entonces, dadas las condiciones iniciales, obtenemos la ecuación del operador (p 2 + 3p) Y (p) + = p + 2 = Y (p) = p + 3 (p + 3) 2 p. Expandamos la función racional a fracciones simples: p + 2 (p + 3) 2 p = A p + B p C (p + 3) 2 = A(p2 + 6p + 9) + B(p 2 + 3p) + Cp p (p + 3) 2. Componer un sistema de ecuaciones para encontrar los coeficientes A, B y C: A + B =, 6A + 3B + C =, 9A = 2, resolviendo cuál encontramos A = 2/9 , B = 2/9, C = /3. Por lo tanto, Y (p) = 2 9 p p (p + 3) 2. Usando la tabla, obtenemos la respuesta. Respuesta: y(x) = e 3x 3 xe 3x. Ejemplo. Encuentre una solución a la ecuación diferencial: y (x) + 2y (x) + 5y (x) = satisfaciendo las condiciones: y() =, y () = 2, y () =. Decisión. Sea y(x) Y (p). Dado que, dadas las condiciones dadas, tenemos y (x) p Y (p) y() = py (p) () = py (p) +, y (x) p 2 Y (p) p y() y ( ) = = p 2 Y (p) p () 2 = p 2 Y (p) + p 2, y (x) p 3 Y (p) p 2 y() p y () y () = = p 3 Y (p) p 2 () p 2 = p 3 Y (p) + p 2 2p,

15 luego de aplicar la transformada de Laplace a la ecuación dada, obtenemos la siguiente ecuación del operador: p 3 Y (p) + p 2 2p + 2p 2 Y (p) + 2p 4 + 5pY (p) + 5 = o después de las transformaciones : Y (p) (p 3 + 2p 2 + 5p) = p 2. Resolviendo esta ecuación para Y (p), obtenemos Y (p) = p 2 p(p 2 + 2p + 5). Expandimos la expresión resultante en fracciones simples: p 2 p (p 2 + 2p + 5) = A p + Bp + C p 2 + 2p + 5. Usando el método de coeficientes indefinidos, encontramos A, B, C. Para hacemos esto, reducimos las fracciones a un denominador común e igualamos los coeficientes a iguales potencias p: p 2 p(p 2 + 2p + 5) = Ap2 + 2Ap + 5A + Bp 2 + Cp p(p p + 5) Obtenemos un sistema de ecuaciones algebraicas para A, B, C: resolviendo cual sera: A + B =, 2A + C =, 5A =, A = 5, B = 4 5, C = 2 5. Entonces Y(p) = 5p + 5 4p + 2p 2 + 2p + 5. Para encontrar el original de la segunda fracción, seleccione el cuadrado completo en su denominador: p 2 + 2p + 5 = (p +) 2 + 4, luego seleccione el término p+ en el numerador: 4p+2 = 4(p+)+6 y expandir la fracción a la suma de dos fracciones: 5 4p + 2 p 2 + 2p + 5 = 4 5 p + (p +) (p +) Respuesta: y(x) = e x cos 2x e x sen 2x.

16 6 La solución general de la Ec. (3) también se puede construir por el método operacional. Para ello, los valores específicos y, y,..., y(n) de las condiciones iniciales deben ser reemplazados por constantes arbitrarias C, C 2,..., C n. Bibliografía. Alexandrova N. V. Historia de términos matemáticos, conceptos, designaciones: Libro de referencia del diccionario. M.: Editorial LKI, p. 2. Vasilyeva A. B., Medvedev G. N., Tikhonov N. A., Urazgildina T. A. Ecuaciones diferenciales e integrales, cálculo de variaciones en ejemplos y problemas. M.: FIZ-MATLIT, pág. 3. Sidorov Yu. V. Conferencias sobre la teoría de funciones de una variable compleja / Yu. V. Sidorov, M. V. Fedoryuk, M. I. Shabunin M.: Nauka, 989.

CÁLCULO OPERACIONAL El cálculo operacional es un cálculo simbólico basado en la construcción del análisis matemático como un sistema de operaciones formales sobre

Lección 18 Originales y sus imágenes El cálculo operacional es uno de los métodos de análisis matemático, que aplicaremos a la solución de ecuaciones diferenciales y sistemas. La esencia de este método.

Ecuaciones de Física Matemática Colección de Ejemplos y Ejercicios Petrozavodsk 1 Universidad Estatal de Petrozavodsk Facultad de Matemáticas Ecuaciones de Física Matemática Colección de Ejemplos y Ejercicios

Título Introducción. Conceptos básicos.... 4 1. Ecuaciones integrales de Volterra... 5 Opciones de tarea.... 8 2. Resolvente de la ecuación integral de Volterra. 10 Opciones de tarea.... 11

1 Tema 4. Método de operadores para resolver sistemas y ecuaciones diferenciales lineales 4.1 Transformada de Laplace Una original es cualquier función f(t) de una variable real t que satisface las siguientes

ELEMENTOS DE CÁLCULO OPERATIVO EDITORIAL TGTU MINISTERIO DE EDUCACIÓN Y CIENCIA DE LA FEDERACIÓN DE RUSIA GOU VPO "Universidad Técnica Estatal de Tambov" ELEMENTOS DE CÁLCULO OPERATIVO

Análisis matemático Sección: cálculo operativo Tema: Transformada de Laplace y sus propiedades Profesor Pakhomova E.G. 2011 11. Original e imagen. Teorema de inversión DEFINICIÓN 1. Sea: R C. Función

Números complejos, funciones y operaciones sobre ellos y módulo R parte real número real, yim parte imaginaria número real iy notación algebraica de número complejo El valor principal del argumento

La solución de opciones estándar para el trabajo de control sobre el tema Integrales de una función de una variable Pautas UDC 517.91 Las pautas contienen soluciones detalladas para opciones estándar para el trabajo de control

Capítulo 1 Cálculo Operacional. 1. Definición de la transformada de Laplace. La transformada de Laplace asocia la función f(t) de la variable real t con la función F() de la variable compleja = x + iy

MINISTERIO DE TRANSPORTE DE LA FEDERACIÓN DE RUSIA PRESUPUESTO DEL ESTADO FEDERAL INSTITUCIÓN EDUCATIVA DE EDUCACIÓN SUPERIOR "UNIVERSIDAD DE TRANSPORTE DE RUSIA (MIIT)"

INSTITUCIÓN EDUCATIVA PRESUPUESTARIA DEL ESTADO FEDERAL DE EDUCACIÓN SUPERIOR "UNIVERSIDAD ESTATAL DE COMUNICACIÓN DE MOSCÚ EMPERADOR NICHOLAS II" Departamento "Matemáticas Superiores y Computacionales"

82 4. Apartado 4. Series funcionales y de potencia 4.2. Lección 3 4.2. Lección 3 4.2.. Expansión de Taylor de una función DEFINICIÓN 4.2.. Sea la función y = f(x) infinitamente derivable en alguna vecindad

Conferencia INTEGRACIÓN DE FRACCIONES RACIONALES Fracciones racionales Integración de fracciones racionales simples Descomposición de una fracción racional en fracciones simples Integración de fracciones racionales Racional

TEMA 5 Ecuación lineal de Volterra del tipo th Definiciones básicas y teoremas La ecuación y = λ K(,) y() d+ f(), [, o en forma de operador y = λ By+ f, se denomina ecuación de Volterra del th tipo dejar

Lección 6 Cálculo operacional Transformada de Laplace Imágenes de funciones simples Propiedades básicas de la transformada de Laplace Imagen de la derivada del original Cálculo operacional Transformada de Laplace

Lección 19 Resolver ecuaciones diferenciales y sistemas usando el método operacional 19.1 Resolver ecuaciones diferenciales lineales con coeficientes constantes Se requiere encontrar una solución particular de una ecuación lineal

2.2. Método del operador para el cálculo de procesos transitorios. Información teórica. El cálculo de procesos transitorios en circuitos complejos por el método clásico es muy a menudo difícil de encontrar las constantes de integración.

DOROKHOV VM GUÍA PARA RESOLVER PROBLEMAS DE CÁLCULO OPERACIONAL MOSCÚ, 4 PRÓLOGO Este libro de texto describe los fundamentos teóricos del cálculo operacional Métodos para resolver problemas

Ministerio de Educación y Ciencia de la Federación Rusa Institución Educativa Presupuestaria del Estado Federal de Educación Profesional Superior "Universidad Rusa de Tecnología Química nombrada en honor a DI Mendeleev" Instituto Novomoskovsk (sucursal) Prueba 8 en matemáticas (Operacional

UDC 53.7 SOBRE UN MÉTODO PARA ENCONTRAR UNA SOLUCIÓN PARTICULAR DE ECUACIONES DIFERENCIALES LINEALES CON COEFICIENTES CONSTANTES Zhanybekova A.A., [correo electrónico protegido] universidad técnica kazajo-británica,

CÁLCULO INTEGRAL INTEGRAL INCIERTO Función antiderivada e integral indefinida de antiderivada Lema La función F(se llama antiderivada de la función f(en el intervalo X, si F (= f(X Función,

Ecuaciones de primer orden no resueltas con respecto a la derivada Consideraremos ecuaciones de primer orden que no se resuelvan con respecto a la derivada: F (x, y, y) = 0, (1)

II ECUACIONES DIFERENCIALES Ecuaciones Diferenciales de Primer Orden Definición Las relaciones en las que las variables desconocidas y sus funciones están bajo el signo de la derivada o diferencial se denominan

ELEMENTOS DE LA TEORÍA DE FUNCIONES DE UNA VARIABLE COMPLEJA CÁLCULO OPERACIONAL

Ministerio de Educación y Ciencia de la Federación Rusa "MATI" Universidad Tecnológica Estatal Rusa. K.E. Tsiolkovsky Departamento de Matemáticas Superiores Números complejos y cálculo operativo

1 Tema 3. Ecuaciones diferenciales lineales con coeficientes constantes 3.1 Ecuación lineal homogénea Ecuación diferencial de la forma y (n) + a n 1 y (n 1) +... + a 1 y + a 0 y = 0, (3.1) donde un

INTEGRAL INDEFINIDA. Antiderivada e integral indefinida La tarea principal del cálculo diferencial es encontrar la derivada (o diferencial) de una función dada. Cálculo integral

Ministerio de Educación y Ciencia de la Federación Rusa Sucursal de Achinsk de la Institución Educativa Autónoma del Estado Federal de Educación Profesional Superior "Universidad Federal de Siberia" MATEMÁTICAS

Límite de función. La relevancia de estudiar el tema La teoría de los límites juega un papel fundamental en el análisis matemático, pues permite determinar la naturaleza del comportamiento de una función para un cambio dado en el argumento. A través de

Antiderivada e integral indefinida Conceptos básicos y fórmulas 1. Definición de antiderivada e integral indefinida. Definición. La función F(x) se llama antiderivada de la función f(x) en el intervalo

Capítulo 1 Ecuaciones diferenciales 1.1 El concepto de ecuación diferencial 1.1.1 Problemas que conducen a las ecuaciones diferenciales. En la física clásica, a cada cantidad física se le asigna

ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN Conceptos básicos Ecuaciones diferenciales con variables separables Muchos problemas en ciencia y tecnología se reducen a ecuaciones diferenciales Considere

Desarrollo metodológico Resolución de problemas sobre TFKP Números complejos Operaciones con números complejos Plano complejo Un número complejo se puede representar en exponencial algebraico y trigonométrico

Clase 3 Series de Taylor y Maclaurin Aplicación de series de potencias Expansión de funciones en series de potencias Series de Taylor y Maclaurin Para aplicaciones, es importante poder expandir una función dada en una serie de potencias, esas funciones

Variante típica "Números complejos Polinomios y fracciones racionales" Tarea Dados dos números complejos y cos sn Encuentra y escribe el resultado en forma algebraica Escribe el resultado en trigonométrica

Agencia Federal para la Educación Institución Educativa Estatal Federal de Educación Profesional Superior UNIVERSIDAD FEDERAL DEL SUR R. M. Gavrilova, G. S. Kostetskaya Metódico

S P PREOBRAZHENSKY, SR TIKHOMIROV INTEGRACIÓN DE ECUACIONES DIFERENCIALES MEDIANTE SERIE DE POTENCIAS 987 ÍNDICE

Análisis matemático Sección: Integral indefinida Tema: Integración de fracciones racionales Profesor Pakhomova E.G. 0 5. Integración de fracciones racionales DEFINICIÓN. La fracción racional se llama

Ministerio de Transporte de la Federación de Rusia INSTITUCIÓN EDUCATIVA PRESUPUESTARIA DEL ESTADO FEDERAL DE EDUCACIÓN SUPERIOR "UNIVERSIDAD DE TRANSPORTE DE RUSIA (MIIT)" Instituto de Economía y Finanzas

CÁLCULO OPERACIONAL Transformada de Laplace y fórmula de inversión Sea en el intervalo de Dirichlet, a saber: La integral de Fourier (l l) a) está acotada en este intervalo; la función satisface las condiciones b) es continua por tramos

Ministerio de Educación de la Federación Rusa Gubkin Universidad Estatal Rusa de Petróleo y Gas VI Ivanov Directrices para el estudio del tema "ECUACIONES DIFERENCIALES" (para estudiantes

57 Considere la integración de la fracción racional más simple del cuarto tipo (M N) d () p q p Hagamos un cambio de variable estableciendo d. donde a p q. Entonces la integral M N d p p p q q a, M p N Mp q d M (p q) p

Una ecuación diferencial de orden n se llama lineal si es de primer grado con respecto a la función y y sus derivadas y..., y (n), es decir, tiene la forma a 0 y (n) + a 1 y (n 1) +... + a ny = f(x), donde

Análisis matemático Sección: Integral indefinida Tema: Integración de fracciones racionales Profesor Rozhkova S.V. 0 5. Integración de fracciones racionales DEFINICIÓN. La fracción racional se llama

Ministerio de Telecomunicaciones y Comunicaciones Masivas de la Federación Rusa Institución Educativa Estatal de Educación Profesional Superior UNIVERSIDAD ESTATAL DE TELECOMUNICACIONES DEL VOLGA

Ecuaciones diferenciales de primer orden resueltas con respecto a la derivada Teorema de existencia y unicidad para una solución En el caso general, una ecuación diferencial de primer orden tiene la forma F ()

T A Matveeva V B vetlichnaya D K Agisheva A Zotova

CÁLCULO INTEGRAL INTEGRAL INDEFINIDA Una función antiderivada y una integral indefinida de una antiderivada La función F() se llama antiderivada de la función f() en el intervalo X, si F / () = f() X.

5. 4 Métodos básicos de integración Integración directa. Cálculo de integrales basado en llevar el integrando a una forma tabular y usando las propiedades del indefinido

Lección 3 Descripción matemática de los sistemas de control En la teoría de control, en el análisis y síntesis de los sistemas de control, se trata de su modelo matemático El modelo matemático del ACS es una ecuación

Integración de un sistema de ecuaciones diferenciales eliminando variables Uno de los principales métodos para integrar un sistema de ecuaciones diferenciales es el siguiente: a partir de las ecuaciones de la normal

Ecuaciones en derivadas parciales de primer orden Algunos problemas de mecánica clásica, mecánica de medios continuos, acústica, óptica, hidrodinámica, transferencia de radiación se reducen a ecuaciones en derivadas parciales

Las integrales indefinidas más simples Ejemplos de resolución de problemas Las siguientes integrales se reducen a tablas mediante la transformación idéntica del integrando. 1. dx = dx = 2x 2/3/3 + 2x 1/2 + C. >2.

ACTIVIDAD PRÁCTICA Integración de fracciones racionales Una fracción racional es una fracción de la forma P Q, donde P y Q son polinomios Una fracción racional se llama propia si el grado del polinomio P es menor que el grado

[F] Filippov AV Colección de problemas sobre ecuaciones diferenciales Moscú-Izhevsk: Centro de Investigación "Dinámica regular y caótica" 00 URL: http://librarbsaz/kitablar/846pf [M] Matveev NM Colección de problemas y ejercicios sobre

ocupación E. Filas de Taylor. Suma de series de potencias Mat. análisis, aplicación. Matemáticas, 3er semestre Encuentra la expansión de una función en una serie de potencias en potencias, calcula el radio de convergencia de la serie de potencias: A f()

Tarea 1.1. Encuentre soluciones y = y(x) de la ecuación diferencial que no sean idénticamente cero en el área indicada y satisfagan las condiciones de contorno dadas (el problema de Sturm-Liouville) Solución: Considere

9. Antiderivada e integral indefinida 9.. Dada la función f() en el intervalo I R. La función F () se llama función antiderivada f() en el intervalo I, si F () = f() para cualquier I, y la antiderivada

~ ~ Integrales indefinidas y definidas El concepto de antiderivada e integral indefinida. Definición: Una función F se llama antiderivada con respecto a una función f si estas funciones están relacionadas de la siguiente manera

Clase 5 7 Teorema de Hilbert-Schmidt Consideraremos un operador integral A, cuyo núcleo K( satisface las siguientes condiciones: K(s) es simétrico, continuo en el conjunto de variables en [, ]

Ministerio de Educación de la República de Bielorrusia Universidad Estatal de Bielorrusia Facultad de Física Departamento de Matemática Superior y Física Matemática O A Kononova, N I Ilyinkova, N K Filippova Linear

Tema 9 Serie de potencias Una serie de potencias es una serie funcional de la forma, mientras que los números... son los coeficientes de la serie, y el punto de expansión de la serie.,...,...R... se llama el centro Serie de potencias El término general de la serie de potencias

SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES CON COEFICIENTES CONSTANTES Reducción a una sola ecuación del orden th Desde un punto de vista práctico, los sistemas lineales con coeficientes constantes son muy importantes

Integrales y ecuaciones diferenciales Módulo 1. Integral indefinida Tema 1.2 Fracciones racionales abstractas. Descomposición de una fracción racional propia en una suma de unos simples. Integración de protozoos

Fórmula de expansión Heaviside

Sea la imagen de la función una función racional fraccionaria.

Teorema. Sean, donde y funciones diferenciables. Introduzcamos los dos polos de la función, es decir raíces (ceros) de su denominador. Entonces, si obtenemos la fórmula de Heaviside:

Realizaremos la demostración para el caso cuando y sean polinomios de grados t y PAG en consecuencia, mientras t PAG. Entonces es una fracción racional propia. Representémoslo como una suma de fracciones simples:

A partir de aquí encontramos los coeficientes de la identidad (17.2), reescribiéndolos en la forma

Multiplicamos ambos lados de la última igualdad por y pasamos al límite en. Teniendo en cuenta que y, obtenemos

de donde se sigue (17.1). El teorema ha sido probado.

Observación 1. Si los coeficientes de los polinomios y son reales, entonces las raíces complejas del polinomio son conjugadas por pares. En consecuencia, en la fórmula (17.1), las cantidades complejas conjugadas serán los términos correspondientes a las raíces complejas conjugadas del polinomio, y la fórmula de Heaviside tomará la forma

donde la primera suma se extiende a todas las raíces reales del polinomio, la segunda a todas sus raíces complejas con partes imaginarias positivas.

Observación 2. Cada miembro de la fórmula (17.1) es una oscilación escrita en forma compleja, donde. Por lo tanto, las raíces reales () corresponden a oscilaciones aperiódicas, raíces complejas con partes reales negativas - oscilaciones amortiguadas, raíces puramente imaginarias - oscilaciones armónicas no amortiguadas.

Si el denominador no tiene raíces con partes reales positivas, entonces para valores suficientemente grandes obtenemos un estado estacionario:

Raíces puramente imaginarias de un polinomio con partes imaginarias positivas.

Las oscilaciones correspondientes a raíces con partes reales negativas decaen exponencialmente en y por lo tanto no entran en el estado estacionario.

Ejemplo 1 Buscar imagen original

Decisión. Tenemos. Escribimos las raíces del polinomio: .

Por fórmula (17.1)

Aquí, ya que los números son las raíces de la ecuación. Por lo tanto,

Ejemplo 2 Buscar imagen original

donde un 0; .

Decisión. Aquí, la función, además de la raíz obvia, tiene infinitas raíces, que son ceros de la función. Resolviendo la ecuación, llegamos a donde

Así, las raíces del denominador tienen la forma y, donde

Por la fórmula (17.3) encontramos el original

Método del operador para resolver ecuaciones diferenciales

Ecuaciones diferenciales. Considere el problema de Cauchy para la ecuación diferencial lineal

(aquí) con condiciones iniciales

Pasando a imágenes en (18.1), debido a la linealidad de la transformada de Laplace, tenemos

Imágenes de derivadas, usando el Teorema 3 del § 16 y condiciones iniciales (18.2), escribimos en la forma

Sustituyendo (18.4) en (18.3), después de transformaciones simples, obtenemos la ecuación del operador

donde (polinomio característico); .

De la ecuación (18.5) encontramos la solución del operador

La solución del problema de Cauchy (18.1), (18.2) es la solución del operador original (18.6):

Para el problema de Cauchy, en la notación aceptada, podemos escribir

La ecuación del operador tiene la forma

Descompongamos la solución del operador en fracciones simples:

Usando las fórmulas obtenidas en el § 15, obtenemos los originales:

Así, la solución del problema de Cauchy tendrá la forma

Ejemplo 1 Resolver el problema de Cauchy para una ecuación diferencial con condiciones iniciales, donde.

Decisión.

Su solución parece

Usando el Teorema 2 del § 16, encontramos sucesivamente:

Ejemplo 2 Resuelva el problema de Cauchy para una ecuación diferencial con condiciones iniciales cero, donde es una función de impulso de paso.

Decisión. Escribamos la ecuación del operador

y su solucion

El teorema 2 del § 16 implica

de acuerdo con el teorema del retraso (§ 15)

Por fin,

Ejemplo 3 a un punto de masa t unido al resorte por rigidez con y situado en un plano horizontal liso, actúa una fuerza que cambia periódicamente. En el momento del tiempo, el punto fue sometido a un impacto portador de impulso. Despreciando la resistencia, encuentre la ley de movimiento de un punto si en el momento inicial de tiempo estaba en reposo en el origen.

Decisión. Escribimos la ecuación de movimiento en la forma

donde es la fuerza elástica; es la función de Dirac. Resolvamos la ecuación del operador

Si (caso de resonancia), entonces

Según el teorema del retraso

Por fin,

Integral (fórmula) de Duhamel. Considere el problema de Cauchy para la ecuación (18.1) en condiciones iniciales. La solución del operador en este caso tiene la forma

Sea la función de peso la original para. entonces por el Teorema 1 del § 16 obtenemos

La relación (18.7) se llama integral de Duhamel (fórmula).

Comentario. En condiciones iniciales distintas de cero, la fórmula de Duhamel no es directamente aplicable. En este caso, primero es necesario transformar el problema original en un problema con condiciones iniciales homogéneas (cero). Para hacer esto, introducimos una nueva función, configurando

donde son los valores iniciales de la solución deseada.

Como es fácil de ver, y por lo tanto, .

Por lo tanto, la función es la solución de la ecuación (18.1) con el lado derecho obtenido al sustituir (18.8) en (18.1), con datos iniciales cero.

Usando (18.7), encontramos y.

Ejemplo 4 Utilice la integral de Duhamel para encontrar una solución al problema de Cauchy

con condiciones iniciales.

Decisión. Los datos iniciales son distintos de cero. Suponemos, de acuerdo con (18.8), . Entonces, y para la definición, obtenemos una ecuación con condiciones iniciales homogéneas.

Para el problema en consideración, el polinomio característico, la función de peso. Según la fórmula de Duhamel

Por fin,

Sistemas de ecuaciones diferenciales lineales con coeficientes constantes. El problema de Cauchy para un sistema de ecuaciones diferenciales lineales en notación matricial tiene la forma

donde es el vector de las funciones deseadas; - vector de partes derechas; - matriz de coeficientes; - vector de datos iniciales.

El cálculo operativo se ha convertido ahora en uno de los capítulos más importantes del análisis matemático práctico. El método operacional se usa directamente para resolver ecuaciones diferenciales ordinarias y sistemas de tales ecuaciones; también se puede utilizar para resolver ecuaciones diferenciales parciales.

Los fundadores del cálculo simbólico (operacional) son los científicos rusos M. E. Vashchenko-Zakharchenko y A. V. Letnikov.

El cálculo operativo atrajo la atención después de que el ingeniero eléctrico inglés Heaviside, utilizando el cálculo simbólico, obtuviera una serie de resultados importantes. Pero la desconfianza hacia el cálculo simbólico persistió hasta que Georgi, Bromwich, Carson, A. M. Efros, A. I. Lurie, V. A. Ditkin y otros establecieron la conexión entre el cálculo operativo y las transformaciones integrales.

La idea de resolver una ecuación diferencial por el método operacional es que a partir de la ecuación diferencial con respecto a la función deseada-original F ( t ) ir a la ecuación para otra función F ( pag ), llamado una imagen F ( t ) . La ecuación resultante (operacional) generalmente ya es algebraica (lo que significa que es más simple que la original). Resolviéndolo con respecto a la imagen. F ( pag ) y luego procediendo al original correspondiente, encuentran la solución deseada de esta ecuación diferencial.

El método operativo para resolver ecuaciones diferenciales se puede comparar con el cálculo de varias expresiones usando logaritmos, cuando, por ejemplo, al multiplicar, los cálculos no se realizan en los números en sí, sino en sus logaritmos, lo que conduce al reemplazo de la multiplicación con un operación más simple - adición.

Al igual que con el logaritmo, al usar el método operativo, necesita:

1) una tabla de originales y sus correspondientes imágenes;

2) conocimiento de las reglas para realizar operaciones en la imagen, correspondientes a las acciones realizadas en el original.

§uno. Originales e imágenes de funciones según Laplace

Definición 1.Seremos la función real del argumento real F (t) llamar original, si cumple tres requisitos:

1) F (t) 0 , en t 0

2) F ( t ) no aumenta más rápido que alguna función exponencial

, en t0 , donde METRO 0, s00 - algunas constantes reales, s 0 llamado indicador de crecimiento de la función f(t) .

3) Sobre cualquier segmento finito  un , bsemieje positivo Desde función F (t) satisface las condiciones de Dirichlet, es decir,

un limitado,

b) es continua o tiene solo un número finito de puntos de discontinuidad de primera clase,

c) tiene un número finito de extremos.

Las funciones que satisfacen estos tres requisitos se denominan en cálculo operativo interpretado por Laplace o originales .

El original más simple es la función de identidad de Heaviside

Si la función

satisface la condición 2 y no satisface la condición 1, entonces el producto también cumplirá la condición 1, es decir sera original Para simplificar la notación, por regla general utilizaremos el multiplicador H (t) se omitirá, asumiendo que todas las funciones consideradas son iguales a cero para valores negativos t .

Integral de Laplace para el original F (t) se llama integral impropia de la forma