Pronađite kanonski oblik kvadratnog oblika online kalkulatora. Redukcija kvadratnog oblika na kanonski oblik

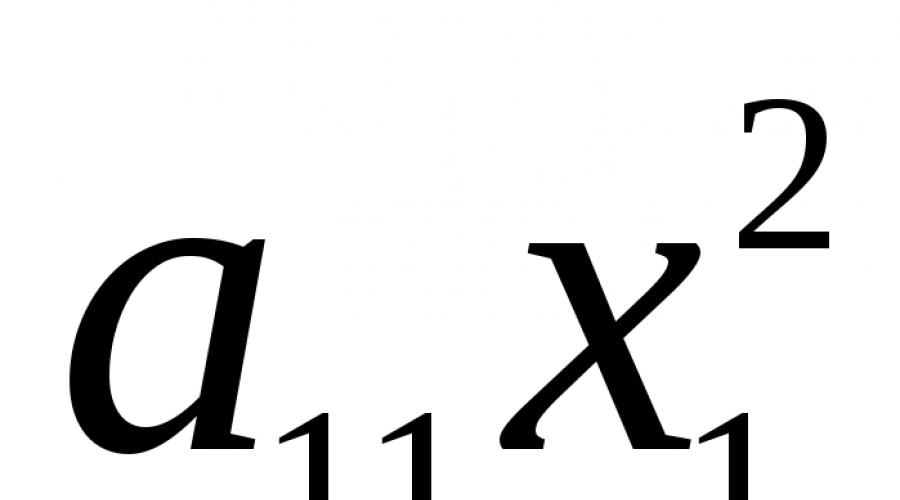
Dat kvadratni oblik (2) A(x, x) = , gdje x = (x 1 , x 2 , …, x n). Razmotrimo kvadratni oblik u prostoru R 3, tj x = (x 1 , x 2 , x 3), A(x, x) =
+
+
+
+
+
+ +
+
+
=
+
+
+ 2
+ 2
+ + 2
(koristili smo uslov simetrije oblika, tj a 12 = a 21 , a 13 = a 31 , a 23 = a 32). Hajde da ispišemo matricu kvadratni oblik A u osnovi ( e}, A(e) =
. Prilikom promjene baze, matrica kvadratnog oblika se mijenja prema formuli A(f) = C t A(e)C, gdje C je prijelazna matrica iz baze ( e) na osnovu ( f), a C t je transponovana matrica C.

Definicija11.12. Vrsta kvadratnog oblika sa dijagonalnom matricom se naziva kanonski.

Pa neka A(f) =
, onda A"(x, x) =
+
+
, gdje x" 1 , x" 2 , x" 3 – vektorske koordinate x u novoj osnovi ( f}.

Definicija11.13. Pusti unutra n V takva osnova je izabrana f = {f 1 , f 2 , …, f n), u kojem kvadratni oblik ima oblik

A(x, x) =
+
+ … +
, (3)

gdje y 1 , y 2 , …, y n su vektorske koordinate x u osnovi ( f). Izraz (3) se poziva kanonski pogled kvadratni oblik. Koeficijenti  1 , λ 2 , …, λ n pozvao kanonski; naziva se baza u kojoj kvadratni oblik ima kanonski oblik kanonska osnova.

Komentar. Ako je kvadratni oblik A(x, x) se svodi na kanonski oblik, onda, općenito govoreći, nisu svi koeficijenti  i razlikuju se od nule. Rang kvadratnog oblika jednak je rangu njegove matrice u bilo kojoj bazi.

Neka je rang kvadratnog oblika A(x, x) je jednako r, gdje r ≤ n. Matrica kvadratnog oblika u kanonskom obliku ima dijagonalni oblik. A(f) =
, jer je njegov rang r, zatim među koeficijentima  i treba biti r, nije jednako nuli. Ovo implicira da je broj kanonskih koeficijenata koji nisu nula jednak rangu kvadratnog oblika.

Komentar. Linearna transformacija koordinata je prijelaz iz varijabli x 1 , x 2 , …, x n na varijable y 1 , y 2 , …, y n, gdje su stare varijable izražene u terminima novih varijabli sa nekim numeričkim koeficijentima.

x 1 = α 11 y 1 + α 12 y 2 + … + α 1 n y n ,

x 2 = α 2 1 y 1 + α 2 2 y 2 + … + α 2 n y n ,

………………………………

x 1 = α n 1 y 1 + a n 2 y 2 + … + α nn y n .

Kako svaka transformacija baze odgovara nedegeneriranoj linearnoj transformaciji koordinata, pitanje svođenja kvadratnog oblika na kanonski oblik može se riješiti odabirom odgovarajuće nedegenerirane transformacije koordinata.

Teorema 11.2 (osnovna teorema o kvadratnim oblicima). Bilo koji kvadratni oblik A(x, x) navedeno u n-dimenzionalni vektorski prostor V, uz pomoć nedegenerirane linearne transformacije koordinata može se svesti na kanonski oblik.

Dokaz. (Lagrangeova metoda) Ideja ove metode je da se kvadratni trinom u svakoj varijabli sukcesivno dopuni do punog kvadrata. Pretpostavićemo to A(x, x) ≠ 0 iu bazi e = {e 1 , e 2 , …, e n) ima oblik (2):

A(x, x) =
.

Ako a A(x, x) = 0, tada ( a ij) = 0, odnosno oblik je već kanonski. Formula A(x, x) može se transformisati tako da koeficijent a 11 ≠ 0. Ako a 11 = 0, tada je koeficijent kvadrata druge varijable drugačiji od nule, tada je prenumeracijom varijabli moguće postići da a 11 ≠ 0. Prenumeracija varijabli je nedegenerirana linearna transformacija. Ako su svi koeficijenti kvadrata varijabli jednaki nuli, tada se potrebne transformacije dobivaju na sljedeći način. Neka, na primjer, a 12 ≠ 0 (A(x, x) ≠ 0, dakle najmanje jedan koeficijent a ij≠ 0). Razmotrite transformaciju

x 1 = y 1 – y 2 ,

x 2 = y 1 + y 2 ,

x i = y i, at i = 3, 4, …, n.

Ova transformacija nije degenerirana, jer determinanta njene matrice nije nula
= = 2 ≠ 0.

Zatim 2 a 12 x 1 x 2 = 2 a 12 (y 1 – y 2)(y 1 + y 2) = 2
– 2
, odnosno u obliku A(x, x) postojat će kvadrati od dvije varijable odjednom.

A(x, x) =
+ 2
+ 2
+
. (4)

Transformirajmo dodijeljenu sumu u oblik:

A(x, x) = a 11
, (5)

dok su koeficijenti a ij promijeniti u . Razmotrite nedegenerisanu transformaciju

y 1 = x 1 + + … + ,

y 2 = x 2 ,

y n = x n .

Onda dobijamo

A(x, x) =
. (6).

Ako je kvadratni oblik
= 0, onda je pitanje ubacivanja A(x, x) na kanonski oblik je riješen.

Ako ovaj oblik nije jednak nuli, onda ponavljamo razmišljanje, uzimajući u obzir transformacije koordinata y 2 , …, y n bez promjene koordinata y jedan . Očigledno, ove transformacije neće biti degenerisane. U konačnom broju koraka, kvadratni oblik A(x, x) će se svesti na kanonski oblik (3).

Komentar 1. Potrebna transformacija početnih koordinata x 1 , x 2 , …, x n može se dobiti množenjem nedegeneriranih transformacija pronađenih u procesu zaključivanja: [ x] = A[y], [y] = B[z], [z] = C[t], zatim [ x] = AB[z] = ABC[t], tj. [ x] = M[t], gdje M = ABC.

Komentar 2. Neka A(x, x) = A(x, x) =
+
+ …+
, gdje je  i ≠ 0, i = 1, 2, …, r, i  1 > 0, λ 2 > 0, …, λ q > 0, λ q +1 < 0, …, λ r < 0.

Razmotrite nedegenerisanu transformaciju

y 1 = z 1 , y 2 = z 2 , …, y q = z q , y q +1 =
z q +1 , …, y r = z r , y r +1 = z r +1 , …, y n = z n. Kao rezultat A(x, x) će imati oblik: A(x, x) = + + … + – – … – , koji se zove normalni kvadratni oblik.

Primjer11.1. Pretvorite kvadratni oblik u kanonski oblik A(x, x) = 2x 1 x 2 – 6x 2 x 3 + 2x 3 x 1 .

Odluka. Ukoliko a 11 = 0, koristite transformaciju

x 1 = y 1 – y 2 ,

x 2 = y 1 + y 2 ,

x 3 = y 3 .

Ova transformacija ima matricu A =
, tj. [ x] = A[y] dobijamo A(x, x) = 2(y 1 – y 2)(y 1 + y 2) – 6(y 1 + y 2)y 3 + 2y 3 (y 1 – y 2) =

2– 2– 6y 1 y 3 – 6y 2 y 3 + 2y 3 y 1 – 2y 3 y 2 = 2– 2– 4y 1 y 3 – 8y 3 y 2 .

Budući da je koeficijent at nije jednako nuli, možete odabrati kvadrat jedne nepoznate, neka bude y jedan . Odaberite sve pojmove koji sadrže y 1 .

A(x, x) = 2(– 2y 1 y 3) – 2– 8y 3 y 2 = 2(– 2y 1 y 3 + ) – 2– 2– 8y 3 y 2 = 2(y 1 – y 3) 2 – 2– 2– 8y 3 y 2 .

Izvršimo transformaciju čija je matrica jednaka B.

z 1 = y 1 – y 3 ,  y 1 = z 1 + z 3 ,

z 2 = y 2 ,  y 2 = z 2 ,

z 3 = y 3 ;  y 3 = z 3 .

B =
, [y] = B[z].

Get A(x, x) = 2– 2–– 8z 2 z 3 . Izdvajamo pojmove koji sadrže z 2. Imamo A(x, x) = 2– 2(+ 4z 2 z 3) – 2= 2– 2(+ 4z 2 z 3 + 4) + + 8 – 2 = 2– 2(z 2 + 2z 3) 2 + 6.

Izvođenje matrične transformacije C:

t 1 = z 1 ,  z 1 = t 1 ,

t 2 = z 2 + 2z 3 ,  z 2 = t 2 – 2t 3 ,

t 3 = z 3 ;  z 3 = t 3 .

C =
, [z] = C[t].

dobio: A(x, x) = 2– 2+ 6kanonski oblik kvadratnog oblika, dok [ x] = A[y], [y] = B[z], [z] = C[t], dakle [ x] = ABC[t];

ABC =


=
. Formule konverzije su sljedeće

x 1 = t 1 – t 2 + t 3 ,

x 2 = t 1 + t 2 – t 3 ,

Definicija 10.4.Canonical view kvadratni oblik (10.1) se zove sljedeći pogled: . (10.4)

Pokažimo da u bazi sopstvenih vektora kvadratni oblik (10.1) poprima kanonski oblik. Neka bude

- normalizovani sopstveni vektori koji odgovaraju sopstvenim vrednostima λ 1 ,λ 2 ,λ 3 matrice (10.3) u ortonormalnoj bazi . Tada će matrica prijelaza sa stare baze na novu biti matrica

. U novoj osnovi, matrica ALI poprima dijagonalni oblik (9.7) (po svojstvu vlastitih vektora). Dakle, transformacija koordinata prema formulama:

,

dobijamo u novoj bazi kanonski oblik kvadratnog oblika sa koeficijentima jednakim sopstvenim vrednostima λ 1 , λ 2 , λ 3:

Napomena 1. Sa geometrijske tačke gledišta, razmatrana koordinatna transformacija je rotacija koordinatnog sistema, koja kombinuje stare koordinatne ose sa novim.

Napomena 2. Ako se bilo koja od svojstvenih vrijednosti matrice (10.3) poklapa, možemo dodati jedinični vektor ortogonan svakom od njih odgovarajućim ortonormalnim vlastitim vektorima i tako konstruirati bazu u kojoj kvadratni oblik poprima kanonski oblik.

Svodimo na kanonski oblik kvadratni oblik

x² + 5 y² + z² + 2 xy + 6xz + 2yz.

Njena matrica ima oblik. U primjeru razmatranom u predavanju 9, pronađene su svojstvene vrijednosti i ortonormalni svojstveni vektori ove matrice:

Sastavimo prijelaznu matricu na osnovu ovih vektora:

(redoslijed vektora se mijenja tako da formiraju desnu trojku). Transformirajmo koordinate prema formulama:

.

Dakle, kvadratni oblik se svodi na kanonski oblik sa koeficijentima jednakim svojstvenim vrijednostima matrice kvadratnog oblika.

Predavanje 11

Krive drugog reda. Elipsa, hiperbola i parabola, njihova svojstva i kanonske jednadžbe. Svođenje jednadžbe drugog reda na kanonski oblik.

Definicija 11.1.Krive drugog reda na ravni nazivaju se linije presjeka kružnog konusa sa ravnima koje ne prolaze kroz njegov vrh.

Ako takva ravnina siječe sve generatore jedne šupljine stošca, onda se u presjeku ispostavlja elipsa, na preseku generatora obe šupljine - hiperbola, a ako je rezna ravan paralelna bilo kojoj generatrisi, tada je presjek konusa parabola.

Komentar. Sve krive drugog reda date su jednačinama drugog stepena u dvije varijable.

Elipsa.

Definicija 11.2.Elipsa je skup tačaka u ravni za koje je zbir udaljenosti do dvije fiksne tačke F 1 i F trikovi, je konstantna vrijednost.

Komentar. Kada se bodovi poklope F 1 i F 2 elipsa se pretvara u krug.

Izvodimo jednačinu elipse odabirom Dekartovog sistema

y M(x, y) koordinate tako da os Oh poklopila sa linijom F 1 F 2, početak

r 1 r 2 koordinate - sa sredinom segmenta F 1 F 2. Neka dužina ovoga

segment je 2 sa, zatim u odabranom koordinatnom sistemu

F 1 O F 2 x F 1 (-c, 0), F 2 (c, 0). Pusti poentu M(x, y) leži na elipsi, i

zbir udaljenosti od njega do F 1 i F 2 jednako 2 a.

Onda r 1 + r 2 = 2a, ali ,

Stoga, uvođenje notacije b² = a²- c² i nakon jednostavnih algebarskih transformacija, dobijamo kanonska jednadžba elipse: (11.1)

Definicija 11.3.ekscentričnost elipsa se naziva količina e=c/a (11.2)

Definicija 11.4.Direktorica D i elipsa koja odgovara fokusu F i F i oko ose OU okomito na osu Oh na daljinu a/e od porijekla.

Komentar. Uz drugačiji izbor koordinatnog sistema, elipsa se može dati ne kanonskom jednačinom (11.1), već jednačinom drugog stepena druge vrste.

Svojstva elipse:

1) Elipsa ima dvije međusobno okomite ose simetrije (glavne ose elipse) i centar simetrije (centar elipse). Ako je elipsa data kanonskom jednačinom, tada su njene glavne ose koordinatne ose, a centar je ishodište. Budući da su dužine segmenata formiranih presjekom elipse sa glavnim osama jednake 2 a i 2 b (2a>2b), tada se glavna osa koja prolazi kroz žarišta naziva glavna os elipse, a druga velika os se naziva sporedna os.

2) Cijela elipsa je sadržana unutar pravokutnika

3) Ekscentricitet elipse e< 1.

stvarno,

4) Direktrise elipse nalaze se izvan elipse (pošto je udaljenost od centra elipse do direktrise a/e, a e<1, следовательно, a/e>a, a cijela elipsa leži u pravokutniku )

5) Odnos udaljenosti r i od tačke elipse do fokusa F i na distancu d i od ove tačke do direktrise koja odgovara fokusu jednaka je ekscentricitetu elipse.

Dokaz.

Udaljenosti od tačke M(x, y)žarišta elipse mogu se predstaviti na sljedeći način:

Sastavljamo jednadžbe direktrise:

(D 1), (D 2). Onda Odavde r i / d i = e, što je trebalo dokazati.

Hiperbola.

Definicija 11.5.Hiperbola je skup tačaka u ravni za koji je modul razlike između udaljenosti do dvije fiksne tačke F 1 i F 2 ovog aviona, tzv trikovi, je konstantna vrijednost.

Kanonsku jednačinu hiperbole izvodimo analogno izvođenju jednadžbe elipse, koristeći istu notaciju.

|r 1 - r 2 | = 2a, odakle Ako označavamo b² = c² - a², odavde možete dobiti

- kanonska jednadžba hiperbole. (11.3)

Definicija 11.6.ekscentričnost hiperbola se naziva količina e = c / a.

Definicija 11.7.Direktorica D i hiperbola koja odgovara fokusu F i, naziva se prava linija koja se nalazi u istoj poluravni sa F i oko ose OU okomito na osu Oh na daljinu a / e od porijekla.

Svojstva hiperbole:

1) Hiperbola ima dvije ose simetrije (glavne ose hiperbole) i centar simetrije (centar hiperbole). Štaviše, jedna od ovih osa seče se sa hiperbolom u dve tačke, koje se nazivaju vrhovi hiperbole. Zove se realna os hiperbole (os Oh za kanonski izbor koordinatnog sistema). Druga osa nema zajedničke tačke s hiperbolom i naziva se njegova imaginarna osa (u kanonskim koordinatama - os OU). Sa obe strane su desna i leva grana hiperbole. Žarišta hiperbole nalaze se na njenoj realnoj osi.

2) Grane hiperbole imaju dvije asimptote definirane jednadžbama

3) Uz hiperbolu (11.3) možemo uzeti u obzir i tzv. konjugiranu hiperbolu definiranu kanonskom jednadžbom

za koje se realna i imaginarna osa zamjenjuju uz zadržavanje istih asimptota.

4) Ekscentricitet hiperbole e> 1.

5) Odnos udaljenosti r i od tačke hiperbole do fokusa F i na distancu d i od ove tačke do direktrise koja odgovara fokusu jednaka je ekscentricitetu hiperbole.

Dokaz se može izvesti na isti način kao i za elipsu.

Parabola.

Definicija 11.8.parabola je skup tačaka u ravni za koje je udaljenost do neke fiksne tačke F ova ravan je jednaka udaljenosti do neke fiksne prave linije. Dot F pozvao fokus parabole, a prava linija - njegova ravnateljica.

U Za izvođenje jednadžbe parabole, biramo kartezijanski

koordinatni sistem tako da mu je ishodište sredina

D M(x,y) okomito FD, spušten iz fokusa u režiju

r su, a koordinatne ose postavljene paralelno i

okomito na direktora. Neka je dužina segmenta FD

D O F x je R. Zatim iz jednakosti r=d sledi to

ukoliko

Algebarske transformacije ova jednačina se može dovesti do oblika: y² = 2 px, (11.4)

pozvao kanonska jednadžba parabole. Vrijednost R pozvao parametar parabole.

Svojstva parabole:

1) Parabola ima os simetrije (osa parabole). Tačka presjeka parabole sa osom naziva se vrh parabole. Ako je parabola data kanonskom jednadžbom, tada je njena osa osa Oh, a vrh je ishodište koordinata.

2) Cijela parabola se nalazi u desnoj poluravnini Ohu.

Komentar. Koristeći svojstva direktrisa elipse i hiperbole i definiciju parabole, možemo dokazati sljedeću tvrdnju:

Skup ravnih tačaka za koji je omjer e udaljenost do neke fiksne tačke do udaljenosti do neke prave linije je konstantna vrijednost, je elipsa (sa e<1), гиперболу (при e>1) ili parabola (kada e=1).

Slične informacije.

Redukcija kvadratnih oblika

Razmotrimo najjednostavniji i najčešće korišten u praksi metod svođenja kvadratnog oblika na kanonski oblik, tzv. Lagrangeova metoda. Zasniva se na odabiru kompletnog kvadrata u kvadratnom obliku.

Teorema 10.1(Lagrangeova teorema) Bilo koji kvadratni oblik (10.1):

upotrebom nesingularne linearne transformacije (10.4) može se svesti na kanonski oblik (10.6):

,

□ Hajde da dokažemo teoremu na konstruktivan način, koristeći Lagrangeovu metodu odabira savršenih kvadrata. Problem je pronaći nesingularnu matricu takvu da linearna transformacija (10.4) rezultira kvadratnim oblikom (10.6) kanonskog oblika. Ova matrica će se dobiti postepeno kao proizvod konačnog broja matrica posebnog tipa.

Tačka 1 (pripremni).

1.1. Među varijablama izdvajamo onu koja istovremeno ulazi u kvadratni oblik u kvadratu i u prvom stepenu (zovemo je vodeća varijabla). Pređimo na tačku 2.

1.2. Ako nema vodeće varijable u kvadratnom obliku (za sve : ), tada biramo par varijabli čiji proizvod ulazi u formu sa koeficijentom koji nije nula i prelazimo na korak 3.

1.3. Ako u kvadratnom obliku nema proizvoda suprotno imenovanih varijabli, tada je dati kvadratni oblik već predstavljen u kanonskom obliku (10.6). Dokaz teoreme je potpun.

Tačka 2 (isticanje cijelog kvadrata).

2.1. Na osnovu vodeće varijable biramo puni kvadrat. Bez gubitka općenitosti, pretpostavljamo da je vodeća varijabla varijabla . Grupiranjem pojmova koji sadrže , dobivamo

.

Izdvajanje punog kvadrata preko varijable in , dobijamo

.

Dakle, kao rezultat odabira punog kvadrata za varijablu, dobijamo zbir kvadrata linearni oblik

koji uključuje vodeću varijablu , i kvadratni oblik od varijabli, u kojima vodeća varijabla više nije uključena. Hajde da izvršimo promjenu varijabli (uvedemo nove varijable)

dobijamo matricu

() nesingularna linearna transformacija , kao rezultat čega kvadratni oblik (10.1) poprima sljedeći oblik

Sa kvadratnom formom Uradimo isto kao u tački 1.

2.1. Ako je vodeća varijabla varijabla, tada postoje dva načina da to učinite: ili odaberite cijeli kvadrat za ovu varijablu ili izvršite preimenovanje (prenumeracija) varijable:

sa nesingularnom transformacijskom matricom:

.

Tačka 3 (kreiranje vodeće varijable). Odabrani par varijabli će biti zamijenjen zbirom i razlikom dvije nove varijable, a ostatak starih varijabli će biti zamijenjen odgovarajućim novim varijablama. Ako je, na primjer, u stavu 1. izraz

tada odgovarajuća promjena varijabli ima oblik

a u kvadratnom obliku (10.1) dobiće se vodeća varijabla.

Na primjer, u slučaju zamjene varijable:

matrica ove nesingularne linearne transformacije ima oblik

.

Kao rezultat gornjeg algoritma (uzastopna primjena tačaka 1, 2, 3), kvadratni oblik (10.1) će se svesti na kanonski oblik (10.6).

Imajte na umu da smo kao rezultat izvršenih transformacija na kvadratnom obliku (odabir punog kvadrata, preimenovanje i kreiranje vodeće varijable) koristili elementarne nesingularne matrice tri tipa (one su prijelazne matrice od baze do baze). Željena matrica nesingularne linearne transformacije (10.4), u kojoj oblik (10.1) ima kanonski oblik (10.6), dobija se množenjem konačnog broja elementarnih nesingularnih matrica tri tipa. ■

Primjer 10.2. Donesite kvadratni oblik

kanonskom obliku Lagrangeovom metodom. Navedite odgovarajuću nesingularnu linearnu transformaciju. Provjeri.

Odluka. Biramo vodeću varijablu (koeficijent ). Grupiranjem pojmova koji sadrže , i odabirom cijelog kvadrata na njemu, dobivamo

gdje je naznačeno

Hajde da izvršimo promjenu varijabli (uvedemo nove varijable)

Izražavanje starih varijabli u terminima novih:

dobijamo matricu