Tabela de ângulos trigonometria completa. Seno, cosseno, tangente e cotangente - tudo o que você precisa saber no OGE e no USE
Leia também
Os conceitos de seno (), cosseno (), tangente (), cotangente () estão inextricavelmente ligados ao conceito de ângulo. Para entender bem esses conceitos, à primeira vista, complexos (que causam um estado de horror em muitos escolares), e ter certeza de que “o diabo não é tão assustador quanto é pintado”, vamos começar do início e entender o conceito de ângulo.
O conceito de ângulo: radiano, grau
Vamos olhar para a imagem. O vetor "virou" em relação ao ponto por uma certa quantidade. Então a medida dessa rotação em relação à posição inicial será canto.
O que mais você precisa saber sobre o conceito de ângulo? Bem, unidades de ângulo, é claro!
O ângulo, tanto em geometria quanto em trigonometria, pode ser medido em graus e radianos.
O ângulo em (um grau) é o ângulo central no círculo, baseado em um arco circular igual à parte do círculo. Assim, todo o círculo consiste em "pedaços" de arcos circulares, ou seja, o ângulo descrito pelo círculo é igual.

Ou seja, a figura acima mostra um ângulo que é igual, ou seja, esse ângulo é baseado em um arco circular do tamanho da circunferência.
Um ângulo em radianos é chamado de ângulo central em um círculo, com base em um arco circular, cujo comprimento é igual ao raio do círculo. Bem, você entendeu? Se não, então vamos olhar para a imagem.

Assim, a figura mostra um ângulo igual a um radiano, ou seja, esse ângulo é baseado em um arco circular, cujo comprimento é igual ao raio do círculo (o comprimento é igual ao comprimento ou o raio é igual a o comprimento do arco). Assim, o comprimento do arco é calculado pela fórmula:
Onde é o ângulo central em radianos.
Bem, sabendo disso, você pode responder quantos radianos contém um ângulo descrito por um círculo? Sim, para isso você precisa se lembrar da fórmula da circunferência de um círculo. Lá está ela:
Bem, agora vamos correlacionar essas duas fórmulas e fazer com que o ângulo descrito pelo círculo seja igual. Ou seja, correlacionando o valor em graus e radianos, obtemos isso. Respectivamente, . Como você pode ver, ao contrário de "graus", a palavra "radiano" é omitida, pois a unidade de medida geralmente é clara no contexto.
Quantos radianos são? Isso mesmo!
Entendi? Em seguida, aperte para a frente:
Alguma dificuldade? Então veja respostas:
Triângulo retângulo: seno, cosseno, tangente, cotangente de um ângulo
Então, com o conceito de ângulo descoberto. Mas o que é o seno, cosseno, tangente, cotangente de um ângulo? Vamos descobrir. Para isso, um triângulo retângulo nos ajudará.

Como se chamam os lados de um triângulo retângulo? Isso mesmo, a hipotenusa e os catetos: a hipotenusa é o lado oposto ao ângulo reto (no nosso exemplo, este é o lado); as pernas são os dois lados restantes e (aqueles que são adjacentes ao ângulo reto), além disso, se considerarmos as pernas em relação ao ângulo, então a perna é a perna adjacente e a perna é a oposta. Então, agora vamos responder a pergunta: quais são o seno, cosseno, tangente e cotangente de um ângulo?
Seno de um ânguloé a razão da perna oposta (distante) para a hipotenusa.
em nosso triângulo.
Cosseno de um ângulo- esta é a razão da perna adjacente (próxima) para a hipotenusa.
em nosso triângulo.
Ângulo tangente- esta é a proporção da perna oposta (distante) para a adjacente (perto).
em nosso triângulo.
Cotangente de um ângulo- esta é a proporção da perna adjacente (próxima) para a oposta (distante).
em nosso triângulo.
Essas definições são necessárias lembrar! Para tornar mais fácil lembrar qual perna dividir por qual, você precisa entender claramente que em tangente e co-tangente apenas as pernas ficam sentadas, e a hipotenusa aparece apenas em seio e cosseno. E então você pode criar uma cadeia de associações. Por exemplo, este:
cosseno→toque→toque→adjacente;
Cotangente→toque→toque→adjacente.
Antes de tudo, é necessário lembrar que o seno, cosseno, tangente e cotangente como razões dos lados de um triângulo não dependem dos comprimentos desses lados (em um ângulo). Não confie? Então certifique-se olhando para a imagem:

Considere, por exemplo, o cosseno de um ângulo. Por definição, a partir de um triângulo: , mas podemos calcular o cosseno de um ângulo a partir de um triângulo: . Você vê, os comprimentos dos lados são diferentes, mas o valor do cosseno de um ângulo é o mesmo. Assim, os valores de seno, cosseno, tangente e cotangente dependem apenas da magnitude do ângulo.
Se você entende as definições, vá em frente e corrija-as!
Para o triângulo mostrado na figura abaixo, encontramos.

Bem, você conseguiu? Então tente você mesmo: calcule o mesmo para o canto.
Círculo unitário (trigonométrico)
Entendendo os conceitos de graus e radianos, consideramos um círculo com um raio igual a. Tal círculo é chamado solteiro. É muito útil no estudo da trigonometria. Portanto, nos debruçamos sobre isso com um pouco mais de detalhes.

Como você pode ver, este círculo é construído no sistema de coordenadas cartesianas. O raio do círculo é igual a um, enquanto o centro do círculo está na origem, a posição inicial do vetor de raio é fixada ao longo da direção positiva do eixo (no nosso exemplo, este é o raio).
Cada ponto do círculo corresponde a dois números: a coordenada ao longo do eixo e a coordenada ao longo do eixo. Quais são esses números de coordenadas? E, em geral, o que eles têm a ver com o tema em questão? Para fazer isso, lembre-se do triângulo retângulo considerado. Na figura acima, você pode ver dois triângulos retângulos inteiros. Considere um triângulo. É retangular porque é perpendicular ao eixo.
O que é igual a de um triângulo? Isso mesmo. Além disso, sabemos que é o raio do círculo unitário e, portanto, . Substitua esse valor em nossa fórmula de cosseno. Aqui está o que acontece:
E o que é igual a de um triângulo? Bem, claro, ! Substitua o valor do raio nesta fórmula e obtenha:
Então, você pode me dizer quais são as coordenadas de um ponto que pertence ao círculo? Bem, de jeito nenhum? E se você perceber isso e são apenas números? A que coordenada corresponde? Bem, é claro, a coordenada! A que coordenada corresponde? Isso mesmo, coordenar! Assim, o ponto.

E o que então são iguais e? Isso mesmo, vamos usar as definições apropriadas de tangente e cotangente e obter isso, a.
E se o ângulo for maior? Aqui, por exemplo, como nesta imagem:

O que mudou neste exemplo? Vamos descobrir. Para fazer isso, voltamos novamente para um triângulo retângulo. Considere um triângulo retângulo: um ângulo (como adjacente a um ângulo). Qual é o valor do seno, cosseno, tangente e cotangente de um ângulo? Isso mesmo, aderimos às definições correspondentes das funções trigonométricas:
Bem, como você pode ver, o valor do seno do ângulo ainda corresponde à coordenada; o valor do cosseno do ângulo - a coordenada; e os valores de tangente e cotangente às razões correspondentes. Assim, essas relações são aplicáveis a quaisquer rotações do vetor raio.
Já foi mencionado que a posição inicial do vetor raio é ao longo da direção positiva do eixo. Até agora, giramos esse vetor no sentido anti-horário, mas o que acontece se o girarmos no sentido horário? Nada de extraordinário, você também obterá um ângulo de um determinado tamanho, mas apenas negativo. Assim, ao girar o vetor raio no sentido anti-horário, obtemos ângulos positivos, e ao girar no sentido horário - negativo.
Então, sabemos que toda uma revolução do vetor raio ao redor do círculo é ou. É possível girar o vetor raio por ou por? Bem, claro que você pode! No primeiro caso, portanto, o vetor raio fará uma revolução completa e parará na posição ou.
No segundo caso, ou seja, o raio vetor fará três voltas completas e parará na posição ou.
Assim, a partir dos exemplos acima, podemos concluir que os ângulos que diferem por ou (onde é qualquer número inteiro) correspondem à mesma posição do vetor raio.
A figura abaixo mostra um ângulo. A mesma imagem corresponde ao canto, e assim por diante. Esta lista pode ser continuada indefinidamente. Todos esses ângulos podem ser escritos com a fórmula geral ou (onde é qualquer número inteiro)

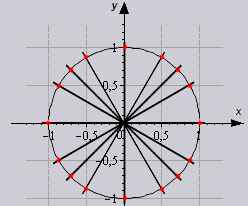
Agora, conhecendo as definições das funções trigonométricas básicas e usando o círculo unitário, tente responder a quais valores são iguais:
Aqui está um círculo unitário para ajudá-lo:

Alguma dificuldade? Então vamos descobrir. Então sabemos que:
A partir daqui, determinamos as coordenadas dos pontos correspondentes a certas medidas do ângulo. Bem, vamos começar pela ordem: o canto em corresponde a um ponto com coordenadas, portanto:
Não existe;
Além disso, seguindo a mesma lógica, descobrimos que os cantos em correspondem a pontos com coordenadas, respectivamente. Sabendo disso, é fácil determinar os valores das funções trigonométricas nos pontos correspondentes. Tente você mesmo primeiro, depois verifique as respostas.
Respostas:
Não existe
Não existe
Não existe
Não existe
Assim, podemos fazer a seguinte tabela:

Não há necessidade de lembrar todos esses valores. Basta lembrar a correspondência entre as coordenadas dos pontos no círculo unitário e os valores das funções trigonométricas:
Mas os valores das funções trigonométricas dos ângulos e, dados na tabela abaixo, deve ser lembrado:

Não tenha medo, agora vamos mostrar um dos exemplos memorização bastante simples dos valores correspondentes:
Para usar este método, é vital lembrar os valores do seno para todas as três medidas do ângulo (), bem como o valor da tangente do ângulo em. Conhecendo esses valores, é bastante fácil restaurar toda a tabela - os valores de cossenosão transferidos de acordo com as setas, ou seja:
Sabendo disso, você pode restaurar os valores para. O numerador " " corresponderá e o denominador " " corresponderá. Os valores cotangentes são transferidos de acordo com as setas mostradas na figura. Se você entender isso e se lembrar do diagrama com setas, será suficiente lembrar o valor inteiro da tabela.
Coordenadas de um ponto em um círculo
É possível encontrar um ponto (suas coordenadas) em um círculo, conhecendo as coordenadas do centro do círculo, seu raio e ângulo de rotação?
Bem, claro que você pode! Vamos trazer para fora fórmula geral para encontrar as coordenadas de um ponto.
Aqui, por exemplo, temos esse círculo:

Nos é dado que o ponto é o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas girando o ponto em graus.
Como pode ser visto na figura, a coordenada do ponto corresponde ao comprimento do segmento. O comprimento do segmento corresponde à coordenada do centro do círculo, ou seja, é igual a. O comprimento de um segmento pode ser expresso usando a definição de cosseno:
Então temos que para o ponto a coordenada.
Pela mesma lógica, encontramos o valor da coordenada y para o ponto. Nesse caminho,
Então, em termos gerais, as coordenadas dos pontos são determinadas pelas fórmulas:
Coordenadas do centro do círculo,
raio do círculo,
Ângulo de rotação do vetor raio.
Como você pode ver, para o círculo unitário que estamos considerando, essas fórmulas são significativamente reduzidas, pois as coordenadas do centro são zero e o raio é igual a um:
Bem, vamos tentar essas fórmulas para dar um gostinho, praticando encontrar pontos em um círculo?
1. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
2. Encontre as coordenadas de um ponto em um círculo unitário obtido pela rotação de um ponto.
3. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
4. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
5. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
Tendo problemas para encontrar as coordenadas de um ponto em um círculo?
Resolva esses cinco exemplos (ou entenda bem a solução) e você aprenderá como encontrá-los!
1.
Pode ser visto que. E sabemos o que corresponde a uma volta completa do ponto de partida. Assim, o ponto desejado estará na mesma posição que ao virar. Sabendo disso, encontramos as coordenadas desejadas do ponto:
2. O círculo é uma unidade com centro em um ponto, o que significa que podemos usar fórmulas simplificadas:
Pode ser visto que. Sabemos o que corresponde a duas rotações completas do ponto de partida. Assim, o ponto desejado estará na mesma posição que ao virar. Sabendo disso, encontramos as coordenadas desejadas do ponto:
Seno e cosseno são valores tabulares. Lembramos seus valores e obtemos:
Assim, o ponto desejado tem coordenadas.
3. O círculo é uma unidade com centro em um ponto, o que significa que podemos usar fórmulas simplificadas:
Pode ser visto que. Vamos descrever o exemplo considerado na figura:

O raio faz ângulos com o eixo igual a e. Sabendo que os valores tabulares do cosseno e do seno são iguais, e tendo determinado que o cosseno aqui assume um valor negativo e o seno é positivo, temos:
Exemplos semelhantes são analisados com mais detalhes ao estudar as fórmulas para reduzir funções trigonométricas no tópico.
Assim, o ponto desejado tem coordenadas.
4.
Ângulo de rotação do vetor de raio (por condição)
Para determinar os sinais correspondentes de seno e cosseno, construímos um círculo unitário e um ângulo:

Como você pode ver, o valor, ou seja, é positivo, e o valor, ou seja, é negativo. Conhecendo os valores tabulares das funções trigonométricas correspondentes, obtemos que:
Vamos substituir os valores obtidos em nossa fórmula e encontrar as coordenadas:
Assim, o ponto desejado tem coordenadas.
5. Para resolver este problema, usamos fórmulas na forma geral, onde
As coordenadas do centro do círculo (no nosso exemplo,
Raio do círculo (por condição)
Ângulo de rotação do vetor raio (por condição).
Substitua todos os valores na fórmula e obtenha:
e - valores da tabela. Lembramos e os substituímos na fórmula:
Assim, o ponto desejado tem coordenadas.
RESUMO E FÓRMULA BÁSICA
O seno de um ângulo é a razão entre o cateto oposto (distante) e a hipotenusa.
O cosseno de um ângulo é a razão entre o cateto adjacente (próximo) e a hipotenusa.
A tangente de um ângulo é a razão entre a perna oposta (distante) e a adjacente (próxima).
A cotangente de um ângulo é a razão entre a perna adjacente (próxima) e a oposta (distante).
No século V aC, o antigo filósofo grego Zenão de Elea formulou suas famosas aporias, das quais a mais famosa é a aporia "Aquiles e a tartaruga". Aqui está como soa:Digamos que Aquiles corra dez vezes mais rápido que a tartaruga e esteja mil passos atrás dela. No tempo que Aquiles leva para percorrer essa distância, a tartaruga rasteja cem passos na mesma direção. Quando Aquiles tiver dado cem passos, a tartaruga rastejará outros dez passos, e assim por diante. O processo continuará indefinidamente, Aquiles nunca alcançará a tartaruga.
Esse raciocínio se tornou um choque lógico para todas as gerações subsequentes. Aristóteles, Diógenes, Kant, Hegel, Gilbert... Todos eles, de uma forma ou de outra, consideravam as aporias de Zenão. O choque foi tão forte que " ... as discussões continuam no momento, a comunidade científica ainda não conseguiu chegar a uma opinião comum sobre a essência dos paradoxos ... análise matemática, teoria dos conjuntos, novas abordagens físicas e filosóficas estiveram envolvidas no estudo do assunto ; nenhum deles se tornou uma solução universalmente aceita para o problema..."[Wikipedia," Zeno's Aporias "]. Todos entendem que estão sendo enganados, mas ninguém entende qual é o engano.
Do ponto de vista da matemática, Zenão em sua aporia demonstrou claramente a transição do valor para. Esta transição implica aplicar em vez de constantes. Tanto quanto eu entendo, o aparato matemático para aplicar unidades de medida variáveis ainda não foi desenvolvido ou não foi aplicado à aporia de Zenão. A aplicação de nossa lógica usual nos leva a uma armadilha. Nós, pela inércia do pensamento, aplicamos unidades constantes de tempo ao recíproco. Do ponto de vista físico, parece que o tempo desacelera até parar completamente no momento em que Aquiles alcança a tartaruga. Se o tempo parar, Aquiles não pode mais ultrapassar a tartaruga.
Se virarmos a lógica a que estamos acostumados, tudo se encaixa. Aquiles corre a uma velocidade constante. Cada segmento subsequente de seu caminho é dez vezes mais curto que o anterior. Assim, o tempo gasto para superá-lo é dez vezes menor que o anterior. Se aplicarmos o conceito de "infinito" nessa situação, seria correto dizer "Aquiles ultrapassará a tartaruga infinitamente rapidamente".
Como evitar essa armadilha lógica? Permaneça em unidades de tempo constantes e não mude para valores recíprocos. Na linguagem de Zeno, fica assim:
No tempo que Aquiles leva para correr mil passos, a tartaruga rasteja cem passos na mesma direção. Durante o próximo intervalo de tempo, igual ao primeiro, Aquiles dará mais mil passos e a tartaruga rastejará cem passos. Agora Aquiles está oitocentos passos à frente da tartaruga.
Esta abordagem descreve adequadamente a realidade sem quaisquer paradoxos lógicos. Mas esta não é uma solução completa para o problema. A afirmação de Einstein sobre a intransponibilidade da velocidade da luz é muito semelhante à aporia de Zenão "Aquiles e a tartaruga". Ainda temos que estudar, repensar e resolver esse problema. E a solução deve ser buscada não em números infinitamente grandes, mas em unidades de medida.
Outra aporia interessante de Zenão fala de uma flecha voadora:
Uma flecha voadora é imóvel, pois em cada momento está em repouso, e como está em repouso em todos os momentos, está sempre em repouso.
Nesta aporia, o paradoxo lógico é superado de forma muito simples - basta esclarecer que a cada momento a flecha voadora está em repouso em diferentes pontos do espaço, o que, na verdade, é movimento. Há outro ponto a ser observado aqui. A partir de uma fotografia de um carro na estrada, é impossível determinar o fato de seu movimento ou a distância até ele. Para determinar o fato do movimento do carro, são necessárias duas fotografias tiradas do mesmo ponto em pontos diferentes no tempo, mas não podem ser usadas para determinar a distância. Para determinar a distância até o carro, você precisa de duas fotografias tiradas de diferentes pontos no espaço ao mesmo tempo, mas não pode determinar o fato do movimento delas (é claro, você ainda precisa de dados adicionais para cálculos, a trigonometria o ajudará) . O que quero salientar em particular é que dois pontos no tempo e dois pontos no espaço são duas coisas diferentes que não devem ser confundidas, pois oferecem diferentes oportunidades de exploração.
quarta-feira, 4 de julho de 2018
Muito bem as diferenças entre set e multiset estão descritas na Wikipedia. Nós olhamos.
Como você pode ver, "o conjunto não pode ter dois elementos idênticos", mas se houver elementos idênticos no conjunto, esse conjunto é chamado de "multiconjunto". Os seres racionais jamais compreenderão tal lógica do absurdo. Este é o nível de papagaios falantes e macacos treinados, no qual a mente está ausente da palavra "completamente". Os matemáticos agem como treinadores comuns, pregando suas ideias absurdas para nós.
Era uma vez, os engenheiros que construíram a ponte estavam em um barco debaixo da ponte durante os testes da ponte. Se a ponte desabasse, o engenheiro medíocre morria sob os escombros de sua criação. Se a ponte pudesse suportar a carga, o talentoso engenheiro construiu outras pontes.
Por mais que os matemáticos se escondam atrás da frase "cuidado comigo, estou em casa", ou melhor, "a matemática estuda conceitos abstratos", há um cordão umbilical que os conecta inextricavelmente com a realidade. Este cordão umbilical é dinheiro. Vamos aplicar a teoria dos conjuntos matemáticos aos próprios matemáticos.
Estudamos matemática muito bem e agora estamos sentados no caixa, pagando salários. Aqui um matemático vem até nós por seu dinheiro. Contamos o valor total para ele e o colocamos em nossa mesa em pilhas diferentes, nas quais colocamos notas do mesmo valor. Em seguida, pegamos uma nota de cada pilha e damos ao matemático seu "conjunto de salários matemáticos". Explicamos a matemática que ele só receberá o restante das contas quando provar que o conjunto sem elementos idênticos não é igual ao conjunto com elementos idênticos. Isto é onde a diversão começa.
Em primeiro lugar, a lógica dos deputados funcionará: "você pode aplicar aos outros, mas não a mim!" Além disso, começarão as garantias de que existem números de notas diferentes nas notas da mesma denominação, o que significa que não podem ser considerados elementos idênticos. Bem, contamos o salário em moedas - não há números nas moedas. Aqui o matemático lembrará freneticamente da física: moedas diferentes têm quantidades diferentes de sujeira, a estrutura cristalina e o arranjo dos átomos para cada moeda são únicos ...
E agora eu tenho a pergunta mais interessante: onde está o limite além do qual elementos de um multiconjunto se transformam em elementos de um conjunto e vice-versa? Tal linha não existe - tudo é decidido pelos xamãs, a ciência aqui não está nem perto.
Olhe aqui. Selecionamos estádios de futebol com a mesma área de campo. A área dos campos é a mesma, o que significa que temos um multiset. Mas se considerarmos os nomes dos mesmos estádios, conseguimos muito, porque os nomes são diferentes. Como você pode ver, o mesmo conjunto de elementos é um conjunto e um multiconjunto ao mesmo tempo. Como certo? E aqui o matemático-xamã-shuller tira um ás de trunfo da manga e começa a nos falar sobre um conjunto ou um multiconjunto. De qualquer forma, ele nos convencerá de que está certo.
Para entender como os xamãs modernos operam com a teoria dos conjuntos, atrelando-a à realidade, basta responder a uma pergunta: como os elementos de um conjunto diferem dos elementos de outro conjunto? Vou lhe mostrar, sem nenhum "concebível como um todo" ou "não concebível como um todo".
domingo, 18 de março de 2018
A soma dos dígitos de um número é uma dança de xamãs com um pandeiro, que nada tem a ver com matemática. Sim, nas aulas de matemática somos ensinados a encontrar a soma dos dígitos de um número e usá-la, mas eles são xamãs para isso, para ensinar seus descendentes suas habilidades e sabedoria, caso contrário os xamãs simplesmente morrerão.
Você precisa de provas? Abra a Wikipedia e tente encontrar a página "Soma de dígitos de um número". Ela não existe. Não existe uma fórmula em matemática pela qual você possa encontrar a soma dos dígitos de qualquer número. Afinal, os números são símbolos gráficos com os quais escrevemos números e, na linguagem da matemática, a tarefa soa assim: "Encontre a soma dos símbolos gráficos que representam qualquer número". Os matemáticos não podem resolver este problema, mas os xamãs podem fazê-lo de forma elementar.
Vamos descobrir o que e como fazemos para encontrar a soma dos dígitos de um determinado número. E assim, digamos que temos o número 12345. O que precisa ser feito para encontrar a soma dos dígitos desse número? Vamos considerar todas as etapas em ordem.
1. Anote o número em um pedaço de papel. O que nos fizemos? Convertemos o número em um símbolo gráfico numérico. Esta não é uma operação matemática.
2. Cortamos uma foto recebida em várias fotos contendo números separados. Cortar uma imagem não é uma operação matemática.
3. Converta caracteres gráficos individuais em números. Esta não é uma operação matemática.
4. Some os números resultantes. Agora isso é matemática.
A soma dos dígitos do número 12345 é 15. São os "cursos de corte e costura" dos xamãs usados pelos matemáticos. Mas isso não é tudo.
Do ponto de vista da matemática, não importa em qual sistema numérico escrevemos o número. Assim, em diferentes sistemas numéricos, a soma dos dígitos do mesmo número será diferente. Em matemática, o sistema numérico é indicado como um subscrito à direita do número. Com um grande número de 12345, não quero enganar minha cabeça, considere o número 26 do artigo sobre. Vamos escrever este número em sistemas numéricos binários, octais, decimais e hexadecimais. Não consideraremos cada etapa sob um microscópio, já fizemos isso. Vejamos o resultado.
Como você pode ver, em diferentes sistemas numéricos, a soma dos dígitos do mesmo número é diferente. Este resultado não tem nada a ver com matemática. É como encontrar a área de um retângulo em metros e centímetros lhe daria resultados completamente diferentes.
Zero em todos os sistemas numéricos parece o mesmo e não tem soma de dígitos. Este é outro argumento a favor do fato de que . Uma pergunta para os matemáticos: como se denota em matemática aquilo que não é um número? O que, para os matemáticos, nada além de números existe? Para os xamãs, posso permitir isso, mas para os cientistas, não. A realidade não é apenas sobre números.
O resultado obtido deve ser considerado como prova de que os sistemas numéricos são unidades de medida dos números. Afinal, não podemos comparar números com unidades de medida diferentes. Se as mesmas ações com diferentes unidades de medida da mesma quantidade levam a resultados diferentes depois de compará-las, isso não tem nada a ver com matemática.
O que é matemática de verdade? É quando o resultado de uma ação matemática não depende do valor do número, da unidade de medida utilizada e de quem realiza essa ação.
Ai! Este não é o banheiro feminino?
- Jovem! Este é um laboratório para estudar a santidade indefinida das almas após a ascensão ao céu! Nimbus no topo e seta para cima. Que outro banheiro?
Feminino... Uma auréola em cima e uma seta para baixo é masculina.
Se você tem uma obra de arte de design piscando diante de seus olhos várias vezes ao dia,
Então não é de surpreender que de repente você encontre um ícone estranho em seu carro:
Pessoalmente, eu me esforço para ver menos quatro graus em uma pessoa fazendo cocô (uma foto) (composição de várias fotos: sinal de menos, número quatro, designação de graus). E eu não considero essa garota uma tola que não sabe física. Ela só tem um estereótipo de arco de percepção de imagens gráficas. E os matemáticos nos ensinam isso o tempo todo. Aqui está um exemplo.
1A não é "menos quatro graus" ou "um a". Isso é "pooping man" ou o número "vinte e seis" no sistema numérico hexadecimal. As pessoas que trabalham constantemente nesse sistema numérico percebem automaticamente o número e a letra como um símbolo gráfico.
No artigo, entenderemos completamente como é tabela de valores trigonométricos, seno, cosseno, tangente e cotangente. Considere o valor básico das funções trigonométricas, de um ângulo de 0,30,45,60,90,...,360 graus. E vamos ver como usar essas tabelas no cálculo do valor das funções trigonométricas.
Primeiro considere tabela de cosseno, seno, tangente e cotangente de um ângulo de 0, 30, 45, 60, 90, .. graus. A definição dessas quantidades permite determinar o valor das funções dos ângulos de 0 e 90 graus:
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, a cotangente de 00 será indefinida
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, a tangente de 90 0 será indefinida
Se tomarmos triângulos retângulos cujos ângulos são de 30 a 90 graus. Nós temos:
sen 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sen 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sen 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3
Representamos todos os valores obtidos na forma tabela trigonométrica:
Tabela de senos, cossenos, tangentes e cotangentes!
Se usarmos a fórmula de elenco, nossa tabela aumentará, valores para ângulos de até 360 graus serão adicionados. Será parecido com:

Além disso, com base nas propriedades da periodicidade, a tabela pode ser aumentada se substituirmos os ângulos por 0 0 +360 0 *z .... 330 0 +360 0 *z, em que z é um número inteiro. Nesta tabela, é possível calcular o valor de todos os ângulos correspondentes a pontos em um único círculo.
Vamos ver claramente como usar a tabela na solução.
Tudo é muito simples. Como o valor de que precisamos está no ponto de interseção das células de que precisamos. Por exemplo, vamos pegar cos de um ângulo de 60 graus, na tabela ficará assim:

Na tabela final dos principais valores das funções trigonométricas, agimos da mesma forma. Mas nesta tabela é possível descobrir quanto será a tangente de um ângulo de 1020 graus, ela = -√3 Vamos verificar 1020 0 = 300 0 +360 0 *2. Vamos encontrar a mesa.

Mesa Bradis. Para seno, cosseno, tangente e cotangente.
As tabelas de Bradys são divididas em várias partes, elas consistem em tabelas de cosseno e seno, tangente e cotangente - que é dividida em duas partes (tg de um ângulo de até 90 graus e ctg de pequenos ângulos).
Seno e cosseno

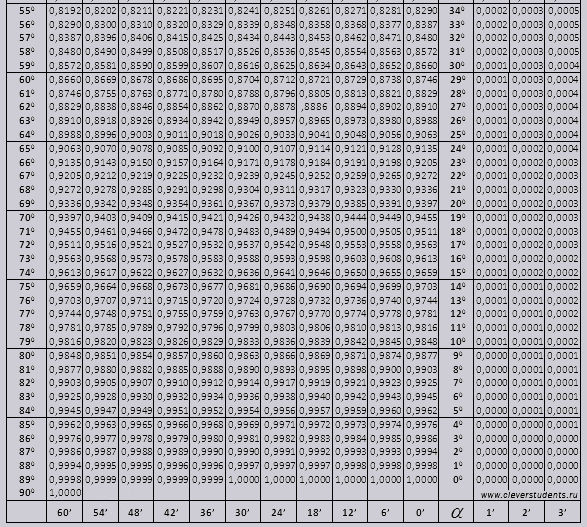
ângulo tg de 00 a 760, ângulo ctg de 140 a 900.
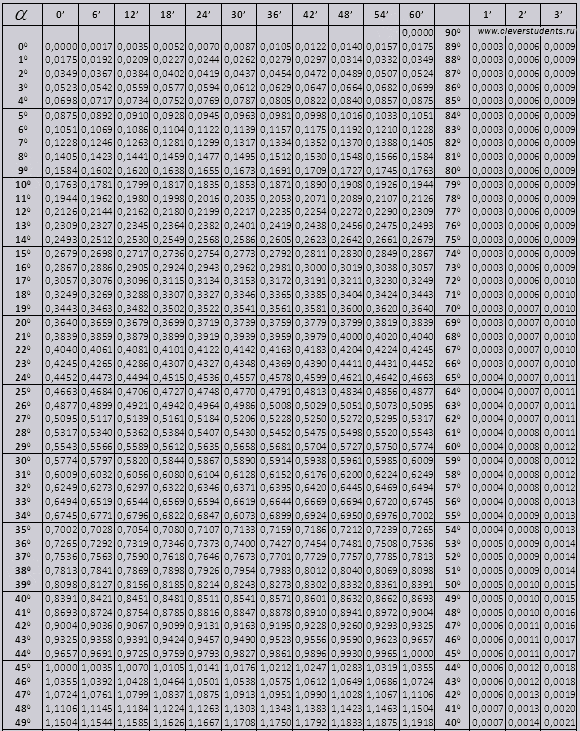

tg até 900 e ctg pequenos ângulos.
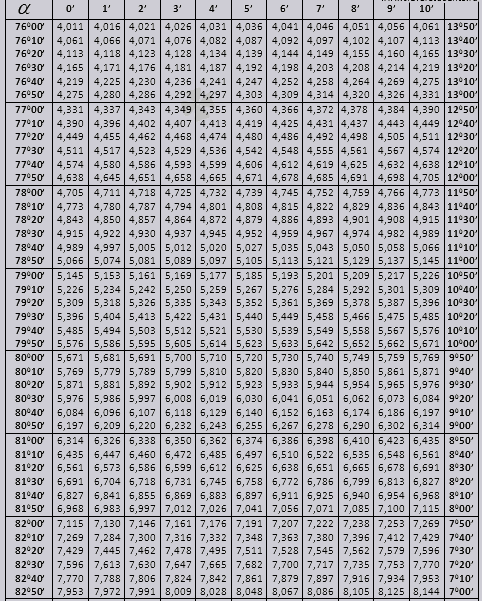

Vamos descobrir como usar as tabelas de Bradis na resolução de problemas.
Vamos encontrar a designação sin (a designação na coluna da borda esquerda) 42 minutos (a designação está na linha superior). Ao cruzar estamos procurando uma designação, é = 0,3040.
Os valores de minutos são indicados com um intervalo de seis minutos, e se o valor que precisamos estiver dentro desse intervalo. Vamos levar 44 minutos, e na tabela são apenas 42. Tomamos 42 como base e usamos as colunas adicionais do lado direito, pegamos a 2ª correção e somamos 0,3040 + 0,0006, obtemos 0,3046.
Com sen 47 min, tomamos 48 min como base e subtraímos 1 correção dele, ou seja, 0,3057 - 0,0003 = 0,3054
Ao calcular cos, trabalhamos de forma semelhante ao sin, apenas tomamos a linha inferior da tabela como base. Por exemplo, cos 20 0 = 0,9397
Os valores tg de um ângulo de até 90 0 e cot de um ângulo pequeno estão corretos e não há correções neles. Por exemplo, encontre tg 78 0 37min = 4,967 
e ctg 20 0 13 min = 25,83 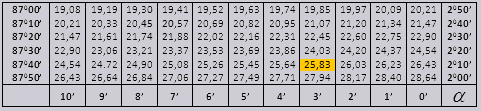
Bem, aqui consideramos as principais tabelas trigonométricas. Esperamos que esta informação tenha sido extremamente útil para você. Suas dúvidas sobre as mesas, se houver, não deixe de escrever nos comentários!
Nota: Guarda-lamas de parede - uma placa de guarda-lamas para proteger as paredes. Siga o link para-lamas sem moldura (http://www.spi-polymer.ru/otboyniki/) e saiba mais.
Começamos nosso estudo de trigonometria com um triângulo retângulo. Vamos definir o que são o seno e o cosseno, assim como a tangente e a cotangente de um ângulo agudo. Estes são os fundamentos da trigonometria.
Lembre-se que ângulo certoé um ângulo igual a 90 graus. Em outras palavras, metade do canto desdobrado.
Canto afiado- menos de 90 graus.
Ângulo obtuso- superior a 90 graus. Em relação a tal ângulo, "blunt" não é um insulto, mas um termo matemático :-)
Vamos desenhar um triângulo retângulo. Um ângulo reto é geralmente denotado. Observe que o lado oposto ao canto é indicado pela mesma letra, apenas pequena. Assim, o lado oposto ao ângulo A é denotado.
Um ângulo é denotado pela letra grega correspondente.

Hipotenusa Um triângulo retângulo é o lado oposto ao ângulo reto.
Pernas- lados opostos a cantos vivos.
A perna oposta ao canto é chamada oposto(relativo ao ângulo). A outra perna, que fica de um lado do canto, é chamada adjacente.
Seioângulo agudo em um triângulo retângulo é a razão entre o cateto oposto e a hipotenusa:
Cossenoângulo agudo em um triângulo retângulo - a razão entre o cateto adjacente e a hipotenusa:
Tangenteângulo agudo em um triângulo retângulo - a proporção da perna oposta para o adjacente:
Outra definição (equivalente): a tangente de um ângulo agudo é a razão entre o seno de um ângulo e seu cosseno:
Co-tangenteângulo agudo em um triângulo retângulo - a razão da perna adjacente para o oposto (ou, equivalentemente, a razão de cosseno para seno):
Preste atenção às razões básicas para seno, cosseno, tangente e cotangente, que são dadas abaixo. Eles serão úteis para nós na resolução de problemas.

Vamos provar alguns deles.
Ok, nós demos definições e fórmulas escritas. Mas por que precisamos de seno, cosseno, tangente e cotangente?
Nós sabemos isso a soma dos ângulos de qualquer triângulo é.
Conhecemos a relação entre partidos triângulo retângulo. Este é o teorema de Pitágoras: .
Acontece que conhecendo dois ângulos em um triângulo, você pode encontrar o terceiro. Conhecendo dois lados de um triângulo retângulo, você pode encontrar o terceiro. Então, para ângulos - sua proporção, para lados - deles próprios. Mas o que fazer se em um triângulo retângulo um ângulo (exceto o direito) e um lado são conhecidos, mas você precisa encontrar outros lados?

Era isso que as pessoas enfrentavam no passado, fazendo mapas da área e do céu estrelado. Afinal, nem sempre é possível medir diretamente todos os lados de um triângulo.
Seno, cosseno e tangente - eles também são chamados funções trigonométricas do ângulo- dê a razão entre partidos e cantos triângulo. Conhecendo o ângulo, você pode encontrar todas as suas funções trigonométricas usando tabelas especiais. E conhecendo os senos, cossenos e tangentes dos ângulos de um triângulo e de um de seus lados, você pode encontrar o resto.
Também desenharemos uma tabela de valores de seno, cosseno, tangente e cotangente para ângulos "bons" de a.
Observe os dois traços vermelhos na tabela. Para os valores correspondentes dos ângulos, a tangente e a cotangente não existem.
Vamos analisar vários problemas em trigonometria das tarefas do Banco de FIPI.
1. Em um triângulo, o ângulo é , . Achar .
O problema é resolvido em quatro segundos.
Porque o , .
2. Em um triângulo, o ângulo é , , . Achar .

Vamos encontrar pelo teorema de Pitágoras.
Problema resolvido.
Muitas vezes em problemas existem triângulos com ângulos e ou com ângulos e . Memorize as proporções básicas para eles de cor!

Para um triângulo com ângulos e o cateto oposto ao ângulo em é igual a metade da hipotenusa.
Um triângulo com ângulos e isósceles. Nele, a hipotenusa é vezes maior que a perna.
Consideramos problemas para resolver triângulos retângulos - isto é, para encontrar lados ou ângulos desconhecidos. Mas isso não é tudo! Nas variantes do exame em matemática, existem muitas tarefas onde aparece o seno, cosseno, tangente ou cotangente do ângulo externo do triângulo. Mais sobre isso no próximo artigo.
Dados de referência para tangente (tg x) e cotangente (ctg x). Definição geométrica, propriedades, gráficos, fórmulas. Tabela de tangentes e cotangentes, derivadas, integrais, expansões em série. Expressões através de variáveis complexas. Conexão com funções hiperbólicas.
Definição geométrica

|BD| - o comprimento do arco de um círculo centrado no ponto A.
α é o ângulo expresso em radianos.
Tangente ( tgα) é uma função trigonométrica que depende do ângulo α entre a hipotenusa e o cateto de um triângulo retângulo, igual à razão do comprimento do cateto oposto |BC| ao comprimento da perna adjacente |AB| .
Cotangente ( ctgα) é uma função trigonométrica que depende do ângulo α entre a hipotenusa e o cateto de um triângulo retângulo, igual à razão do comprimento do cateto adjacente |AB| ao comprimento da perna oposta |BC| .
Tangente
Onde n- todo.
Na literatura ocidental, a tangente é denotada da seguinte forma:
.
;
;
.
Gráfico da função tangente, y = tg x

Co-tangente
Onde n- todo.
Na literatura ocidental, a cotangente é denotada da seguinte forma:
.
A seguinte notação também foi adotada:
;
;
.
Gráfico da função cotangente, y = ctg x

Propriedades da tangente e cotangente
Periodicidade
Funções y= tg x e y= ctg x são periódicas com período π.
Paridade
As funções tangente e cotangente são ímpares.
Domínios de definição e valores, ascendentes, descendentes
As funções tangente e cotangente são contínuas em seu domínio de definição (veja a prova de continuidade). As principais propriedades da tangente e da cotangente são apresentadas na tabela ( n- inteiro).
| y= tg x | y= ctg x | |
| Escopo e continuidade | ||
| Faixa de valores | -∞ < y < +∞ | -∞ < y < +∞ |
| Ascendente | - | |
| descendente | - | |
| Extremos | - | - |
| Zeros, y = 0 | ||
| Pontos de interseção com o eixo y, x = 0 | y= 0 | - |
Fórmulas
Expressões em termos de seno e cosseno
;
;
;
;
;
Fórmulas para tangente e cotangente de soma e diferença
O resto das fórmulas são fáceis de obter, por exemplo
Produto de tangentes
A fórmula da soma e diferença de tangentes
Esta tabela mostra os valores de tangentes e cotangentes para alguns valores do argumento. 
Expressões em termos de números complexos
Expressões em termos de funções hiperbólicas
;
;
Derivativos
; .
.
Derivada da enésima ordem em relação à variável x da função:
.
Derivação de fórmulas para tangente > > > ; para cotangente > > >
Integrais
Expansões em série
Para obter a expansão da tangente em potências de x, você precisa obter vários termos da expansão em uma série de potências para as funções pecado x e cos x e divida esses polinômios entre si , . Isso resulta nas seguintes fórmulas.
No .
no .
Onde B n- Números de Bernoulli. Eles são determinados a partir da relação de recorrência:
;
;
Onde .
Ou de acordo com a fórmula de Laplace: 
Funções inversas
As funções inversas de tangente e cotangente são arcotangente e arcotangente, respectivamente.
Arctangente, arctg
, Onde n- todo.
Arco tangente, arcctg
, Onde n- todo.
Referências:
DENTRO. Bronstein, K. A. Semendyaev, Manual de Matemática para Engenheiros e Estudantes de Instituições de Ensino Superior, Lan, 2009.
G. Korn, Manual de Matemática para Pesquisadores e Engenheiros, 2012.