Zasada rozwiązywania nierówności metodą przedziałową. Metoda przedziałowa: rozwiązywanie najprostszych ścisłych nierówności
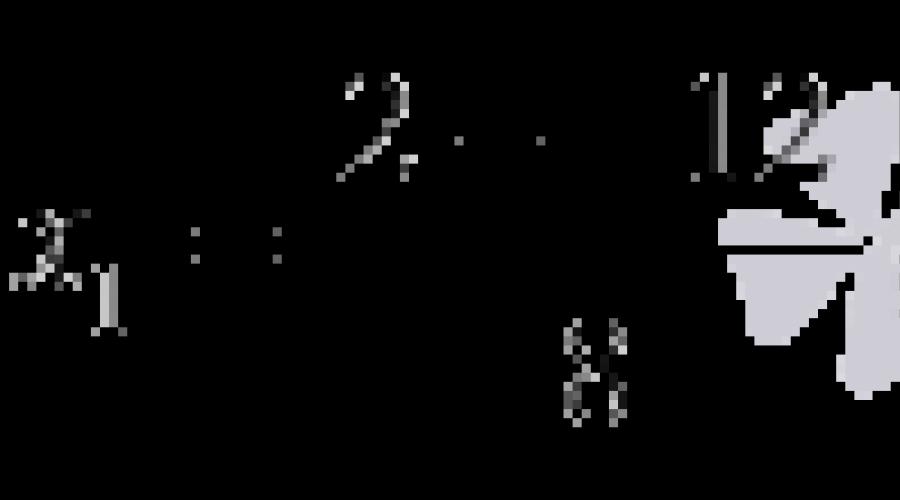
Przeczytaj także
Metoda interwałowa to metoda uniwersalna rozwiązuje nierówności, w szczególności pozwala rozwiązywać nierówności kwadratowe w jednej zmiennej. W tym artykule szczegółowo omówimy wszystkie niuanse rozwiązywania nierówności kwadratowych za pomocą metody przedziałowej. Najpierw przedstawiamy algorytm, po którym przeanalizujemy szczegółowo gotowe rozwiązania typowe przykłady.
Nawigacja strony.
Algorytm
Pierwsza znajomość metody przedziałowej następuje zwykle na lekcjach algebry, kiedy uczą się rozwiązywania nierówności kwadratowych. W tym przypadku algorytm metody przedziałowej podany jest w postaci przystosowanej specjalnie do rozwiązywania nierówności kwadratowych. Składając hołd prostocie, podamy ją również w tej formie, oraz algorytm ogólny Z metodą interwałową możesz zapoznać się korzystając z linku na samym początku tego artykułu.
Więc, algorytm rozwiązywania nierówności kwadratowych metodą przedziałową Jest:
- Znajdowanie zer trójmian kwadratowy a·x 2 +b·x+c od lewej strony nierówności kwadratowej.
- Rysujemy go i jeśli są korzenie, zaznaczamy je na nim. Ponadto, jeśli rozwiązujemy nierówność ścisłą, to oznaczamy je pustymi (przebitymi) punktami, a jeśli rozwiązujemy nieścisłą nierówność, to punktami zwykłymi. Psują się oś współrzędnych w przerwach.
- Ustalamy, które znaki mają wartości trójmianu na każdym przedziale (jeśli w pierwszym kroku znaleziono zera) lub na całej osi liczbowej (jeśli nie ma zer), powiemy Ci, jak to zrobić poniżej. I stawiamy + lub - nad tymi przedziałami zgodnie z pewnymi znakami.
- Jeśli zdecydujemy nierówność kwadratowa ze znakiem > lub ≥, to cieniujemy przedziały ze znakiem +, natomiast jeśli nierówność rozwiązujemy znakiem< или ≤, то наносим штриховку над промежутками со знаком −. В результате получаем , которое и является искомым решением неравенства.
- Zapisujemy odpowiedź.
Zgodnie z obietnicą wyjaśniamy trzeci krok zapowiadanego algorytmu. Istnieje kilka podstawowych podejść, które pozwalają znaleźć znaki w odstępach czasu. Przeanalizujemy je na przykładach i zaczniemy od wiarygodnych, ale nie najbardziej szybki sposób, która polega na obliczeniu wartości trójmianu w poszczególnych punktach przedziałów.
Weźmy trójmian x 2 +4 x−5, jego pierwiastkami są liczby −5 i 1, dzielą one oś liczbową na trzy przedziały (−∞, −5), (−5, 1) i (1, +∞ ).
Wyznaczmy znak trójmianu x 2 +4·x−5 na przedziale (1, +∞) . Aby to zrobić, obliczamy wartość tego trójmianu dla pewnej wartości x z tego przedziału. Wskazane jest przyjęcie wartości zmiennej, aby obliczenia były proste. W naszym przypadku możemy przyjąć np. x=2 (przy tej liczbie łatwiej przeprowadzić obliczenia niż np. przy 1,3, 74 lub). Podstawiamy go do trójmianu zamiast zmiennej x, w wyniku czego otrzymujemy 2 2 +4 2−5=7. 7 jest liczbą dodatnią, co oznacza, że dowolna wartość trójmianu kwadratowego na przedziale (1, +∞) będzie dodatnia. W ten sposób zdefiniowaliśmy znak +.
Aby utrwalić umiejętności, określimy znaki na pozostałych dwóch polach. Zacznijmy od znaku na przedziale (−5, 1) . Z tego przedziału najlepiej wziąć x=0 i obliczyć wartość trójmianu kwadratowego dla tej wartości zmiennej, mamy 0 2 +4·0−5=−5. Od -5 – liczba ujemna, to w tym przedziale wszystkie wartości trójmianu będą ujemne, dlatego zdefiniowaliśmy znak minus.
Pozostaje znaleźć znak na przedziale (−∞, −5) . Weźmy x=−6, podstawmy za x i otrzymamy (−6) 2 +4·(−6)−5=7, zatem wymaganym znakiem będzie plus.
Ale następujące fakty pozwalają na szybsze umieszczanie znaków:
- Gdy trójmian kwadratowy ma dwa pierwiastki (z dodatnim dyskryminatorem), wówczas znaki jego wartości w przedziałach, na które te pierwiastki dzielą oś liczbową, naprzemiennie (jak w poprzednim przykładzie). Oznacza to, że wystarczy określić znak w jednym z trzech przedziałów i umieścić znaki na pozostałych przedziałach, naprzemiennie. W rezultacie możliwy jest jeden z dwóch ciągów znaków: +, -, + lub -, +, -. Co więcej, ogólnie można obejść się bez obliczania wartości trójmianu kwadratowego w punkcie przedziału i wyciągać wnioski na temat znaków na podstawie wartości współczynnika wiodącego a: jeśli a>0, to mamy ciąg znaków + , -, + i jeśli a<0 – то −, +, −.
- Jeśli trójmian kwadratowy ma jeden pierwiastek (gdy dyskryminator wynosi zero), to pierwiastek ten dzieli oś liczbową na dwa przedziały, a znaki nad nimi będą takie same. Oznacza to, że wystarczy określić znak nad jednym z nich, a nad drugim - umieścić ten sam. Spowoduje to +, + lub -, -. Wnioski na podstawie znaków można także wyciągnąć na podstawie wartości współczynnika a: jeśli a > 0, to będzie to +, +, a jeśli a<0 , то −, −.
- Gdy trójmian kwadratowy nie ma pierwiastków, wówczas znaki jego wartości na całej osi liczbowej pokrywają się zarówno ze znakiem wiodącego współczynnika a, jak i znakiem wolnego terminu c. Rozważmy na przykład kwadratowy trójmian −4 x 2 −7, nie ma on pierwiastków (jego wyróżnik jest ujemny), a na przedziale (−∞, +∞) jego wartości są ujemne, ponieważ współczynnik x 2 wynosi liczba ujemna -4, a wyraz wolny -7 jest również ujemny.
Teraz przeanalizowaliśmy wszystkie kroki algorytmu i pozostaje rozważyć przykłady rozwiązywania nierówności kwadratowych za jego pomocą.
Przykłady z rozwiązaniami
Przejdźmy do ćwiczeń. Rozwiążmy kilka nierówności kwadratowych metodą przedziałową i omówmy główne charakterystyczne przypadki.
Przykład.
Rozwiąż nierówność 8 x 2 −4 x−1≥0 .
Rozwiązanie.
Rozwiążmy tę nierówność kwadratową metodą przedziałową. W pierwszym kroku polega to na poszukiwaniu pierwiastków trójmianu kwadratowego 8 x 2 −4 x −1 . Współczynnik x jest parzysty, więc wygodniej jest obliczyć nie dyskryminator, ale jego czwartą część: D"=(−2) 2 −8·(−1)=12. Ponieważ jest on większy od zera, znajdujemy dwa korzenie  I
I  .
.
Teraz zaznaczamy je na linii współrzędnych. Łatwo zobaczyć, że x 1 
Następnie, stosując metodę przedziałową, wyznaczamy znaki na każdym z trzech otrzymanych przedziałów. Jest to najwygodniejsze i najszybsze w oparciu o wartość współczynnika przy x 2, jest ona równa 8, czyli dodatnia, zatem sekwencja znaków będzie następująca: +, -, +: 
Ponieważ rozwiązujemy nierówność ze znakiem ≥, rysujemy cieniowanie na przedziałach ze znakami plus: 
Na podstawie powstałego obrazu zbioru liczbowego nie jest trudno opisać go analitycznie:  lub tak
lub tak  . W ten sposób rozwiązaliśmy pierwotną nierówność kwadratową.
. W ten sposób rozwiązaliśmy pierwotną nierówność kwadratową.
Odpowiedź:
 Lub
Lub  .
.
Przykład.
Rozwiąż nierówność kwadratową  metoda interwałowa.
metoda interwałowa.
Rozwiązanie.
Znajdź pierwiastki trójmianu kwadratowego po lewej stronie nierówności: 
Ponieważ rozwiązujemy ścisłą nierówność, przedstawiamy punkt przebity o współrzędnej 7 na linii współrzędnych: ![]()
Teraz wyznaczamy znaki na dwóch powstałych przedziałach (−∞, 7) i (7, +∞). Łatwo to zrobić, biorąc pod uwagę, że dyskryminator trójmianu kwadratowego jest równy zerom, a współczynnik wiodący jest ujemny. Mamy znaki −, −: ![]()
Ponieważ rozwiązujemy nierówność ze znakiem<, то изображаем штриховку над интервалами со знаками минус:![]()
Widać wyraźnie, że oba przedziały (−∞, 7), (7, +∞) są rozwiązaniami.
Odpowiedź:
(−∞, 7)∪(7, +∞) lub w innym zapisie x≠7 .
Przykład.
Czy nierówność kwadratowa x 2 +x+7<0 решения?
Rozwiązanie.
Aby odpowiedzieć na postawione pytanie, rozwiążemy tę nierówność kwadratową, a ponieważ analizujemy metodę przedziałów, zastosujemy ją. Jak zwykle zaczynamy od znalezienia pierwiastków trójmianu kwadratowego po lewej stronie. Znajdujemy dyskryminator: D=1 2 −4·1·7=1−28=−27, jest on mniejszy od zera, co oznacza, że nie ma pierwiastków rzeczywistych.
Dlatego po prostu rysujemy linię współrzędnych bez zaznaczania na niej żadnych punktów: ![]()
Teraz określamy znak wartości trójmianu kwadratowego. w D<0
он совпадает со знаком коэффициента при x 2
, то есть, со знаком числа 1
, оно положительное, следовательно, имеем знак +:![]()
Rozwiązujemy nierówność ze znakiem<, поэтому штриховку следует изобразить над промежутками со знаком −, но таковых нет, и в силу этого штриховку не наносим, а чертеж сохраняет свой вид.![]()
W rezultacie mamy zbiór pusty, co oznacza, że pierwotna nierówność kwadratowa nie ma rozwiązań.
Odpowiedź:
Bibliografia.
- Algebra: podręcznik dla 8 klasy. ogólne wykształcenie instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
- Algebra: Klasa 9: edukacyjna. dla edukacji ogólnej instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2009. - 271 s. : chory. - ISBN 978-5-09-021134-5.
- Mordkovich A. G. Algebra. 8 klasa. Za 2 godziny Część 1. Podręcznik dla uczniów szkół ogólnokształcących / A. G. Mordkovich. - wyd. 11, usunięte. - M.: Mnemosyne, 2009. - 215 s.: il. ISBN 978-5-346-01155-2.
- Mordkovich A. G. Algebra. 9. klasa. Za 2 godziny Część 1. Podręcznik dla uczniów szkół ogólnokształcących / A. G. Mordkovich, P. V. Semenov. - wyd. 13, usunięte. - M.: Mnemosyne, 2011. - 222 s.: il. ISBN 978-5-346-01752-3.
- Mordkovich A. G. Algebra i początki analizy matematycznej. Klasa 11. Za 2 godziny Część 1. Podręcznik dla uczniów szkół ogólnokształcących (poziom profilu) / A. G. Mordkovich, P. V. Semenov. - wyd. 2, skreślone. - M.: Mnemosyne, 2008. - 287 s.: il. ISBN 978-5-346-01027-2.
Ważne notatki!
1. Jeśli zamiast formuł widzisz Gobbledygook, wyczyść pamięć podręczną. Jak to zrobić w przeglądarce jest napisane tutaj:
2. Zanim zaczniesz czytać artykuł, zwróć uwagę na nasz nawigator, aby uzyskać najbardziej przydatne zasoby
Trzeba tylko zrozumieć tę metodę i znać ją jak własną kieszeń! Choćby dlatego, że służy do rozwiązywania nierówności wymiernych i dlatego, że znając tę metodę, rozwiązanie tych nierówności jest zaskakująco proste. Nieco później zdradzę Ci kilka sekretów, jak zaoszczędzić czas na rozwiązywaniu tych nierówności. Jesteś zaintrygowany? Więc chodźmy!
Istota tej metody polega na rozłożeniu nierówności na czynniki (powtórz temat) i wyznaczeniu ODZ oraz znaku czynników; teraz wszystko wyjaśnię; Weźmy najprostszy przykład: .
Nie ma potrzeby wpisywania tutaj zakresu dopuszczalnych wartości (), ponieważ nie ma podziału przez zmienną i nie obserwuje się tu żadnych pierwiastków (pierwiastków). Wszystko tutaj jest już dla nas rozłożone na czynniki. Ale nie relaksuj się, to wszystko po to, żeby przypomnieć Ci podstawy i zrozumieć istotę!
Powiedzmy, że nie znasz metody przedziałowej. Jak rozwiązałbyś tę nierówność? Podejdź logicznie i opieraj się na tym, co już wiesz. Po pierwsze, lewa strona będzie większa od zera, jeśli oba wyrażenia w nawiasach będą większe od zera lub mniejsze od zera, ponieważ „plus” za „plus” daje „plus”, a „minus” za „minus” daje „plus”, prawda? A jeśli znaki wyrażeń w nawiasach są różne, to ostatecznie lewa strona będzie mniejsza od zera. Czego potrzebujemy, aby znaleźć te wartości, przy których wyrażenia w nawiasach będą ujemne lub dodatnie?
Musimy rozwiązać równanie, jest dokładnie tak samo jak nierówność, tylko zamiast znaku będzie znak, pierwiastki tego równania pozwolą nam wyznaczyć te wartości brzegowe, od których odejdziemy, czynniki będą większe lub mniej niż zero.
A teraz same interwały. Co to jest interwał? Jest to pewien przedział osi liczbowej, czyli wszystkie możliwe liczby zawarte między dwiema liczbami - końcami przedziału. Nie jest łatwo wyobrazić sobie te interwały w głowie, dlatego często rysuje się interwały, nauczę cię teraz.
Rysujemy oś; na niej znajduje się cała seria liczb od i do. Na osi nanoszone są punkty, czyli tzw. zera funkcji, czyli wartości, przy których wyrażenie jest równe zeru. Punkty te są „przypięte”, co oznacza, że nie należą do wartości, przy których nierówność jest prawdziwa. W tym przypadku są one przebite, ponieważ znak nierówności, a nie, to znaczy ściśle większy i nie większy lub równy.
Chcę powiedzieć, że nie trzeba zaznaczać zera, jest tutaj bez kółek, ale tylko dla zrozumienia i orientacji wzdłuż osi. OK, narysowaliśmy oś, postawiliśmy kropki (dokładniej kółka), co dalej, w jaki sposób pomoże mi to w rozwiązaniu? - ty pytasz. Teraz po prostu weź wartość x z przedziałów w odpowiedniej kolejności i podstaw je do nierówności i zobacz, jaki będzie znak mnożenia.
Krótko mówiąc, po prostu weźmiemy to na przykład, podstawimy tutaj, wyjdzie, co oznacza, że nierówność będzie obowiązywać w całym przedziale (na całym przedziale) od do, z którego ją wzięliśmy. Innymi słowy, jeśli x wynosi od do, to nierówność jest prawdziwa.
To samo robimy z odstępem od do, bierzemy lub np. podstawiamy, ustalamy znak, znak będzie „minus”. I to samo robimy z ostatnim, trzecim odstępem od do, gdzie znak okazuje się być „plus”. Tekstu jest mnóstwo, ale za mało przejrzystości, prawda?
Przyjrzyj się jeszcze raz nierównościom.
Teraz stosujemy również znaki, które zostaną uzyskane w wyniku, na tej samej osi. W moim przykładzie linia przerywana oznacza dodatni i ujemny odcinek osi.

Spójrz na nierówność - na rysunek, jeszcze raz na nierówność - i jeszcze raz na rysunek, czy coś jest jasne? Spróbuj teraz powiedzieć, w jakich przedziałach X nierówność będzie prawdziwa. Zgadza się, od do nierówność będzie również prawdziwa od do, ale na przedziale od do nierówność wynosi zero i ten przedział nas mało interesuje, bo mamy znak w nierówności.
Cóż, skoro już to zrozumiałeś, pozostaje Ci tylko zapisać odpowiedź! W odpowiedzi zapisujemy te przedziały, dla których lewa strona jest większa od zera, co oznacza, że X należy do przedziału od minus nieskończoności do minus jeden i od dwóch do plus nieskończoności. Warto doprecyzować, że nawiasy oznaczają, że wartości, którymi ograniczony jest przedział, nie są rozwiązaniami nierówności, czyli nie są uwzględniane w odpowiedzi, a jedynie wskazują, że do np. rozwiązanie.
Teraz przykład, w którym nie tylko będziesz musiał narysować odstęp:
Jak myślisz, co należy zrobić przed umieszczeniem punktów na osi? Tak, rozłóż to na czynniki:
Rysujemy odstępy i stawiamy znaki, zauważmy, że przebiliśmy kropki, bo znak jest ściśle mniejszy od zera:

Czas zdradzić Wam jeden sekret, który obiecałem na początku tego tematu! A co jeśli powiem Ci, że nie musisz podstawiać wartości z każdego przedziału, aby wyznaczyć znak, ale możesz wyznaczyć znak w jednym z przedziałów, a w pozostałych po prostu zamieniać znaki!
W ten sposób zaoszczędziliśmy trochę czasu na stawianiu znaków - myślę, że ten zyskany czas na Unified State Exam nie zaszkodzi!
Piszemy odpowiedź:
Rozważmy teraz przykład nierówności ułamkowo-racjonalnej - nierówności, której obie części są wyrażeniami wymiernymi (patrz).
Co możesz powiedzieć o tej nierówności? Patrzysz na to jak na równanie ułamkowo-wymierne. Co zrobimy najpierw? Od razu widzimy, że nie ma pierwiastków, czyli na pewno jest wymierny, ale wtedy jest to ułamek i to nawet z niewiadomą w mianowniku!
Zgadza się, potrzebujemy ODZ!
Zatem pójdźmy dalej, tutaj wszystkie czynniki oprócz jednego mają zmienną pierwszego stopnia, ale istnieje czynnik, w którym x ma drugi stopień. Zwykle nasz znak zmieniał się po przejściu przez jeden z punktów, w którym lewa strona nierówności przyjmuje wartość zerową, dla czego ustaliliśmy, jakie x powinno być równe w każdym czynniku. Ale tutaj zawsze jest to pozytywne, ponieważ dowolna liczba do kwadratu > zero i wyraz dodatni.
Czy sądzisz, że będzie to miało wpływ na znaczenie nierówności? Zgadza się – to nie będzie miało wpływu! Możemy bezpiecznie podzielić nierówność na obie części i tym samym usunąć ten czynnik, aby nie był razi w oczy.
Nadszedł czas na narysowanie przedziałów; aby to zrobić, musisz określić te wartości graniczne, od których odejdą mnożniki będą większe i mniejsze od zera. Ale zwróćcie uwagę, że tu jest znak, oznacza to, że nie będziemy wyłapywać punktu, w którym lewa strona nierówności przyjmuje wartość zerową, jest to wliczane do liczby rozwiązań, mamy tylko jeden taki punkt, jest to punkt, w którym x jest równe jeden. Czy pokolorujemy punkt, w którym mianownik jest ujemny? - Oczywiście nie!
Mianownik nie może wynosić zero, więc przedział będzie wyglądał następująco:

Korzystając z tego schematu, możesz łatwo napisać odpowiedź, powiem tylko, że teraz masz do dyspozycji nowy typ zamka - kwadratowy! Oto wspornik [ mówi, że wartość jest zawarta w przedziale rozwiązania, tj. jest częścią odpowiedzi, ten nawias odpowiada wypełnionemu (nie przypiętemu) punktowi na osi.
Czy otrzymałeś tę samą odpowiedź?
Rozkładamy to na czynniki i przenosimy wszystko na jedną stronę, w końcu wystarczy zostawić zero po prawej stronie, aby z nim porównać:
Zwracam uwagę, że w ostatnim przekształceniu, aby otrzymać w liczniku i mianowniku, mnożę obie strony nierówności przez. Pamiętaj, że gdy pomnożymy obie strony nierówności, znak nierówności zmieni się na przeciwny!!!
Piszemy ODZ:
W przeciwnym razie mianownik spadnie do zera i, jak pamiętasz, nie można dzielić przez zero!
Zgadzam się, wynikająca z tego nierówność kusi, aby zmniejszyć licznik i mianownik! Nie da się tego zrobić; możesz stracić część decyzji lub ODZ!
Teraz spróbuj samodzielnie umieścić punkty na osi. Zwrócę tylko uwagę, że przy wykreślaniu punktów trzeba zwrócić uwagę na to, że punkt o wartości, która na podstawie znaku wydawałaby się naniesiona na osi jako zacieniony, nie będzie zacieniony, będzie wydłubany! Dlaczego pytasz? I pamiętaj o ODZ, nie będziesz dzielić przez zero w ten sposób?
Pamiętaj, ODZ jest na pierwszym miejscu! Jeśli wszystkie nierówności i znaki równości mówią jedno, a ODZ co innego, zaufajcie ODZ, wielkiemu i potężnemu! Cóż, zbudowałeś interwały, jestem pewien, że wziąłeś moją wskazówkę dotyczącą naprzemienności i masz to w ten sposób (patrz obrazek poniżej). Teraz przekreśl to i nie popełniaj więcej tego błędu! Jaki błąd? - ty pytasz.

Faktem jest, że w tej nierówności współczynnik został powtórzony dwukrotnie (pamiętasz, jak próbowałeś go zmniejszyć?). Jeśli więc jakiś czynnik w nierówności powtórzy się parzystą liczbę razy, to przy przejściu przez punkt na osi, który zamienia ten współczynnik na zero (w tym przypadku przez punkt), znak nie ulegnie zmianie, jeśli jest nieparzysty; , wtedy znak się zmienia!
Prawidłowa będzie następująca oś z odstępami i znakami:

I proszę zwrócić uwagę, że znak, który nas interesuje, to nie jest ten, który był na początku (kiedy pierwszy raz zobaczyliśmy nierówność, znak tam był), po przekształceniach znak zmienił się na, czyli interesują nas przedziały ze znakiem.
Odpowiedź:
Powiem też, że zdarzają się sytuacje, gdy istnieją pierwiastki nierówności, które nie mieszczą się w żadnym przedziale, w odpowiedzi zapisuje się je w nawiasach klamrowych, np. tak: . Więcej o takich sytuacjach przeczytasz w artykule Poziom średni.
Podsumujmy, jak rozwiązywać nierówności za pomocą metody przedziałowej:
- Przesuwamy wszystko na lewą stronę, zostawiając tylko zero po prawej stronie;
- Znajdujemy ODZ;
- Na osi wykreślamy wszystkie pierwiastki nierówności;
- Bierzemy dowolny z jednego z przedziałów i określamy znak w przedziale, do którego należy pierwiastek, naprzemiennie znaki, zwracając uwagę na pierwiastki, które powtarzają się kilkakrotnie w nierówności, zależy od tego, czy znak zmienia się podczas przechodzenia przez nie; na parzystości lub nieparzystości liczby powtórzeń lub nie;
- W odpowiedzi zapisujemy odstępy, obserwując punkty przerywane i nieprzebite (patrz ODZ), umieszczając pomiędzy nimi niezbędne rodzaje nawiasów.
I na koniec nasza ulubiona sekcja „zrób to sam”!
Przykłady:
Odpowiedzi:
METODA INTERWAŁOWA. ŚREDNI POZIOM
Funkcja liniowa
Funkcję postaci nazywa się liniową. Weźmy na przykład funkcję. Jest dodatni w i ujemny w. Punkt jest zerem funkcji (). Pokażmy znaki tej funkcji na osi liczbowej:

Mówimy, że „funkcja zmienia znak przy przejściu przez punkt”.
Można zauważyć, że znaki funkcji odpowiadają położeniu wykresu funkcji: jeśli wykres znajduje się nad osią, znakiem jest „ ”, jeśli poniżej – „ ”.
Jeśli uogólnimy otrzymaną regułę na dowolną funkcję liniową, otrzymamy następujący algorytm:
- Znajdowanie zera funkcji;
- Zaznaczamy to na osi liczbowej;
- Wyznaczamy znak funkcji po przeciwnych stronach zera.
Funkcja kwadratowa
Mam nadzieję, że pamiętasz, jak rozwiązywać nierówności kwadratowe? Jeżeli nie to przeczytaj temat. Przypomnę ogólną postać funkcji kwadratowej: .
Przypomnijmy sobie teraz, jakie znaki przyjmuje funkcja kwadratowa. Jej wykresem jest parabola, a funkcja przyjmuje znak „” dla tych, w których parabola znajduje się powyżej osi, oraz „” – jeśli parabola znajduje się poniżej osi:

Jeśli funkcja ma zera (wartości, przy których), parabola przecina oś w dwóch punktach - pierwiastkach odpowiedniego równania kwadratowego. Zatem oś jest podzielona na trzy przedziały, a znaki funkcji zmieniają się naprzemiennie podczas przechodzenia przez każdy pierwiastek.
Czy można w jakiś sposób określić znaki bez każdorazowego rysowania paraboli?
Przypomnijmy, że trójmian kwadratowy można rozłożyć na czynniki:
Na przykład: .
Zaznaczmy pierwiastki na osi:
Pamiętamy, że znak funkcji może się zmienić tylko podczas przejścia przez pierwiastek. Wykorzystajmy ten fakt: dla każdego z trzech przedziałów, na które oś jest podzielona przez pierwiastki, wystarczy wyznaczyć znak funkcji tylko w jednym, dowolnie wybranym punkcie: w pozostałych punktach przedziału znak będzie taki sam .
W naszym przykładzie: w obu wyrażeniach w nawiasach są liczby dodatnie (podstaw, na przykład:). Na osi stawiamy znak „ ”:


Cóż, gdy (na przykład podstawienie) oba nawiasy są ujemne, co oznacza, że iloczyn jest dodatni:

To jest to metoda interwałowa: znając znaki czynników w każdym przedziale, wyznaczamy znak całego iloczynu.
Rozważmy także przypadki, gdy funkcja nie ma zer lub ma tylko jeden.
Jeśli ich tam nie ma, nie ma korzeni. Oznacza to, że nie będzie żadnego „przechodzenia przez korzeń”. Oznacza to, że funkcja przyjmuje tylko jeden znak na całej osi liczbowej. Można to łatwo ustalić, podstawiając go do funkcji.
Jeśli jest tylko jeden pierwiastek, parabola dotyka osi, więc znak funkcji nie zmienia się przy przejściu przez pierwiastek. Jaką regułę możemy wymyślić na takie sytuacje?
Jeśli uwzględnisz taką funkcję, otrzymasz dwa identyczne czynniki:
A każde wyrażenie kwadratowe jest nieujemne! Zatem znak funkcji się nie zmienia. W takich przypadkach zaznaczymy pierwiastek, przechodząc przez który znak się nie zmienia, zakreślając go kwadratem:
Taki pierwiastek nazwiemy wielokrotnością.
Metoda przedziałowa w nierównościach
Teraz każdą nierówność kwadratową można rozwiązać bez rysowania paraboli. Wystarczy postawić na osi znaki funkcji kwadratowej i dobrać przedziały w zależności od znaku nierówności. Na przykład:
Zmierzmy korzenie na osi i umieśćmy znaki:

Potrzebujemy części osi ze znakiem „”; ponieważ nierówność nie jest ścisła, w rozwiązaniu uwzględnione są również same pierwiastki:
Rozważmy teraz racjonalną nierówność - nierówność, której obie strony są wyrażeniami racjonalnymi (patrz).
Przykład:
Wszystkie czynniki oprócz jednego są tutaj „liniowe”, to znaczy zawierają zmienną tylko do pierwszej potęgi. Potrzebujemy takich współczynników liniowych, aby zastosować metodę przedziałową - znak zmienia się przy przejściu przez ich pierwiastki. Ale mnożnik w ogóle nie ma pierwiastków. Oznacza to, że jest on zawsze dodatni (sprawdź to sam), a zatem nie wpływa na znak całej nierówności. Oznacza to, że możemy podzielić przez nią lewą i prawą stronę nierówności i w ten sposób się jej pozbyć:
Teraz wszystko jest tak jak było z nierównościami kwadratowymi: ustalamy, w których punktach każdy z czynników zanika, zaznaczamy te punkty na osi i układamy znaki. Pragnę zwrócić Państwa uwagę na bardzo istotny fakt:

Odpowiedź: . Przykład: .
Aby zastosować metodę przedziałową, jedna z części nierówności musi mieć. Dlatego przesuńmy prawą stronę w lewą stronę:
Licznik i mianownik mają ten sam współczynnik, ale nie spiesz się, aby go zmniejszyć! W końcu możemy zapomnieć o nakłuciu tego punktu. Lepiej oznaczyć ten pierwiastek jako wielokrotność, to znaczy przechodząc przez niego znak się nie zmieni: 
Odpowiedź: .
I jeszcze jeden bardzo ilustrujący przykład:
Ponownie nie usuwamy tych samych współczynników licznika i mianownika, ponieważ jeśli to zrobimy, będziemy musieli szczególnie pamiętać o przebiciu kropki.
- : powtarzane razy;
- : razy;
- : razy (w liczniku i jeden w mianowniku).
W przypadku liczby parzystej postępujemy tak samo jak poprzednio: zakreślamy punkt kwadratem i nie zmieniamy znaku przy przejściu przez pierwiastek. Ale w przypadku liczby nieparzystej ta zasada nie ma zastosowania: znak nadal będzie się zmieniał podczas przejścia przez pierwiastek. Dlatego z takim pierwiastkiem nie robimy nic dodatkowego, jakby nie był on wielokrotnością. Powyższe zasady dotyczą wszystkich potęg parzystych i nieparzystych. 
Co powinniśmy napisać w odpowiedzi?
W przypadku naruszenia naprzemienności znaków należy zachować szczególną ostrożność, ponieważ jeśli nierówność nie jest ścisła, odpowiedź powinna obejmować wszystkie zacienione punkty. Ale niektóre z nich często wyróżniają się, to znaczy nie są uwzględnione w zacienionym obszarze. W tym przypadku dodajemy je do odpowiedzi jako izolowane punkty (w nawiasach klamrowych):
Przykłady (zdecyduj sam):
Odpowiedzi:
- Jeśli wśród czynników jest to proste, jest to pierwiastek, ponieważ można go przedstawić jako.
.
METODA INTERWALOWA. KRÓTKO O NAJWAŻNIEJSZYCH RZECZACH
Do rozwiązywania nierówności wymiernych stosuje się metodę przedziałową. Polega na wyznaczeniu znaku iloczynu na podstawie znaków czynników w różnych przedziałach.
Algorytm rozwiązywania nierówności wymiernych metodą przedziałową.
- Przesuwamy wszystko na lewą stronę, zostawiając tylko zero po prawej stronie;
- Znajdujemy ODZ;
- Na osi wykreślamy wszystkie pierwiastki nierówności;
- Bierzemy dowolny z jednego z przedziałów i określamy znak w przedziale, do którego należy pierwiastek, naprzemiennie znaki, zwracając uwagę na pierwiastki, które powtarzają się kilkakrotnie w nierówności, zależy od tego, czy znak zmienia się podczas przechodzenia przez nie; na parzystości lub nieparzystości liczby powtórzeń lub nie;
- W odpowiedzi zapisujemy odstępy, obserwując punkty przerywane i nieprzebite (patrz ODZ), umieszczając pomiędzy nimi niezbędne rodzaje nawiasów.
No cóż, temat się skończył. Jeśli czytasz te słowa, oznacza to, że jesteś bardzo fajny.
Bo tylko 5% ludzi jest w stanie samodzielnie coś opanować. A jeśli przeczytasz do końca, to jesteś w tych 5%!
Teraz najważniejsza rzecz.
Zrozumiełeś teorię na ten temat. I powtarzam, to... to jest po prostu super! Już jesteś lepszy od zdecydowanej większości Twoich rówieśników.
Problem w tym, że to może nie wystarczyć...
Po co?
Za pomyślne zdanie egzaminu Unified State Exam, za rozpoczęcie studiów z ograniczonym budżetem i, CO NAJWAŻNIEJSZE, za całe życie.
Nie będę Cię do niczego przekonywał, powiem tylko jedno...
Ludzie, którzy otrzymali dobre wykształcenie, zarabiają znacznie więcej niż ci, którzy go nie otrzymali. To jest statystyka.
Ale to nie jest najważniejsze.
Najważniejsze, że są BARDZIEJ SZCZĘŚLIWI (są takie badania). Być może dlatego, że otwiera się przed nimi o wiele więcej możliwości i życie staje się jaśniejsze? nie wiem...
Ale pomyśl samodzielnie...
Czego potrzeba, aby na egzaminie Unified State Exam wypaść lepiej od innych i ostatecznie… być szczęśliwszym?
Zdobądź rękę, rozwiązując problemy z tego tematu.
Podczas egzaminu nie będziesz proszony o zadawanie teorii.
Będziesz potrzebować rozwiązywać problemy z czasem.
A jeśli ich nie rozwiązałeś (DUŻO!), na pewno popełnisz gdzieś głupi błąd lub po prostu nie będziesz miał czasu.
To jak w sporcie – trzeba to powtarzać wiele razy, żeby na pewno wygrać.
Znajdź kolekcję gdziekolwiek chcesz, koniecznie z rozwiązaniami, szczegółową analizą i decyduj, decyduj, decyduj!
Możesz skorzystać z naszych zadań (opcjonalnie) i oczywiście je polecamy.
Aby lepiej radzić sobie z naszymi zadaniami, musisz pomóc przedłużyć żywotność podręcznika YouClever, który aktualnie czytasz.
Jak? Istnieją dwie opcje:
- Odblokuj wszystkie ukryte zadania w tym artykule -
- Odblokuj dostęp do wszystkich ukrytych zadań we wszystkich 99 artykułach podręcznika - Kup podręcznik - 499 RUR
Tak, w naszym podręczniku mamy 99 takich artykułów i dostęp do wszystkich zadań oraz wszystkich ukrytych w nich tekstów można od razu otworzyć.
Dostęp do wszystkich ukrytych zadań jest zapewniony przez CAŁY okres istnienia witryny.
Podsumowując...
Jeśli nie podobają Ci się nasze zadania, znajdź inne. Tylko nie poprzestawaj na teorii.
„Rozumiem” i „Umiem rozwiązać” to zupełnie różne umiejętności. Potrzebujesz obu.
Znajdź problemy i rozwiąż je!
Ale dzisiaj racjonalne nierówności nie mogą rozwiązać wszystkiego. Dokładniej, nie tylko każdy może decydować. Niewiele osób może to zrobić.
Kliczko
Ta lekcja będzie trudna. Tak trudne, że tylko Wybrani dotrą do końca. Dlatego przed rozpoczęciem czytania polecam usunąć kobiety, koty, dzieci w ciąży i... z ekranów.
Daj spokój, to właściwie proste. Załóżmy, że opanowałeś metodę przedziałów (jeśli jej nie opanowałeś, polecam wrócić i przeczytać ją) i nauczyłeś się rozwiązywać nierówności w postaci $P\left(x \right) \gt 0$, gdzie $ P\left(x \right)$ jest jakimś wielomianem lub iloczynem wielomianów.
Myślę, że nie będzie Ci trudno rozwiązać np. coś takiego (swoją drogą, spróbuj na rozgrzewkę):
\[\begin(align) & \left(2((x)^(2))+3x+4 \right)\left(4x+25 \right) \gt 0; \\ & x\left(2((x)^(2))-3x-20 \right)\left(x-1 \right)\ge 0; \\ & \left(8x-((x)^(4)) \right)((\left(x-5 \right))^(6))\le 0. \\ \end(align)\]
Teraz skomplikujmy trochę problem i rozważmy nie tylko wielomiany, ale tak zwane ułamki wymierne postaci:
gdzie $P\left(x \right)$ i $Q\left(x \right)$ są tymi samymi wielomianami postaci $((a)_(n))((x)^(n))+( ( a)_(n-1))((x)^(n-1))+...+((a)_(0))$, czyli iloczyn takich wielomianów.
Będzie to nierówność racjonalna. Zasadniczą kwestią jest obecność zmiennej $x$ w mianowniku. Są to na przykład nierówności racjonalne:
\[\begin(align) & \frac(x-3)(x+7) \lt 0; \\ & \frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4)\ge 0; \\ & \frac(3((x)^(2))+10x+3)(((\left(3-x \right))^(2))\left(4-((x)^( 2)) \right))\ge 0. \\ \end(align)\]
I nie jest to nierówność wymierna, ale najczęstsza nierówność, którą można rozwiązać metodą przedziałową:
\[\frac(((x)^(2))+6x+9)(5)\ge 0\]
Patrząc w przyszłość, powiem od razu: istnieją co najmniej dwa sposoby rozwiązywania nierówności racjonalnych, ale wszystkie w ten czy inny sposób sprowadzają się do znanej nam metody przedziałów. Dlatego zanim przeanalizujemy te metody, przypomnijmy sobie stare fakty, inaczej nowy materiał nie będzie miał sensu.
Co już musisz wiedzieć
Ważnych faktów nigdy za wiele. Tak naprawdę potrzebujemy tylko czterech.
Skrócone wzory na mnożenie
Tak, tak: będą nas prześladować przez cały szkolny program nauczania matematyki. I na uniwersytecie też. Istnieje wiele takich formuł, ale potrzebujemy tylko następujących:
\[\begin(align) & ((a)^(2))\pm 2ab+((b)^(2))=((\left(a\pm b \right))^(2)); \\ & ((a)^(2))-((b)^(2))=\lewo(a-b \prawo)\lewo(a+b \prawo); \\ & ((a)^(3))+((b)^(3))=\lewo(a+b \prawo)\lewo(((a)^(2))-ab+((b) ^(2)) \prawo); \\ & ((a)^(3))-((b)^(3))=\lewo(a-b \prawo)\lewo(((a)^(2))+ab+((b)^( 2))\prawo). \\ \end(align)\]
Zwróć uwagę na dwa ostatnie wzory - są to suma i różnica kostek (a nie sześcian sumy lub różnicy!). Łatwo je zapamiętać, jeśli zauważymy, że znak w pierwszym nawiasie pokrywa się ze znakiem w wyrażeniu oryginalnym, a w drugim jest przeciwny do znaku w wyrażeniu oryginalnym.
Równania liniowe
Są to najprostsze równania w postaci $ax+b=0$, gdzie $a$ i $b$ to liczby zwykłe, a $a\ne 0$. Równanie to można rozwiązać w prosty sposób:
\[\begin(align) & ax+b=0; \\&ax=-b; \\ & x=-\frac(b)(a). \\ \end(align)\]
Zaznaczę, że mamy prawo dzielić przez współczynnik $a$, bo $a\ne 0$. To wymaganie jest całkiem logiczne, ponieważ dla $a=0$ otrzymujemy to:
Po pierwsze, w tym równaniu nie ma zmiennej $x$. To, ogólnie rzecz biorąc, nie powinno nas mylić (dzieje się to, powiedzmy, w geometrii i dość często), ale mimo to nie jest to już równanie liniowe.
Po drugie, rozwiązanie tego równania zależy wyłącznie od współczynnika $b$. Jeśli $b$ również wynosi zero, to nasze równanie ma postać $0=0$. Ta równość jest zawsze prawdziwa; oznacza to, że $x$ to dowolna liczba (zwykle zapisana w ten sposób: $x\in \mathbb(R)$). Jeśli współczynnik $b$ nie jest równy zero, to równość $b=0$ nigdy nie jest spełniona, tzn. nie ma odpowiedzi (wpisz $x\in \varnothing $ i przeczytaj „zestaw rozwiązań jest pusty”).
Aby uniknąć tych wszystkich trudności, przyjmujemy po prostu $a\ne 0$, co wcale nie ogranicza nas w dalszym myśleniu.
Równania kwadratowe
Przypomnę, że tak nazywa się równanie kwadratowe:
Tutaj po lewej stronie wielomian drugiego stopnia i znowu $a\ne 0$ (w przeciwnym razie zamiast równania kwadratowego otrzymamy równanie liniowe). Za pomocą dyskryminatora rozwiązuje się następujące równania:
- Jeśli $D \gt 0$, otrzymamy dwa różne pierwiastki;
- Jeśli $D=0$, to będzie jeden pierwiastek, ale drugiej krotności (co to za krotność i jak ją uwzględnić - o tym później). Lub możemy powiedzieć, że równanie ma dwa identyczne pierwiastki;
- Dla $D \lt 0$ w ogóle nie ma pierwiastków, a znak wielomianu $a((x)^(2))+bx+c$ dla dowolnego $x$ pokrywa się ze znakiem współczynnika $a $. Nawiasem mówiąc, jest to bardzo przydatny fakt, o którym z jakiegoś powodu zapominają mówić na lekcjach algebry.
Same korzenie oblicza się za pomocą dobrze znanego wzoru:
\[((x)_(1,2))=\frac(-b\pm \sqrt(D))(2a)\]
Stąd, nawiasem mówiąc, ograniczenia dotyczące dyskryminatora. Przecież pierwiastek kwadratowy z liczby ujemnej nie istnieje. Wielu uczniów ma straszny mętlik w głowie odnośnie pierwiastków, dlatego specjalnie zapisałam sobie całą lekcję: czym jest pierwiastek w algebrze i jak go obliczyć - gorąco polecam przeczytać :)
Działania na ułamkach wymiernych
Wiesz już wszystko, co napisano powyżej, jeśli przestudiowałeś metodę interwałową. Ale to, co teraz przeanalizujemy, nie ma analogii w przeszłości - to zupełnie nowy fakt.
Definicja. Ułamek wymierny jest wyrazem formy
\[\frac(P\lewo(x \prawo))(Q\lewo(x \prawo))\]
gdzie $P\lewo(x \prawo)$ i $Q\lewo(x \prawo)$ są wielomianami.
Oczywiście łatwo jest uzyskać nierówność z takiego ułamka – wystarczy dodać znak „większy niż” lub „mniejszy niż” po prawej stronie. A nieco dalej odkryjemy, że rozwiązywanie takich problemów to przyjemność, wszystko jest bardzo proste.
Problemy zaczynają się, gdy w jednym wyrażeniu występuje kilka takich ułamków. Trzeba je sprowadzić do wspólnego mianownika – a to właśnie w tym momencie popełnia się dużą liczbę błędów w ofensywie.
Dlatego, aby skutecznie rozwiązywać równania wymierne, musisz mocno zrozumieć dwie umiejętności:
- Rozkładanie wielomianu na czynniki $P\left(x \right)$;
- A właściwie sprowadzanie ułamków do wspólnego mianownika.
Jak rozłożyć wielomian na czynniki? Bardzo prosta. Załóżmy, że mamy wielomian w postaci
Przyrównujemy to do zera. Otrzymujemy równanie $n$tego stopnia:
\[((a)_(n))((x)^(n))+((a)_(n-1))((x)^(n-1))+...+(( a)_(1))x+((a)_(0))=0\]
Powiedzmy, że rozwiązaliśmy to równanie i otrzymaliśmy pierwiastki $((x)_(1)),\ ...,\ ((x)_(n))$ (nie przejmuj się: w większości przypadków będzie nie więcej niż dwa z tych korzeni). W tym przypadku nasz pierwotny wielomian można przepisać w następujący sposób:
\[\begin(align) & P\left(x \right)=((a)_(n))((x)^(n))+((a)_(n-1))((x )^(n-1))+...+((a)_(1))x+((a)_(0))= \\ & =((a)_(n))\lewo(x -((x)_(1)) \right)\cdot \left(x-((x)_(2)) \right)\cdot ...\cdot \left(x-((x)_( n)) \right) \end(align)\]
To wszystko! Uwaga: wiodący współczynnik $((a)_(n))$ nigdzie nie zniknął - będzie to osobny mnożnik przed nawiasami i w razie potrzeby można go wstawić w którykolwiek z tych nawiasów (pokazuje praktyka) że przy $((a)_ (n))\ne \pm 1$ prawie zawsze są ułamki pomiędzy pierwiastkami).
Zadanie. Uprość wyrażenie:
\[\frac(((x)^(2))+x-20)(x-4)-\frac(2((x)^(2))-5x+3)(2x-3)-\ frac(4-8x-5((x)^(2)))(x+2)\]
Rozwiązanie. Najpierw spójrzmy na mianowniki: wszystkie są dwumianami liniowymi i nie ma tu nic do uwzględnienia. Rozłóżmy więc liczniki na czynniki:
\[\begin(align) & ((x)^(2))+x-20=\left(x+5 \right)\left(x-4 \right); \\ & 2((x)^(2))-5x+3=2\lewo(x-\frac(3)(2) \prawo)\lewo(x-1 \prawo)=\lewo(2x- 3 \prawo)\lewo(x-1 \prawo); \\ & 4-8x-5((x)^(2))=-5\lewo(x+2 \prawo)\lewo(x-\frac(2)(5) \prawo)=\lewo(x +2 \prawo)\lewo(2-5x \prawo). \\\end(align)\]
Uwaga: w drugim wielomianie wiodący współczynnik „2”, zgodnie z naszym schematem, najpierw pojawił się przed nawiasem, a następnie został uwzględniony w pierwszym nawiasie, ponieważ tam pojawił się ułamek.
To samo wydarzyło się w trzecim wielomianie, tylko tam również kolejność wyrazów jest odwrotna. Jednak współczynnik „-5” został ostatecznie uwzględniony w drugim nawiasie (pamiętajcie: współczynnik można wpisać w jednym i tylko jednym nawiasie!), co oszczędziło nam niedogodności związanych z pierwiastkami ułamkowymi.
Jeśli chodzi o pierwszy wielomian, wszystko jest proste: jego pierwiastków szukamy albo standardowo poprzez dyskryminator, albo korzystając z twierdzenia Viety.
Wróćmy do pierwotnego wyrażenia i przepiszmy je z uwzględnieniem liczników:
\[\begin(macierz) \frac(\left(x+5 \right)\left(x-4 \right))(x-4)-\frac(\left(2x-3 \right)\left( x-1 \right))(2x-3)-\frac(\left(x+2 \right)\left(2-5x \right))(x+2)= \\ =\left(x+5 \right)-\left(x-1 \right)-\left(2-5x \right)= \\ =x+5-x+1-2+5x= \\ =5x+4. \\ \end(macierz)\]
Odpowiedź: $5x+4$.
Jak widać nic skomplikowanego. Trochę matematyki dla klas 7-8 i to wszystko. Celem wszystkich transformacji jest uzyskanie czegoś prostego i łatwego w obsłudze ze złożonej i przerażającej ekspresji.
Jednak nie zawsze tak będzie. Zatem teraz zajmiemy się poważniejszym problemem.
Ale najpierw wymyślmy, jak doprowadzić dwa ułamki do wspólnego mianownika. Algorytm jest niezwykle prosty:
- Uwzględnij oba mianowniki;
- Rozważ pierwszy mianownik i dodaj do niego czynniki, które występują w drugim mianowniku, ale nie w pierwszym. Powstały produkt będzie wspólnym mianownikiem;
- Dowiedz się, jakich czynników brakuje każdemu z pierwotnych ułamków, aby mianowniki stały się równe wspólnemu.
Może się wydawać, że ten algorytm przypomina po prostu tekst zawierający „dużo liter”. Dlatego spójrzmy na wszystko na konkretnym przykładzie.
Zadanie. Uprość wyrażenie:
\[\left(\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3) )-8)-\frac(1)(x-2) \right)\cdot \left(\frac(((x)^(2)))(((x)^(2))-4)- \frac(2)(2-x) \right)\]
Rozwiązanie. Lepiej jest rozwiązywać tak duże problemy w częściach. Zapiszmy, co jest w pierwszym nawiasie:
\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3))-8 )-\frac(1)(x-2)\]
W przeciwieństwie do poprzedniego problemu, tutaj mianowniki nie są takie proste. Rozważmy każdy z nich.
Trójmianu kwadratowego $((x)^(2))+2x+4$ nie można rozłożyć na czynniki, ponieważ równanie $((x)^(2))+2x+4=0$ nie ma pierwiastków (wyróżnik jest ujemny ). Pozostawiamy to bez zmian.
Drugi mianownik - wielomian sześcienny $((x)^(3))-8$ - po dokładnym zbadaniu jest różnicą sześcianów i można go łatwo rozszerzyć za pomocą skróconych wzorów na mnożenie:
\[((x)^(3))-8=((x)^(3))-((2)^(3))=\lewo(x-2 \prawo)\lewo(((x) ^(2))+2x+4 \prawo)\]
Nic innego nie można rozłożyć na czynniki, ponieważ w pierwszym nawiasie znajduje się dwumian liniowy, a w drugim jest już nam znana konstrukcja, która nie ma rzeczywistych pierwiastków.
Wreszcie trzeci mianownik to dwumian liniowy, którego nie można rozwinąć. Zatem nasze równanie będzie miało postać:
\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(\lewo(x-2 \prawo)\lewo (((x)^(2))+2x+4 \prawo))-\frac(1)(x-2)\]
Jest całkiem oczywiste, że wspólnym mianownikiem będzie dokładnie $\left(x-2 \right)\left(((x)^(2))+2x+4 \right)$ i aby sprowadzić do niego wszystkie ułamki zwykłe należy pomnożyć pierwszy ułamek przez $\left(x-2 \right)$, a ostatni przez $\left(((x)^(2))+2x+4 \right)$. Następnie pozostaje tylko podać podobne:
\[\begin(macierz) \frac(x\cdot \left(x-2 \right))(\left(x-2 \right)\left(((x)^(2))+2x+4 \ prawo))+\frac(((x)^(2))+8)(\lewo(x-2 \prawo)\lewo(((x)^(2))+2x+4 \prawo))- \frac(1\cdot \left(((x)^(2))+2x+4 \right))(\left(x-2 \right)\left(((x)^(2))+2x +4 \right))= \\ =\frac(x\cdot \left(x-2 \right)+\left(((x)^(2))+8 \right)-\left(((x )^(2))+2x+4 \prawo))(\lewo(x-2 \prawo)\lewo(((x)^(2))+2x+4 \prawo))= \\ =\frac (((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\lewo(x-2\prawo)\lewo (((x)^(2))+2x+4 \prawo))= \\ =\frac(((x)^(2))-4x+4)(\lewo(x-2 \prawo)\ lewy(((x)^(2))+2x+4 \prawy)). \\ \end(macierz)\]
Zwróć uwagę na drugą linię: gdy mianownik jest już wspólny, tj. Zamiast trzech oddzielnych ułamków pisaliśmy jeden duży; nie należy od razu pozbywać się nawiasów. Lepiej napisać dodatkową linię i zauważyć, że powiedzmy, przed trzecim ułamkiem był minus - i nigdzie nie pójdzie, ale „zawiesi się” w liczniku przed nawiasem. Dzięki temu unikniesz wielu błędów.
Cóż, w ostatniej linijce warto rozłożyć licznik na czynniki. Co więcej, jest to dokładny kwadrat i znowu pomagają nam skrócone formuły mnożenia. Mamy:
\[\frac(((x)^(2))-4x+4)(\lewo(x-2 \prawo)\lewo(((x)^(2))+2x+4 \prawo))= \frac(((\left(x-2 \right))^(2)))(\left(x-2 \right)\left(((x)^(2))+2x+4 \right) )=\frac(x-2)(((x)^(2))+2x+4)\]
Teraz zajmiemy się drugim nawiasem dokładnie w ten sam sposób. Tutaj napiszę po prostu łańcuch równości:
\[\begin(macierz) \frac(((x)^(2)))(((x)^(2))-4)-\frac(2)(2-x)=\frac((( x)^(2)))(\lewo(x-2 \prawo)\lewo(x+2 \prawo))-\frac(2)(2-x)= \\ =\frac(((x) ^(2)))(\lewo(x-2 \prawo)\lewo(x+2 \prawo))+\frac(2)(x-2)= \\ =\frac(((x)^( 2)))(\left(x-2 \right)\left(x+2 \right))+\frac(2\cdot \left(x+2 \right))(\left(x-2 \right) )\cdot \left(x+2 \right))= \\ =\frac(((x)^(2))+2\cdot \left(x+2 \right))(\left(x-2 \right)\left(x+2 \right))=\frac(((x)^(2))+2x+4)(\left(x-2 \right)\left(x+2 \right) ). \\ \end(macierz)\]
Wróćmy do pierwotnego problemu i spójrzmy na produkt:
\[\frac(x-2)(((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2 \prawo)\lewo(x+2 \prawo))=\frac(1)(x+2)\]
Odpowiedź: \[\frac(1)(x+2)\].
Znaczenie tego zadania jest takie samo jak poprzedniego: pokazać, jak można uprościć wyrażenia wymierne, jeśli mądrze podejdzie się do ich przekształcenia.
A teraz, gdy już to wszystko wiesz, przejdźmy do głównego tematu dzisiejszej lekcji - rozwiązywania ułamkowych nierówności racjonalnych. Co więcej, po takim przygotowaniu same nierówności będziecie łamać jak orzechy :)
Główny sposób rozwiązywania racjonalnych nierówności
Istnieją co najmniej dwa podejścia do rozwiązywania racjonalnych nierówności. Teraz przyjrzymy się jednemu z nich - temu, który jest ogólnie przyjęty na szkolnym kursie matematyki.
Ale najpierw zwróćmy uwagę na ważny szczegół. Wszystkie nierówności dzielą się na dwa typy:
- Ścisłe: $f\left(x \right) \gt 0$ lub $f\left(x \right) \lt 0$;
- Lax: $f\lewo(x \prawo)\ge 0$ lub $f\lewo(x \prawo)\le 0$.
Nierówności drugiego typu można łatwo sprowadzić do pierwszego, a także równania:
Ten mały „dodatek” $f\left(x \right)=0$ prowadzi do tak nieprzyjemnej rzeczy jak wypełnione punkty - poznaliśmy je w metodzie interwałowej. W przeciwnym razie nie ma różnic między nierównościami ścisłymi i nieścisłymi, więc spójrzmy na uniwersalny algorytm:
- Zbierz wszystkie niezerowe elementy po jednej stronie znaku nierówności. Na przykład po lewej stronie;
- Sprowadź wszystkie ułamki do wspólnego mianownika (jeśli jest kilka takich ułamków), przynieś podobne. Następnie, jeśli to możliwe, rozłóż licznik i mianownik na czynniki. Tak czy inaczej otrzymamy nierówność postaci $\frac(P\left(x \right))(Q\left(x \right))\vee 0$, gdzie „ptaszek” jest znakiem nierówności .
- Przyrównujemy licznik do zera: $P\left(x \right)=0$. Rozwiązujemy to równanie i otrzymujemy pierwiastki $((x)_(1))$, $((x)_(2))$, $((x)_(3))$, ... Następnie wymagamy że mianownik nie jest równy zero: $Q\left(x \right)\ne 0$. Oczywiście w skrócie musimy rozwiązać równanie $Q\left(x \right)=0$ i otrzymamy pierwiastki $x_(1)^(*)$, $x_(2)^(*)$ , $x_(3 )^(*)$, ... (w rzeczywistych problemach nie będzie więcej niż trzy takie pierwiastki).
- Wszystkie te pierwiastki (zarówno z gwiazdkami, jak i bez) zaznaczamy na jednej osi liczbowej, pierwiastki bez gwiazdek zamalowujemy, a te z gwiazdkami przebijamy.
- Umieszczamy znaki „plus” i „minus”, wybieramy potrzebne interwały. Jeżeli nierówność ma postać $f\left(x \right) \gt 0$, to odpowiedzią będą przedziały oznaczone „plusem”. Jeśli $f\left(x \right) \lt 0$, to patrzymy na przedziały z „minusami”.
Praktyka pokazuje, że największe trudności sprawiają punkty 2 i 4 - właściwe przekształcenia i prawidłowe ułożenie liczb w kolejności rosnącej. Cóż, na ostatnim etapie zachowaj szczególną ostrożność: zawsze umieszczamy znaki na podstawie ostatnia nierówność zapisana przed przejściem do równań. Jest to uniwersalna reguła, odziedziczona z metody przedziałowej.
Zatem istnieje pewien schemat. Poćwiczmy.
Zadanie. Rozwiąż nierówność:
\[\frac(x-3)(x+7) \lt 0\]
Rozwiązanie. Mamy ścisłą nierówność w postaci $f\left(x \right) \lt 0$. Oczywiście punkty 1 i 2 naszego schematu zostały już spełnione: wszystkie elementy nierówności zebrano po lewej stronie, nie ma potrzeby sprowadzania czegokolwiek do wspólnego mianownika. Przejdźmy zatem od razu do punktu trzeciego.
Przyrównujemy licznik do zera:
\[\begin(wyrównaj) & x-3=0; \\ & x=3. \end(align)\]
I mianownik:
\[\begin(wyrównaj) & x+7=0; \\ & ((x)^(*))=-7. \\ \end(align)\]
W tym miejscu wiele osób utknie, ponieważ teoretycznie trzeba zapisać $x+7\ne 0$, zgodnie z wymogami ODZ (nie można dzielić przez zero, to wszystko). Ale w przyszłości będziemy wybijać punkty, które pochodzą z mianownika, więc nie ma potrzeby ponownie komplikować obliczeń - pisz wszędzie znak równości i nie martw się. Nikt nie odejmie za to punktów :)
Czwarty punkt. Wynikowe pierwiastki zaznaczamy na osi liczbowej:
Wszystkie punkty są przypięte, ponieważ nierówność jest ścisła
Notatka: wszystkie punkty są przypięte, ponieważ pierwotna nierówność jest ścisła. I tutaj nie ma znaczenia, czy te punkty pochodziły z licznika, czy z mianownika.
Cóż, spójrzmy na znaki. Weźmy dowolną liczbę $((x)_(0)) \gt 3$. Na przykład $((x)_(0))=100$ (ale z takim samym sukcesem można przyjąć $((x)_(0))=3,1$ lub $((x)_(0)) = 1\ 000\ 000 $). Otrzymujemy:
Zatem na prawo od wszystkich pierwiastków mamy obszar dodatni. A przechodząc przez każdy korzeń, znak się zmienia (nie zawsze tak będzie, ale o tym później). Przejdźmy zatem do punktu piątego: ułóż znaki i wybierz ten, którego potrzebujesz:
Wróćmy do ostatniej nierówności, która była przed rozwiązaniem równań. Właściwie pokrywa się z pierwotną, gdyż w tym zadaniu nie wykonywaliśmy żadnych przekształceń.
Ponieważ musimy rozwiązać nierówność w postaci $f\left(x \right) \lt 0$, zacieniowałem przedział $x\in \left(-7;3 \right)$ - jest to jedyny zaznaczony ze znakiem minus. To jest odpowiedź.
Odpowiedź: $x\in \left(-7;3 \right)$
To wszystko! Czy to jest trudne? Nie, to nie jest trudne. To prawda, że zadanie było łatwe. Teraz skomplikujmy trochę misję i rozważmy bardziej „wyrafinowaną” nierówność. Rozwiązując go, nie będę już podawać tak szczegółowych obliczeń - po prostu nakreślę kluczowe punkty. Generalnie sformatujemy go tak samo jak sformatowalibyśmy go podczas samodzielnej pracy czy egzaminu :)
Zadanie. Rozwiąż nierówność:
\[\frac(\lewo(7x+1 \prawo)\lewo(11x+2 \prawo))(13x-4)\ge 0\]
Rozwiązanie. Jest to nieścisła nierówność postaci $f\left(x \right)\ge 0$. Wszystkie niezerowe elementy są zbierane po lewej stronie, nie ma różnych mianowników. Przejdźmy do równań.
Licznik ułamka:
\[\begin(align) & \left(7x+1 \right)\left(11x+2 \right)=0 \\ & 7x+1=0\Rightarrow ((x)_(1))=-\ frac(1)(7); \\ & 11x+2=0\Strzałka w prawo ((x)_(2))=-\frac(2)(11). \\ \end(align)\]
Mianownik:
\[\begin(wyrównaj) & 13x-4=0; \\ & 13x=4; \\ & ((x)^(*))=\frac(4)(13). \\ \end(align)\]
Nie wiem, jaki zboczeniec stworzył ten problem, ale korzenie nie wyszły zbyt dobrze: trudno byłoby je umieścić na osi liczbowej. A jeśli przy pierwiastku $((x)^(*))=(4)/(13)\;$ wszystko jest mniej więcej jasne (to jest jedyna liczba dodatnia - będzie po prawej), to $ ((x)_(1 ))=-(1)/(7)\;$ i $((x)_(2))=-(2)/(11)\;$ wymagają dodatkowych badań: który z nich jest większy?
Można się tego dowiedzieć na przykład w ten sposób:
\[((x)_(1))=-\frac(1)(7)=-\frac(2)(14) \gt -\frac(2)(11)=((x)_(2 ))\]
Mam nadzieję, że nie trzeba wyjaśniać, dlaczego ułamek liczbowy $-(2)/(14)\; \gt -(2)/(11)\;$? W razie potrzeby radzę pamiętać, jak wykonywać operacje na ułamkach.
I zaznaczamy wszystkie trzy pierwiastki na osi liczbowej:
Kropki z licznika są wypełniane, kropki z mianownika są przebijane
Stawiamy znaki. Na przykład możesz wziąć $((x)_(0))=1$ i znaleźć znak w tym miejscu:
\[\begin(align) & f\left(x \right)=\frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4); \\ & f\left(1 \right)=\frac(\left(7\cdot 1+1 \right)\left(11\cdot 1+2 \right))(13\cdot 1-4)=\ frac(8\cdot 13)(9) \gt 0. \\\end(align)\]
Ostatnia nierówność przed równaniami to $f\left(x \right)\ge 0$, więc interesuje nas znak plus.
Mamy dwa zbiory: jeden to odcinek zwyczajny, a drugi to półprosta otwarta na osi liczbowej.
Odpowiedź: $x\in \left[ -\frac(2)(11);-\frac(1)(7) \right]\bigcup \left(\frac(4)(13);+\infty \right )$
Ważna uwaga dotycząca liczb, które podstawiamy, aby znaleźć znak w przedziale skrajnym na prawo. Absolutnie nie jest konieczne zastępowanie liczby znajdującej się najbliżej pierwiastka znajdującego się najbardziej na prawo. Możesz wziąć miliardy, a nawet „plus nieskończoność” - w tym przypadku znak wielomianu w nawiasie, liczniku lub mianowniku jest określony wyłącznie przez znak wiodącego współczynnika.
Przyjrzyjmy się jeszcze raz funkcji $f\left(x \right)$ z ostatniej nierówności:
Jego zapis zawiera trzy wielomiany:
\[\begin(align) & ((P)_(1))\left(x \right)=7x+1; \\ & ((P)_(2))\left(x \right)=11x+2; \\ & Q\lewo(x \prawo)=13x-4. \end(align)\]
Wszystkie są dwumianami liniowymi i wszystkie ich współczynniki wiodące (cyfry 7, 11 i 13) są dodatnie. W konsekwencji przy podstawieniu bardzo dużych liczb same wielomiany również będą dodatnie :)
Zasada ta może wydawać się zbyt skomplikowana, ale tylko na początku, gdy analizujemy bardzo łatwe problemy. W przypadku poważnych nierówności podstawienie „plus-nieskończoność” pozwoli nam znaleźć znaki znacznie szybciej niż standardowe $((x)_(0))=100$.
Już niedługo będziemy musieli stawić czoła takim wyzwaniom. Ale najpierw przyjrzyjmy się alternatywnemu sposobowi rozwiązywania ułamkowych nierówności racjonalnych.
Alternatywny sposób
Tę technikę zaproponował mi jeden z moich uczniów. Sam nigdy z tego nie korzystałem, ale praktyka pokazała, że wielu uczniom naprawdę wygodniej jest rozwiązywać nierówności w ten sposób.
Zatem początkowe dane są takie same. Musimy rozwiązać ułamkową nierówność wymierną:
\[\frac(P\lewo(x \prawo))(Q\lewo(x \prawo)) \gt 0\]
Zastanówmy się: dlaczego wielomian $Q\left(x \right)$ jest „gorszy” niż wielomian $P\left(x \right)$? Dlaczego musimy rozważać osobne grupy korzeni (z gwiazdką i bez), myśleć o punktach przebicia itp.? To proste: ułamek ma dziedzinę definicji, zgodnie z którą ułamek ma sens tylko wtedy, gdy jego mianownik jest różny od zera.
W przeciwnym razie nie ma różnicy między licznikiem a mianownikiem: przyrównujemy go również do zera, szukamy pierwiastków, a następnie zaznaczamy je na osi liczbowej. Dlaczego więc nie zastąpić linii ułamkowej (właściwie znaku podziału) zwykłym mnożeniem i zapisać wszystkie wymagania ODZ w postaci osobnej nierówności? Na przykład tak:
\[\frac(P\left(x \right))(Q\left(x \right)) \gt 0\Rightarrow \left\( \begin(align) & P\left(x \right)\cdot Q \left(x \right) \gt 0, \\ & Q\left(x \right)\ne 0. \\ \end(align) \right.\]
Uwaga: takie podejście sprowadzi problem do metody interwałowej, ale wcale nie skomplikuje rozwiązania. Przecież nadal będziemy przyrównywać wielomian $Q\left(x \right)$ do zera.
Zobaczmy, jak to działa na rzeczywistych problemach.
Zadanie. Rozwiąż nierówność:
\[\frac(x+8)(x-11) \gt 0\]
Rozwiązanie. Przejdźmy więc do metody interwałowej:
\[\frac(x+8)(x-11) \gt 0\Rightarrow \left\( \begin(align) & \left(x+8 \right)\left(x-11 \right) \gt 0 , \\ & x-11\ne 0. \\ \end(align) \right.\]
Pierwszą nierówność można rozwiązać w sposób elementarny. Po prostu przyrównujemy każdy nawias do zera:
\[\begin(align) & x+8=0\Rightarrow ((x)_(1))=-8; \\ & x-11=0\Strzałka w prawo ((x)_(2))=11. \\ \end(align)\]
Druga nierówność jest również prosta:
Zaznacz punkty $((x)_(1))$ i $((x)_(2))$ na osi liczbowej. Wszystkie są odrzucane, ponieważ nierówność jest ścisła:
Prawy punkt został wyłupiony dwukrotnie. Jest okej.Zwróć uwagę na punkt $x=11$. Okazuje się, że jest „podwójnie nakłuty”: z jednej strony nakłuwamy go ze względu na nasilenie nierówności, z drugiej zaś ze względu na dodatkowy wymóg DL.
W każdym razie będzie to po prostu punkt przebicia. Ustawiamy zatem znaki nierówności $\left(x+8 \right)\left(x-11 \right) \gt 0$ - ostatni, który widzieliśmy przed przystąpieniem do rozwiązywania równań:
Nas interesują obszary dodatnie, gdyż rozwiązujemy nierówność postaci $f\left(x \right) \gt 0$ - zacieniujemy je. Pozostaje tylko zapisać odpowiedź.
Odpowiedź. $x\in \left(-\infty ;-8 \right)\bigcup \left(11;+\infty \right)$
Na przykładzie tego rozwiązania chcę Cię przestrzec przed częstym błędem wśród początkujących uczniów. Mianowicie: nigdy nie otwieraj nawiasów w nierównościach! Wręcz przeciwnie, spróbuj wszystko uwzględnić - uprości to rozwiązanie i pozwoli uniknąć wielu problemów.
Teraz spróbujmy czegoś bardziej skomplikowanego.
Zadanie. Rozwiąż nierówność:
\[\frac(\left(2x-13 \right)\left(12x-9 \right))(15x+33)\le 0\]
Rozwiązanie. Jest to nieścisła nierówność postaci $f\left(x \right)\le 0$, więc tutaj należy zwrócić szczególną uwagę na zacienione punkty.
Przejdźmy do metody interwałowej:
\[\left\( \begin(align) & \left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)\le 0, \\ & 15x+33\ ne 0. \\ \end(align) \right.\]
Przejdźmy do równania:
\[\begin(align) & \left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)=0 \\ & 2x-13=0\Rightarrow ((x )_(1))=6,5; \\ & 12x-9=0\Strzałka w prawo ((x)_(2))=0,75; \\ & 15x+33=0\Strzałka w prawo ((x)_(3))=-2.2. \\ \end(align)\]
Bierzemy pod uwagę dodatkowy wymóg:
Zaznaczamy wszystkie powstałe pierwiastki na osi liczbowej:
Jeśli punkt jest jednocześnie przebity i wypełniony, uważa się go za przebityZnów dwa punkty „nakładają się” na siebie - to normalne, zawsze tak będzie. Ważne jest tylko, aby zrozumieć, że punkt oznaczony jako przebity i zamalowany jest w rzeczywistości punktem przebitym. Te. „Kłucie” jest działaniem silniejszym niż „malowanie”.
Jest to całkowicie logiczne, ponieważ ściskając zaznaczamy punkty, które wpływają na znak funkcji, ale same nie biorą udziału w odpowiedzi. A jeśli w pewnym momencie liczba już nam nie odpowiada (np. nie wpada do ODZ), to skreślamy ją z rozważań aż do samego końca zadania.
Generalnie przestań filozofować. Umieszczamy znaki i malujemy odstępy oznaczone znakiem minus:
Odpowiedź. $x\in \left(-\infty ;-2,2 \right)\bigcup \left[ 0,75;6,5 \right]$.
I znowu chciałem zwrócić uwagę na to równanie:
\[\lewo(2x-13 \prawo)\lewo(12x-9 \prawo)\lewo(15x+33 \prawo)=0\]
Jeszcze raz: nigdy nie otwieraj nawiasów w takich równaniach! Tylko sobie utrudnisz sprawę. Pamiętaj: iloczyn jest równy zero, gdy przynajmniej jeden z czynników jest równy zero. W rezultacie równanie to po prostu „rozpada się” na kilka mniejszych, które rozwiązaliśmy w poprzednim zadaniu.
Biorąc pod uwagę wielość korzeni
Z poprzednich problemów łatwo zauważyć, że najtrudniejsze są nierówności nieścisłe, bo trzeba w nich śledzić zacienione punkty.
Ale na świecie jest jeszcze większe zło – są to liczne korzenie nierówności. Tutaj nie trzeba już podążać za zacienionymi kropkami - tutaj znak nierówności nie może się nagle zmienić, przechodząc przez te właśnie kropki.
W tej lekcji nie rozważaliśmy jeszcze czegoś takiego (chociaż podobny problem często napotykano w metodzie przedziałowej). Dlatego wprowadzamy nową definicję:
Definicja. Pierwiastek równania $((\left(x-a \right))^(n))=0$ jest równy $x=a$ i nazywany jest pierwiastkiem $n$-tej krotności.
Właściwie nie jesteśmy szczególnie zainteresowani dokładną wartością krotności. Liczy się tylko to, czy ta sama liczba $n$ jest parzysta czy nieparzysta. Ponieważ:
- Jeśli $x=a$ jest pierwiastkiem parzystej wielokrotności, to znak funkcji nie zmienia się przy przejściu przez niego;
- I odwrotnie, jeśli $x=a$ jest pierwiastkiem nieparzystej wielokrotności, to znak funkcji ulegnie zmianie.
Wszystkie poprzednie problemy omówione w tej lekcji są szczególnym przypadkiem pierwiastka nieparzystej wielokrotności: wszędzie krotność jest równa jeden.
I dalej. Zanim przystąpimy do rozwiązywania problemów, chciałbym zwrócić uwagę na jedną subtelność, która dla doświadczonego ucznia wydaje się oczywista, ale wielu początkujących wprawia w osłupienie. Mianowicie:
Pierwiastek wielokrotności $n$ powstaje tylko w przypadku, gdy całe wyrażenie zostanie podniesione do tej potęgi: $((\left(x-a \right))^(n))$, a nie $\left(((x) ^(n))-a \right)$.
Jeszcze raz: nawias $((\left(x-a \right))^(n))$ daje nam pierwiastek $x=a$ krotności $n$, ale nawias $\left(((x)^( n)) -a \right)$ lub, jak to często bywa, $(a-((x)^(n)))$ daje nam pierwiastek (lub dwa pierwiastki, jeśli $n$ jest parzyste) pierwszej wielokrotności , niezależnie od tego, co wynosi $n$.
Porównywać:
\[((\lewo(x-3 \prawo))^(5))=0\Strzałka w prawo x=3\lewo(5k \prawo)\]
Tutaj wszystko jest jasne: cały nawias został podniesiony do potęgi piątej, więc na wyjściu otrzymaliśmy pierwiastek z potęgi piątej. I teraz:
\[\left(((x)^(2))-4 \right)=0\Strzałka w prawo ((x)^(2))=4\Strzałka w prawo x=\pm 2\]
Mamy dwa pierwiastki, ale oba mają pierwszą wielokrotność. Albo oto inny:
\[\left(((x)^(10))-1024 \right)=0\Rightarrow ((x)^(10))=1024\Rightarrow x=\pm 2\]
I nie pozwól, aby dziesiąty stopień przeszkadzał ci. Najważniejsze, że 10 jest liczbą parzystą, więc na wyjściu mamy dwa pierwiastki i oba znowu mają pierwszą wielokrotność.
Ogólnie rzecz biorąc, bądź ostrożny: wielość występuje tylko wtedy, gdy stopień odnosi się do całego nawiasu, a nie tylko do zmiennej.
Zadanie. Rozwiąż nierówność:
\[\frac(((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right))(((\left(x+7 \right))^(5)))\ge 0\]
Rozwiązanie. Spróbujmy rozwiązać to w alternatywny sposób - poprzez przejście od ilorazu do iloczynu:
\[\left\(\begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right)\cdot ( (\left(x+7 \right))^(5))\ge 0, \\ & ((\left(x+7 \right))^(5))\ne 0. \\ \end(align )\Prawidłowy.\]
Zajmijmy się pierwszą nierównością metodą przedziałową:
\[\begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right)\cdot ((\left( x+7 \prawo))^(5))=0; \\ & ((x)^(2))=0\Strzałka w prawo x=0\left(2k \right); \\ & ((\left(6-x \right))^(3))=0\RightStrzałka x=6\left(3k \right); \\ & x+4=0\Strzałka w prawo x=-4; \\ & ((\left(x+7 \right))^(5))=0\RightStrzałka x=-7\left(5k \right). \\ \end(align)\]
Dodatkowo rozwiązujemy drugą nierówność. Właściwie już to rozwiązaliśmy, ale żeby recenzenci nie znaleźli błędów w rozwiązaniu, lepiej rozwiązać je jeszcze raz:
\[((\lewo(x+7 \prawo))^(5))\ne 0\Strzałka w prawo x\ne -7\]
Uwaga: w ostatniej nierówności nie ma krotności. Właściwie: jaką różnicę robi to, ile razy skreślisz punkt $x=-7$ na osi liczbowej? Przynajmniej raz, co najmniej pięć razy wynik będzie taki sam: przebity punkt.
Zaznaczmy wszystko, co mamy na osi liczbowej:
Jak powiedziałem, punkt $x=-7$ w końcu zostanie przebity. Wielości ułożone są w oparciu o rozwiązanie nierówności metodą przedziałową.
Pozostaje tylko umieścić znaki:
Ponieważ punkt $x=0$ jest pierwiastkiem parzystej wielokrotności, znak nie zmienia się przy przejściu przez niego. Pozostałe punkty mają dziwną mnogość i wszystko jest z nimi proste.
Odpowiedź. $x\in \left(-\infty ;-7 \right)\bigcup \left[ -4;6 \right]$
Jeszcze raz zwróć uwagę na $x=0$. Dzięki równej wielości powstaje ciekawy efekt: wszystko na lewo od niego jest zamalowane, wszystko na prawo jest również zamalowane, a sam punkt jest całkowicie zamalowany.
Dzięki temu nie trzeba go izolować podczas zapisywania odpowiedzi. Te. nie ma potrzeby pisać czegoś w stylu $x\in \left[ -4;0 \right]\bigcup \left[ 0;6 \right]$ (choć formalnie taka odpowiedź też byłaby poprawna). Zamiast tego natychmiast zapisujemy $x\in \left[ -4;6 \right]$.
Takie efekty są możliwe tylko przy pierwiastkach o parzystej wielokrotności. A w kolejnym zadaniu spotkamy się z odwrotną „manifestacją” tego efektu. Gotowy?
Zadanie. Rozwiąż nierówność:
\[\frac(((\lewo(x-3 \prawo))^(4))\lewo(x-4 \prawo))(((\lewo(x-1 \prawo))^(2)) \left(7x-10-((x)^(2)) \right))\ge 0\]
Rozwiązanie. Tym razem będziemy postępować według standardowego schematu. Przyrównujemy licznik do zera:
\[\begin(align) & ((\left(x-3 \right))^(4))\left(x-4 \right)=0; \\ & ((\left(x-3 \right))^(4))=0\Rightarrow ((x)_(1))=3\left(4k \right); \\ & x-4=0\Strzałka w prawo ((x)_(2))=4. \\ \end(align)\]
I mianownik:
\[\begin(align) & ((\left(x-1 \right))^(2))\left(7x-10-((x)^(2)) \right)=0; \\ & ((\left(x-1 \right))^(2))=0\Rightarrow x_(1)^(*)=1\left(2k \right); \\ & 7x-10-((x)^(2))=0\Strzałka w prawo x_(2)^(*)=5;\ x_(3)^(*)=2. \\ \end(align)\]
Ponieważ rozwiązujemy nieścisłą nierówność w postaci $f\left(x \right)\ge 0$, pierwiastki z mianownika (które mają gwiazdki) zostaną usunięte, a pierwiastki z licznika zostaną zacienione.
Ustawiamy znaki i zacieniamy obszary oznaczone „plusem”:
Punkt $x=3$ jest izolowany. To jest część odpowiedzi
Zanim napiszemy ostateczną odpowiedź, przyjrzyjmy się bliżej zdjęciu:
- Punkt $x=1$ ma parzystą wielokrotność, ale sam jest przebity. W związku z tym trzeba będzie to wyodrębnić w odpowiedzi: musisz napisać $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)$, a nie $x\in \left(-\ infty ;2 \right)$.
- Punkt $x=3$ również ma parzystą wielokrotność i jest zacieniony. Układ znaków wskazuje, że sam punkt nam odpowiada, ale krok w lewo lub w prawo – i znajdziemy się w obszarze, który zdecydowanie nam nie odpowiada. Takie punkty nazywane są izolowanymi i zapisywane są w postaci $x\in \left\( 3 \right\)$.
Wszystkie otrzymane kawałki łączymy we wspólny zestaw i zapisujemy odpowiedź.
Odpowiedź: $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;5 \right) $
Definicja. Rozwiązanie nierówności oznacza znaleźć zbiór wszystkich jego rozwiązań lub udowodnij, że ten zbiór jest pusty.
Wydawałoby się: co tu może być niezrozumiałego? Tak, prawda jest taka, że zbiory można definiować na różne sposoby. Zapiszmy jeszcze raz odpowiedź na ostatnie zadanie:
Dosłownie czytamy to, co jest napisane. Zmienna „x” należy do pewnego zbioru, który uzyskuje się poprzez połączenie (znak „U”) czterech odrębnych zbiorów:
- Interwał $\left(-\infty ;1 \right)$, co dosłownie oznacza „wszystkie liczby mniejsze od jeden, ale nie samą jednostkę”;
- Interwał $\lewo(1;2 \prawo)$, tj. „wszystkie liczby z zakresu od 1 do 2, ale nie same liczby 1 i 2”;
- Zbiór $\left\( 3 \right\)$, składający się z jednej liczby - trzech;
- Przedział $\left[ 4;5 \right)$ zawierający wszystkie liczby z zakresu od 4 do 5, a także samą czwórkę, ale nie piątkę.
Interesująca jest tutaj trzecia kwestia. W przeciwieństwie do przedziałów, które definiują nieskończone zbiory liczb i wskazują jedynie granice tych zbiorów, zbiór $\left\( 3 \right\)$ określa ściśle jedną liczbę poprzez wyliczenie.
Aby zrozumieć, że podajemy konkretne liczby zawarte w zbiorze (a nie wyznaczamy granic ani niczego innego), zastosowano nawiasy klamrowe. Na przykład zapis $\left\( 1;2 \right\)$ oznacza dokładnie „zbiór składający się z dwóch liczb: 1 i 2”, ale nie segment od 1 do 2. W żadnym wypadku nie należy mylić tych pojęć .
Zasada dodawania wielokrotności
Cóż, na koniec dzisiejszej lekcji mała puszka od Pawła Berdowa :)
Uważni uczniowie zapewne zastanawiali się już: co się stanie, jeśli licznik i mianownik będą miały ten sam pierwiastek? Zatem działa następująca reguła:
Dodawane są wielokrotności identycznych pierwiastków. Zawsze. Nawet jeśli ten pierwiastek występuje zarówno w liczniku, jak i mianowniku.
Czasem lepiej podjąć decyzję, niż rozmawiać. Dlatego rozwiązujemy następujący problem:
Zadanie. Rozwiąż nierówność:
\[\frac(((x)^(2))+6x+8)(\left(((x)^(2))-16 \right)\left(((x)^(2))+ 9x+14 \prawo))\ge 0\]
\[\begin(align) & ((x)^(2))+6x+8=0 \\ & ((x)_(1))=-2;\ ((x)_(2))= -4. \\ \end(align)\]
Jeszcze nic specjalnego. Przyrównujemy mianownik do zera:
\[\begin(align) & \left(((x)^(2))-16 \right)\left(((x)^(2))+9x+14 \right)=0 \\ & ( (x)^(2))-16=0\Strzałka w prawo x_(1)^(*)=4;\ x_(2)^(*)=-4; \\ & ((x)^(2))+9x+14=0\Strzałka w prawo x_(3)^(*)=-7;\ x_(4)^(*)=-2. \\ \end(align)\]
Odkryto dwa identyczne pierwiastki: $((x)_(1))=-2$ i $x_(4)^(*)=-2$. Obydwa mają pierwszą wielokrotność. Dlatego zastępujemy je jednym pierwiastkiem $x_(4)^(*)=-2$, ale wielokrotnością 1+1=2.
Ponadto istnieją również identyczne pierwiastki: $((x)_(2))=-4$ i $x_(2)^(*)=-4$. Należą także do pierwszej krotności, więc pozostanie tylko $x_(2)^(*)=-4$ z krotności 1+1=2.
Uwaga: w obu przypadkach pozostawiliśmy dokładnie „przebity” korzeń i wykluczyliśmy z rozważań „malowany”. Ponieważ na początku lekcji zgodziliśmy się: jeśli punkt jest jednocześnie przebity i zamalowany, to i tak uważamy go za przebity.
W rezultacie mamy cztery korzenie i wszystkie zostały wycięte:
\[\begin(align) & x_(1)^(*)=4; \\ & x_(2)^(*)=-4\left(2k \right); \\ & x_(3)^(*)=-7; \\ & x_(4)^(*)=-2\lewo(2k \prawo). \\ \end(align)\]
Zaznaczamy je na osi liczbowej, biorąc pod uwagę krotność:
Umieszczamy znaki i malujemy interesujące nas obszary:
Wszystko. Żadnych izolowanych punktów i innych perwersji. Możesz zapisać odpowiedź.
Odpowiedź. $x\in \left(-\infty ;-7 \right)\bigcup \left(4;+\infty \right)$.
Zasada mnożenia wielokrotności
Czasami dochodzi do jeszcze bardziej nieprzyjemnej sytuacji: równanie, które ma wiele pierwiastków, samo zostaje podniesione do pewnej potęgi. W tym przypadku zmienia się wielokrotność wszystkich oryginalnych korzeni.
Jest to rzadkie zjawisko, dlatego większość uczniów nie ma doświadczenia w rozwiązywaniu takich problemów. A zasada jest tutaj taka:
Gdy równanie zostanie podniesione do potęgi $n$, krotność wszystkich jego pierwiastków również wzrośnie n$ razy.
Innymi słowy, podniesienie do potęgi prowadzi do pomnożenia wielokrotności przez tę samą potęgę. Przyjrzyjmy się tej zasadzie na przykładzie:
Zadanie. Rozwiąż nierówność:
\[\frac(x((\lewo(((x)^(2))-6x+9 \prawo))^(2))((\lewo(x-4 \prawo))^(5)) )(((\lewo(2-x \prawo))^(3))((\lewo(x-1 \prawo))^(2)))\le 0\]
Rozwiązanie. Przyrównujemy licznik do zera:
Iloczyn wynosi zero, gdy co najmniej jeden z czynników wynosi zero. Wszystko jest jasne z pierwszym czynnikiem: $x=0$. Ale potem zaczynają się problemy:
\[\begin(align) & ((\left(((x)^(2))-6x+9 \right))^(2))=0; \\ & ((x)^(2))-6x+9=0\lewo(2k \prawo); \\ & D=((6)^(3))-4\cdot 9=0 \\ & ((x)_(2))=3\left(2k \right)\left(2k \right) \ \& ((x)_(2))=3\left(4k \right) \\\end(align)\]
Jak widzimy, równanie $((x)^(2))-6x+9=0$ ma pojedynczy pierwiastek drugiej krotności: $x=3$. Całe to równanie jest następnie podnoszone do kwadratu. Zatem wielokrotność pierwiastka będzie wynosić 2 $\cdot 2=4$, co ostatecznie zapisaliśmy.
\[((\lewo(x-4 \prawo))^(5))=0\Strzałka w prawo x=4\lewo(5k \prawo)\]
Z mianownikiem też nie ma problemów:
\[\begin(align) & ((\left(2-x \right))^(3))((\left(x-1 \right))^(2))=0; \\ & ((\left(2-x \right))^(3))=0\Rightarrow x_(1)^(*)=2\left(3k \right); \\ & ((\left(x-1 \right))^(2))=0\Rightarrow x_(2)^(*)=1\left(2k \right). \\ \end(align)\]
W sumie otrzymaliśmy pięć kropek: dwie przebite i trzy pomalowane. W liczniku i mianowniku nie ma pokrywających się pierwiastków, więc po prostu zaznaczamy je na osi liczbowej:
Znaki układamy uwzględniając krotności i malujemy interesujące nas interwały:
Znów jeden izolowany punkt i jeden przebity
Ze względu na korzenie parzystej wielokrotności ponownie otrzymaliśmy kilka „niestandardowych” elementów. To jest $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)$, a nie $x\in \left[ 0;2 \right)$, a także izolowany punkt $ x\w \lewo\( 3 \prawo\)$.
Odpowiedź. $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;+\infty \right)$
Jak widać, wszystko nie jest takie skomplikowane. Najważniejsze jest uważność. Ostatnia część tej lekcji poświęcona jest przekształceniom - tym samym, które omawialiśmy na samym początku.
Konwersje wstępne
Nierówności, które zbadamy w tej sekcji, nie można nazwać złożonymi. Jednak w przeciwieństwie do poprzednich zadań, tutaj będziesz musiał zastosować umiejętności z teorii ułamków wymiernych - faktoryzację i redukcję do wspólnego mianownika.
Zagadnienie to szczegółowo omawialiśmy na samym początku dzisiejszej lekcji. Jeśli nie jesteś pewien, czy rozumiesz, o czym mówię, gorąco polecam wrócić i powtórzyć. Ponieważ nie ma sensu wkuwać metod rozwiązywania nierówności, jeśli „pływa” w konwersji ułamków.
Nawiasem mówiąc, w zadaniach domowych będzie również wiele podobnych zadań. Umieszczono je w osobnym podrozdziale. I tam znajdziesz bardzo nietrywialne przykłady. Ale to będzie w pracy domowej, a teraz spójrzmy na kilka takich nierówności.
Zadanie. Rozwiąż nierówność:
\[\frac(x)(x-1)\le \frac(x-2)(x)\]
Rozwiązanie. Przesuń wszystko w lewo:
\[\frac(x)(x-1)-\frac(x-2)(x)\le 0\]
Sprowadzamy do wspólnego mianownika, otwieramy nawiasy i wstawiamy podobne wyrazy do licznika:
\[\begin(align) & \frac(x\cdot x)(\left(x-1 \right)\cdot x)-\frac(\left(x-2 \right)\left(x-1 \ prawo))(x\cdot \lewo(x-1 \prawo))\le 0; \\ & \frac(((x)^(2))-\left(((x)^(2))-2x-x+2 \right))(x\left(x-1 \right)) \le 0; \\ & \frac(((x)^(2))-((x)^(2))+3x-2)(x\left(x-1 \right))\le 0; \\ & \frac(3x-2)(x\left(x-1 \right))\le 0. \\\end(align)\]
Teraz mamy przed sobą klasyczną nierówność ułamkowo-racjonalną, której rozwiązanie nie jest już trudne. Proponuję rozwiązać to metodą alternatywną – metodą przedziałów:
\[\begin(align) & \left(3x-2 \right)\cdot x\cdot \left(x-1 \right)=0; \\ & ((x)_(1))=\frac(2)(3);\ ((x)_(2))=0;\ ((x)_(3))=1. \\ \end(align)\]
Nie zapomnij o ograniczeniu wynikającym z mianownika:
Wszystkie liczby i ograniczenia zaznaczamy na osi liczbowej:
Wszystkie korzenie mają pierwszą wielokrotność. Bez problemu. Po prostu umieszczamy znaki i malujemy potrzebne obszary:
To wszystko. Możesz zapisać odpowiedź.
Odpowiedź. $x\in \left(-\infty ;0 \right)\bigcup \left[ (2)/(3)\;;1 \right)$.
Oczywiście był to bardzo prosty przykład. Zatem teraz spójrzmy na problem poważniej. A tak na marginesie, poziom tego zadania jest w miarę zgodny z samodzielną i testową pracą na ten temat w 8 klasie.
Zadanie. Rozwiąż nierówność:
\[\frac(1)(((x)^(2))+8x-9)\ge \frac(1)(3((x)^(2))-5x+2)\]
Rozwiązanie. Przesuń wszystko w lewo:
\[\frac(1)(((x)^(2))+8x-9)-\frac(1)(3((x)^(2))-5x+2)\ge 0\]
Zanim sprowadzimy oba ułamki do wspólnego mianownika, rozłóżmy te mianowniki na czynniki. A co jeśli wyjdą te same nawiasy? Z pierwszym mianownikiem jest to proste:
\[((x)^(2))+8x-9=\lewo(x-1 \prawo)\lewo(x+9 \prawo)\]
To drugie jest trochę trudniejsze. Możesz dodać stały współczynnik do nawiasu, w którym pojawia się ułamek. Pamiętaj: pierwotny wielomian miał współczynniki całkowite, więc istnieje duża szansa, że rozkład na czynniki będzie miał współczynniki całkowite (w rzeczywistości zawsze tak będzie, chyba że dyskryminator jest irracjonalny).
\[\begin(align) & 3((x)^(2))-5x+2=3\left(x-1 \right)\left(x-\frac(2)(3) \right)= \\ & =\left(x-1 \right)\left(3x-2 \right) \end(align)\]
Jak widać, istnieje wspólny nawias: $\left(x-1 \right)$. Wracamy do nierówności i sprowadzamy oba ułamki do wspólnego mianownika:
\[\begin(align) & \frac(1)(\left(x-1 \right)\left(x+9 \right))-\frac(1)(\left(x-1 \right)\ lewo(3x-2 \prawo))\ge 0; \\ & \frac(1\cdot \left(3x-2 \right)-1\cdot \left(x+9 \right))(\left(x-1 \right)\left(x+9 \right) )\lewo(3x-2 \prawo))\ge 0; \\ & \frac(3x-2-x-9)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ & \frac(2x-11)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ \end(align)\]
Przyrównujemy mianownik do zera:
\[\begin(align) & \left(x-1 \right)\left(x+9 \right)\left(3x-2 \right)=0; \\ & x_(1)^(*)=1;\ x_(2)^(*)=-9;\ x_(3)^(*)=\frac(2)(3) \\ \end( wyrównywać)\]
Żadnych wielokrotności ani zbieżnych pierwiastków. Na linii zaznaczamy cztery liczby:
Ustawiamy znaki:
Zapisujemy odpowiedź.
Odpowiedź: $x\in \left(-\infty ;-9 \right)\bigcup \left((2)/(3)\;;1 \right)\bigcup \left[ 5.5;+\infty \right) $.
Już od czasów starożytnych konieczne było porównywanie ilości i ilości przy rozwiązywaniu problemów praktycznych. Jednocześnie pojawiły się słowa takie jak coraz mniej, wyżej i niżej, lżej i ciężej, ciszej i głośniej, taniej i drożej itp., oznaczające wyniki porównywania jednorodnych wielkości.
Pojęcia więcej i mniej powstały w związku z liczeniem obiektów, mierzeniem i porównywaniem ilości. Na przykład matematycy starożytnej Grecji wiedzieli, że bok dowolnego trójkąta jest mniejszy od sumy dwóch pozostałych boków i że większy bok trójkąta leży naprzeciw większego kąta. Archimedes, obliczając obwód, ustalił, że obwód dowolnego koła jest równy trzykrotności średnicy z nadmiarem mniejszym niż jedna siódma średnicy, ale większym niż dziesięć siedemdziesiąt razy średnicy.
Zapisz symbolicznie relacje między liczbami i wielkościami, używając znaków > i b. Zapisy, w których dwie liczby są połączone jednym ze znaków: > (większy niż), Z nierównościami liczbowymi spotkałeś się także w klasach niższych. Wiesz, że nierówności mogą być prawdziwe lub fałszywe. Na przykład \(\frac(1)(2) > \frac(1)(3)\) jest poprawną nierównością numeryczną, 0,23 > 0,235 jest niepoprawną nierównością liczbową.
Nierówności z niewiadomymi mogą być prawdziwe dla niektórych wartości niewiadomych i fałszywe dla innych. Na przykład nierówność 2x+1>5 jest prawdziwa dla x = 3, ale fałszywa dla x = -3. W przypadku nierówności z jedną niewiadomą możesz ustawić zadanie: rozwiązać nierówność. W praktyce problemy rozwiązywania nierówności są stawiane i rozwiązywane nie rzadziej niż problemy rozwiązywania równań. Na przykład wiele problemów ekonomicznych sprowadza się do badania i rozwiązywania systemów nierówności liniowych. W wielu gałęziach matematyki nierówności są częstsze niż równania.
Niektóre nierówności służą jako jedyny pomocniczy sposób udowodnienia lub obalenia istnienia określonego obiektu, na przykład pierwiastka równania.
Nierówności numeryczne
Można porównywać liczby całkowite i ułamki dziesiętne. Zna zasady porównywania ułamków zwykłych o tych samych mianownikach, ale różnych licznikach; o tych samych licznikach, ale różnych mianownikach. Tutaj dowiesz się, jak porównać dwie dowolne liczby, znajdując znak ich różnicy.
Porównywanie liczb jest szeroko stosowane w praktyce. Na przykład ekonomista porównuje zaplanowane wskaźniki z rzeczywistymi, lekarz porównuje temperaturę pacjenta z normalną, tokarz porównuje wymiary obrabianej części ze standardem. We wszystkich takich przypadkach niektóre liczby są porównywane. W wyniku porównywania liczb powstają nierówności liczbowe.
Definicja. Liczba a jest większa od liczby b, jeśli różnica a-b jest dodatnia. Liczba a jest mniejsza niż liczba b, jeśli różnica a-b jest ujemna.
Jeżeli a jest większe od b, to piszą: a > b; jeśli a jest mniejsze od b, to piszą: a Zatem nierówność a > b oznacza, że różnica a - b jest dodatnia, tj. a - b > 0. Nierówność a Dla dowolnych dwóch liczb aib z trzech relacji a > b, a = b, a Porównanie liczb aib oznacza sprawdzenie, który ze znaków >, = lub Twierdzenie. Jeśli a > b i b > c, to a > c.
Twierdzenie. Jeśli do obu stron nierówności dodamy tę samą liczbę, znak nierówności nie ulegnie zmianie.
Konsekwencja. Każdy wyraz można przenieść z jednej części nierówności do drugiej, zmieniając znak tego wyrazu na przeciwny.
Twierdzenie. Jeżeli obie strony nierówności pomnożymy przez tę samą liczbę dodatnią, to znak nierówności nie ulegnie zmianie. Jeśli obie strony nierówności zostaną pomnożone przez tę samą liczbę ujemną, wówczas znak nierówności zmieni się na przeciwny.
Konsekwencja. Jeśli obie strony nierówności podzielimy przez tę samą liczbę dodatnią, to znak nierówności nie ulegnie zmianie. Jeżeli obie strony nierówności podzielimy przez tę samą liczbę ujemną, to znak nierówności zmieni się na przeciwny.
Wiesz, że równości liczbowe można dodawać i mnożyć wyraz po wyrazie. Następnie dowiesz się, jak wykonywać podobne działania z nierównościami. W praktyce często wykorzystuje się umiejętność dodawania i mnożenia nierówności wyraz po wyrazie. Działania te pomagają rozwiązać problemy oceny i porównania znaczeń wyrażeń.
Podczas rozwiązywania różnych problemów często konieczne jest dodanie lub pomnożenie lewej i prawej strony nierówności. Jednocześnie czasami mówi się, że nierówności sumują się lub mnożą. Przykładowo, jeśli turysta pierwszego dnia przeszedł ponad 20 km, a drugiego ponad 25 km, to można powiedzieć, że w ciągu dwóch dni przeszedł ponad 45 km. Podobnie, jeśli długość prostokąta jest mniejsza niż 13 cm, a szerokość mniejsza niż 5 cm, to możemy powiedzieć, że pole tego prostokąta jest mniejsze niż 65 cm2.
Rozważając te przykłady, wykorzystano następujące przykłady: twierdzenia o dodawaniu i mnożeniu nierówności:
Twierdzenie. Dodając nierówności tego samego znaku, otrzymujemy nierówność tego samego znaku: jeśli a > b i c > d, to a + c > b + d.
Twierdzenie. Mnożąc nierówności tego samego znaku, którego lewa i prawa strona są dodatnie, otrzymujemy nierówność tego samego znaku: jeśli a > b, c > d oraz a, b, c, d są liczbami dodatnimi, to ac > bd.
Nierówności ze znakiem > (większe niż) i 1/2, 3/4 b, c Wraz ze znakami nierówności ścisłych > i W ten sam sposób nierówność \(a \geq b \) oznacza, że liczba a jest większy lub równy b, tj. i nie mniejszy niż b.
Nierówności zawierające znak \(\geq \) lub \(\leq \) nazywane są nieścisłymi. Na przykład \(18 \geq 12 , \; 11 \leq 12 \) nie są nierównościami ścisłymi.
Wszystkie właściwości nierówności ścisłych obowiązują również w przypadku nierówności nieścisłych. Co więcej, jeśli dla nierówności ścisłych znaki > uznano za przeciwne i wiadomo, że aby rozwiązać szereg zastosowanych problemów, należy stworzyć model matematyczny w postaci równania lub układu równań. Następnie dowiesz się, że modele matematyczne służące do rozwiązywania wielu problemów to nierówności z niewiadomymi. Wprowadzone zostanie pojęcie rozwiązania nierówności oraz zostanie pokazane, jak sprawdzić, czy dana liczba jest rozwiązaniem konkretnej nierówności.
Nierówności formy
\(ax > b, \quad ax, w którym aib mają podane liczby, a x jest niewiadomą, nazywane są nierówności liniowe z jedną niewiadomą.
Definicja. Rozwiązaniem nierówności z jedną niewiadomą jest wartość niewiadomej, przy której nierówność ta staje się prawdziwą nierównością liczbową. Rozwiązanie nierówności polega na znalezieniu wszystkich jej rozwiązań lub stwierdzeniu, że ich nie ma.
Rozwiązałeś równania, sprowadzając je do najprostszych równań. Podobnie rozwiązując nierówności, próbuje się je sprowadzić za pomocą właściwości do postaci prostych nierówności.
Rozwiązywanie nierówności drugiego stopnia za pomocą jednej zmiennej
Nierówności formy
\(ax^2+bx+c >0 \) i \(ax^2+bx+c gdzie x jest zmienną, a, b i c to pewne liczby, a \(a \neq 0 \), zwane nierówności drugiego stopnia z jedną zmienną.
Rozwiązanie nierówności
\(ax^2+bx+c >0 \) lub \(ax^2+bx+c można uznać za znalezienie przedziałów, w których funkcja \(y= ax^2+bx+c \) przyjmuje wartość dodatnią lub ujemną wartości W tym celu wystarczy przeanalizować, jak wykres funkcji \(y= ax^2+bx+c\) leży w płaszczyźnie współrzędnych: gdzie skierowane są ramiona paraboli - w górę czy w dół, czy parabola przecina oś x, a jeśli tak, to w jakich punktach.
Algorytm rozwiązywania nierówności drugiego stopnia z jedną zmienną:
1) znajdź dyskryminator trójmianu kwadratowego \(ax^2+bx+c\) i dowiedz się, czy trójmian ma pierwiastek;
2) jeśli trójmian ma pierwiastki, to zaznaczamy je na osi x i przez zaznaczone punkty narysujemy schematyczną parabolę, której gałęzie są skierowane w górę dla a > 0 lub w dół dla 0 lub w dół dla 3) znajdź przedziały na osi x, dla których parabole punktów znajdują się powyżej osi x (jeśli rozwiązują nierówność \(ax^2+bx+c >0\)) lub poniżej osi x (jeśli rozwiązują nierówność nierówność
\(ax^2+bx+c Rozwiązywanie nierówności metodą przedziałową
Rozważ funkcję
f(x) = (x + 2)(x - 3)(x - 5)
Dziedziną tej funkcji jest zbiór wszystkich liczb. Zerami funkcji są liczby -2, 3, 5. Dzielą one dziedzinę definicji funkcji na przedziały \((-\infty; -2), \; (-2; 3), \; ( 3; 5) \) i \( (5; +\infty)\)
Przekonajmy się, jakie są znaki tej funkcji w każdym ze wskazanych przedziałów.
Wyrażenie (x + 2)(x - 3)(x - 5) jest iloczynem trzech czynników. Znak każdego z tych czynników w rozważanych przedziałach pokazano w tabeli:
Ogólnie rzecz biorąc, niech funkcja będzie dana wzorem
f(x) = (x-x 1)(x-x 2) ... (x-x n),
gdzie x jest zmienną, a x 1, x 2, ..., x n to liczby, które nie są sobie równe. Liczby x 1 , x 2 , ..., x n są zerami funkcji. W każdym z przedziałów, na które dzieli się dziedzinę definicji przez zera funkcji, znak funkcji zostaje zachowany, a przy przejściu przez zero zmienia się jej znak.
Właściwość ta służy do rozwiązywania nierówności postaci
(x-x 1)(x-x 2) ... (x-x n) > 0,
(x-x 1)(x-x 2) ... (x-x n) gdzie x 1, x 2, ..., x n są liczbami, które nie są sobie równe
Rozważana metoda rozwiązywanie nierówności nazywa się metodą przedziałową.
Podajmy przykłady rozwiązywania nierówności metodą przedziałową.
Rozwiąż nierówność:
\(x(0,5-x)(x+4) Oczywiście zera funkcji f(x) = x(0,5-x)(x+4) to punkty \(x=0, \; x= \ frac(1)(2) , \; x=-4 \)Wykreślamy zera funkcji na osi liczb i obliczamy znak na każdym przedziale:
Wybieramy te przedziały, w których funkcja jest mniejsza lub równa zero i zapisujemy odpowiedź.
Odpowiedź:
\(x \in \left(-\infty; \; 1 \right) \cup \left[ 4; \; +\infty \right) \)
Metoda interwałowa to specjalny algorytm przeznaczony do rozwiązywania złożonych nierówności w postaci f(x) > 0. Algorytm składa się z 5 kroków:
- Rozwiąż równanie f(x) = 0. Zamiast nierówności otrzymamy równanie, które jest znacznie prostsze do rozwiązania;
- Zaznacz wszystkie uzyskane pierwiastki na linii współrzędnych. W ten sposób linia prosta zostanie podzielona na kilka przedziałów;
- Znajdź wielokrotność pierwiastków. Jeśli korzenie są parzyste, narysuj pętlę nad korzeniem. (Korzeń uważa się za wielokrotność, jeśli istnieje parzysta liczba identycznych rozwiązań)
- Znajdź znak (plus lub minus) funkcji f(x) w skrajnym prawym przedziale. Aby to zrobić, wystarczy podstawić w f(x) dowolną liczbę, która będzie na prawo od wszystkich zaznaczonych pierwiastków;
- Zaznacz znaki w pozostałych odstępach, naprzemiennie.
Następnie pozostaje już tylko zapisać interesujące nas interwały. Oznaczono je znakiem „+”, jeśli nierówność miała postać f(x) > 0, lub znakiem „-”, jeśli nierówność miała postać f(x)< 0.
W przypadku nierówności nieścisłych (≤ , ≥) należy w przedziałach uwzględnić punkty będące rozwiązaniem równania f(x) = 0;
Przykład 1:
Rozwiąż nierówność:
(x - 2) (x + 7)< 0
Pracujemy metodą interwałową.
Krok 1: zastąp nierówność równaniem i rozwiąż ją:
(x - 2)(x + 7) = 0
Iloczyn wynosi zero wtedy i tylko wtedy, gdy co najmniej jeden z czynników wynosi zero:
x - 2 = 0 => x = 2
x + 7 = 0 => x = -7
Mamy dwa korzenie.
Krok 2: Zaznaczamy te pierwiastki na linii współrzędnych. Mamy:
Krok 3: znajdujemy znak funkcji w skrajnym prawym przedziale (na prawo od zaznaczonego punktu x = 2). Aby to zrobić, musisz wziąć dowolną liczbę większą niż liczba x = 2. Weźmy na przykład x = 3 (ale nikt nie zabrania przyjmowania x = 4, x = 10, a nawet x = 10 000).
f(x) = (x - 2)(x + 7)
f(3)=(3 - 2)(3 + 7) = 1*10 = 10
Otrzymujemy, że f(3) = 10 > 0 (10 jest liczbą dodatnią), więc umieszczamy znak plus w skrajnym prawym przedziale.
Krok 4: należy zwrócić uwagę na znaki na pozostałych odstępach. Pamiętamy, że przechodząc przez każdy korzeń, znak musi się zmienić. Na przykład na prawo od pierwiastka x = 2 znajduje się plus (upewniliśmy się o tym w poprzednim kroku), więc po lewej stronie musi być minus. Ten minus rozciąga się na cały przedział (-7; 2), więc na prawo od pierwiastka x = -7 znajduje się minus. Dlatego na lewo od pierwiastka x = −7 znajduje się plus. Pozostaje zaznaczyć te znaki na osi współrzędnych.
Wróćmy do pierwotnej nierówności, która miała postać:
(x - 2) (x + 7)< 0
Zatem funkcja musi być mniejsza od zera. Oznacza to, że interesuje nas znak minus, który występuje tylko w jednym przedziale: (−7; 2). To będzie odpowiedź.
Przykład 2:
Rozwiąż nierówność:
(9x 2 - 6x + 1)(x - 2) ≥ 0
Rozwiązanie:
Najpierw musisz znaleźć pierwiastki równania
(9x 2 - 6x + 1)(x - 2) = 0
Zwińmy pierwszy nawias i otrzymamy:
(3x - 1) 2 (x - 2) = 0
x - 2 = 0; (3x - 1) 2 = 0
Rozwiązując te równania otrzymujemy:
Narysujmy punkty na osi liczbowej:
Ponieważ x 2 i x 3 są wielokrotnymi pierwiastkami, wówczas na prostej i nad nią będzie jeden punkt „ pętla”.
Weźmy dowolną liczbę mniejszą niż skrajny lewy punkt i podstawmy ją do pierwotnej nierówności. Weźmy liczbę -1.
Nie zapomnij podać rozwiązania równania (znaleziono X), ponieważ nasza nierówność nie jest ścisła.
Odpowiedź: ()U)











