Jak rozwiązywać równania i nierówności logarytmiczne. Złożone nierówności logarytmiczne

14.10.2019

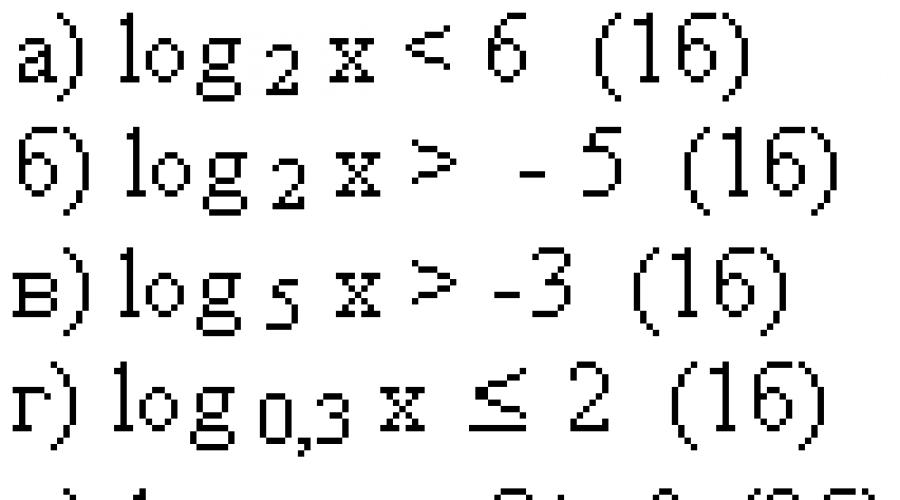
Przeczytaj także

Czynność rozliczeniowa – co to jest?

Zobacz, co „Sergey Anatolyevich Storchak” znajduje się w innych słownikach Sergey Anatolyevich Storchak

Rola polityki pieniężnej na obecnym etapie Rola państwa w polityce pieniężnej

Ogólna charakterystyka Eurazji

Alexander Starovoitov: biografia, działalność polityczna Osoba publiczna Alexander Starovoitov

Cele Lekcji:

Dydaktyczny:

Poziom 1 – uczy rozwiązywania najprostszych nierówności logarytmicznych, korzystając z definicji logarytmu i własności logarytmów;
Poziom 2 – rozwiązujemy nierówności logarytmiczne, wybierając własną metodę rozwiązania;
Poziom 3 – potrafi zastosować wiedzę i umiejętności w niestandardowych sytuacjach.

Edukacyjny: rozwijać pamięć, uwagę, logiczne myślenie, umiejętność porównywania, umiejętność generalizowania i wyciągania wniosków

Edukacyjny: kultywuj dokładność, odpowiedzialność za wykonywane zadanie i wzajemną pomoc.

Metody nauczania: werbalny , wizualny , praktyczny , wyszukiwanie częściowe , samorządność , kontrola.

Formy organizacji aktywność poznawcza studenci: czołowy , indywidualny , pracować w parach.

Sprzęt: zestaw zadań testowych, podsumowanie referencyjne, czyste arkusze rozwiązań.

Typ lekcji: nauka nowego materiału.

Podczas zajęć

1. Moment organizacyjny. Ogłaszany jest temat i cele lekcji, plan lekcji: każdy uczeń otrzymuje kartę oceny, którą wypełnia w trakcie lekcji; dla każdej pary uczniów – drukowane materiały z zadaniami należy wykonać w parach; puste arkusze rozwiązań; arkusze pomocnicze: definicja logarytmu; wykres funkcji logarytmicznej, jej własności; właściwości logarytmów; algorytm rozwiązania nierówności logarytmiczne.

Wszelkie decyzje po dokonaniu samooceny przekazywane są nauczycielowi.

Arkusz ocen ucznia

2. Aktualizowanie wiedzy.

Instrukcje nauczyciela. Przypomnij sobie definicję logarytmu, wykres funkcji logarytmicznej i jej właściwości. Aby to zrobić, przeczytaj tekst na s. 88–90, 98–101 podręcznika „Algebra i początki analizy 10–11” pod redakcją Sh.A Alimova, Yu.M Kolyagina i innych.

Uczniowie otrzymują arkusze, na których zapisano: definicję logarytmu; pokazuje wykres funkcji logarytmicznej i jej własności; właściwości logarytmów; algorytm rozwiązywania nierówności logarytmicznych, przykład rozwiązania nierówności logarytmicznej sprowadzającej się do kwadratowej.

3. Studiowanie nowego materiału.

Rozwiązywanie nierówności logarytmicznych opiera się na monotoniczności funkcji logarytmicznej.

Algorytm rozwiązywania nierówności logarytmicznych:

A) Znajdź dziedzinę definicji nierówności (wyrażenie sublogarytmiczne jest większe od zera).
B) Przedstaw (jeśli to możliwe) lewą i prawą stronę nierówności jako logarytmy o tej samej podstawie.
C) Ustal, czy funkcja logarytmiczna: jeśli t>1, to rośnie; jeśli 0 1, a następnie maleje.
D) Przejdź do więcej prosta nierówność(wyrażenia sublogarytmiczne), biorąc pod uwagę, że znak nierówności pozostanie, jeśli funkcja wzrośnie, i zmieni się, jeśli funkcja maleje.

Element edukacyjny nr 1.

Cel: skonsolidować rozwiązanie najprostszych nierówności logarytmicznych

Forma organizacji aktywności poznawczej studentów: praca indywidualna.

Zadania dla niezależna praca za 10 minut. Dla każdej nierówności istnieje kilka możliwych odpowiedzi; należy wybrać właściwą i sprawdzić ją za pomocą klawisza.

KLUCZ: 13321, maksymalna liczba punktów – 6 punktów.

Element edukacyjny nr 2.

Cel: skonsolidować rozwiązanie nierówności logarytmicznych za pomocą właściwości logarytmów.

Instrukcje nauczyciela. Zapamiętaj podstawowe własności logarytmów. W tym celu zapoznaj się z tekstem podręcznika na s. 92, 103–104.

Zadania do samodzielnej pracy przez 10 minut.

KLUCZ: 2113, maksymalna liczba punktów – 8 punktów.

Element edukacyjny nr 3.

Cel: badanie rozwiązania nierówności logarytmicznych metodą redukcji do kwadratu.

Instrukcja nauczyciela: metoda sprowadzenia nierówności do kwadratu polega na przekształceniu nierówności do takiej postaci, że pewna funkcja logarytmiczna jest oznaczona przez nową zmienną, uzyskując w ten sposób nierówność kwadratową względem tej zmiennej.

Skorzystajmy z metody interwałowej.

Przeszedłeś pierwszy poziom opanowania materiału. Teraz będziesz musiał samodzielnie wybrać metodę rozwiązywania równań logarytmicznych, wykorzystując całą swoją wiedzę i możliwości.

Element edukacyjny nr 4.

Cel: utrwalić rozwiązanie nierówności logarytmicznych samodzielnie wybierając racjonalną metodę rozwiązania.

Zadania do samodzielnej pracy przez 10 minut

Element edukacyjny nr 5.

Instrukcje nauczyciela. Dobrze zrobiony! Opanowałeś rozwiązywanie równań drugiego stopnia złożoności. Celem Twojej dalszej pracy jest zastosowanie wiedzy i umiejętności w bardziej złożonych i niestandardowych sytuacjach.

Zadania do samodzielnego rozwiązania:

Instrukcje nauczyciela. Świetnie, jeśli wykonałeś całe zadanie. Dobrze zrobiony!

Ocena z całej lekcji uzależniona jest od ilości punktów zdobytych za wszystkie elementy edukacyjne:

jeśli N ≥ 20 to otrzymujesz ocenę „5”,
dla 16 ≤ N ≤ 19 – ocena „4”,
dla 8 ≤ N ≤ 15 – ocena „3”,
w N< 8 выполнить работу над ошибками к следующему уроку (решения можно взять у учителя).

Prześlij arkusze ocen nauczycielowi.

5. Praca domowa: jeśli zdobyłeś nie więcej niż 15 punktów, popracuj nad swoimi błędami (rozwiązania można pobrać od nauczyciela), jeśli zdobyłeś więcej niż 15 punktów, wykonaj kreatywne zadanie na temat „Nierówności logarytmiczne”.

Z nimi są logarytmy wewnętrzne.

Przykłady:

$\log_3⁡x≥\log_3⁡9$
$\log_3⁡ ((x^2-3))< \log_3⁡{(2x)}$
$\log_(x+1)⁡((x^2+3x-7))>2$
$\lg^2⁡((x+1))+10≤11 \lg⁡((x+1))$

Jak rozwiązać nierówności logarytmiczne:

Powinniśmy dążyć do sprowadzenia dowolnej nierówności logarytmicznej do postaci $\log_a⁡(f(x)) ˅ \log_a(⁡g(x))$ (symbol $˅$ oznacza dowolne z ). Ten typ pozwala pozbyć się logarytmów i ich podstaw, dokonując przejścia do nierówności wyrażeń pod logarytmami, czyli do postaci $f(x) ˅ g(x)$.

Ale przy dokonywaniu tego przejścia istnieje jedna bardzo ważna subtelność:
$-$ jeśli jest liczbą i jest większa od 1, znak nierówności pozostaje taki sam podczas przejścia,
$-$ jeśli podstawa jest liczbą większą od 0, ale mniejszą od 1 (leży między zerem a jedynką), to znak nierówności powinien zmienić się na przeciwny, tj.

Przykłady:

$\log_2⁡((8-x))<1$
ODZ: $8-x>0$
$-x>-8$
$X<8$

Rozwiązanie:
$\log$$_2$ $(8-x)<\log$$_2$ ${2}$
$8-x$$<$ $2$
$8-2\(x>6$
Odpowiedź: $(6;8)$

$\log$$_(0,5⁡)$ $(2x-4)$≥$\log$$_(0,5)$ ⁡$((x+ 1))$
ODZ: $\begin(przypadki)2x-4>0\\x+1 > 0\koniec(przypadki)$
$\begin(cases)2x>4\\x > -1\end(cases)$ $\Leftrightarrow$ $\begin(cases)x>2\\x > -1\end(cases) $ $\Leftrightarrow$ $x\in(2;\infty)$

Rozwiązanie:
$2x-4$$≤$ $x+1$
$2x-x≤4+1$
$x≤5$
Odpowiedź: $(2;5]$

Bardzo ważne! W dowolnej nierówności przejście z postaci $\log_a(⁡f(x)) ˅ \log_a⁡(g(x))$ do porównywania wyrażeń pod logarytmami można wykonać tylko wtedy, gdy:

Przykład . Rozwiąż nierówność: $\log$$≤-1$

Rozwiązanie:

$\dziennik$ $_(\frac(1)(3))⁡(\frac(3x-2)(2x-3))$$≤-1$	Napiszmy ODZ.
ODZ: $\frac(3x-2)(2x-3)$ $>0$
$⁡\frac(3x-2-3(2x-3))(2x-3)$$≥$ $0$	Otwieramy nawiasy i przynosimy .
$⁡\frac(-3x+7)(2x-3)$ $≥$ $0$	Mnożymy nierówność przez $-1$, nie zapominając o odwróceniu znaku porównania.
$⁡\frac(3x-7)(2x-3)$ $≤$ $0$
$⁡\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))$$≤$ $0$	Skonstruujmy oś liczbową i zaznaczmy na niej punkty $\frac(7)(3)$ i $\frac(3)(2)$. Należy pamiętać, że kropka jest usuwana z mianownika, mimo że nierówność nie jest ścisła. Faktem jest, że ten punkt nie będzie rozwiązaniem, ponieważ podstawiony do nierówności doprowadzi nas do dzielenia przez zero.
$x∈($$\frac(3)(2)$ $;$$\frac(7)(3)]$	Teraz wykreślamy ODZ na tej samej osi liczbowej i w odpowiedzi zapisujemy przedział mieszczący się w ODZ.
	Zapisujemy ostateczną odpowiedź.

Odpowiedź: $x∈($$\frac(3)(2)$ $;$$\frac(7)(3)]$

Przykład . Rozwiąż nierówność: $\log^2_3⁡x-\log_3⁡x-2>0$

Rozwiązanie:

$\log^2_3⁡x-\log_3⁡x-2>0$	Napiszmy ODZ.
ODZ: $x>0$	Przejdźmy do rozwiązania.
Rozwiązanie: $\log^2_3⁡x-\log_3⁡x-2>0$	Mamy tu typową nierówność logarytmiczną kwadratową. Zróbmy to.
$t=\log_3⁡x$ $t^2-t-2>0$	Układ lewa strona nierówności na.
$D=1+8=9$ $t_1= \frac(1+3)(2)=2$ $t_2=\frac(1-3)(2)=-1$ $(t+1)(t-2)>0$
	Teraz musimy wrócić do pierwotnej zmiennej - x. Aby to zrobić, przejdźmy do , który ma to samo rozwiązanie i dokonajmy odwrotnego podstawienia.
$\left[ \begin(zebrane) t>2 \\ t<-1 \end{gathered} \right.$ $\Leftrightarrow$ $\left[ \begin{gathered} \log_3⁡x>2\\\log_3⁡x<-1 \end{gathered} \right.$	Przekształć $2=\log_3⁡9$, $-1=\log_3⁡\frac(1)(3)$.
$\left[ \begin(zebrane) \log_3⁡x>\log_39 \\ \log_3⁡x<\log_3\frac{1}{3} \end{gathered} \right.$	Przejdźmy do porównywania argumentów. Podstawy logarytmów są większe niż $1$, więc znak nierówności się nie zmienia.
$\left[ \begin(zebrane) x>9 \\ x<\frac{1}{3} \end{gathered} \right.$	Połączmy rozwiązanie nierówności i ODZ na jednym rysunku.
	Zapiszmy odpowiedź.

Odpowiedź: $(0; \frac(1)(3))∪(9;∞)$

Nierówność nazywa się logarytmiczną, jeśli zawiera funkcję logarytmiczną.

Metody rozwiązywania nierówności logarytmicznych nie różnią się od, z wyjątkiem dwóch rzeczy.

Po pierwsze, przechodząc od nierówności logarytmicznej do nierówności funkcji sublogarytmicznych, należy podążaj za znakiem powstałej nierówności. Przestrzega następującej zasady.

Jeżeli podstawa funkcji logarytmicznej jest większa niż 1$, to przy przejściu od nierówności logarytmicznej do nierówności funkcji sublogarytmicznych znak nierówności zostaje zachowany, natomiast jeśli jest mniejszy niż 1$, to zmienia się na przeciwny .

Po drugie, rozwiązaniem dowolnej nierówności jest przedział, dlatego na końcu rozwiązywania nierówności funkcji sublogarytmicznych konieczne jest utworzenie układu dwóch nierówności: pierwszą nierównością tego układu będzie nierówność funkcji sublogarytmicznych, a drugi będzie przedziałem dziedziny definicji funkcji logarytmicznych zawartych w nierówności logarytmicznej.

Ćwiczyć.

Rozwiążmy nierówności:

1. $\log_(2)((x+3)) \geq 3.$

$D(y): \x+3>0.$

$x \in (-3;+\infty)$

Podstawą logarytmu jest $2>1$, więc znak się nie zmienia. Korzystając z definicji logarytmu otrzymujemy:

$x+3 \geq 2^(3),$

$x \in )

\(\dziennik\) \(_(\frac(1)(3))⁡(\frac(3x-2)(2x-3))\)\(≤-1\)	Napiszmy ODZ.
ODZ: \(\frac(3x-2)(2x-3)\) \(>0\)
\(⁡\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\)	Otwieramy nawiasy i przynosimy .
\(⁡\frac(-3x+7)(2x-3)\) \(≥\) \(0\)	Mnożymy nierówność przez \(-1\), nie zapominając o odwróceniu znaku porównania.
\(⁡\frac(3x-7)(2x-3)\) \(≤\) \(0\)
\(⁡\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\)	Skonstruujmy oś liczbową i zaznaczmy na niej punkty \(\frac(7)(3)\) i \(\frac(3)(2)\). Należy pamiętać, że kropka jest usuwana z mianownika, mimo że nierówność nie jest ścisła. Faktem jest, że ten punkt nie będzie rozwiązaniem, ponieważ podstawiony do nierówności doprowadzi nas do dzielenia przez zero.
\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)	Teraz wykreślamy ODZ na tej samej osi liczbowej i w odpowiedzi zapisujemy przedział mieszczący się w ODZ.
	Zapisujemy ostateczną odpowiedź.

\(\log^2_3⁡x-\log_3⁡x-2>0\)	Napiszmy ODZ.
ODZ: \(x>0\)	Przejdźmy do rozwiązania.
Rozwiązanie: \(\log^2_3⁡x-\log_3⁡x-2>0\)	Mamy tu typową nierówność logarytmiczną kwadratową. Zróbmy to.
\(t=\log_3⁡x\) \(t^2-t-2>0\)	Układ lewa strona nierówności na.
\(D=1+8=9\) \(t_1= \frac(1+3)(2)=2\) \(t_2=\frac(1-3)(2)=-1\) \((t+1)(t-2)>0\)
	Teraz musimy wrócić do pierwotnej zmiennej - x. Aby to zrobić, przejdźmy do , który ma to samo rozwiązanie i dokonajmy odwrotnego podstawienia.
\(\left[ \begin(zebrane) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3⁡x>2\\\log_3⁡x<-1 \end{gathered} \right.\)	Przekształć \(2=\log_3⁡9\), \(-1=\log_3⁡\frac(1)(3)\).
\(\left[ \begin(zebrane) \log_3⁡x>\log_39 \\ \log_3⁡x<\log_3\frac{1}{3} \end{gathered} \right.\)	Przejdźmy do porównywania argumentów. Podstawy logarytmów są większe niż \(1\), więc znak nierówności się nie zmienia.
\(\left[ \begin(zebrane) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\)	Połączmy rozwiązanie nierówności i ODZ na jednym rysunku.
	Zapiszmy odpowiedź.