Modulo jednadžbe. Modul broja (apsolutna vrijednost broja), definicije, primjeri, svojstva

Jedna od najtežih tema za studente je rješavanje jednadžbi koje sadrže varijablu pod predznakom modula. Pogledajmo za početak s čime je to povezano? Zašto, na primjer, kvadratne jednadžbe većina djece klikće kao orasi, ali s takvim daleko od najsloženijem konceptom kao što je modul ima toliko problema?

Po mom mišljenju, sve te poteškoće povezane su s nedostatkom jasno formuliranih pravila za rješavanje jednadžbi s modulom. Da, odlučujući kvadratna jednadžba, učenik sigurno zna da prvo treba primijeniti diskriminantnu formulu, a zatim formule za korijene kvadratne jednadžbe. Ali što ako se u jednadžbi susreće modul? Pokušat ćemo jasno opisati potreban plan radnje za slučaj kada jednadžba sadrži nepoznanicu pod predznakom modula. Za svaki slučaj dajemo nekoliko primjera.

Ali prvo, prisjetimo se definicija modula. Dakle, modul broja a sam broj se zove ako a nenegativni i -a ako je broj a manje od nule. Možete to napisati ovako:

|a| = a ako je a ≥ 0 i |a| = -a ako a< 0

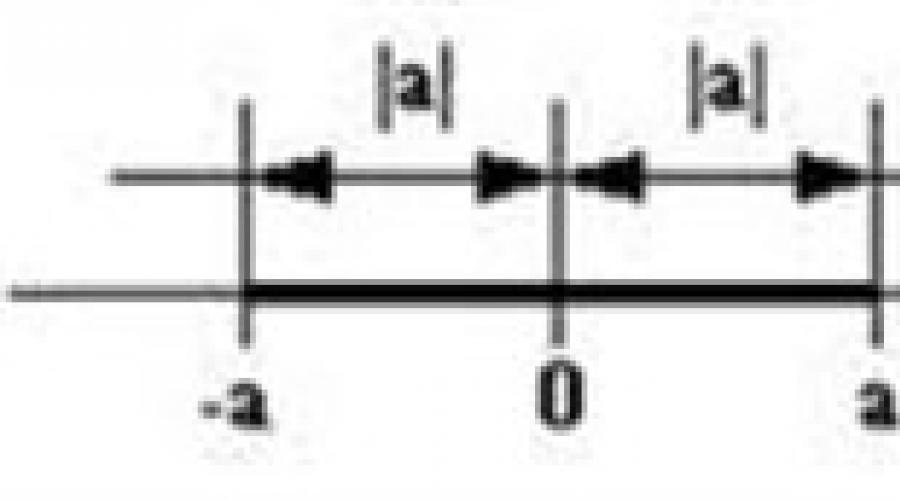
Govoreći o geometrijski smisao modula, treba imati na umu da svaki realni broj odgovara određenoj točki na brojevnoj osi - svom do Koordinirati. Dakle, modul ili apsolutna vrijednost broja je udaljenost od ove točke do ishodišta brojčane osi. Udaljenost se uvijek daje kao pozitivan broj. Dakle, modul bilo kojeg negativan broj je pozitivan broj. Usput, čak iu ovoj fazi mnogi studenti počinju biti zbunjeni. U modulu može biti bilo koji broj, ali rezultat primjene modula je uvijek pozitivan broj.

Sada prijeđimo na rješavanje jednadžbi.

1. Razmotrimo jednadžbu oblika |x| = c, gdje je c realan broj. Ova se jednadžba može riješiti pomoću definicije modula.

Sve realne brojeve dijelimo u tri skupine: one koji su veći od nule, one koji su manji od nule, a treća skupina je broj 0. Rješenje zapisujemo u obliku dijagrama:

(±c ako je c > 0

Ako je |x| = c, tada je x = (0 ako je c = 0

(bez korijena ako ima< 0

1) |x| = 5, jer 5 > 0, tada je x = ±5;

2) |x| = -5, jer -5< 0, то уравнение не имеет корней;

3) |x| = 0, tada je x = 0.

2. Jednadžba oblika |f(x)| = b, gdje je b > 0. Za rješavanje ove jednadžbe potrebno je riješiti se modula. Činimo to ovako: f(x) = b ili f(x) = -b. Sada je potrebno svaku od dobivenih jednadžbi posebno riješiti. Ako je u izvornoj jednadžbi b< 0, решений не будет.

1) |x + 2| = 4, jer 4 > 0, dakle

x + 2 = 4 ili x + 2 = -4

2) |x 2 – 5| = 11, jer 11 > 0, dakle

x 2 - 5 = 11 ili x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 nema korijena

3) |x 2 – 5x| = -8 , jer -osam< 0, то уравнение не имеет корней.

3. Jednadžba oblika |f(x)| = g(x). Prema značenju modula, takva će jednadžba imati rješenja ako joj je desna strana veća ili jednaka nuli, t.j. g(x) ≥ 0. Tada imamo:

f(x) = g(x) ili f(x) = -g(x).

1) |2x – 1| = 5x - 10. Ova će jednadžba imati korijen ako je 5x - 10 ≥ 0. Ovdje počinje rješenje takvih jednadžbi.

1. O.D.Z. 5x – 10 ≥ 0

2. Rješenje:

2x - 1 = 5x - 10 ili 2x - 1 = -(5x - 10)

3. Kombinirajte O.D.Z. i rješenje, dobivamo:

Korijen x \u003d 11/7 ne odgovara prema O.D.Z., manji je od 2, a x \u003d 3 zadovoljava ovaj uvjet.

Odgovor: x = 3

2) |x – 1| \u003d 1 - x 2.

1. O.D.Z. 1 - x 2 ≥ 0. Riješimo ovu nejednakost metodom intervala:

(1 – x)(1 + x) ≥ 0

2. Rješenje:

x - 1 \u003d 1 - x 2 ili x - 1 \u003d - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 ili x = 1 x = 0 ili x = 1

3. Kombinirajte otopinu i O.D.Z.:

Prikladni su samo korijeni x = 1 i x = 0.

Odgovor: x = 0, x = 1.

4. Jednadžba oblika |f(x)| = |g(x)|. Takva je jednadžba ekvivalentna sljedećim dvjema jednadžbama f(x) = g(x) ili f(x) = -g(x).

1) |x 2 - 5x + 7| = |2x – 5|. Ova jednadžba je ekvivalentna sljedećim dvjema:

x 2 - 5x + 7 = 2x - 5 ili x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 ili x = 4 x = 2 ili x = 1

Odgovor: x = 1, x = 2, x = 3, x = 4.

5. Jednadžbe riješene metodom supstitucije (promjena varijable). Ova metoda rješenja je najlakše objasniti u konkretan primjer. Dakle, neka je dana kvadratna jednadžba s modulom:

x 2 – 6|x| + 5 = 0. Svojstvom modula x 2 = |x| 2, pa se jednadžba može prepisati na sljedeći način:

|x| 2–6|x| + 5 = 0. Napravimo promjenu |x| = t ≥ 0, tada ćemo imati:

t 2 - 6t + 5 = 0. Rješavajući ovu jednadžbu, dobivamo da je t = 1 ili t = 5. Vratimo se na zamjenu:

|x| = 1 ili |x| = 5

x = ±1 x = ±5

Odgovor: x = -5, x = -1, x = 1, x = 5.

Pogledajmo još jedan primjer:

x 2 + |x| – 2 = 0. Svojstvom modula x 2 = |x| 2, dakle

|x| 2 + |x| – 2 = 0. Napravimo promjenu |x| = t ≥ 0, tada:

t 2 + t - 2 \u003d 0. Rješavanjem ove jednadžbe dobivamo, t = -2 ili t = 1. Vratimo se na zamjenu:

|x| = -2 ili |x| = 1

Nema korijena x = ± 1

Odgovor: x = -1, x = 1.

6. Druga vrsta jednadžbi su jednadžbe sa "složenim" modulom. Takve jednadžbe uključuju jednadžbe koje imaju "module unutar modula". Jednadžbe ovog tipa mogu se riješiti korištenjem svojstava modula.

1) |3 – |x|| = 4. Postupit ćemo na isti način kao u jednadžbama druge vrste. Jer 4 > 0, tada dobivamo dvije jednadžbe:

3 – |x| = 4 ili 3 – |x| = -4.

Sada izrazimo modul x u svakoj jednadžbi, zatim |x| = -1 ili |x| = 7.

Rješavamo svaku od rezultirajućih jednadžbi. U prvoj jednadžbi nema korijena, jer -jedan< 0, а во втором x = ±7.

Odgovor x = -7, x = 7.

2) |3 + |x + 1|| = 5. Ovu jednadžbu rješavamo na sličan način:

3 + |x + 1| = 5 ili 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 ili x + 1 = -2. Nema korijena.

Odgovor: x = -3, x = 1.

Postoji također generička metoda rješenje jednadžbi s modulom. Ovo je metoda razmaka. Ali razmotrit ćemo to dalje.

blog.site, uz potpuno ili djelomično kopiranje materijala, potrebna je poveznica na izvor.

U ovom članku ćemo detaljno analizirati apsolutna vrijednost broja. mi ćemo dati razne definicije modula broja, uvodimo zapis i dajemo grafičke ilustracije. Pritom razmislite razni primjeri nalaženje modula broja po definiciji. Nakon toga navodimo i obrazlažemo glavna svojstva modula. Na kraju članka govorit ćemo o tome kako se određuje i pronalazi modul kompleksnog broja.

Navigacija po stranici.

Modul broja - definicija, zapis i primjeri

Prvo predstavljamo oznaka modula. Modul broja a zapisati ćemo kao , odnosno lijevo i desno od broja stavit ćemo okomite linije koje čine znak modula. Navedimo par primjera. Na primjer, modulo -7 može se napisati kao ; modul 4,125 je napisan kao , a modul je napisan kao .

Sljedeća definicija modula odnosi se na, dakle, na, i na cijele brojeve, te na racionalne i iracionalne brojeve, kao na sastavne dijelove skupa realnih brojeva. Govorit ćemo o modulu kompleksnog broja u.

Definicija.

Modul a je ili sam broj a, ako je a pozitivan broj, ili broj −a, suprotan broju a, ako je a negativan broj, ili 0, ako je a=0.

Zvučna definicija modula broja često je zapisana sljedeći obrazac , ova oznaka znači da ako je a>0, ako je a=0, i ako je a<0 .

Zapis se može predstaviti u kompaktnijem obliku . Ova oznaka znači da ako (a je veće ili jednako 0), i ako je a<0 .

Postoji i zapis . Ovdje treba posebno objasniti slučaj kada je a=0. U ovom slučaju imamo , ali −0=0, budući da se nula smatra brojem koji je suprotan samom sebi.

Donesimo primjeri nalaženja modula broja uz zadanu definiciju. Na primjer, pronađimo module brojeva 15 i . Počnimo s pronalaženjem. Budući da je broj 15 pozitivan, njegov je modul po definiciji jednak samom ovom broju, odnosno . Koliki je modul broja? Budući da je broj negativan, onda je njegov modul jednak broju suprotnom broju, odnosno broju . Tako, .

U zaključku ovog odlomka dajemo jedan zaključak, koji je vrlo zgodno primijeniti u praksi pri pronalaženju modula broja. Iz definicije modula broja proizlazi da modul broja jednak je broju pod predznakom modula, bez obzira na njegov predznak, a iz gore navedenih primjera to je vrlo jasno vidljivo. Izražena izjava objašnjava zašto se naziva i modul broja apsolutnu vrijednost broja. Dakle, modul broja i apsolutna vrijednost broja su jedno te isto.

Modul broja kao udaljenost

Geometrijski se modul broja može tumačiti kao udaljenosti. Donesimo određivanje modula broja u smislu udaljenosti.

Definicija.

Modul a je udaljenost od ishodišta na koordinatnoj liniji do točke koja odgovara broju a.

Ova definicija je u skladu s definicijom modula broja danom u prvom odlomku. Objasnimo ovu točku. Udaljenost od ishodišta do točke koja odgovara pozitivnom broju jednaka je ovom broju. Nula odgovara referentnoj točki, stoga je udaljenost od referentne točke do točke s koordinatom 0 jednaka nuli (nije potreban niti jedan segment niti segment koji čini bilo koji dio jednog segmenta da bi se došlo od točke O do točke s koordinata 0). Udaljenost od ishodišta do točke s negativnom koordinatom jednaka je broju suprotnom od koordinata zadane točke, budući da je jednaka udaljenosti od ishodišta do točke čija je koordinata suprotan broj.

Na primjer, modul broja 9 je 9, budući da je udaljenost od ishodišta do točke s koordinatom 9 devet. Uzmimo još jedan primjer. Točka s koordinatom −3,25 nalazi se na udaljenosti 3,25 od točke O, dakle .

Zvučna definicija modula broja poseban je slučaj definiranja modula razlike dvaju brojeva.

Definicija.

Modul razlike dva broja a i b jednaka je udaljenosti između točaka koordinatnog pravca s koordinatama a i b .

To jest, ako su zadane točke na koordinatnoj liniji A(a) i B(b), tada je udaljenost od točke A do točke B jednaka modulu razlike između brojeva a i b. Ako uzmemo točku O (referentnu točku) kao točku B, tada ćemo dobiti definiciju modula broja danu na početku ovog odlomka.

Određivanje modula broja kroz aritmetički kvadratni korijen

Ponekad se nađe određivanje modula kroz aritmetički kvadratni korijen.

Na primjer, izračunajmo module brojeva −30 i na temelju ove definicije. Imamo . Slično, izračunavamo modul od dvije trećine: .

Definicija modula broja u smislu aritmetičkog kvadratnog korijena također je u skladu s definicijom danom u prvom stavku ovog članka. Pokažimo to. Neka je a pozitivan broj, a −a negativan. Zatim i , ako je a=0, onda .

Svojstva modula

Modul ima niz karakterističnih rezultata - svojstva modula. Sada ćemo dati glavne i najčešće korištene od njih. Prilikom potkrijepljivanja ovih svojstava oslanjat ćemo se na definiciju modula broja u smislu udaljenosti.

Počnimo s najočitijim svojstvom modula − modul broja ne može biti negativan broj. U doslovnom obliku, ovo svojstvo ima oblik za bilo koji broj a . Ovo svojstvo je vrlo lako opravdati: modul broja je udaljenost, a udaljenost se ne može izraziti kao negativan broj.

Prijeđimo na sljedeće svojstvo modula. Modul broja jednak je nuli ako i samo ako je taj broj nula. Modul nule je po definiciji nula. Nula odgovara ishodištu, nijedna druga točka na koordinatnoj liniji ne odgovara nuli, budući da je svaki realni broj povezan s jednom točkom na koordinatnoj liniji. Iz istog razloga, bilo koji broj osim nule odgovara točki koja nije ishodište. A udaljenost od ishodišta do bilo koje točke osim točke O nije jednaka nuli, budući da je udaljenost između dvije točke jednaka nuli ako i samo ako se te točke podudaraju. Gornje obrazloženje dokazuje da je samo modul nule jednak nuli.

Krenuti dalje. Suprotni brojevi imaju jednake module, odnosno za bilo koji broj a . Doista, dvije točke na koordinatnoj liniji, čije su koordinate suprotni brojevi, nalaze se na istoj udaljenosti od ishodišta, što znači da su moduli suprotnih brojeva jednaki.

Sljedeće svojstvo modula je: modul umnoška dvaju brojeva jednak je umnošku modula tih brojeva, tj. . Po definiciji, modul umnoška brojeva a i b je ili a b ako je , ili −(a b) ako je . Iz pravila množenja realnih brojeva slijedi da je umnožak modula brojeva a i b jednak ili a b , , ili −(a b) , ako je , što dokazuje razmatrano svojstvo.

Modul kvocijenta dijeljenja a sa b jednak je kvocijentu dijeljenja modula a s modulom b, tj. . Opravdamo ovo svojstvo modula. Budući da je kvocijent jednak proizvodu, onda . Na temelju prethodnog svojstva imamo . Ostaje samo koristiti jednakost , koja vrijedi zbog definicije modula broja.

Sljedeće svojstvo modula zapisuje se kao nejednakost: , a , b i c su proizvoljni realni brojevi. Napisana nejednakost nije ništa drugo do nejednakost trokuta. Da bismo to razjasnili, uzmimo točke A(a), B(b), C(c) na koordinatnoj liniji i razmotrimo degenerirani trokut ABC, čiji vrhovi leže na istoj liniji. Po definiciji, modul razlike jednak je duljini odsječka AB, - duljini odsječka AC, i - duljini odsječka CB. Budući da duljina bilo koje stranice trokuta ne prelazi zbroj duljina druge dvije stranice, nejednakost , dakle, vrijedi i nejednakost.

Upravo dokazana nejednakost mnogo je češća u obliku . Napisana nejednakost se obično smatra zasebnim svojstvom modula s formulacijom: “ Modul zbroja dvaju brojeva ne prelazi zbroj modula tih brojeva". Ali nejednakost izravno proizlazi iz nejednakosti , ako u nju stavimo −b umjesto b i uzmemo c=0 .

Modul kompleksnog broja

dajmo određivanje modula kompleksnog broja. Neka nam se da kompleksni broj, napisan u algebarskom obliku , gdje su x i y neki realni brojevi, koji predstavljaju, redom, stvarni i imaginarni dio zadanog kompleksnog broja z, i imaginarna je jedinica.

Tochilkina Julia

U radu su prikazane različite metode rješavanja jednadžbi s modulom.

Preuzimanje datoteka:

Pregled:

Općinska proračunska obrazovna ustanova

"Srednja škola br.59"

Modulo jednadžbe

Apstraktni rad

Izvedena Učenik 9. razreda

MBOU "Srednja škola br. 59", Barnaul

Tochilkina Julia

Nadglednik

Zakharova Ljudmila Vladimirovna,

nastavnik matematike

MBOU "Srednja škola br. 59", Barnaul

Barnaul 2015

Uvod

Ja sam deveti razred. Ove akademske godine moram položiti završnu ovjeru za tečaj osnovne škole. Za pripremu ispita kupili smo zbirku matematike D. A. Maltseva. 9. razred Pregledavajući zbirku, pronašao sam jednadžbe koje sadrže ne samo jedan, već i nekoliko modula. Učiteljica je objasnila meni i mojim kolegama iz razreda da se takve jednadžbe nazivaju jednadžbe "ugniježđenih modula". Taj nam se naziv činio neobičnim, a rješenje na prvi pogled prilično kompliciranim. Tako se pojavila tema za moj rad “Jednadžbe s modulom”. Odlučio sam detaljnije proučiti ovu temu, pogotovo jer će mi dobro doći pri polaganju ispita na kraju školske godine i mislim da će mi trebati u 10. i 11. razredu. Sve navedeno određuje relevantnost teme koju sam odabrao.

Cilj:

1. Razmotrite različite metode za rješavanje jednadžbi s modulom.
2. Naučiti rješavati jednadžbe koje sadrže predznak apsolutne vrijednosti različitim metodama

Za rad na temi formulirani su sljedeći zadaci:

Zadaci:

1. Proučiti teorijsko gradivo na temu "Modul realnog broja."
2. Razmotriti metode rješavanja jednadžbi i učvrstiti znanje stečeno rješavanjem problema.
3. Stečeno znanje primijeniti u rješavanju različitih jednadžbi koje sadrže predznak modula u srednjoj školi

Predmet studija:metode za rješavanje jednadžbi s modulom

Predmet studija:modulo jednadžbe

Metode istraživanja:

Teorijski : proučavanje literature na temu istraživanja;

Internet – informacije.

Analiza informacije dobivene proučavanjem književnosti; rezultati dobiveni rješavanjem jednadžbi s modulom na različite načine.

Usporedba načini rješavanja jednadžbi, predmet racionalnosti njihove uporabe u rješavanju različitih jednadžbi s modulom.

"Počinjemo razmišljati kada naletimo na nešto." Paul Valerie.

1. Pojmovi i definicije.

Koncept "modula" naširoko se koristi u mnogim dijelovima školskog tečaja matematike, na primjer, u proučavanju apsolutnih i relativnih pogrešaka približnog broja; u geometriji i fizici proučavaju se pojmovi vektora i njegove duljine (modul vektora). Koncept modula koristi se u kolegijima visoke matematike, fizike i tehničkih znanosti koji se izučavaju na visokim učilištima.

Riječ "modul" dolazi od latinske riječi "modulus", što u prijevodu znači "mjera". Ova riječ ima mnogo značenja i koristi se ne samo u matematici, fizici i tehnologiji, već iu arhitekturi, programiranju i drugim egzaktnim znanostima.

Vjeruje se da je taj izraz predložio Kots, Newtonov učenik. Znak modula uveo je u 19. stoljeću Weierstrass.

U arhitekturi, modul je početna jedinica mjere uspostavljena za danu arhitektonsku strukturu.

U strojarstvu je to pojam koji se koristi u raznim područjima tehnologije, koji služi za označavanje različitih koeficijenata i veličina, na primjer, modul elastičnosti, modul zahvata...

U matematici modul ima nekoliko značenja, ali ja ću ga tretirati kao apsolutnu vrijednost broja.

Definicija 1: Modul (apsolutna vrijednost) realnog broja a sam broj se zove ako a ≥0, ili suprotan broj - i ako a modul nule je nula.

Kod rješavanja jednadžbi s modulom zgodno je koristiti svojstva modula.

Razmotrimo dokaze svojstava 5,6,7.

Izjava 5. Jednakost │ je istina ako av ≥ 0.

Dokaz. Doista, nakon kvadriranja oba dijela ove jednakosti, dobivamo, │ a+v │²=│ a │²+2│ ab │+│ do │²,

a² + 2 av + b² \u003d a² + 2│ av │ + b², odakle je │ av │ = av

I posljednja će jednakost vrijediti za av ≥0.

Tvrdnja 6. Jednakost │ a-c │=│ a │+│ c │ istina je kada av ≤0.

Dokaz. Da bismo to dokazali, dovoljna je jednakost

│ a + in │=│ a │+│ u │ zamijeniti in sa - in, zatim a (- in) ≥0, odakle je av ≤0.

Tvrdnja 7. Jednakost │ a │+│ u │= a + in izvedeno na a ≥0 i b ≥0.

Dokaz . Uzimajući u obzir četiri slučaja a ≥0 i b ≥0; a ≥0 i b a na ≥0; a u a ≥0 i b ≥0.

(a-c) u ≥0.

Geometrijska interpretacija

|a| je udaljenost na koordinatnoj liniji od točke s koordinatom a , do ishodišta koordinata.

|-a| |a|

A 0 a x

Geometrijsko tumačenje značenja |a| jasno potvrđuje da |-a|=|a|

Ako je a 0, tada se na koordinatnoj liniji nalaze dvije točke a i -a, jednako udaljene od nule, čiji su moduli jednaki.

Ako je a=0, tada na koordinatnoj liniji |a| predstavljen točkom 0.

2. definicija: Jednadžba s modulom je jednadžba koja sadrži varijablu pod predznakom apsolutne vrijednosti (pod predznakom modula). Na primjer: |x +3|=1

3. definicija: Rješavanje jednadžbe znači pronaći sve njezine korijene, odnosno dokazati da nema korijena.

2. Metode rješenja

Iz definicije i svojstava modula slijede glavne metode rješavanja jednadžbi s modulom:

1. "Proširivanje" modula (tj. korištenje definicije);
2. Korištenje geometrijskog značenja modula (svojstvo 2);
3. Metoda grafičkog rješenja;
4. Korištenje ekvivalentnih transformacija (svojstva 4.6);
5. Zamjena varijable (ovo koristi svojstvo 5).
6. intervalna metoda.

Riješio sam prilično velik broj primjera, ali u svom radu Vam predstavljam samo nekoliko, po mom mišljenju, tipičnih primjera riješenih na različite načine, jer se ostali dupliciraju i kako biste razumjeli kako riješiti jednadžbe s modula, nema potrebe za razmatranjem svih riješenih primjera.

RJEŠENJE JEDNADŽBI | f(x)| = a

Razmotrimo jednadžbu | f(x)| = a, i R

Jednadžba ove vrste može se riješiti definiranjem modula:

Ako je a a tada jednadžba nema korijena.

Ako je a= 0, tada je jednadžba ekvivalentna f(x)=0.

Ako je a>0, tada je jednadžba ekvivalentna skupu

Primjer. Riješite jednadžbu |3x+2|=4.

Odluka.

|3x+2|=4, zatim 3x+2=4,

3x+2= -4;

X=-2,

X=2/3

Odgovor: -2;2/3.

RJEŠENJE JEDNADŽBI UZ POMOĆ GEOMETRIJSKIH SVOJSTVA MODULA.

Primjer 1 Riješite jednadžbu /x-1/+/x-3/=6.

Odluka.

Riješiti ovu jednadžbu znači pronaći sve takve točke na brojevnoj osi Ox, za svaku od kojih je zbroj udaljenosti od nje do točaka s koordinatama 1 i 3 jednak 6.

Nijedna točka na segmentune zadovoljava ovaj uvjet, jer zbroj navedenih udaljenosti je 2. Izvan ovog segmenta postoje dvije točke: 5 i -1.

1 1 3 5

Odgovor: -1;5

Primjer 2 Riješite jednadžbu |x 2 +x-5|+|x 2 +x-9|=10.

Odluka.

Označite x 2 + x-5 \u003d a, zatim / a / + / a-4 /=10. Nađimo točke na x-osi tako da je za svaku od njih zbroj udaljenosti do točaka s koordinatama 0 i 4 jednak 10. Ovaj uvjet je zadovoljen sa -4 i 7.

3 0 4 7

Dakle, x 2 + x-5 \u003d 4 x 2 + x-5 \u003d 7

X 2 + x-2 \u003d 0 x 2 + x-12 \u003d 0

X 1 \u003d 1, x 2 \u003d -2 x 1 \u003d -4, x 2 \u003d 3 Odgovor: -4; -2; jedan; 3.

RJEŠENJE JEDNADŽBI | f(x)| = | g(x)|.

1. Od | a |=|b |, ako je a=b, onda jednadžba oblika | f(x)| = | g(x )| jednak je agregatu

Primjer 1.

Riješite jednadžbu | x–2| = |3 - x |.

Odluka.

Ova jednadžba je ekvivalentna dvjema jednadžbama:

x - 2 = 3 - x (1) i x - 2 \u003d -3 + x (2)

2 x = 5 -2 = -3 - netočno

x = 2,5 jednadžba nema rješenja.

Odgovor: 2.5.

Primjer 2

Riješite jednadžbu |x 2 + 3x-20|= |x 2 -3x+ 2|.

Odluka.

Budući da su obje strane jednadžbe nenegativne, ondakvadriranje je ekvivalentna transformacija:

(x 2 + 3x-20) 2 \u003d (x 2 -3x + 2) 2

(x 2 + 3x-20) 2 - (x 2 -3x + 2) 2 \u003d 0,

(x 2 + 3x-20-x 2 + 3x-2) (x 2 + 3x-20 + x 2 -3x + 2) \u003d 0,

(6x-22)(2x 2 -18)=0,

6x-22=0 ili 2x 2 -18=0;

X=22/6, x=3, x=-3.

X=11/3

Odgovor: -3; 3; 11/3.

RJEŠENJE JEDNADŽBI GLEDA | f(x)| = g(x).

Razlika između ovih jednadžbi i| f(x)| = a u tome što je desna strana također varijabla. A može biti i pozitivno i negativno. Stoga morate biti sigurni da nije negativan, jer modul ne može biti jednak negativnom broju (svojstvo№1 )

1 način

Rješenje jednadžbe | f(x)| = g(x ) svodi se na skup rješenja jednadžbii provjera valjanosti nejednakosti g(x )>0 za pronađene vrijednosti nepoznate.

2 načina (prema definiciji modula)

Od | f(x)| = g (x) ako je f (x) = 0; | f(x)| = - f(x) ako je f(x)

Primjer.

Riješite jednadžbu |3 x –10| = x - 2.

Odluka.

Ova jednadžba je ekvivalentna kombinaciji dvaju sustava:

O t e t: 3; 4.

RJEŠENJE JEDNADŽBI OBRASCA |f 1 (x)|+|f 2 (x)|+…+|f n (x)|=g(x)

Rješenje ovakvih jednadžbi temelji se na definiciji modula. Za svaku funkciju f 1 (x), f 2 (x), …, f n (x) potrebno je pronaći područje definicije, njegove nule i točke diskontinuiteta koje se prekidaju opće područje definicije u intervale, u svakom od kojih su funkcije f 1 (x), f 2 (x), …, f n (x) zadržati svoj znak. Nadalje, koristeći definiciju modula, za svako od pronađenih područja dobivamo jednadžbu koja se mora riješiti na zadanom intervalu. Ova metoda se zove "intervalna metoda»

Primjer.

Riješite jednadžbu |x-2|-3|x+4|=1.

Odluka.

Nađimo točke u kojima su izrazi podmodula jednaki nuli

x-2=0, x+4=0,

x=2; x=-4.

Razbijmo brojevni pravac na intervale x

Rješenje jednadžbe svodi se na rješenje triju sustava:

Odgovor: -15, -1,8.

GRAFIČKA METODA ZA RJEŠAVANJE JEDNADŽBI KOJE SADRŽE ZNAK MODULA.

Grafički način rješavanja jednadžbi je približan, budući da točnost ovisi o odabranom segmentu jedinice, debljini olovke, kutovima pod kojima se prave sijeku itd. Ali ova metoda vam omogućuje da procijenite koliko rješenja ima određena jednadžba.

Primjer. Riješite grafički jednadžbu |x - 2| + |x - 3| + |2x - 8| = 9

Odluka. Konstruirajmo grafove funkcija u jednom koordinatnom sustavu

y=|x - 2| + |x - 3| + |2x - 8| i y=9.

Da biste izgradili graf, razmotrite ovu funkciju na svakom intervalu (-∞; 2); [3/2; ∞)

Odgovor: (- ∞ ; 4/3] [ 3/2 ; ∞ )

Također smo koristili metodu ekvivalentnih transformacija u rješavanju jednadžbi | f(x)| = | g(x)|.

JEDNADŽBE SA "KOMPLEKSNIM MODULOM"

Druga vrsta jednadžbi su jednadžbe sa "složenim" modulom. Takve jednadžbe uključuju jednadžbe koje imaju "module unutar modula". Jednadžbe ovog tipa mogu se riješiti raznim metodama.

Primjer 1

Riješite jednadžbu ||||x| – |–2| –1| –2| = 2.

Odluka.

Po definiciji modula imamo:

Riješimo prvu jednadžbu.

1. ||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

x = 7.

Riješimo drugu jednadžbu.

1. ||| x | –2| –1| = 0,

|| x | –2| = 1,

| x | -2 = 1,

| x | = 3 i | x | = 1,

x = 3; x = 1.

O n e t: 1; 3; 7.

Primjer 2

Riješite jednadžbu |2 – |x + 1|| = 3.

Odluka.

Riješimo jednadžbu uvođenjem nove varijable.

Neka | x + 1| = y , tada |2 – y | = 3, dakle

Napravimo obrnutu zamjenu:

(1) | x + 1| = -1 - nema rješenja.

(2) | x + 1| = 5

A n e t: -6; 4.

Primjer3 .

Koliko korijena ima jednadžba | 2 | x | -6 | = 5 - x?

Odluka. Riješimo jednadžbu koristeći sheme ekvivalencije.

Jednadžba | 2 | x | -6 | = 5 -x je ekvivalentno sistemu:

Apsolutna vrijednost broja a je udaljenost od ishodišta do točke ALI(a).

Da bismo razumjeli ovu definiciju, zamjenjujemo umjesto varijable a bilo koji broj, na primjer 3 i pokušajte ga ponovno pročitati:

Apsolutna vrijednost broja 3 je udaljenost od ishodišta do točke ALI(3 ).

Postaje jasno da modul nije ništa više od uobičajene udaljenosti. Pokušajmo vidjeti udaljenost od ishodišta do točke A( 3 )

Udaljenost od ishodišta koordinata do točke A( 3 ) jednako je 3 (tri jedinice ili tri koraka).

Modul broja označen je s dvije okomite linije, na primjer:

Modul broja 3 označava se na sljedeći način: |3|

Modul broja 4 označava se na sljedeći način: |4|

Modul broja 5 označava se ovako: |5|

Tražili smo modul broja 3 i saznali da je jednak 3. Pa pišemo:

Čita se kao: "Modul tri je tri"

Pokušajmo sada pronaći modul broja -3. Opet se vraćamo na definiciju i u nju zamjenjujemo broj -3. Samo umjesto točke A koristiti nova točka B. točka A već smo koristili u prvom primjeru.

Modul broja je 3 nazivati ​​udaljenost od ishodišta do točke B(—3 ).

Udaljenost od jedne točke do druge ne može biti negativna. Stoga, modul bilo kojeg negativnog broja, budući da je udaljenost, također neće biti negativan. Modul broja -3 bit će broj 3. Udaljenost od ishodišta do točke B(-3) također je jednaka tri jedinice:

Čita se kao: "Modul broja minus tri je tri"

Modul broja 0 je 0, budući da se točka s koordinatom 0 poklapa s ishodištem, tj. udaljenost od ishodišta do točke O(0) jednako nuli:

"Modul nule je nula"

Izvlačimo zaključke:

• Modul broja ne može biti negativan;
• Za pozitivan broj i nulu modul je jednak samom broju, a za negativan suprotnom broju;
• Suprotni brojevi imaju jednake module.

Suprotni brojevi

Zovu se brojevi koji se razlikuju samo u znakovima suprotan. Na primjer, brojevi −2 i 2 su suprotni. Razlikuju se samo u znakovima. Broj −2 ima znak minus, a 2 ima predznak plus, ali ga ne vidimo, jer se plus, kao što smo ranije rekli, tradicionalno ne piše.

Još primjera suprotnih brojeva:

Suprotni brojevi imaju jednake module. Na primjer, pronađimo module za −2 i 2

Slika pokazuje da je udaljenost od ishodišta do točaka A(−2) i B(2) jednaka dva koraka.

Svidjela ti se lekcija?
Pridružite nam se nova grupa Vkontakte i počnite primati obavijesti o novim lekcijama

Modul je apsolutna vrijednost izraza. Da biste barem nekako označili modul, uobičajeno je koristiti ravne zagrade. Vrijednost koja se nalazi u parnim zagradama je vrijednost koja se uzima po modulu. Proces rješavanja bilo kojeg modula sastoji se u otvaranju istih izravnih zagrada, koje se u matematičkom jeziku nazivaju modularne zagrade. Njihovo otkrivanje događa se prema određenom broju pravila. Također, u redoslijedu rješavanja modula postoje i skupovi vrijednosti onih izraza koji su bili u zagradama modula. U većini slučajeva, modul se proširuje na način da izraz koji je bio podmodul dobije i pozitivne i negativne vrijednosti, uključujući vrijednost nula. Ako pođemo od utvrđenih svojstava modula, tada se u procesu sastavljaju različite jednadžbe ili nejednadžbe iz izvornog izraza koje je potrebno riješiti. Idemo shvatiti kako riješiti module.

Proces rješenja

Rješenje modula počinje pisanjem izvorne jednadžbe s modulom. Da biste odgovorili na pitanje kako riješiti jednadžbe s modulom, morate ga potpuno otvoriti. Za rješavanje takve jednadžbe modul se proširuje. Moraju se uzeti u obzir svi modularni izrazi. Potrebno je utvrditi pri kojim vrijednostima nepoznatih veličina uključenih u njegov sastav, modularni izraz u zagradama nestaje. Da bismo to učinili, dovoljno je izraz u modularnim zagradama izjednačiti s nulom, a zatim izračunati rješenje rezultirajuće jednadžbe. Pronađene vrijednosti moraju se zabilježiti. Na isti način, također morate odrediti vrijednost svih nepoznatih varijabli za sve module u ovoj jednadžbi. Dalje, potrebno je pozabaviti se definicijom i razmatranjem svih slučajeva postojanja varijabli u izrazima kada su različite od vrijednosti nula. Da biste to učinili, trebate zapisati neki sustav nejednakosti koji odgovara svim modulima u izvornoj nejednakosti. Nejednadžbe moraju biti sastavljene na način da pokriju sve dostupne i moguće vrijednosti varijable koje se nalaze na brojevnoj liniji. Zatim morate za vizualizaciju nacrtati ovu istu brojevnu liniju, na koju ćete staviti sve dobivene vrijednosti u budućnosti.

Gotovo sve se sada može učiniti online. Modul nije iznimka od pravila. Možete ga riješiti online na jednom od mnogih suvremeni resursi. Sve one vrijednosti varijable koje se nalaze u nultom modulu bit će posebno ograničenje koje će se koristiti u procesu rješavanja modularne jednadžbe. U izvornoj jednadžbi potrebno je proširiti sve dostupne modularne zagrade, mijenjajući predznak izraza tako da se vrijednosti željene varijable podudaraju s onim vrijednostima koje su vidljive na brojevnoj liniji. Rezultirajuća jednadžba se mora riješiti. Vrijednost varijable, koja će se dobiti tijekom rješavanja jednadžbe, mora se provjeriti u odnosu na ograničenje koje postavlja sam modul. Ako vrijednost varijable u potpunosti zadovoljava uvjet, onda je točna. Svi korijeni koji će se dobiti tijekom rješavanja jednadžbe, ali neće odgovarati ograničenjima, moraju se odbaciti.