Nok 34 i 2 odluka. Kako pronaći najmanji zajednički višekratnik dvaju brojeva
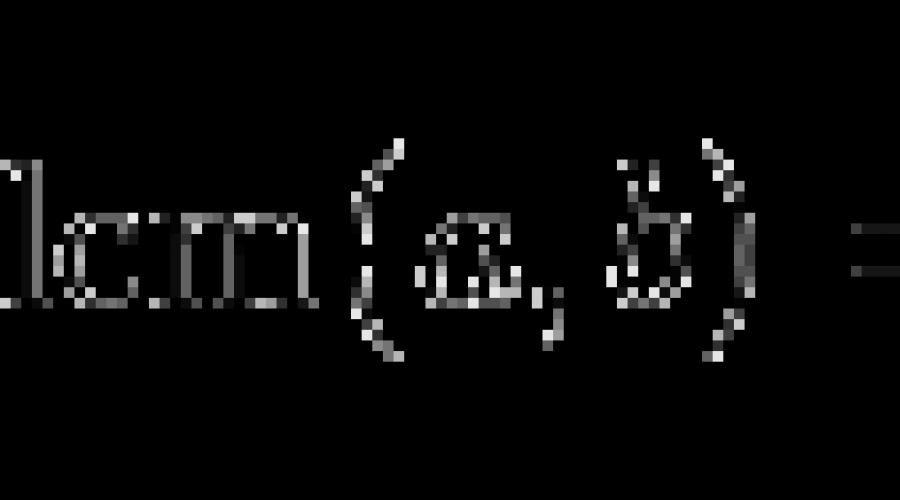
Pročitajte također
Najveći zajednički djelitelj i najmanji zajednički višekratnik ključni su aritmetički koncepti koji vam omogućuju rad bez napora obični razlomci. LCM i najčešće se koriste za pronalaženje zajedničkog nazivnika nekoliko razlomaka.
Osnovni koncepti
Djelitelj cijelog broja X je drugi cijeli broj Y kojim je X djeljiv bez ostatka. Na primjer, djelitelj broja 4 je 2, a 36 je 4, 6, 9. Višekratnik cijelog broja X je broj Y koji je djeljiv s X bez ostatka. Na primjer, 3 je višekratnik od 15, a 6 je višekratnik od 12.
Za bilo koji par brojeva možemo pronaći njihove zajedničke djelitelje i višekratnike. Na primjer, za 6 i 9, zajednički višekratnik je 18, a zajednički djelitelj je 3. Očito, parovi mogu imati nekoliko djelitelja i višekratnika, pa se u izračunima koriste najveći djelitelj GCD-a i najmanji djelitelj LCM-a. .
Najmanji djelitelj nema smisla, jer je za bilo koji broj uvijek jedan. Najveći višekratnik je također besmislen, budući da niz višekratnika teži beskonačnosti.
Pronalaženje GCD
Postoje mnoge metode za pronalaženje najvećeg zajedničkog djelitelja, od kojih su najpoznatije:
- sekvencijalno nabrajanje djelitelja, odabir zajedničkih za par i traženje najvećeg od njih;
- razlaganje brojeva na nedjeljive faktore;
- Euklidov algoritam;
- binarni algoritam.
Danas u obrazovne ustanove Najpopularnije metode su razlaganje na primarni čimbenici i Euklidov algoritam. Potonji se, pak, koristi u rješavanju Diofantovih jednadžbi: traženje GCD-a je potrebno da bi se provjeravala mogućnost da se jednadžba riješi u cijelim brojevima.
Pronalaženje NOC-a
Najmanji zajednički višekratnik također je točno određen iterativnim nabrajanjem ili faktorizacijom u nedjeljive faktore. Osim toga, lako je pronaći LCM ako je najveći djelitelj već određen. Za brojeve X i Y, LCM i GCD povezani su sljedećim odnosom:
LCM(X,Y) = X × Y / GCM(X,Y).
Na primjer, ako je gcd(15,18) = 3, tada je LCM(15,18) = 15 × 18 / 3 = 90. Najočitija upotreba LCM-a je pronaći zajednički nazivnik, koji je najmanji zajednički višekratnik zadane razlomke.
Koprosti brojevi
Ako par brojeva nema zajedničkih djelitelja, onda se takav par naziva koprostor. GCM za takve parove uvijek je jednak jedan, a na temelju veze djelitelja i višekratnika, GCM za koprime jednak je njihovom umnošku. Na primjer, brojevi 25 i 28 su međusobno prosti, jer nemaju zajedničkih djelitelja, a LCM(25, 28) = 700, što odgovara njihovom umnošku. Bilo koja dva nedjeljiva broja uvijek će biti koprosta.
Zajednički djelitelj i višestruki kalkulator
S našim kalkulatorom možete izračunati GCD i LCM za bilo koji broj brojeva koje možete izabrati. Zadaci za izračunavanje zajedničkih djelitelja i višekratnika nalaze se u aritmetici 5. i 6. razreda, međutim, GCD i LCM su ključni pojmovi matematike i koriste se u teoriji brojeva, planimetriji i komunikacijskoj algebri.
Primjeri iz stvarnog života
Zajednički nazivnik razlomaka
Najmanji zajednički višekratnik koristi se pri pronalaženju zajedničkog nazivnika nekoliko razlomaka. Neka je u aritmetičkom zadatku potrebno zbrojiti 5 razlomaka:
1/8 + 1/9 + 1/12 + 1/15 + 1/18.
Za zbrajanje razlomaka, izraz se mora svesti na zajednički nazivnik, što se svodi na problem pronalaženja LCM-a. Da biste to učinili, odaberite 5 brojeva u kalkulatoru i unesite vrijednosti nazivnika u odgovarajuće ćelije. Program će izračunati LCM (8, 9, 12, 15, 18) = 360. Sada morate izračunati dodatne faktore za svaki razlomak, koji su definirani kao omjer LCM-a i nazivnika. Dakle, dodatni množitelji bi izgledali ovako:
- 360/8 = 45
- 360/9 = 40
- 360/12 = 30
- 360/15 = 24
- 360/18 = 20.
Nakon toga pomnožimo sve razlomke s odgovarajućim dodatnim faktorom i dobijemo:
45/360 + 40/360 + 30/360 + 24/360 + 20/360.
Lako možemo zbrojiti takve razlomke i dobiti rezultat u obliku 159/360. Smanjujemo razlomak za 3 i vidimo konačni odgovor - 53/120.
Rješenje linearnih Diofantovih jednadžbi
Linearne Diofantove jednadžbe su izrazi oblika ax + by = d. Ako je omjer d/gcd(a, b) cijeli broj, tada je jednadžba rješiva u cijelim brojevima. Provjerimo nekoliko jednadžbi za mogućnost cjelobrojnog rješenja. Prvo provjerite jednadžbu 150x + 8y = 37. Koristeći kalkulator, nalazimo gcd (150,8) = 2. Podijelite 37/2 = 18,5. Broj nije cijeli broj, dakle, jednadžba nema cjelobrojne korijene.
Provjerimo jednadžbu 1320x + 1760y = 10120. Pomoću kalkulatora pronađimo gcd(1320, 1760) = 440. Podijelimo 10120/440 = 23. Kao rezultat, dobivamo cijeli broj, stoga je Diofantov koeficijent u .
Zaključak
GCD i LCM igraju veliku ulogu u teoriji brojeva, a sami koncepti se najčešće koriste različitim područjima matematika. Koristite naš kalkulator za izračunavanje najvećih djelitelja i najmanjih višekratnika bilo kojeg broja brojeva.
Ali mnogi prirodni brojevi su jednako djeljivi s drugim prirodnim brojevima.
Na primjer:
Broj 12 je djeljiv sa 1, sa 2, sa 3, sa 4, sa 6, sa 12;
Broj 36 je djeljiv sa 1, sa 2, sa 3, sa 4, sa 6, sa 12, sa 18, sa 36.
Brojevi kojima je broj djeljiv (za 12 je 1, 2, 3, 4, 6 i 12) nazivaju se djelitelji brojeva. Djelitelj prirodnog broja a je prirodan broj koji dijeli dati broj a bez traga. Prirodni broj koji ima više od dva faktora naziva se kompozitni .
Imajte na umu da brojevi 12 i 36 imaju zajedničke djelitelje. To su brojevi: 1, 2, 3, 4, 6, 12. Najveći djelitelj ovih brojeva je 12. Zajednički djelitelj ova dva broja a i b je broj kojim su oba data broja djeljiva bez ostatka a i b.
zajednički višestruki nekoliko brojeva naziva se broj koji je djeljiv sa svakim od tih brojeva. Na primjer, brojevi 9, 18 i 45 imaju zajednički višekratnik 180. Ali 90 i 360 su također njihovi zajednički višekratnici. Među svim zajedničkim višekratnicima uvijek postoji najmanji, in ovaj slučaj to je 90. Ovaj broj se zove najmanjezajednički višekratnik (LCM).
LCM je uvijek prirodan broj, koji mora biti veći od najvećeg broja za koji je definiran.
Najmanji zajednički višekratnik (LCM). Svojstva.
komutativnost:
asocijativnost:
![]()
Konkretno, ako i su međusobno prosti brojevi , tada:
Najmanji zajednički višekratnik dvaju cijelih brojeva m i n je djelitelj svih ostalih zajedničkih višekratnika m i n. Štoviše, skup zajedničkih višekratnika m,n podudara se sa skupom višekratnika za LCM( m,n).
Asimptotika za može se izraziti u terminima nekih teoretskih funkcija.
Tako, Čebiševljeva funkcija. Kao i:
To proizlazi iz definicije i svojstava Landauove funkcije g(n).
Što slijedi iz zakona raspodjele prostih brojeva.
Pronalaženje najmanjeg zajedničkog višekratnika (LCM).
NOC( a, b) može se izračunati na nekoliko načina:
1. Ako je najveći zajednički djelitelj poznat, možete koristiti njegov odnos s LCM:
![]()
2. Neka je poznata kanonska dekompozicija oba broja na proste faktore:
![]()
gdje p 1 ,...,p k- razne primarni brojevi, a d 1 ,...,d k i e 1 ,...,ek su nenegativni cijeli brojevi (mogu biti nula ako odgovarajući prosti broj nije u proširenju).
Zatim LCM ( a,b) izračunava se po formuli:
Drugim riječima, LCM ekspanzija sadrži sve proste faktore koji su uključeni u barem jedno proširenje brojeva a, b, a uzima se najveći od dva eksponenta ovog faktora.
Primjer:
Izračun najmanjeg zajedničkog višekratnika nekoliko brojeva može se svesti na nekoliko uzastopnih izračuna LCM-a dvaju brojeva:
Pravilo. Da biste pronašli LCM niza brojeva, trebate:
- rastaviti brojeve na proste faktore;
- prenesite najveću ekspanziju u faktore željenog proizvoda (umnožak faktora veliki broj od zadanih), a zatim dodaju faktore iz razlaganja drugih brojeva koji se ne pojavljuju u prvom broju ili su u njemu manji broj puta;
- rezultirajući umnožak prostih faktora bit će LCM zadanih brojeva.
Bilo koje dvije ili više prirodni brojevi imaju svoj NOC. Ako brojevi nisu međusobno višekratnici ili nemaju iste faktore u proširenju, tada je njihov LCM jednak umnošku tih brojeva.

Prosti faktori broja 28 (2, 2, 7) dopunjeni su faktorom 3 (broj 21), rezultirajući proizvod (84) bit će najmanji broj, što je djeljivo s 21 i 28 .

Prosti faktori najvećeg broja 30 dopunjeni su faktorom 5 od broja 25, rezultirajući umnožak 150 veći je od najvećeg broja 30 i djeljiv je sa svim zadanim brojevima bez ostatka. Ovo je najmanji mogući umnožak (150, 250, 300...) čiji su svi dati brojevi višekratnici.

Brojevi 2,3,11,37 su prosti, pa je njihov LCM jednak umnošku zadanih brojeva.
Pravilo. Da biste izračunali LCM prostih brojeva, trebate sve te brojeve pomnožiti zajedno.
Druga opcija:
Da biste pronašli najmanji zajednički višekratnik (LCM) nekoliko brojeva trebate:
1) predstavljaju svaki broj kao proizvod njegovih prostih faktora, na primjer:
504 \u003d 2 2 2 3 3 7,
2) zapišite potencije svih prostih faktora:
504 \u003d 2 2 2 3 3 7 \u003d 2 3 3 2 7 1,
3) zapišite sve proste djelitelje (množitelje) svakog od ovih brojeva;
4) izabrati najveći stupanj svakog od njih, koji se nalazi u svim proširenjima ovih brojeva;
5) pomnožite ove moći.
Primjer. Pronađite LCM brojeva: 168, 180 i 3024.
Riješenje. 168 \u003d 2 2 2 3 7 \u003d 2 3 3 1 7 1,
180 \u003d 2 2 3 3 5 \u003d 2 2 3 2 5 1,
3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1 .
Zapisujemo najveće potencije svih prostih djelitelja i množimo ih:
LCM = 2 4 3 3 5 1 7 1 = 15120.
Višekratnik broja je broj koji je djeljiv danim brojem bez ostatka. Najmanji zajednički višekratnik (LCM) grupe brojeva je najmanji broj koji je jednako djeljiv sa svakim brojem u skupini. Da biste pronašli najmanji zajednički višekratnik, morate pronaći proste faktore zadanih brojeva. Također, LCM se može izračunati korištenjem niza drugih metoda koje su primjenjive na grupe od dva ili više brojeva.
Koraci
Broj višekratnika
- Na primjer, pronađite najmanji zajednički višekratnik brojeva 5 i 8. To su mali brojevi, pa se ova metoda može koristiti.
-
Višekratnik broja je broj koji je djeljiv danim brojem bez ostatka. U tablici množenja može se pronaći više brojeva.
- Na primjer, brojevi koji su višekratnici broja 5 su: 5, 10, 15, 20, 25, 30, 35, 40.
-
Zapišite niz brojeva koji su višekratnici prvog broja. Učinite to pod višekratnicima prvog broja da biste usporedili dva reda brojeva.
- Na primjer, brojevi koji su višekratnici broja 8 su: 8, 16, 24, 32, 40, 48, 56 i 64.
-
Pronađite najmanji broj koji se pojavljuje u oba niza višekratnika. Možda ćete morati napisati duge nizove višekratnika da biste ih pronašli ukupni broj. Najmanji broj koji se pojavljuje u oba niza višekratnika je najmanji zajednički višekratnik.
- Na primjer, najmanji broj koji se pojavljuje u nizu višekratnika 5 i 8 je 40. Stoga je 40 najmanji zajednički višekratnik 5 i 8.
Primena faktorizacija
-
Pogledajte ove brojke. Ovdje opisanu metodu najbolje je koristiti kada su data dva broja koja su oba veća od 10. Ako su dati manji brojevi, upotrijebite drugu metodu.
- Na primjer, pronađite najmanji zajednički višekratnik brojeva 20 i 84. Svaki od brojeva je veći od 10, pa se ova metoda može koristiti.
-
Faktorizirajte prvi broj. Odnosno, trebate pronaći takve proste brojeve, kada se pomnožite, dobijete zadani broj. Nakon što ste pronašli proste faktore, zapišite ih kao jednakost.
- Na primjer, 2 × 10 = 20 (\displaystyle (\mathbf (2))\puta 10=20) i 2 × 5 = 10 (\displaystyle (\mathbf (2) )\puta (\mathbf (5) )=10). Dakle, prosti faktori broja 20 su brojevi 2, 2 i 5. Zapišite ih kao izraz: .
-
Razdijelite drugi broj u proste faktore. Učinite to na isti način kao što ste rastavili na faktor prvi broj, odnosno pronađite takve proste brojeve koji će, kada se pomnože, dobiti ovaj broj.
- Na primjer, 2 × 42 = 84 (\displaystyle (\mathbf (2) )\puta 42=84), 7 × 6 = 42 (\displaystyle (\mathbf (7) )\puta 6=42) i 3 × 2 = 6 (\displaystyle (\mathbf (3) )\puta (\mathbf (2) )=6). Dakle, prosti faktori broja 84 su brojevi 2, 7, 3 i 2. Zapišite ih kao izraz: .
-
Zapišite čimbenike zajedničke za oba broja. Napišite takve faktore kao operaciju množenja. Dok zapisujete svaki faktor, prekrižite ga u oba izraza (izrazi koji opisuju razlaganje brojeva na proste faktore).
- Na primjer, zajednički faktor za oba broja je 2, pa napišite 2 × (\displaystyle 2\puta) i prekriži 2 u oba izraza.
- Zajednički faktor za oba broja je još jedan faktor 2, pa napišite 2 × 2 (\displaystyle 2\puta 2) a druga 2 prekriži u oba izraza.
-
Dodajte preostale faktore operaciji množenja. To su faktori koji nisu precrtani u oba izraza, odnosno faktori koji nisu zajednički za oba broja.
- Na primjer, u izrazu 20 = 2 × 2 × 5 (\displaystyle 20=2\put 2\put 5) obje dvojke (2) su precrtane jer su zajednički čimbenici. Faktor 5 nije precrtan, pa zapišite operaciju množenja na sljedeći način: 2 × 2 × 5 (\displaystyle 2\put 2\puts 5)
- U izrazu 84 = 2 × 7 × 3 × 2 (\displaystyle 84=2\put 7\put 3\puts 2) obje su dvojke (2) također prekrižene. Faktori 7 i 3 nisu precrtani, pa operaciju množenja zapišite na sljedeći način: 2 × 2 × 5 × 7 × 3 (\displaystyle 2\put 2\put 5\put 7\puts 3).
-
Izračunajte najmanji zajednički višekratnik. Da biste to učinili, pomnožite brojeve u napisanoj operaciji množenja.
- Na primjer, 2 × 2 × 5 × 7 × 3 = 420 (\displaystyle 2\put 2\put 5\put 7\puts 3=420). Dakle, najmanji zajednički višekratnik 20 i 84 je 420.
Pronalaženje zajedničkih djelitelja
-
Nacrtajte mrežu kao što biste to učinili za igru tic-tac-toe. Takva se mreža sastoji od dvije paralelne linije koje se sijeku (pod pravim kutom) s dvije druge paralelne linije. To će rezultirati u tri retka i tri stupca (rešetka izgleda kao znak #). Upišite prvi broj u prvi red i drugi stupac. U prvi red i treći stupac upiši drugi broj.
- Na primjer, pronađite najmanji zajednički višekratnik 18 i 30. U prvi red i drugi stupac upišite 18, a u prvi red i treći stupac upišite 30.
-
Pronađite djelitelj zajednički za oba broja. Zapišite to u prvi red i prvi stupac. Bolje je tražiti proste djelitelje, ali to nije preduvjet.
- Na primjer, 18 i 30 su parni brojevi, pa je njihov zajednički djelitelj 2. Dakle, upišite 2 u prvi red i prvi stupac.
-
Podijelite svaki broj s prvim djeliteljem. Svaki količnik upiši ispod odgovarajućeg broja. Kvocijent je rezultat dijeljenja dva broja.
- Na primjer, 18 ÷ 2 = 9 (\displaystyle 18\div 2=9), pa napiši 9 ispod 18.
- 30 ÷ 2 = 15 (\displaystyle 30\div 2=15), pa napiši 15 ispod 30.
-
Pronađite djelitelj zajednički za oba kvocijenta. Ako takvog djelitelja nema, preskočite sljedeća dva koraka. U suprotnom, upišite djelitelj u drugi red i prvi stupac.
- Na primjer, 9 i 15 su djeljivi s 3, pa upišite 3 u drugi red i prvi stupac.
-
Svaki kvocijent podijelite s drugim djeliteljem. Zapišite svaki rezultat dijeljenja ispod odgovarajućeg kvocijenta.
- Na primjer, 9 ÷ 3 = 3 (\displaystyle 9\div 3=3), pa napiši 3 pod 9.
- 15 ÷ 3 = 5 (\displaystyle 15\div 3=5), pa napiši 5 ispod 15.
-
Ako je potrebno, nadopunite mrežu dodatnim ćelijama. Ponavljajte gornje korake sve dok kvocijent ne dobije zajednički djelitelj.
-
Zaokružite brojeve u prvom stupcu i posljednjem retku mreže. Zatim napišite označene brojeve kao operaciju množenja.
- Na primjer, brojevi 2 i 3 su u prvom stupcu, a brojevi 3 i 5 su u posljednjem redu, pa napišite operaciju množenja ovako: 2 × 3 × 3 × 5 (\displaystyle 2\put 3\put 3\puts 5).
-
Pronađite rezultat množenja brojeva. Time će se izračunati najmanji zajednički višekratnik dva zadana broja.
- Na primjer, 2 × 3 × 3 × 5 = 90 (\displaystyle 2\put 3\put 3\puts 5=90). Dakle, najmanji zajednički višekratnik 18 i 30 je 90.
Euklidov algoritam
-
Zapamtite terminologiju povezanu s operacijom dijeljenja. Dividenda je broj koji se dijeli. Djelitelj je broj kojim se dijeli. Kvocijent je rezultat dijeljenja dva broja. Ostatak je broj koji ostane kada se podijele dva broja.
- Na primjer, u izrazu 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) odmor. 3:
15 je djeljivo
6 je djelitelj
2 je privatno
3 je ostatak.
- Na primjer, u izrazu 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) odmor. 3:
Pogledajte ove brojke. Ovdje opisanu metodu najbolje je koristiti kada su data dva broja koja su oba manja od 10. Ako su dati veliki brojevi, upotrijebite drugu metodu.
Materijal u nastavku je logičan nastavak teorije iz članka pod naslovom LCM - Najmanji zajednički višestruki, definicija, primjeri, odnos između LCM i GCM. Ovdje ćemo govoriti o pronalaženje najmanjeg zajedničkog višekratnika (LCM), i Posebna pažnja Pogledajmo primjere. Najprije pokažimo kako se LCM dvaju brojeva izračunava u terminima GCD tih brojeva. Zatim razmotrite pronalaženje najmanjeg zajedničkog višekratnika faktoringom brojeva u proste faktore. Nakon toga ćemo se usredotočiti na pronalaženje LCM-a od tri i više brojeva, a također obratite pozornost na izračun LCM negativnih brojeva.
Navigacija po stranici.
Izračun najmanjeg zajedničkog višekratnika (LCM) kroz gcd
Jedan od načina za pronalaženje najmanjeg zajedničkog višekratnika temelji se na odnosu između LCM-a i GCD-a. Postojeći odnos između LCM-a i GCD-a omogućuje vam da izračunate najmanji zajednički višekratnik dva pozitivna cijela broja kroz poznati najveći zajednički djelitelj. Odgovarajuća formula ima oblik LCM(a, b)=a b: GCD(a, b) . Razmotrimo primjere pronalaženja LCM-a prema gornjoj formuli.
Primjer.
Pronađite najmanji zajednički višekratnik dvaju brojeva 126 i 70 .
Riješenje.
U ovom primjeru a=126, b=70. Upotrijebimo odnos između LCM i GCD izražen formulom LCM(a, b)=a b: GCD(a, b). Odnosno, prvo moramo pronaći najveći zajednički djelitelj brojeva 70 i 126, nakon čega možemo izračunati LCM ovih brojeva prema napisanoj formuli.
Pronađite gcd(126, 70) koristeći Euklidov algoritam: 126=70 1+56 , 70=56 1+14 , 56=14 4 , dakle gcd(126, 70)=14 .
Sada nalazimo traženi najmanji zajednički višekratnik: LCM(126, 70)=126 70: GCM(126, 70)= 126 70:14 = 630 .
Odgovor:
LCM (126, 70) = 630 .
Primjer.
Što je LCM(68, 34)?
Riješenje.
Jer 68 je jednako djeljivo s 34, tada je gcd(68, 34)=34. Sada izračunavamo najmanji zajednički višekratnik: LCM(68, 34)=68 34: LCM(68, 34)= 68 34:34 = 68 .
Odgovor:
LCM (68, 34) = 68 .
Imajte na umu da prethodni primjer odgovara sljedećem pravilu za pronalaženje LCM-a za pozitivne cijele brojeve a i b: ako je broj a djeljiv s b, tada je najmanji zajednički višekratnik ovih brojeva a.
Pronalaženje LCM-a faktoriranjem brojeva u proste faktore
Drugi način pronalaženja najmanjeg zajedničkog višekratnika temelji se na faktoriranju brojeva u proste faktore. Ako napravimo umnožak svih prostih čimbenika ovih brojeva, nakon čega iz tog umnožaka izuzmemo sve zajedničke proste faktore koji su prisutni u proširenjima tih brojeva, tada će rezultirajući umnožak biti jednak najmanjem zajedničkom višekratniku tih brojeva.
Najavljeno pravilo za pronalaženje LCM proizlazi iz jednakosti LCM(a, b)=a b: GCD(a, b). Doista, umnožak brojeva a i b jednak je umnošku svih čimbenika uključenih u proširenja brojeva a i b. Zauzvrat, gcd(a, b) je jednak umnošku svih prostih čimbenika koji su istovremeno prisutni u proširenjima brojeva a i b (što je opisano u odjeljku o pronalaženju gcd pomoću dekompozicije brojeva na proste faktore ).
Uzmimo primjer. Neka znamo da je 75=3 5 5 i 210=2 3 5 7 . Sastavite umnožak svih faktora ovih proširenja: 2 3 3 5 5 5 7 . Sada iz ovog proizvoda izuzimamo sve čimbenike koji su prisutni i u proširenju broja 75 i u proširenju broja 210 (takvi faktori su 3 i 5), tada će proizvod dobiti oblik 2 3 5 5 7 . Vrijednost ovog proizvoda jednaka je najmanjem zajedničkom višekratniku brojeva 75 i 210, tj. LCM(75, 210)= 2 3 5 5 7=1 050.
Primjer.
Nakon faktoringa brojeva 441 i 700 u proste faktore, pronađite najmanji zajednički višekratnik tih brojeva.
Riješenje.
Razložimo brojeve 441 i 700 na proste faktore:
Dobivamo 441=3 3 7 7 i 700=2 2 5 5 7 .
Sada napravimo umnožak svih čimbenika koji sudjeluju u proširenjima ovih brojeva: 2 2 3 3 5 5 7 7 7 . Isključimo iz ovog proizvoda sve čimbenike koji su istovremeno prisutni u oba proširenja (postoji samo jedan takav faktor - to je broj 7): 2 2 3 3 5 5 7 7 . Na ovaj način, LCM(441, 700)=2 2 3 3 5 5 7 7=44 100.
Odgovor:
LCM (441, 700) = 44 100 .
Pravilo za pronalaženje LCM-a pomoću dekompozicije brojeva na proste faktore može se formulirati malo drugačije. Ako faktorima iz proširenja broja a dodamo čimbenike koji nedostaju iz proširenja broja a, tada će vrijednost rezultirajućeg proizvoda biti jednaka najmanjem zajedničkom višekratniku brojeva a i b.
Na primjer, uzmimo sve iste brojeve 75 i 210, njihova proširenja u proste faktore su sljedeća: 75=3 5 5 i 210=2 3 5 7 . Faktorima 3, 5 i 5 iz proširenja broja 75 dodamo čimbenike koji nedostaju 2 i 7 iz proširenja broja 210, dobijemo umnožak 2 3 5 5 7 , čija je vrijednost LCM(75 , 210) .
Primjer.
Pronađite najmanji zajednički višekratnik brojeva 84 i 648.
Riješenje.
Prvo dobivamo razlaganje brojeva 84 i 648 na proste faktore. Izgledaju kao 84=2 2 3 7 i 648=2 2 2 3 3 3 3 . Faktorima 2 , 2 , 3 i 7 iz proširenja broja 84 dodamo čimbenike koji nedostaju 2 , 3 , 3 i 3 iz proširenja broja 648 , dobijemo umnožak 2 2 2 3 3 3 3 7 , što je jednako 4 536 . Dakle, željeni najmanji zajednički višekratnik brojeva 84 i 648 je 4,536.
Odgovor:
LCM (84, 648) = 4 536 .
Pronalaženje LCM-a tri ili više brojeva
Najmanji zajednički višekratnik tri ili više brojeva može se pronaći uzastopnim pronalaženjem LCM dva broja. Prisjetimo se odgovarajućeg teorema, koji daje način da se pronađe LCM od tri ili više brojeva.
Teorema.
Neka su dati pozitivni cijeli brojevi a 1 , a 2 , …, a k, najmanji zajednički višekratnik m k ovih brojeva nalazi se u sekvencijalnom izračunu m 2 = LCM (a 1 , a 2) , m 3 = LCM (m 2 , a 3) , … , m k =LCM(m k−1 , a k) .
Razmotrimo primjenu ovog teorema na primjeru pronalaženja najmanjeg zajedničkog višekratnika četiri broja.
Primjer.
Pronađite LCM četiri broja 140 , 9 , 54 i 250 .
Riješenje.
U ovom primjeru a 1 =140, a 2 =9, a 3 =54, a 4 =250.
Prvo pronađemo m 2 \u003d LCM (a 1, a 2) \u003d LCM (140, 9). Da bismo to učinili, koristeći Euklidov algoritam, određujemo gcd(140, 9) , imamo 140=9 15+5 , 9=5 1+4 , 5=4 1+1 , 4=1 4 , dakle, gcd( 140, 9)=1 , odakle LCM(140, 9)=140 9: LCM(140, 9)= 140 9:1 = 1 260 . To jest, m 2 =1 260 .
Sada nalazimo m 3 = LCM (m 2, a 3) \u003d LCM (1 260, 54). Izračunajmo ga kroz gcd(1 260, 54) , što je također određeno Euklidovim algoritmom: 1 260=54 23+18 , 54=18 3 . Tada je gcd(1 260, 54)=18, odakle je LCM(1 260, 54)= 1 260 54:gcd(1 260, 54)= 1 260 54:18=3 780 . To jest, m 3 \u003d 3 780.
Ostalo da se pronađe m 4 \u003d LCM (m 3, a 4) \u003d LCM (3 780, 250). Da bismo to učinili, nalazimo GCD(3 780, 250) koristeći Euklid algoritam: 3 780=250 15+30 , 250=30 8+10 , 30=10 3 . Prema tome, gcd(3 780, 250)=10, odakle je gcd(3 780, 250)= 3 780 250: gcd (3 780, 250)= 3 780 250:10 = 94 500 . To jest, m 4 \u003d 94 500.
Dakle, najmanji zajednički višekratnik izvorna četiri broja je 94 500.
Odgovor:
LCM (140, 9, 54, 250) = 94 500.
U mnogim slučajevima, najmanji zajednički višekratnik tri ili više brojeva prikladno se nalazi korištenjem prostih faktorizacija zadanih brojeva. U tom slučaju treba se pridržavati sljedećeg pravila. Najmanji zajednički višekratnik nekoliko brojeva jednak je umnošku koji se sastoji na sljedeći način: čimbenici koji nedostaju iz proširenja drugog broja dodaju se svim čimbenicima iz proširenja prvog broja, faktori koji nedostaju iz proširenja broja treći broj se dodaje dobivenim faktorima i tako dalje.
Razmotrimo primjer pronalaženja najmanjeg zajedničkog višekratnika pomoću dekompozicije brojeva na proste faktore.
Primjer.
Nađi najmanji zajednički višekratnik pet brojeva 84 , 6 , 48 , 7 , 143 .
Riješenje.
Prvo dobivamo proširenja ovih brojeva u proste faktore: 84=2 2 3 7 , 6=2 3 , 48=2 2 2 2 3 , 7 prosti faktori) i 143=11 13 .
Da biste pronašli LCM ovih brojeva, faktorima prvog broja 84 (oni su 2 , 2 , 3 i 7 ) trebate dodati faktore koji nedostaju iz proširenja drugog broja 6 . Proširivanje broja 6 ne sadrži faktore koji nedostaju, budući da su i 2 i 3 već prisutni u proširenju prvog broja 84 . Osim faktora 2, 2, 3 i 7 dodajemo faktore koji nedostaju 2 i 2 iz proširenja trećeg broja 48, dobivamo skup faktora 2, 2, 2, 2, 3 i 7. Nema potrebe dodavati faktore ovom skupu u sljedećem koraku, budući da je 7 već sadržano u njemu. Konačno, faktorima 2, 2, 2, 2, 3 i 7 dodajemo faktore koji nedostaju 11 i 13 iz proširenja broja 143. Dobivamo umnožak 2 2 2 2 3 7 11 13 koji je jednak 48 048 .
Najveći zajednički djelitelj
Definicija 2
Ako je prirodni broj a djeljiv prirodnim brojem $b$, tada se $b$ naziva djelitelj od $a$, a broj $a$ naziva se višekratnik od $b$.
Neka su $a$ i $b$ prirodni brojevi. Broj $c$ naziva se zajedničkim djeliteljem i za $a$ i za $b$.
Skup zajedničkih djelitelja brojeva $a$ i $b$ je konačan, jer nijedan od tih djelitelja ne može biti veći od $a$. To znači da među tim djeliteljima postoji najveći, koji se naziva najveći zajednički djelitelj brojeva $a$ i $b$, a za označavanje se koristi oznaka:
$gcd \ (a;b) \ ili \ D \ (a;b)$
Da biste pronašli najveći zajednički djelitelj dvaju brojeva:
- Pronađite umnožak brojeva pronađenih u koraku 2. Rezultirajući broj bit će željeni najveći zajednički djelitelj.
Primjer 1
Pronađite gcd brojeva $121$ i $132.$
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Odaberite brojeve koji su uključeni u proširenje ovih brojeva
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Pronađite umnožak brojeva pronađenih u koraku 2. Rezultirajući broj bit će željeni najveći zajednički djelitelj.
$gcd=2\cdot 11=22$
Primjer 2
Pronađite GCD monoma $63$ i $81$.
Pronaći ćemo prema prikazanom algoritmu. Za ovo:
Razložimo brojeve na proste faktore
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Odabiremo brojeve koji su uključeni u proširenje ovih brojeva
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Nađimo umnožak brojeva pronađenih u koraku 2. Dobiveni broj će biti željeni najveći zajednički djelitelj.
$gcd=3\cdot 3=9$
GCD dvaju brojeva možete pronaći na drugi način, koristeći skup djelitelja brojeva.
Primjer 3
Pronađite gcd brojeva $48$ i $60$.
Riješenje:
Pronađite skup djelitelja $48$: $\lijevo\((\rm 1,2,3.4.6,8,12,16,24,48)\desno\)$
Sada pronađimo skup djelitelja $60$:$\ \left\((\rm 1,2,3,4,5,6,10,12,15,20,30,60)\right\)$
Nađimo presjek ovih skupova: $\left\((\rm 1,2,3,4,6,12)\right\)$ - ovaj skup će odrediti skup zajedničkih djelitelja brojeva $48$ i $60 $. Najveći element u zadanog skupa bit će broj 12$. Dakle, najveći zajednički djelitelj $48$ i $60$ je $12$.
Definicija NOC-a
Definicija 3
zajednički višekratnik prirodnih brojeva$a$ i $b$ je prirodan broj koji je višekratnik i $a$ i $b$.
Uobičajeni višekratnici brojeva su brojevi koji su djeljivi izvornikom bez ostatka. Na primjer, za brojeve 25$ i 50$ zajednički će višekratnici biti brojevi 50,100,150,200$ itd.
Najmanji zajednički višekratnik nazivat će se najmanjim zajedničkim višekratnikom i označavati ga s LCM$(a;b)$ ili K$(a;b).$
Da biste pronašli LCM dva broja, trebate:
- Rastaviti brojeve na proste faktore
- Napišite čimbenike koji su dio prvog broja i dodajte im faktore koji su dio drugog i ne idu na prvi
Primjer 4
Pronađite LCM brojeva $99$ i $77$.
Pronaći ćemo prema prikazanom algoritmu. Za ovo
Rastaviti brojeve na proste faktore
$99=3\cdot 3\cdot 11$
Zapišite čimbenike uključene u prvi
dodajte im čimbenike koji su dio drugog i ne idu u prvi
Pronađite umnožak brojeva pronađenih u koraku 2. Rezultirajući broj bit će željeni najmanji zajednički višekratnik
$LCC=3\cdot 3\cdot 11\cdot 7=693$
Sastavljanje popisa djelitelja brojeva često je vrlo dugotrajno. Postoji način da se pronađe GCD koji se zove Euklidov algoritam.
Izjave na kojima se temelji Euklidov algoritam:
Ako su $a$ i $b$ prirodni brojevi, a $a\vdots b$, tada je $D(a;b)=b$
Ako su $a$ i $b$ prirodni brojevi takvi da je $b
Koristeći $D(a;b)= D(a-b;b)$, možemo sukcesivno smanjivati brojeve koji se razmatraju dok ne dođemo do para brojeva tako da je jedan od njih djeljiv drugim. Tada će manji od ovih brojeva biti željeni najveći zajednički djelitelj za brojeve $a$ i $b$.
Svojstva GCD i LCM
- Svaki zajednički višekratnik $a$ i $b$ djeljiv je s K$(a;b)$
- Ako je $a\vdots b$, tada je K$(a;b)=a$
Ako je K$(a;b)=k$ i $m$-prirodni broj, tada je K$(am;bm)=km$
Ako je $d$ zajednički djelitelj za $a$ i $b$, tada je K($\frac(a)(d);\frac(b)(d)$)=$\ \frac(k)(d ) $
Ako je $a\vdots c$ i $b\vdots c$, tada je $\frac(ab)(c)$ zajednički višekratnik $a$ i $b$
Za bilo koje prirodne brojeve $a$ i $b$ jednakost
$D(a;b)\cdot K(a;b)=ab$
Svaki zajednički djelitelj $a$ i $b$ je djelitelj $D(a;b)$