Kako pronaći ukupnu površinu formule piramide. Pronađite površinu pravilne trokutaste piramide

Prilikom pripreme za Jedinstveni državni ispit iz matematike, studenti moraju sistematizovati svoja znanja iz algebre i geometrije. Želio bih kombinirati sve poznate informacije, na primjer, o tome kako izračunati površinu piramide. Štoviše, počevši od baze i bočnih rubova do cijele površine. Ako je situacija sa bočnim stranama jasna, budući da su trouglovi, onda je baza uvijek drugačija.

Kako pronaći površinu osnove piramide?

To može biti apsolutno bilo koja figura: od proizvoljnog trougla do n-ugla. A ova baza, pored razlike u broju uglova, može biti pravilna ili nepravilna figura. U zadacima Jedinstvenog državnog ispita koji zanimaju školarce, postoje samo zadaci s tačnim brojkama u osnovi. Stoga ćemo govoriti samo o njima.

Pravilan trougao

Odnosno, jednakostraničan. Onaj u kojem su sve strane jednake i označene slovom "a". U ovom slučaju, površina baze piramide se izračunava po formuli:

S = (a 2 * √3) / 4.

Square

Formula za izračunavanje njegove površine je najjednostavnija, ovdje je "a" opet strana:

Proizvoljni regularni n-ugao

Strana poligona ima istu notaciju. Za broj uglova koristi se latinično slovo n.

S = (n * a 2) / (4 * tg (180º/n)).

Što učiniti pri izračunavanju bočne i ukupne površine?

Jer u osnovi leži tačna figura, tada se ispostavljaju da su sve strane piramide jednake. Štaviše, svaki od njih je jednakokraki trokut, jer su bočne ivice jednake. Zatim da bi izračunali bočno područje piramide, trebat će vam formula koja se sastoji od zbira identičnih monoma. Broj pojmova je određen brojem stranica baze.

Square jednakokraki trougao izračunava se pomoću formule u kojoj se polovina proizvoda baze pomnoži sa visinom. Ova visina u piramidi naziva se apotema. Njegova oznaka je "A". Opća formula za bočnu površinu to izgleda ovako:

S = ½ P*A, gdje je P obim osnove piramide.

Postoje situacije kada stranice baze nisu poznate, ali su date bočne ivice (c) i ravan ugao na njenom vrhu (α). Zatim morate koristiti sljedeću formulu za izračunavanje bočne površine piramide:

S = n/2 * u 2 sin α .

Zadatak br. 1

Stanje. Nađi ukupne površine piramida, ako njena osnova ima stranu 4 cm, a apotema ima vrijednost √3 cm.

Rješenje. Morate početi s izračunavanjem perimetra baze. Pošto je ovo pravilan trokut, onda je P = 3*4 = 12 cm Pošto je apotema poznata, možemo odmah izračunati površinu cijele bočne površine: ½*12*√3 = 6√3 cm 2.

Za trougao u osnovi dobijate sljedeću vrijednost površine: (4 2 *√3) / 4 = 4√3 cm 2.

Da biste odredili cijelu površinu, morat ćete sabrati dvije rezultirajuće vrijednosti: 6√3 + 4√3 = 10√3 cm 2.

Odgovori. 10√3 cm 2.

Problem br. 2

Stanje. Postoji pravilna četvorougaona piramida. Dužina donje strane je 7 mm, bočne ivice 16 mm. Potrebno je saznati njegovu površinu.

Rješenje. Pošto je poliedar četvorougao i pravilan, njegova osnova je kvadrat. Kada znate površinu baze i bočnih strana, moći ćete izračunati površinu piramide. Formula za kvadrat je data gore. A za bočne strane poznate su sve strane trougla. Stoga možete koristiti Heronovu formulu da izračunate njihove površine.

Prvi proračuni su jednostavni i vode do sljedećeg broja: 49 mm 2. Za drugu vrijednost, morat ćete izračunati poluperimetar: (7 + 16*2): 2 = 19,5 mm. Sada možete izračunati površinu jednakokračnog trougla: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 mm 2. Postoje samo četiri takva trokuta, tako da ćete prilikom izračunavanja konačnog broja morati da ga pomnožite sa 4.

Ispada: 49 + 4 * 54,644 = 267,576 mm 2.

Odgovori. Željena vrijednost je 267,576 mm 2.

Zadatak br. 3

Stanje. Za pravilnu četvorougaonu piramidu morate izračunati površinu. Poznato je da je stranica kvadrata 6 cm, a visina 4 cm.

Rješenje. Najlakši način je korištenje formule s umnoškom perimetra i apoteme. Prvu vrijednost je lako pronaći. Drugi je malo komplikovaniji.

Morat ćemo se sjetiti Pitagorine teoreme i razmotriti da je formirana visinom piramide i apoteme, koja je hipotenuza. Drugi krak je jednak polovini stranice kvadrata, jer visina poliedra pada na njegovu sredinu.

Tražena apotema (hipotenuza pravouglog trougla) je jednaka √(3 2 + 4 2) = 5 (cm).

Sada možete izračunati potrebnu vrijednost: ½*(4*6)*5+6 2 = 96 (cm 2).

Odgovori. 96 cm 2.

Problem br. 4

Stanje. Dana ispravna strana njegove osnove su 22 mm, bočna rebra su 61 mm. Kolika je bočna površina ovog poliedra?

Rješenje. Obrazloženje u njemu je isto kao ono opisano u zadatku br. 2. Samo tamo je data piramida sa kvadratom u osnovi, a sada je to šestougao.

Prije svega, osnovna površina se izračunava korištenjem gornje formule: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 cm 2.

Sada morate saznati polu-perimetar jednakokračnog trokuta, što je bočna strana. (22+61*2):2 = 72 cm Preostaje samo da pomoću Heronove formule izračunate površinu svakog takvog trokuta, a zatim ga pomnožite sa šest i dodate onom dobijenom za osnovu.

Proračuni pomoću Heronove formule: √(72*(72-22)*(72-61) 2)=√435600=660 cm 2. Izračuni koji će dati površinu bočne površine: 660 * 6 = 3960 cm 2. Ostaje da ih zbrojimo kako bismo saznali cijelu površinu: 5217,47≈5217 cm 2.

Odgovori. Baza je 726√3 cm 2, bočna površina je 3960 cm 2, cijela površina je 5217 cm 2.

Piramida- jedna od varijanti poliedra formiranog od mnogouglova i trokuta koji leže u osnovi i koji su njegova lica.

Štaviše, na vrhu piramide (tj. u jednoj tački) sva lica su ujedinjena.

Da bi se izračunala površina piramide, vrijedi utvrditi da se njena bočna površina sastoji od nekoliko trokuta. I lako možemo pronaći njihove oblasti koristeći

razne formule. U zavisnosti od toga koje podatke znamo o trouglovima, tražimo njihovu površinu.

Navodimo neke formule koje se mogu koristiti za pronalaženje površine trokuta:

1. S = (a*h)/2 . IN u ovom slučaju znamo visinu trougla h , koji je spušten u stranu a .
2. S = a*b*sinβ . Evo stranica trougla a , b , a ugao između njih je β .
3. S = (r*(a + b + c))/2 . Evo stranica trougla a, b, c . Polumjer kružnice koja je upisana u trokut je r .
4. S = (a*b*c)/4*R . Polumjer opisane kružnice oko trougla je R .
5. S = (a*b)/2 = r² + 2*r*R . Ova formula treba koristiti samo kada je trokut pravokutni trokut.
6. S = (a²*√3)/4 . Ovu formulu primjenjujemo na jednakostranični trokut.

Tek nakon što izračunamo površine svih trokuta koji su lica naše piramide, možemo izračunati površinu njene bočne površine. Da bismo to učinili, koristit ćemo gornje formule.

Da biste izračunali površinu bočne površine piramide, nema poteškoća: morate saznati zbroj površina svih trokuta. Izrazimo to formulom:

Sp = ΣSi

Evo Si je površina prvog trokuta, i S P - površina bočne površine piramide.

Pogledajmo primjer. S obzirom na pravilnu piramidu, njene bočne strane čine nekoliko jednakostraničnih trokuta,

« Geometrija je najmoćniji alat za izoštravanje naših mentalnih sposobnosti».

Galileo Galilei.

a kvadrat je osnova piramide. Štaviše, ivica piramide ima dužinu od 17 cm. Nađimo površinu bočne površine ove piramide.

Razmišljamo ovako: znamo da su lica piramide trouglovi, da su jednakostranična. Takođe znamo koja je dužina ivice ove piramide. Iz toga proizilazi da svi trokuti imaju jednake stranice i da im je dužina 17 cm.

Da biste izračunali površinu svakog od ovih trokuta, možete koristiti sljedeću formulu:

S = (17²*√3)/4 = (289*1,732)/4 = 125,137 cm²

Dakle, pošto znamo da kvadrat leži u osnovi piramide, ispada da imamo četiri jednakostranična trougla. To znači da se bočna površina piramide može lako izračunati pomoću sljedeće formule: 125,137 cm² * 4 = 500,548 cm²

Naš odgovor je sljedeći: 500,548 cm² - ovo je površina bočne površine ove piramide.

Površina piramide. U ovom članku ćemo se osvrnuti na probleme s pravilnim piramidama. Da vas podsjetim da je pravilna piramida piramida čija je osnova pravilan poligon, vrh piramide je projektovan na centar ovog poligona.

Bočna strana takve piramide je jednakokraki trokut.Visina ovog trougla, povučena iz vrha pravilne piramide, naziva se apotema, SF - apotema:

U tipu problema predstavljenom u nastavku, morate pronaći površinu cijele piramide ili površinu njene bočne površine. Na blogu se već raspravljalo o nekoliko problema sa pravilnim piramidama, gdje se postavljalo pitanje pronalaženja elemenata (visina, osnovna ivica, bočna ivica).

IN Zadaci objedinjenog državnog ispita U pravilu se razmatraju pravilne trouglaste, četverokutne i šesterokutne piramide. Nisam vidio nikakve probleme sa pravilnim petougaonim i sedmougaonim piramidama.

Formula za površinu cijele površine je jednostavna - morate pronaći zbir površine osnove piramide i površine njene bočne površine:

Razmotrimo zadatke:

Stranice osnove pravilne četvorougaone piramide su 72, bočne ivice su 164. Nađite površinu ove piramide.

Površina piramide jednaka je zbroju površina bočne površine i baze:

*Bočna površina se sastoji od četiri trougla jednake površine. Osnova piramide je kvadrat.

Možemo izračunati površinu stranice piramide koristeći:

Dakle, površina piramide je:

Odgovor: 28224

Stranice osnove pravilne šesterokutne piramide jednake su 22, bočne ivice jednake su 61. Nađite površinu bočne površine ove piramide.

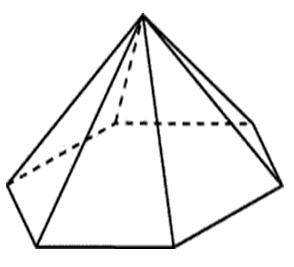
Osnova pravilne šestougaone piramide je pravilan šestougao.

Bočna površina ove piramide sastoji se od šest površina jednakih trokuta sa stranicama 61,61 i 22:

Nađimo površinu trokuta koristeći Heronovu formulu:

Dakle, bočna površina je:

Odgovor: 3240

*U gore navedenim problemima, površina bočne strane se može naći pomoću druge formule trokuta, ali za to morate izračunati apotemu.

27155. Nađi površinu pravilne četvorougaone piramide čije su osnovne stranice 6, a visina 4.

Da bismo pronašli površinu piramide, moramo znati površinu baze i površinu bočne površine:

Površina osnove je 36 jer je kvadrat sa stranicom 6.

Bočna površina se sastoji od četiri lica, koja su jednakih trouglova. Da biste pronašli površinu takvog trokuta, morate znati njegovu osnovu i visinu (apotemu):

*Površina trokuta jednaka je polovini umnoška osnove i visine povučene ovoj osnovici.

Baza je poznata, jednaka je šest. Hajde da nađemo visinu. Hajde da razmotrimo pravougaonog trougla(naglašeno je žutom bojom):

Jedna noga je jednaka 4, pošto je ovo visina piramide, druga je jednaka 3, jer je jednaka polovini ivice baze. Hipotenuzu možemo pronaći pomoću Pitagorine teoreme:

To znači da je površina bočne površine piramide:

Dakle, površina cijele piramide je:

Odgovor: 96

27069. Stranice osnove pravilne četvorougaone piramide jednake su 10, bočne ivice jednake su 13. Nađite površinu ove piramide.

27070. Stranice osnove pravilne šesterokutne piramide jednake su 10, bočne ivice jednake su 13. Nađite površinu bočne površine ove piramide.

Postoje i formule za bočnu površinu pravilne piramide. U pravilnoj piramidi osnova je ortogonalna projekcija bočne površine, dakle:

P- perimetar baze, l- apotema piramide

*Ova formula se zasniva na formuli za površinu trokuta.

Ako želite saznati više o tome kako se te formule izvode, ne propustite, pratite objavljivanje članaka.To je sve. Sretno ti!

S poštovanjem, Alexander Krutitskikh.

P.S: Bio bih vam zahvalan ako mi kažete nešto o stranici na društvenim mrežama.

Cilindar je geometrijsko tijelo omeđeno dvama paralelne ravni i cilindrične površine. U članku ćemo govoriti o tome kako pronaći površinu cilindra i, koristeći formulu, riješit ćemo nekoliko problema kao primjer.

Cilindar ima tri površine: gornju, bazu i bočnu površinu.

Vrh i baza cilindra su krugovi i lako ih je prepoznati.

Poznato je da je površina kruga jednaka πr 2. Stoga će formula za površinu dva kruga (vrh i baza cilindra) biti πr 2 + πr 2 = 2πr 2.

Treća, bočna površina cilindra, je zakrivljeni zid cilindra. Kako bismo što bolje predstavili ovu površinu, pokušajmo je transformirati da dobijemo prepoznatljivog oblika. Zamislite da je cilindar običan lim, koji nema gornji ili donji poklopac. Napravimo okomiti rez na bočnom zidu od vrha do dna limenke (korak 1 na slici) i pokušajmo otvoriti (ispraviti) rezultirajuću figuru što je više moguće (korak 2).

Nakon što se dobijena staklenka potpuno otvori, vidjet ćemo poznatu figuru (korak 3), ovo je pravougaonik. Površinu pravougaonika je lako izračunati. Ali prije toga, vratimo se na trenutak originalnom cilindru. Vrh originalnog cilindra je krug, a znamo da se obim izračunava po formuli: L = 2πr. Na slici je označeno crvenom bojom.

Kada bočni zid cilindar je potpuno otvoren, vidimo da obim postaje dužina rezultirajućeg pravokutnika. Stranice ovog pravougaonika biće obim (L = 2πr) i visina cilindra (h). Površina pravokutnika jednaka je proizvodu njegovih stranica - S = dužina x širina = L x h = 2πr x h = 2πrh. Kao rezultat toga, dobili smo formulu za izračunavanje površine bočne površine cilindra.

Formula za bočnu površinu cilindra
S strana = 2πrh

Ukupna površina cilindra

Konačno, ako zbrojimo površinu svega tri površine, dobijamo formulu površine puna površina cilindar. Površina cilindra jednaka je površini vrha cilindra + površini osnove cilindra + površini bočne površine cilindra ili S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Ponekad se ovaj izraz piše identično formuli 2πr (r + h).

Formula za ukupnu površinu cilindra
S = 2πr 2 + 2πrh = 2πr(r + h)
r – poluprečnik cilindra, h – visina cilindra

Primjeri izračunavanja površine cilindra

Da bismo razumjeli gornje formule, pokušajmo izračunati površinu cilindra koristeći primjere.

1. Poluprečnik osnove cilindra je 2, visina je 3. Odredite površinu bočne površine cilindra.

Ukupna površina se izračunava pomoću formule: S strana. = 2πrh

S strana = 2 * 3,14 * 2 * 3

S strana = 6,28 * 6

S strana = 37,68

Bočna površina cilindra je 37,68.

2. Kako pronaći površinu cilindra ako je visina 4, a polumjer 6?

Ukupna površina se izračunava pomoću formule: S = 2πr 2 + 2πrh

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Površina bočne površine proizvoljne piramide jednaka je zbiru površina njenih bočnih strana. Ima smisla dati posebnu formulu za izražavanje ove površine u slučaju pravilne piramide. Dakle, neka nam je dana pravilna piramida, u čijoj osnovi leži pravilan n-ugao sa stranicom jednakom a. Neka je h visina bočne strane, koja se također naziva apothem piramide. Površina jedne bočne strane je jednaka 1/2ah, a cijela bočna površina piramide ima površinu jednaku n/2ha Pošto je na obim osnove piramide, možemo zapisati pronađenu formulu u obliku:

Bočna površina pravilne piramide jednak je umnošku njene apoteme i polovine perimetra osnove.

U vezi ukupna površina, onda jednostavno dodamo površinu baze bočnoj.

Upisana i opisana sfera i lopta. Treba napomenuti da centar sfere upisane u piramidu leži na presjeku simetralnih ravni unutrašnjih diedralnih uglova piramide. Središte sfere opisane u blizini piramide nalazi se na sjecištu ravnina koje prolaze kroz sredine ivica piramide i okomite na njih.

Krnja piramida. Ako piramidu preseče ravan paralelna njenoj osnovi, tada se deo zatvoren između presečne ravni i baze naziva krnje piramide. Na slici je prikazana piramida odbacivanjem njenog dijela koji leži iznad rezne ravnine, dobijamo skraćenu piramidu. Jasno je da je mala odbačena piramida homotetična velikoj piramidi sa centrom homotetije na vrhu. Koeficijent sličnosti jednak omjeru visine: k=h 2 /h 1, ili bočna rebra, ili drugo prikladno linearne dimenzije obe piramide. Znamo da su površine sličnih figura povezane kao kvadrati linearnih dimenzija; pa su površine osnova obe piramide (tj. površina osnova krnje piramide) povezane kao

Ovdje je S 1 površina donje baze, a S 2 površina gornje osnove skraćene piramide. U istoj vezi su bočne površine piramide Slično pravilo postoji i za volumene.

Zapremine sličnih tijela povezani su kao kocke svojih linearnih dimenzija; na primjer, zapremine piramida su povezane kao proizvod njihovih visina i površine baza, iz čega se odmah dobija naše pravilo. Ima apsolutno opšti karakter a to direktno proizilazi iz činjenice da volumen uvijek ima dimenziju trećeg stepena dužine. Koristeći ovo pravilo, izvodimo formulu koja izražava volumen krnje piramide kroz visinu i površinu baza.

Neka je data skraćena piramida visine h i baza S 1 i S 2. Ako zamislimo da se to nastavi puna piramida, tada je koeficijent sličnosti između pune piramide i male piramide lako pronaći kao korijen omjera S 2 /S 1 . Visina skraćene piramide izražava se kao h = h 1 - h 2 = h 1 (1 - k). Sada imamo za zapreminu krnje piramide (V 1 i V 2 označavaju zapremine pune i male piramide)

formula za zapreminu krnje piramide

Izvedemo formulu za površinu S bočne površine pravilne krnje piramide kroz perimetre P 1 i P 2 osnova i dužinu apoteme a. Razmišljamo na potpuno isti način kao kada izvodimo formulu za volumen. Dopunjavamo piramidu gornjim dijelom, imamo P 2 = kP 1, S 2 = k 2 S 1, gdje je k koeficijent sličnosti, P 1 i P 2 su perimetri baza, a S 1 i S 2 su površine bočnih površina cijele rezultirajuće piramide i prema tome njenog gornjeg dijela. Za bočnu površinu nalazimo (a 1 i a 2 su apotemi piramida, a = a 1 - a 2 = a 1 (1-k))

formula za bočnu površinu pravilne skraćene piramide