خصائص الدالة هي أكبر وأصغر قيمة. كيف تجد أصغر قيمة للدالة

ولحلها ، تحتاج إلى الحد الأدنى من المعرفة بالموضوع. ينتهي العام الدراسي القادم ، ويريد الجميع الذهاب في إجازة ، ولأقرب هذه اللحظة ، أبدأ العمل على الفور:

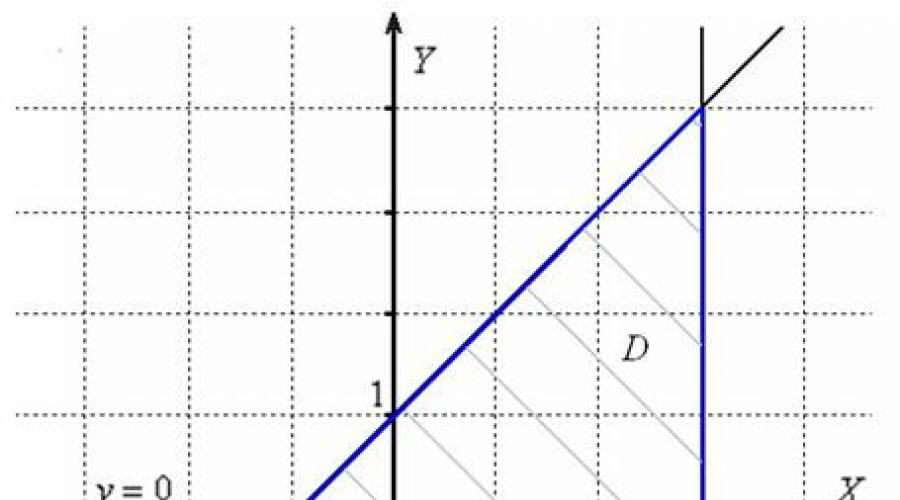
لنبدأ بالمنطقة. المنطقة المشار إليها في الشرط هي محدود مغلق مجموعة من النقاط في الطائرة. على سبيل المثال ، مجموعة من النقاط يحدها مثلث ، بما في ذلك المثلث الكامل (إذا كان من الحدود"اخرج" نقطة واحدة على الأقل ، فلن تكون المنطقة مغلقة بعد ذلك). من الناحية العملية ، هناك أيضًا مناطق مستطيلة ودائرية وأكثر قليلاً أشكال معقدة. وتجدر الإشارة إلى ذلك من الناحية النظرية التحليل الرياضييتم إعطاء تعريفات صارمة القيود ، العزلة ، الحدود ، إلخ.، لكني أعتقد أن الجميع على دراية بهذه المفاهيم على مستوى حدسي ، وليس هناك حاجة إلى المزيد الآن.

يتم الإشارة إلى المنطقة المسطحة بشكل قياسي بالحرف ، وكقاعدة عامة ، يتم تحديدها بشكل تحليلي - من خلال عدة معادلات (ليس بالضرورة خطي)؛ أقل في كثير من الأحيان عدم المساواة. معدل دوران لفظي نموذجي: "منطقة مغلقة محدودة بأسطر".

جزء لا يتجزأ من المهمة قيد النظر هو بناء المنطقة على الرسم. كيف افعلها؟ من الضروري رسم جميع الخطوط المذكورة (بتنسيق هذه القضية 3 مباشرة) وتحليل ما حدث. عادةً ما يتم تظليل المنطقة المرغوبة قليلاً ، ويتم تمييز حدودها بخط عريض:


يمكن تعيين نفس المنطقة المتباينات الخطية: ، والتي لسبب ما تتم كتابتها في الغالب كقائمة تعداد ، وليس النظام.
بما أن الحدود تنتمي إلى المنطقة ، فإن كل التفاوتات ، بالطبع ، غير صارم.

والآن جوهر الأمر. تخيل أن المحور ينتقل إليك مباشرة من أصل الإحداثيات. النظر في وظيفة مستمر في كلنقطة المنطقة. الرسم البياني لهذه الوظيفة السطحية، والسعادة الصغيرة هي أنه من أجل حل مشكلة اليوم ، لا نحتاج إلى معرفة شكل هذا السطح على الإطلاق. يمكن أن تكون موجودة فوق ، أسفل ، عبور الطائرة - كل هذا ليس مهمًا. و ما يلي مهم: بحسب نظريات ويرستراس, مستمرفي محدودة مغلقةالمنطقة ، تصل الوظيفة إلى الحد الأقصى (من "الأعلى")وأقل (من "الأدنى")القيم التي يمكن العثور عليها. تتحقق هذه القيم أوفي نقاط ثابتة, ينتمون إلى المنطقةد , أوفي النقاط التي تقع على حدود هذه المنطقة. مما يلي خوارزمية حل بسيطة وشفافة:

مثال 1

في منطقة مغلقة محدودة

قرار: بادئ ذي بدء ، تحتاج إلى تصوير المنطقة على الرسم. لسوء الحظ ، من الصعب تقنيًا عمل نموذج تفاعلي للمشكلة ، وبالتالي سأقدم على الفور الرسم التوضيحي الأخير الذي يوضح جميع النقاط "المشبوهة" التي تم العثور عليها أثناء الدراسة. عادة ما يتم وضعها واحدة تلو الأخرى عند العثور عليها:

بناءً على التمهيد ، يمكن تقسيم القرار بسهولة إلى نقطتين:

I) لنجد نقاط ثابتة. هذا إجراء قياسي قمنا به مرارًا وتكرارًا في الدرس. حول القيم القصوى للعديد من المتغيرات:

تم العثور على نقطة ثابتة ينتميالمناطق: (ضع علامة على الرسم)، مما يعني أنه يجب علينا حساب قيمة الوظيفة عند نقطة معينة:

- كما في المقال أكبر وأصغر قيم للدالة في مقطعسأقوم بتسليط الضوء على النتائج الهامة بالخط العريض. في دفتر ملاحظات ، من الملائم وضع دائرة عليها بقلم رصاص.

انتبه لسعادتنا الثانية - لا فائدة من التحقق حالة كافية لأقصى حد. لماذا ا؟ حتى إذا وصلت الوظيفة ، على سبيل المثال ، الحد الأدنى المحلي، فهذا لا يعني أن القيمة الناتجة ستكون الحد الأدنىفي جميع أنحاء المنطقة (انظر بداية الدرس حول التطرف غير المشروط) .

ماذا لو كانت النقطة الثابتة لا تنتمي إلى المنطقة؟ لا شيء تقريبا! وتجدر الإشارة إلى ذلك وانتقل إلى الفقرة التالية.

ب) نحقق في حدود المنطقة.

نظرًا لأن الحد يتكون من جوانب مثلث ، فمن المناسب تقسيم الدراسة إلى 3 فقرات فرعية. لكن من الأفضل ألا تفعل ذلك بأي حال من الأحوال. من وجهة نظري ، من الأفضل التفكير أولاً في الشرائح الموازية تنسيق المحاور، وقبل كل شيء ، أولئك الذين يرقدون على المحاور أنفسهم. لفهم تسلسل الإجراءات ومنطقها بالكامل ، حاول دراسة النهاية "في نفس واحد":

1) دعونا نتعامل مع الجانب السفلي من المثلث. للقيام بذلك ، نعوض مباشرة في الدالة:

بدلاً من ذلك ، يمكنك القيام بذلك على النحو التالي:

هندسيًا ، هذا يعني أن المستوى الإحداثي (والتي يتم تقديمها أيضًا بواسطة المعادلة)"قطع" من الأسطحالقطع المكافئ "المكاني" ، الذي يقع الجزء العلوي منه تحت الشك على الفور. هيا نكتشف أين هي:

- القيمة الناتجة "ضرب" في المنطقة ، وقد تكون كذلك عند هذه النقطة (علامة على الرسم)تصل الدالة إلى أكبر أو أصغر قيمة في المنطقة بأكملها. على أي حال ، لنقم بالحسابات:

"المرشحون" الآخرون هم بالطبع أطراف هذا المقطع. احسب قيم الدالة عند النقاط (علامة على الرسم):

هنا ، بالمناسبة ، يمكنك إجراء فحص شفهي قصير على الإصدار "المُجرد":

2) لدراسة الجانب الأيمن من المثلث ، نقوم باستبداله في الدالة و "رتب الأشياء هناك":

هنا نقوم على الفور بإجراء فحص تقريبي ، "رنين" نهاية المقطع المعالجة بالفعل:
، في احسن الاحوال.

يرتبط الوضع الهندسي بالنقطة السابقة:

- القيمة الناتجة أيضًا "دخلت في نطاق اهتماماتنا" ، مما يعني أننا بحاجة إلى حساب ما تساوي الوظيفة عند النقطة التي ظهرت:

دعنا نفحص الطرف الثاني من المقطع:

استخدام الوظيفة ، دعونا تحقق:

3) ربما يعرف الجميع كيفية استكشاف الجانب المتبقي. نستبدل الدالة وننفذ التبسيط:

ينتهي الخط تم التحقيق بالفعل ، ولكن في المسودة ما زلنا نتحقق مما إذا وجدنا الوظيفة بشكل صحيح :
- تزامن مع نتيجة الفقرة الفرعية الأولى ؛
- تصادف مع نتيجة الفقرة الفرعية الثانية.

يبقى معرفة ما إذا كان هناك شيء مثير للاهتمام داخل المقطع:

- هناك! بالتعويض عن خط مستقيم في المعادلة ، نحصل على إحداثيات هذه "الاهتمام":

نحدد نقطة على الرسم ونجد القيمة المقابلة للوظيفة:

دعونا نتحكم في الحسابات وفقا لنسخة "الميزانية" :
، طلب.

والخطوة الأخيرة: انظر بعناية في جميع الأرقام "السمين" ، أوصي حتى للمبتدئين بعمل قائمة واحدة:

التي نختار منها أكبر وأصغر القيم. إجابهاكتب في اسلوب مشكلة البحث أكبر وأصغر قيم للدالة في المقطع:

سأعلق مرة أخرى فقط في حالة. المعنى الهندسينتيجة:
- هنا أعلى نقطة على السطح في المنطقة ؛
- هنا أدنى نقطة على السطح في المنطقة.

في المشكلة التي تم تحليلها ، وجدنا 7 نقاط "مشبوهة" ، لكن عددها يختلف من مهمة إلى أخرى. بالنسبة للمنطقة المثلثة ، يتكون الحد الأدنى من "مجموعة الاستكشاف" من ثلاث نقاط. يحدث هذا عندما يتم تعيين الوظيفة ، على سبيل المثال طائرة- من الواضح تمامًا أنه لا توجد نقاط ثابتة ، ويمكن أن تصل الوظيفة إلى القيم القصوى / الدنيا فقط عند رؤوس المثلث. لكن لا توجد مثل هذه الأمثلة مرة أو مرتين - عادة ما يتعين عليك التعامل مع نوع ما سطح الترتيب الثاني.

إذا قمت بحل مثل هذه المهام قليلاً ، فيمكن للمثلثات أن تجعل رأسك يدور ، وبالتالي فقد أعددت لك أمثلة غير عاديةلجعلها مربعة :)

مثال 2

أوجد أكبر وأصغر قيم للدالة في منطقة مغلقة تحدها خطوط

مثال 3

أوجد أكبر وأصغر قيم للدالة في منطقة مغلقة محدودة.

انتباه خاصانتبه إلى الترتيب المنطقي وتقنية دراسة حدود المنطقة ، بالإضافة إلى سلسلة الفحوصات الوسيطة ، والتي ستتجنب الأخطاء الحسابية تمامًا تقريبًا. بشكل عام ، يمكنك حلها كما تريد ، ولكن في بعض المشاكل ، على سبيل المثال ، في نفس المثال 2 ، هناك كل فرصة لتعقيد حياتك بشكل كبير. عينة عينةإنهاء الواجبات في نهاية الدرس.

نقوم بتنظيم خوارزمية الحل ، وإلا ، مع اجتهادي عنكبوت ، ضاعت بطريقة ما في سلسلة طويلة من التعليقات للمثال الأول:

- في الخطوة الأولى نبني مساحة ، من المستحسن تظليلها وإبراز الحدود بخط سميك. أثناء الحل ، ستظهر النقاط التي يجب وضعها على الرسم.

- البحث عن نقاط ثابتة وحساب قيم الوظيفة فقط في هؤلاءالتي تنتمي إلى المنطقة. يتم تمييز القيم التي تم الحصول عليها في النص (على سبيل المثال ، محاطة بدائرة بقلم رصاص). إذا كانت النقطة الثابتة لا تنتمي إلى المنطقة ، فإننا نضع علامة على هذه الحقيقة برمز أو لفظيًا. إذا لم تكن هناك نقاط ثابتة على الإطلاق ، فإننا نخلص إلى نتيجة مكتوبة مفادها أنها غائبة. على أي حال ، لا يمكن تخطي هذا العنصر!

- استكشاف المنطقة الحدودية. أولاً ، من المفيد التعامل مع الخطوط المستقيمة الموازية لمحاور الإحداثيات (إن وجد). يتم أيضًا تمييز قيم الوظيفة المحسوبة عند النقاط "المشبوهة". لقد قيل الكثير عن تقنية الحل أعلاه وسيتم ذكر شيء آخر أدناه - اقرأ ، وأعد قراءته ، وتعمق فيه!

- من الأرقام المحددة ، حدد أكبر وأصغر القيم وأعطي إجابة. يحدث أحيانًا أن تصل الوظيفة إلى هذه القيم في عدة نقاط في وقت واحد - في هذه الحالة ، يجب أن تنعكس كل هذه النقاط في الإجابة. دعونا ، على سبيل المثال ، واتضح أن أصغر قيمة. ثم نكتب ذلك

الأمثلة النهائية مخصصة للآخرين أفكار مفيدةمفيد في الممارسة:

مثال 4

أوجد أكبر وأصغر قيم للدالة في منطقة مغلقة .

لقد احتفظت بصيغة المؤلف ، حيث يتم إعطاء المنطقة على أنها عدم مساواة مزدوجة. يمكن كتابة هذا الشرط في نظام مكافئ أو بشكل أكثر تقليدية لهذه المشكلة:

أذكرك ذلك مع غير خطيواجهنا عدم المساواة في ، وإذا كنت لا تفهم المعنى الهندسي للإدخال ، فيرجى عدم التأخير وتوضيح الموقف الآن ؛-)

قرار، كالعادة ، يبدأ ببناء المنطقة ، وهو نوع من "النعل":

حسنًا ، عليك أحيانًا أن تقضم ليس فقط جرانيت العلم ....

ط) البحث عن نقاط ثابتة:

نظام أحلام الأبله :)

النقطة الثابتة تنتمي إلى المنطقة ، أي تقع على حدودها.

وهكذا ، لا شيء ... ذهب الدرس الممتع - هذا ما يعنيه شرب الشاي المناسب =)

ب) نحقق في حدود المنطقة. بدون مزيد من اللغط ، لنبدأ بالمحور السيني:

1) إذا ، إذن

اكتشف مكان قمة القطع المكافئ:
- قدر مثل هذه اللحظات - "اضغط" مباشرة إلى النقطة التي من خلالها أصبح كل شيء واضحًا بالفعل. لكن لا تنس التحقق من:

دعنا نحسب قيم الوظيفة في نهايات المقطع:

2) ج الأسفلدعنا نكتشف "النعال" "في جلسة واحدة" - بدون أي معقدات نقوم باستبدالها في الوظيفة ، علاوة على ذلك ، سنكون مهتمين فقط بالقسم:

السيطرة:

الآن هذا يجلب بالفعل بعض الإحياء إلى الركوب الرتيب على مسار مخرش. لنجد النقاط الحرجة:

نحن نقرر معادلة من الدرجة الثانيةهل تذكر هذا؟ ... ومع ذلك ، تذكر ، بالطبع ، وإلا فلن تقرأ هذه السطور =) إذا كانت الحسابات في المثالين السابقين مريحة في الكسور العشرية(وهو أمر نادر بالمناسبة) ، فنحن ننتظر ما هو معتاد الكسور المشتركة. نجد الجذور "x" وباستخدام المعادلة ، نحدد إحداثيات "اللعبة" المقابلة للنقاط "المرشحة":


دعنا نحسب قيم الوظيفة عند النقاط الموجودة:

تحقق من الوظيفة بنفسك.

الآن ندرس بعناية الجوائز التي تم ربحها ونكتبها إجابه:

ها هم "المرشحون" ، لذا فإن "المرشحين"!

لحل مستقل:

مثال 5

أوجد أصغر وأكبر قيم للدالة في منطقة مغلقة

يُقرأ الإدخال الذي يحتوي على أقواس معقوفة على النحو التالي: "مجموعة من النقاط من هذا القبيل".

في بعض الأحيان يستخدمون في مثل هذه الأمثلة طريقة لاغرانج المضاعف، لكن حاجة حقيقيةمن غير المحتمل أن يتم استخدامها. لذلك ، على سبيل المثال ، إذا تم إعطاء دالة بنفس المنطقة "de" ، فبعد الاستبدال بها - بمشتق لا توجد صعوبات ؛ علاوة على ذلك ، يتم رسم كل شيء في "سطر واحد" (بعلامات) دون الحاجة إلى النظر في أنصاف الدائرة العلوية والسفلية بشكل منفصل. لكن ، بالطبع ، هناك المزيد الحالات الصعبة، حيث بدون وظيفة لاغرانج (حيث ، على سبيل المثال ، نفس معادلة الدائرة)من الصعب أن تتدبر أمرها - ما مدى صعوبة تدبر الأمر دون راحة جيدة!

كل التوفيق لاجتياز الدورة ونراكم قريبا الموسم المقبل!

الحلول والأجوبة:

المثال 2: قرار: ارسم المنطقة على الرسم:

أحيانًا في المسائل B15 توجد وظائف "سيئة" يصعب العثور على مشتقاتها. في السابق ، كان هذا يقتصر على المسابير فقط ، ولكن الآن أصبحت هذه المهام شائعة جدًا لدرجة أنه لم يعد من الممكن تجاهلها عند التحضير لهذا الاختبار.

في هذه الحالة ، تعمل الحيل الأخرى ، إحداها - روتيني.

تسمى الوظيفة f (x) زيادة رتيبة على المقطع إذا كان ما يلي صحيحًا لأي نقطة x 1 و x 2 من هذا المقطع:

× 1< x 2 ⇒ f (× 1) < f (x2).

تسمى الوظيفة f (x) متناقصة بشكل رتيب على المقطع إذا كان ما يلي صحيحًا لأي نقطتين x 1 و x 2 من هذا المقطع:

× 1< x 2 ⇒ f (× 1)> و ( x2).

بعبارة أخرى ، بالنسبة للدالة المتزايدة ، كلما كان x أكبر ، كلما كان f (x) أكبر. بالنسبة للدالة المتناقصة ، يكون العكس هو الصحيح: كلما زاد عدد x ، كلما زاد حجم الأصغرو (خ).

على سبيل المثال ، يزيد اللوغاريتم بشكل رتيب إذا كانت القاعدة a> 1 وتنخفض بشكل رتيب إذا كانت 0< a < 1. Не забывайте про область القيم المسموح بهااللوغاريتم: x> 0.

و (س) = السجل أ س (أ> 0 ؛ أ ≠ 1 ؛ س> 0)

يزيد الجذر التربيعي الحسابي (وليس فقط التربيعي) بشكل رتيب على نطاق التعريف بالكامل:

تتصرف الدالة الأسية بشكل مشابه للوغاريتم: فهي تزيد لـ a> 1 وتنقص لـ 0< a < 1. Но в отличие от логарифма, دالة أسيةمُعرَّف لجميع الأرقام ، وليس فقط x> 0:

و (س) = أ س (أ> 0)

أخيرًا ، الدرجات ذات الأس السالب. يمكنك كتابتها على شكل كسر. لديهم نقطة انقطاع حيث يتم كسر الرتابة.

لم يتم العثور على كل هذه الميزات في شكل نقي. تتم إضافة كثيرات الحدود والكسور وغير ذلك من الهراء إليها ، مما يجعل من الصعب حساب المشتق. ماذا يحدث في هذه الحالة - الآن سنحلل.

إحداثيات رأس القطع المكافئ

في أغلب الأحيان ، يتم استبدال وسيطة الوظيفة بـ ثلاثي الحدود مربعمن الشكل y = ax 2 + bx + c. الرسم البياني الخاص به عبارة عن قطع مكافئ قياسي ، ونحن مهتمون به:

1. فروع القطع المكافئ - يمكن أن ترتفع (لـ> 0) أو لأسفل (أ< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. رأس القطع المكافئ هو النقطة القصوى للدالة التربيعية ، حيث تأخذ هذه الوظيفة أصغرها (ل> 0) أو أكبرها (أ< 0) значение.

الأكثر أهمية قمة القطع المكافئ، يتم حساب الحد الفاصل بواسطة الصيغة:

إذن ، وجدنا النقطة القصوى للدالة التربيعية. ولكن إذا كانت الوظيفة الأصلية رتيبة ، فإن النقطة x 0 ستكون أيضًا نقطة نهائية. وبالتالي ، فإننا نصوغ القاعدة الأساسية:

النقاط القصوى ثلاثي الحدود مربعو وظيفة معقدةالتي تدخل فيها هي نفسها. لذلك ، يمكنك البحث عن x 0 لمربع ثلاثي الحدود ، وتجاهل الدالة.

من المنطق أعلاه ، لا يزال من غير الواضح نوع النقطة التي نحصل عليها: الحد الأقصى أو الحد الأدنى. ومع ذلك ، تم تصميم المهام على وجه التحديد بحيث لا يهم. أحكم لنفسك:

1. لا يوجد جزء في حالة المشكلة. لذلك ، ليس مطلوبًا حساب f (a) و f (b). يبقى فقط النظر في النقاط القصوى ؛
2. ولكن لا توجد سوى نقطة واحدة من هذا القبيل - هذه هي قمة القطع المكافئ × 0 ، ويتم حساب إحداثياتها شفهيًا وبدون أي مشتقات.

وبالتالي ، يتم تبسيط حل المشكلة إلى حد كبير وتقليله إلى خطوتين فقط:

1. اكتب معادلة القطع المكافئ y = ax 2 + bx + c وابحث عن رأسه باستخدام الصيغة: x 0 = −b / 2a؛
2. أوجد قيمة الوظيفة الأصلية في هذه المرحلة: f (x 0). إذا لم تكن هناك شروط إضافية ، فسيكون هذا هو الحل.

للوهلة الأولى ، قد تبدو هذه الخوارزمية ومبرراتها معقدة. لا أنشر عمداً مخطط حل "مكشوف" ، لأن التطبيق غير المدروس لمثل هذه القواعد محفوف بالأخطاء.

دعونا ننظر في المشاكل الحقيقية من امتحان تجريبيفي الرياضيات - هذا هو المكان الذي تحدث فيه هذه التقنية في أغلب الأحيان. في الوقت نفسه ، سوف نتأكد من أنه بهذه الطريقة تصبح العديد من مشاكل B15 شفهية تقريبًا.

تحت الجذر وظيفة من الدرجة الثانية y \ u003d x 2 + 6x + 13. الرسم البياني لهذه الوظيفة عبارة عن قطع مكافئ بفروع لأعلى ، نظرًا لأن المعامل a \ u003d 1 \ u003e 0.

قمة القطع المكافئ:

× 0 \ u003d -b / (2a) \ u003d -6 / (2 1) \ u003d -6 / 2 \ u003d -3

نظرًا لأن فروع القطع المكافئ موجهة لأعلى ، عند النقطة x 0 \ u003d −3 ، تأخذ الوظيفة y \ u003d x 2 + 6x + 13 أصغر قيمة.

يتزايد الجذر بشكل رتيب ، لذا فإن x 0 هي النقطة الدنيا للدالة بأكملها. نملك:

مهمة. ابحث عن أصغر قيمة للدالة:

ص = سجل 2 (س 2 + 2 س + 9)

تحت اللوغاريتم مرة أخرى دالة تربيعية: y \ u003d x 2 + 2x + 9. الرسم البياني عبارة عن قطع مكافئ مع فروع لأعلى ، لأن أ = 1> 0.

قمة القطع المكافئ:

× 0 \ u003d -b / (2a) \ u003d -2 / (2 1) \ u003d -2/2 \ u003d -1

لذلك ، عند النقطة x 0 = −1 ، تأخذ الدالة التربيعية أصغر قيمة. لكن الوظيفة y = log 2 x رتيبة ، لذلك:

y min = y (−1) = log 2 ((1) 2 + 2 (−1) + 9) = ... = log 2 8 = 3

الأس هو دالة تربيعية y = 1 - 4x - x 2. دعونا نعيد كتابته بالصيغة العادية: y = −x 2 - 4x + 1.

من الواضح أن الرسم البياني لهذه الوظيفة هو قطع مكافئ ، يتفرع لأسفل (أ = -1< 0). Поэтому вершина будет точкой максимума:

س 0 = −b / (2a) = - (- 4) / (2 (−1)) = 4 / (- 2) = −2

الوظيفة الأصلية أسية ، إنها رتيبة ، لذا أعلى قيمةستكون عند النقطة التي تم العثور عليها × 0 = −2:

سيلاحظ القارئ اليقظ بالتأكيد أننا لم نكتب منطقة القيم المسموح بها للجذر واللوغاريتم. لكن هذا لم يكن مطلوبًا: يوجد بالداخل وظائف تكون قيمها دائمًا موجبة.

النتائج من نطاق الوظيفة

في بعض الأحيان ، لحل المسألة B15 ، لا يكفي مجرد إيجاد رأس القطع المكافئ. قد تكمن القيمة المطلوبة في نهاية المقطع، ولكن ليس في أقصى نقطة. إذا لم تحدد المهمة مقطعًا على الإطلاق ، فراجع مجموعة التسامحالوظيفة الأصلية. يسمى:

انتبه مرة أخرى: قد يكون الصفر تحت الجذر ، ولكن ليس في لوغاريتم أو مقام كسر. دعونا نرى كيف يعمل مع أمثلة محددة:

مهمة. أوجد أكبر قيمة للدالة:

تحت الجذر مرة أخرى وظيفة تربيعية: y \ u003d 3 - 2x - x 2. التمثيل البياني الخاص به عبارة عن قطع مكافئ ، لكنه يتفرع إلى الأسفل حيث أن a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический الجذر التربيعيمن رقم سالب غير موجود.

نكتب منطقة القيم المسموح بها (ODZ):

3 - 2x - x 2 ≥ 0 ⇒ x 2 + 2x - 3 ≤ 0 ⇒ (x + 3) (x - 1) ≤ 0 ⇒ x ∈ [−3 ؛ واحد]

الآن ابحث عن رأس القطع المكافئ:

س 0 = b / (2a) = - (- 2) / (2 (−1)) = 2 / (- 2) = 1

النقطة x 0 = −1 تنتمي إلى مقطع ODZ - وهذا جيد. الآن نعتبر قيمة الوظيفة عند النقطة x 0 ، وكذلك في نهايات ODZ:

ص (−3) = ص (1) = 0

إذن ، حصلنا على العددين 2 و 0. مطلوب منا إيجاد أكبرهما - هذا هو الرقم 2.

مهمة. ابحث عن أصغر قيمة للدالة:

ص = تسجيل 0.5 (6 س - س 2-5)

يوجد داخل اللوغاريتم دالة تربيعية y = 6x - x 2 - 5. هذا قطع مكافئ بفروع لأسفل ، لكن في اللوغاريتم لا يمكن أن يكون أرقام سالبة، لذلك نكتب ODZ:

6x - x 2-5> 0 x 2-6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

يرجى ملاحظة: عدم المساواة صارم ، وبالتالي فإن النهايات لا تنتمي إلى ODZ. بهذه الطريقة ، يختلف اللوغاريتم عن الجذر ، حيث تناسبنا نهايات المقطع تمامًا.

البحث عن قمة القطع المكافئ:

س 0 = b / (2a) = −6 / (2 (−1)) = −6 / (- 2) = 3

الجزء العلوي من القطع المكافئ يناسب طول ODZ: x 0 = 3 ∈ (1 ؛ 5). ولكن نظرًا لأن نهايات المقطع لا تهمنا ، فإننا نعتبر قيمة الوظيفة فقط عند النقطة × 0:

y min = y (3) = log 0.5 (6 3 - 3 2-5) = log 0.5 (18-9-5) = log 0.5 4 = −2

مع نقطة عمليةالأكثر أهمية هو استخدام المشتق لإيجاد أكبر وأصغر قيمة للدالة. بماذا ترتبط؟ تعظيم الأرباح ، وتقليل التكاليف ، وتحديد الحمل الأمثل للمعدات ... بمعنى آخر ، في العديد من مجالات الحياة ، يتعين على المرء حل مشكلة تحسين بعض المعلمات. وهذه هي مشكلة إيجاد أكبر وأصغر قيم للدالة.

وتجدر الإشارة إلى أن أكبر وأصغر قيمة لوظيفة ما يتم البحث عنها عادة في بعض الفترات X ، والتي تكون إما المجال الكامل للوظيفة أو جزء من المجال. يمكن أن يكون الفاصل الزمني X نفسه مقطعًا خطيًا ، أي فاصل زمني مفتوح ، فاصل زمني لانهائي.

في هذا المقال سنتحدث عن إيجاد القيم الأكبر والأصغر صراحة. وظيفة معينةمتغير واحد y = f (x).

التنقل في الصفحة.

أكبر وأصغر قيمة للدالة - التعريفات ، الرسوم التوضيحية.

دعونا نتناول بإيجاز التعاريف الرئيسية.

أكبر قيمة للدالة ، أي عدم المساواة هو الصحيح.

أصغر قيمة للدالة y = f (x) في الفترة الزمنية X تسمى هذه القيمة ، أي عدم المساواة هو الصحيح.

هذه التعريفات بديهية: القيمة الأكبر (الأصغر) للدالة هي أكبر (أصغر) قيمة مقبولة في الفترة قيد النظر مع الإحداثي السيني.

نقاط ثابتةهي قيم الحجة التي يختفي عندها مشتق الوظيفة.

لماذا نحتاج إلى نقاط ثابتة عند إيجاد أكبر وأصغر القيم؟ الإجابة على هذا السؤال مقدمة من نظرية فيرما. ويترتب على هذه النظرية أنه إذا كان للدالة القابلة للتفاضل حد أقصى (الحد الأدنى المحلي أو الحد الأقصى المحلي) عند نقطة ما ، فإن هذه النقطة تكون ثابتة. وبالتالي ، غالبًا ما تأخذ الوظيفة الحد الأقصى (الأصغر) لقيمتها على الفاصل الزمني X عند إحدى النقاط الثابتة من هذا الفاصل الزمني.

أيضًا ، يمكن أن تأخذ الوظيفة في كثير من الأحيان أكبر وأصغر القيم عند النقاط التي لا يوجد فيها المشتق الأول لهذه الوظيفة ، ويتم تعريف الوظيفة نفسها.

دعنا نجيب على الفور على أحد الأسئلة الأكثر شيوعًا حول هذا الموضوع: "هل من الممكن دائمًا تحديد أكبر (أصغر) قيمة للدالة"؟ لا، ليس دائما. في بعض الأحيان ، تتطابق حدود الفاصل الزمني X مع حدود مجال الوظيفة ، أو يكون الفاصل X غير محدود. ويمكن لبعض الدوال في اللانهاية وعلى حدود مجال التعريف أن تأخذ قيمًا كبيرة بلا حدود وقيم صغيرة بلا حدود. في هذه الحالات ، لا يمكن قول أي شيء عن أكبر وأصغر قيمة للدالة.

من أجل الوضوح ، نقدم توضيحًا بيانيًا. انظر إلى الصور - وسيتضح الكثير.

في الجزء

في الشكل الأول ، تأخذ الدالة أكبر قيم (max y) وأصغر (min y) عند نقاط ثابتة داخل المقطع [-6 ؛ 6].

تأمل الحالة الموضحة في الشكل الثاني. قم بتغيير المقطع إلى. في هذا المثال ، يتم تحقيق أصغر قيمة للدالة عند نقطة ثابتة ، والأكبر - عند نقطة مع إحداثية تتطابق مع الحد الأيمن للفاصل الزمني.

في الشكل رقم 3 ، النقاط الحدودية للقطاع [-3 ؛ 2] هي حدود النقاط المقابلة لأكبر وأصغر قيمة للدالة.

في النطاق المفتوح

في الشكل الرابع ، تأخذ الدالة أكبر قيم (max y) وأصغر (min y) عند نقاط ثابتة ضمن الفاصل الزمني المفتوح (-6 ؛ 6).

في الفاصل الزمني ، لا يمكن استخلاص استنتاجات حول القيمة الأكبر.

في اللانهاية

في المثال الموضح في الشكل السابع ، تأخذ الوظيفة أكبر قيمة (max y) عند نقطة ثابتة مع الإحداثي x = 1 ، ويتم الوصول إلى أصغر قيمة (min y) عند الحد الأيمن للفاصل الزمني. عند سالب اللانهاية ، تقترب قيم الدالة بشكل مقارب من y = 3.

في الفاصل الزمني ، لا تصل الوظيفة إلى القيمة الأصغر أو الأكبر. نظرًا لأن x = 2 تميل إلى اليمين ، فإن قيم الدالة تميل إلى سالب ما لا نهاية (الخط المستقيم x = 2 خط مقارب عمودي) ، وبما أن الحد الفاصل يميل إلى زائد اللانهاية ، فإن قيم الدالة تقترب من y = 3 . يظهر الرسم التوضيحي لهذا المثال في الشكل 8.

خوارزمية لإيجاد أكبر وأصغر قيم للدالة المستمرة في المقطع.

نكتب خوارزمية تسمح لنا بالعثور على أكبر وأصغر قيمة لدالة في مقطع ما.

1. نجد مجال الوظيفة ونتحقق مما إذا كانت تحتوي على المقطع بأكمله.
2. نجد جميع النقاط التي لا يوجد عندها المشتق الأول والمضمنة في المقطع (عادةً ما تحدث هذه النقاط في وظائف ذات وسيطة تحت علامة الوحدة النمطية وفي وظائف الطاقةمع الأس المنطقي الكسري). إذا لم تكن هناك مثل هذه النقاط ، فانتقل إلى النقطة التالية.
3. نحدد جميع النقاط الثابتة التي تقع في المقطع. للقيام بذلك ، نساويها بالصفر ، ونحل المعادلة الناتجة ونختار الجذور المناسبة. إذا لم تكن هناك نقاط ثابتة أو لم يقع أي منها في المقطع ، فانتقل إلى الخطوة التالية.
4. نحسب قيم الوظيفة عند النقاط الثابتة المحددة (إن وجدت) ، عند النقاط التي لا يوجد فيها المشتق الأول (إن وجد) ، وأيضًا عند x = a و x = b.
5. من القيم التي تم الحصول عليها للوظيفة ، نختار الأكبر والأصغر - ستكون القيم القصوى والأصغر المرغوبة للوظيفة ، على التوالي.

دعنا نحلل الخوارزمية عند حل مثال للعثور على أكبر وأصغر قيم لدالة في مقطع ما.

مثال.

أوجد أكبر وأصغر قيمة للدالة

• في الجزء
• على الفاصل الزمني [-4 ؛ -1].

قرار.

مجال الوظيفة هو مجموعة الأعداد الحقيقية بأكملها ، باستثناء الصفر ، أي. كلا الجزأين يقعان ضمن مجال التعريف.

نجد مشتق الوظيفة فيما يتعلق:

من الواضح أن مشتق الوظيفة موجود في جميع نقاط المقاطع و [-4 ؛ -1].

يتم تحديد النقاط الثابتة من المعادلة. الجذر الحقيقي الوحيد هو x = 2. تقع هذه النقطة الثابتة في الجزء الأول.

بالنسبة للحالة الأولى ، نحسب قيم الوظيفة في نهايات المقطع وعند نقطة ثابتة ، أي بالنسبة إلى x = 1 و x = 2 و x = 4:

لذلك ، أكبر قيمة للدالة يتم الوصول إليها عند x = 1 ، وأصغر قيمة - عند x = 2.

بالنسبة للحالة الثانية ، نحسب قيم الوظيفة فقط في نهايات المقطع [-4 ؛ -1] (لأنها لا تحتوي على نقطة ثابتة واحدة):

إعطاء دالة معرّفة ومستمرة في بعض الفترات. مطلوب العثور على أكبر (أصغر) قيمة للدالة في هذا الفاصل الزمني.

اساس نظرى.
نظرية (الثانية Weierstrass Theorem):

إذا تم تعريف دالة واستمرارها في فترة زمنية مغلقة ، فإنها تصل إلى قيمها القصوى والدنيا في هذا الفاصل الزمني.

يمكن أن تصل الوظيفة إلى قيمها القصوى والدنيا إما عند النقاط الداخلية للفاصل الزمني أو عند حدودها. دعونا نوضح كل شيء الخيارات الممكنة.

تفسير:
1) تصل الوظيفة إلى قيمتها القصوى على الحد الأيسر للفاصل الزمني عند النقطة ، وقيمتها الدنيا على الحد الأيمن للفاصل الزمني عند النقطة.
2) تصل الوظيفة إلى أقصى قيمتها عند النقطة (هذه هي النقطة القصوى) ، وقيمتها الدنيا عند الحد الأيمن للفاصل الزمني عند النقطة.
3) تصل الوظيفة إلى أقصى قيمتها على الحد الأيسر للفاصل الزمني عند النقطة ، وقيمتها الدنيا عند النقطة (هذه هي النقطة الدنيا).
4) الوظيفة ثابتة في الفترة الزمنية ، أي تصل إلى قيمها الدنيا والقصوى في أي نقطة في الفاصل الزمني ، والقيم الدنيا والقصوى متساوية مع بعضها البعض.
5) تصل الوظيفة إلى أقصى قيمتها عند النقطة ، وقيمتها الدنيا عند النقطة (على الرغم من حقيقة أن الوظيفة لها حد أقصى وأدنى في هذه الفترة).
6) تصل الوظيفة إلى أقصى قيمتها عند نقطة (هذه هي النقطة القصوى) ، وقيمتها الدنيا عند نقطة ما (هذه هي النقطة الدنيا).
تعليق:

"الحد الأقصى" و "القيمة القصوى" شيئان مختلفان. يأتي هذا من تعريف الحد الأقصى والفهم البديهي لعبارة "القيمة القصوى".

خوارزمية لحل المشكلة 2.



4) اختر من بين القيم التي تم الحصول عليها الأكبر (الأصغر) واكتب الإجابة.

المثال 4:

حدد أكبر وأصغر قيمة للدالة في الجزء.
قرار:
1) أوجد مشتق التابع.

2) ابحث عن النقاط الثابتة (والنقاط المشكوك فيها بحد أقصى) عن طريق حل المعادلة. انتبه إلى النقاط التي لا يوجد فيها مشتق محدود ذو وجهين.

3) احسب قيم الوظيفة عند نقاط ثابتة وعند حدود الفاصل الزمني.

4) اختر من بين القيم التي تم الحصول عليها الأكبر (الأصغر) واكتب الإجابة.

تصل الوظيفة في هذا المقطع إلى قيمتها القصوى عند النقطة ذات الإحداثيات.

تصل الوظيفة في هذا المقطع إلى قيمتها الدنيا عند النقطة ذات الإحداثيات.

يمكنك التحقق من صحة الحسابات من خلال النظر إلى الرسم البياني للوظيفة قيد الدراسة.


تعليق:تصل الوظيفة إلى قيمتها القصوى عند النقطة القصوى ، والحد الأدنى للقيمة عند حدود المقطع.

حالة خاصة.

افترض أننا نريد إيجاد الحد الأقصى و الحد الأدنى للقيمةبعض الوظائف في الفترة. بعد تنفيذ الفقرة الأولى من الخوارزمية ، أي عند حساب المشتق ، يصبح من الواضح ، على سبيل المثال ، أنه يأخذ فقط قيمًا سالبة على المقطع بأكمله قيد الدراسة. تذكر أنه إذا كانت المشتقة سالبة ، فإن الدالة تتناقص. وجدنا أن الدالة تتناقص في الفترة بأكملها. يظهر هذا الوضع في الرسم البياني رقم 1 في بداية المقال.

تقل الوظيفة في الفترة الزمنية ، أي ليس لديها نقاط متطرفة. يمكن أن نرى من الصورة أن الوظيفة ستأخذ أصغر قيمة على الحد الأيمن من المقطع ، وأكبر قيمة على اليسار. إذا كان المشتق في الفترة موجبًا في كل مكان ، فإن الدالة تتزايد. تكون القيمة الأصغر على الحد الأيسر من المقطع ، وتكون القيمة الأكبر على الجانب الأيمن.

في هذا المقال سوف أتحدث عنه خوارزمية لإيجاد أكبر وأصغر قيمةالوظيفة ، الحد الأدنى والحد الأقصى من النقاط.

من الناحية النظرية ، سنحتاج بالتأكيد جدول مشتقو قواعد التمايز. كل شيء في هذا المنتدى:

خوارزمية لإيجاد أكبر وأصغر القيم.

أجد أنه من الأسهل أن أشرح مثال محدد. يعتبر:

مثال:أوجد أكبر قيمة للدالة y = x ^ 5 + 20x ^ 3–65x في المقطع [–4 ؛ 0].

الخطوة 1.نأخذ المشتق.

ص "= (x ^ 5 + 20x ^ 3–65x)" = 5x ^ 4 + 20 * 3x ^ 2 - 65 = 5x ^ 4 + 60x ^ 2 - 65

الخطوة 2إيجاد النقاط القصوى.

النقطة القصوىنقوم بتسمية النقاط التي تصل عندها الوظيفة إلى الحد الأقصى أو الحد الأدنى لقيمتها.

للعثور على النقاط القصوى ، من الضروري مساواة مشتق الدالة بالصفر (y "= 0)

5x ^ 4 + 60x ^ 2-65 = 0

الآن دعونا نحل هذا معادلة من الدرجة الثانيةوالجذور التي تم العثور عليها هي نقاطنا القصوى.

لقد قمت بحل هذه المعادلات عن طريق استبدال t = x ^ 2 ، ثم 5t ^ 2 + 60t - 65 = 0.

قلل المعادلة بمقدار 5 ، نحصل على: t ^ 2 + 12t - 13 = 0

د = 12 ^ 2 - 4 * 1 * (- 13) = 196

T_ (1) = (-12 + sqrt (196)) / 2 = (-12 + 14) / 2 = 1

T_ (2) = (-12 - الجذر التربيعي (196)) / 2 = (-12-14) / 2 = -13

نجري الاستبدال العكسي x ^ 2 = t:

X_ (1 و 2) = ± sqrt (1) = ± 1
x_ (3 و 4) = ± sqrt (-13) (نستبعد ، لا يمكن أن يكون هناك أرقام سالبة تحت الجذر ، ما لم نتحدث بالطبع عن أرقام مركبة)

المجموع: x_ (1) = 1 و x_ (2) = -1 - هذه هي نقاطنا القصوى.

الخطوه 3حدد أكبر وأصغر قيمة.

طريقة الاستبدال.

في الحالة ، حصلنا على المقطع [ب] [- 4 ؛ 0]. لم يتم تضمين النقطة x = 1 في هذا المقطع. لذلك نحن لا نعتبرها. لكن بالإضافة إلى النقطة x = -1 ، نحتاج أيضًا إلى النظر في الحدود اليمنى واليسرى للقطاع ، أي النقطتين -4 و 0. للقيام بذلك ، نعوض بكل هذه النقاط الثلاث في الدالة الأصلية. لاحظ أن الأصل هو المعطى في الشرط (y = x ^ 5 + 20x ^ 3–65x) ، يبدأ البعض بالتعويض في المشتق ...

ص (-1) = (-1) ^ 5 + 20 * (- 1) ^ 3 - 65 * (- 1) = -1 - 20 + 65 = [ب] 44
ص (0) = (0) ^ 5 + 20 * (0) ^ 3-65 * (0) = 0
ص (-4) = (-4) ^ 5 + 20 * (- 4) ^ 3-65 * (- 4) = -1024-1280 + 260 = -2044

هذا يعني أن القيمة القصوى للدالة هي [b] 44 ويتم الوصول إليها عند النقاط [b] -1 ، والتي تسمى النقطة القصوى للدالة في المقطع [-4 ؛ 0].

قررنا وحصلنا على إجابة ، نحن رائعون ، يمكنك الاسترخاء. لكن توقف! ألا تعتقد أن عد ص (-4) معقد جدًا بطريقة ما؟ في ظروف زمنية محدودة يفضل استخدام طريقة أخرى أسميها كالتالي:

من خلال فترات الثبات.

تم العثور على هذه الفجوات لمشتق الدالة ، أي لمعادلتنا البيكوادر.

أفعل ذلك بالطريقة التالية. أرسم خط اتجاه. لقد قمت بتعيين النقاط: -4 ، -1 ، 0 ، 1. على الرغم من حقيقة أن 1 لم يتم تضمينه في المقطع المحدد ، إلا أنه لا يزال يتعين ملاحظته من أجل تحديد فترات الثبات بشكل صحيح. لنأخذ عددًا أكبر من 1 عدة مرات ، دعنا نقول 100 ، استبدلها ذهنيًا في معادلتنا ثنائية التكافؤ 5 (100) ^ 4 + 60 (100) ^ 2 - 65. حتى بدون احتساب أي شيء ، يصبح من الواضح أنه عند النقطة 100 الوظيفة لها علامة زائد. هذا يعني أنه بالنسبة للفترات من 1 إلى 100 ، فإنه يحتوي على علامة زائد. عند المرور من خلال 1 (ننتقل من اليمين إلى اليسار) ، ستتغير الوظيفة إلى علامة ناقص. عند المرور عبر النقطة 0 ، ستحتفظ الوظيفة بعلامتها ، لأن هذه ليست سوى حدود المقطع ، وليس جذر المعادلة. عند المرور عبر -1 ، ستتغير الوظيفة مرة أخرى إلى علامة الجمع.

من الناحية النظرية ، نعلم أن مكان اشتقاق الوظيفة (وقد رسمنا هذا من أجلها) يغير علامة من زائد إلى ناقص (النقطة -1 في حالتنا)تصل الوظيفة الحد الأقصى المحلي (ص (-1) = 44 كما تم حسابه سابقًا)في هذا الجزء (هذا واضح جدًا من الناحية المنطقية ، توقفت الوظيفة عن الزيادة ، حيث وصلت إلى الحد الأقصى وبدأت في الانخفاض).

تبعا لذلك ، حيث يكون مشتق الوظيفة علامة التغييرات من ناقص إلى زائد، حقق الحد الأدنى المحلي للدالة. نعم ، نعم ، وجدنا أيضًا النقطة الدنيا المحلية ، وهي 1 ، و y (1) هي الحد الأدنى لقيمة الوظيفة في الفترة ، دعنا نقول من -1 إلى +. يرجى ملاحظة أن هذا ليس سوى حد أدنى محلي ، أي حد أدنى في جزء معين. نظرًا لأن الحد الأدنى الفعلي (العالمي) للدالة سيصل إلى مكان ما هناك ، في-.

في رأيي ، الطريقة الأولى أبسط من الناحية النظرية ، والطريقة الثانية أبسط من حيث العمليات الحسابية ، ولكنها أكثر صعوبة من الناحية النظرية. بعد كل شيء ، في بعض الأحيان هناك حالات لا تتغير فيها الوظيفة عند المرور بجذر المعادلة ، وفي الواقع يمكنك الخلط بين هذه الحدود القصوى والدنيا المحلية والعالمية ، على الرغم من أنه سيتعين عليك إتقان ذلك جيدًا على أي حال إذا كنت تخطط للدخول إلى جامعة تقنية (ولماذا عليك إجراء امتحان الملف الشخصي وحل هذه المهمة). لكن الممارسة والممارسة فقط ستعلمك كيفية حل هذه المشكلات مرة واحدة وإلى الأبد. ويمكنك التدريب على موقعنا. هنا .

إذا كان لديك أي أسئلة ، أو كان هناك شيء غير واضح ، فتأكد من طرحه. يسعدني الرد عليكم وإجراء التغييرات والإضافات على المقال. تذكر أننا نصنع هذا الموقع معًا!