صيغ ظل التمام لجيب جيب التمام. الجيب وجيب التمام والظل والظل لزاوية حادة. الدوال المثلثية
علم المثلثات هو فرع من فروع الرياضيات يدرس الدوال المثلثية واستخدامها في الهندسة. بدأ تطوير علم المثلثات في ذلك الوقت اليونان القديمة. خلال العصور الوسطى ، قدم علماء من الشرق الأوسط والهند مساهمة مهمة في تطوير هذا العلم.
هذا المقال عن مفاهيم أساسيةوتعريفات علم المثلثات. يناقش تعريفات الدوال المثلثية الرئيسية: الجيب وجيب التمام والظل والظل. يتم شرح وتوضيح معناها في سياق الهندسة.
Yandex.RTB R-A-339285-1
في البداية ، تم التعبير عن تعريفات الدوال المثلثية ، التي تكون حجتها زاوية ، من خلال نسبة أضلاع المثلث القائم.
تعريفات الدوال المثلثية
جيب الزاوية (sin α) هو نسبة الضلع المقابلة لهذه الزاوية على الوتر.
جيب تمام الزاوية (cos α) هو نسبة الضلع المجاورة إلى الوتر.
ظل الزاوية (t g α) هو نسبة الساق المقابلة إلى المجاورة.
ظل التمام للزاوية (ct g α) هو نسبة الساق المجاورة إلى الأخرى.
يتم إعطاء هذه التعاريف ل زاوية حادةمثلث قائم!
دعونا نعطي توضيحا.
في المثلث ABC بالزاوية القائمة C ، جيب الزاوية A يساوي النسبةالضلع BC إلى الوتر AB.
تجعل تعريفات الجيب وجيب التمام والظل والظل من الممكن حساب قيم هذه الوظائف من الأطوال المعروفة لأضلاع المثلث.
من المهم أن تتذكر!
نطاق قيم الجيب وجيب التمام: من -1 إلى 1. بمعنى آخر ، يأخذ الجيب وجيب التمام قيمًا من -1 إلى 1. نطاق قيم الظل وجيب التمام هو خط الأرقام بالكامل ، أي هذه يمكن أن تأخذ الوظائف أي قيمة.
التعريفات الواردة أعلاه تشير إلى الزوايا الحادة. في علم المثلثات ، يتم تقديم مفهوم زاوية الدوران ، والتي لا تقتصر قيمتها ، على عكس الزاوية الحادة ، على إطارات من 0 إلى 90 درجة. يتم التعبير عن زاوية الدوران بالدرجات أو بالراديان بأي رقم حقيقي من - ∞ إلى + ∞.
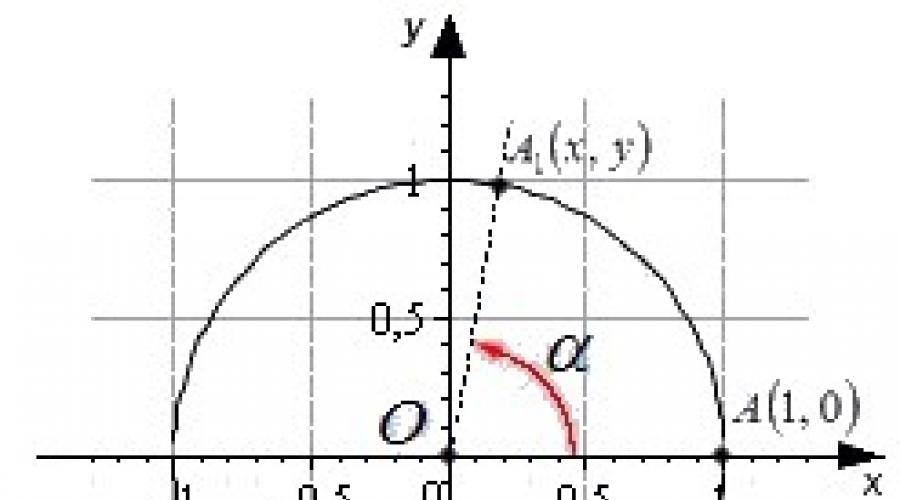
في هذا السياق ، يمكن للمرء تحديد الجيب وجيب التمام والظل والظل لزاوية مقدار تعسفي. تخيل دائرة وحدة متمركزة في أصل نظام الإحداثيات الديكارتية.

نقطة البداية أ ذات الإحداثيات (1 ، 0) تدور حول مركز دائرة الوحدة بزاوية ما α وتنتقل إلى النقطة أ 1. يتم تقديم التعريف من خلال إحداثيات النقطة A 1 (x ، y).
جيب الزاوية لزاوية الدوران
جيب الزاوية α هو إحداثي النقطة A 1 (x، y). sinα = ذ
جيب التمام (كوس) لزاوية الدوران
جيب تمام زاوية الدوران α هو حدود النقطة A 1 (x، y). كوس α = س
الظل (tg) لزاوية الدوران
ظل زاوية الدوران α هو نسبة إحداثي النقطة A 1 (x، y) إلى الحد الفاصل لها. t g α = y x
ظل التمام (ctg) لزاوية الدوران
ظل التمام لزاوية الدوران α هو نسبة الحد الأقصى للنقطة A 1 (س ، ص) إلى إحداثيتها. ج t ز α = س ص
يتم تحديد الجيب وجيب التمام لأي زاوية دوران. هذا أمر منطقي ، لأنه يمكن تحديد إحداثيات النقطة والإحداثيات بعد الدوران بأي زاوية. يختلف الوضع مع الظل والظل. لا يتم تعريف الظل عندما تنتقل النقطة بعد الدوران إلى النقطة التي لا تحتوي على حد أقصى (0 ، 1) و (0 ، - 1). في مثل هذه الحالات ، فإن التعبير عن الظل t g α = y x ببساطة لا معنى له ، لأنه يحتوي على قسمة على صفر. الوضع مشابه مع ظل التمام. الفرق هو أن ظل التمام لم يتم تعريفه في الحالات التي يختفي فيها إحداثيات النقطة.
من المهم أن تتذكر!
يتم تعريف الجيب وجيب التمام لأي زوايا α.
يتم تحديد الظل لجميع الزوايا باستثناء α = 90 ° + 180 ° k، k ∈ Z (α = π 2 + π k، k ∈ Z)
يتم تعريف ظل التمام لجميع الزوايا باستثناء α = 180 ° k، k ∈ Z (α = π k، k ∈ Z)
عند اتخاذ القرار أمثلة عمليةلا تقل "جيب زاوية الدوران α". تم حذف الكلمات "زاوية الدوران" ببساطة ، مما يعني أنه من الواضح بالفعل من السياق ما هو على المحك.
أعداد
ماذا عن تعريف الجيب وجيب التمام والظل والظل لعدد ، وليس زاوية الدوران؟
الجيب وجيب التمام والظل والظل لعدد
الجيب وجيب التمام والظل والظل لعدد ريسمى الرقم ، والذي يساوي على التوالي الجيب وجيب التمام والظل والظل في رراديان.
على سبيل المثال ، جيب 10 π يساوي الجيبزاوية دوران 10 π rad.
هناك نهج آخر لتعريف الجيب وجيب التمام والظل وظل التمام لرقم. دعونا ننظر في الأمر بمزيد من التفصيل.
أي رقم حقيقي ريتم وضع نقطة على دائرة الوحدة بالتوافق مع المركز في أصل نظام الإحداثيات الديكارتية المستطيل. يتم تعريف الجيب وجيب التمام والظل والظل من حيث إحداثيات هذه النقطة.
نقطة البداية على الدائرة هي النقطة أ ذات الإحداثيات (1 ، 0).
رقم موجب، عدد إيجابي ر
عدد السلبي ريتوافق مع النقطة التي ستتحرك إليها نقطة البداية إذا تحركت عكس اتجاه عقارب الساعة على طول الدائرة و سوف يمر الطريقر.
الآن وقد تم إنشاء الاتصال بين الرقم والنقطة على الدائرة ، ننتقل إلى تعريف الجيب وجيب التمام والظل والظل.
الجيب (الخطيئة) للعدد t
جيب رقم ر- إحداثيات نقطة دائرة الوحدة المقابلة للرقم ر. الخطيئة ر = ذ
جيب التمام (كوس) من ر
جيب التمام لعدد ر- حدود نقطة دائرة الوحدة المقابلة للرقم ر. كوس تي = س
الظل (tg) من t
ظل رقم ر- نسبة الإحداثي إلى إحداثيات نقطة دائرة الوحدة المقابلة للرقم ر. t g t = y x = sin t cos t
تتوافق التعريفات الأخيرة مع التعريف الوارد في بداية هذا القسم ولا تتعارض معه. أشر إلى دائرة مقابلة لرقم ر، يتزامن مع النقطة التي تمر إليها نقطة البداية بعد الالتفاف عبر الزاوية رراديان.
الدوال المثلثية للحجة الزاوية والرقمية
تتوافق كل قيمة للزاوية α مع قيمة معينة لجيب وجيب التمام لهذه الزاوية. تمامًا مثل جميع الزوايا α بخلاف α = 90 ° + 180 ° · k ، فإن k ∈ Z (α = π 2 + π · k، k ∈ Z) يتوافق مع قيمة معينة للماس. يتم تعريف ظل التمام ، كما هو مذكور أعلاه ، لجميع α ، باستثناء α = 180 ° k ، k ∈ Z (α = π k ، k ∈ Z).
يمكننا القول أن sin α و cos α و t g α و c t g α هي دوال للزاوية ألفا أو وظائف للوسيطة الزاوية.
وبالمثل ، يمكن للمرء أن يتحدث عن الجيب وجيب التمام والظل والظل كوظائف في حجة عددية. كل رقم حقيقي ريتوافق مع قيمة محددة لجيب أو جيب التمام لرقم ر. جميع الأرقام ما عدا π 2 + π · k ، k ∈ Z ، تتوافق مع قيمة الظل. يتم تعريف ظل التمام بالمثل لجميع الأرقام باستثناء π · k، k ∈ Z.
الوظائف الأساسية لعلم المثلثات
الجيب وجيب التمام والظل والظل هي الدوال المثلثية الأساسية.
من السياق ، يكون من الواضح عادةً أي حجة للدالة المثلثية ( حجة الزاويةأو حجة رقمية) نتعامل معها.
دعنا نعود إلى البيانات في بداية التعريفات والزاوية ألفا ، التي تقع في النطاق من 0 إلى 90 درجة. التعريفات المثلثيةتتوافق تمامًا مع الجيب وجيب التمام والظل والظل التعاريف الهندسية، من خلال نسب أضلاع المثلث القائم الزاوية. دعونا نظهر ذلك.

خذ دائرة وحدة متمركزة على نظام إحداثيات ديكارتي مستطيل. دعنا ندير نقطة البداية أ (1 ، 0) بزاوية تصل إلى 90 درجة ونرسم من النقطة الناتجة أ 1 (س ، ص) عموديًا على المحور س. في المثلث الأيمن الناتج ، تكون الزاوية A 1 O H يساوي الزاويةبدوره α ، طول الساق O H يساوي حدودي النقطة A 1 (x ، y). طول الضلع المقابل للزاوية يساوي إحداثي النقطة A 1 (x، y) ، وطول الوتر يساوي واحدًا ، لأنه نصف قطر دائرة الوحدة.
وفقًا للتعريف الهندسي ، فإن جيب الزاوية α يساوي نسبة الساق المقابلة إلى الوتر.
الخطيئة α \ u003d A 1 H O A 1 \ u003d y 1 \ u003d y
هذا يعني أن تعريف جيب الزاوية الحادة في مثلث قائم الزاوية من خلال نسبة العرض إلى الارتفاع يكافئ تعريف جيب زاوية الدوران α ، مع وجود ألفا في النطاق من 0 إلى 90 درجة.
وبالمثل ، يمكن إظهار تطابق التعاريف لجيب التمام والظل والظل.

إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter
عندما تم النظر في مهام حل مثلث قائم الزاوية ، فقد وعدت بتقديم تقنية لحفظ تعريفات الجيب وجيب التمام. باستخدامه ، ستتذكر دائمًا بسرعة أي رجل تنتمي إلى الوتر (المجاور أو المقابل). قررت عدم تأجيله إلى أجل غير مسمى ، المواد اللازمةأدناه ، من فضلك انظر
الحقيقة هي أنني لاحظت مرارًا وتكرارًا كيف يجد الطلاب في الصفوف 10-11 صعوبة في تذكر هذه التعريفات. يتذكرون جيدًا أن الساق تشير إلى الوتر ، لكن أي واحد يشير إلى الوتر- تنسى و مشوش. ثمن الخطأ ، كما تعلم في الامتحان ، هو النتيجة المفقودة.
المعلومات التي سأقدمها مباشرة للرياضيات ليس لها علاقة. هي مرتبطة ب التفكير المجازيوطرق الاتصال المنطقي اللفظي. هذا صحيح ، أنا نفسي ، تذكرت مرة واحدة وإلى الأبدبيانات التعريف. إذا كنت لا تزال تنساها ، فمن السهل دائمًا تذكرها بمساعدة التقنيات المقدمة.
دعني أذكرك بتعريف الجيب وجيب التمام في مثلث قائم الزاوية:
جيب التمامالزاوية الحادة في المثلث القائم هي نسبة الضلع المجاورة إلى الوتر:

التجويفالزاوية الحادة في المثلث القائم هي نسبة الضلع المقابلة إلى الوتر:

إذن ، ما هي الارتباطات التي تثيرها كلمة جيب التمام فيك؟
ربما كل شخص لديه ما يخصهتذكر الرابط:
وهكذا ، سيكون لديك على الفور تعبير في ذاكرتك -
«… نسبة الضلع من الضلع إلى الوتر».
تم حل مشكلة تعريف جيب التمام.
إذا كنت بحاجة إلى تذكر تعريف الجيب في مثلث قائم الزاوية ، ثم تذكر تعريف جيب التمام ، يمكنك بسهولة إثبات أن جيب الزاوية الحادة في المثلث القائم هو نسبة الضلع المقابلة إلى الوتر. بعد كل شيء ، هناك ساقان فقط ، إذا كانت الساق المجاورة "مشغولة" بجيب التمام ، فسيبقى الجانب المقابل فقط للجيب.
ماذا عن الظل وظل التمام؟ نفس الارتباك. يعرف الطلاب أن هذه هي نسبة الأرجل ، لكن المشكلة تكمن في تذكر أي واحد يشير إلى أيهما - إما عكس المجاور ، أو العكس.
تعريفات:
الظلالزاوية الحادة في مثلث قائم الزاوية هي نسبة الضلع المقابلة إلى المجاورة:

ظل التمامالزاوية الحادة في المثلث القائم هي نسبة الضلع المجاورة إلى الضلع المقابل:

كيف تتذكر؟ هناك طريقتان. يستخدم أحدهما أيضًا اتصالًا منطقيًا لفظيًا ، والآخر - اتصال رياضي.
الطريقة الرياضية
يوجد تعريف كهذا - ظل الزاوية الحادة هو نسبة جيب الزاوية إلى جيب التمام:

* بتذكر الصيغة ، يمكنك دائمًا تحديد أن ظل الزاوية الحادة في المثلث القائم هو نسبة الضلع المقابلة إلى الضلع المجاورة.
على نفس المنوال.ظل التمام للزاوية الحادة هو نسبة جيب تمام الزاوية إلى جيبها:

لذا! عند تذكر هذه الصيغ ، يمكنك دائمًا تحديد ما يلي:
- ظل الزاوية الحادة في المثلث القائم هو نسبة الضلع المقابلة إلى المجاورة
- ظل التمام لزاوية حادة في مثلث قائم الزاوية هو نسبة الضلع المجاورة إلى الضلع المقابل.
الطريقة المنطقية اللفظية
حول الظل. تذكر الرابط:

أي ، إذا كنت بحاجة إلى تذكر تعريف الظل ، باستخدام هذا الاتصال المنطقي ، يمكنك بسهولة تذكر ما هو
"... نسبة الساق المقابلة إلى المجاورة"
إذا كان الأمر يتعلق بـ cotangent ، ثم تذكر تعريف الظل ، فيمكنك بسهولة التعبير عن تعريف cotangent -
"... نسبة الرجل المجاورة إلى الأخرى"
هناك تقنية مثيرة للاهتمام لحفظ الظل والظل في الموقع " الترادف الرياضي " ، بحث.
طريقة عالمية
يمكنك فقط طحن.ولكن كما تبين الممارسة ، وبفضل الروابط المنطقية اللفظية ، يتذكر الشخص المعلومات لفترة طويلة ، وليس المعلومات الرياضية فقط.
آمل أن تكون المادة مفيدة لك.
مع خالص التقدير ، الكسندر كروتسكيخ
ملاحظة: سأكون ممتنًا إذا تحدثت عن الموقع في الشبكات الاجتماعية.
كيف تجد الجيب؟



تساعد دراسة الهندسة على تنمية التفكير. يتم تضمين هذا الموضوع في المناهج الدراسية. في الحياة ، يمكن أن تكون معرفة هذا الموضوع مفيدة - على سبيل المثال ، عند التخطيط لشقة.
من التاريخ
كجزء من دورة الهندسة ، تمت دراسة علم المثلثات أيضًا ، والذي يستكشف الدوال المثلثية. في علم المثلثات ، ندرس الجيب وجيب التمام والظل والظل لزاوية.
لكن على هذه اللحظةلنبدأ بأبسط جيب. دعنا نلقي نظرة فاحصة على المفهوم الأول - جيب الزاوية في الهندسة. ما هو الجيب وكيفية العثور عليه؟
مفهوم "جيب الزاوية" والجيوب الأنفية
جيب الزاوية هو النسبة بين قيم الضلع المقابل والوتر في المثلث القائم. هذه دالة مثلثية مباشرة ، مكتوبة كـ "sin (x)" ، حيث (x) هي زاوية المثلث.
على الرسم البياني ، يُشار إلى جيب الزاوية بخصائصه الخاصة. يشبه الجيب الجيبي خطًا متموجًا مستمرًا يقع ضمن حدود معينة على مستوى الإحداثيات. الوظيفة فردية ، وبالتالي فهي متماثلة بالنسبة إلى 0 على مستوى الإحداثيات (تترك أصل الإحداثيات).
يقع مجال هذه الوظيفة في النطاق من -1 إلى +1 على نظام الإحداثيات الديكارتية. فترة دالة جيب الزاوية هي 2 Pi. هذا يعني أن كل 2 Pi يتكرر النمط وأن الموجة الجيبية تمر بدورة كاملة.
المعادلة الجيبية
- الخطيئة س = أ / ج
- حيث a هي الساق المقابلة لزاوية المثلث
- ج - وتر المثلث القائم
خصائص جيب الزاوية
- الخطيئة (س) = - الخطيئة (س). توضح هذه الميزة أن الوظيفة متماثلة ، وإذا تم وضع القيمتين x و (-x) جانبًا على نظام الإحداثيات في كلا الاتجاهين ، فستكون إحداثيات هذه النقاط معاكسة. سيكونون على مسافة متساوية من بعضهم البعض.
- ميزة أخرى لهذه الوظيفة هي أن الرسم البياني للوظيفة يزيد على المقطع [- P / 2 + 2 Pn] ؛ [P / 2 + 2Pn] ، حيث n هو أي عدد صحيح. سيُلاحظ انخفاض في الرسم البياني لجيب الزاوية على المقطع: [P / 2 + 2 Pn] ؛ [3P / 2 + 2Pn].
- sin (x)> 0 عندما تكون x في النطاق (2Pn، P + 2Pn)
- (خ)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)
يتم تحديد قيم جيب الزاوية بواسطة جداول خاصة. تم إنشاء هذه الجداول لتسهيل عملية العد. الصيغ المعقدةوالمعادلات. إنه سهل الاستخدام ويحتوي على قيم ليس فقط وظائف الخطيئة(x) ، ولكن أيضًا قيم الوظائف الأخرى.
علاوة على ذلك ، يتم تضمين جدول القيم القياسية لهذه الوظائف في دراسة اجباريةللذاكرة ، مثل جدول الضرب. هذا ينطبق بشكل خاص على الفصول ذات التحيز المادي والرياضي. في الجدول يمكنك رؤية قيم الزوايا الرئيسية المستخدمة في حساب المثلثات: 0 ، 15 ، 30 ، 45 ، 60 ، 75 ، 90 ، 120 ، 135 ، 150 ، 180 ، 270 ، 360 درجة.
يوجد أيضًا جدول يحدد قيم الدوال المثلثية للزوايا غير القياسية. الاستفادة طاولات مختلفة، يمكنك بسهولة حساب الجيب وجيب التمام والظل وظل التمام لبعض الزوايا.
تتكون المعادلات من الدوال المثلثية. حل هذه المعادلات سهل إذا كنت تعرف البساطة الهويات المثلثيةوتخفيضات الوظائف ، على سبيل المثال ، مثل الخطيئة (P / 2 + x) = cos (x) وغيرها. كما تم تجميع جدول منفصل لمثل هذه القوالب.
كيفية إيجاد جيب الزاوية
عندما تكون المهمة هي إيجاد جيب الزاوية ، وبحسب الشرط لدينا فقط جيب التمام أو الظل أو ظل التمام للزاوية ، يمكننا بسهولة حساب ما نحتاج إليه باستخدام المتطابقات المثلثية.
- الخطيئة 2 س + كوس 2 س = 1
من هذه المعادلة ، يمكننا إيجاد كل من الجيب وجيب التمام ، اعتمادًا على القيمة غير المعروفة. سننجح المعادلة المثلثيةمع واحد غير معروف:
- sin 2 x = 1 - cos 2 x
- sin x = ± √ 1 - cos 2 x
- ctg 2 x + 1 = 1 / sin 2 x
من هذه المعادلة ، يمكنك إيجاد قيمة الجيب ، مع معرفة قيمة ظل التمام للزاوية. للتبسيط ، استبدل sin 2 x = y ، وستحصل على معادلة بسيطة. على سبيل المثال ، قيمة ظل التمام هي 1 ، ثم:
- 1 + 1 = 1 / ص
- 2 = 1 / ص
- 2 ص = 1
- ص = 1/2
الآن نقوم بالاستبدال العكسي للاعب:
- الخطيئة 2 س = ½
- الخطيئة س = 1 / √2
نظرًا لأننا أخذنا قيمة ظل التمام للزاوية القياسية (45 0) ، يمكن التحقق من القيم التي تم الحصول عليها مقابل الجدول.
إذا كانت لديك قيمة ظل ، لكنك تحتاج إلى إيجاد الجيب ، فستساعدك هوية مثلثية أخرى:
- tg x * ctg x = 1
إنه يتبع هذا:
- ctg x = 1 / tg x
لإيجاد جيب الزاوية غير القياسي ، على سبيل المثال ، 240 0 ، تحتاج إلى استخدام صيغ تقليل الزاوية. نعلم أن π تقابل 180 0 بالنسبة لنا. وبالتالي ، سوف نعبر عن مساواتنا باستخدام الزوايا القياسية عن طريق التوسع.
- 240 0 = 180 0 + 60 0
علينا إيجاد ما يلي: sin (180 0 + 60 0). في علم المثلثات ، توجد صيغ اختزال ، في هذه القضيةتأتي في متناول اليدين. هذه هي الصيغة:
- الخطيئة (π + س) = - الخطيئة (س)
إذن ، جيب الزاوية 240 درجة هو:
- الخطيئة (180 0 + 60 0) = - الخطيئة (60 0) = - √3 / 2
في حالتنا ، x = 60 ، و P على التوالي ، 180 درجة. وجدنا القيمة (-3 / 2) من جدول قيم وظائف الزوايا القياسية.
وبالتالي فمن الممكن أن تتحلل زوايا غير قياسية، على سبيل المثال: 210 = 180 + 30.
ترتبط مفاهيم الجيب () وجيب التمام () والظل () والظل () ارتباطًا وثيقًا بمفهوم الزاوية. من أجل فهم هذه المفاهيم المعقدة جيدًا للوهلة الأولى (التي تسبب حالة من الرعب لدى العديد من أطفال المدارس) ، وللتأكد من أن "الشيطان ليس مخيفًا كما يرسم" ، فلنبدأ من البداية ونفهم مفهوم الزاوية.
مفهوم الزاوية: راديان ، درجة
دعونا نلقي نظرة على الصورة. المتجه "تحول" بالنسبة للنقطة بمقدار معين. لذلك سيكون قياس هذا الدوران بالنسبة للموضع الأولي حقنة.
ماذا تريد أن تعرف أيضًا عن مفهوم الزاوية؟ حسنًا ، وحدات الزاوية بالطبع!
يمكن قياس الزاوية ، في كل من الهندسة وعلم المثلثات ، بالدرجات والراديان.
الزاوية عند (درجة واحدة) هي الزاوية المركزية في الدائرة ، بناءً على قوس دائري يساوي جزء الدائرة. وهكذا ، تتكون الدائرة بأكملها من "قطع" من أقواس دائرية ، أو أن الزاوية الموصوفة بالدائرة متساوية.

أي أن الشكل أعلاه يوضح زاوية متساوية ، أي أن هذه الزاوية تستند إلى قوس دائري بحجم المحيط.
الزاوية بالتقدير الدائري تسمى الزاوية المركزية في الدائرة ، بناءً على قوس دائري ، طوله يساوي نصف قطر الدائرة. حسنا هل فهمت إذا لم يكن كذلك ، فلنلقِ نظرة على الصورة.

إذن ، يوضح الشكل زاوية تساوي راديان ، أي أن هذه الزاوية تستند إلى قوس دائري ، طوله يساوي نصف قطر الدائرة (الطول يساوي الطول أو نصف القطر يساوي الطولأقواس). وبالتالي ، يتم حساب طول القوس بالصيغة التالية:
أين الزاوية المركزية بالتقدير الدائري.
حسنًا ، بمعرفة ذلك ، هل يمكنك الإجابة على عدد الراديان التي تحتوي على زاوية موصوفة بالدائرة؟ نعم ، لهذا عليك أن تتذكر صيغة محيط الدائرة. ها هي:
حسنًا ، دعونا الآن نربط هاتين الصيغتين ونحصل على أن الزاوية الموضحة بالدائرة متساوية. أي بربط القيمة بالدرجات والراديان ، نحصل على ذلك. على التوالى، . كما ترى ، على عكس "الدرجات" ، تم حذف كلمة "راديان" ، لأن وحدة القياس عادة ما تكون واضحة من السياق.
كم عدد الراديان؟ هذا صحيح!
فهمتك؟ ثم اربط للأمام:
أي صعوبات؟ ثم ابحث الإجابات:
المثلث الأيمن: الجيب ، جيب التمام ، الظل ، ظل التمام لزاوية
لذلك ، مع مفهوم الزاوية برزت. ولكن ما هو الجيب وجيب التمام والظل والظل لزاوية؟ دعونا نفهم ذلك. لهذا ، سوف يساعدنا المثلث القائم.

ماذا تسمى أضلاع المثلث القائم الزاوية؟ هذا صحيح ، الوتر والساقان: الوتر هو الضلع المقابل زاوية مستقيمة(في مثالنا ، هذا هو الجانب) ؛ الأرجل هي الضلعان المتبقيان و (تلك المجاورة للزاوية القائمة) ، علاوة على ذلك ، إذا أخذنا في الاعتبار الساقين بالنسبة للزاوية ، فإن الساق هي الساق المجاورة ، والساق هي الضلع المقابل. الآن ، دعنا نجيب على السؤال: ما هو الجيب وجيب التمام والظل والظل لزاوية؟
جيب الزاويةهي نسبة الضلع المقابلة (البعيدة) إلى الوتر.
في مثلثنا.
جيب التمام لزاوية- هذه هي نسبة الضلع المجاورة (القريبة) إلى الوتر.
في مثلثنا.
ظل الزاوية- هذه هي نسبة الضلع المقابلة (البعيدة) إلى المجاورة (القريبة).
في مثلثنا.
ظل التمام لزاوية- هذه هي نسبة الضلع المجاورة (القريبة) إلى الضلع المقابل (البعيد).
في مثلثنا.
هذه التعريفات ضرورية يتذكر! لتسهيل تذكر الساق التي تقسم على ماذا ، عليك أن تفهم ذلك بوضوح ظلو ظل التمامفقط الساقان تجلسان ، ويظهر الوتر فقط في التجويفو جيب التمام. وبعد ذلك يمكنك الخروج بسلسلة من الجمعيات. على سبيل المثال ، هذا:
جيب التمام ← اللمس ← اللمس ← المجاور ؛
ظل التمام ← اللمس ← اللمس ← المجاور.
بادئ ذي بدء ، من الضروري أن نتذكر أن الجيب وجيب التمام والظل والظل كنسب لأضلاع المثلث لا تعتمد على أطوال هذه الجوانب (بزاوية واحدة). لا تصدق؟ ثم تأكد من خلال النظر إلى الصورة:

ضع في اعتبارك ، على سبيل المثال ، جيب التمام لزاوية. حسب التعريف ، من مثلث: ، لكن يمكننا حساب جيب تمام الزاوية من مثلث:. كما ترى ، أطوال الأضلاع مختلفة ، لكن قيمة جيب التمام لزاوية واحدة هي نفسها. وبالتالي ، فإن قيم الجيب وجيب التمام والظل والظل تعتمد فقط على حجم الزاوية.
إذا فهمت التعاريف ، فابدأ في إصلاحها!
للمثلث الموضح في الشكل أدناه ، نجد.

حسنًا ، هل فهمت ذلك؟ ثم جربها بنفسك: احسب نفس الزاوية.
دائرة الوحدة (المثلثية)
من خلال فهم مفاهيم الدرجات والراديان ، اعتبرنا الدائرة التي يساوي نصف قطرها. تسمى هذه الدائرة غير متزوج. إنه مفيد للغاية في دراسة علم المثلثات. لذلك ، فإننا نتناولها بمزيد من التفصيل.

كما ترى ، هذه الدائرة مبنية في نظام الإحداثيات الديكارتية. نصف قطر الدائرة يساوي واحدًا ، بينما يقع مركز الدائرة عند نقطة الأصل ، والموضع الأولي لمتجه نصف القطر ثابتًا على طول الاتجاه الموجب للمحور (في مثالنا ، هذا هو نصف القطر).
تتوافق كل نقطة في الدائرة مع رقمين: التنسيق على طول المحور والإحداثيات على طول المحور. ما هي هذه الأرقام الإحداثي؟ وبشكل عام ، ما علاقتهم بالموضوع المطروح؟ للقيام بذلك ، تذكر معلومات المثلث القائم الزاوية. في الشكل أعلاه ، يمكنك أن ترى مثلثين قائمين كاملين. خذ بعين الاعتبار المثلث. إنه مستطيل لأنه عمودي على المحور.
ماذا يساوي المثلث؟ هذا صحيح. بالإضافة إلى ذلك ، نعلم أن هذا هو نصف قطر دائرة الوحدة ، وبالتالي ،. عوّض بهذه القيمة في صيغة جيب التمام. إليك ما يحدث:
وماذا يساوي المثلث؟ حسنا بالطبع، ! عوض بقيمة نصف القطر في هذه الصيغة واحصل على:
لذا ، هل يمكنك تحديد إحداثيات نقطة ما ، تنتمي إلى الدائرة؟ حسنًا ، مستحيل؟ وإذا أدركت ذلك وهل هي مجرد أرقام؟ ما هو التنسيق الذي يتوافق معه؟ حسنًا ، بالطبع ، التنسيق! ما هو التنسيق الذي يتوافق معه؟ هذا صحيح ، قم بالتنسيق! وهكذا ، فإن النقطة.

وماذا بعد ذلك متساوون و؟ هذا صحيح ، دعنا نستخدم التعريفات المناسبة لـ tangent و cotangent ونحصل على ذلك ، a.
ماذا لو كانت الزاوية أكبر؟ هنا على سبيل المثال كما في هذه الصورة:

ما الذي تغير في هذا المثال؟ دعونا نفهم ذلك. للقيام بذلك ، ننتقل مرة أخرى إلى مثلث قائم الزاوية. ضع في اعتبارك مثلث قائم الزاوية: زاوية (كمجاورة لزاوية). ما هي قيمة الجيب وجيب التمام والظل وظل التمام لزاوية؟ هذا صحيح ، نحن نلتزم بالتعريفات المقابلة للوظائف المثلثية:
حسنًا ، كما ترى ، لا تزال قيمة جيب الزاوية تتوافق مع الإحداثي ؛ قيمة جيب التمام للزاوية - الإحداثي ؛ وقيم الظل والظل للنسب المقابلة. وبالتالي ، فإن هذه العلاقات قابلة للتطبيق على أي دوران لمتجه نصف القطر.
لقد سبق أن ذكرنا أن الموضع الأولي لمتجه نصف القطر يقع على طول الاتجاه الإيجابي للمحور. حتى الآن قمنا بتدوير هذا المتجه عكس اتجاه عقارب الساعة ، ولكن ماذا يحدث إذا قمنا بتدويره في اتجاه عقارب الساعة؟ لا شيء غير عادي ، ستحصل أيضًا على زاوية بحجم معين ، لكنها ستكون سالبة فقط. وهكذا ، عند تدوير متجه نصف القطر عكس اتجاه عقارب الساعة ، نحصل على زوايا موجبة، وعند الدوران في اتجاه عقارب الساعة - نفي.
لذلك ، نعلم أن الثورة الكاملة لمتجه نصف القطر حول الدائرة تساوي أو. هل من الممكن تدوير متجه نصف القطر بواسطة أم بجانبه؟ حسنا بالطبع يمكنك! لذلك ، في الحالة الأولى ، يقوم متجه نصف القطر بعمل ثورة كاملة ويتوقف عند الموضع أو.
في الحالة الثانية ، أي ، يقوم متجه نصف القطر بثلاث دورات كاملة ويتوقف عند الموضع أو.
وبالتالي ، من الأمثلة المذكورة أعلاه ، يمكننا أن نستنتج أن الزوايا التي تختلف في أو (أين يوجد أي عدد صحيح) تتوافق مع نفس موضع متجه نصف القطر.
يوضح الشكل أدناه زاوية. نفس الصورة تتوافق مع الزاوية ، وهكذا. يمكن أن تستمر هذه القائمة إلى أجل غير مسمى. يمكن كتابة كل هذه الزوايا بالصيغة العامة أو (أين يوجد أي عدد صحيح)

الآن ، بعد معرفة تعريفات الدوال المثلثية الأساسية واستخدام دائرة الوحدة ، حاول الإجابة عن القيم التي تساويها:
إليك دائرة الوحدة لمساعدتك:

أي صعوبات؟ ثم دعونا نكتشف ذلك. لذلك نحن نعلم أن:
من هنا نحدد إحداثيات النقاط المقابلة لقياسات معينة للزاوية. حسنًا ، لنبدأ بالترتيب: الزاوية عند تتوافق مع نقطة ذات إحداثيات ، لذلك:
غير موجود؛
علاوة على ذلك ، بالالتزام بالمنطق نفسه ، نجد أن الزوايا تتوافق مع النقاط ذات الإحداثيات ، على التوالي. بمعرفة ذلك ، من السهل تحديد قيم الدوال المثلثية في النقاط المقابلة. جربها بنفسك أولاً ، ثم تحقق من الإجابات.
الإجابات:
غير موجود
غير موجود
غير موجود
غير موجود
وهكذا يمكننا عمل الجدول التالي:

ليست هناك حاجة لتذكر كل هذه القيم. يكفي تذكر المراسلات بين إحداثيات النقاط على دائرة الوحدة وقيم الدوال المثلثية:
لكن قيم الدوال المثلثية للزوايا في ، والمذكورة في الجدول أدناه ، يجب تذكرها:

لا تخافوا ، الآن سنعرض أحد الأمثلة إلى حد ما حفظ بسيط للقيم المقابلة:
لاستخدام هذه الطريقة ، من الضروري تذكر قيم الجيب لجميع مقاييس الزاوية () ، بالإضافة إلى قيمة ظل الزاوية في. من خلال معرفة هذه القيم ، من السهل جدًا استعادة الجدول بأكمله - يتم نقل قيم جيب التمام وفقًا للأسهم ، أي:
بمعرفة هذا ، يمكنك استعادة قيم. سيتطابق البسط "" ويتطابق المقام "". يتم نقل قيم ظل التمام وفقًا للأسهم الموضحة في الشكل. إذا فهمت هذا وتذكرت الرسم التخطيطي بالسهام ، فسيكون ذلك كافيًا لتذكر القيمة بأكملها من الجدول.
إحداثيات نقطة على دائرة
هل من الممكن إيجاد نقطة (إحداثياتها) على دائرة ، معرفة إحداثيات مركز الدائرة ونصف قطرها وزاوية الدوران?
حسنا بالطبع يمكنك! دعونا نخرج الصيغة العامةللعثور على إحداثيات نقطة.
هنا ، على سبيل المثال ، لدينا مثل هذه الدائرة:

نعلم أن النقطة هي مركز الدائرة. نصف قطر الدائرة متساوي. من الضروري إيجاد إحداثيات النقطة التي تم الحصول عليها عن طريق تدوير النقطة بالدرجات.
كما يتضح من الشكل ، فإن تنسيق النقطة يتوافق مع طول المقطع. يتوافق طول المقطع مع إحداثيات مركز الدائرة ، أي أنه يساوي. يمكن التعبير عن طول المقطع باستخدام تعريف جيب التمام:
ثم لدينا هذا بالنسبة للنقطة الإحداثي.
بنفس المنطق ، نجد قيمة إحداثي ص للنقطة. هكذا،
حتى في نظرة عامةيتم تحديد إحداثيات النقاط بواسطة الصيغ:
إحداثيات مركز الدائرة ،
دائرة نصف قطرها
زاوية دوران متجه نصف القطر.
كما ترى ، بالنسبة لدائرة الوحدة التي ندرسها ، يتم تقليل هذه الصيغ بشكل كبير ، نظرًا لأن إحداثيات المركز تساوي صفرًا ونصف القطر يساوي واحدًا:
حسنًا ، لنجرب هذه الصيغ للتذوق ، ونتدرب على إيجاد النقاط على الدائرة؟
1. أوجد إحداثيات نقطة على دائرة الوحدة التي تم الحصول عليها عن طريق تشغيل نقطة.
2. أوجد إحداثيات نقطة على دائرة الوحدة التي تم الحصول عليها بتدوير نقطة على.
3. أوجد إحداثيات نقطة على دائرة الوحدة التي تم الحصول عليها عن طريق تشغيل نقطة.
4. نقطة - مركز الدائرة. نصف قطر الدائرة متساوي. من الضروري إيجاد إحداثيات النقطة التي تم الحصول عليها بتدوير متجه نصف القطر الأولي بمقدار.
5. نقطة - مركز الدائرة. نصف قطر الدائرة متساوي. من الضروري إيجاد إحداثيات النقطة التي تم الحصول عليها بتدوير متجه نصف القطر الأولي بمقدار.
هل تواجه مشكلة في العثور على إحداثيات نقطة في دائرة؟
قم بحل هذه الأمثلة الخمسة (أو افهم الحل جيدًا) وسوف تتعلم كيفية العثور عليها!
1.
ويمكن أن نرى أن. ونعرف ما يتوافق مع الانعطاف الكامل لنقطة البداية. وبالتالي ، ستكون النقطة المرغوبة في نفس الموضع عند التحول إلى. بمعرفة هذا نجد الإحداثيات المرغوبة للنقطة:
2. الدائرة عبارة عن وحدة مركزها نقطة ، مما يعني أنه يمكننا استخدام صيغ مبسطة:
ويمكن أن نرى أن. نحن نعلم ما يتوافق مع دورتين كاملتين لنقطة البداية. وبالتالي ، ستكون النقطة المرغوبة في نفس الموضع عند التحول إلى. بمعرفة هذا نجد الإحداثيات المرغوبة للنقطة:
الجيب وجيب التمام قيم الجدول. نتذكر قيمهم ونحصل على:
وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.
3. الدائرة عبارة عن وحدة مركزها نقطة ، مما يعني أنه يمكننا استخدام صيغ مبسطة:
ويمكن أن نرى أن. دعنا نصور المثال المدروس في الشكل:

يجعل نصف القطر زوايا مع المحور تساوي و. مع العلم أن القيم الجدولية لجيب التمام والجيب متساوية ، وبعد تحديد أن جيب التمام هنا يأخذ قيمة سالبة ، وجيب الجيب موجب ، لدينا:
يتم تحليل أمثلة مماثلة بمزيد من التفصيل عند دراسة الصيغ لتقليل الدوال المثلثية في الموضوع.
وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.
4.
زاوية دوران متجه نصف القطر (حسب الشرط)
لتحديد علامات الجيب وجيب التمام المقابلة ، نقوم ببناء دائرة وحدة وزاوية:

كما ترى ، القيمة ، أي موجبة ، والقيمة أي سالبة. بمعرفة القيم الجدولية للوظائف المثلثية المقابلة ، نحصل على ما يلي:
دعنا نعوض بالقيم التي تم الحصول عليها في الصيغة الخاصة بنا ونوجد الإحداثيات:
وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.
5. لحل هذه المشكلة ، نستخدم الصيغ بشكل عام ، أين
إحداثيات مركز الدائرة (في مثالنا ،
نصف قطر الدائرة (حسب الشرط)
زاوية دوران متجه نصف القطر (حسب الشرط).
عوّض بكل القيم في الصيغة واحصل على:
و- قيم الجدول. نتذكرها ونستبدلها بالصيغة:
وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.
ملخص وصيغة أساسية
جيب الزاوية هو نسبة الضلع المقابل (البعيد) إلى الوتر.
جيب تمام الزاوية هو نسبة الضلع المجاورة (القريبة) إلى الوتر.
ظل الزاوية هو نسبة الضلع المقابلة (البعيدة) إلى المجاورة (القريبة).
ظل التمام لزاوية هو نسبة الضلع المجاورة (القريبة) إلى الضلع المقابل (البعيد).
تعليمات
استخدم الدالة القوسية لحساب قيمة الزاوية بالدرجات إذا كنت تعرف قيمة تلك الزاوية. اذا كان حقنةيُشار إليه بالحرف α ، بشكل عام ، يمكن كتابة الحل على النحو التالي: α = arcsin (sin (α)).
إذا كانت لديك الفرصة لاستخدام الكمبيوتر ، فمن الأسهل استخدام نظام التشغيل المدمج لإجراء عمليات حسابية عملية. في أحدث إصدارين من Windows ، يمكنك بدء تشغيله على النحو التالي: اضغط على مفتاح Win ، واكتب "ka" واضغط على Enter. في الإصدارات السابقة من نظام التشغيل هذا ، ابحث عن رابط "الآلة الحاسبة" في القسم الفرعي "القياسي" بقسم "كافة البرامج" في القائمة الرئيسية للنظام.
بعد تشغيل التطبيق ، قم بتبديله إلى الوضع الذي يسمح لك بالعمل مع الدوال المثلثية. يمكن القيام بذلك عن طريق تحديد سطر "الهندسة" في قسم "العرض" بقائمة الآلة الحاسبة أو بالضغط على Alt + 2.
أدخل قيمة شرط. بشكل افتراضي ، لا تحتوي واجهة الآلة الحاسبة على زر لحساب القوس. لتتمكن من استخدام هذه الوظيفة ، تحتاج إلى عكس القيم الافتراضية للأزرار - انقر فوق الزر Inv في نافذة البرنامج. في المزيد الإصدارات القديمةيتم استبدال هذا الزر بخانة اختيار بنفس التعيين - حدده.
يمكنك الاستعانة في الحسابات والخدمات المتنوعة التي تعتبر أكثر من كافية على الإنترنت. على سبيل المثال ، انتقل إلى الصفحة http://planetcalc.com/326/ ، وانتقل لأسفل قليلاً وفي حقل الإدخال ، أدخل قيمة الجيب. لبدء إجراء الحساب ، يوجد زر يسمى احسب - انقر فوقه. سوف تجد نتيجة الحسابات في السطر الأول من الجدول تحت هذا الزر. بالإضافة إلى القوسين ، فإنه يعرض كلاً من القيم وظل القوس للقيمة التي تم إدخالها.
تسمى دالة الجيب المثلثية المعكوسة قوس. يمكن أن يأخذ قيمًا تقع ضمن نصف عدد pi ، موجبًا وسالبًا. الجانب السلبيعند القياس بالراديان. عند القياس بالدرجات ، ستكون هذه القيم ، على التوالي ، في النطاق من -90 درجة إلى + 90 درجة.
تعليمات
لا يلزم حساب بعض القيم "المستديرة" ، فمن السهل تذكرها. على سبيل المثال: - إذا كانت وسيطة الدالة تساوي صفرًا ، فإن قيمة القوس منها تساوي أيضًا صفرًا ؛ - من 1/2 تساوي 30 درجة أو 1/6 Pi ، إذا تم قياسها ؛ - القوس من -1/2 يساوي إلى -30 درجة أو -1 / 6 من pi في ؛ - قوس قوس من 1 هو 90 درجة أو 1/2 من باي بالراديان ؛ - قوس قوس -1 هو -90 درجة أو -1 / 2 باي بالراديان ؛
لقياس قيم هذه الوظيفة من وسيطات أخرى ، فإن أسهل طريقة هي استخدام حاسبة Windows القياسية ، إذا كان لديك. للبدء ، افتح القائمة الرئيسية على زر "ابدأ" (أو بالضغط على مفتاح WIN) ، انتقل إلى قسم "كافة البرامج" ، ثم إلى القسم الفرعي "الملحقات" وانقر على عنصر "الحاسبة".
قم بتبديل واجهة الآلة الحاسبة إلى وضع التشغيل الذي يسمح لك بحساب الدوال المثلثية. للقيام بذلك ، افتح قسم "عرض" في قائمته وحدد العنصر "هندسة" أو "علمي" (حسب نظام التشغيل المستخدم).
أدخل قيمة الوسيطة التي تريد من خلالها حساب ظل القوس. يمكن القيام بذلك عن طريق النقر على أزرار واجهة الآلة الحاسبة بالماوس ، أو بالضغط على المفاتيح ، أو بنسخ القيمة (CTRL + C) ثم لصقها (CTRL + V) في حقل إدخال الآلة الحاسبة.
حدد الوحدات التي تريد الحصول على نتيجة حساب الدالة بها. يوجد أسفل حقل الإدخال ثلاثة خيارات ، والتي تحتاج إلى تحديد (بالنقر فوقها بالماوس) خيار واحد - أو راديان أو راديان.
حدد مربع الاختيار الذي يعكس الوظائف المشار إليها في أزرار واجهة الآلة الحاسبة. بجانبه يوجد نقش قصير Inv.
انقر فوق زر الخطيئة. ستعكس الآلة الحاسبة الوظيفة المرفقة بها وتجري الحساب وتقدم لك النتيجة في الوحدات المحددة.
فيديوهات ذات علاقة
على مثلث قائم الزاوية ، كأبسط مضلعات ، شحذ العديد من العلماء معرفتهم في مجال علم المثلثات في تلك الأيام التي لم يطلق فيها أحد على هذا المجال من الرياضيات بهذه الكلمة. لذلك أشر إلى المؤلف الذي حدد الأنماط في نسبة أطوال الأضلاع وقيم الزوايا في هذا المسطح الشكل الهندسياليوم غير ممكن. وتسمى هذه العلاقات بالوظائف المثلثية وتنقسم إلى عدة مجموعات ، يعتبر معظمها تقليديًا وظائف "مباشرة". تم تعيين وظيفتين فقط لهذه المجموعة ، إحداهما هي شرط.

تعليمات
حسب التعريف ، في مثلث قائم الزاوية ، تساوي إحدى الزوايا 90 درجة ، وبسبب حقيقة أن مجموع زواياه في الهندسة الإقليدية يجب أن يساوي 180 درجة ، فإن الزاويتين الأخريين هما (أي 90 درجة). تصف انتظامات نسب هذه الزوايا وأطوال الأضلاع بدقة الدوال المثلثية.
تحدد الوظيفة ، التي تسمى جيب الزاوية الحادة ، النسبة بين أطوال ضلعي مثلث قائم الزاوية ، يقع أحدهما مقابل هذه الزاوية الحادة والآخر بجوارها ويقع مقابل الزاوية القائمة. نظرًا لأن الضلع المقابل للزاوية اليمنى في مثل هذا المثلث يسمى الوتر ، والاثنان الآخران هما الأرجل ، يمكن صياغة وظائف الجيب كنسبة بين أطوال الساق والوتر.
بالإضافة إلى هذا التعريف البسيط لهذه الوظيفة المثلثية ، هناك المزيد من التعقيدات: من خلال دائرة في الإحداثيات الديكارتية ، من خلال سلسلة ، من خلال المعادلات التفاضلية والوظيفية. هذه الوظيفة مستمرة ، أي أن حججها ("مجال التعريفات") يمكن أن تكون أي رقم - من سالب بلا حدود إلى موجب بلا حدود. والقيم القصوى لهذه الوظيفة محدودة بنطاق من -1 إلى +1 - وهذا هو "نطاق قيمها". الحد الأدنى للقيمةيأخذ الجيب بزاوية 270 درجة ، والتي تقابل 3 / Pi ، ويتم الحصول على الحد الأقصى عند 90 درجة (½ من Pi). تصبح قيم الوظيفة صفرًا عند 0 درجة ، 180 درجة ، 360 درجة ، إلخ. من كل هذا يترتب على أن الجيب هو دالة دورية وأن مدته تساوي 360 درجة أو ضعف الرقم Pi.
لإجراء حسابات عملية لقيم هذه الوظيفة من وسيطة معينة ، يمكنك استخدام - الغالبية العظمى منها (بما في ذلك الآلة الحاسبة المضمنة في نظام التشغيلجهاز الكمبيوتر الخاص بك) لديه الخيار المقابل.
فيديوهات ذات علاقة
التجويفو جيب التمام- هذه دوال مثلثية مباشرة لها عدة تعريفات - من خلال دائرة في نظام الإحداثيات الديكارتية ، من خلال الحلول المعادلة التفاضلية، من خلال الزوايا الحادة في مثلث قائم الزاوية. يسمح لك كل تعريف من هذه التعريفات باستنتاج العلاقة بين هاتين الوظيفتين. ربما يكون التالي هو أبسط طريقة للتعبير جيب التماممن خلال الجيب - من خلال تعريفاتهم للزوايا الحادة للمثلث القائم.

تعليمات
عبر عن جيب الزاوية الحادة لمثلث قائم الزاوية بدلالة أطوال أضلاع هذا الشكل. وفقًا للتعريف ، يجب أن يكون جيب الزاوية (α) هو نسبة طول الضلع (أ) المقابل لها - الساق - إلى طول الضلع (ج) المقابل للزاوية اليمنى - الوتر: (α) = أ / ج.
ابحث عن صيغة مماثلة لـ جيب التماملكن نفس الزاوية. حسب التعريف ، يجب التعبير عن هذه القيمة كنسبة طول الضلع (ب) المجاور لهذه الزاوية (الضلع الثاني) إلى طول الجانب (ج) الواقع مقابل الزاوية اليمنى: cos (a) \ u003d أ / ج.
أعد كتابة المعادلة التالية من نظرية فيثاغورس بحيث تستخدم العلاقات بين الأرجل والوتر المشتقة في الخطوتين السابقتين. للقيام بذلك ، قسّم أولاً كلا من أصل هذه النظرية (a² + b² = c²) على مربع الوتر (a² / c² + b² / c² = 1) ، ثم أعد كتابة المساواة الناتجة بهذا الشكل: (a / ج) ² + (ب / ج) ² = 1.
استبدل في التعبير الناتج نسبة أطوال الأرجل والوتر بالدوال المثلثية ، بناءً على صيغ الخطوتين الأولى والثانية: sin² (a) + cos² (a) \ u003d 1. Express جيب التماممن المساواة الناتجة: cos (a) = √ (1 - sin² (a)). يمكن حل هذه المشكلة بطريقة عامة.
إذا كنت بحاجة ، بالإضافة إلى النتيجة العامة ، إلى الحصول على نتيجة عددية ، فاستخدم ، على سبيل المثال ، آلة حاسبة مدمجة في غرفة العمليات نظام ويندوز. رابط لإطلاقه في القسم الفرعي "قياسي" بقسم "كافة البرامج" في قائمة نظام التشغيل. تمت صياغة هذا الرابط بإيجاز - "آلة حاسبة". لتتمكن من حساب الدوال المثلثية من هذا البرنامج ، قم بتمكين واجهته "الهندسية" - اضغط على مجموعة المفاتيح Alt + 2.
أدخل قيمة جيب الزاوية في الشروط وانقر على زر الواجهة بالتعيين x² - سيؤدي هذا إلى تربيع القيمة الأصلية. ثم اكتب * -1 على لوحة المفاتيح ، واضغط على Enter ، واكتب +1 واضغط على Enter مرة أخرى - بهذه الطريقة ستطرح مربع الجيب من الوحدة. انقر فوق مفتاح رمز الجذر لاستخراج المربع والحصول على النتيجة النهائية.
قام علماء الرياضيات بدراسة المثلثات منذ آلاف السنين. يستخدم علم المثلثات - علم المثلثات - كميات خاصة: الجيب وجيب التمام.

مثلث قائم
في البداية ، نشأ الجيب وجيب التمام بسبب الحاجة إلى حساب الكميات في المثلثات القائمة. لوحظ أنه إذا لم تتغير قيمة قياس درجة الزوايا في مثلث قائم الزاوية ، فإن نسبة العرض إلى الارتفاع ، بغض النظر عن مقدار تغير هذه الأضلاع في الطول ، تظل كما هي.
هذه هي الطريقة التي تم بها تقديم مفاهيم الجيب وجيب التمام. جيب الزاوية الحادة في مثلث قائم الزاوية هو نسبة الضلع المقابلة إلى الوتر ، وجيب التمام هو نسبة الضلع المجاورة إلى الوتر.
نظريات الجيب والجيب
ولكن لا يمكن استخدام جيب التمام والجيب ليس فقط في المثلثات القائمة. لإيجاد قيمة زاوية منفرجة أو حادة ، أي جانب أي مثلث ، يكفي تطبيق نظرية جيب التمام والجيب.
نظرية جيب التمام بسيطة للغاية: "مربع جانب من المثلث يساوي مجموع مربعات الضلعين الآخرين مطروحًا منه ضعف حاصل ضرب هذين الضلعين بجيب الزاوية بينهما".
هناك تفسيران لنظرية الجيب: صغير وممتد. وبحسب الصغير: "في المثلث تكون الزوايا متناسبة مع الضلعين المتقابلين". غالبًا ما يتم تمديد هذه النظرية بسبب خاصية الدائرة المحصورة حول مثلث: "في المثلث ، تكون الزوايا متناسبة مع الأضلاع المتقابلة ، ونسبتها تساوي قطر الدائرة المحددة".
المشتقات
المشتق هو أداة رياضية توضح مدى سرعة تغير الوظيفة فيما يتعلق بالتغيير في حجتها. تستخدم المشتقات في الهندسة وفي عدد من التخصصات الفنية.
عند حل المشكلات ، تحتاج إلى معرفة القيم الجدولية لمشتقات الدوال المثلثية: الجيب وجيب التمام. مشتق الجيب هو جيب التمام ، ومشتق الجيب هو الجيب ، ولكن بعلامة الطرح.
التطبيق في الرياضيات
غالبًا ما يتم استخدام الجيب وجيب التمام في الحل مثلثات قائمةوالمهام المرتبطة بها.
تنعكس راحة الجيب وجيب التمام أيضًا في التكنولوجيا. كان من السهل تقييم الزوايا والجوانب باستخدام نظريتي جيب التمام والجيب ، حيث تم تقسيم الأشكال والأشياء المعقدة إلى مثلثات "بسيطة". أمضى المهندسون ، الذين غالبًا ما يتعاملون مع حسابات نسبة العرض إلى الارتفاع ومقاييس الدرجة ، الكثير من الوقت والجهد في حساب جيب التمام وجيب الزوايا غير الجدولية.
ثم جاءت جداول Bradis للإنقاذ ، والتي تحتوي على آلاف قيم الجيب وجيب التمام والظل والظل. زوايا مختلفة. في العهد السوفياتي ، أجبر بعض المعلمين عنابرهم على حفظ صفحات طاولات Bradis.
راديان - الحجم الزاويأقواس بالطول يساوي نصف القطرأو 57.295779513 درجة.
الدرجة (في الهندسة) - 1/360 من الدائرة أو 1/90 من الزاوية اليمنى.
π = 3.141592653589793238462 ... (القيمة التقريبية للبي).
جدول جيب التمام للزوايا: 0 درجة ، 30 درجة ، 45 درجة ، 60 درجة ، 90 درجة ، 120 درجة ، 135 درجة ، 150 درجة ، 180 درجة ، 210 درجة ، 225 درجة ، 240 درجة ، 270 درجة ، 300 درجة ، 315 درجة ، 330 درجة ، 360 درجة.
| الزاوية س (بالدرجات) | 0° | 30 درجة | 45 درجة | 60 درجة | 90 درجة | 120 درجة | 135 درجة | 150 درجة | 180 درجة | 210 درجة | 225 درجة | 240 درجة | 270 درجة | 300 درجة | 315 درجة | 330 درجة | 360 درجة |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| الزاوية x (بالتقدير الدائري) | 0 | π / 6 | / 4 | π / 3 | π / 2 | 2 × / 3 | 3xπ / 4 | 5xπ / 6 | π | 7xπ / 6 | 5xπ / 4 | 4xπ / 3 | 3xπ / 2 | 5xπ / 3 | 7xπ / 4 | 11xπ / 6 | 2xπ |
| كوس x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |