Уравнения с модулем. Модуль числа (абсолютная величина числа), определения, примеры, свойства

Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?

На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.

Но для начала вспомним определение модуля . Итак, модулем числа a называется само это число, если a неотрицательно и -a , если число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a < 0

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:

{±c, если с > 0

Если |x| = c, то x = {0, если с = 0

{нет корней, если с < 0

1) |x| = 5, т.к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.

1) |x + 2| = 4, т.к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

2) |x 2 – 5| = 11, т.к. 11 > 0, то

x 2 – 5 = 11 или x 2 – 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 нет корней

3) |x 2 – 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x) .

1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x – 10 ≥ 0

2. Решение:

2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3

2) |x – 1| = 1 – x 2 .

1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:

(1 – x)(1 + x) ≥ 0

2. Решение:

x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)

x 2 + x – 2 = 0 x 2 – x = 0

x = -2 или x = 1 x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1.

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:

x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5

x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0

x = 3 или x = 4 x = 2 или x = 1

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:

|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1 x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5.

Рассмотрим еще один пример:

x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому

|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2 или |x| = 1

Нет корней x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 – |x| = 4 или 3 – |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5 или 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 или x + 1 = -2. Нет корней.

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

В этой статье мы детально разберем модуль числа . Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.

Навигация по странице.

Модуль числа – определение, обозначение и примеры

Сначала введем обозначение модуля числа . Модуль числа a будем записывать как , то есть, слева и справа от числа будем ставить вертикальные черточки, образующие знак модуля. Приведем пару примеров. Например, модуль −7 можно записать как ; модуль 4,125 записывается как , а модуль имеет запись вида .

Следующее определение модуля относится к , а следовательно, и к , и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в .

Определение.

Модуль числа a – это либо само число a , если a – положительное число, либо число −a , противоположное числу a , если a – отрицательное число, либо 0 , если a=0 .

Озвученное определение модуля числа часто записывают в следующем виде , эта запись означает, что , если a>0 , , если a=0 , и , если a<0 .

Запись можно представить в более компактной форме . Эта запись означает, что , если (a больше или равно 0 ), и , если a<0 .

Также имеет место и запись . Здесь отдельно следует пояснить случай, когда a=0 . В этом случае имеем , но −0=0 , так как нуль считают числом, которое противоположно самому себе.

Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и . Начнем с нахождения . Так как число 15 – положительное, то его модуль по определению равен самому этому числу, то есть, . А чему равен модуль числа ? Так как - отрицательное число, то его модуль равен числу, противоположному числу , то есть, числу . Таким образом, .

В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака , а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа . Так модуль числа и абсолютная величина числа – это одно и то же.

Модуль числа как расстояние

Геометрически модуль числа можно интерпретировать как расстояние . Приведем определение модуля числа через расстояние .

Определение.

Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.

Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0 ). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.

Например, модуль числа 9 равен 9 , так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25 , поэтому .

Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.

Определение.

Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b .

То есть, если даны точки на координатной прямой A(a) и B(b) , то расстояние от точки A до точки B равно модулю разности чисел a и b . Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.

Определение модуля числа через арифметический квадратный корень

Иногда встречается определение модуля через арифметический квадратный корень .

Для примера вычислим модули чисел −30 и на основании данного определения. Имеем . Аналогично вычисляем модуль двух третьих: .

Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда и , если же a=0 , то .

Свойства модуля

Модулю присущ ряд характерных результатов - свойства модуля . Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.

Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом . В буквенном виде это свойство имеет запись вида для любого числа a . Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.

Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль . Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O , не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.

Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a . Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.

Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел , то есть, . По определению модуль произведения чисел a и b равен либо a·b , если , либо −(a·b) , если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b , , либо −(a·b) , если , что доказывает рассматриваемое свойство.

Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b , то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.

Следующее свойство модуля записывается в виде неравенства: , a , b и c – произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника . Чтобы это стало понятно, возьмем точки A(a) , B(b) , C(c) на координатной прямой, и рассмотрим вырожденный треугольник АВС , у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ , - длине отрезка АС , а - длине отрезка СВ . Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .

Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел ». Но неравенство напрямую следует из неравенства , если в нем вместо b положить −b , и принять c=0 .

Модуль комплексного числа

Дадим определение модуля комплексного числа . Пусть нам дано комплексное число , записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z , а – мнимая единица.

Точилкина Юлия

В работе представлены различные способы решения уравнений с модулем.

Скачать:

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 59»

Уравнения с модулем

Реферативная работа

Выполнила ученица 9А класса

МБОУ «СОШ № 59» г. Барнаула

Точилкина Юлия

Руководитель

Захарова Людмила Владимировна,

учитель математики

МБОУ «СОШ № 59» г. Барнаула

Барнаул 2015

Введение

Я учусь в девятом классе. В этом учебном году мне предстоит сдавать итоговую аттестацию за курс основной школы. Для подготовки к экзамену мы приобрели сборник Д. А. Мальцева Математика. 9 класс. Просматривая сборник, я обнаружила уравнения, содержащие не только один, но и несколько модулей. Учитель объяснила мне и моим одноклассникам, что такие уравнения называют уравнениями с «вложенными модулями». Такое название показалось для нас необычным, а решение на первый взгляд, довольно сложным. Так появилась тема для моей работы «Уравнения с модулем». Я решила глубже изучить эту тему, тем более, что она мне пригодится при сдаче экзаменов в конце учебного года и думаю, что понадобится в 10 и 11 классах. Все сказанное выше определяет актуальность выбранной мною темы.

Цель работы :

1. Рассмотреть различные методы решения уравнений с модулем.
2. Научиться решать уравнения, содержащие знак абсолютной величины, различными методами

Для работы над темой были сформулированы следующие задачи:

Задачи:

1. Изучить теоретический материал по теме «Модуль действительного числа».
2. Рассмотреть методы решения уравнений и закрепить полученные знания решением задач.
3. Полученные знания применять при решении различных уравнений, содержащих знак модуля в старших классах

Объект исследования: методы решения уравнений с модулем

Предмет исследования: уравнения с модулем

Методы исследования:

Теоретические : изучение литературы по теме исследования;

Internet – информации.

Анализ информации, полученной при изучении литературы; результатов полученных при решении уравнений с модулем различными способами.

Сравнение способов решения уравнений предмет рациональности их использования при решении различных уравнений с модулем.

«Мы начинаем думать, когда обо что-то стукнемся». Поль Валери.

1. Понятия и определения.

Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике изучаются понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это слово имеет множество значений и применяется не только в математике, физике и технике, но и в архитектуре, программировании и других точных науках.

Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля был введен в XIX веке Вейерштрассом.

В архитектуре модуль– исходная единица измерения, устанавливаемая для данного архитектурного сооружения.

В технике – это термин, применяемый в различных областях техники, служащий для обозначения различных коэффициентов и величин, например, модуль упругости, модуль зацепления…

В математике модуль имеет несколько значений, но я буду рассматривать его как абсолютную величину числа.

Определение1 : Модулем (абсолютной величиной) действительного числа а называется само это число, если а ≥0, или противоположное число – а , если а модуль нуля равен нулю.

При решении уравнений с модулем, удобно использовать свойства модуля.

Рассмотрим доказательства 5,6, 7 свойств.

Утверждение 5. Равенство │ а+в │=│ а │+│ в │ является верным, если ав ≥ 0.

Доказательство. Действительно, после возведения обеих частей данного равенства в квадрат, получим, │ а+в │²=│ а │²+2│ ав │+│ в │²,

а²+ 2 ав+в²=а²+ 2│ ав │+ в², откуда │ ав │= ав

А последнее равенство будет верным при ав ≥0.

Утверждение 6. Равенство │ а-в │=│ а │+│ в │ является верным при ав ≤0.

Доказательство. Для доказательства достаточно в равенстве

│ а+в │=│ а │+│ в │ заменить в на - в, тогда а· (- в ) ≥0, откуда ав ≤0.

Утверждение 7.Равенство │ а │+│ в │= а+в выполняется при а ≥0 и в ≥0.

Доказательство . Рассмотрев четыре случая а ≥0 и в ≥0; а ≥0 и в а в ≥0; а в а ≥0 и в ≥0.

(а-в ) в ≥0.

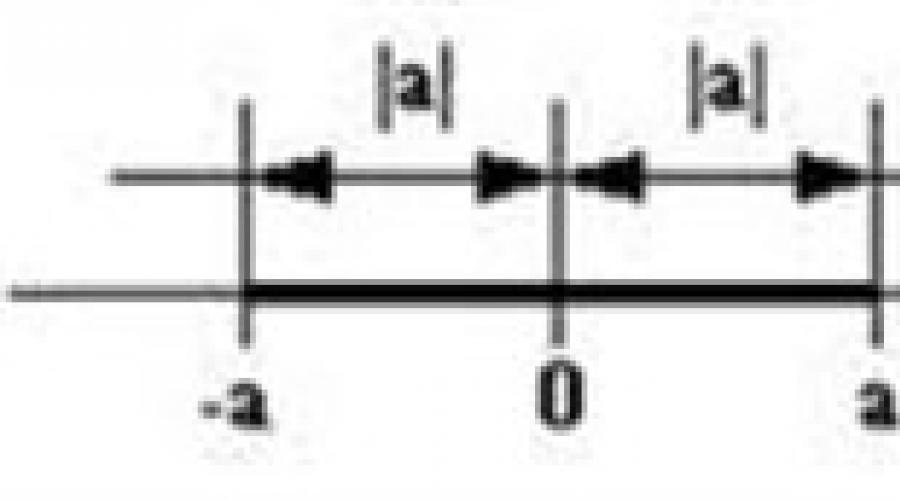
Геометрическая интерпретация

|а| - это расстояние на координатной прямой от точки с координатой а , до начала координат.

|-а| |а|

А 0 а х

Геометрическое толкование смысла |а| наглядно подтверждает, что |-а|=|а|

Если а 0, то на координатной прямой существует две точки а и –а, равноудаленные от нуля, модули которых равны.

Если а=0, то на координатной прямой |а| изображается точкой 0.

Определение 2: Уравнение с модулем – это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Например: |х +3|=1

Определение 3: Решить уравнение-это значит найти все его корни, или доказать, что корней нет.

2. Методы решения

Из определения и свойств модуля вытекают основные методы решения уравнений с модулем:

1. «Раскрытие» модуля (т.е. использование определения);
2. Использование геометрического смыла модуля (свойство 2);
3. Графический метод решения;
4. Использование равносильных преобразований (свойства 4,6);
5. Замена переменной (при этом используется свойство 5).
6. Метод интервалов.

Я решила достаточно большое количество примеров, но в работе представляю вашему вниманию только несколько, на мой взгляд, типичных примеров, решенных различными способами, потому что остальные дублируют друг друга и чтобы понять, как решать уравнения с модулем нет необходимости рассматривать все решенные примеры.

РЕШЕНИЕ УРАВНЕНИЙ | f(x)| = a

Рассмотрим уравнение | f(x)| = a, а R

Уравнение данного вида может быть решено по определению модуля:

Если а то уравнение корней не имеет.

Если а= 0, то уравнение равносильно f(x)=0.

Если а>0, то уравнение равносильно совокупности

Пример. Решить уравнение |3х+2|=4.

Р е ш е н и е.

|3х+2|=4, тогда 3х+2=4,

3х+2= -4;

Х=-2,

Х=2/3

О т в е т: -2;2/3.

РЕШЕНИЕ УРАВНЕНИЙ с ИСПОЛЬЗОВАНИЕМ ГЕОМЕТРИЧЕСКОГО СВОЙСТВА МОДУЛЯ.

Пример 1. Решить уравнение /х-1/+/х-3/=6.

Решение.

Решить данное уравнение значит найти все такие точки на числовой оси Ох, для каждой из которых сумма расстояний от нее до точек с координатами 1 и 3 равна 6.

Ни одна точка из отрезка не удовлетворяет этому условию, т.к. сумма указанных расстояний равна 2. Вне этого отрезка есть две точки это 5 и -1.

1 1 3 5

Ответ: -1;5

Пример 2. Решить уравнение |х 2 +х-5|+|х 2 +х-9|=10.

Решение.

Обозначим х 2 +х-5= а, тогда / а /+/ а-4 /=10. Найдем точки на оси Ох такие, что для каждой из них сумма расстояний до точек с координатами 0 и 4 равна 10. Этому условию удовлетворяют -4 и 7.

3 0 4 7

Значит х 2 +х-5= 4 х 2 +х-5=7

Х 2 +х-2=0 х 2 +х-12=0

Х 1= 1, х 2= -2 х 1= -4, х 2= 3 Ответ:-4;-2; 1; 3.

РЕШЕНИЕ УРАВНЕНИЙ | f (x )| = | g (x )|.

1. Так как | а |=|в |, если а= в, то уравнение вида | f (x )| = | g (x )| равносильно совокупности

Пример1.

Решить уравнение | x –2| = |3 – х |.

Р е ш е н и е.

Данное уравнение равносильно двум уравнениям:

х – 2 = 3 – х (1) и х – 2 = –3 + х (2)

2 х = 5 –2 = –3 – неверно

х = 2,5 уравнение не имеет решений.

О т в е т: 2,5.

Пример 2.

Решить уравнение |х 2 +3х-20|= |х 2 -3х+ 2|.

Р е ш е н и е.

Так как обе части уравнения неотрицательны, то возведение в квадрат является равносильным преобразованием:

(х 2 +3х-20) 2 = (х 2 -3х+2) 2

(х 2 +3х-20) 2 - (х 2 -3х+2) 2 =0,

(х 2 +3х-20-х 2 +3х-2) (х 2 +3х-20+х 2 -3х+2)=0,

(6х-22)(2х 2 -18)=0,

6х-22=0 или 2х 2 -18=0;

Х=22/6, х=3, х=-3.

Х=11/3

Ответ: -3; 3; 11/3.

РЕШЕНИЕ УРАВНЕНИЙ ВИДА | f (x )| = g (x ).

Отличие данных уравнений от | f(x)| = a в том, что в правой части тоже переменная. А она может быть как положительной, так и отрицательной. Поэтому в ее неотрицательности нужно специально убедиться, ведь модуль не может равняться отрицательному числу (свойство №1 )

1 способ

Решение уравнения | f (x )| = g (x ) сводится к совокупности решения уравнений и проверке справедливости неравенства g (x )>0 для найденных значений неизвестной.

2 способ (по определению модуля)

Так как | f (x )| = g (x ), если f (x) = 0; | f (x )| = - f (x ), если f (x )

Пример.

Решить уравнение |3 х –10| = х – 2.

Р е ш е н и е.

Данное уравнение равносильно совокупности двух систем:

О т в е т: 3; 4.

РЕШЕНИЕ УРАВНЕНИЙ ВИДА |f 1 (x)|+|f 2 (x)|+…+|f n (x)|=g(х)

Решение уравнений данного вида основано на определении модуля. Для каждой функции f 1 (x), f 2 (x), …, f n (x) необходимо найти область определения, ее нули и точки разрыва, разбивающие общую область определения на промежутки, в каждом из которых функции f 1 (x), f 2 (x), …, f n (x) сохраняют свой знак. Далее используя определение модуля, для каждой из найденных областей получим уравнение, которое необходимо решить на данном промежутке. Данный метод получил название « метод интервалов »

Пример .

Решить уравнение |х-2|-3|х+4|=1.

Р е ш е н и е.

Найдем точки, в которых подмодульные выражения равны нулю

х-2=0, х+4=0,

х=2; х=-4.

Разобьем числовую прямую на промежутки х

Решение уравнения сводится к решению трех систем:

О т в е т: -15, -1,8.

ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ УРАВНЕНИЙ, СОДЕРЖАЩИХ ЗНАК МОДУЛЯ.

Графический способ решения уравнений является приближенным, так ка точность зависит от выбранного единичнрого отрезка, толщины карандаша, углов под которыми пересекаются линии и т.д. Но этот метод позволяет оценивать сколько решений имеет то или иное уравнение.

Пример . Решить графически уравнение |x - 2| + |x - 3| + |2x - 8| = 9

Решение. Построим в одной системе координат графики функций

у=|x - 2| + |x - 3| + |2x - 8| и у=9.

Для построения графика необходимо рассмотреть данную функцию на каждом промежутке (-∞; 2); [ 3/2 ; ∞ )

Ответ: (- ∞ ; 4/3] [ 3/2 ; ∞ )

Метод равносильных преобразований мы использовали и при решении уравнений | f (x )| = | g (x )|.

УРАВНЕНИЯ СО «СЛОЖНЫМ МОДУЛЕМ»

Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя различные методы.

Пример 1.

Решить уравнение ||||x| – |–2| –1| –2| = 2.

Решение.

По определению модуля, имеем:

Решим первое уравнение.

1. ||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

х = 7.

Решим второе уравнение.

1. ||| x | –2| –1| = 0,

|| x | –2| = 1,

| x | –2 = 1 ,

| x | = 3 и | x | = 1,

х = 3; х = 1.

О т в е т: 1; 3; 7.

Пример 2.

Решить уравнение |2 – |x + 1|| = 3.

Р е ш е н и е.

Решим уравнение с помощью введения новой переменной.

Пусть | x + 1| = y , тогда |2 – y | = 3, отсюда

Выполним обратную замену:

(1) | x + 1| = –1 – нет решений.

(2) | x + 1| = 5

О т в е т: –6; 4.

Пример3 .

Сколько корней имеет уравнение | 2 | х | -6 | = 5 - х?

Решение. Решим уравнение, используя схемы равносильности.

Уравнение | 2 | х | -6 | = 5 -х равносильно системе:

Модуль числа a — это расстояние от начала координат до точки А (a ).

Чтобы понять это определение, подставим вместо переменной a любое число, например 3 и попробуем снова прочитать его:

Модуль числа 3 — это расстояние от начала координат до точки А (3 ).

Становится ясно, что модуль это ни что иное, как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3 )

Расстояние от начала координат до точки А(3 ) равно 3 (трём единицам или трём шагам).

Модуль числа обозначает двумя вертикальными линиями, например:

Модуль числа 3 обозначается так: |3|

Модуль числа 4 обозначается так: |4|

Модуль числа 5 обозначается так: |5|

Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:

Читается как: «Модуль числа три равен три»

Теперь попробуем найти модуль числа -3. Опять же возвращаемся к определению и подставляем в него число -3. Только вместо точки A используем новую точку B . Точку A мы уже использовали в первом примере.

Модулем числа —3 называют расстояние от начала координат до точки B (—3 ).

Расстояние от одного пункта до другого не может быть отрицательным. Поэтому и модуль любого отрицательного числа, будучи являясь расстоянием тоже не будет отрицательным. Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:

Читается как: «Модуль числа минус три равен три»

Модуль числа 0 равен 0, та как точка с координатой 0 совпадает с началом координат, т.е. расстояние от начала координат до точки O(0) равно нулю:

«Модуль нуля равен нулю»

Делаем выводы:

• Модуль числа не может быть отрицательным;
• Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу;
• Противоположные числа имеют равные модули.

Противоположные числа

Числа, отличающиеся только знаками называют противоположными . Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числа −2 знак минуса, а у 2 знак плюса, но мы его не видим, потому что плюс, как мы говорили ранее, по традиции не пишут.

Еще примеры противоположных чисел:

Противоположные числа имеют равные модули. Например, найдём модули для −2 и 2

На рисунке видно, что расстояние от начала координат до точек A(−2) и B(2) одинаково равно двум шагам.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Модуль – это абсолютная величина выражения. Чтобы хоть как-то обозначить модуль, принято использовать прямые скобки. То значение, которое заключено в ровных скобках, и является тем значением, которое взято по модулю. Процесс решения любого модуля заключается в раскрытии тех самых прямых скобок, которые математическим языком именуются модульными скобками. Их раскрытие происходит по определенному ряду правил. Также, в порядке решения модулей, находятся и множества значений тех выражений, которые находились в модульных скобках. В большей части всех случаев, модуль раскрывается таким способом, что выражение, которое было подмодульным, получает и положительные, и отрицательные значения, в числе которых также и значение ноль. Если отталкиваться от установленных свойств модуля, то в процессе составляются различные уравнения или же неравенства от исходного выражения, которые затем необходимо решить. Разберемся же с тем, как решать модули.

Процесс решения

Решение модуля начинается с записи исходного уравнения с модулем. Чтобы ответить на вопрос о том, как решать уравнения с модулем, нужно раскрыть его полностью. Для решения такого уравнения, модуль раскрывается. Все модульные выражения должны быть рассмотрены. Следует определить при каких значениях неизвестных величин, входящих в его состав, модульное выражение в скобках обращается в ноль. Для того чтобы это сделать, достаточно приравнять выражение в модульных скобках к нулю, а затем высчитать решение образовавшегося уравнения. Найденные значения нужно зафиксировать. Таким же способом нужно определить еще и значение всех неизвестных переменных для всех модулей в данном уравнении. Далее необходимо заняться определением и рассмотрением всех случаев существования переменных в выражениях, когда они отличны от значения ноль. Для этого нужно записать некоторую систему из неравенств соответственно всем модулям в исходном неравенстве. Неравенства должны быть составлены так, чтоб они охватывали все имеющиеся и возможные значения для переменной, которые находят на числовой прямой. Затем нужно начертить для визуализации эту самую числовую прямую, на которой в дальнейшем отложить все полученные значения.

Практически все сейчас можно сделать в интернете. Не является исключением из правил и модуль. Решить онлайн его можно на одном из многочисленных современных ресурсов. Все те значения переменной, которые находятся в нулевом модуле, будут особым ограничением, которое будет использовано в процессе решения модульного уравнения. В исходном уравнении требуется раскрыть все имеющиеся модульные скобки, при этом, изменяя знак выражения, таким образом, чтобы значения искомой переменной совпадали с теми значениями, которые видно на числовой прямой. Полученное уравнение необходимо решить. То значение переменной, которое будет получено в ходе решения уравнения, нужно проверять на ограничение, которое задано самим модулем. Если значение переменной полностью удовлетворяет условие, то оно является правильным. Все корни, которые будут получены в ходе решения уравнения, но не будут подходить по ограничениям, должны быть отброшены.