Свойства функции наибольшее и наименьшее значение. Как найти наименьшее значение функции

И для её решения потребуется минимальное знание темы. Заканчивается очередной учебный год, всем хочется на каникулы, и чтобы приблизить этот момент я сразу же перехожу к делу:

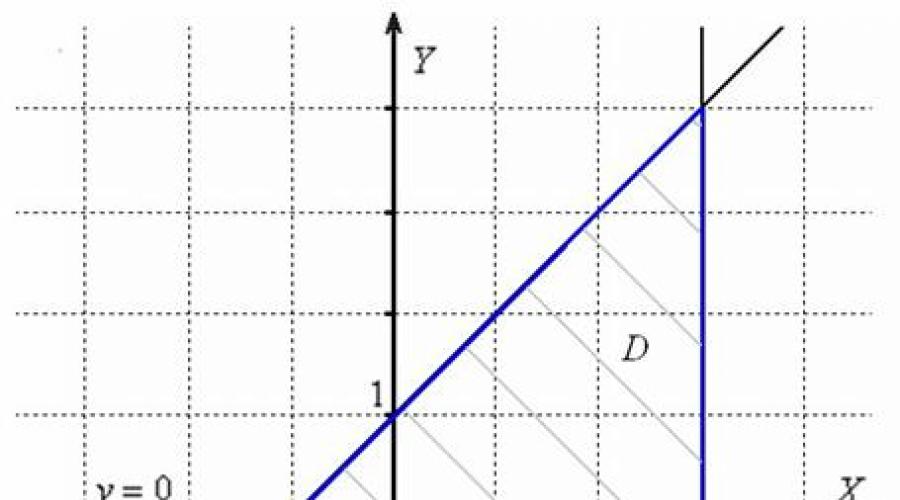
Начнём с области. Область, о которой идёт речь в условии, представляет собой ограниченное замкнутое множество точек плоскости . Например, множество точек, ограниченное треугольником, включая ВЕСЬ треугольник (если из границы «выколоть» хотя бы одну точку, то область перестанет быть замкнутой) . На практике также встречаются области прямоугольной, круглой и чуть более сложных форм. Следует отметить, что в теории математического анализа даются строгие определения ограниченности, замкнутости, границы и т.д. , но, думаю, все осознаЮт эти понятия на интуитивном уровне, а бОльшего сейчас и не надо.

Плоская область стандартно обозначается буквой , и, как правило, задаётся аналитически – несколькими уравнениями (не обязательно линейными) ; реже неравенствами. Типичный словесный оборот: «замкнутая область , ограниченная линиями ».

Неотъемлемой частью рассматриваемого задания является построение области на чертеже. Как это сделать? Нужно начертить все перечисленные линии (в данном случае 3 прямые ) и проанализировать, что же получилось. Искомую область обычно слегка штрихуют, а её границу выделяют жирной линией:


Эту же область можно задать и линейными неравенствами : , которые почему-то чаще записывают перечислительным списком, а не системой .
Так как граница принадлежит области, то все неравенства, разумеется, нестрогие .

А теперь суть задачи. Представьте, что из начала координат прямо на вас выходит ось . Рассмотрим функцию , которая непрерывна в каждой точке области . График данной функции представляет собой некоторую поверхность , и маленькое счастье состоит в том, что для решения сегодняшней задачи нам совсем не обязательно знать, как эта поверхность выглядит. Она может располагаться выше, ниже, пересекать плоскость – всё это не важно. А важно следующее: согласно теоремам Вейерштрасса , непрерывная в ограниченной замкнутой области функция достигает в ней наибольшего (самого «высокого») и наименьшего (самого «низкого») значений, которые и требуется найти. Такие значения достигаются либо в стационарных точках , принадлежащих области D , либо в точках, которые лежат на границе этой области. Из чего следует простой и прозрачный алгоритм решения:

Пример 1

В ограниченной замкнутой области

Решение : прежде всего, нужно изобразить область на чертеже. К сожалению, мне технически трудно сделать интерактивную модель задачи, и поэтому я сразу приведу финальную иллюстрацию, на которой изображены все «подозрительные» точки , найденные в ходе исследования. Обычно они проставляются одна за другой по мере их обнаружения:

Исходя из преамбулы, решение удобно разбить на два пункта:

I) Найдём стационарные точки. Это стандартное действие, которые мы неоднократно выполняли на уроке об экстремумах нескольких переменных :

Найденная стационарная точка принадлежит области: (отмечаем её на чертеже) , а значит, нам следует вычислить значение функции в данной точке:

– как и в статье Наибольшее и наименьшее значения функции на отрезке , важные результаты я буду выделять жирным шрифтом. В тетради их удобно обводить карандашом.

Обратите внимание на наше второе счастье – нет никакого смысла проверять достаточное условие экстремума . Почему? Даже если в точке функция достигает, например, локального минимума , то это ЕЩЁ НЕ ЗНАЧИТ, что полученное значение будет минимальным во всей области (см. начало урока о безусловных экстремумах ) .

Что делать, если стационарная точка НЕ принадлежит области? Почти ничего! Нужно отметить, что и перейти к следующему пункту.

II) Исследуем границу области.

Поскольку граница состоит из сторон треугольника, то исследование удобно разбить на 3 подпункта. Но лучше это сделать не абы как. С моей точки зрения, сначала выгоднее рассмотреть отрезки, параллельные координатным осям, и в первую очередь – лежащие на самих осях. Чтобы уловить всю последовательность и логику действий постарайтесь изучить концовку «на одном дыхании»:

1) Разберёмся с нижней стороной треугольника. Для этого подставим непосредственно в функцию:

Как вариант, можно оформить и так:

Геометрически это означает, что координатная плоскость (которая тоже задаётся уравнением ) «высекает» из поверхности «пространственную» параболу , вершина которой немедленно попадает под подозрение. Выясним, где она находится :

– полученное значение «попало» в область, и вполне может статься, что в точке (отмечаем на чертеже) функция достигает наибольшего либо наименьшего значения во всей области . Так или иначе, проводим вычисления:

Другие «кандидаты» – это, конечно же, концы отрезка. Вычислим значения функции в точках (отмечаем на чертеже) :

Тут, кстати, можно выполнить устную мини-проверку по «урезанной» версии :

2) Для исследования правой стороны треугольника подставляем в функцию и «наводим там порядок»:

Здесь сразу же выполним черновую проверку, «прозванивая» уже обработанный конец отрезка:
, отлично.

Геометрическая ситуация родственна предыдущему пункту:

– полученное значение тоже «вошло в сферу наших интересов», а значит, нужно вычислить, чему равна функция в появившейся точке :

Исследуем второй конец отрезка :

Используя функцию , выполним контрольную проверку:

3) Наверное, все догадываются, как исследовать оставшуюся сторону . Подставляем в функцию и проводим упрощения:

Концы отрезка уже исследованы, но на черновике всё равно проверяем, правильно ли мы нашли функцию :
– совпало с результатом 1-го подпункта;
– совпало с результатом 2-го подпункта.

Осталось выяснить, если ли что-то интересное внутри отрезка :

– есть! Подставляя в уравнение прямой , получим ординату этой «интересности»:

Отмечаем на чертеже точку и находим соответствующее значение функции :

Проконтролируем вычисления по «бюджетной» версии :
, порядок.

И заключительный шаг : ВНИМАТЕЛЬНО просматриваем все «жирные» числа, начинающим рекомендую даже составить единый список:

из которого выбираем наибольшее и наименьшее значения. Ответ запишем в стилистике задачи нахождения наибольшего и наименьшего значений функции на отрезке :

На всякий случай ещё раз закомментирую геометрический смысл результата:
– здесь самая высокая точка поверхности в области ;
– здесь самая низкая точка поверхности в области .

В разобранной задаче у нас выявилось 7 «подозрительных» точек, но от задачи к задаче их количество варьируется. Для треугольной области минимальный «исследовательский набор» состоит из трёх точек. Такое бывает, когда функция , например, задаёт плоскость – совершенно понятно, что стационарные точки отсутствуют, и функция может достигать наибольшего/наименьшего значений только в вершинах треугольника. Но подобных примеров раз, два и обчёлся – обычно приходится иметь дело с какой-нибудь поверхностью 2-го порядка .

Если вы немного порешаете такие задания, то от треугольников голова может пойти кругом, и поэтому я приготовил для вас необычные примеры чтобы она стала квадратной:))

Пример 2

Найти наибольшее и наименьшее значения функции в замкнутой области, ограниченной линиями

Пример 3

Найти наибольшее и наименьшее значения функции в ограниченной замкнутой области .

Особое внимание обратите на рациональный порядок и технику исследования границы области, а также на цепочку промежуточных проверок, которая практически стопроцентно позволит избежать вычислительных ошибок. Вообще говоря, решать можно как угодно, но в некоторых задачах, например, в том же Примере 2, есть все шансы значительно усложнить себе жизнь. Примерный образец чистового оформления заданий в конце урока.

Систематизируем алгоритм решения, а то с моей прилежностью паука он как-то затерялся в длинной нити комментариев 1-го примера:

– На первом шаге строим область , её желательно заштриховать, а границу выделить жирной линией. В ходе решения будут появляться точки, которые нужно проставлять на чертеже.

– Найдём стационарные точки и вычислим значения функции только в тех из них , которые принадлежат области . Полученные значения выделяем в тексте (например, обводим карандашом). Если стационарная точка НЕ принадлежит области, то отмечаем этот факт значком либо словесно. Если же стационарных точек нет вовсе, то делаем письменный вывод о том, что они отсутствуют. В любом случае данный пункт пропускать нельзя!

– Исследуем границу области. Сначала выгодно разобраться с прямыми, которые параллельны координатным осям (если таковые есть вообще) . Значения функции, вычисленные в «подозрительных» точках, также выделяем. О технике решения очень много сказано выше и ещё кое-что будет сказано ниже – читайте, перечитывайте, вникайте!

– Из выделенных чисел выбираем наибольшее и наименьшее значения и даём ответ. Иногда бывает, что такие значения функция достигает сразу в нескольких точках – в этом случае все эти точки следует отразить в ответе. Пусть, например, и оказалось, что это наименьшее значение. Тогда записываем, что

Заключительные примеры посвящены другим полезным идеям, которые пригодятся на практике:

Пример 4

Найти наибольшее и наименьшее значения функции в замкнутой области .

Я сохранил авторскую формулировку, в которой область задана в виде двойного неравенства. Это условие можно записать эквивалентной системой или же в более традиционном для данной задачи виде:

Напоминаю, что с нелинейными неравенствами мы сталкивались на , и если вам не понятен геометрический смысл записи , то, пожалуйста, не откладывайте и проясните ситуацию прямо сейчас;-)

Решение , как всегда, начинается с построения области, которая представляет собой своеобразную «подошву»:

Мда, иногда приходится грызть не только гранит науки….

I) Найдём стационарные точки:

Система-мечта идиота:)

Стационарная точка принадлежит области, а именно, лежит на её границе.

А так, оно, ничего… весело урок пошёл – вот что значит попить правильного чая =)

II) Исследуем границу области. Не мудрствуя лукаво, начнём с оси абсцисс:

1) Если , то

Найдём, где вершина параболы:
– ценИте такие моменты – «попали» прямо в точку , с которой уже всё ясно. Но о проверке всё равно не забываем:

Вычислим значения функции на концах отрезка:

2) С нижней частью «подошвы» разберёмся «за один присест» – безо всяких комплексов подставляем в функцию, причём, интересовать нас будет лишь отрезок :

Контроль:

Вот это уже вносит некоторое оживление в монотонную езду по накатанной колее. Найдём критические точки:

Решаем квадратное уравнение , помните ещё о таком? …Впрочем, помните, конечно, иначе бы не читали эти строки =) Если в двух предыдущих примерах были удобны вычисления в десятичных дробях (что, кстати, редкость), то здесь нас поджидают привычные обыкновенные дроби. Находим «иксовые» корни и по уравнению определяем соответствующие «игрековые» координаты точек-«кандидатов»:


Вычислим значения функции в найденных точках:

Проверку по функции проведите самостоятельно.

Теперь внимательно изучаем завоёванные трофеи и записываем ответ :

Вот это «кандидаты», так «кандидаты»!

Для самостоятельного решения:

Пример 5

Найти наименьшее и наибольшее значения функции в замкнутой области

Запись с фигурными скобками читается так: «множество точек , таких, что ».

Иногда в подобных примерах используют метод множителей Лагранжа , но реальная необходимость его применять вряд ли возникнет. Так, например, если дана функция с той же областью «дэ», то после подстановки в неё – с производной от никаких трудностей; причём оформляется всё «одной строкой» (со знаками ) без надобности рассматривать верхнюю и нижнюю полуокружности по отдельности. Но, конечно, бывают и более сложные случаи, где без функции Лагранжа (где , например, то же уравнение окружности) обойтись трудно – как трудно обойтись и без хорошего отдыха!

Всем хорошо сдать сессию и до скорых встреч в следующем сезоне!

Решения и ответы:

Пример 2: Решение : изобразим область на чертеже:

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых - монотонность .

Функция f (x ) называется монотонно возрастающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:

x 1 < x 2 ⇒ f (x 1 ) < f (x 2 ).

Функция f (x ) называется монотонно убывающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:

x 1 < x 2 ⇒ f (x 1 ) > f (x 2 ).

Другими словами, для возрастающей функции чем больше x , тем больше f (x ). Для убывающей функции все наоборот: чем больше x , тем меньше f (x ).

Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 < a < 1. Не забывайте про область допустимых значений логарифма: x > 0.

f (x ) = log a x (a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 < a < 1. Но в отличие от логарифма, показательная функция определена для всех чисел, а не только для x > 0:

f (x ) = a x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит - сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax 2 + bx + c . Его график - стандартная парабола, в которой нас интересуют:

1. Ветви параболы - могут уходить вверх (при a > 0) или вниз (a < 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы - точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a < 0) значение.

Наибольший интерес представляет именно вершина параболы , абсцисса которой рассчитывается по формуле:

Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x 0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x 0 для квадратного трехчлена, а на функцию - забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок в условии задачи отсутствует. Следовательно, вычислять f (a ) и f (b ) не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна - это вершина параболы x 0 , координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы y = ax 2 + bx + c и найти ее вершину по формуле: x 0 = −b /2a ;
2. Найти значение исходной функции в этой точке: f (x 0). Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике - именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Под корнем стоит квадратичная функция y = x 2 + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.

Вершина параболы:

x 0 = −b /(2a ) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке x 0 = −3 функция y = x 2 + 6x + 13 принимает наименьшее значение.

Корень монотонно возрастает, значит x 0 - точка минимума всей функции. Имеем:

Задача. Найдите наименьшее значение функции:

y = log 2 (x 2 + 2x + 9)

Под логарифмом снова квадратичная функция: y = x 2 + 2x + 9. График - парабола ветвями вверх, т.к. a = 1 > 0.

Вершина параболы:

x 0 = −b /(2a ) = −2/(2 · 1) = −2/2 = −1

Итак, в точке x 0 = −1 квадратичная функция принимает наименьшее значение. Но функция y = log 2 x - монотонная, поэтому:

y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = ... = log 2 8 = 3

В показателе стоит квадратичная функция y = 1 − 4x − x 2 . Перепишем ее в нормальном виде: y = −x 2 − 4x + 1.

Очевидно, что график этой функции - парабола, ветви вниз (a = −1 < 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2

Исходная функция - показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x 0 = −2:

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка , а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби - никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

Под корнем снова квадратичная функция: y = 3 − 2x − x 2 . Ее график - парабола, но ветви вниз, поскольку a = −1 < 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Теперь найдем вершину параболы:

x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1

Точка x 0 = −1 принадлежит отрезку ОДЗ - и это хорошо. Теперь считаем значение функции в точке x 0 , а также на концах ОДЗ:

y (−3) = y (1) = 0

Итак, получили числа 2 и 0. Нас просят найти наибольшее - это число 2.

Задача. Найдите наименьшее значение функции:

y = log 0,5 (6x − x 2 − 5)

Внутри логарифма стоит квадратичная функция y = 6x − x 2 − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5 < 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.

Ищем вершину параболы:

x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: x 0 = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x 0:

y min = y (3) = log 0,5 (6 · 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2

С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования... Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.

Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X , который является или всей областью определения функции или частью области определения. Сам интервал X может быть отрезком , открытым интервалом , бесконечным промежутком .

В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x) .

Навигация по странице.

Наибольшее и наименьшее значение функции - определения, иллюстрации.

Кратко остановимся на основных определениях.

Наибольшим значением функции , что для любого справедливо неравенство .

Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .

Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.

Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.

Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.

Сразу ответим на один из самых распространенных вопросов по этой теме:"Всегда ли можно определить наибольшее (наименьшее) значение функции"? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.

Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.

На отрезке

На первом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри отрезка [-6;6] .

Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на . В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее - в точке с абсциссой, соответствующей правой границе интервала.

На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.

На открытом интервале

На четвертом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри открытого интервала (-6;6) .

На интервале , о наибольшем значении никаких выводов сделать нельзя.

На бесконечности

В примере, представленном на седьмом рисунке, функция принимает наибольшее значение (max y ) в стационарной точке с абсциссой x=1 , а наименьшее значение (min y ) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3 .

На интервале функция не достигает ни наименьшего, ни наибольшего значения. При стремлении к x=2 справа значения функции стремятся к минус бесконечности (прямая x=2 является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3 . Графическая иллюстрация этого примера приведена на рисунке №8.

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке .

Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.

1. Находим область определения функции и проверяем, содержится ли в ней весь отрезок .
2. Находим все точки, в которых не существует первая производная и которые содержатся в отрезке (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
3. Определяем все стационарные точки, попадающие в отрезок . Для этого, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
4. Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b .
5. Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми наибольшим и наименьшим значениями функции соответственно.

Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.

Пример.

Найти наибольшее и наименьшее значение функции

• на отрезке ;
• на отрезке [-4;-1] .

Решение.

Областью определения функции является все множество действительных чисел, за исключением нуля, то есть . Оба отрезка попадают в область определения.

Находим производную функции по :

Очевидно, производная функции существует во всех точках отрезков и [-4;-1] .

Стационарные точки определим из уравнения . Единственным действительным корнем является x=2 . Эта стационарная точка попадает в первый отрезок .

Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1 , x=2 и x=4 :

Следовательно, наибольшее значение функции достигается при x=1 , а наименьшее значение – при x=2 .

Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1] (так как он не содержит ни одной стационарной точки):

Дана функция , определенная и непрерывная на некотором промежутке . Требуется найти наибольшее (наименьшее) значение функции на этом промежутке.

Теоретические основы.
Теорема (Вторая теорема Вейерштрасса):

Если функция определена и непрерывна в замкнутом промежутке , то она достигает в этом промежутке своих наибольшего и наименьшего значений.

Функция может достигать своих наибольших и наименьших значений либо на внутренних точках промежутка, либо на его границах. Проиллюстрируем все возможные варианты.

Пояснение:
1) Функция достигает своего наибольшего значения на левой границе промежутка в точке , а своего наименьшего значения на правой границе промежутка в точке .
2) Функция достигает своего наибольшего значения в точке (это точка максимума) , а своего наименьшего значения на правой границе промежутка в точке .
3) Функция достигает своего наибольшего значения на левой границе промежутка в точке , а своего наименьшего значения в точке (это точка минимума).
4) Функция постоянна на промежутке, т.е. она достигает своего минимального и максимального значения в любой точке промежутка, причем минимальное и максимальное значения равны между собой.
5) Функция достигает своего наибольшего значения в точке , а своего наименьшего значения точке (несмотря на то, что функция имеет на этом промежутке как максимум, так и минимум).
6) Функция достигает своего наибольшего значения в точке (это точка максимума), а своего наименьшего значения в точке (это точка минимума).
Замечание:

«Максимум» и «максимальное значение» — разные вещи. Это следует из определения максимума и интуитивного понимания словосочетания «максимальное значение».

Алгоритм решения задачи 2.



4) Выбрать из полученных значений наибольшее (наименьшее) и записать ответ.

Пример 4:

Определить наибольшее и наименьшее значение функции на отрезке .
Решение:
1) Найти производную функции .

2) Найти стационарные точки (и точки, подозрительные на экстремум), решив уравнение . Обратить внимание на точки, в которых не существует двусторонней конечной производной.

3) Вычислить значения функции в стационарных точках и на границах интервала.

4) Выбрать из полученных значений наибольшее (наименьшее) и записать ответ.

Функция на этом отрезке достигает своего наибольшего значения в точке с координатами .

Функция на этом отрезке достигает своего наименьшего значения в точке с координатами .

В правильность вычислений можно убедиться, взглянув на график исследуемой функции.


Замечание: Наибольшего значения функция достигает в точке максимума, а наименьшего – на границе отрезка.

Частный случай.

Предположим, требуется найти максимально и минимальное значение некоторой функции на отрезке. После выполнение первого пункта алгоритма, т.е. вычисления производной, становится ясно, что, например, она принимает только отрицательные значения на всем рассматриваемом отрезке. Помним, что если производная отрицательна, то функция убывает. Получили, что на всем отрезке функция убывает. Эта ситуация отображена на графике № 1 в начале статьи.

На отрезке функция убывает, т.е. точек экстремумов у нее нет. Из картинки видно, что наименьшее значение функция примет на правой границе отрезка, а наибольшее значение — на левой. если же производная на отрезке всюду положительна, то функция возрастает. Наименьшее значение — на левой границе отрезка, наибольшее — на правой.

В этой статье я расскажу про алгоритм поиска наибольшего и наименьшего значения функции, точек минимума и максимума.

Из теории нам точно пригодится таблица производных и правила дифференцирования . Все это есть в этой табличке:

Алгоритм поиска наибольшего и наименьшего значения.

Мне удобнее объяснять на конкретном примере. Рассмотрим:

Пример: Найдите наибольшее значение функции y=x^5+20x^3–65x на отрезке [–4;0].

Шаг 1. Берем производную.

Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Шаг 2. Находим точки экстремума.

Точкой экстремума мы называем такие точки, в которых функция достигает своего наибольшего или наименьшего значения.

Чтобы найти точки экстремума, надо приравнять производную функции к нулю (y" = 0)

5x^4 + 60x^2 - 65 = 0

Теперь решаем это биквадратное уравнение и найденные корни есть наши точки экстремума.

Я решаю такие уравнения заменой t = x^2, тогда 5t^2 + 60t - 65 = 0.

Сократим уравнение на 5, получим: t^2 + 12t - 13 = 0

D = 12^2 - 4*1*(-13) = 196

T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

Делаем обратную замену x^2 = t:

X_(1 и 2) = ±sqrt(1) = ±1
x_(3 и 4) = ±sqrt(-13) (исключаем, под корнем не может быть отрицательных чисел, если конечно речь не идет о комплексных числах)

Итого: x_(1) = 1 и x_(2) = -1 - это и есть наши точки экстремума.

Шаг 3. Определяем наибольшее и наименьшее значение.

Метод подстановки.

В условии нам был дан отрезок [b][–4;0]. Точка x=1 в этот отрезок не входит. Значит ее мы не рассматриваем. Но помимо точки x=-1 нам также надо рассмотреть левую и правую границу нашего отрезка, то есть точки -4 и 0. Для этого подставляем все эти три точки в исходную функцию. Заметьте исходную - это ту, которая дана в условии (y=x^5+20x^3–65x), некоторые начинают подставлять в производную...

Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

Значит наибольшее значение функции это [b]44 и достигается оно в точки [b]-1, которая называется точкой максимума функции на отрезке [-4; 0].

Мы решили и получили ответ, мы молодцы, можно расслабиться. Но стоп! Вам не кажется, что считать y(-4) как-то слишком сложно? В условиях ограниченного времени лучше воспользоваться другим способом, я называю его так:

Через промежутки знакопостоянства.

Находятся эти промежутки для производной функции, то есть для нашего биквадратного уравнения.

Я делаю это следующим образом. Рисую направленный отрезок. Расставляю точки: -4, -1, 0, 1. Не смотря на то, что 1 не входит в заданный отрезок, ее все равно следует отметить для того, чтобы корректно определить промежутки знакопостоянства. Возьмем какое-нибудь число во много раз больше 1, допустим 100, мысленно подставим его в наше биквадратное уравнение 5(100)^4 + 60(100)^2 - 65. Даже ничего не считая становится очевидно, что в точке 100 функция имеет знак плюс. А значит и на промежутки от 1 до 100 она имеет знак плюс. При переходе через 1 (мы идем справа налево)функция сменит знак на минус. При переходе через точку 0 функция сохранит свой знак, так как это лишь граница отрезка, а не корень уравнения. При переходе через -1 функция опять сменит знак на плюс.

Из теории мы знаем, что там, где производная функции (а мы именно для нее это и чертили) меняет знак с плюса на минус (точка -1 в нашем случае) функция достигает своего локального максимума (y(-1)=44, как была посчитано ранее) на данном отрезке (это логически очень понятно, функция перестала возрастать, так как достигла своего максимума и начала убывать).

Соответственно, там где производная функции меняет знак с минуса на плюс , достигается локальный минимум функции . Да, да, мы также нашли точку локального минимума это 1, а y(1) - это минимальное значение функции на отрезке, допустим от -1 до +∞. Обратите огромное внимание, что это лишь ЛОКАЛЬНЫЙ МИНИМУМ, то есть минимум на определенном отрезке. Так как действительный (глобальный) минимум функция достигнет где-то там, в -∞.

На мой взгляд первый способ проще теоретически, а второй проще с точки зрения арифметических действий, но намного сложнее с точки зрения теории. Ведь иногда бывают случаи, когда функция не меняет знак при переходе через корень уравнения, да и вообще можно запутаться с этими локальными, глобальными максимумами и минимумами, хотя Вам так и так придется это хорошо освоить, если вы планируете поступать в технический ВУЗ (а для чего иначе сдавать профильное ЕГЭ и решать это задание). Но практика и только практика раз и навсегда научит Вас решать такие задачи. А тренироваться можете на нашем сайте. Вот .

Если появились какие-то вопросы, или что-то непонятно - обязательно спросите. Я с радостью Вам отвечу, и внесу изменения, дополнения в статью. Помните мы делаем этот сайт вместе!