Faça um estudo da função e construa seu gráfico. Exame completo da função e plotagem do gráfico
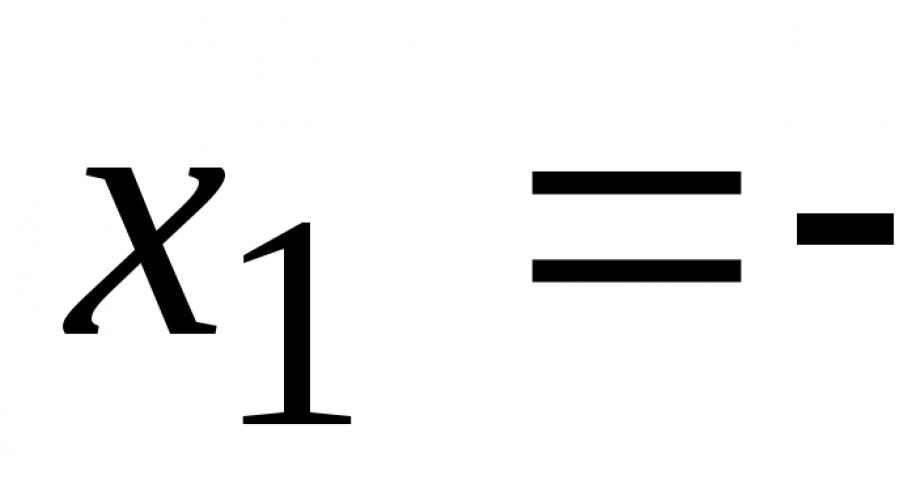
Leia também
Para estudar completamente a função e traçar seu gráfico, é recomendado usar o seguinte esquema:
1) encontre o domínio de definição da função;
2) encontrar os pontos de descontinuidade da função e assíntotas verticais (se existirem);
3) investigar o comportamento da função no infinito, encontrar assíntotas horizontais e oblíquas;
4) examinar a função quanto à paridade (estranha) e periodicidade (para funções trigonométricas);
5) encontrar extremos e intervalos de monotonicidade da função;
6) determinar os intervalos de convexidade e pontos de inflexão;
7) encontre os pontos de intersecção com os eixos coordenados e, se possível, alguns pontos adicionais que esclarecem o gráfico.
O estudo da função é realizado simultaneamente à construção do seu gráfico.
Exemplo 9 Explore a função e construa um gráfico.
1. Âmbito de definição: ;
2. A função sofre descontinuidade em pontos  ,
, ;
;
Examinamos a função quanto à presença de assíntotas verticais.
 ;
; ,
,
 ─ assíntota vertical.
─ assíntota vertical.
 ;
; ,
,
 ─ assíntota vertical.
─ assíntota vertical.
3. Examinamos a função quanto à presença de assíntotas oblíquas e horizontais.
Direto  ─ assíntota oblíqua, se
─ assíntota oblíqua, se  ,
,
 .
.
 ,
, .
.
Direto  ─ assíntota horizontal.
─ assíntota horizontal.
4. A função é par porque  . A paridade da função indica a simetria do gráfico em relação ao eixo y.
. A paridade da função indica a simetria do gráfico em relação ao eixo y.
5. Encontre os intervalos de monotonicidade e extremos da função.
Vamos encontrar os pontos críticos, ou seja, pontos em que a derivada é 0 ou não existe:  ;
; . Temos três pontos
. Temos três pontos  ;
;
 . Esses pontos dividem todo o eixo real em quatro intervalos. Vamos definir os sinais
. Esses pontos dividem todo o eixo real em quatro intervalos. Vamos definir os sinais  em cada um deles.
em cada um deles.

Nos intervalos (-∞; -1) e (-1; 0) a função aumenta, nos intervalos (0; 1) e (1; +∞) ─ diminui. Ao passar por um ponto  a derivada muda de sinal de mais para menos, portanto, neste ponto a função tem um máximo
a derivada muda de sinal de mais para menos, portanto, neste ponto a função tem um máximo  .
.
6. Encontre os intervalos de convexidade e pontos de inflexão.

Vamos encontrar os pontos em que  é 0 ou não existe.
é 0 ou não existe.
 não tem raízes reais.
não tem raízes reais.  ,
,
 ,
,

Pontos  E
E  divida o eixo real em três intervalos. Vamos definir o sinal
divida o eixo real em três intervalos. Vamos definir o sinal  em cada intervalo.
em cada intervalo.

Assim, a curva nos intervalos  E
E  convexo para baixo, no intervalo (-1;1) convexo para cima; não há pontos de inflexão, pois a função está em pontos
convexo para baixo, no intervalo (-1;1) convexo para cima; não há pontos de inflexão, pois a função está em pontos  E
E  não determinado.
não determinado.
7. Encontre os pontos de intersecção com os eixos.
Com eixo  o gráfico da função cruza no ponto (0; -1) e com o eixo
o gráfico da função cruza no ponto (0; -1) e com o eixo  o gráfico não se cruza, porque o numerador desta função não tem raízes reais.
o gráfico não se cruza, porque o numerador desta função não tem raízes reais.
O gráfico da função dada é mostrado na Figura 1.

Figura 1 ─ Gráfico da função 
Aplicação do conceito de derivada em economia. Função de elasticidade
Para estudar processos econômicos e resolver outros problemas aplicados, o conceito de elasticidade de uma função é frequentemente utilizado.
Definição. Função de elasticidade  é chamado de limite da razão do incremento relativo da função
é chamado de limite da razão do incremento relativo da função  ao incremento relativo da variável
ao incremento relativo da variável  no
no  , . (VII)
, . (VII)
A elasticidade de uma função mostra aproximadamente quantos por cento a função mudará  quando a variável independente muda
quando a variável independente muda  em 1%.
em 1%.
A função elasticidade é utilizada na análise da demanda e do consumo. Se a elasticidade da demanda (em valor absoluto)  , então a demanda é considerada elástica se
, então a demanda é considerada elástica se  ─ neutro se
─ neutro se  ─ inelástico em relação ao preço (ou renda).
─ inelástico em relação ao preço (ou renda).
Exemplo 10 Calcule a elasticidade da função  e encontre o valor do índice de elasticidade para
e encontre o valor do índice de elasticidade para  = 3.
= 3.
Solução: de acordo com a fórmula (VII), a elasticidade da função é:
Seja x = 3, então  .Isso significa que se a variável independente aumentar 1%, então o valor da variável dependente aumentará 1,42%.
.Isso significa que se a variável independente aumentar 1%, então o valor da variável dependente aumentará 1,42%.
Exemplo 11 Deixe a demanda funcionar  em relação ao preço
em relação ao preço  parece
parece  , Onde
, Onde  ─ coeficiente constante. Encontre o valor do indicador de elasticidade da função de demanda ao preço x = 3 den. unidades
─ coeficiente constante. Encontre o valor do indicador de elasticidade da função de demanda ao preço x = 3 den. unidades
Solução: calcule a elasticidade da função demanda usando a fórmula (VII)
Acreditar  unidades monetárias, obtemos
unidades monetárias, obtemos  . Isto significa que a um preço
. Isto significa que a um preço  unidades monetárias um aumento de 1% no preço causará uma diminuição de 6% na demanda, ou seja, a demanda é elástica.
unidades monetárias um aumento de 1% no preço causará uma diminuição de 6% na demanda, ou seja, a demanda é elástica.
Hoje convidamos você a explorar e construir o gráfico de uma função conosco. Depois de estudar cuidadosamente este artigo, você não precisará suar muito para concluir esse tipo de tarefa. Não é fácil estudar e construir o gráfico de uma função; é um trabalho volumoso que exige máxima atenção e precisão nos cálculos. Para facilitar a compreensão do material, estudaremos passo a passo a mesma função e explicaremos todas as nossas ações e cálculos. Bem-vindo ao incrível e mundo fascinante matemática! Ir!
Domínio
Para explorar e representar graficamente uma função, você precisa conhecer várias definições. Função é um dos conceitos principais (básicos) da matemática. Reflete a dependência entre diversas variáveis (duas, três ou mais) durante as mudanças. A função também mostra a dependência dos conjuntos.
Imagine que temos duas variáveis que possuem uma certa faixa de variação. Portanto, y é função de x, desde que cada valor da segunda variável corresponda a um valor da segunda. Neste caso, a variável y é dependente e é chamada de função. Costuma-se dizer que as variáveis x e y estão em Para maior clareza dessa dependência, é construído um gráfico da função. O que é um gráfico de uma função? Este é um conjunto de pontos no plano de coordenadas, onde cada valor de x corresponde a um valor de y. Os gráficos podem ser diferentes - linha reta, hipérbole, parábola, onda senoidal e assim por diante.
É impossível representar graficamente uma função sem pesquisa. Hoje aprenderemos como realizar pesquisas e construir o gráfico de uma função. É muito importante fazer anotações durante o estudo. Isso tornará a tarefa muito mais fácil de realizar. O plano de pesquisa mais conveniente:
- Domínio.
- Continuidade.
- Par ou ímpar.
- Periodicidade.
- Assíntotas.
- Zeros.
- Assine constância.
- Aumentando e diminuindo.
- Extremos.
- Convexidade e concavidade.
Vamos começar com o primeiro ponto. Vamos encontrar o domínio de definição, ou seja, em quais intervalos nossa função existe: y=1/3(x^3-14x^2+49x-36). No nosso caso, a função existe para quaisquer valores de x, ou seja, o domínio de definição é igual a R. Isso pode ser escrito da seguinte forma xÎR.
Continuidade
Agora examinaremos a função de descontinuidade. Na matemática, o termo “continuidade” surgiu como resultado do estudo das leis do movimento. O que é infinito? Espaço, tempo, algumas dependências (um exemplo é a dependência das variáveis S e t em problemas de movimento), a temperatura de um objeto aquecido (água, frigideira, termômetro, etc.), uma linha contínua (ou seja, aquela que pode ser desenhado sem levantá-lo da folha com um lápis).

Um gráfico é considerado contínuo se não quebrar em algum ponto. Um dos mais exemplos ilustrativos Esse gráfico é uma senóide, que você pode ver na imagem desta seção. Uma função é contínua em algum ponto x0 se uma série de condições forem atendidas:
- uma função é definida em um determinado ponto;
- os limites direito e esquerdo num ponto são iguais;
- o limite é igual ao valor da função no ponto x0.
Se pelo menos uma condição não for atendida, diz-se que a função falhou. E os pontos em que a função quebra são geralmente chamados de pontos de interrupção. Um exemplo de função que irá “quebrar” quando exibida graficamente é: y=(x+4)/(x-3). Além disso, y não existe no ponto x = 3 (já que é impossível dividir por zero).
Na função que estamos estudando (y=1/3(x^3-14x^2+49x-36)) tudo acabou sendo simples, pois o gráfico será contínuo.
Par ou ímpar

Agora examine a função para paridade. Primeiro, um pouco de teoria. Uma função par é aquela que satisfaz a condição f(-x)=f(x) para qualquer valor da variável x (do intervalo de valores). Exemplos incluem:
- módulo x (o gráfico parece uma gralha, a bissetriz do primeiro e segundo trimestres do gráfico);
- x ao quadrado (parábola);
- cosseno x (cosseno).
Observe que todos esses gráficos são simétricos quando vistos em relação ao eixo y (ou seja, o eixo y).
O que então é chamado de função ímpar? Estas são aquelas funções que satisfazem a condição: f(-x)=-f(x) para qualquer valor da variável x. Exemplos:
- hipérbole;
- parábola cúbica;
- sinusóide;
- tangente e assim por diante.
Observe que essas funções são simétricas em relação ao ponto (0:0), ou seja, a origem. Com base no que foi dito nesta seção do artigo, mesmo e Função estranha deve ter a propriedade: x pertence ao conjunto de definição e -x também.
Vamos examinar a função de paridade. Podemos ver que ela não se enquadra em nenhuma das descrições. Portanto, nossa função não é par nem ímpar.
Assíntotas
Vamos começar com uma definição. Uma assíntota é uma curva o mais próxima possível do gráfico, ou seja, a distância de um determinado ponto tende a zero. No total, existem três tipos de assíntotas:
- vertical, isto é, paralelo ao eixo y;
- horizontal, isto é, paralelo ao eixo x;
- inclinado.
Quanto ao primeiro tipo, essas linhas devem ser procuradas em alguns pontos:
- brecha;
- extremidades do domínio de definição.
No nosso caso, a função é contínua e o domínio de definição é igual a R. Portanto, não existem assíntotas verticais.
O gráfico de uma função possui uma assíntota horizontal, que corresponde a próximo requisito: se x tende ao infinito ou menos infinito, e o limite é igual a algum número (por exemplo, a). Neste caso, y=a é a assíntota horizontal. Não existem assíntotas horizontais na função que estamos estudando.
Uma assíntota oblíqua existe apenas se duas condições forem atendidas:
- lim(f(x))/x=k;
- lim f(x)-kx=b.
Então ele pode ser encontrado usando a fórmula: y=kx+b. Novamente, no nosso caso não existem assíntotas oblíquas.
Zeros de função

A próxima etapa é examinar o gráfico da função em busca de zeros. Também é muito importante notar que a tarefa associada a encontrar os zeros de uma função ocorre não apenas no estudo e construção de um gráfico de uma função, mas também como uma tarefa independente e como forma de resolver desigualdades. Pode ser necessário encontrar os zeros de uma função em um gráfico ou usar notação matemática.
Encontrar esses valores o ajudará a representar graficamente a função com mais precisão. Se conversarmos em linguagem simples, então o zero da função é o valor da variável x em que y = 0. Se você estiver procurando os zeros de uma função em um gráfico, deverá prestar atenção aos pontos em que o gráfico cruza o eixo x.
Para encontrar os zeros da função, você precisa resolver a seguinte equação: y=1/3(x^3-14x^2+49x-36)=0. Após realizar os cálculos necessários, obtemos a seguinte resposta:
Constância de sinal
A próxima etapa da pesquisa e construção de uma função (gráfico) é encontrar intervalos de sinal constante. Isso significa que devemos determinar em quais intervalos a função assume um valor positivo e em quais intervalos ela assume um valor negativo. As funções zero encontradas na última seção nos ajudarão a fazer isso. Então, precisamos construir uma linha reta (separada do gráfico) e em na ordem certa distribua os zeros da função sobre ela, do menor para o maior. Agora você precisa determinar qual dos intervalos resultantes tem um sinal “+” e qual tem um “-”.
No nosso caso, a função assume um valor positivo nos intervalos:
- de 1 a 4;
- de 9 ao infinito.
Significado negativo:
- de menos infinito a 1;
- das 4 às 9.
Isso é muito fácil de determinar. Substitua qualquer número do intervalo na função e veja qual sinal a resposta tem (menos ou mais).
Função crescente e decrescente
Para explorar e construir uma função, precisamos saber onde o gráfico aumentará (subirá ao longo do eixo Oy) e onde irá cair (rastejará para baixo ao longo do eixo y).

A função aumenta apenas se o valor maior da variável x corresponder a valor mais alto você. Ou seja, x2 é maior que x1 e f(x2) é maior que f(x1). E observamos um fenômeno completamente oposto com função decrescente (quanto mais x, menos y). Para determinar os intervalos de aumento e diminuição, você precisa encontrar o seguinte:
- domínio de definição (já temos);
- derivada (no nosso caso: 1/3(3x^2-28x+49);
- resolva a equação 1/3(3x^2-28x+49)=0.
Após os cálculos obtemos o resultado:
Obtemos: a função aumenta nos intervalos de menos infinito a 7/3 e de 7 ao infinito, e diminui no intervalo de 7/3 a 7.
Extremos

A função em estudo y=1/3(x^3-14x^2+49x-36) é contínua e existe para qualquer valor da variável x. O ponto extremo mostra o máximo e o mínimo de uma determinada função. No nosso caso não existem, o que simplifica muito a tarefa de construção. Caso contrário, eles também podem ser encontrados usando a função derivada. Uma vez encontrados, não esqueça de marcá-los no gráfico.
Convexidade e concavidade
Continuamos a explorar ainda mais a função y(x). Agora precisamos verificar a convexidade e a concavidade. As definições desses conceitos são bastante difíceis de compreender, é melhor analisar tudo por meio de exemplos. Para o teste: uma função é convexa se for uma função não decrescente. Concordo, isso é incompreensível!
Precisamos de determinar a derivada de uma função de segunda ordem. Obtemos: y=1/3(6x-28). Agora vamos igualar o lado direito a zero e resolver a equação. Resposta: x=14/3. Encontramos o ponto de inflexão, ou seja, o local onde o gráfico muda de convexidade para concavidade ou vice-versa. No intervalo de menos infinito a 14/3 a função é convexa, e de 14/3 a mais infinito é côncava. Também é muito importante notar que o ponto de inflexão no gráfico deve ser suave e suave, sem cantos afiados não deveria estar presente.
Definindo pontos adicionais
Nossa tarefa é investigar e construir um gráfico da função. Concluímos o estudo; construir um gráfico da função agora não é difícil. Para uma reprodução mais precisa e detalhada de uma curva ou linha reta no plano coordenado, você pode encontrar vários pontos auxiliares. Eles são bastante fáceis de calcular. Por exemplo, tomamos x=3, resolvemos a equação resultante e encontramos y=4. Ou x=5 e y=-5 e assim por diante. Você pode pegar quantos pontos adicionais forem necessários para a construção. Pelo menos 3-5 deles são encontrados.
Traçando um gráfico

Precisávamos investigar a função (x^3-14x^2+49x-36)*1/3=y. Todas as marcações necessárias durante os cálculos foram feitas no plano de coordenadas. Resta construir um gráfico, ou seja, conectar todos os pontos. A ligação dos pontos deve ser suave e precisa, é uma questão de habilidade - um pouco de prática e sua programação ficará perfeita.
Manter sua privacidade é importante para nós. Por este motivo, desenvolvemos uma Política de Privacidade que descreve como utilizamos e armazenamos as suas informações. Revise nossas práticas de privacidade e informe-nos se tiver alguma dúvida.
Coleta e uso de informações pessoais
Informações pessoais referem-se a dados que podem ser usados para identificar ou contatar uma pessoa específica.
Você pode ser solicitado a fornecer suas informações pessoais a qualquer momento quando entrar em contato conosco.
Abaixo estão alguns exemplos dos tipos de informações pessoais que podemos coletar e como podemos usar essas informações.
Quais informações pessoais coletamos:
- Quando você envia uma inscrição no site, podemos coletar diversas informações, incluindo seu nome, número de telefone, endereço E-mail etc.
Como usamos suas informações pessoais:
- Coletado por nós informações pessoais nos permite entrar em contato com você e informá-lo sobre ofertas exclusivas, promoções e outros eventos e eventos futuros.
- De tempos em tempos, poderemos usar suas informações pessoais para enviar avisos e comunicações importantes.
- Também podemos usar informações pessoais para fins internos, como auditoria, análise de dados e vários estudos a fim de melhorar os serviços que prestamos e fornecer recomendações sobre nossos serviços.
- Se você participar de um sorteio, concurso ou promoção semelhante, poderemos usar as informações que você fornecer para administrar tais programas.
Divulgação de informações a terceiros
Não divulgamos as informações recebidas de você a terceiros.
Exceções:
- Se necessário, de acordo com a lei, procedimento judicial, V. julgamento e/ou com base em solicitações públicas ou solicitações de agências governamentais no território da Federação Russa - divulgue suas informações pessoais. Também poderemos divulgar informações sobre você se determinarmos que tal divulgação é necessária ou apropriada para fins de segurança, aplicação da lei ou outros fins de saúde pública. casos importantes.
- No caso de uma reorganização, fusão ou venda, poderemos transferir as informações pessoais que coletamos para o terceiro sucessor aplicável.
Proteção de informações pessoais
Tomamos precauções - inclusive administrativas, técnicas e físicas - para proteger suas informações pessoais contra perda, roubo e uso indevido, bem como acesso não autorizado, divulgação, alteração e destruição.
Respeitando sua privacidade no nível da empresa
Para garantir que suas informações pessoais estejam seguras, comunicamos padrões de privacidade e segurança aos nossos funcionários e aplicamos rigorosamente as práticas de privacidade.