Tipos simples de resistência. curva plana. Curva reta Curva transversal plana Curva reta e transversal

Curva reta. Curvatura transversal plana Traçar diagramas de fatores de força internos para vigas Traçar diagramas Q e M segundo equações Traçar diagramas Q e M usando seções características (pontos) Cálculos de resistência em flexão direta de vigas Tensões principais na flexão. Verificação completa da resistência das vigas Compreensão do centro de flexão Determinação dos deslocamentos nas vigas durante a flexão. Conceitos de deformação de vigas e condições de sua rigidez Equação diferencial do eixo dobrado da viga Método de integração direta Exemplos de determinação de deslocamentos em vigas pelo método de integração direta Significado físico das constantes de integração Método de parâmetros iniciais (equação universal de o eixo dobrado da viga). Exemplos de determinação de deslocamentos em uma viga pelo método de parâmetros iniciais Determinação de deslocamentos pelo método de Mohr. Regra de A.K. Vereschagin. Cálculo da integral de Mohr de acordo com A.K. Vereshchagin Exemplos de determinação de deslocamentos por meio da integral de Mohr Bibliografia Curvatura direta. Curva transversal plana. 1.1. Traçar diagramas de fatores de força internos para vigas A flexão direta é um tipo de deformação em que surgem dois fatores de força internos nas seções transversais da barra: um momento fletor e uma força transversal. Em um caso particular, a força transversal pode ser igual a zero, então a dobra é chamada de pura. Com uma flexão transversal plana, todas as forças estão localizadas em um dos principais planos de inércia da haste e são perpendiculares ao seu eixo longitudinal, os momentos estão localizados no mesmo plano (Fig. 1.1, a, b). Arroz. 1.1 A força transversal em uma seção transversal arbitrária da viga é numericamente igual à soma algébrica das projeções sobre a normal ao eixo da viga de todas as forças externas que atuam em um lado da seção considerada. A força transversal na seção m-n da viga (Fig. 1.2, a) é considerada positiva se a resultante das forças externas à esquerda da seção for direcionada para cima e para a direita - para baixo e negativa - no caso oposto (Fig. 1.2, b). Arroz. 1.2 Ao calcular a força transversal em uma determinada seção, as forças externas situadas à esquerda da seção são tomadas com um sinal de mais se forem direcionadas para cima e com um sinal de menos se forem direcionadas para baixo. Para o lado direito do feixe - vice-versa. 5 O momento fletor em uma seção transversal de viga arbitrária é numericamente igual à soma algébrica dos momentos em torno do eixo central z da seção de todas as forças externas que atuam em um lado da seção considerada. O momento fletor na seção m-n da viga (Fig. 1.3, a) é considerado positivo se o momento resultante das forças externas é direcionado no sentido horário da seção à esquerda da seção e no sentido anti-horário para a direita, e negativo na seção caso contrário (Fig. 1.3b). Arroz. 1.3 Ao calcular o momento fletor em uma determinada seção, os momentos das forças externas situadas à esquerda da seção são considerados positivos se forem direcionados no sentido horário. Para o lado direito do feixe - vice-versa. É conveniente determinar o sinal do momento fletor pela natureza da deformação da viga. O momento fletor é considerado positivo se, na seção considerada, a parte de corte da viga se curva com convexidade para baixo, ou seja, as fibras inferiores são esticadas. Caso contrário, o momento fletor na seção é negativo. Entre o momento fletor M, a força transversal Q e a intensidade da carga q, existem dependências diferenciais. 1. A primeira derivada da força transversal ao longo da abcissa da seção é igual à intensidade da carga distribuída, ou seja, . (1.1) 2. A primeira derivada do momento fletor ao longo da abcissa da seção é igual à força transversal, ou seja . (1.2) 3. A segunda derivada em relação à abcissa da seção é igual à intensidade da carga distribuída, ou seja . (1.3) Consideramos positiva a carga distribuída direcionada para cima. Algumas conclusões importantes decorrem das dependências diferenciais entre M, Q, q: 1. Se na seção da viga: a) a força transversal é positiva, então o momento fletor aumenta; b) a força transversal é negativa, então o momento fletor diminui; c) a força transversal é zero, então o momento fletor tem valor constante (flexão pura); 6 d) a força transversal passa por zero, mudando o sinal de mais para menos, máx M M, caso contrário M Mmin. 2. Se não houver carga distribuída na seção da viga, a força transversal é constante e o momento fletor muda linearmente. 3. Se houver uma carga uniformemente distribuída na seção da viga, a força transversal muda de acordo com uma lei linear e o momento fletor - de acordo com a lei de uma parábola quadrada, convexa invertida em direção à carga (no caso de plotagem M do lado das fibras tensionadas). 4. Na seção sob a força concentrada, o diagrama Q tem um salto (pela magnitude da força), o diagrama M tem uma quebra na direção da força. 5. Na seção onde é aplicado um momento concentrado, o diagrama M tem um salto igual ao valor desse momento. Isso não se reflete no gráfico Q. Sob carregamento complexo, as vigas constroem diagramas de forças transversais Q e momentos fletores M. O gráfico Q (M) é um gráfico que mostra a lei da mudança na força transversal (momento fletor) ao longo do comprimento da viga. Com base na análise dos diagramas M e Q, são estabelecidas seções perigosas do feixe. As ordenadas positivas do diagrama Q são traçadas para cima e as ordenadas negativas são traçadas para baixo a partir da linha de base traçada paralelamente ao eixo longitudinal da viga. As ordenadas positivas do diagrama M são estabelecidas e as ordenadas negativas são plotadas para cima, ou seja, o diagrama M é construído a partir do lado das fibras esticadas. A construção dos diagramas Q e M para vigas deve começar com a definição das reações de apoio. Para uma viga com uma extremidade fixa e a outra extremidade livre, a plotagem de Q e M pode ser iniciada a partir da extremidade livre sem definir reações no embutimento. 1.2. A construção dos diagramas Q e M de acordo com as equações de Balk é dividida em seções, dentro das quais as funções para o momento fletor e a força cortante permanecem constantes (não possuem descontinuidades). Os limites das seções são os pontos de aplicação de forças concentradas, pares de forças e locais de variação da intensidade da carga distribuída. Uma seção arbitrária é tomada em cada seção a uma distância x da origem, e as equações para Q e M são elaboradas para esta seção. Os gráficos Q e M são construídos usando essas equações. Exemplo 1.1 Construir gráficos de forças cortantes Q e momentos fletores M para uma determinada viga (Fig. 1.4a). Solução: 1. Determinação das reações dos apoios. Compomos as equações de equilíbrio: das quais obtemos As reações dos apoios estão definidas corretamente. A viga tem quatro seções Fig. 1.4 carregamentos: CA, AD, DB, BE. 2. Plotagem Q. Plot SA. Na seção CA 1, desenhamos uma seção arbitrária 1-1 a uma distância x1 da extremidade esquerda da viga. Definimos Q como a soma algébrica de todas as forças externas que atuam à esquerda da seção 1-1: O sinal de menos é tomado porque a força que atua à esquerda da seção é direcionada para baixo. A expressão para Q não depende da variável x1. O gráfico Q nesta seção será representado como uma linha reta paralela ao eixo x. Lote AD. No site, desenhamos uma seção arbitrária 2-2 a uma distância x2 da extremidade esquerda da viga. Definimos Q2 como a soma algébrica de todas as forças externas que atuam à esquerda da seção 2-2: 8 O valor de Q é constante na seção (não depende da variável x2). O gráfico Q no gráfico é uma linha reta paralela ao eixo x. local do banco de dados. No site, desenhamos uma seção arbitrária 3-3 a uma distância x3 da extremidade direita da viga. Definimos Q3 como a soma algébrica de todas as forças externas que atuam à direita da seção 3-3: A expressão resultante é a equação de uma linha reta inclinada. Lote B.E. No site, desenhamos uma seção 4-4 a uma distância x4 da extremidade direita da viga. Definimos Q como a soma algébrica de todas as forças externas que atuam à direita da seção 4-4: 4 Aqui, o sinal de mais é tomado porque a carga resultante à direita da seção 4-4 é direcionada para baixo. Com base nos valores obtidos, construímos os diagramas Q (Fig. 1.4, b). 3. Plotando M. Lote m1. Definimos o momento fletor na seção 1-1 como a soma algébrica dos momentos das forças que atuam à esquerda da seção 1-1. é a equação de uma reta. Seção A 3 Defina o momento fletor na seção 2-2 como a soma algébrica dos momentos das forças que atuam à esquerda da seção 2-2. é a equação de uma reta. Plot DB 4 Definimos o momento fletor na seção 3-3 como a soma algébrica dos momentos das forças que atuam à direita da seção 3-3. é a equação de uma parábola quadrada. 9 Encontre três valores nas extremidades da seção e no ponto com coordenada xk , onde Seção BE 1 Defina o momento fletor na seção 4-4 como a soma algébrica dos momentos das forças que atuam à direita da seção 4- 4. - na equação de uma parábola quadrada encontramos três valores de M4: Com base nos valores obtidos, construímos um gráfico M (Fig. 1.4, c). Nos trechos CA e AD, o gráfico Q é limitado por retas paralelas ao eixo das abcissas, e nos trechos DB e BE, por retas oblíquas. Nos trechos C, A e B do diagrama Q há saltos da magnitude das forças correspondentes, que servem para verificar a exatidão da construção do diagrama Q. Nos trechos onde Q  0, os momentos aumentam de da esquerda para direita. Nos trechos onde Q  0, os momentos diminuem. Sob as forças concentradas, há dobras na direção da ação das forças. Sob o momento concentrado, há um salto pelo valor do momento. Isso indica a correção da construção do diagrama M. Exemplo 1.2 Construir os diagramas Q e M para uma viga sobre dois apoios, carregada com uma carga distribuída, cuja intensidade varia de acordo com uma lei linear (Fig. 1.5, a). Solução Determinação de reações de suporte. A resultante da carga distribuída é igual à área do triângulo que representa o diagrama de carga e é aplicada no centro de gravidade deste triângulo. Fazemos as somas dos momentos de todas as forças em relação aos pontos A e B: Traçando Q. Vamos desenhar uma seção arbitrária a uma distância x do suporte esquerdo. A ordenada do diagrama de carga correspondente à seção é determinada a partir da semelhança dos triângulos. A resultante daquela parte da carga que está localizada à esquerda da seção zero: O gráfico Q é mostrado na fig. 1.5, B. O momento fletor em uma seção arbitrária é igual a O momento fletor muda de acordo com a lei de uma parábola cúbica: O valor máximo do momento fletor está na seção, onde 0, ou seja, em 1,5, c. 1.3. Construção dos diagramas Q e M por seções características (pontos) Utilizando as relações diferenciais entre M, Q, q e as conclusões delas decorrentes, é aconselhável construir os diagramas Q e M por seções características (sem formular equações). Usando este método, os valores de Q e M são calculados em seções características. As seções características são as seções limítrofes das seções, bem como as seções onde o fator de força interno dado tem um valor extremo. Dentro dos limites entre as seções características, o esboço 12 do diagrama é estabelecido com base nas dependências diferenciais entre M, Q, q e as conclusões deles decorrentes. Exemplo 1.3 Construa os diagramas Q e M para a viga mostrada na fig. 1.6, a. Arroz. 1.6. Solução: Começamos a plotar os diagramas Q e M a partir da extremidade livre da viga, enquanto as reações no embutimento podem ser omitidas. A viga tem três áreas de carregamento: AB, BC, CD. Não há carga distribuída nas seções AB e BC. As forças transversais são constantes. O gráfico Q é limitado por linhas retas paralelas ao eixo x. Os momentos fletores mudam linearmente. O gráfico M é limitado a linhas retas inclinadas ao eixo x. Na seção CD há uma carga uniformemente distribuída. As forças transversais mudam linearmente e os momentos fletores mudam de acordo com a lei de uma parábola quadrada com uma convexidade na direção da carga distribuída. No limite das seções AB e BC, a força transversal muda abruptamente. No limite das seções BC e CD, o momento fletor muda abruptamente. 1. Plotando Q. Calculamos os valores das forças transversais Q nas seções de limite das seções: Com base nos resultados dos cálculos, construímos um diagrama Q para a viga (Fig. 1, b). Segue-se do diagrama Q que a força transversal na seção CD é igual a zero na seção espaçada a uma distância qa a q do início desta seção. Nesta seção, o momento fletor tem um valor máximo. 2. Construção do diagrama M. Calculamos os valores dos momentos fletores nas seções limite das seções: Exemplo 1.4 De acordo com o diagrama de momentos fletores (Fig. 1.7, a) para a viga (Fig. 1.7, b), determine as cargas atuantes e trace Q. O círculo indica o vértice da parábola quadrada. Solução: Determine as cargas que atuam na viga. A seção AC é carregada com uma carga uniformemente distribuída, pois o diagrama M nesta seção é uma parábola quadrada. Na seção de referência B, um momento concentrado é aplicado à viga, agindo no sentido horário, pois no diagrama M temos um salto para cima da magnitude do momento. Na seção NE, a viga não é carregada, pois o diagrama M nesta seção é limitado por uma reta inclinada. A reação do apoio B é determinada a partir da condição de que o momento fletor na seção C seja igual a zero, ou seja, para determinar a intensidade da carga distribuída, compomos uma expressão para o momento fletor na seção A como a soma dos momentos de forças à direita e igual a zero. Agora determinamos a reação do apoio A. Para isso, compomos uma expressão para os momentos fletores na seção como a soma dos momentos das forças à esquerda.O esquema de cálculo de uma viga com carga é mostrado na fig. 1.7, c. A partir da extremidade esquerda da viga, calculamos os valores das forças transversais nas seções de limite das seções: O gráfico Q é mostrado na fig. 1.7, d. O problema considerado pode ser resolvido compilando dependências funcionais para M, Q em cada seção. Vamos escolher a origem das coordenadas na extremidade esquerda da viga. Na seção AC, o gráfico M é expresso por uma parábola quadrada, cuja equação é da forma Constantes a, b, c, encontramos a partir da condição de que a parábola passe por três pontos com coordenadas conhecidas: Substituindo as coordenadas de os pontos na equação da parábola, obtemos: A expressão para o momento fletor será Diferenciando a função M1 , obtemos a dependência para a força transversal Após a diferenciação da função Q obtemos uma expressão para a intensidade da carga distribuída. Na seção NE, a expressão para o momento fletor é representada como uma função linear. Para determinar as constantes aeb, usamos as condições em que essa reta passa por dois pontos cujas coordenadas são conhecidas. Obtemos duas equações: ,b de que temos um 20. A equação para o momento fletor na seção NE será Após uma diferenciação dupla de M2, encontraremos. Com base nos valores encontrados de M e Q, construímos diagramas de momentos fletores e forças de cisalhamento para a viga. Além da carga distribuída, forças concentradas são aplicadas à viga em três seções, onde há saltos no diagrama Q, e momentos concentrados na seção onde há salto no diagrama M. Exemplo 1.5 Para uma viga (Fig. 1.8, a), determine a posição racional da rótula C, na qual o maior momento fletor no vão é igual ao momento fletor no engaste (em valor absoluto). Construir diagramas Q e M. Solução Determinação de reações de apoios. Apesar do número total de ligações de apoio ser quatro, a viga é estaticamente determinada. O momento fletor na dobradiça C é igual a zero, o que nos permite fazer uma equação adicional: a soma dos momentos sobre a dobradiça de todas as forças externas que atuam em um lado dessa dobradiça é igual a zero. Faça a soma dos momentos de todas as forças à direita da rótula C. O diagrama Q da viga é limitado por uma reta inclinada, pois q = const. Determinamos os valores das forças transversais nas seções de limite da viga: A abscissa xK da seção, onde Q = 0, é determinada a partir da equação de onde o gráfico M para a viga é limitado por uma parábola quadrada. Expressões para momentos fletores nas seções, onde Q = 0, e na terminação são escritas respectivamente da seguinte forma: Da condição de igualdade dos momentos, obtemos uma equação quadrática em relação ao parâmetro desejado x: O valor real é x 2x 1,029 m. Determinamos os valores numéricos das forças transversais e momentos fletores nas seções características da viga. 1.8, c - parcela M. O problema considerado poderia ser resolvido dividindo a viga articulada em seus elementos constituintes, conforme mostrado na fig. 1.8, d. No início, as reações dos apoios VC e VB são determinadas. As parcelas Q e M são construídas para a viga suspensa SV a partir da ação da carga aplicada a ela. Em seguida, eles se movem para a viga principal AC, carregando-a com uma força adicional VC, que é a força de pressão da viga CB na viga AC. Depois disso, os diagramas Q e M são construídos para a viga CA. 1.4. Cálculos de resistência para flexão direta de vigas Cálculo de resistência para tensões normais e de cisalhamento. Com uma flexão direta de uma viga, tensões normais e de cisalhamento surgem em suas seções transversais (Fig. 1.9). 18 Fig. 1.9 As tensões normais estão relacionadas ao momento fletor, as tensões de cisalhamento estão relacionadas à força transversal. Na flexão pura direta, as tensões de cisalhamento são iguais a zero. As tensões normais em um ponto arbitrário da seção transversal da viga são determinadas pela fórmula (1.4) onde M é o momento fletor na seção dada; Iz é o momento de inércia da seção em relação ao eixo neutro z; y é a distância do ponto onde a tensão normal é determinada ao eixo z neutro. As tensões normais ao longo da altura da seção mudam linearmente e atingem o maior valor nos pontos mais distantes do eixo neutro. Se a seção é simétrica em relação ao eixo neutro (Fig. 1.11), então 1.11 as maiores tensões de tração e compressão são as mesmas e são determinadas pela fórmula,  - momento axial de resistência da seção à flexão. Para uma seção retangular com uma largura b e uma altura h: (1.7) Para uma seção circular com um diâmetro d: (1.8) Para uma seção anular   são os diâmetros interno e externo do anel, respectivamente. Para vigas feitas de materiais plásticos, as mais racionais são as formas simétricas de 20 seções (viga I, em forma de caixa, anular). Para vigas feitas de materiais frágeis que não resistem igualmente à tração e compressão, as seções que são assimétricas em torno do eixo neutro z (ta-br., em forma de U, viga I assimétrica) são racionais. Para vigas de seção constante feitas de materiais plásticos com perfis de seção simétrica, a condição de resistência é escrita da seguinte forma: (1.10) onde Mmax é o módulo do momento fletor máximo; - tensão admissível para o material. Para vigas de seção constante feitas de materiais plásticos com perfis de seção assimétrica, a condição de resistência é escrita da seguinte forma: (1. 11) Para vigas feitas de materiais frágeis com seções assimétricas em relação ao eixo neutro, se o diagrama M não for ambíguo (Fig. 1.12), duas condições de resistência devem ser escritas - a distância do eixo neutro aos pontos mais distantes do eixo zonas esticadas e comprimidas da seção perigosa, respectivamente; P - tensões admissíveis, respectivamente, em tração e compressão. Fig.1.12. 21 Se o diagrama de momento fletor tiver seções de sinais diferentes (Fig. 1.13), então, além de verificar a seção 1-1, onde Mmax atua, é necessário calcular as tensões de tração máximas para a seção 2-2 (com a maior momento do sinal oposto). Arroz. 1.13 Juntamente com o cálculo básico para tensões normais, em alguns casos é necessário verificar a resistência da viga para tensões de cisalhamento. As tensões de cisalhamento em vigas são calculadas pela fórmula de D. I. Zhuravsky (1.13) onde Q é a força transversal na seção transversal considerada da viga; Szots é o momento estático em torno do eixo neutro da área da parte da seção localizada em um lado da linha reta traçada através do ponto dado e paralela ao eixo z; b é a largura da seção ao nível do ponto considerado; Iz é o momento de inércia de toda a seção em torno do eixo neutro z. Em muitos casos, as tensões de cisalhamento máximas ocorrem no nível da camada neutra da viga (retângulo, viga I, círculo). Nesses casos, a condição de resistência para tensões de cisalhamento é escrita como (1.14) onde Qmax é a força transversal com o maior módulo; - tensão de cisalhamento admissível para o material. Para uma seção de viga retangular, a condição de resistência tem a forma (1.15) A é a área da seção transversal da viga. Para uma seção circular, a condição de resistência é representada como (1.16) Para uma seção I, a condição de resistência é escrita da seguinte forma: (1.17) d é a espessura da parede da viga I. Normalmente, as dimensões da seção transversal da viga são determinadas a partir da condição de resistência para tensões normais. A verificação da resistência das vigas para tensões de cisalhamento é obrigatória para vigas curtas e vigas de qualquer comprimento, se houver grandes forças concentradas próximas aos apoios, bem como para vigas de madeira, rebitadas e soldadas. Exemplo 1.6 Verifique a resistência de uma viga de seção em caixa (Fig. 1.14) para tensões normais e de cisalhamento, se MPa. Construa diagramas na seção perigosa da viga. Arroz. 1.14 Decisão 23 1. Plote os gráficos Q e M de seções características. Considerando o lado esquerdo da viga, obtemos O diagrama das forças transversais é mostrado na fig. 1.14, c. O gráfico dos momentos fletores é mostrado na fig. 5.14, G. 2. Características geométricas da seção transversal 3. As tensões normais mais altas na seção C, onde Mmax atua (módulo): MPa. As tensões normais máximas na viga são praticamente iguais às admissíveis. 4. As maiores tensões tangenciais na seção C (ou A), onde max Q atua (módulo): Aqui é o momento estático da área da meia seção em relação ao eixo neutro; b2 cm é a largura da seção ao nível da linha neutra. Fig. 5. Tensões tangenciais em um ponto (na parede) na seção C: Fig. 1.15 Aqui Szomc 834,5 = 108 cm3 é o momento estático da área da parte da seção localizada acima da linha que passa pelo ponto K1; b2 cm é a espessura da parede ao nível do ponto K1. Os gráficos  e  para a seção C da viga são mostrados na fig. 1.15. Exemplo 1.7 Para a viga mostrada na fig. 1.16, a, é necessário: 1. Construir diagramas de forças transversais e momentos fletores ao longo de seções características (pontos). 2. Determine as dimensões da seção transversal na forma de um círculo, retângulo e viga I a partir da condição de resistência para tensões normais, compare as áreas da seção transversal. 3. Verifique as dimensões selecionadas das seções da viga para tensões de cisalhamento. Dado: Solução: 1. Determinar as reações dos apoios da viga Verificar: 2. Traçar os diagramas Q e M. Valores das forças transversais em seções características da viga 25 Fig. 1.16 Nos trechos CA e AD, a intensidade de carga q = const. Portanto, nestas seções, o diagrama Q é limitado a linhas retas inclinadas ao eixo. Na seção DB, a intensidade da carga distribuída q \u003d 0, portanto, nesta seção, o diagrama Q é limitado a uma linha reta paralela ao eixo x. O diagrama Q para a viga é mostrado na fig. 1.16b. Valores de momentos fletores nas seções características da viga: Na segunda seção, determinamos a abcissa x2 da seção, em que Q = 0: O momento máximo na segunda seção Diagrama M para a viga é mostrado na fig . 1.16, c. 2. Compor a condição de resistência para tensões normais, a partir da qual determinamos o módulo de seção axial necessário a partir da expressão determinada o diâmetro necessário d de uma viga de seção circular Área de seção circular Para uma viga retangular Altura de seção necessária Área de seção retangular De acordo com as tabelas do GOST 8239-89, encontramos o maior valor mais próximo do momento de resistência axial 597 cm3, que corresponde à viga I nº 33 com as características: A z 9840 cm4. Verificação da tolerância: (subcarga em 1% dos 5% permitidos) a viga I mais próxima nº 30 (W 2 cm3) leva a uma sobrecarga significativa (mais de 5%). Finalmente aceitamos a viga I nº 33. Comparamos as áreas das seções circulares e retangulares com a menor área A da viga I: Das três seções consideradas, a seção I é a mais econômica. 3. Calculamos as maiores tensões normais na seção perigosa 27 da viga I (Fig. 1.17, a): Tensões normais na parede próxima ao banzo da seção da viga I. 1.17b. 5. Determinamos as maiores tensões de cisalhamento para as seções selecionadas da viga. a) seção retangular da viga: b) seção circular da viga: c) seção I da viga: tensões de cisalhamento na parede próxima ao banzo da viga I na seção perigosa A (à direita) (em ponto 2): Na fig. 1.17, em. As tensões de cisalhamento máximas na viga não excedem as tensões admissíveis Exemplo 1.8 Determine a carga admissível na viga (Fig. 1.18, a), se 60 MPa, as dimensões da seção transversal são dadas (Fig. 1.19, a). Construa um diagrama de tensões normais na seção perigosa da viga sob a carga admissível. Fig 1.18 1. Determinação das reações dos apoios das vigas. Tendo em conta a simetria do sistema 2. Construção dos diagramas Q e M a partir de secções características. Forças de cisalhamento nas seções características da viga: O diagrama Q da viga é mostrado na fig. 5.18b. Momentos fletores nas seções características da viga Para a segunda metade da viga, as ordenadas M estão ao longo dos eixos de simetria. O diagrama M para a viga é mostrado na fig. 1.18b. 3. Características geométricas da seção (Fig. 1.19). Dividimos a figura em dois elementos simples: uma viga I - 1 e um retângulo - 2. Fig. 1.19 De acordo com o sortimento para viga I nº 20, temos Para um retângulo: Momento estático da área da seção em relação ao eixo z1 Distância do eixo z1 ao centro de gravidade da seção Momento de inércia da seção em relação ao eixo central principal z de toda a seção de acordo com as fórmulas para a transição para eixos paralelos ponto perigoso "a" (Fig. 1.19) na seção perigosa I (Fig. 1.18): Após a substituição dos dados numéricos 5. Com um valor permitido carga na seção perigosa, as tensões normais nos pontos "a" e "b" serão iguais: a seção perigosa 1-1 é mostrada na fig. 1.19b.

curva reta- este é um tipo de deformação em que surgem dois fatores de força internos nas seções transversais da haste: um momento fletor e uma força transversal.

Curva pura- este é um caso especial de flexão direta, em que apenas um momento fletor ocorre nas seções transversais da haste e a força transversal é zero.

Exemplo de Dobra Pura - Plotagem CD na haste AB. Momento de flexãoé o valor Pai par de forças externas causando flexão. Do equilíbrio da parte da haste à esquerda da seção transversal mn segue que as forças internas distribuídas sobre esta seção são estaticamente equivalentes ao momento M, igual e oposto ao momento fletor Pai.

Para encontrar a distribuição dessas forças internas ao longo da seção transversal, é necessário considerar a deformação da barra.

No caso mais simples, a haste possui um plano longitudinal de simetria e está sujeita à ação de pares de forças de flexão externas localizadas neste plano. Então a dobra ocorrerá no mesmo plano.

eixo da haste nn 1é uma linha que passa pelos centros de gravidade de suas seções transversais.

Seja a seção transversal da haste um retângulo. Desenhe duas linhas verticais em suas faces milímetros e pp. Quando dobradas, essas linhas permanecem retas e giram de modo que permaneçam perpendiculares às fibras longitudinais da haste.

Uma outra teoria de flexão é baseada na suposição de que não apenas as linhas milímetros e pp, mas toda a seção transversal plana da haste permanece plana após a flexão e normal às fibras longitudinais da haste. Portanto, ao dobrar, as seções transversais milímetros e pp girar em relação um ao outro em torno de eixos perpendiculares ao plano de dobra (plano de desenho). Neste caso, as fibras longitudinais do lado convexo sofrem tensão e as fibras do lado côncavo sofrem compressão.

superfície neutraé uma superfície que não sofre deformação durante a flexão. (Agora está localizado perpendicular ao desenho, o eixo deformado da haste nn 1 pertence a esta superfície).

Eixo seccional neutro- esta é a interseção de uma superfície neutra com qualquer uma com qualquer seção transversal (agora também localizada perpendicular ao desenho).

Deixe uma fibra arbitrária estar a uma distância y de uma superfície neutra. ρ é o raio de curvatura do eixo curvo. Ponto Oé o centro de curvatura. Vamos desenhar uma linha n 1 s 1 paralelo milímetros.ss 1é o alongamento absoluto da fibra.

Extensão relativa ε x fibras

Segue que deformação das fibras longitudinais proporcional à distância y da superfície neutra e inversamente proporcional ao raio de curvatura ρ .

O alongamento longitudinal das fibras do lado convexo da haste é acompanhado por constrição lateral, e o encurtamento longitudinal do lado côncavo - extensão lateral, como no caso de alongamento e contração simples. Por causa disso, a aparência de todas as seções transversais muda, os lados verticais do retângulo ficam inclinados. Deformação lateral z:

μ - Razão de Poisson.

Como resultado dessa distorção, todas as linhas retas de seção transversal paralelas ao eixo z, são dobrados de modo a permanecerem normais aos lados da seção. O raio de curvatura desta curva R será mais do que ρ Da mesma maneira que ε x é maior em valor absoluto do que ε z, e obtemos

Essas deformações das fibras longitudinais correspondem a tensões

A tensão em qualquer fibra é proporcional à sua distância do eixo neutro. n 1 n 2. Posição do eixo neutro e raio de curvatura ρ são duas incógnitas na equação para σ x - pode ser determinado a partir da condição de que as forças distribuídas em qualquer seção transversal formam um par de forças que equilibra o momento externo M.

Todos os itens acima também são verdadeiros se a haste não tiver um plano longitudinal de simetria no qual o momento fletor atua, desde que o momento fletor atue no plano axial, que contém um dos dois eixos principais corte transversal. Esses planos são chamados principais planos de flexão.

Quando existe um plano de simetria e o momento fletor atua nesse plano, nele ocorre a deflexão. Momentos de forças internas em torno do eixo z equilibrar o momento externo M. Momentos de esforço em relação ao eixo y são mutuamente destruídos.

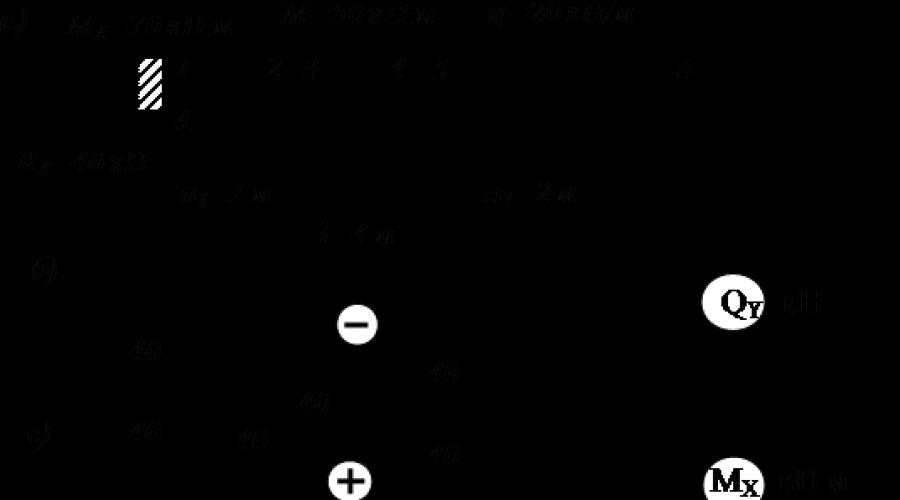
Para uma viga engastada carregada com uma carga distribuída de intensidade kN / m e um momento concentrado kN m (Fig. 3.12), é necessário: para construir diagramas de forças cortantes e momentos fletores, selecione uma viga de seção transversal circular a uma altura admissível tensão normal kN/cm2 e verificar a resistência da viga de acordo com as tensões de cisalhamento na tensão de cisalhamento admissível kN/cm2. Dimensões da viga m; m; m.

Esquema de projeto para o problema de flexão transversal direta

Arroz. 3.12

Resolvendo o problema de "flexão transversal direta"

Determinando reações de suporte

A reação horizontal no embutimento é zero, pois as cargas externas na direção do eixo z não atuam na viga.

Escolhemos as direções das forças reativas restantes que surgem no encaixe: vamos direcionar a reação vertical, por exemplo, para baixo e o momento - no sentido horário. Seus valores são determinados a partir das equações da estática:

Compilando essas equações, consideramos o momento positivo ao girar no sentido anti-horário, e a projeção da força é positiva se sua direção coincidir com a direção positiva do eixo y.

Da primeira equação encontramos o momento na terminação:

Da segunda equação - reação vertical:

Os valores positivos obtidos por nós no momento e a reação vertical na terminação indicam que adivinhamos suas direções.

De acordo com a natureza da fixação e carregamento da viga, dividimos seu comprimento em duas seções. Ao longo dos limites de cada uma dessas seções, descrevemos quatro seções transversais (ver Fig. 3.12), nas quais calcularemos os valores de forças cortantes e momentos fletores pelo método das seções (ROZU).

Seção 1. Vamos descartar mentalmente o lado direito do feixe. Vamos substituir sua ação no lado esquerdo restante por uma força cortante e um momento fletor. Para a conveniência de calcular seus valores, fechamos o lado direito do feixe descartado por nós com um pedaço de papel, alinhando a borda esquerda da folha com a seção em consideração.

Lembre-se de que a força cortante que surge em qualquer seção transversal deve equilibrar todas as forças externas (ativas e reativas) que atuam na parte da viga que estamos considerando (ou seja, visível). Portanto, a força de cisalhamento deve ser igual à soma algébrica de todas as forças que vemos.

Também damos a regra dos sinais para a força cortante: uma força externa atuando na parte considerada da viga e tendendo a “girar” essa parte em relação à seção no sentido horário causa uma força cortante positiva na seção. Essa força externa é incluída na soma algébrica para a definição com um sinal de mais.

No nosso caso, vemos apenas a reação do suporte, que gira a parte visível da viga em relação à primeira seção (em relação à borda do papel) no sentido anti-horário. É por isso

kN.

O momento fletor em qualquer seção deve equilibrar o momento criado por forças externas que vemos em relação à seção em consideração. Portanto, é igual à soma algébrica dos momentos de todos os esforços que atuam na parte da viga que estamos considerando, em relação à seção considerada (ou seja, em relação à borda do papel). Neste caso, uma carga externa dobrando a parte considerada da viga com convexidade para baixo causa um momento fletor positivo na seção. E o momento criado por tal carga é incluído na soma algébrica para a definição com um sinal de mais.

Vemos dois esforços: a reação e o momento de rescisão. No entanto, o braço da força em relação à seção 1 é igual a zero. É por isso

kNm

Tomamos o sinal de mais porque o momento reativo dobra a parte visível da viga com uma convexidade para baixo.

Seção 2. Como antes, cobriremos todo o lado direito da viga com um pedaço de papel. Agora, ao contrário da primeira seção, a força tem um ombro: m. Portanto

kN; kNm

Seção 3. Fechando o lado direito da viga, encontramos

kN;

Seção 4. Vamos fechar o lado esquerdo da viga com uma folha. Então

kNm

kNm

.

Com base nos valores encontrados, construímos diagramas de esforços cortantes (Fig. 3.12, b) e momentos fletores (Fig. 3.12, c).

Sob seções sem carga, o diagrama de forças cortantes corre paralelamente ao eixo da viga e sob uma carga distribuída q, ao longo de uma linha reta inclinada para cima. Sob a reação de apoio no diagrama há um salto para baixo no valor dessa reação, ou seja, de 40 kN.

No diagrama de momentos fletores, vemos uma quebra sob a reação de apoio. O ângulo de fratura é direcionado para a reação do suporte. Sob uma carga distribuída q, o diagrama muda ao longo de uma parábola quadrática, cuja convexidade é direcionada para a carga. Na seção 6 do diagrama há um extremo, pois o diagrama da força cortante neste local passa pelo valor zero aqui.

Determine o diâmetro necessário da seção transversal da viga

A condição de resistência para tensões normais tem a forma:

,

onde é o momento de resistência da viga na flexão. Para uma viga de seção transversal circular, é igual a:

.

O momento fletor com maior valor absoluto ocorre na terceira seção da viga: kN cm

Então o diâmetro de viga necessário é determinado pela fórmula

cm.

Aceitamos mm. Então

kN/cm2 kN/cm2.

"Sobretensão" é

,

o que é permitido.

Verificamos a resistência da viga para as maiores tensões tangenciais

As maiores tensões de cisalhamento que ocorrem na seção transversal de uma viga circular são calculadas pela fórmula

,

onde é a área da seção transversal.

De acordo com o gráfico, o maior valor algébrico da força cortante é igual a kN. Então

kN/cm2 kN/cm2,

ou seja, a condição de resistência e tensão de cisalhamento é cumprida, além disso, com uma grande margem.

Um exemplo de solução do problema "flexão transversal direta" nº 2

Condição do exemplo de problema para flexão transversal direta

Para uma viga articulada carregada com uma carga distribuída de intensidade kN / m, uma força concentrada kN e um momento concentrado kN m (Fig. 3.13), é necessário traçar as forças cortantes e momentos fletores e selecionar uma seção transversal da viga I com uma tensão normal admissível kN/cm2 e tensão de cisalhamento admissível kN/cm2. Vão da viga m.

Um exemplo de tarefa para uma curva reta - um esquema de design

Arroz. 3.13

Solução de um exemplo de um problema de dobra reta

Determinando reações de suporte

Para uma determinada viga apoiada articuladamente, é necessário encontrar três reações de apoio: , e . Como somente cargas verticais atuam na viga, perpendiculares ao seu eixo, a reação horizontal do suporte articulado fixo A é igual a zero: .

As direções das reações verticais e são escolhidas arbitrariamente. Vamos direcionar, por exemplo, ambas as reações verticais para cima. Para calcular seus valores, compomos duas equações de estática:

Lembre-se de que a carga linear resultante, uniformemente distribuída ao longo de uma seção de comprimento l, é igual, ou seja, igual à área do diagrama dessa carga e é aplicada no centro de gravidade desse diagrama, isto é, no meio do comprimento.

;

kN.

Verificamos: .

Lembre-se de que as forças cuja direção coincide com a direção positiva do eixo y são projetadas (projetadas) nesse eixo com um sinal de mais:

está correto.

Construímos diagramas de forças cortantes e momentos fletores

Quebramos o comprimento da viga em seções separadas. Os limites dessas seções são os pontos de aplicação de forças concentradas (ativas e/ou reativas), bem como os pontos correspondentes ao início e fim da carga distribuída. Existem três dessas áreas em nosso problema. Ao longo dos limites dessas seções, traçamos seis seções transversais, nas quais calcularemos os valores de forças cortantes e momentos fletores (Fig. 3.13, a).

Seção 1. Vamos descartar mentalmente o lado direito do feixe. Para a conveniência de calcular a força cortante e o momento fletor que surgem nesta seção, fechamos a parte da viga descartada por nós com um pedaço de papel, alinhando a borda esquerda do pedaço de papel com a própria seção.

A força de cisalhamento na seção da viga é igual à soma algébrica de todas as forças externas (ativas e reativas) que vemos. Neste caso, vemos a reação do apoio e a carga linear q, distribuídas em um comprimento infinitamente pequeno. A carga linear resultante é zero. É por isso

kN.

O sinal de mais é obtido porque a força gira a parte visível do feixe em relação à primeira seção (a borda do pedaço de papel) no sentido horário.

O momento fletor na seção da viga é igual à soma algébrica dos momentos de todas as forças que vemos, em relação à seção em consideração (ou seja, em relação à borda de um pedaço de papel). Vemos a reação do suporte e a carga linear q, distribuída por um comprimento infinitamente pequeno. No entanto, a alavancagem da força é zero. A carga linear resultante também é igual a zero. É por isso

Seção 2. Como antes, cobriremos todo o lado direito da viga com um pedaço de papel. Agora vemos a reação e a carga q atuando em uma seção de comprimento . A carga linear resultante é igual a . Ele é anexado no meio de uma seção com um comprimento de . É por isso

Lembre-se de que, ao determinar o sinal do momento fletor, liberamos mentalmente a parte da viga que vemos de todas as fixações de apoio reais e a imaginamos como se estivesse presa na seção em consideração (ou seja, a borda esquerda da peça de papel é representado mentalmente por nós como um selo rígido).

Seção 3. Vamos fechar a parte direita. Pegue

Seção 4. Fechamos o lado direito da viga com uma folha. Então

Agora, para controlar a exatidão dos cálculos, vamos cobrir o lado esquerdo da viga com um pedaço de papel. Vemos a força concentrada P, a reação do suporte direito e a carga linear q, distribuída ao longo de um comprimento infinitamente pequeno. A carga linear resultante é zero. É por isso

kNm

Ou seja, está tudo certo.

Seção 5. Ainda feche o lado esquerdo do feixe. Terá

kN;

kNm

Seção 6. Vamos fechar o lado esquerdo do feixe novamente. Pegue

kN;

Com base nos valores encontrados, construímos diagramas de esforços cortantes (Fig. 3.13, b) e momentos fletores (Fig. 3.13, c).

Estamos convencidos de que sob a seção sem carga o diagrama de força cortante corre paralelo ao eixo da viga e sob uma carga distribuída q - ao longo de uma linha reta com inclinação descendente. Existem três saltos no diagrama: sob a reação - para cima em 37,5 kN, sob a reação - em 132,5 kN e sob a força P - para baixo em 50 kN.

No diagrama de momentos fletores, vemos rupturas sob a força concentrada P e sob as reações de apoio. Os ângulos de fratura são direcionados para essas forças. Sob uma carga distribuída de intensidade q, o diagrama muda ao longo de uma parábola quadrática, cuja convexidade é direcionada para a carga. Sob o momento concentrado há um salto de 60 kN m, ou seja, pela magnitude do próprio momento. Na seção 7 do diagrama há um extremo, pois o diagrama da força cortante para esta seção passa pelo valor zero (). Vamos determinar a distância da seção 7 ao suporte esquerdo.

Começamos com o caso mais simples, a chamada flexão pura.

A flexão pura é um caso especial de flexão, em que a força transversal nas seções da viga é zero. A flexão pura só pode ocorrer quando o peso próprio da viga é tão pequeno que sua influência pode ser desprezada. Para vigas em dois apoios, exemplos de cargas que causam

curva, mostrada na Fig. 88. Em seções dessas vigas, onde Q \u003d 0 e, portanto, M \u003d const; há uma curva pura.

As forças em qualquer seção da viga com flexão pura são reduzidas a um par de forças, cujo plano de ação passa pelo eixo da viga e o momento é constante.

As tensões podem ser determinadas com base nas seguintes considerações.

1. As componentes tangenciais das forças nas áreas elementares da seção transversal da viga não podem ser reduzidas a um par de forças cujo plano de ação é perpendicular ao plano da seção. Segue-se que a força de flexão na seção é o resultado da ação em áreas elementares

apenas forças normais e, portanto, com flexão pura, as tensões são reduzidas apenas às normais.

2. Para que os esforços em áreas elementares sejam reduzidos a apenas algumas forças, deve haver forças positivas e negativas entre elas. Portanto, devem existir fibras de viga tensionadas e comprimidas.

3. Devido ao fato de que as forças em diferentes seções são as mesmas, as tensões nos pontos correspondentes das seções são as mesmas.

Considere qualquer elemento próximo à superfície (Fig. 89, a). Como nenhuma força é aplicada ao longo de sua face inferior, que coincide com a superfície da viga, também não há tensões sobre ela. Portanto, não há tensões na face superior do elemento, pois caso contrário o elemento não estaria em equilíbrio. Considerando o elemento adjacente a ele em altura (Fig. 89, b), chegamos a

A mesma conclusão, etc. Segue-se que não há tensões ao longo das faces horizontais de qualquer elemento. Considerando os elementos que compõem a camada horizontal, começando pelo elemento próximo à superfície da viga (Fig. 90), chegamos à conclusão de que não há tensões ao longo das faces verticais laterais de nenhum elemento. Assim, o estado de tensão de qualquer elemento (Fig. 91, a), e no limite da fibra, deve ser representado como mostrado na Fig. 91b, ou seja, pode ser tensão axial ou compressão axial.

4. Devido à simetria da aplicação de forças externas, a seção ao longo do meio do comprimento da viga após a deformação deve permanecer plana e normal ao eixo da viga (Fig. 92, a). Pela mesma razão, seções em quartos do comprimento da viga também permanecem planas e normais ao eixo da viga (Fig. 92, b), se apenas as seções extremas da viga permanecerem planas e normais ao eixo da viga durante a deformação. Uma conclusão semelhante também é válida para seções em oitavos do comprimento da viga (Fig. 92, c), etc. Portanto, se as seções extremas da viga permanecerem planas durante a flexão, então para qualquer seção ela permanecerá

é justo dizer que após a deformação ela permanece plana e normal ao eixo da viga curvada. Mas, neste caso, é óbvio que a mudança no alongamento das fibras da viga ao longo de sua altura deve ocorrer não apenas continuamente, mas também monotonamente. Se chamarmos uma camada de um conjunto de fibras com os mesmos alongamentos, segue-se do que foi dito que as fibras esticadas e comprimidas da viga devem estar localizadas em lados opostos da camada em que os alongamentos das fibras são iguais a zero. Chamaremos de neutras as fibras cujos alongamentos são iguais a zero; uma camada composta por fibras neutras - uma camada neutra; a linha de interseção da camada neutra com o plano da seção transversal da viga - a linha neutra desta seção. Então, com base nas considerações anteriores, pode-se argumentar que com uma flexão pura da viga em cada uma de suas seções existe uma linha neutra que divide esta seção em duas partes (zonas): a zona de fibras esticadas (zona tensionada) e a zona de fibras comprimidas (zona comprimida). Assim, as tensões normais de tração devem atuar nos pontos da zona esticada da seção transversal, as tensões de compressão nos pontos da zona comprimida e nos pontos da linha neutra as tensões são iguais a zero.

Assim, com uma flexão pura de uma viga de seção transversal constante:

1) apenas tensões normais atuam nas seções;

2) toda a seção pode ser dividida em duas partes (zonas) - esticada e comprimida; o limite das zonas é a linha neutra da seção, nos pontos em que as tensões normais são iguais a zero;

3) qualquer elemento longitudinal da viga (no limite, qualquer fibra) é submetido a tração ou compressão axial, de modo que as fibras adjacentes não interagem entre si;

4) se as seções extremas da viga durante a deformação permanecerem planas e normais ao eixo, então todas as suas seções transversais permanecerão planas e normais ao eixo da viga curvada.

Estado de tensão de uma viga em flexão pura

Considere um elemento de uma viga sujeito à flexão pura, concluindo medidos entre as seções m-m e n-n, que são espaçadas uma da outra a uma distância dx infinitamente pequena (Fig. 93). Devido ao disposto (4) do parágrafo anterior, as seções m-m e n-n, que eram paralelas antes da deformação, após a flexão, permanecendo planas, formarão um ângulo dQ e se cruzarão ao longo de uma linha reta que passa pelo ponto C, que é o centro de curvatura da fibra neutra NN. Então a parte da fibra AB contida entre eles, localizada a uma distância z da fibra neutra (a direção positiva do eixo z é tomada em direção à convexidade da viga durante a flexão), se transformará em um arco A "B" após Um segmento da fibra neutra O1O2, transformando-se em um arco O1O2, não mudará seu comprimento, enquanto a fibra AB receberá um alongamento:

antes da deformação

após a deformação

onde p é o raio de curvatura da fibra neutra.

Portanto, o alongamento absoluto do segmento AB é

e alongamento

Uma vez que, de acordo com a posição (3), a fibra AB é submetida a tração axial, então com deformação elástica

A partir disso, pode-se ver que as tensões normais ao longo da altura da viga são distribuídas de acordo com uma lei linear (Fig. 94). Como a força igual de todos os esforços em todas as seções elementares da seção deve ser igual a zero, então

de onde, substituindo o valor de (5.8), encontramos

Mas a última integral é um momento estático em torno do eixo Oy, que é perpendicular ao plano de ação das forças de flexão.

Devido à sua igualdade a zero, este eixo deve passar pelo centro de gravidade O da seção. Assim, a linha neutra da seção da viga é uma linha reta yy, perpendicular ao plano de ação das forças de flexão. É chamado de eixo neutro da seção da viga. Então, de (5.8), segue-se que as tensões em pontos situados à mesma distância do eixo neutro são as mesmas.

O caso da flexão pura, em que as forças de flexão atuam em apenas um plano, causando flexão somente nesse plano, é uma flexão plana pura. Se o plano nomeado passa pelo eixo Oz, então o momento dos esforços elementares em relação a este eixo deve ser igual a zero, ou seja,

Substituindo aqui o valor de σ de (5.8), encontramos

A integral do lado esquerdo desta igualdade, como é conhecida, é o momento de inércia centrífuga da seção em torno dos eixos y e z, de modo que

Os eixos em relação aos quais o momento de inércia centrífugo da seção é igual a zero são chamados de eixos principais de inércia desta seção. Se, além disso, eles passam pelo centro de gravidade da seção, podem ser chamados de eixos centrais principais de inércia da seção. Assim, com uma flexão pura plana, a direção do plano de ação das forças de flexão e o eixo neutro da seção são os principais eixos centrais de inércia desta última. Em outras palavras, para obter uma flexão plana e limpa de uma viga, uma carga não pode ser aplicada a ela arbitrariamente: ela deve ser reduzida a forças atuantes em um plano que passa por um dos principais eixos centrais de inércia das seções da viga; neste caso, o outro eixo central principal de inércia será o eixo neutro da seção.

Como se sabe, no caso de uma seção simétrica em relação a qualquer eixo, o eixo de simetria é um de seus principais eixos centrais de inércia. Portanto, neste caso específico, certamente obteremos uma flexão pura aplicando as cargas analógicas apropriadas no plano que passa pelo eixo longitudinal da viga e pelo eixo de simetria de sua seção. A linha reta, perpendicular ao eixo de simetria e passando pelo centro de gravidade da seção, é o eixo neutro desta seção.

Tendo estabelecido a posição do eixo neutro, não é difícil encontrar a magnitude da tensão em qualquer ponto da seção. De fato, como a soma dos momentos das forças elementares em relação ao eixo neutro yy deve ser igual ao momento fletor, então

de onde, substituindo o valor de σ de (5.8), encontramos

Desde a integral é. momento de inércia da seção em torno do eixo y, então

e da expressão (5.8) obtemos

O produto EI Y é chamado de rigidez à flexão da viga.

As maiores tensões de tração e compressão em valor absoluto atuam nos pontos da seção para os quais o valor absoluto de z é maior, ou seja, nos pontos mais distantes do eixo neutro. Com as designações, Fig. 95 tem

O valor de Jy/h1 é chamado de momento de resistência da seção ao alongamento e é denotado por Wyr; da mesma forma, Jy/h2 é chamado de momento de resistência da seção à compressão

e denotam Wyc, então

e, portanto,

Se o eixo neutro é o eixo de simetria da seção, então h1 = h2 = h/2 e, consequentemente, Wyp = Wyc, então não há necessidade de distinção entre eles, e eles usam a mesma designação:

chamando W y simplesmente o módulo de seção. Portanto, no caso de uma seção simétrica em torno do eixo neutro,

Todas as conclusões acima são obtidas com base na suposição de que as seções transversais da viga, quando dobradas, permanecem planas e normais ao seu eixo (a hipótese das seções planas). Como mostrado, esta suposição é válida apenas se as seções extremas (extremidades) da viga permanecerem planas durante a flexão. Por outro lado, decorre da hipótese das seções planas que as forças elementares nessas seções devem ser distribuídas de acordo com uma lei linear. Portanto, para a validade da teoria obtida da flexão pura plana, é necessário que os momentos fletores nas extremidades da viga sejam aplicados na forma de forças elementares distribuídas ao longo da altura da seção de acordo com uma lei linear (Fig. 96), que coincide com a lei de distribuição de tensões ao longo da altura das vigas de seção. No entanto, com base no princípio de Saint-Venant, pode-se argumentar que uma mudança no método de aplicação dos momentos fletores nas extremidades da viga causará apenas deformações locais, cuja influência afetará apenas a uma certa distância dessas extremidades (aproximadamente igual à altura da seção). As seções localizadas no restante do comprimento da viga permanecerão planas. Consequentemente, a teoria da flexão pura plana, com qualquer método de aplicação de momentos fletores, é válida apenas na parte média do comprimento da viga, localizada a distâncias de suas extremidades aproximadamente iguais à altura da seção. A partir disso, fica claro que esta teoria é obviamente inaplicável se a altura da seção exceder a metade do comprimento ou vão da viga.

Classificação dos tipos de flexão da haste

dobrar chamado esse tipo de deformação, na qual ocorrem momentos fletores nas seções transversais da haste. Uma haste trabalhando em flexão é chamada feixe. Se os momentos fletores são os únicos fatores de força internos nas seções transversais, então a haste experimenta curva limpa. Se os momentos fletores ocorrerem junto com as forças transversais, então tal flexão é chamada transversal.

Vigas, eixos, eixos e outros detalhes estruturais trabalham na flexão.

Vamos introduzir alguns conceitos. O plano que passa por um dos principais eixos centrais da seção e pelo eixo geométrico da barra é chamado de plano principal. O plano no qual as cargas externas atuam, fazendo com que a viga se curve, é chamado de plano de força. A linha de interseção do plano de força com o plano da seção transversal da barra é chamada linha de energia. Dependendo da posição relativa da potência e dos planos principais do feixe, é distinguida uma curva reta ou oblíqua. Se o plano de força coincide com um dos planos principais, então a barra experimenta curva reta(Fig. 5.1, uma), se não corresponder - oblíquo(Fig. 5.1, b).

Arroz. 5.1. Curvatura da haste: uma- direto; b- oblíquo

Do ponto de vista geométrico, a flexão da haste é acompanhada por uma mudança na curvatura do eixo da haste. O eixo inicialmente retilíneo da haste torna-se curvilíneo quando é dobrado. Com flexão direta, o eixo dobrado da haste encontra-se no plano de força, com flexão oblíqua, em um plano diferente do plano de força.

Observando a flexão de uma haste de borracha, pode-se notar que parte de suas fibras longitudinais é esticada, enquanto a outra parte é comprimida. Obviamente, entre as fibras esticadas e comprimidas da haste existe uma camada de fibras que não sofre tensão nem compressão, a chamada camada neutra. A linha de interseção da camada neutra da haste com o plano de sua seção transversal é chamada linha de seção neutra.

Como regra, as cargas que atuam na viga podem ser atribuídas a um dos três tipos: forças concentradas R, momentos concentrados M intensidade de cargas distribuídas c(Fig. 5.2). A parte I da viga, localizada entre os apoios, é chamada de período, parte II da viga, localizada em um lado do suporte, - console.