Wyznacz współrzędne środka ciężkości przekroju T. Obliczanie belek teowych żelbetowych. Wyznaczanie środka ciężkości przekroju T
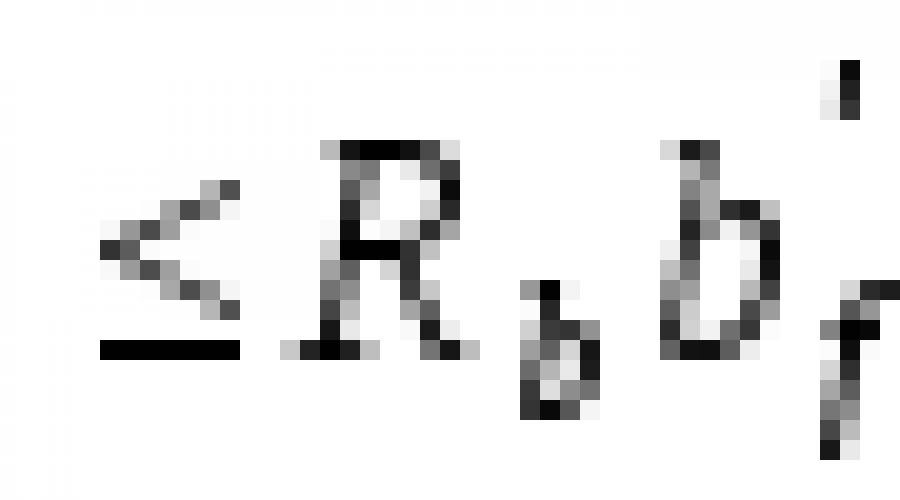
Przeczytaj także
Obliczenia są takie same jak dla belki przekrój prostokątny. Obejmują wyznaczanie sił w belce i na narożach płyty. Siły te następnie kierują się do środka ciężkości nowego przekroju T.
Oś przechodzi przez środek ciężkości płyty.
Uproszczone podejście do uwzględniania sił płyty polega na pomnożeniu sił w węzłach płyty (wspólnych węzłach płyty i belek) przez projektową szerokość płyty. Podczas pozycjonowania belki względem płyty uwzględniane są przemieszczenia (również przemieszczenia względne). Otrzymane wyniki skrócone są takie same, jak gdyby teownik został podniesiony od płaszczyzny płyty o wielkość przemieszczenia równą odległości od środka ciężkości płyty do środka ciężkości teownika (patrz Niżej wymienione).
Doprowadzenie sił do środka ciężkości przekroju T następuje w następujący sposób:
M = Mb + Mp * B + Np * B * e1 + Nb * e2
B = beff1+b+beff2
Wyznaczanie środka ciężkości przekroju T
Moment statyczny obliczony w środku ciężkości płyty
S = b*h* (przesunięcie)
A = (beff1+b+beff2)*hpl + b*h
Środek ciężkości podniesiony względem środka ciężkości płyty:
b - szerokość belki;
h - wysokość belki;
beff1, beff2 - obliczone szerokości płyt;
hpl - wysokość płyty (grubość płyty);
przemieszczenie to przemieszczenie belki względem płyty.
NOTATKA.
- Należy wziąć pod uwagę, że może tak być całkowite obszary płyty i belki, co niestety będzie obliczane dwukrotnie, co doprowadzi do wzrostu sztywności belki teowej. W rezultacie siły i ugięcia są zmniejszone.
- Wyniki płyty odczytywane są z węzłów elementów skończonych; zagęszczenie siatki wpływa na wyniki.
- W modelu oś przekroju T przechodzi przez środek ciężkości płyty.
- Mnożenie odpowiednich sił przez przyjętą projektową szerokość płyty jest uproszczeniem, które prowadzi do przybliżonych wyników.
Zginany konstrukcje żelbetowe przekroje prostokątne nie są efektywne z ekonomicznego punktu widzenia. Wynika to z faktu, że naprężenia normalne na wysokości przekroju podczas zginania elementu rozkładają się nierównomiernie. W porównaniu do przekrojów prostokątnych, przekroje teowe są znacznie bardziej opłacalne, ponieważ w tym samym nośność Zużycie betonu w elementach o profilu T jest mniejsze.
Sekcja T z reguły ma pojedyncze wzmocnienie.
W obliczeniach wytrzymałościowych przekrojów normalnych zginanych elementów profili T występują dwa przypadki obliczeniowe.
Algorytm dla pierwszego przypadku obliczeniowego opiera się na założeniu, że oś neutralna elementu zginanego znajduje się w obrębie ściskanego kołnierza.
Algorytm dla drugiego przypadku obliczeniowego opiera się na założeniu, że oś neutralna elementu zginanego znajduje się na zewnątrz ściskanego kołnierza (przechodzi wzdłuż krawędzi teownika elementu).
Obliczanie wytrzymałości przekroju normalnego elementu żelbetowego na zginanie z pojedynczym zbrojeniem w przypadku, gdy oś neutralna znajduje się w ściskanym pasie jest identyczne z algorytmem obliczania przekroju prostokątnego z pojedynczym zbrojeniem o szerokości przekroju równej szerokość kołnierza trójnika.
Schemat projektowy dla tego przypadku przedstawiono na rys. 3.3.
Ryż. 3.3. Do obliczenia wytrzymałości przekroju normalnego elementu żelbetowego na zginanie w przypadku, gdy oś neutralna znajduje się w obrębie ściskanego pasa.
Geometrycznie przypadek, gdy oś neutralna znajduje się w obrębie ściskanego kołnierza oznacza, że wysokość strefy ściskanej przekroju trójnika () jest nie większa niż wysokość ściskanego kołnierza i wyraża się warunkiem: .
Z punktu widzenia sił działających od obciążenia zewnętrznego i sił wewnętrznych warunek ten oznacza, że wytrzymałość przekroju jest zapewniona, jeśli obliczona wartość momentu zginającego od obciążenia zewnętrznego (M ) nie przekroczy obliczonej wartości momentu sił wewnętrznych względem środka ciężkości przekroju zbrojenia rozciąganego przy wartościach .
M ![]() (3.25)
(3.25)
Jeżeli warunek (3.25) jest spełniony, to rzeczywiście oś neutralna znajduje się w obrębie ściśniętego kołnierza. W takim przypadku konieczne jest wyjaśnienie, jaki rozmiar szerokości ściśniętego kołnierza należy uwzględnić w obliczeniach. Normy ustanawiają następujące zasady:
Oznaczający B " F , ujęte w obliczeniach; wynika z warunku, że szerokość zwisu półki w każdym kierunku z żebra nie powinna być większa 1 / 6 zakres elementów i nic więcej:
a) w obecności żeber poprzecznych lub gdy H " F ≥ 0,1 H - 1 / 2 wyraźne odległości pomiędzy żebrami podłużnymi;
b) w przypadku braku żeber poprzecznych (lub gdy odległości między nimi są większe niż odległości między żebrami podłużnymi) oraz H " F < 0,1 H - 6 H " F
c) ze wspornikowymi zwisami półki:
Na H " F ≥ 0,1 H - 6 H " F ;
Na 0,05 H ≤ H " F < 0,1 H - 3 H " F ;
Na H " F < 0,05 H - zwisy nie są brane pod uwagę.
Zapiszmy warunek wytrzymałościowy względem środka ciężkości rozciąganego zbrojenia podłużnego
M ![]() (3.26)
(3.26)
Przekształćmy równanie (3.26) analogicznie do przekształceń wyrażeń (3.3). (3.4) otrzymujemy wyrażenie
M (3.27)
Stąd określamy wartość
= (3.28)
Według wartości z tabeli ![]() Określmy wartości 𝛈.
Określmy wartości 𝛈.
Porównajmy wartość . sekcje elementów. Jeżeli warunek 𝛏 jest spełniony, to stanowi on warunek wytrzymałościowy względem środka ciężkości ściśniętej strefy trójnika.
M ![]() (3.29)
(3.29)
Po przeprowadzeniu transformacji wyrażenia (3.29) podobnej do transformacji wyrażenia (3.12) otrzymujemy:
= (3.30)
![]() konieczne jest wybranie wartości powierzchni rozciągniętego podłużnego zbrojenia roboczego.
konieczne jest wybranie wartości powierzchni rozciągniętego podłużnego zbrojenia roboczego.
Obliczanie wytrzymałości przekroju normalnego elementu żelbetowego na zginanie z pojedynczym zbrojeniem w przypadku, gdy oś neutralna znajduje się na zewnątrz ściskanego pasa (przechodzi wzdłuż krawędzi trójnika) różni się nieco od omówionych powyżej.
Schemat projektowy dla tego przypadku przedstawiono na rys. 3.4.

Ryż. 3.4. Do obliczeń wytrzymałości przekroju normalnego elementu żelbetowego na zginanie w przypadku, gdy oś neutralna znajduje się na zewnątrz ściskanego pasa.
Rozważmy przekrój poprzeczny strefy ściskanej trójnika jako sumę składającą się z dwóch prostokątów (nawisów kołnierzy) i prostokąta związanego z ściskaną częścią żebra.
Stan wytrzymałości względem środka ciężkości zbrojenia na rozciąganie.
M + (3.31)
Gdzie – siła w ściśniętych zwisach półek;
Ramię od środka ciężkości naprężonego zbrojenia do środka ciężkości zwisów półki;
– siła działająca w ściskanej części żebra teownika;
- ramię od środka ciężkości zbrojenia rozciąganego do środka ciężkości ściśniętej części żebra.
= (3.32)
= (3.33)
= B (3.34)
= (3.35)
Podstawmy wyrażenia (3.32 – 3.35) do wzoru (3.31).
M + B (3.36)
Przekształćmy drugi wyraz po prawej stronie równania w wyrażeniu (3.36) analogicznie do przekształceń wykonanych powyżej (wzory 3.3; 3.4; 3.5)
Otrzymujemy następujące wyrażenie:
M + (3.37)
Stąd definiujemy wartość numeryczna .
=![]() (3.38)
(3.38)
Według wartości z tabeli ![]() Określmy wartości 𝛈.
Określmy wartości 𝛈.
Porównajmy tę wartość z wartością graniczną względnej wysokości strefy ściśniętej . sekcje elementów. Jeżeli warunek 𝛏 jest spełniony, wówczas powstaje warunek równowagi rzutów sił na oś podłużną elementu. Σ N=0
--=0 (3.39)
=+ B (3.40)
Stąd definiujemy wymagany obszar odcinki rozciąganego, podłużnego zbrojenia roboczego.
=![]() (3.41)
(3.41)
Według asortymentu zbrojenia prętów ![]() konieczne jest wybranie wartości powierzchni rozciągniętego podłużnego zbrojenia roboczego.
konieczne jest wybranie wartości powierzchni rozciągniętego podłużnego zbrojenia roboczego.
Cechą środka ciężkości jest to, że siła ta nie działa na ciało w żadnym jednym punkcie, ale jest rozłożona na całą objętość ciała. Siły grawitacji, na które działają poszczególne elementy ciała (które można uznać za punkty materialne) są skierowane w stronę środka Ziemi i nie są ściśle równoległe. Ale ponieważ rozmiary większości ciał na Ziemi są znacznie mniejsze niż jego promień, dlatego siły te uważa się za równoległe.
Wyznaczanie środka ciężkości
Definicja
Punkt, przez który przechodzi wypadkowa wszystkich równoległych sił grawitacji, działających na elementy ciała w dowolnym miejscu ciała w przestrzeni, nazywa się Środek ciężkości.
Innymi słowy: środek ciężkości to punkt, do którego przyłożona jest siła ciężkości w dowolnym położeniu ciała w przestrzeni. Jeśli znane jest położenie środka ciężkości, możemy założyć, że siła ciężkości jest jedną siłą i jest przykładana w środku ciężkości.
Zadanie znalezienia środka ciężkości jest istotnym zadaniem w technologii, ponieważ stabilność wszystkich konstrukcji zależy od położenia środka ciężkości.
Metoda wyznaczania środka ciężkości ciała
Wyznaczanie położenia środka ciężkości ciała złożony kształt Możesz najpierw w myślach rozbić ciało na części o prostym kształcie i znaleźć dla nich środki ciężkości. W przypadku ciał o prostym kształcie środek ciężkości można natychmiast wyznaczyć na podstawie rozważań o symetrii. Siła ciężkości jednorodnego dysku i kuli znajduje się w ich środku, a jednorodnego walca w punkcie pośrodku jego osi; jednorodny równoległościan na przecięciu jego przekątnych itp. Dla wszystkich ciał jednorodnych środek ciężkości pokrywa się ze środkiem symetrii. Środek ciężkości może znajdować się na zewnątrz ciała, na przykład na pierścieniu.
Znajdźmy położenie środków ciężkości części ciała, znajdź położenie środka ciężkości ciała jako całości. Aby to zrobić, ciało jest reprezentowane jako zbiór punkty materialne. Każdy taki punkt znajduje się w środku ciężkości swojej części ciała i ma masę tej części.
Współrzędne środka ciężkości
W przestrzeni trójwymiarowej współrzędne punktu przyłożenia wypadkowej wszystkich równoległych sił ciężkości (współrzędne środka ciężkości), dla solidny są obliczane jako:
\[\left\( \begin(array)(c) x_c=\frac(\sum\limits_i(\Delta m_ix_i))(m); \\ y_c=\frac(\sum\limits_i(\Delta m_iy_i) )(m);; \\ z_c=\frac(\suma\limits_i(\Delta m_iz_i))(m) \end(array) \right.\left(1\right),\]
gdzie $m$ jest masą ciała.$;;x_i$ jest współrzędną na osi X masy elementarnej $\Delta m_i$; $y_i$ - współrzędna na osi Y masy elementarnej $\Delta m_i$; ; $z_i$ jest współrzędną na osi Z elementarnej masy $\Delta m_i$.
W notacji wektorowej układ trzech równań (1) zapisuje się jako:
\[(\overline(r))_c=\frac(1)(m)\sum\limits_i(m_i(\overline(r))_i\left(2\right),)\]
$(\overline(r))_c$ - promień - wektor określający położenie środka ciężkości; $(\overline(r))_i$ to wektory promieniowe określające położenie mas elementarnych.
Środek ciężkości, środek masy i środek bezwładności ciała
Wzór (2) pokrywa się z wyrażeniami wyznaczającymi środek masy ciała. Jeżeli rozmiar ciała jest mały w porównaniu z odległością do środka Ziemi, przyjmuje się, że środek ciężkości pokrywa się ze środkiem masy ciała. W większości problemów środek ciężkości pokrywa się ze środkiem masy ciała.
Siła bezwładności w nieinercyjnych układach odniesienia poruszających się translacyjnie przykładana jest do środka ciężkości ciała.
Należy jednak wziąć pod uwagę, że siła odśrodkowa bezwładności (w ogólnym przypadku) nie jest przykładana do środka ciężkości, ponieważ w nieinercjalnym układzie odniesienia na elementy ciała (nawet jeśli masy elementów są równe), ponieważ odległości do osi obrotu są różne.
Przykłady problemów z rozwiązaniami
Przykład 1
Ćwiczenia. Układ składa się z czterech małych kulek (rys. 1). Jakie są współrzędne jego środka ciężkości?
Rozwiązanie. Spójrzmy na ryc. 1. Środek ciężkości w tym przypadku będzie miał jedną współrzędną $x_c$, którą definiujemy jako:
Masa ciała w naszym przypadku wynosi:
Licznik ułamka po prawej stronie wyrażenia (1.1) w przypadku (1(a)) przyjmuje postać:
\[\sum\limits_(i=4)(\Delta m_ix_i=m\cdot 0+2m\cdot a+3m\cdot 2a+4m\cdot 3a=20m\cdot a).\]
Otrzymujemy:
Odpowiedź.$x_c=2a;$
Przykład 2
Ćwiczenia. Układ składa się z czterech małych kulek (rys. 2). Jakie są współrzędne jego środka ciężkości?

Rozwiązanie. Spójrzmy na ryc. 2. Środek ciężkości układu znajduje się na płaszczyźnie, dlatego ma on dwie współrzędne ($x_c,y_c$). Znajdźmy je za pomocą wzorów:
\[\left\( \begin(array)(c) x_c=\frac(\sum\limits_i(\Delta m_ix_i))(m); \\ y_с=\frac(\sum\limits_i(\Delta m_iy_i) )(m).\end(tablica)\right.\]
Waga systemu:
Znajdźmy współrzędną $x_c$:
Współrzędna $y_с$:
Odpowiedź.$x_c=0,5\ a$; $y_с=0,3\ a$