Hookeov zakon napetosti i kompresije. Uzdužne i poprečne deformacije Određivanje relativne uzdužne deformacije

Razmotrimo deformacije koje nastaju tijekom napetosti i kompresije štapova. Kada se rasteže, duljina šipke se povećava, a poprečne dimenzije smanjuju. Kada se stisne, naprotiv, duljina šipke se smanjuje, a poprečne dimenzije se povećavaju. Na slici 2.7 isprekidana linija prikazuje deformirani pogled na istegnuti štap.

ℓ – duljina štapa prije primjene opterećenja;

ℓ 1 – duljina štapa nakon primjene opterećenja;

b – poprečna dimenzija prije primjene opterećenja;

b 1 – poprečna veličina nakon primjene opterećenja.

Apsolutna uzdužna deformacija ∆ℓ = ℓ 1 – ℓ.

Apsolutna poprečna deformacija ∆b = b 1 – b.

Vrijednost relativne linearne deformacije ε može se definirati kao omjer apsolutnog istezanja ∆ℓ i početne duljine grede ℓ

Poprečne deformacije nalaze se na sličan način

Kod istezanja se poprečne dimenzije smanjuju: ε > 0, ε′< 0; при сжатии: ε < 0, ε′ >0. Iskustvo pokazuje da je kod elastičnih deformacija poprečna deformacija uvijek upravno proporcionalna uzdužnoj.

ε′ = – νε. (2.7)

Koeficijent proporcionalnosti ν naziva se Poissonov omjer ili omjer poprečne deformacije. Predstavlja apsolutnu vrijednost omjera poprečne i uzdužne deformacije pri aksijalna napetost

Ime je dobio po francuskom znanstveniku koji ga je prvi predložio u početkom XIX stoljeća. Poissonov omjer je stalna vrijednost za materijal unutar granica elastičnih deformacija (tj. deformacija koje nestaju nakon uklanjanja opterećenja). Za raznih materijala Poissonov omjer varira unutar 0 ≤ ν ≤ 0,5: za čelik ν = 0,28…0,32; za gumu ν = 0,5; za čep ν = 0.

Postoji odnos između naprezanja i elastične deformacije poznat kao Hookeov zakon:

σ = Eε. (2.9)

Koeficijent proporcionalnosti E između naprezanja i deformacija naziva se normalni elastični modul ili Youngov modul. Dimenzija E je ista kao i dimenzija napona. Kao i ν, E je elastičan materijalna konstanta. Kako više vrijednosti E, manje je uzdužna deformacija, pod jednakim uvjetima. Za čelik E = (2...2,2)10 5 MPa ili E = (2...2,2)10 4 kN/cm 2.

Zamjenom u formulu (2.9) vrijednosti σ prema formuli (2.2) i ε prema formuli (2.5), dobivamo izraz za apsolutnu deformaciju

Umnožak EF naziva se krutost drveta na napetost i pritisak.

Formule (2.9) i (2.10) su različite oblike zapisi o Hookeovom zakonu predloženom u sredinom 17. stoljeća stoljeća. Moderna forma snimci ovog temeljnog zakona fizike pojavili su se mnogo kasnije - početkom 19. stoljeća.

Formula (2.10) vrijedi samo unutar onih područja gdje su sila N i krutost EF konstantne. Za stepenasti štap i štap opterećen s nekoliko sila, produžeci se izračunavaju u presjecima s konstantnim N i F i rezultati se algebarski zbrajaju

Ako se te veličine mijenjaju prema kontinuiranom zakonu, ∆ℓ se izračunava po formuli

U nekim slučajevima, kako bi se osiguralo normalna operacija strojeva i konstrukcija, dimenzije njihovih dijelova moraju biti odabrane tako da se, osim stanja čvrstoće, osigura i stanje krutosti

gdje je ∆ℓ – promjena dimenzija dijela;

[∆ℓ] – dopuštena vrijednost ove promjene.

Naglašavamo da proračun krutosti uvijek nadopunjuje proračun čvrstoće.

2.4. Izračun šipke uzimajući u obzir vlastitu težinu

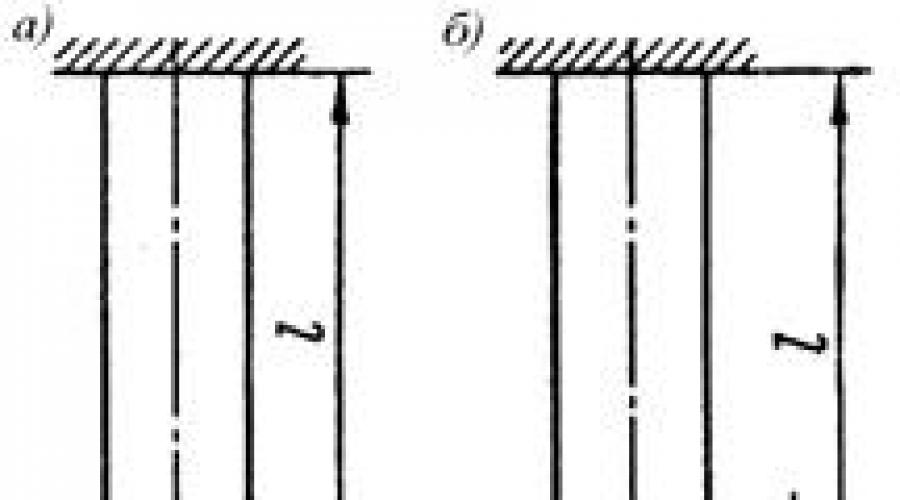
Najjednostavniji primjer problema rastezanja štapa s parametrima koji se mijenjaju po duljini je problem rastezanja prizmatičnog štapa pod utjecajem vlastite težine (slika 2.8a). Uzdužna sila N x u presjeku ove grede (na udaljenosti x od njenog donjeg kraja) jednaka je sili gravitacije donjeg dijela grede (slika 2.8, b), tj.

N x = γFx, (2.14)

gdje je γ – volumenska težina materijal šipke.

Uzdužna sila i naprezanje variraju linearno, dostižući maksimum u ugradnji. Aksijalni pomak proizvoljnog presjeka jednak je izduženju gornjeg dijela grede. Stoga se mora odrediti pomoću formule (2.12), iz koje se provodi integracija Trenutna vrijednost x do x = l:

Dobili smo izraz za proizvoljan presjek štapa

Pri x = ℓ pomak je najveći, jednak je izduženju štapa

Slika 2.8, c, d, e prikazuje grafove N x, σ x i u x

Pomnožimo brojnik i nazivnik formule (2.17) s F i dobijemo:

Izraz γFℓ jednak je vlastitoj težini štapa G. Prema tome

Formulu (2.18) možemo odmah dobiti iz (2.10), ako se sjetimo da se rezultanta vlastite težine G mora primijeniti na težište štapa i stoga uzrokuje istezanje samo gornje polovice štapa (Sl. 2.8, a).

Ako su štapovi, osim vlastite težine, opterećeni i koncentriranim uzdužnim silama, tada se naprezanja i deformacije određuju na temelju načela neovisnosti djelovanja sila odvojeno od koncentriranih sila i od vlastite težine, nakon čega se dobivaju: zbrajaju se.

Načelo neovisnog djelovanja sila slijedi iz linearne deformabilnosti elastičnih tijela. Njegova bit leži u činjenici da se bilo koja vrijednost (naprezanje, pomak, deformacija) iz djelovanja skupine sila može dobiti kao zbroj vrijednosti pronađenih iz svake sile zasebno.

Razmotrimo ravni štap konstantnog poprečnog presjeka, kruto fiksiran na vrhu. Neka štap ima duljinu i neka je opterećen vlačnom silom F . Djelovanje te sile povećava duljinu štapa za određeni iznos Δ (Slika 9.7, a).

Kad se štap sabija istom silom F duljina štapa će se smanjiti za isti iznos Δ (Slika 9.7, b).

Veličina Δ , jednaka razlici između duljina štapa nakon deformacije i prije deformacije, naziva se apsolutna linearna deformacija (izduženje ili skraćivanje) štapa kada se rasteže ili stisne.

Apsolutni linearni omjer deformacija Δ na izvornu duljinu štapa naziva se relativna linearna deformacija i označava se slovom ε ili ε x ( gdje je indeks x označava smjer deformacije). Kada je štap rastegnut ili stisnut, količina ε jednostavno se naziva relativna uzdužna deformacija štapa. Određuje se formulom:

Opetovana istraživanja procesa deformacije istegnutog ili stisnutog štapa u elastičnom stadiju potvrdila su postojanje ravne linije. proporcionalna ovisnost između normalnog naprezanja i relativne uzdužne deformacije. Ovaj odnos se zove Hookeov zakon i ima oblik:

Veličina E koji se naziva modulom uzdužne elastičnosti ili modulom prve vrste. To je fizikalna konstanta (konstanta) za svaku vrstu materijala štapa i karakterizira njegovu krutost. Što je vrijednost veća E , manja će biti uzdužna deformacija štapa. Veličina E mjereno u istim jedinicama kao i napon, to jest in Godišnje , MPa itd. Vrijednosti modula elastičnosti sadržane su u tablicama referentne i obrazovne literature. Na primjer, vrijednost modula uzdužne elastičnosti čelika uzima se jednakom E = 2∙10 5 MPa , i drvo

E = 0,8∙10 5 MPa.

Pri proračunu štapova na napetost ili pritisak često se javlja potreba za određivanjem vrijednosti apsolutne uzdužne deformacije ako je poznata veličina uzdužne sile, površina presjeka i materijal štapa. Iz formule (9.8) nalazimo: . Zamijenimo u ovom izrazu ε njegova vrijednost iz formule (9.9). Kao rezultat dobivamo = . Ako koristimo formulu normalnog naprezanja , tada dobivamo konačnu formulu za određivanje apsolutne uzdužne deformacije:

Umnožak modula uzdužne elastičnosti i površine poprečnog presjeka štapa naziva se njegov krutost kada se istegnu ili stisnu.

Analizirajući formulu (9.10), možemo izvući značajan zaključak: apsolutna uzdužna deformacija štapa tijekom napetosti (kompresije) izravno je proporcionalna umnošku uzdužne sile i duljine štapa i obrnuto proporcionalna njegovoj krutosti.

Imajte na umu da se formula (9.10) može koristiti u slučaju kada je presjek štapa i uzdužna sila ima konstantne vrijednosti cijelom dužinom. U općem slučaju, kada šipka ima stepenasto promjenjivu krutost i opterećena je duž svoje duljine s nekoliko sila, potrebno ju je podijeliti na dijelove i odrediti apsolutne deformacije svakog od njih pomoću formule (9.10).

Algebarski zbroj apsolutnih deformacija svakog presjeka bit će jednak apsolutnoj deformaciji cijelog štapa, to jest:

Uzdužne deformacije štapa uslijed jednolikog djelovanja raspodijeljeno opterećenje duž svoje osi (na primjer, djelovanjem vlastite težine), određuje se sljedećom formulom koju iznosimo bez dokaza:

Kod napetosti ili pritiska štapa, osim uzdužnih deformacija, javljaju se i poprečne deformacije, apsolutne i relativne. Označimo sa b veličina poprečnog presjeka štapa prije deformacije. Kad se štap silom rasteže F ova će se veličina smanjiti za Δb , što je apsolutna poprečna deformacija štapa. Naprotiv, apsolutna poprečna deformacija će imati negativan predznak pozitivan znak(Slika 9.8).

Razmotrimo ravnu gredu konstantne duljine poprečnog presjeka (slika 1.5), ugrađenu na jednom kraju, a na drugom kraju opterećenu vlačnom silom R. Pod silom R greda se produljuje za određeni iznos , što se naziva totalno (ili apsolutno) istezanje (apsolutna uzdužna deformacija).

Riža. 1.5. Deformacija grede

U bilo kojoj točki grede koja se razmatra postoji identično stanje naprezanja i, prema tome, linearne deformacije za sve njegove točke su iste. Stoga se vrijednost e može definirati kao omjer apsolutnog produljenja prema izvornoj duljini grede, tj.

Šipke izrađene od različitih materijala različito se izdužuju. Za slučajeve u kojima naprezanja u gredi ne prelaze granicu proporcionalnosti, iskustvom je utvrđen sljedeći odnos:

Gdje N- uzdužna sila u presjeci drvena građa; F- površina poprečnog presjeka grede; E- koeficijent ovisno o fizička svojstva materijal.

S obzirom da je normalno naprezanje u presjeku grede σ = N/F dobivamo ε = σ/E. Odakle σ = εE.

Apsolutno produljenje grede izražava se formulom

Sljedeća formulacija Hookeovog zakona je općenitija: relativna uzdužna deformacija izravno je proporcionalna normalnom naprezanju. U ovoj se formulaciji Hookeov zakon koristi ne samo u proučavanju napetosti i kompresije greda, već iu drugim dijelovima tečaja.

Veličina E koji se naziva modul elastičnosti prve vrste. Ovo je fizička konstanta materijala koja karakterizira njegovu krutost. Što je vrijednost veća E, manja je, ako su ostale stvari jednake, uzdužna deformacija. Modul elastičnosti izražava se u istim jedinicama kao i naprezanje, tj. u paskalima (Pa) (čelik E=2* 10 5 MPa, bakar E= 1 * 10 5 MPa).

Raditi E.F. naziva se krutost presjeka grede na napetost i pritisak.

Uz uzdužnu deformaciju, kada na gredu djeluje tlačna ili vlačna sila, uočava se i poprečna deformacija. Kada se greda sabija, njezine poprečne dimenzije se povećavaju, a kada se rastežu, smanjuju se. Ako poprečna veličina grede prije djelovanja tlačnih sila na nju R odrediti U, a nakon primjene ovih sila B - ∆B, zatim vrijednost ∆V pokazat će apsolutnu poprečnu deformaciju grede.

Omjer je relativna poprečna deformacija.

Iskustvo pokazuje da je pri naprezanjima koja ne prelaze granicu elastičnosti relativna poprečna deformacija izravno proporcionalna relativnoj uzdužnoj deformaciji, ali ima suprotan predznak:

Koeficijent proporcionalnosti q ovisi o materijalu drveta. Naziva se koeficijent poprečne deformacije (ili Poissonov omjer ) i je omjer relativne poprečne i uzdužne deformacije, uzet prema apsolutna vrijednost, tj. Poissonov omjer zajedno s modulom elastičnosti E karakterizira elastična svojstva materijala.

Poissonov omjer se određuje eksperimentalno. Za različite materijale ima vrijednosti od nule (za pluto) do vrijednosti blizu 0,50 (za gumu i parafin). Za čelik, Poissonov omjer je 0,25 ... 0,30; za niz drugih metala (lijevano željezo, cink, bronca, bakar) it

ima vrijednosti od 0,23 do 0,36.

Riža. 1.6. Greda promjenjivog presjeka

Određivanje vrijednosti poprečnog presjeka šipke provodi se na temelju stanja čvrstoće

gdje je [σ] dopušteno naprezanje.

Definirajmo uzdužni pomak δ a bodova A os grede rastegnute silom R( riža. 1.6).

Jednaka je apsolutnoj deformaciji dijela grede oglas zatvoren između ugradnje i presjeka nacrtanog kroz točku d, oni. uzdužna deformacija grede određena je formulom

Ova formula je primjenjiva samo kada su, unutar cijele duljine presjeka, uzdužne sile N i krutost E.F. presjeci grede su konstantni. U slučaju koji se razmatra, na mjestu ab uzdužna sila N jednaka je nuli (ne uzimamo u obzir vlastitu težinu drveta), au površini bd jednako je R, osim toga, površina poprečnog presjeka drveta u tom području ak razlikuje se od površine poprečnog presjeka na gradilištu CD. Stoga, uzdužna deformacija područja oglas treba odrediti kao zbroj uzdužnih deformacija tri presjeka ab, pr I CD, za svaki od kojih vrijednosti N I E.F. konstantna cijelom dužinom:

Uzdužne sile na razmatranim presjecima grede

Stoga,

Slično, možete odrediti pomake δ bilo koje točke na osi grede i koristiti njihove vrijednosti za konstruiranje dijagrama uzdužna kretanja (epureδ), tj. graf koji prikazuje promjenu tih kretanja duž duljine osi grede.

4.2.3. Uvjeti čvrstoće. Proračuni krutosti.

Pri provjeri naprezanja površine presjeka F a poznate su i uzdužne sile te se proračun sastoji od proračuna računskih (stvarnih) naprezanja σ u karakterističnim presjecima elemenata. Zatim se dobiveni maksimalni napon uspoređuje s dopuštenim:

Prilikom odabira odjeljaka odrediti potrebna područja [F] poprečni presjeci elementa (na temelju poznatih uzdužnih sila N i dopušteno naprezanje [σ]). Prihvaćene površine presjeka F mora zadovoljiti uvjet čvrstoće izražen u sljedeći obrazac:

Pri određivanju nosivosti Po poznate vrijednosti F i dopuštenog naprezanja [σ], izračunavaju se dopuštene vrijednosti [N] uzdužnih sila:

Na temelju dobivenih vrijednosti [N] zatim se određuju dopuštene vrijednosti vanjskih opterećenja [ P].

Za ovaj slučaj, uvjet čvrstoće ima oblik

Količine standardni koeficijenti granice sigurnosti utvrđene su standardima. Oni ovise o klasi konstrukcije (kapitalna, privremena itd.), predviđenom vijeku trajanja, opterećenju (statičko, cikličko itd.), mogućoj heterogenosti u izradi materijala (na primjer, beton) i vrsti deformacija (napetost, kompresija, savijanje itd.) i drugi čimbenici. U nekim slučajevima potrebno je smanjiti faktor sigurnosti kako bi se smanjila težina konstrukcije, a ponekad povećati faktor sigurnosti - po potrebi uzeti u obzir istrošenost trljajućih dijelova strojeva, koroziju i propadanje materijal.

Vrijednosti standardnih faktora sigurnosti za različite materijale, konstrukcije i opterećenja u većini slučajeva imaju sljedeće vrijednosti: - 2,5...5 i - 1,5...2,5.

Pod provjerom krutosti konstrukcijskog elementa u stanju čistog naprezanja-tlaka podrazumijeva se traženje odgovora na pitanje: jesu li dovoljne vrijednosti karakteristika krutosti elementa (modula elastičnosti materijala)? E i površina presjeka F), tako da maksimum svih vrijednosti pomaka točaka elementa uzrokovanih vanjske sile, u max nije premašio neku specificiranu graničnu vrijednost [u]. Smatra se da ako je nejednakost u max< [u] конструкция переходит в предельное состояние.

Razmotrimo ravnu gredu konstantnog poprečnog presjeka s duljinom ugrađenom na jednom kraju i opterećenom na drugom kraju s vlačnom silom P (slika 8.2, a). Pod djelovanjem sile P greda se izduži za određeni iznos, što se naziva potpuno, odnosno apsolutno istezanje (apsolutna uzdužna deformacija).

U bilo kojoj točki grede koja se razmatra postoji identično stanje naprezanja i, prema tome, linearne deformacije (vidi § 5.1) za sve njene točke su iste. Stoga se vrijednost može definirati kao omjer apsolutnog istezanja prema početnoj duljini grede I, tj. Linearna deformacija pri zatezanju ili sabijanju greda obično se naziva relativno izduženje, odnosno relativna uzdužna deformacija i označava se.

Stoga,

Relativna uzdužna deformacija mjeri se u apstraktnim jedinicama. Složimo se da deformacija rastezanja bude pozitivna (slika 8.2, a), a deformacija kompresije negativna (slika 8.2, b).

Što je veća veličina sile koja rasteže gredu, to je veće, ako su ostale stvari jednake, produljenje grede; kako veća površina presjeka grede, manje je istezanje grede. Šipke izrađene od različitih materijala različito se izdužuju. Za slučajeve u kojima naprezanja u gredi ne prelaze granicu proporcionalnosti (vidi § 6.1, paragraf 4), iskustvom je utvrđen sljedeći odnos:

Ovdje je N uzdužna sila u presjecima grede; - površina poprečnog presjeka grede; E je koeficijent koji ovisi o fizičkim svojstvima materijala.

S obzirom da normalno naprezanje u presjeku grede dobijemo

Apsolutno produljenje grede izražava se formulom

odnosno apsolutna uzdužna deformacija upravno je proporcionalna uzdužnoj sili.

Prvi put je formuliran zakon izravne proporcionalnosti između sila i deformacija (1660.). Formule (10.2)-(13.2) su matematički izrazi Hookeovog zakona za napetost i sabijanje grede.

Sljedeća formulacija Hookeovog zakona je općenitija [vidi. formule (11.2) i (12.2)]: relativna uzdužna deformacija izravno je proporcionalna normalnom naprezanju. U ovoj se formulaciji Hookeov zakon koristi ne samo u proučavanju napetosti i kompresije greda, već iu drugim dijelovima tečaja.

Veličina E uključena u formule (10.2)-(13.2) naziva se modulom elastičnosti prve vrste (skraćeno modulom elastičnosti). Što je veća vrijednost E, manja je uzdužna deformacija, ako su ostale stvari jednake.

Umnožak ćemo nazvati krutošću poprečnog presjeka grede na napetost i pritisak.

Dodatak I prikazuje vrijednosti modula elastičnosti E za različite materijale.

Formula (13.2) može se koristiti za izračunavanje apsolutne uzdužne deformacije jednog dijela grede duljine samo pod uvjetom da je presjek grede unutar tog presjeka konstantan i da je uzdužna sila N ista u svim presjecima.

Uz uzdužnu deformaciju, kada na gredu djeluje tlačna ili vlačna sila, uočava se i poprečna deformacija. Kada se greda sabija, njezine poprečne dimenzije se povećavaju, a kada se rastežu, smanjuju se. Ako je poprečna veličina grede prije primjene tlačne sile P na nju označena b, a nakon primjene tih sila (slika 9.2), tada će vrijednost označavati apsolutnu poprečnu deformaciju grede.

Omjer je relativna poprečna deformacija.

Iskustvo pokazuje da je pri naprezanjima koja ne prelaze granicu elastičnosti (vidi § 6.1, paragraf 3), relativna poprečna deformacija izravno proporcionalna relativnoj uzdužnoj deformaciji, ali ima suprotan predznak:

Koeficijent proporcionalnosti u formuli (14.2) ovisi o materijalu grede. Naziva se omjer poprečne deformacije ili Poissonov omjer i omjer je relativne poprečne deformacije prema uzdužnoj deformaciji, uzet u apsolutnoj vrijednosti, tj.

Poissonov omjer, zajedno s modulom elastičnosti E, karakterizira elastična svojstva materijala.

Vrijednost Poissonovog omjera određuje se eksperimentalno. Za različite materijale ima vrijednosti od nule (za pluto) do vrijednosti blizu 0,50 (za gumu i parafin). Za čelik, Poissonov omjer je 0,25-0,30; za niz drugih metala (lijevano željezo, cink, bronca, bakar) ima vrijednosti od 0,23 do 0,36. Približne vrijednosti Poissonovog omjera za različite materijale dane su u Dodatku I.

Kada vlačne sile djeluju duž osi grede, njezina se duljina povećava, a poprečne dimenzije smanjuju. Kada djeluju tlačne sile, događa se suprotna pojava. Na sl. Na slici 6 prikazana je greda rastegnuta dvjema silama P. Uslijed napetosti greda se produžila za iznos Δ l, koji se zove apsolutna elongacija, i dobivamo apsolutna transverzalna kontrakcija Δa .

Omjer apsolutnog produljenja i skraćivanja prema izvornoj duljini ili širini grede naziva se relativna deformacija. U u ovom slučaju naziva se relativna deformacija uzdužna deformacija, A - relativna poprečna deformacija. Omjer relativne poprečne deformacije prema relativnoj uzdužnoj deformaciji naziva se Poissonov omjer: (3.1)

Određuje se Poissonov koeficijent za svaki materijal kao konstanta elastičnosti empirijski i nalazi se unutar: ; za čelik.

U granicama elastičnih deformacija utvrđeno je da je normalno naprezanje izravno proporcionalno relativnoj uzdužnoj deformaciji. Ta se ovisnost naziva Hookeov zakon:

, (3.2)

Gdje E- koeficijent proporcionalnosti, tzv modul normalne elastičnosti.