Suriin ang solusyon ng pinakamalaki at pinakamaliit sa segment. Ang pinakamalaki at pinakamaliit na halaga ng function. Gawain B15 (2014)

Tingnan natin kung paano galugarin ang isang function gamit ang isang graph. Lumalabas na ang pagtingin sa graph, maaari mong malaman ang lahat ng bagay na interesado sa amin, lalo na:

• saklaw ng function
• saklaw ng pag-andar
• mga function na zero
• mga panahon ng pagtaas at pagbaba
• mataas at mababang puntos
• ang pinakamalaki at pinakamaliit na halaga ng function sa segment.

Linawin natin ang terminolohiya:

Abscissa ay ang pahalang na coordinate ng punto.
Mag-orden- patayong coordinate.
abscissa- ang pahalang na axis, kadalasang tinatawag na axis.
Y-axis - patayong axis, o axis .

Pangangatwiran ay isang malayang variable kung saan nakasalalay ang mga halaga ng function. Kadalasang ipinahiwatig.
Sa madaling salita, tayo mismo ang pumili , pumalit sa formula ng function at makakuha ng .

Domain function - ang hanay ng mga (at ang mga lamang) na halaga ng argumento kung saan umiiral ang function.
Tinutukoy: o .

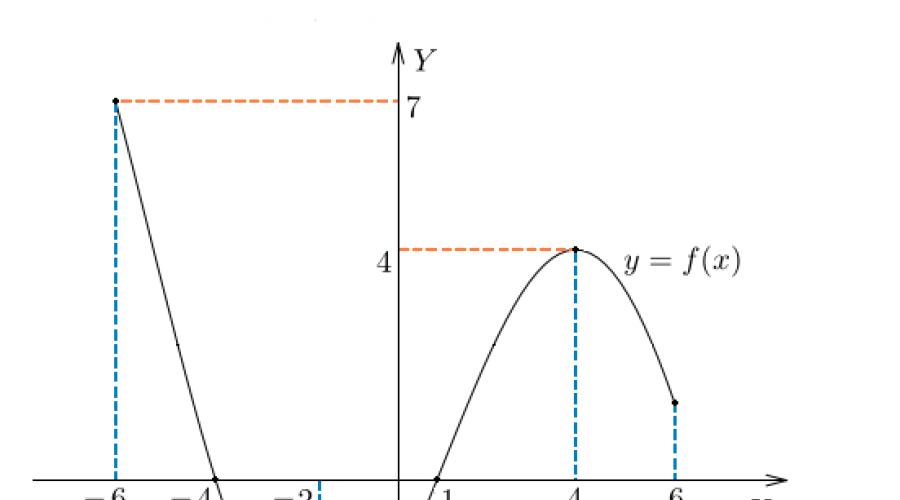
Sa aming figure, ang domain ng function ay isang segment. Sa segment na ito iginuhit ang graph ng function. Dito lang ibinigay na function umiral.

Saklaw ng pag-andar ay ang hanay ng mga halaga na kinukuha ng variable. Sa aming figure, ito ay isang segment - mula sa pinakamababa hanggang sa pinakamataas na halaga.

Mga function na zero- mga punto kung saan ang halaga ng function ay katumbas ng zero, ibig sabihin. Sa aming figure, ito ang mga punto at .

Ang mga halaga ng pag-andar ay positibo saan . Sa aming figure, ito ang mga pagitan at .
Ang mga halaga ng pag-andar ay negatibo saan . Mayroon kaming ganitong interval (o interval) mula hanggang.

Ang pinakamahalagang konsepto - pagtaas at pagbaba ng mga function sa ilang set. Bilang isang set, maaari kang kumuha ng segment, interval, unyon ng interval, o buong number line.

Function nadadagdagan

Sa madaling salita, mas marami , mas marami , ibig sabihin, ang graph ay papunta sa kanan at pataas.

Function bumababa sa set kung para sa alinman at kabilang sa set ang hindi pagkakapantay-pantay ay nagpapahiwatig ng hindi pagkakapantay-pantay .

Para sa isang bumababa na function, ang isang mas malaking halaga ay tumutugma sa isang mas maliit na halaga. Pakanan at pababa ang graph.

Sa aming figure, ang function ay tumataas sa pagitan at bumababa sa pagitan at .

Tukuyin natin kung ano ang maximum at minimum na puntos ng function.

Pinakamataas na punto- ito ay isang panloob na punto ng domain ng kahulugan, na ang halaga ng function sa loob nito ay mas malaki kaysa sa lahat ng mga puntong sapat na malapit dito.
Sa madaling salita, ang pinakamataas na punto ay tulad ng isang punto, ang halaga ng function kung saan higit pa kaysa sa mga kapitbahay. Ito ay isang lokal na "burol" sa tsart.

Sa aming figure - ang pinakamataas na punto.

Mababang punto- isang panloob na punto ng domain ng kahulugan, na ang halaga ng function sa loob nito ay mas mababa kaysa sa lahat ng mga punto na sapat na malapit dito.
Iyon ay, ang pinakamababang punto ay tulad na ang halaga ng pag-andar sa loob nito ay mas mababa kaysa sa mga kalapit. Sa graph, ito ay isang lokal na "butas".

Sa aming figure - ang pinakamababang punto.

Ang punto ay ang hangganan. Ito ay hindi isang panloob na punto ng domain ng kahulugan at samakatuwid ay hindi akma sa kahulugan ng isang pinakamataas na punto. Kung tutuusin, wala siyang kapitbahay sa kaliwa. Sa parehong paraan, maaaring walang pinakamababang punto sa aming tsart.

Ang maximum at minimum na mga puntos ay sama-samang tinatawag matinding mga punto ng pag-andar. Sa aming kaso, ito ay at .

Ngunit paano kung kailangan mong hanapin, halimbawa, minimum na function sa hiwa? AT kasong ito sagot: . kasi minimum na function ay ang halaga nito sa pinakamababang punto.

Katulad nito, ang maximum ng aming function ay . Ito ay naabot sa punto.

Masasabi nating ang extrema ng function ay katumbas ng at .

Minsan sa mga gawain kailangan mong hanapin ang pinakamalaki at pinakamaliit na halaga ng function sa isang partikular na segment. Ang mga ito ay hindi kinakailangang nag-tutugma sa mga sukdulan.

Sa kaso natin pinakamaliit na halaga ng function sa pagitan ay katumbas at tumutugma sa pinakamababa ng function. Ngunit ang pinakamalaking halaga nito sa segment na ito ay katumbas ng . Naabot ito sa kaliwang dulo ng segment.

Sa anumang kaso, ang pinakamalaki at pinakamaliit na halaga ng isang tuluy-tuloy na pag-andar sa isang segment ay nakakamit alinman sa mga extremum point o sa mga dulo ng segment.

maliit at maganda simpleng gawain mula sa kategorya ng mga nagsisilbing lifeline para sa isang lumulutang na estudyante. Sa kalikasan, ang inaantok na kaharian ng kalagitnaan ng Hulyo, kaya oras na upang manirahan sa isang laptop sa beach. Maaga sa umaga, nagsimulang tumugtog ang isang sinag ng araw ng teorya upang tumutok sa lalong madaling panahon sa pagsasanay, na, sa kabila ng ipinahayag nitong kagaanan, ay naglalaman ng mga fragment ng salamin sa buhangin. Kaugnay nito, inirerekumenda kong maingat na isaalang-alang ang ilang mga halimbawa ng pahinang ito. Upang malutas ang mga praktikal na gawain, kailangan mong magawa maghanap ng mga derivatives at unawain ang materyal ng artikulo Mga agwat ng monotonicity at extrema ng isang function.

Una, maikling tungkol sa pangunahing bagay. Sa isang aralin tungkol sa pagpapatuloy ng pag-andar Ibinigay ko ang kahulugan ng continuity sa isang punto at continuity sa isang interval. Ang huwarang pag-uugali ng isang function sa isang segment ay nabuo sa katulad na paraan. Ang isang function ay tuloy-tuloy sa isang segment kung:

1) ito ay tuloy-tuloy sa pagitan;
2) tuloy-tuloy sa isang punto sa kanan at sa punto umalis.

Ang ikalawang talata ay tumatalakay sa tinatawag na unilateral na pagpapatuloy gumagana sa isang punto. Mayroong ilang mga diskarte sa kahulugan nito, ngunit mananatili ako sa linya na nagsimula nang mas maaga:

Ang function ay tuloy-tuloy sa isang punto sa kanan, kung ito ay tinukoy sa isang partikular na punto at ang kanang-kamay na limitasyon ay tumutugma sa halaga ng function sa isang partikular na punto: . Ito ay tuloy-tuloy sa punto umalis, kung tinukoy sa isang partikular na punto at ang kaliwang limitasyon nito ay katumbas ng halaga sa puntong iyon:

Isipin na ang mga berdeng tuldok ay ang mga kuko kung saan nakakabit ang magic rubber band:

Sa isip, kunin ang pulang linya sa iyong mga kamay. Malinaw, gaano man kalayo natin iunat ang graph pataas at pababa (sa kahabaan ng axis), mananatili pa rin ang function limitado- isang hedge sa itaas, isang hedge sa ibaba, at ang aming produkto ay nanginginain sa isang paddock. kaya, ang isang function na tuloy-tuloy sa isang segment ay nakatali dito. Sa kurso ng mathematical analysis, ang tila simpleng katotohanang ito ay nakasaad at mahigpit na pinatunayan Ang unang teorama ni Weierstrass.… Maraming tao ang naiinis na ang mga elementarya na pahayag ay nakakapagod na pinatunayan sa matematika, ngunit ito ay may mahalagang kahulugan. Ipagpalagay na ang isang tiyak na naninirahan sa terry Middle Ages ay hinila ang graph sa kalangitan na lampas sa mga limitasyon ng visibility, ito ay ipinasok. Bago ang pag-imbento ng teleskopyo, ang limitadong pag-andar sa espasyo ay hindi halata! Sa katunayan, paano mo malalaman kung ano ang naghihintay sa atin sa kabila ng abot-tanaw? Pagkatapos ng lahat, sa sandaling ang Earth ay itinuturing na patag, kaya ngayon kahit na ang ordinaryong teleportasyon ay nangangailangan ng patunay =)

Ayon kay pangalawang Weierstrass theorem, tuloy-tuloy sa segmentumabot ang function nito eksaktong tuktok na gilid at ang kanyang eksaktong ilalim na gilid .

Tinatawag din ang numero ang maximum na halaga ng function sa segment at tinutukoy ng , at ang bilang - ang pinakamababang halaga ng function sa segment may markang .

Sa kaso natin:

Tandaan : sa teorya, ang mga tala ay karaniwan .

Sa madaling salita, pinakamataas na halaga ay matatagpuan kung saan ang pinakamataas na punto ng graph, at ang pinakamaliit - kung saan ang pinakamababang punto.

Mahalaga! Gaya ng itinuro na sa artikulo sa extrema ng function, ang pinakamalaking halaga ng function at pinakamaliit na halaga ng function – IBA, Ano maximum na function at minimum na function. Kaya, sa halimbawang ito, ang numero ay ang minimum ng function, ngunit hindi ang pinakamababang halaga.

By the way, ano ang nangyayari sa labas ng segment? Oo, kahit ang baha, sa konteksto ng problemang isinasaalang-alang, hindi ito interesado sa amin. Ang gawain ay nagsasangkot lamang ng paghahanap ng dalawang numero at yun lang!

Bukod dito, ang solusyon ay purong analytical, samakatuwid, hindi na kailangang gumuhit!

Ang algorithm ay namamalagi sa ibabaw at nagmumungkahi ng sarili mula sa figure sa itaas:

1) Hanapin ang mga halaga ng function sa kritikal na mga punto, na kabilang sa segment na ito.

Makakuha ng isa pang goodie: hindi na kailangang suriin ang isang sapat na kondisyon para sa isang extremum, dahil, tulad ng ipinakita lamang, ang pagkakaroon ng isang minimum o maximum hindi pa garantisado ano ang pinakamababa o pinakamataas na halaga. Ang demonstration function ay umabot sa pinakamataas nito at, ayon sa kalooban ng tadhana, ang parehong numero ay ang pinakamalaking halaga ng function sa pagitan . Ngunit, siyempre, ang gayong pagkakataon ay hindi palaging nagaganap.

Kaya, sa unang hakbang, mas mabilis at mas madaling kalkulahin ang mga halaga ng pag-andar sa mga kritikal na punto na kabilang sa segment, nang hindi naaabala kung mayroon silang extrema o wala.

2) Kinakalkula namin ang mga halaga ng function sa mga dulo ng segment.

3) Kabilang sa mga halaga ng function na matatagpuan sa ika-1 at ika-2 talata, pipiliin namin ang pinakamaliit at pinakamaraming malaking numero, isulat ang sagot.

Umupo kami sa baybayin ng asul na dagat at tumama sa mga takong sa mababaw na tubig:

Halimbawa 1

Hanapin ang pinakamalaki at pinakamaliit na value ng isang function sa isang segment

Desisyon:
1) Kalkulahin ang mga halaga ng function sa mga kritikal na punto na kabilang sa segment na ito:

Kalkulahin natin ang halaga ng function sa pangalawang kritikal na punto:

2) Kalkulahin ang mga halaga ng function sa mga dulo ng segment:

3) Ang mga "Bold" na resulta ay nakuha gamit ang mga exponential at logarithms, na makabuluhang nagpapalubha sa kanilang paghahambing. Para sa kadahilanang ito, kami ay armado ng isang calculator o Excel at kalkulahin ang tinatayang mga halaga, hindi nakakalimutan na:

Ngayon malinaw na ang lahat.

Sagot:

Fractional-rational na halimbawa para sa malayang solusyon:

Halimbawa 6

Hanapin ang maximum at pinakamababang halaga mga function sa segment

Ang proseso ng paghahanap ng pinakamaliit at pinakamalaking halaga ng isang function sa isang segment ay nagpapaalala sa isang kamangha-manghang paglipad sa paligid ng isang bagay (isang graph ng isang function) sa isang helicopter na may pagpapaputok mula sa isang long-range na kanyon sa ilang mga punto at pagpili mula sa ang mga puntong ito ay napakaespesyal na mga punto para sa mga control shot. Pinipili ang mga puntos sa isang tiyak na paraan at ayon sa ilang mga patakaran. Sa anong mga tuntunin? Pag-uusapan pa natin ito.

Kung ang function y = f(x) tuloy-tuloy sa segment [ a, b] , pagkatapos ay umabot ito sa segment na ito hindi bababa sa at pinakamataas na halaga . Maaaring mangyari ito sa matinding puntos o sa dulo ng segment. Samakatuwid, upang mahanap hindi bababa sa at ang pinakamalaking halaga ng function , tuloy-tuloy sa segment [ a, b] , kailangan mong kalkulahin ang mga halaga nito sa lahat kritikal na mga punto at sa mga dulo ng segment, at pagkatapos ay piliin ang pinakamaliit at pinakamalaki sa kanila.

Hayaan, halimbawa, kinakailangan upang matukoy ang maximum na halaga ng function f(x) sa segment [ a, b] . Upang gawin ito, hanapin ang lahat ng mga kritikal na punto nito na nasa [ a, b] .

kritikal na punto ay tinatawag na punto kung saan tinukoy ang function, at siya derivative ay alinman sa zero o wala. Pagkatapos ay dapat mong kalkulahin ang mga halaga ng pag-andar sa mga kritikal na punto. At, sa wakas, dapat ihambing ng isa ang mga halaga ng function sa mga kritikal na punto at sa mga dulo ng segment ( f(a) at f(b) ). Ang pinakamalaki sa mga bilang na ito ay magiging ang pinakamalaking halaga ng function sa pagitan [a, b] .

Ang problema sa paghahanap ang pinakamaliit na halaga ng function .

Hinahanap namin ang pinakamaliit at pinakamalaking halaga ng function nang magkasama

Halimbawa 1. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment [-1, 2] .

Desisyon. Nahanap namin ang derivative ng function na ito. I-equate ang derivative sa zero () at makakuha ng dalawang kritikal na puntos: at . Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, sapat na upang kalkulahin ang mga halaga nito sa mga dulo ng segment at sa punto , dahil ang punto ay hindi kabilang sa segment [-1, 2] . Ang mga value ng function na ito ay ang mga sumusunod: , , . Sinusundan nito iyon pinakamaliit na halaga ng function(minarkahan ng pula sa graph sa ibaba), katumbas ng -7, ay naabot sa kanang dulo ng segment - sa punto , at pinakadakila(pula din sa graph), ay katumbas ng 9, - sa kritikal na punto .

Kung ang function ay tuloy-tuloy sa isang tiyak na agwat at ang agwat na ito ay hindi isang segment (ngunit, halimbawa, isang agwat; ang pagkakaiba sa pagitan ng isang agwat at isang segment: ang mga hangganan na punto ng agwat ay hindi kasama sa agwat, ngunit ang Ang mga hangganan ng mga punto ng segment ay kasama sa segment), pagkatapos ay kabilang sa mga halaga ng pag-andar ay maaaring walang pinakamaliit at pinakamalaki. Kaya, halimbawa, ang function na inilalarawan sa figure sa ibaba ay tuloy-tuloy sa ]-∞, +∞[ at walang pinakamalaking halaga.

Gayunpaman, para sa anumang agwat (sarado, bukas, o walang katapusan), ang sumusunod na katangian ng tuluy-tuloy na pag-andar ay nananatili.

Halimbawa 4. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment [-1, 3] .

Desisyon. Nakita namin ang derivative ng function na ito bilang derivative ng quotient:

.

Tinutumbas namin ang derivative sa zero, na nagbibigay sa amin ng isang kritikal na punto: . Ito ay kabilang sa pagitan [-1, 3] . Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, makikita namin ang mga halaga nito sa mga dulo ng segment at sa natagpuang kritikal na punto:

Ihambing natin ang mga halagang ito. Konklusyon: katumbas ng -5/13, sa punto at ang pinakamalaking halaga katumbas ng 1 sa punto .

Patuloy kaming naghahanap ng pinakamaliit at pinakamalaking value ng function nang magkasama

Mayroong mga guro na, sa paksa ng paghahanap ng pinakamaliit at pinakamalaking halaga ng isang function, ay hindi nagbibigay sa mga mag-aaral ng mga halimbawa na mas kumplikado kaysa sa mga isinasaalang-alang lamang, iyon ay, ang mga kung saan ang function ay isang polynomial o isang fraction, ang numerator. at denominator nito ay mga polynomial. Ngunit hindi namin lilimitahan ang ating sarili sa gayong mga halimbawa, dahil sa mga guro ay may mga mahilig sa pag-iisip ng mga mag-aaral nang buo (talahanayan ng mga derivatives). Samakatuwid, ang logarithm at ang trigonometric function ay gagamitin.

Halimbawa 6. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment .

Desisyon. Nakikita namin ang derivative ng function na ito bilang derivative ng produkto :

Tinutumbas namin ang derivative sa zero, na nagbibigay ng isang kritikal na punto: . Ito ay kabilang sa segment. Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, makikita namin ang mga halaga nito sa mga dulo ng segment at sa natagpuang kritikal na punto:

Ang resulta ng lahat ng mga aksyon: naabot ng function ang pinakamababang halaga nito, katumbas ng 0, sa isang punto at sa isang punto at ang pinakamalaking halaga katumbas ng e² , sa punto .

Halimbawa 7. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment .

Desisyon. Nahanap namin ang derivative ng function na ito:

I-equate ang derivative sa zero:

Ang tanging kritikal na punto ay nabibilang sa segment . Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, makikita namin ang mga halaga nito sa mga dulo ng segment at sa natagpuang kritikal na punto:

Konklusyon: naabot ng function ang pinakamababang halaga nito, katumbas ng , sa punto at ang pinakamalaking halaga, katumbas ng , sa punto .

Sa mga inilapat na matinding problema, ang paghahanap ng pinakamaliit (pinakamalaking) mga halaga ng function, bilang panuntunan, ay binabawasan sa paghahanap ng pinakamababa (maximum). Ngunit hindi ang minima o maxima mismo ang mas praktikal na interes, ngunit ang mga halaga ng argumento kung saan nakamit ang mga ito. Kapag nilulutas ang mga inilapat na problema, lumitaw ang isang karagdagang kahirapan - ang pagsasama-sama ng mga pag-andar na naglalarawan sa kababalaghan o proseso na isinasaalang-alang.

Halimbawa 8 Ang isang tangke na may kapasidad na 4, na may hugis ng parallelepiped na may parisukat na base at bukas sa itaas, ay dapat na tinned. Ano ang dapat na mga sukat ng tangke upang masakop ito ng hindi bababa sa dami ng materyal?

Desisyon. Hayaan x- gilid ng base h- taas ng tangke, S- ang ibabaw nitong lugar na walang takip, V- ang dami nito. Ang ibabaw na lugar ng tangke ay ipinahayag ng formula, i.e. ay isang function ng dalawang variable. Upang ipahayag S bilang isang function ng isang variable, ginagamit namin ang katotohanan na , kung saan . Pagpapalit sa nahanap na expression h sa pormula para sa S:

Suriin natin ang function na ito para sa isang extremum. Ito ay tinukoy at naiba sa lahat ng dako sa ]0, +∞[ , at

.

Itinutumbas namin ang derivative sa zero () at hanapin ang kritikal na punto. Bilang karagdagan, sa , ang derivative ay hindi umiiral, ngunit ang halagang ito ay hindi kasama sa domain ng kahulugan at samakatuwid ay hindi maaaring maging isang extremum point. Kaya, - ang tanging kritikal na punto. Suriin natin ito para sa pagkakaroon ng extremum gamit ang pangalawa sapat na tanda. Hanapin natin ang pangalawang derivative. Kapag ang pangalawang derivative ay mas malaki sa zero (). Nangangahulugan ito na kapag ang function ay umabot sa isang minimum . Dahil ito minimum - ang tanging extremum ng function na ito, ito ang pinakamaliit na halaga nito. Kaya, ang gilid ng base ng tangke ay dapat na katumbas ng 2 m, at ang taas nito.

Halimbawa 9 Mula sa talata A, na matatagpuan sa linya ng tren, hanggang sa punto Sa, sa malayo mula dito l, kailangang dalhin ang mga kalakal. Ang halaga ng pagbibiyahe ng isang yunit ng timbang sa bawat yunit ng distansya sa pamamagitan ng tren ay katumbas ng , at sa pamamagitan ng highway ito ay katumbas ng . Hanggang saang punto M mga linya riles ng tren isang highway ay dapat na itayo upang ang transportasyon ng mga kalakal mula sa PERO sa Sa ay ang pinaka matipid AB ang riles ay ipinapalagay na tuwid)?

Sa pagsasagawa, karaniwan nang gumamit ng derivative upang makalkula ang pinakamalaki at pinakamaliit na halaga ng isang function. Ginagawa namin ang pagkilos na ito kapag nalaman namin kung paano bawasan ang mga gastos, dagdagan ang kita, kalkulahin pinakamainam na pagkarga para sa produksyon, atbp., iyon ay, sa mga kaso kung saan kinakailangan upang matukoy pinakamainam na halaga anumang parameter. Upang malutas nang tama ang mga naturang problema, dapat magkaroon ng isang mahusay na pag-unawa sa kung ano ang pinakamalaki at pinakamaliit na halaga ng isang function.

Yandex.RTB R-A-339285-1

Karaniwan naming tinutukoy ang mga halagang ito sa loob ng ilang pagitan x , na maaaring tumutugma sa buong saklaw ng function o bahagi nito. Maaari itong maging isang segment [ a ; b ] , at open interval (a ; b), (a ; b ] , [ a ; b), infinite interval (a ; b), (a ; b ] , [ a ; b) o infinite interval - ∞ ; a , (- ∞ ; a ] , [ a ; + ∞), (- ∞ ; + ∞) .

Sa artikulong ito, ipapaliwanag namin kung paano tahasang kinakalkula ang pinakamalaki at pinakamaliit na halaga. ibinigay na function na may isang variable y=f(x) y = f (x) .

Mga pangunahing kahulugan

Nagsisimula kami, gaya ng dati, sa pagbabalangkas ng mga pangunahing kahulugan.

Kahulugan 1

Ang pinakamalaking halaga ng function na y = f (x) sa ilang interval x ay ang value m a x y = f (x 0) x ∈ X , na, para sa anumang halaga x x ∈ X , x ≠ x 0, ginagawa ang hindi pagkakapantay-pantay f (x ) ≤ f (x 0) .

Kahulugan 2

Ang pinakamaliit na value ng function na y = f (x) sa ilang interval x ay ang value m i n x ∈ X y = f (x 0) , na, para sa anumang value x ∈ X , x ≠ x 0, ginagawa ang hindi pagkakapantay-pantay f(X f (x) ≥ f(x0) .

Ang mga kahulugan na ito ay medyo halata. Kahit na mas madali, maaari mong sabihin ito: ang pinakamalaking halaga ng isang function ay ang pinaka pinakamahalaga sa isang kilalang agwat sa abscissa x 0 , at ang pinakamaliit ay ang pinakamaliit na tinatanggap na halaga sa parehong pagitan sa x 0 .

Kahulugan 3

Ang mga nakatigil na puntos ay ang mga halaga ng argumento ng function kung saan ang derivative nito ay nagiging 0.

Bakit kailangan nating malaman kung ano ang mga nakatigil na punto? Upang masagot ang tanong na ito, kailangan nating tandaan ang teorama ni Fermat. Ito ay sumusunod mula dito na ang isang nakatigil na punto ay isang punto kung saan matatagpuan ang extremum ng isang differentiable function (ibig sabihin, ang lokal na minimum o maximum nito). Dahil dito, kukunin ng function ang pinakamaliit o pinakamalaking halaga sa isang tiyak na pagitan nang eksakto sa isa sa mga nakatigil na punto.

Ang isa pang function ay maaaring tumagal sa pinakamalaki o pinakamaliit na halaga sa mga puntong iyon kung saan ang function mismo ay tiyak, at ang unang derivative nito ay wala.

Ang unang tanong na bumangon kapag pinag-aaralan ang paksang ito ay: sa lahat ng pagkakataon, matutukoy ba natin ang maximum o minimum na halaga ng isang function sa isang naibigay na agwat? Hindi, hindi natin ito magagawa kapag ang mga hangganan ng ibinigay na pagitan ay magkakasabay sa mga hangganan ng domain ng kahulugan, o kung tayo ay nakikitungo sa isang walang katapusang pagitan. Nangyayari rin na ang isang function sa isang ibinigay na pagitan o sa infinity ay kukuha ng infinitesimal o infinite malalaking halaga. Sa mga kasong ito, hindi posibleng matukoy ang pinakamalaki at/o pinakamaliit na halaga.

Ang mga sandaling ito ay magiging mas mauunawaan pagkatapos ng larawan sa mga graph:

Ang unang figure ay nagpapakita sa amin ng isang function na tumatagal sa pinakamalaki at pinakamaliit na halaga (m a xy at m i n y) sa mga nakatigil na punto na matatagpuan sa pagitan [- 6 ; 6].

Suriin natin nang detalyado ang kaso na ipinahiwatig sa pangalawang graph. Baguhin natin ang halaga ng segment sa [ 1 ; 6] at nakuha namin na ang pinakamalaking halaga ng function ay makakamit sa punto na may abscissa sa kanang hangganan ng pagitan, at ang pinakamaliit - sa nakatigil na punto.

Sa ikatlong figure, ang abscissas ng mga puntos ay kumakatawan sa mga hangganan ng mga punto ng segment [- 3 ; 2]. Tumutugma ang mga ito sa pinakamalaki at pinakamaliit na halaga ng ibinigay na function.

Ngayon tingnan natin ang ikaapat na larawan. Sa loob nito, ang function ay tumatagal ng m a x y (ang pinakamalaking halaga) at m i n y (ang pinakamaliit na halaga) sa mga nakatigil na punto sa bukas na pagitan (- 6 ; 6) .

Kung kukunin natin ang pagitan [1; 6) , pagkatapos ay maaari nating sabihin na ang pinakamaliit na halaga ng function dito ay maaabot sa isang nakatigil na punto. Hindi natin malalaman ang pinakamataas na halaga. Maaaring kunin ng function ang pinakamalaking halaga sa x katumbas ng 6 kung ang x = 6 ay kabilang sa pagitan. Ito ang kasong ito na ipinapakita sa Figure 5.

Sa graph 6, nakukuha ng function na ito ang pinakamaliit na halaga sa kanang hangganan ng pagitan (- 3 ; 2 ] , at hindi kami makakagawa ng mga tiyak na konklusyon tungkol sa pinakamalaking halaga.

Sa figure 7, makikita natin na ang function ay magkakaroon ng m a x y sa nakatigil na punto, na mayroong abscissa na katumbas ng 1 . Naabot ng function ang pinakamababang halaga nito sa hangganan ng pagitan sa kanang bahagi. Sa minus infinity, ang mga halaga ng function ay asymptotically lalapit sa y = 3 .

Kung kukuha tayo ng pagitan x ∈ 2 ; + ∞ , pagkatapos ay makikita natin na ang ibinigay na function ay hindi kukuha ng alinman sa pinakamaliit o pinakamalaking halaga. Kung ang x ay may posibilidad na 2, kung gayon ang mga halaga ng function ay may posibilidad na minus infinity, dahil ang tuwid na linya na x = 2 ay isang patayong asymptote. Kung ang abscissa ay may posibilidad na plus infinity, ang mga halaga ng function ay asymptotically lalapit sa y = 3. Ito ang kaso na ipinapakita sa Figure 8.

Sa talatang ito, magbibigay kami ng isang pagkakasunud-sunod ng mga aksyon na dapat gawin upang mahanap ang pinakamalaki o pinakamaliit na halaga ng isang function sa isang tiyak na agwat.

1. Una, hanapin natin ang domain ng function. Suriin natin kung ang segment na tinukoy sa kundisyon ay kasama dito.
2. Ngayon kalkulahin natin ang mga puntong nakapaloob sa segment na ito kung saan wala ang unang derivative. Kadalasan ay matatagpuan ang mga ito sa mga function na ang argumento ay nakasulat sa ilalim ng module sign, o in mga function ng kapangyarihan, na ang exponent ay isang fractionally rational na numero.
3. Susunod, malalaman natin kung aling mga nakatigil na punto ang nahuhulog sa isang partikular na segment. Upang gawin ito, kailangan mong kalkulahin ang derivative ng function, pagkatapos ay i-equate ito sa 0 at lutasin ang resultang equation, at pagkatapos ay piliin ang naaangkop na mga ugat. Kung hindi tayo nakakuha ng isang nakatigil na punto o hindi sila nahuhulog sa isang partikular na segment, pagkatapos ay magpapatuloy tayo sa susunod na hakbang.
4. Tukuyin natin kung anong mga halaga ang kukunin ng function sa mga naibigay na nakatigil na mga punto (kung mayroon man), o sa mga puntong iyon kung saan ang unang derivative ay hindi umiiral (kung mayroon), o kinakalkula namin ang mga halaga para sa x = a at x = b .
5. 5. Mayroon kaming isang serye ng mga halaga ng pag-andar, kung saan kailangan na nating piliin ang pinakamalaki at pinakamaliit. Ito ang magiging pinakamalaki at pinakamaliit na value ng function na kailangan nating hanapin.

Tingnan natin kung paano ilapat nang tama ang algorithm na ito kapag nilulutas ang mga problema.

Halimbawa 1

Kundisyon: ang function na y = x 3 + 4 x 2 ay ibinigay. Tukuyin ang pinakamalaki at pinakamaliit na halaga nito sa mga segment [1; 4 ] at [ - 4 ; - isa ] .

Desisyon:

Magsimula tayo sa paghahanap ng domain ng function na ito. Sa kasong ito, ito ang magiging set ng lahat ng totoong numero maliban sa 0 . Sa madaling salita, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; +∞ . Ang parehong mga segment na tinukoy sa kundisyon ay nasa loob ng lugar ng kahulugan.

Ngayon kinakalkula namin ang derivative ng function ayon sa panuntunan ng pagkita ng kaibahan ng isang fraction:

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x 3

Nalaman namin na ang derivative ng function ay iiral sa lahat ng punto ng mga segment [1; 4 ] at [ - 4 ; - isa ] .

Ngayon kailangan nating matukoy ang mga nakatigil na punto ng pag-andar. Gawin natin ito gamit ang equation x 3 - 8 x 3 = 0. Mayroon lamang itong tunay na ugat, na 2. Ito ay magiging isang nakatigil na punto ng function at mahuhulog sa unang segment [1; 4 ] .

Kalkulahin natin ang mga halaga ng function sa mga dulo ng unang segment at sa ibinigay na punto, i.e. para sa x = 1 , x = 2 at x = 4:

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

Nakuha namin na ang pinakamalaking halaga ng function na m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 ay makakamit sa x = 1 , at ang pinakamaliit na m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – sa x = 2 .

Ang pangalawang segment ay hindi kasama ang anumang nakatigil na mga punto, kaya kailangan nating kalkulahin ang mga halaga ng pag-andar lamang sa mga dulo ng ibinigay na segment:

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Kaya naman, m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Sagot: Para sa segment [1; 4 ] - m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , para sa segment [ - 4 ; - 1 ] - m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Tingnan ang larawan:

Bago mag-aral ang pamamaraang ito, ipinapayo namin sa iyo na ulitin kung paano kalkulahin nang tama ang isang panig na limitasyon at ang limitasyon sa infinity, pati na rin matutunan ang mga pangunahing pamamaraan para sa paghahanap ng mga ito. Upang mahanap ang pinakamalaki at / o pinakamaliit na halaga ng isang function sa isang bukas o walang katapusan na pagitan, ginagawa namin ang mga sumusunod na hakbang sa pagkakasunud-sunod.

1. Una kailangan mong suriin kung ang ibinigay na pagitan ay magiging isang subset ng domain ng ibinigay na function.
2. Tukuyin natin ang lahat ng mga punto na nakapaloob sa kinakailangang pagitan at kung saan wala ang unang hinalaw. Kadalasan ang mga ito ay para sa mga function kung saan ang argument ay nakapaloob sa modulus sign, at para sa mga power function na may fractional. makatwirang tagapagpahiwatig. Kung nawawala ang mga puntong ito, maaari kang magpatuloy sa susunod na hakbang.
3. Ngayon ay tinutukoy namin kung aling mga nakatigil na punto ang nahuhulog sa isang naibigay na agwat. Una, itinutumbas natin ang derivative sa 0, lutasin ang equation at hanapin ang mga angkop na ugat. Kung wala kaming isang nakatigil na punto o hindi sila nahuhulog sa isang naibigay na agwat, pagkatapos ay pumunta kami kaagad sa karagdagang aksyon. Ang mga ito ay tinutukoy ng uri ng agwat.

• Kung ang pagitan ay mukhang [ a ; b) , pagkatapos ay kailangan nating kalkulahin ang halaga ng function sa puntong x = a at ang one-sided na limitasyon lim x → b - 0 f (x) .
• Kung ang pagitan ay may anyo (a ; b ] , pagkatapos ay kailangan nating kalkulahin ang halaga ng function sa puntong x = b at ang one-sided na limitasyon lim x → a + 0 f (x) .
• Kung ang pagitan ay may anyo (a ; b) , kailangan nating kalkulahin ang mga one-sided na limitasyon lim x → b - 0 f (x) , lim x → a + 0 f (x) .
• Kung ang pagitan ay mukhang [ a ; + ∞) , pagkatapos ay kinakailangan upang kalkulahin ang halaga sa puntong x = a at ang limitasyon sa plus infinity lim x → + ∞ f (x) .
• Kung ang pagitan ay mukhang (- ∞ ; b ] , kinakalkula namin ang halaga sa puntong x = b at ang limitasyon sa minus infinity lim x → - ∞ f (x) .
• Kung - ∞ ; b , pagkatapos ay isinasaalang-alang namin ang isang panig na limitasyon lim x → b - 0 f (x) at ang limitasyon sa minus infinity lim x → - ∞ f (x)
• Kung - ∞ ; + ∞ , pagkatapos ay isinasaalang-alang namin ang mga limitasyon sa minus at plus infinity lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. Sa dulo, kailangan mong gumuhit ng isang konklusyon batay sa nakuha na mga halaga ng pag-andar at mga limitasyon. Mayroong maraming mga pagpipilian dito. Kaya, kung ang one-sided na limitasyon ay katumbas ng minus infinity o plus infinity, agad na malinaw na walang masasabi tungkol sa pinakamaliit at pinakamalaking halaga ng function. Sa ibaba ay isasaalang-alang natin ang isang tipikal na halimbawa. Mga detalyadong paglalarawan tulungan kang maunawaan kung ano. Kung kinakailangan, maaari kang bumalik sa mga numero 4 - 8 sa unang bahagi ng materyal.

Kundisyon: binigyan ng function na y = 3 e 1 x 2 + x - 6 - 4 . Kalkulahin ang pinakamalaki at pinakamaliit na halaga nito sa mga pagitan - ∞ ; - 4 , - ∞ ; - 3 , (- 3 ; 1 ] , (- 3 ; 2), [ 1 ; 2), 2 ; + ∞ , [ 4 ; +∞) .

Desisyon

Una sa lahat, nakita namin ang domain ng function. Ang denominator ng fraction ay square trinomial, na hindi dapat maging 0:

x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Nakuha namin ang saklaw ng function, kung saan nabibilang ang lahat ng mga agwat na tinukoy sa kundisyon.

Ngayon pag-iba-ibahin natin ang function at makuha ang:

y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

Dahil dito, ang mga derivatives ng isang function ay umiiral sa buong domain ng kahulugan nito.

Lumipat tayo sa paghahanap ng mga nakatigil na puntos. Ang derivative ng function ay nagiging 0 sa x = - 1 2 . Ito ay isang nakatigil na punto na nasa pagitan (- 3 ; 1 ] at (- 3 ; 2) .

Kalkulahin natin ang halaga ng function sa x = - 4 para sa pagitan (- ∞ ; - 4 ] , pati na rin ang limitasyon sa minus infinity:

y (- 4) \u003d 3 e 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 e 1 6 - 4 ≈ - 0. 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1

Dahil 3 e 1 6 - 4 > - 1 , pagkatapos ay m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4. Hindi ito nagpapahintulot sa amin na natatanging matukoy ang pinakamaliit na halaga ng function. Maaari lamang nating tapusin na may limitasyon sa ibaba - 1 , dahil sa halagang ito na ang function ay lumalapit sa asymptotically sa minus infinity.

Ang isang tampok ng ikalawang pagitan ay na ito ay walang isang nakatigil na punto at hindi isang solong mahigpit na hangganan. Samakatuwid, hindi namin makalkula ang alinman sa pinakamalaki o pinakamaliit na halaga ng function. Sa pamamagitan ng pagtukoy sa limitasyon sa minus infinity at bilang ang argumento ay may posibilidad na - 3 sa kaliwang bahagi, makuha lamang namin ang hanay ng mga halaga:

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Nangangahulugan ito na ang mga halaga ng function ay matatagpuan sa pagitan - 1; +∞

Upang mahanap ang pinakamataas na halaga ng function sa ikatlong pagitan, tinutukoy namin ang halaga nito sa nakatigil na punto x = - 1 2 kung x = 1 . Kailangan din nating malaman ang isang panig na limitasyon para sa kaso kapag ang argumento ay may posibilidad na - 3 sa kanang bahagi:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Ito ay lumabas na ang function ay kukuha ng pinakamalaking halaga sa isang nakatigil na punto m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4. Tulad ng para sa pinakamaliit na halaga, hindi namin matukoy ito. Lahat ng iyon ay alam , ay ang pagkakaroon ng isang mas mababang limitasyon sa - 4 .

Para sa agwat (- 3 ; 2), kunin natin ang mga resulta ng nakaraang kalkulasyon at muling kalkulahin kung ano ang katumbas ng one-sided na limitasyon kapag may tending sa 2 mula sa kaliwang bahagi:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Kaya naman, m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4 , at hindi matutukoy ang pinakamaliit na halaga, at ang mga halaga ng function ay nililimitahan mula sa ibaba ng numero - 4 .

Batay sa ginawa natin sa dalawang nakaraang kalkulasyon, maaari nating igiit iyon sa pagitan [1; 2) ang function ay kukuha ng pinakamalaking halaga sa x = 1, at imposibleng mahanap ang pinakamaliit.

Sa pagitan (2 ; + ∞), hindi maaabot ng function ang alinman sa pinakamalaki o pinakamaliit na halaga, i.e. kukuha ito ng mga halaga mula sa pagitan - 1; +∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Matapos makalkula kung ano ang magiging katumbas ng halaga ng function sa x = 4 , malalaman natin na m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , at ang ibinigay na function sa plus infinity ay asymptotically lalapit sa linyang y = - 1 .

Ihambing natin ang nakuha natin sa bawat pagkalkula sa graph ng ibinigay na function. Sa figure, ang mga asymptotes ay ipinapakita sa pamamagitan ng mga tuldok na linya.

Iyon lang ang gusto naming pag-usapan tungkol sa paghahanap ng pinakamalaki at pinakamaliit na halaga ng isang function. Ang mga pagkakasunud-sunod ng mga aksyon na ibinigay namin ay makakatulong sa iyong gawin ang mga kinakailangang kalkulasyon nang mabilis at simple hangga't maaari. Ngunit tandaan na madalas na kapaki-pakinabang na malaman muna kung anong mga agwat ang babawasan ng pag-andar at kung anong mga agwat ang tataas nito, pagkatapos ay maaaring makagawa ng karagdagang mga konklusyon. Upang mas tumpak mong matukoy ang pinakamalaki at pinakamaliit na halaga ng function at bigyang-katwiran ang mga resulta.

Kung may napansin kang pagkakamali sa text, mangyaring i-highlight ito at pindutin ang Ctrl+Enter