Nok 34 at 2 na desisyon. Paano mahanap ang hindi bababa sa karaniwang maramihang ng dalawang numero
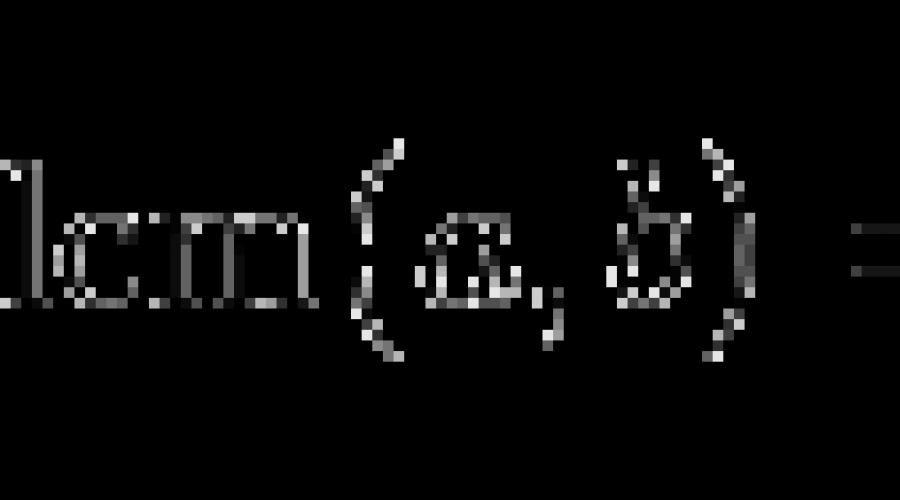
Basahin din
Ang pinakadakilang common divisor at ang least common multiple ay ang mga pangunahing konsepto ng arithmetic na nagbibigay-daan sa iyong gumana nang walang kahirap-hirap. ordinaryong fraction. LCM at kadalasang ginagamit upang mahanap ang karaniwang denominator ng ilang fraction.
Pangunahing konsepto
Ang divisor ng isang integer X ay isa pang integer Y kung saan ang X ay nahahati nang walang natitira. Halimbawa, ang divisor ng 4 ay 2, at ang 36 ay 4, 6, 9. Ang multiple ng integer X ay isang numerong Y na nahahati ng X na walang natitira. Halimbawa, ang 3 ay isang multiple ng 15, at ang 6 ay isang multiple ng 12.
Para sa anumang pares ng mga numero, mahahanap natin ang kanilang mga karaniwang divisors at multiple. Halimbawa, para sa 6 at 9, ang common multiple ay 18, at ang common divisor ay 3. Malinaw, ang mga pares ay maaaring magkaroon ng ilang divisor at multiple, kaya ang pinakamalaking divisor ng GCD at ang pinakamaliit na multiple ng LCM ay ginagamit sa mga kalkulasyon .
Ang pinakamaliit na divisor ay hindi makatwiran, dahil para sa anumang numero ito ay palaging isa. Ang pinakamalaking maramihan ay wala ring kahulugan, dahil ang pagkakasunud-sunod ng mga maramihan ay may posibilidad na walang katapusan.
Paghahanap ng GCD
Mayroong maraming mga paraan para sa paghahanap ng pinakadakilang karaniwang divisor, ang pinakasikat sa mga ito ay:
- sunud-sunod na enumeration ng mga divisors, pagpili ng mga karaniwan para sa isang pares at hanapin ang pinakamalaki sa kanila;
- agnas ng mga numero sa hindi mahahati na mga kadahilanan;
- Euclid's algorithm;
- binary algorithm.
Ngayon sa institusyong pang-edukasyon Ang pinakasikat na paraan ay ang agnas sa pangunahing mga kadahilanan at algorithm ni Euclid. Ang huli, sa turn, ay ginagamit sa paglutas ng mga equation ng Diophantine: ang paghahanap para sa GCD ay kinakailangan upang suriin ang equation para sa posibilidad na malutas ito sa mga integer.
Paghahanap ng NOC
Ang hindi bababa sa karaniwang maramihang ay eksaktong tinutukoy din ng umuulit na enumeration o factorization sa hindi mahahati na mga salik. Bilang karagdagan, madaling mahanap ang LCM kung ang pinakamalaking divisor ay natukoy na. Para sa mga numerong X at Y, ang LCM at GCD ay nauugnay sa sumusunod na relasyon:
LCM(X,Y) = X × Y / GCM(X,Y).
Halimbawa, kung ang gcd(15,18) = 3, ang LCM(15,18) = 15 × 18 / 3 = 90. Ang pinaka-halatang paggamit ng LCM ay upang mahanap ang common denominator, na siyang pinakamaliit na common multiple ng binigay na mga fraction.
Mga numero ng koprime
Kung ang isang pares ng mga numero ay walang karaniwang divisors, kung gayon ang naturang pares ay tinatawag na coprime. Ang GCM para sa mga naturang pares ay palaging katumbas ng isa, at batay sa koneksyon ng mga divisors at multiple, ang GCM para sa coprime ay katumbas ng kanilang produkto. Halimbawa, ang mga numerong 25 at 28 ay coprime, dahil wala silang karaniwang divisors, at LCM(25, 28) = 700, na tumutugma sa kanilang produkto. Anumang dalawang hindi mahahati na numero ay palaging magiging coprime.
Karaniwang Divisor at Maramihang Calculator
Sa aming calculator maaari mong kalkulahin ang GCD at LCM para sa anumang bilang ng mga numerong mapagpipilian. Ang mga gawain para sa pagkalkula ng mga karaniwang divisors at multiple ay matatagpuan sa aritmetika ng mga baitang 5 at 6, gayunpaman, ang GCD at LCM ay ang mga pangunahing konsepto ng matematika at ginagamit sa teorya ng numero, planimetry at communicative algebra.
Mga halimbawa sa totoong buhay
Common denominator ng mga fraction
Ginagamit ang least common multiple kapag hinahanap ang common denominator ng ilang fraction. Ipagpalagay na sa isang problema sa aritmetika kinakailangan na magsama ng 5 fraction:
1/8 + 1/9 + 1/12 + 1/15 + 1/18.
Upang magdagdag ng mga fraction, ang expression ay dapat na bawasan sa karaniwang denominador, na binabawasan ang problema sa paghahanap ng LCM. Upang gawin ito, pumili ng 5 numero sa calculator at ipasok ang mga halaga ng denominator sa naaangkop na mga cell. Kakalkulahin ng programa ang LCM (8, 9, 12, 15, 18) = 360. Ngayon ay kailangan mong kalkulahin ang mga karagdagang salik para sa bawat fraction, na tinukoy bilang ratio ng LCM sa denominator. Kaya ang mga dagdag na multiplier ay magiging ganito:
- 360/8 = 45
- 360/9 = 40
- 360/12 = 30
- 360/15 = 24
- 360/18 = 20.
Pagkatapos nito, i-multiply namin ang lahat ng mga fraction sa pamamagitan ng kaukulang karagdagang kadahilanan at makakuha ng:
45/360 + 40/360 + 30/360 + 24/360 + 20/360.
Madali tayong magdagdag ng mga fraction at makuha ang resulta sa anyo ng 159/360. Binabawasan namin ang fraction ng 3 at makita ang huling sagot - 53/120.
Solusyon ng mga linear na Diophantine equation
Ang mga linear na Diophantine equation ay mga expression ng anyong ax + by = d. Kung ang ratio d / gcd(a, b) ay isang integer, kung gayon ang equation ay malulutas sa mga integer. Suriin natin ang ilang mga equation para sa posibilidad ng isang integer na solusyon. Una, suriin ang equation na 150x + 8y = 37. Gamit ang calculator, makikita natin ang gcd (150.8) = 2. Hatiin ang 37/2 = 18.5. Ang numero ay hindi isang integer, samakatuwid, ang equation ay walang mga integer na ugat.
Suriin natin ang equation na 1320x + 1760y = 10120. Gumamit ng calculator para mahanap ang gcd(1320, 1760) = 440. Hatiin ang 10120/440 = 23. Bilang resulta, nakakakuha tayo ng integer, samakatuwid, ang Diophantine cosolveble infficient in ay .
Konklusyon
Malaki ang ginagampanan ng GCD at LCM sa teorya ng numero, at ang mga konsepto mismo ay malawakang ginagamit sa karamihan iba't ibang lugar matematika. Gamitin ang aming calculator upang kalkulahin ang pinakamalaking divisors at pinakamaliit na multiple ng anumang bilang ng mga numero.
Ngunit maraming natural na numero ang pantay na nahahati ng iba pang natural na numero.
Halimbawa:
Ang bilang na 12 ay nahahati ng 1, ng 2, ng 3, ng 4, ng 6, ng 12;
Ang bilang na 36 ay nahahati ng 1, ng 2, ng 3, ng 4, ng 6, ng 12, ng 18, ng 36.
Ang mga numero kung saan ang numero ay nahahati (para sa 12 ito ay 1, 2, 3, 4, 6 at 12) ay tinatawag mga divisors ng numero. Divisor ng isang natural na numero a ay ang natural na numero na naghahati sa ibinigay na numero a walang bakas. Ang isang natural na numero na may higit sa dalawang mga kadahilanan ay tinatawag pinagsama-sama .
Tandaan na ang mga numero 12 at 36 ay may mga karaniwang divisors. Ito ang mga numero: 1, 2, 3, 4, 6, 12. Ang pinakamalaking divisor ng mga numerong ito ay 12. Ang karaniwang divisor ng dalawang numerong ito a at b ay ang bilang kung saan ang parehong ibinigay na mga numero ay nahahati nang walang natitira a at b.
karaniwang maramihan ilang mga numero ang tinatawag na bilang na nahahati sa bawat isa sa mga numerong ito. Halimbawa, ang mga numerong 9, 18 at 45 ay may common multiple na 180. Ngunit 90 at 360 din ang kanilang common multiple. Sa lahat ng jcommon multiples, palaging may pinakamaliit, in kasong ito ito ay 90. Ang numerong ito ay tinatawag hindi bababa sacommon multiple (LCM).
Ang LCM ay palaging isang natural na numero, na dapat na mas malaki kaysa sa pinakamalaki sa mga numero kung saan ito tinukoy.
Least common multiple (LCM). Ari-arian.
Commutativity:
Pagkakaisa:
![]()
Sa partikular, kung at mga coprime na numero , kung gayon:
Hindi bababa sa karaniwang maramihang ng dalawang integer m at n ay isang divisor ng lahat ng iba pang common multiples m at n. Bukod dito, ang hanay ng mga karaniwang multiple m,n tumutugma sa hanay ng mga multiple para sa LCM( m,n).
Ang mga asymptotics para sa ay maaaring ipahayag sa mga tuntunin ng ilang mga function ng number-theoretic.
Kaya, Pag-andar ng Chebyshev. Pati na rin ang:
Ito ay sumusunod mula sa kahulugan at mga katangian ng Landau function g(n).
Ano ang sumusunod mula sa batas ng pamamahagi ng mga prime number.
Paghahanap ng least common multiple (LCM).
NOC( a, b) ay maaaring kalkulahin sa maraming paraan:
1. Kung kilala ang pinakamalaking karaniwang divisor, maaari mong gamitin ang kaugnayan nito sa LCM:
![]()
2. Hayaang malaman ang canonical decomposition ng parehong mga numero sa prime factor:
![]()
saan p 1 ,...,p k- iba-iba mga pangunahing numero, a d 1 ,...,d k at e 1 ,...,ek ay mga di-negatibong integer (maaari silang maging zero kung ang kaukulang prime ay wala sa decomposition).
Pagkatapos LCM ( a,b) ay kinakalkula ng formula:
Sa madaling salita, ang pagpapalawak ng LCM ay naglalaman ng lahat ng pangunahing salik na kasama sa kahit isa sa mga pagpapalawak ng numero a, b, at ang pinakamalaki sa dalawang exponent ng salik na ito ay kinuha.
Halimbawa:
Ang pagkalkula ng hindi bababa sa karaniwang multiple ng ilang numero ay maaaring bawasan sa ilang sunud-sunod na kalkulasyon ng LCM ng dalawang numero:
Panuntunan. Upang mahanap ang LCM ng isang serye ng mga numero, kailangan mo:
- mabulok ang mga numero sa pangunahing mga kadahilanan;
- ilipat ang pinakamalaking pagpapalawak sa mga kadahilanan ng nais na produkto (ang produkto ng mga kadahilanan ng isang malaking bilang mula sa mga ibinigay), at pagkatapos ay magdagdag ng mga kadahilanan mula sa pagkabulok ng iba pang mga numero na hindi nangyayari sa unang numero o nasa loob nito ng mas maliit na bilang ng beses;
- ang magreresultang produkto ng prime factor ay ang LCM ng mga ibinigay na numero.
Anumang dalawa o higit pa natural na mga numero may sariling NOC. Kung ang mga numero ay hindi multiple ng bawat isa o walang parehong mga salik sa pagpapalawak, ang kanilang LCM ay katumbas ng produkto ng mga numerong ito.

Ang mga pangunahing salik ng numerong 28 (2, 2, 7) ay dinagdagan ng salik na 3 (bilang 21), ang magreresultang produkto (84) ay ang pinakamaliit na bilang, na nahahati sa 21 at 28 .

Ang mga pangunahing kadahilanan ng pinakamalaking bilang 30 ay dinagdagan ng isang kadahilanan na 5 ng bilang 25, ang nagresultang produkto 150 ay mas malaki kaysa sa pinakamalaking bilang 30 at nahahati sa lahat ng ibinigay na mga numero nang walang natitira. Ito ang pinakamaliit na posibleng produkto (150, 250, 300...) na ang lahat ng ibinigay na numero ay multiple.

Ang mga numerong 2,3,11,37 ay prime, kaya ang kanilang LCM ay katumbas ng produkto ng mga ibinigay na numero.
tuntunin. Upang kalkulahin ang LCM ng mga prime number, kailangan mong i-multiply ang lahat ng mga numerong ito nang magkasama.
Iba pang Pagpipilian:
Para mahanap ang least common multiple (LCM) ng ilang numero kailangan mo:
1) kinakatawan ang bawat numero bilang produkto ng mga pangunahing salik nito, halimbawa:
504 \u003d 2 2 2 3 3 7,
2) isulat ang mga kapangyarihan ng lahat ng pangunahing mga kadahilanan:
504 \u003d 2 2 2 3 3 7 \u003d 2 3 3 2 7 1,
3) isulat ang lahat ng prime divisors (multipliers) ng bawat isa sa mga numerong ito;
4) piliin ang pinakamalaking antas ng bawat isa sa kanila, na makikita sa lahat ng pagpapalawak ng mga numerong ito;
5) paramihin ang mga kapangyarihang ito.
Halimbawa. Hanapin ang LCM ng mga numero: 168, 180 at 3024.
Desisyon. 168 \u003d 2 2 2 3 7 \u003d 2 3 3 1 7 1,
180 \u003d 2 2 3 3 5 \u003d 2 2 3 2 5 1,
3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1 .
Isinulat namin ang pinakamalaking kapangyarihan ng lahat ng pangunahing divisors at i-multiply ang mga ito:
LCM = 2 4 3 3 5 1 7 1 = 15120.
Ang multiple ng isang numero ay isang numero na nahahati sa isang naibigay na numero nang walang natitira. Ang least common multiple (LCM) ng isang pangkat ng mga numero ay ang pinakamaliit na bilang na pantay na nahahati ng bawat numero sa pangkat. Upang mahanap ang hindi bababa sa karaniwang maramihang, kailangan mong hanapin ang mga pangunahing kadahilanan ng mga ibinigay na numero. Gayundin, maaaring kalkulahin ang LCM gamit ang ilang iba pang mga pamamaraan na naaangkop sa mga pangkat ng dalawa o higit pang mga numero.
Mga hakbang
Isang bilang ng mga multiple
- Halimbawa, hanapin ang hindi bababa sa karaniwang multiple ng mga numero 5 at 8. Ito ay maliliit na numero, kaya maaaring gamitin ang paraang ito.
-
Ang multiple ng isang numero ay isang numero na nahahati sa isang naibigay na numero nang walang natitira. Maramihang mga numero ay matatagpuan sa multiplication table.
- Halimbawa, ang mga numero na multiple ng 5 ay: 5, 10, 15, 20, 25, 30, 35, 40.
-
Isulat ang isang serye ng mga numero na multiple ng unang numero. Gawin ito sa ilalim ng multiple ng unang numero upang paghambingin ang dalawang hanay ng mga numero.
- Halimbawa, ang mga numero na multiple ng 8 ay: 8, 16, 24, 32, 40, 48, 56, at 64.
-
Hanapin ang pinakamaliit na numero na lumilitaw sa parehong serye ng mga multiple. Maaaring kailanganin mong magsulat ng mahabang serye ng mga multiple upang mahanap kabuuang bilang. Ang pinakamaliit na numero na lumilitaw sa parehong serye ng mga multiple ay ang hindi bababa sa karaniwang maramihang.
- Halimbawa, ang pinakamaliit na numero na lumilitaw sa serye ng mga multiple ng 5 at 8 ay 40. Samakatuwid, ang 40 ay ang hindi bababa sa karaniwang multiple ng 5 at 8.
Prime factorization
-
Tingnan ang mga numerong ito. Ang pamamaraang inilarawan dito ay pinakamahusay na ginagamit kapag binigyan ng dalawang numero na parehong mas malaki sa 10. Kung mas maliit na mga numero ang ibinigay, gumamit ng ibang paraan.
- Halimbawa, hanapin ang hindi bababa sa karaniwang multiple ng mga numero 20 at 84. Ang bawat isa sa mga numero ay mas malaki sa 10, kaya maaaring gamitin ang paraang ito.
-
I-factor ang unang numero. Iyon ay, kailangan mong hanapin ang gayong mga prime number, kapag pinarami, makakakuha ka ng isang naibigay na numero. Kapag natagpuan ang pangunahing mga kadahilanan, isulat ang mga ito bilang isang pagkakapantay-pantay.
- Halimbawa, 2 × 10 = 20 (\displaystyle (\mathbf (2) )\times 10=20) at 2 × 5 = 10 (\displaystyle (\mathbf (2) )\times (\mathbf (5) )=10). Kaya, ang mga pangunahing kadahilanan ng bilang 20 ay ang mga numero 2, 2 at 5. Isulat ang mga ito bilang isang expression: .
-
I-factor ang pangalawang numero sa prime factor. Gawin ito sa parehong paraan tulad ng pag-factor mo sa unang numero, iyon ay, hanapin ang mga prime number na, kapag pinarami, ay makakakuha ng numerong ito.
- Halimbawa, 2 × 42 = 84 (\displaystyle (\mathbf (2) )\times 42=84), 7 × 6 = 42 (\displaystyle (\mathbf (7) )\times 6=42) at 3 × 2 = 6 (\displaystyle (\mathbf (3) )\times (\mathbf (2) )=6). Kaya, ang mga pangunahing kadahilanan ng numero 84 ay ang mga numero 2, 7, 3 at 2. Isulat ang mga ito bilang isang expression: .
-
Isulat ang mga salik na karaniwan sa parehong mga numero. Isulat ang mga salik bilang pagpaparami. Habang isinusulat mo ang bawat salik, i-cross out ito sa parehong mga expression (mga expression na naglalarawan sa decomposition ng mga numero sa prime factor).
- Halimbawa, ang karaniwang kadahilanan para sa parehong mga numero ay 2, kaya isulat 2 × (\displaystyle 2\beses ) at ekis ang 2 sa parehong expression.
- Ang karaniwang kadahilanan para sa parehong mga numero ay isa pang kadahilanan ng 2, kaya sumulat 2 × 2 (\displaystyle 2\beses 2) at ekis ang pangalawang 2 sa parehong mga expression.
-
Idagdag ang natitirang mga kadahilanan sa pagpaparami. Ito ang mga salik na hindi natatanggal sa parehong mga expression, iyon ay, mga salik na hindi karaniwan sa parehong mga numero.
- Halimbawa, sa expression 20 = 2 × 2 × 5 (\displaystyle 20=2\beses 2\beses 5) parehong dalawa (2) ang ekis dahil sila ay karaniwang mga kadahilanan. Ang kadahilanan 5 ay hindi na-cross out, kaya isulat ang pagpaparami ng operasyon tulad ng sumusunod: 2 × 2 × 5 (\displaystyle 2\beses 2\beses 5)
- Sa ekspresyon 84 = 2 × 7 × 3 × 2 (\displaystyle 84=2\beses 7\beses 3\beses 2) parehong deuces (2) ay ekis din. Ang mga salik 7 at 3 ay hindi natatanggal, kaya isulat ang pagpaparami bilang sumusunod: 2 × 2 × 5 × 7 × 3 (\displaystyle 2\beses 2\beses 5\beses 7\beses 3).
-
Kalkulahin ang hindi bababa sa karaniwang maramihang. Upang gawin ito, i-multiply ang mga numero sa nakasulat na multiplication operation.
- Halimbawa, 2 × 2 × 5 × 7 × 3 = 420 (\displaystyle 2\beses 2\beses 5\beses 7\beses 3=420). Kaya ang hindi bababa sa karaniwang maramihang ng 20 at 84 ay 420.
Paghahanap ng mga karaniwang divisors
-
Gumuhit ng grid tulad ng gagawin mo para sa isang laro ng tic-tac-toe. Ang nasabing grid ay binubuo ng dalawang parallel na linya na nagsa-intersect (sa tamang mga anggulo) sa dalawang iba pang parallel na linya. Magreresulta ito sa tatlong row at tatlong column (ang grid ay kamukha ng # sign). Isulat ang unang numero sa unang hanay at ikalawang hanay. Isulat ang pangalawang numero sa unang hanay at ikatlong hanay.
- Halimbawa, hanapin ang hindi bababa sa karaniwang multiple ng 18 at 30. Isulat ang 18 sa unang hanay at ikalawang hanay, at isulat ang 30 sa unang hanay at ikatlong hanay.
-
Hanapin ang divisor na karaniwan sa parehong mga numero. Isulat ito sa unang hanay at unang hanay. Mas mainam na maghanap ng mga pangunahing divisors, ngunit hindi ito isang kinakailangan.
- Halimbawa, ang 18 at 30 ay mga numerong pantay, kaya ang kanilang karaniwang divisor ay 2. Kaya't isulat ang 2 sa unang hanay at unang hanay.
-
Hatiin ang bawat numero sa unang divisor. Isulat ang bawat quotient sa ilalim ng katumbas na numero. Ang quotient ay ang resulta ng paghahati ng dalawang numero.
- Halimbawa, 18 ÷ 2 = 9 (\displaystyle 18\div 2=9), kaya sumulat ng 9 sa ilalim ng 18.
- 30 ÷ 2 = 15 (\displaystyle 30\div 2=15), kaya sumulat ng 15 sa ilalim ng 30.
-
Maghanap ng divisor na karaniwan sa parehong quotient. Kung walang ganoong divisor, laktawan ang susunod na dalawang hakbang. Kung hindi, isulat ang divisor sa ikalawang hanay at unang hanay.
- Halimbawa, ang 9 at 15 ay nahahati sa 3, kaya isulat ang 3 sa pangalawang hanay at unang hanay.
-
Hatiin ang bawat quotient sa pangalawang divisor. Isulat ang bawat resulta ng paghahati sa ilalim ng katumbas na quotient.
- Halimbawa, 9 ÷ 3 = 3 (\displaystyle 9\div 3=3), kaya sumulat ng 3 sa ilalim ng 9.
- 15 ÷ 3 = 5 (\displaystyle 15\div 3=5), kaya sumulat ng 5 sa ilalim ng 15.
-
Kung kinakailangan, dagdagan ang grid na may karagdagang mga cell. Ulitin ang mga hakbang sa itaas hanggang sa magkaroon ng karaniwang divisor ang mga quotient.
-
Bilugan ang mga numero sa unang hanay at huling hilera ng grid. Pagkatapos ay isulat ang mga naka-highlight na numero bilang isang multiplication operation.
- Halimbawa, ang mga numero 2 at 3 ay nasa unang hanay, at ang mga numero 3 at 5 ay nasa huling hilera, kaya't isulat ang pagpaparami nang ganito: 2 × 3 × 3 × 5 (\displaystyle 2\beses 3\beses 3\beses 5).
-
Hanapin ang resulta ng pagpaparami ng mga numero. Kakalkulahin nito ang hindi bababa sa karaniwang multiple ng dalawang ibinigay na numero.
- Halimbawa, 2 × 3 × 3 × 5 = 90 (\displaystyle 2\beses 3\beses 3\beses 5=90). Kaya ang hindi bababa sa karaniwang maramihang ng 18 at 30 ay 90.
Ang algorithm ni Euclid
-
Alalahanin ang terminolohiya na nauugnay sa operasyon ng paghahati. Ang dibidendo ay ang bilang na hinahati. Ang divisor ay ang numero kung saan hahatiin. Ang quotient ay ang resulta ng paghahati ng dalawang numero. Ang natitira ay ang numerong natitira kapag hinati ang dalawang numero.
- Halimbawa, sa expression 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) magpahinga. 3:
15 ang mahahati
6 ang divisor
2 ay pribado
3 ang natitira.
- Halimbawa, sa expression 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) magpahinga. 3:
Tingnan ang mga numerong ito. Ang pamamaraang inilarawan dito ay pinakamahusay na ginagamit kapag binibigyan ng dalawang numero na ang bawat isa ay mas mababa sa 10. Kung malaking numero ang ibinigay, gumamit ng ibang paraan.
Ang materyal sa ibaba ay lohikal na pagpapatuloy mga teorya mula sa artikulong pinamagatang LCM - Least Common Multiple, kahulugan, mga halimbawa, relasyon sa pagitan ng LCM at GCM. Dito natin pag-uusapan paghahanap ng least common multiple (LCM), at Espesyal na atensyon Tingnan natin ang mga halimbawa. Ipakita muna natin kung paano kinakalkula ang LCM ng dalawang numero sa mga tuntunin ng GCD ng mga numerong ito. Susunod, isaalang-alang ang paghahanap ng hindi bababa sa karaniwang maramihang sa pamamagitan ng pag-factor ng mga numero sa prime factor. Pagkatapos nito, tututukan natin ang paghahanap ng LCM ng tatlo at higit pa mga numero, at bigyang-pansin din ang pagkalkula ng LCM ng mga negatibong numero.
Pag-navigate sa pahina.
Pagkalkula ng least common multiple (LCM) sa pamamagitan ng gcd
Ang isang paraan upang mahanap ang least common multiple ay batay sa relasyon sa pagitan ng LCM at GCD. Ang umiiral na ugnayan sa pagitan ng LCM at GCD ay nagbibigay-daan sa iyong kalkulahin ang hindi bababa sa karaniwang multiple ng dalawang positive integer sa pamamagitan ng kilalang pinakadakilang karaniwang divisor. Ang kaukulang formula ay may anyo LCM(a, b)=a b: GCD(a, b) . Isaalang-alang ang mga halimbawa ng paghahanap ng LCM ayon sa formula sa itaas.
Halimbawa.
Hanapin ang least common multiple ng dalawang numero 126 at 70 .
Desisyon.
Sa halimbawang ito a=126 , b=70 . Gamitin natin ang relasyon sa pagitan ng LCM at GCD na ipinahayag ng formula LCM(a, b)=a b: GCD(a, b). Iyon ay, kailangan muna nating hanapin ang pinakamalaking karaniwang divisor ng mga numerong 70 at 126, pagkatapos nito ay maaari nating kalkulahin ang LCM ng mga numerong ito ayon sa nakasulat na formula.
Hanapin ang gcd(126, 70) gamit ang algorithm ni Euclid: 126=70 1+56 , 70=56 1+14 , 56=14 4 , kaya gcd(126, 70)=14 .
Ngayon nakita namin ang kinakailangang hindi bababa sa karaniwang maramihang: LCM(126, 70)=126 70: GCM(126, 70)= 126 70:14=630 .
Sagot:
LCM(126, 70)=630 .
Halimbawa.
Ano ang LCM(68, 34) ?
Desisyon.
Bilang Ang 68 ay pantay na nahahati ng 34 , pagkatapos ay gcd(68, 34)=34 . Ngayon kinakalkula namin ang hindi bababa sa karaniwang maramihang: LCM(68, 34)=68 34: LCM(68, 34)= 68 34:34=68 .
Sagot:
LCM(68, 34)=68 .
Tandaan na ang nakaraang halimbawa ay umaangkop sa sumusunod na panuntunan para sa paghahanap ng LCM para sa mga positibong integer a at b : kung ang numero a ay nahahati sa b , kung gayon ang hindi bababa sa karaniwang multiple ng mga numerong ito ay a .
Paghahanap ng LCM sa pamamagitan ng Factoring Numbers into Prime Factors
Ang isa pang paraan upang mahanap ang hindi bababa sa karaniwang maramihang ay batay sa mga numero ng factoring sa prime factor. Kung gagawin namin ang isang produkto ng lahat ng prime factor ng mga numerong ito, pagkatapos nito ay ibubukod namin mula sa produktong ito ang lahat ng karaniwang prime factor na naroroon sa mga pagpapalawak ng mga numerong ito, ang resultang produkto ay magiging katumbas ng hindi bababa sa common multiple ng mga numerong ito.
Ang inihayag na panuntunan para sa paghahanap ng LCM ay sumusunod sa pagkakapantay-pantay LCM(a, b)=a b: GCD(a, b). Sa katunayan, ang produkto ng mga numerong a at b ay katumbas ng produkto ng lahat ng mga salik na kasangkot sa pagpapalawak ng mga numerong a at b. Sa turn, ang gcd(a, b) ay katumbas ng produkto ng lahat ng prime factor na sabay-sabay na naroroon sa mga pagpapalawak ng mga numerong a at b (na inilalarawan sa seksyon sa paghahanap ng gcd gamit ang decomposition ng mga numero sa prime factor. ).
Kumuha tayo ng isang halimbawa. Ipaalam sa amin na 75=3 5 5 at 210=2 3 5 7 . Buuin ang produkto ng lahat ng salik ng mga pagpapalawak na ito: 2 3 3 5 5 5 7 . Ngayon ay ibinubukod namin mula sa produktong ito ang lahat ng mga kadahilanan na naroroon kapwa sa pagpapalawak ng numero 75 at sa pagpapalawak ng bilang 210 (ang mga naturang kadahilanan ay 3 at 5), pagkatapos ay ang produkto ay kukuha ng anyo 2 3 5 5 7 . Ang halaga ng produktong ito ay katumbas ng hindi bababa sa karaniwang multiple ng mga numero 75 at 210, iyon ay, LCM(75, 210)= 2 3 5 5 7=1 050.
Halimbawa.
Pagkatapos i-factor ang mga numerong 441 at 700 sa prime factor, hanapin ang least common multiple ng mga numerong ito.
Desisyon.
I-decompose natin ang mga numerong 441 at 700 sa prime factors:
Nakukuha natin ang 441=3 3 7 7 at 700=2 2 5 5 7 .
Ngayon, gumawa tayo ng produkto ng lahat ng mga salik na kasangkot sa pagpapalawak ng mga bilang na ito: 2 2 3 3 5 5 7 7 7 . Ibukod natin sa produktong ito ang lahat ng mga salik na sabay-sabay na naroroon sa parehong mga pagpapalawak (mayroong isa lamang salik na ito - ito ang numero 7): 2 2 3 3 5 5 7 7 . kaya, LCM(441, 700)=2 2 3 3 5 5 7 7=44 100.
Sagot:
LCM(441, 700)= 44 100 .
Ang panuntunan para sa paghahanap ng LCM gamit ang decomposition ng mga numero sa prime factor ay maaaring mabuo nang medyo naiiba. Kung idaragdag natin ang nawawalang mga salik mula sa pagpapalawak ng bilang b sa mga salik mula sa pagkabulok ng numero a, kung gayon ang halaga ng resultang produkto ay magiging katumbas ng hindi bababa sa karaniwang maramihang ng mga numerong a at b.
Halimbawa, kunin natin ang lahat ng parehong numero 75 at 210, ang kanilang mga pagpapalawak sa prime factor ay ang mga sumusunod: 75=3 5 5 at 210=2 3 5 7 . Sa mga salik 3, 5 at 5 mula sa pagpapalawak ng bilang na 75, idinaragdag namin ang nawawalang mga salik 2 at 7 mula sa pagpapalawak ng bilang 210, nakukuha namin ang produkto 2 3 5 5 7 , ang halaga nito ay LCM(75). , 210).
Halimbawa.
Hanapin ang hindi bababa sa karaniwang multiple ng 84 at 648.
Desisyon.
Una naming makuha ang agnas ng mga numero 84 at 648 sa pangunahing mga kadahilanan. Kamukha nila ang 84=2 2 3 7 at 648=2 2 2 3 3 3 3 . Sa mga salik 2 , 2 , 3 at 7 mula sa pagpapalawak ng bilang na 84 idinaragdag namin ang nawawalang salik 2 , 3 , 3 at 3 mula sa pagpapalawak ng bilang na 648 , nakukuha namin ang produkto 2 2 2 3 3 3 3 7 , na katumbas ng 4 536 . Kaya, ang nais na hindi bababa sa karaniwang maramihang ng mga numero 84 at 648 ay 4,536.
Sagot:
LCM(84, 648)=4 536 .
Paghahanap ng LCM ng tatlo o higit pang mga numero
Ang hindi bababa sa karaniwang multiple ng tatlo o higit pang mga numero ay makikita sa pamamagitan ng sunud-sunod na paghahanap ng LCM ng dalawang numero. Alalahanin ang kaukulang theorem, na nagbibigay ng paraan upang mahanap ang LCM ng tatlo o higit pang mga numero.
Teorama.
Hayaang ibigay ang positive integers a 1 , a 2 , …, a k, ang hindi bababa sa karaniwang multiple m k ng mga numerong ito ay makikita sa sequential kalkulasyon m 2 = LCM (a 1 , a 2) , m 3 = LCM (m 2, a 3) , … , m k =LCM(m k−1 , a k) .
Isaalang-alang ang aplikasyon ng theorem na ito sa halimbawa ng paghahanap ng hindi bababa sa karaniwang maramihang ng apat na numero.
Halimbawa.
Hanapin ang LCM ng apat na numero 140 , 9 , 54 at 250 .
Desisyon.
Sa halimbawang ito a 1 =140 , a 2 =9 , a 3 =54 , a 4 =250 .
Una naming mahanap m 2 \u003d LCM (a 1, a 2) \u003d LCM (140, 9). Upang gawin ito, gamit ang Euclidean algorithm, tinutukoy namin ang gcd(140, 9) , mayroon kaming 140=9 15+5 , 9=5 1+4 , 5=4 1+1 , 4=1 4 , samakatuwid, gcd( 140, 9)=1 , kung saan LCM(140, 9)=140 9: LCM(140, 9)= 140 9:1=1 260 . Ibig sabihin, m 2 =1 260 .
Ngayon nahanap namin m 3 \u003d LCM (m 2, a 3) \u003d LCM (1 260, 54). Kalkulahin natin ito sa pamamagitan ng gcd(1 260, 54) , na tinutukoy din ng Euclid algorithm: 1 260=54 23+18 , 54=18 3 . Pagkatapos gcd(1 260, 54)=18 , kung saan LCM(1 260, 54)= 1 260 54:gcd(1 260, 54)= 1 260 54:18=3 780 . Iyon ay, m 3 \u003d 3 780.
Kaliwa upang mahanap m 4 \u003d LCM (m 3, a 4) \u003d LCM (3 780, 250). Para magawa ito, hanapin natin ang GCD(3 780, 250) gamit ang Euclid algorithm: 3 780=250 15+30 , 250=30 8+10 , 30=10 3 . Samakatuwid, gcd(3 780, 250)=10 , kung saan gcd(3 780, 250)= 3 780 250:gcd(3 780, 250)= 3 780 250:10=94 500 . Iyon ay, m 4 \u003d 94 500.
Kaya ang hindi bababa sa karaniwang maramihang ng orihinal na apat na numero ay 94,500.
Sagot:
LCM(140, 9, 54, 250)=94,500.
Sa maraming mga kaso, ang hindi bababa sa karaniwang maramihang ng tatlo o higit pang mga numero ay madaling makita gamit ang mga prime factorization ng mga ibinigay na numero. Sa kasong ito, dapat sundin ang sumusunod na panuntunan. Ang hindi bababa sa karaniwang multiple ng ilang mga numero ay katumbas ng produkto, na binubuo ng mga sumusunod: ang nawawalang mga salik mula sa pagpapalawak ng pangalawang numero ay idinaragdag sa lahat ng mga salik mula sa pagpapalawak ng unang numero, ang nawawalang mga salik mula sa pagpapalawak ng ang ikatlong numero ay idinagdag sa nakuha na mga kadahilanan, at iba pa.
Isaalang-alang ang isang halimbawa ng paghahanap ng hindi bababa sa karaniwang maramihang gamit ang decomposition ng mga numero sa prime factor.
Halimbawa.
Hanapin ang hindi bababa sa karaniwang multiple ng limang numero 84 , 6 , 48 , 7 , 143 .
Desisyon.
Una, nakuha natin ang mga pagpapalawak ng mga numerong ito sa prime factor: 84=2 2 3 7 , 6=2 3 , 48=2 2 2 2 3 , 7 prime factor) at 143=11 13 .
Upang mahanap ang LCM ng mga numerong ito, sa mga salik ng unang numero 84 (sila ay 2 , 2 , 3 at 7 ) kailangan mong idagdag ang nawawalang mga salik mula sa pagpapalawak ng pangalawang numero 6 . Ang pagpapalawak ng numero 6 ay hindi naglalaman ng mga nawawalang kadahilanan, dahil ang parehong 2 at 3 ay naroroon na sa pagpapalawak ng unang numero 84 . Dagdag pa sa mga salik 2 , 2 , 3 at 7 idinaragdag namin ang nawawalang salik 2 at 2 mula sa pagpapalawak ng ikatlong numero 48 , nakakakuha kami ng isang hanay ng mga salik 2 , 2 , 2 , 2 , 3 at 7 . Hindi na kailangang magdagdag ng mga salik sa set na ito sa susunod na hakbang, dahil ang 7 ay nakapaloob na dito. Sa wakas, sa mga salik 2 , 2 , 2 , 2 , 3 at 7 idinaragdag namin ang nawawalang salik 11 at 13 mula sa pagpapalawak ng bilang na 143 . Nakukuha namin ang produkto 2 2 2 2 3 7 11 13 , na katumbas ng 48 048 .
Pinakamahusay na Common Divisor
Kahulugan 2
Kung ang isang natural na numerong a ay nahahati sa natural na bilang na $b$, kung gayon ang $b$ ay tinatawag na divisor ng $a$, at ang bilang na $a$ ay tinatawag na multiple ng $b$.
Hayaang maging natural na mga numero ang $a$ at $b$. Ang numerong $c$ ay tinatawag na karaniwang divisor para sa parehong $a$ at $b$.
Ang hanay ng mga karaniwang divisors ng mga numerong $a$ at $b$ ay may hangganan, dahil wala sa mga divisors na ito ang maaaring mas malaki sa $a$. Nangangahulugan ito na sa mga divisor na ito ay mayroong pinakamalaki, na tinatawag na pinakamalaking karaniwang divisor ng mga numerong $a$ at $b$, at ang notasyon ay ginagamit upang tukuyin ito:
$gcd \ (a;b) \ o \ D \ (a;b)$
Upang mahanap ang pinakamalaking karaniwang divisor ng dalawang numero:
- Hanapin ang produkto ng mga numerong makikita sa hakbang 2. Ang resultang numero ay ang nais na pinakamalaking karaniwang divisor.
Halimbawa 1
Hanapin ang gcd ng mga numerong $121$ at $132.$
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Piliin ang mga numerong kasama sa pagpapalawak ng mga numerong ito
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Hanapin ang produkto ng mga numerong makikita sa hakbang 2. Ang resultang numero ay ang nais na pinakamalaking karaniwang divisor.
$gcd=2\cdot 11=22$
Halimbawa 2
Hanapin ang GCD ng mga monomial na $63$ at $81$.
Mahahanap namin ayon sa ipinakita na algorithm. Para dito:
I-decompose natin ang mga numero sa prime factors
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Pinipili namin ang mga numero na kasama sa pagpapalawak ng mga numerong ito
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Hanapin natin ang produkto ng mga numerong makikita sa hakbang 2. Ang resultang numero ay ang nais na pinakamalaking karaniwang divisor.
$gcd=3\cdot 3=9$
Mahahanap mo ang GCD ng dalawang numero sa ibang paraan, gamit ang hanay ng mga divisors ng mga numero.
Halimbawa 3
Hanapin ang gcd ng mga numerong $48$ at $60$.
Desisyon:
Hanapin ang hanay ng mga divisors na $48$: $\left\((\rm 1,2,3.4.6,8,12,16,24,48)\right\)$
Ngayon hanapin natin ang hanay ng mga divisors ng numerong $60$:$\ \left\((\rm 1,2,3,4,5,6,10,12,15,20,30,60)\right\) $
Hanapin natin ang intersection ng mga set na ito: $\left\((\rm 1,2,3,4,6,12)\right\)$ - tutukuyin ng set na ito ang set ng mga common divisors ng mga numero $48$ at $60 $. Ang pinakamalaking elemento sa ibinigay na set ang magiging numerong $12$. Kaya ang pinakamalaking karaniwang divisor ng $48$ at $60$ ay $12$.
Kahulugan ng NOC
Kahulugan 3
karaniwang maramihan ng mga natural na numero Ang $a$ at $b$ ay isang natural na numero na isang multiple ng parehong $a$ at $b$.
Ang mga karaniwang multiple ng mga numero ay mga numero na nahahati sa orihinal na walang nalalabi. Halimbawa, para sa mga numerong $25$ at $50$, ang mga karaniwang multiple ay ang mga numerong $50,100,150,200$, atbp.
Ang least common multiple ay tatawaging least common multiple at tinutukoy ng LCM$(a;b)$ o K$(a;b).$
Upang mahanap ang LCM ng dalawang numero, kailangan mo:
- I-decompose ang mga numero sa prime factor
- Isulat ang mga salik na bahagi ng unang numero at idagdag sa kanila ang mga salik na bahagi ng pangalawa at huwag pumunta sa una
Halimbawa 4
Hanapin ang LCM ng mga numerong $99$ at $77$.
Mahahanap namin ayon sa ipinakita na algorithm. Para dito
I-decompose ang mga numero sa prime factor
$99=3\cdot 3\cdot 11$
Isulat ang mga salik na kasama sa una
idagdag sa kanila ang mga salik na bahagi ng pangalawa at huwag pumunta sa una
Hanapin ang produkto ng mga numerong makikita sa hakbang 2. Ang resultang numero ay ang nais na hindi bababa sa karaniwang maramihang
$LCC=3\cdot 3\cdot 11\cdot 7=693$
Ang pag-compile ng mga listahan ng mga divisors ng mga numero ay kadalasang napakatagal. Mayroong isang paraan upang mahanap ang GCD na tinatawag na Euclid's algorithm.
Mga pahayag kung saan nakabatay ang algorithm ni Euclid:
Kung ang $a$ at $b$ ay mga natural na numero, at ang $a\vdots b$, kung gayon ang $D(a;b)=b$
Kung ang $a$ at $b$ ay mga natural na numero tulad ng $b
Gamit ang $D(a;b)= D(a-b;b)$, maaari naming sunud-sunod na bawasan ang mga numerong isinasaalang-alang hanggang sa maabot namin ang isang pares ng mga numero upang ang isa sa mga ito ay mahahati ng isa. Kung gayon ang mas maliit sa mga numerong ito ay ang nais na pinakamalaking karaniwang divisor para sa mga numerong $a$ at $b$.
Mga katangian ng GCD at LCM
- Anumang common multiple ng $a$ at $b$ ay nahahati ng K$(a;b)$
- Kung $a\vdots b$ , kung gayon K$(a;b)=a$
Kung K$(a;b)=k$ at $m$-natural na numero, kung gayon ang K$(am;bm)=km$
Kung ang $d$ ay karaniwang divisor para sa $a$ at $b$, kung gayon ang K($\frac(a)(d);\frac(b)(d)$)=$\ \frac(k)(d ) $
Kung ang $a\vdots c$ at $b\vdots c$ , ang $\frac(ab)(c)$ ay isang common multiple ng $a$ at $b$
Para sa anumang natural na bilang na $a$ at $b$ ang pagkakapantay-pantay
$D(a;b)\cdot K(a;b)=ab$
Anumang karaniwang divisor ng $a$ at $b$ ay isang divisor ng $D(a;b)$