Matematyczne oczekiwanie dyskretnej zmiennej losowej online. Podstawy teorii prawdopodobieństwa. Matematyczne oczekiwanie wartości
Przeczytaj także
Oczekiwanie matematyczne (wartość średnia) zmienna losowa X dane na dyskretnej przestrzeni prawdopodobieństwa nazywa się liczbą m =M[X]=∑x i p i, jeśli szereg jest zbieżny bezwzględnie.
Cel usługi. Korzystanie z usługi w tryb online obliczane są oczekiwania matematyczne, wariancja i odchylenie standardowe(patrz przykład). Dodatkowo wykreślany jest wykres funkcji rozkładu F(X).
Własności oczekiwań matematycznych zmiennej losowej
- Matematyczne oczekiwanie wartości stałej jest sobie równe: M[C]=C, C – stała;
- M=C M[X]
- Oczekiwanie matematyczne sumy zmiennych losowych jest równe sumie ich oczekiwań matematycznych: M=M[X]+M[Y]
- Oczekiwanie matematyczne iloczynu niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych: M=M[X] M[Y] , jeśli X i Y są niezależne.
Właściwości dyspersyjne
- Wariancja stałej wartości wynosi zero: D(c)=0.
- Stały współczynnik można wyjąć spod znaku dyspersji podnosząc go do kwadratu: D(k*X)= k 2 D(X).
- Jeżeli zmienne losowe X i Y są niezależne, to wariancja sumy jest równa sumie wariancji: D(X+Y)=D(X)+D(Y).
- Jeżeli zmienne losowe X i Y są zależne: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- Dla dyspersji obowiązuje następujący wzór obliczeniowy:
D(X)=M(X 2)-(M(X)) 2
Przykład. Znane są matematyczne oczekiwania i wariancje dwóch niezależnych zmiennych losowych X i Y: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Znajdź matematyczne oczekiwanie i wariancję zmiennej losowej Z=9X-8Y+7.
Rozwiązanie. Bazując na własnościach oczekiwań matematycznych: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23 .
Bazując na własnościach dyspersji: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
Algorytm obliczania oczekiwań matematycznych
Właściwości dyskretnych zmiennych losowych: wszystkie ich wartości można przenumerować liczby naturalne; Przypisz każdej wartości niezerowe prawdopodobieństwo.- Pary mnożymy jeden po drugim: x i przez p i .
- Dodaj iloczyn każdej pary x i p i .
Na przykład dla n = 4: m = ∑x i p ja = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Przykład nr 1.
| x ja | 1 | 3 | 4 | 7 | 9 |
| Liczba Pi | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
Oczekiwanie matematyczne znajdujemy za pomocą wzoru m = ∑x i p i .
Oczekiwanie M[X].
M[x] = 1*0,1 + 3*0,2 + 4*0,1 + 7*0,3 + 9*0,3 = 5,9
Wariancję znajdujemy za pomocą wzoru d = ∑x 2 i p i - M[x] 2 .
Wariancja D[X].
D[X] = 1 2 *0,1 + 3 2 *0,2 + 4 2 *0,1 + 7 2 *0,3 + 9 2 *0,3 - 5,9 2 = 7,69
Odchylenie standardowe σ(x).
σ = sqrt(D[X]) = sqrt(7,69) = 2,78
Przykład nr 2. Dyskretna zmienna losowa ma następujący szereg rozkładów:
| X | -10 | -5 | 0 | 5 | 10 |
| R | A | 0,32 | 2A | 0,41 | 0,03 |
Rozwiązanie. Wartość a wyznaczamy z zależności: Σp i = 1
Σp ja = za + 0,32 + 2 za + 0,41 + 0,03 = 0,76 + 3 za = 1
0,76 + 3 a = 1 lub 0,24=3 a , skąd a = 0,08
Przykład nr 3. Wyznacz prawo rozkładu dyskretnej zmiennej losowej, jeśli znana jest jej wariancja, oraz x 1
p1 = 0,3; p2 = 0,3; p3 = 0,1; p4 =0,3
d(x)=12,96
Rozwiązanie.
Tutaj musisz utworzyć wzór na znalezienie wariancji d(x):
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
gdzie oczekiwanie m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
Dla naszych danych
m(x)=6*0,3+9*0,3+x 3 *0,1+15*0,3=9+0,1x 3
12,96 = 6 2 0,3+9 2 0,3+x 3 2 0,1+15 2 0,3-(9+0,1x 3) 2
lub -9/100 (x 2 -20x+96)=0
W związku z tym musimy znaleźć pierwiastki równania, a będą dwa z nich.
x 3 = 8, x 3 = 12
Wybierz ten, który spełnia warunek x 1
Prawo rozkładu dyskretnej zmiennej losowej
x 1 = 6; x2 =9; x 3 = 12; x 4 = 15
p1 = 0,3; p2 = 0,3; p3 = 0,1; p4 =0,3
Oczekiwanie i wariancja to najczęściej używane cechy liczbowe zmiennej losowej. Charakteryzują najważniejsze cechy rozkładu: jego położenie i stopień rozproszenia. W wielu praktycznych problemach pełna, wyczerpująca charakterystyka zmiennej losowej – prawo dystrybucji – albo w ogóle nie może zostać uzyskana, albo w ogóle nie jest potrzebna. W takich przypadkach ogranicza się do przybliżonego opisu zmiennej losowej za pomocą charakterystyk numerycznych.
Wartość oczekiwana jest często nazywana po prostu średnią wartością zmiennej losowej. Rozproszenie zmiennej losowej jest cechą dyspersji, rozproszenia zmiennej losowej wokół jej oczekiwań matematycznych.
Oczekiwanie dyskretnej zmiennej losowej
Przyjrzyjmy się koncepcji oczekiwań matematycznych, opierając się najpierw na mechanicznej interpretacji rozkładu dyskretnej zmiennej losowej. Niech masa jednostkowa zostanie rozłożona pomiędzy punktami osi x X1 , X 2 , ..., X N, a każdemu punktowi materialnemu odpowiada masa P1 , P 2 , ..., P N. Należy wybrać jeden punkt na osi odciętych, charakteryzujący położenie całego układu punktów materialnych, z uwzględnieniem ich mas. Naturalnym jest, że za taki punkt przyjmuje się środek masy układu punktów materialnych. Jest to średnia ważona zmiennej losowej X, do której odcięta jest każdy punkt XI wchodzi z „wagą” równą odpowiedniemu prawdopodobieństwu. Uzyskana w ten sposób średnia wartość zmiennej losowej X nazywa się jego oczekiwaniem matematycznym.
Matematyczne oczekiwanie dyskretnej zmiennej losowej jest sumą iloczynów wszystkich jej możliwych wartości i prawdopodobieństw tych wartości:

Przykład 1. Zorganizowano loterię, w której wygrywają obie strony. Wygranych jest 1000, z czego 400 to 10 rubli. 300 - 20 rubli za sztukę. 200 - 100 rubli za sztukę. i 100 - 200 rubli za sztukę. Jaka jest średnia wygrana osoby, która kupi jeden los?
Rozwiązanie. Średnie wygrane znajdziemy, jeśli podzielimy całkowitą kwotę wygranych, która wynosi 10*400 + 20*300 + 100*200 + 200*100 = 50 000 rubli, przez 1000 (całkowita kwota wygranych). Następnie otrzymujemy 50000/1000 = 50 rubli. Jednak wyrażenie służące do obliczenia średnich wygranych można przedstawić w następującej formie:
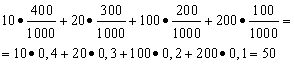
Z drugiej strony, w tych warunkach zwycięska wielkość jest zmienną losową, która może przyjmować wartości 10, 20, 100 i 200 rubli. z prawdopodobieństwem równym odpowiednio 0,4; 0,3; 0,2; 0,1. Dlatego oczekiwana średnia wygrana jest równa sumie iloczynów wielkości wygranych i prawdopodobieństwa ich otrzymania.
Przykład 2. Wydawca podjął decyzję o wydaniu nowej książki. Planuje sprzedać książkę za 280 rubli, z czego sam otrzyma 200, 50 – księgarnia i 30 – autor. Tabela zawiera informacje o kosztach wydania książki i prawdopodobieństwie sprzedaży określonej liczby egzemplarzy książki.
Znajdź oczekiwany zysk wydawcy.
Rozwiązanie. Zmienna losowa „zysk” jest równa różnicy między przychodem ze sprzedaży a kosztem wydatków. Na przykład, jeśli sprzeda się 500 egzemplarzy książki, dochód ze sprzedaży wynosi 200 * 500 = 100 000, a koszt publikacji to 225 000 rubli. Tym samym wydawcy grozi strata 125 000 rubli. Poniższa tabela podsumowuje oczekiwane wartości zmiennej losowej – zysk:
| Numer | Zysk XI | Prawdopodobieństwo PI | XI P I |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Całkowity: | 1,00 | 25000 |
Otrzymujemy w ten sposób matematyczne oczekiwanie zysku wydawcy:
![]() .
.
Przykład 3. Prawdopodobieństwo trafienia jednym strzałem P= 0,2. Określ zużycie pocisków, które zapewniają matematyczną oczekiwaną liczbę trafień równą 5.
Rozwiązanie. Z tego samego matematycznego wzoru oczekiwań, którego używaliśmy do tej pory, wyrażamy X- zużycie powłoki:
![]() .
.
Przykład 4. Określ oczekiwanie matematyczne zmiennej losowej X liczba trafień trzema strzałami, jeżeli prawdopodobieństwo trafienia przy każdym strzale P = 0,4 .
Wskazówka: znajdź prawdopodobieństwo wartości zmiennych losowych według Wzór Bernoulliego .
Właściwości oczekiwań matematycznych
Rozważmy właściwości oczekiwań matematycznych.
Właściwość 1. Matematyczne oczekiwanie na stałą wartość jest równe tej stałej:
Własność 2. Stały współczynnik można wyjąć z matematycznego znaku oczekiwania:
![]()
Własność 3. Oczekiwanie matematyczne sumy (różnicy) zmiennych losowych jest równe sumie (różnicy) ich oczekiwań matematycznych:
Właściwość 4. Oczekiwanie matematyczne iloczynu zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych:
Własność 5. Jeśli wszystkie wartości zmiennej losowej X zmniejszyć (zwiększyć) o tę samą liczbę Z, to jego oczekiwanie matematyczne zmniejszy się (zwiększy) o tę samą liczbę:
![]()
Kiedy nie możesz ograniczyć się tylko do oczekiwań matematycznych
W większości przypadków jedynie oczekiwanie matematyczne nie jest w stanie w wystarczającym stopniu scharakteryzować zmiennej losowej.
Niech zmienne losowe X I Y wynikają z następujących praw dystrybucji:
| Oznaczający X | Prawdopodobieństwo |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Oznaczający Y | Prawdopodobieństwo |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Oczekiwania matematyczne tych wielkości są takie same – równe zeru:
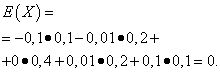
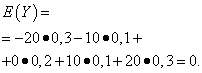
Jednak ich schematy dystrybucji są różne. Losowa wartość X może przyjmować jedynie wartości niewiele różniące się od oczekiwań matematycznych oraz zmienną losową Y może przyjmować wartości znacznie odbiegające od oczekiwań matematycznych. Podobny przykład: przeciętne wynagrodzenie nie pozwala ocenić udziału wysoko i nisko opłacanych pracowników. Innymi słowy, na podstawie oczekiwań matematycznych nie można ocenić, jakie odchylenia od nich, przynajmniej średnio, są możliwe. Aby to zrobić, musisz znaleźć wariancję zmiennej losowej.
Wariancja dyskretnej zmiennej losowej
Zmienność Dyskretna zmienna losowa X nazywa się oczekiwaniem matematycznym kwadratu jego odchylenia od oczekiwania matematycznego:
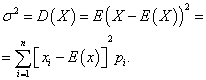
Odchylenie standardowe zmiennej losowej X wartość arytmetyczną pierwiastka kwadratowego z jej wariancji nazywa się:
![]() .
.
Przykład 5. Obliczanie wariancji i odchyleń standardowych zmiennych losowych X I Y, których prawa dystrybucji podano w tabelach powyżej.
Rozwiązanie. Matematyczne oczekiwania zmiennych losowych X I Y, jak stwierdzono powyżej, są równe zeru. Zgodnie ze wzorem dyspersji przy mi(X)=mi(y)=0 otrzymujemy:

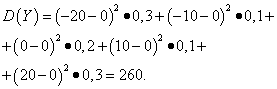
Następnie odchylenia standardowe zmiennych losowych X I Y makijaż
![]() .
.
Zatem przy tych samych oczekiwaniach matematycznych wariancja zmiennej losowej X bardzo mała, ale zmienna losowa Y- istotne. Jest to konsekwencja różnic w ich rozmieszczeniu.
Przykład 6. Inwestor posiada 4 alternatywne projekty inwestycyjne. Tabela podsumowuje oczekiwany zysk w tych projektach z odpowiednim prawdopodobieństwem.
| Projekt 1 | Projekt 2 | Projekt 3 | Projekt 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Znajdź dla każdej alternatywy matematyczne oczekiwanie, wariancję i odchylenie standardowe.
Rozwiązanie. Pokażmy, jak obliczane są te wartości dla 3. alternatywy:
Tabela podsumowuje znalezione wartości dla wszystkich alternatyw.
Wszystkie alternatywy mają te same oczekiwania matematyczne. Oznacza to, że w dłuższej perspektywie wszyscy mają takie same dochody. Odchylenie standardowe można interpretować jako miarę ryzyka – im jest ono wyższe, tym większe ryzyko inwestycji. Inwestor, który nie chce dużego ryzyka, wybierze projekt 1, ponieważ ma najmniejsze odchylenie standardowe (0). Jeżeli inwestor preferuje ryzyko i wysokie zyski w krótkim czasie, to wybierze projekt o największym odchyleniu standardowym – projekt 4.
Właściwości dyspersyjne
Przedstawmy właściwości dyspersji.
Właściwość 1. Wariancja stałej wartości wynosi zero:
Własność 2. Stały współczynnik można usunąć ze znaku dyspersji podnosząc go do kwadratu:
![]() .
.
Własność 3. Wariancja zmiennej losowej jest równa matematycznemu oczekiwaniu kwadratu tej wartości, od którego odejmuje się kwadrat matematycznego oczekiwania samej wartości:
![]() ,
,
Gdzie ![]() .
.
Właściwość 4. Wariancja sumy (różnicy) zmiennych losowych jest równa sumie (różnicy) ich wariancji:
Przykład 7. Wiadomo, że dyskretna zmienna losowa X przyjmuje tylko dwie wartości: −3 i 7. Ponadto znane jest oczekiwanie matematyczne: mi(X) = 4 . Znajdź wariancję dyskretnej zmiennej losowej.
Rozwiązanie. Oznaczmy przez P prawdopodobieństwo, z jakim zmienna losowa przyjmuje wartość X1 = −3 . Następnie prawdopodobieństwo wartości X2 = 7 będzie 1- P. Wyprowadźmy równanie na oczekiwanie matematyczne:
mi(X) = X 1 P + X 2 (1 − P) = −3P + 7(1 − P) = 4 ,
gdzie otrzymujemy prawdopodobieństwa: P= 0,3 i 1 − P = 0,7 .
Prawo rozkładu zmiennej losowej:
| X | −3 | 7 |
| P | 0,3 | 0,7 |
Wariancję tej zmiennej losowej obliczamy korzystając ze wzoru z właściwości 3 dyspersji:
D(X) = 2,7 + 34,3 − 16 = 21 .
Znajdź samodzielnie matematyczne oczekiwanie zmiennej losowej, a następnie spójrz na rozwiązanie
Przykład 8. Dyskretna zmienna losowa X przyjmuje tylko dwie wartości. Przyjmuje większą z wartości 3 z prawdopodobieństwem 0,4. Ponadto znana jest wariancja zmiennej losowej D(X) = 6 . Znajdź matematyczne oczekiwanie zmiennej losowej.
Przykład 9. W urnie jest 6 kul białych i 4 czarne. Z urny losujemy 3 kule. Liczba białych kul wśród wylosowanych kul jest dyskretną zmienną losową X. Znajdź matematyczne oczekiwanie i wariancję tej zmiennej losowej.
Rozwiązanie. Losowa wartość X może przyjmować wartości 0, 1, 2, 3. Z odpowiednich prawdopodobieństw można obliczyć reguła mnożenia prawdopodobieństwa. Prawo rozkładu zmiennej losowej:
| X | 0 | 1 | 2 | 3 |
| P | 1/30 | 3/10 | 1/2 | 1/6 |
Stąd matematyczne oczekiwanie tej zmiennej losowej:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Wariancja danej zmiennej losowej wynosi:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Oczekiwanie i wariancja ciągłej zmiennej losowej
W przypadku ciągłej zmiennej losowej mechaniczna interpretacja oczekiwań matematycznych zachowa to samo znaczenie: środek masy jednostki masy rozłożonej w sposób ciągły na osi x z gęstością F(X). W przeciwieństwie do dyskretnej zmiennej losowej, której argumentem jest funkcja XI zmienia się gwałtownie; w przypadku ciągłej zmiennej losowej argument zmienia się w sposób ciągły. Ale matematyczne oczekiwanie ciągłej zmiennej losowej jest również powiązane z jej średnią wartością.
Aby znaleźć matematyczne oczekiwanie i wariancję ciągłej zmiennej losowej, należy znaleźć całki oznaczone . Jeśli podana jest funkcja gęstości ciągłej zmiennej losowej, to wchodzi ona bezpośrednio do całki. Jeśli podana jest funkcja rozkładu prawdopodobieństwa, to różniczkując ją, musisz znaleźć funkcję gęstości.
Nazywa się ją średnią arytmetyczną wszystkich możliwych wartości ciągłej zmiennej losowej oczekiwanie matematyczne, oznaczone lub .
– liczba chłopców na 10 noworodków.
Jest rzeczą oczywistą, że liczba ta nie jest z góry znana, a wśród kolejnych dziesięciorga urodzonych dzieci mogą znajdować się:
Albo chłopcy - jeden i tylko jeden z wymienionych opcji.
A żeby utrzymać formę, trochę wychowania fizycznego:
– odległość skoku w dal (w niektórych jednostkach).
Nawet mistrz sportu nie jest w stanie tego przewidzieć :)
Jednak Twoje hipotezy?
2) Ciągła zmienna losowa – akceptuje Wszystko wartości liczbowe z jakiegoś skończonego lub nieskończonego przedziału.
Notatka : skróty DSV i NSV są popularne w literaturze edukacyjnej
Najpierw przeanalizujmy dyskretną zmienną losową, a następnie - ciągły.
Prawo rozkładu dyskretnej zmiennej losowej
- Ten korespondencja między możliwymi wartościami tej wielkości a ich prawdopodobieństwami. Najczęściej prawo jest zapisane w tabeli: 
Termin ten jest używany dość często wiersz
dystrybucja, ale w niektórych sytuacjach brzmi to dwuznacznie, dlatego będę się trzymał „prawa”.
I teraz bardzo ważny punkt: od zmiennej losowej Koniecznie zaakceptuje jedna z wartości, następnie tworzą się odpowiednie zdarzenia pełna grupa a suma prawdopodobieństw ich wystąpienia jest równa jeden:
lub, jeśli napisano w formie skondensowanej:
I tak na przykład prawo rozkładu prawdopodobieństwa punktów wyrzuconych na kostce ma następującą postać: 
Bez komentarza.
Możesz mieć wrażenie, że dyskretna zmienna losowa może przyjmować tylko „dobre” wartości całkowite. Rozwiejmy złudzenia – mogą być dowolne:
Przykład 1
W niektórych grach obowiązuje następujące prawo dotyczące zwycięskiej dystrybucji: 
...o takich zadaniach pewnie marzyłeś już od dawna :) Zdradzę Ci sekret - ja też. Zwłaszcza po tym, jak skończyłem pracować teoria pola.
Rozwiązanie: ponieważ zmienna losowa może przyjmować tylko jedną z trzech wartości, powstają odpowiednie zdarzenia pełna grupa, co oznacza, że suma ich prawdopodobieństw jest równa jedności: ![]()
Demaskowanie „partyzanta”: ![]()
– zatem prawdopodobieństwo wygrania jednostek konwencjonalnych wynosi 0,4.
Kontrola: tego właśnie musieliśmy się upewnić.
Odpowiedź:
Nierzadko zdarza się, że musisz samodzielnie sporządzić prawo dystrybucyjne. Do tego używają klasyczna definicja prawdopodobieństwa, twierdzenia o mnożeniu/dodawaniu dotyczące prawdopodobieństw zdarzeń i inne chipsy tervera:
Przykład 2
Pudełko zawiera 50 losów na loterię, spośród których 12 wygrywa, a 2 z nich wygrywają po 1000 rubli, a pozostałe po 100 rubli. Narysuj prawo rozkładu zmiennej losowej – wielkości wygranej, jeśli z pudełka zostanie wylosowany jeden los.
Rozwiązanie: jak zauważyłeś, zwykle umieszczane są wartości zmiennej losowej w kolejności rosnącej. Dlatego zaczynamy od najmniejszych wygranych, czyli rubli.
Takich biletów jest w sumie 50 – 12 = 38 i wg klasyczna definicja:
– prawdopodobieństwo, że losowo wylosowany los okaże się przegrany.
W innych przypadkach wszystko jest proste. Prawdopodobieństwo wygrania rubli wynosi:
Sprawdź: – i to jest szczególnie przyjemny moment takich zadań!
Odpowiedź: pożądane prawo podziału wygranych: ![]()
Poniższe zadanie należy rozwiązać samodzielnie:
Przykład 3
Prawdopodobieństwo, że strzelec trafi w cel wynosi . Narysuj prawo rozkładu zmiennej losowej – liczby trafień po 2 strzałach.
...Wiedziałem, że za nim tęskniliście :) Pamiętajmy Twierdzenia o mnożeniu i dodawaniu. Rozwiązanie i odpowiedź znajdują się na końcu lekcji.
Prawo dystrybucji całkowicie opisuje zmienną losową, ale w praktyce przydatna (a czasem bardziej przydatna) może być znajomość tylko jej części charakterystyki numeryczne .
Oczekiwanie dyskretnej zmiennej losowej
W prostych słowach tak jest średnia wartość oczekiwana gdy testowanie jest powtarzane wiele razy. Niech zmienna losowa przyjmuje wartości z prawdopodobieństwem ![]() odpowiednio. Wtedy matematyczne oczekiwanie tej zmiennej losowej jest równe suma produktów wszystkie jego wartości do odpowiednich prawdopodobieństw:
odpowiednio. Wtedy matematyczne oczekiwanie tej zmiennej losowej jest równe suma produktów wszystkie jego wartości do odpowiednich prawdopodobieństw:
lub upadł: ![]()
Obliczmy na przykład matematyczne oczekiwanie zmiennej losowej – liczby punktów wyrzuconych na kostce:
Przypomnijmy sobie teraz naszą hipotetyczną grę: 
Powstaje pytanie: czy w ogóle opłaca się grać w tę grę? ...kto ma jakieś wrażenia? Nie można więc tego powiedzieć „od ręki”! Ale na to pytanie można łatwo odpowiedzieć, obliczając oczekiwanie matematyczne, zasadniczo - Średnia ważona według prawdopodobieństwa wygranej:
Zatem matematyczne oczekiwanie na tę grę przegrywający.
Nie ufaj swoim wrażeniom – zaufaj liczbom!
Tak, tutaj można wygrać 10, a nawet 20-30 razy z rzędu, ale na dłuższą metę czeka nas nieunikniona ruina. I nie radzę Ci grać w takie gry :) No, może tylko dla zabawy.
Z powyższego wynika, że oczekiwanie matematyczne nie jest już wartością LOSOWĄ.
Zadanie twórcze do niezależnych badań:
Przykład 4
Pan X gra w ruletkę europejską według następującego systemu: stale stawia 100 rubli na „czerwone”. Narysuj prawo rozkładu zmiennej losowej – jej wygranej. Oblicz matematyczne oczekiwanie wygranej i zaokrąglij je do najbliższej kopiejki. Ile przeciętny Czy gracz przegrywa za każdą postawioną setkę?
Odniesienie : Ruletka europejska zawiera 18 czerwonych, 18 czarnych i 1 zielony sektor („zero”). Jeśli pojawi się „czerwony”, gracz otrzymuje podwójną stawkę, w przeciwnym razie trafia ona do dochodu kasyna
Istnieje wiele innych systemów ruletki, dla których możesz tworzyć własne tabele prawdopodobieństwa. Ale tak jest w przypadku, gdy nie potrzebujemy żadnych praw i tabel rozkładu, ponieważ ustalono z całą pewnością, że matematyczne oczekiwania gracza będą dokładnie takie same. Jedyną rzeczą, która zmienia się z systemu na system, jest
Pojęcie oczekiwań matematycznych można rozważyć na przykładzie rzutu kostką. Przy każdym rzucie rejestrowane są utracone punkty. Aby je wyrazić, stosuje się wartości naturalne z zakresu 1 – 6.
Po określonej liczbie rzutów, korzystając z prostych obliczeń, można znaleźć średnią arytmetyczną zdobytych punktów.
Podobnie jak wystąpienie dowolnej wartości z zakresu, tak i ta wartość będzie losowa.
A co jeśli kilkukrotnie zwiększysz liczbę rzutów? Przy dużej liczbie rzutów średnia arytmetyczna punktów będzie zbliżać się do określonej liczby, co w teorii prawdopodobieństwa nazywa się oczekiwaniem matematycznym.
Zatem przez oczekiwanie matematyczne rozumiemy średnią wartość zmiennej losowej. Wskaźnik ten można również przedstawić jako sumę ważoną wartości prawdopodobnych.
Pojęcie to ma kilka synonimów:
- Średnia wartość;
- Średnia wartość;
- wskaźnik tendencji centralnej;
- pierwsza chwila.
Inaczej mówiąc, jest to nic innego jak liczba, wokół której rozłożone są wartości zmiennej losowej.
W różnych sferach ludzkiej działalności podejścia do zrozumienia oczekiwań matematycznych będą nieco inne.
Można to uznać za:
- średnia korzyść uzyskana z podjęcia decyzji, gdy taką decyzję rozważa się z punktu widzenia teorii wielkich liczb;
- możliwa wysokość wygranej lub przegranej (teoria hazardu), obliczona średnio dla każdego zakładu. W slangu brzmią jak „przewaga gracza” (pozytywna dla gracza) lub „przewaga kasyna” (negatywna dla gracza);
- procent zysku uzyskanego z wygranych.
Oczekiwanie nie jest obowiązkowe dla absolutnie wszystkich zmiennych losowych. Jest nieobecny dla tych, którzy mają rozbieżność w odpowiedniej sumie lub całce.
Właściwości oczekiwań matematycznych
Jak każdy parametr statystyczny, oczekiwanie matematyczne ma następujące właściwości:

Podstawowe wzory na oczekiwania matematyczne
Obliczenia oczekiwania matematycznego można dokonać zarówno dla zmiennych losowych charakteryzujących się zarówno ciągłością (wzór A), jak i dyskretnością (wzór B):
- M(X)=∑i=1nxi⋅pi, gdzie xi to wartości zmiennej losowej, pi to prawdopodobieństwa:
- M(X)=∫+∞−∞f(x)⋅xdx, gdzie f(x) to podana gęstość prawdopodobieństwa.
Przykłady obliczania oczekiwań matematycznych
Przykład A.
Czy można poznać średni wzrost krasnoludków w bajce o Królewnie Śnieżce? Wiadomo, że każdy z 7 krasnoludków miał określony wzrost: 1,25; 0,98; 1,05; 0,71; 0,56; 0,95 i 0,81 m.
Algorytm obliczeń jest dość prosty:
- znajdujemy sumę wszystkich wartości wskaźnika wzrostu (zmienna losowa):
1,25+0,98+1,05+0,71+0,56+0,95+ 0,81 = 6,31; - Otrzymaną kwotę podziel przez liczbę krasnali:
6,31:7=0,90.
Zatem średni wzrost krasnali w bajce wynosi 90 cm, innymi słowy, jest to matematyczne oczekiwanie wzrostu krasnali.
Wzór roboczy - M(x)=4 0,2+6 0,3+10 0,5=6
Praktyczna realizacja oczekiwań matematycznych
Obliczanie statystycznego wskaźnika oczekiwań matematycznych stosuje się w różnych obszarach działalności praktycznej. Przede wszystkim mówimy o sferze komercyjnej. Przecież wprowadzenie tego wskaźnika przez Huygensa wiąże się z określeniem szans, które mogą być korzystne lub przeciwnie, niekorzystne dla jakiegoś zdarzenia.
 Parametr ten jest szeroko stosowany do oceny ryzyka, szczególnie w przypadku inwestycji finansowych.
Parametr ten jest szeroko stosowany do oceny ryzyka, szczególnie w przypadku inwestycji finansowych.
Zatem w biznesie kalkulacja oczekiwań matematycznych służy jako metoda oceny ryzyka przy obliczaniu cen.
Wskaźnik ten można również wykorzystać do obliczenia skuteczności niektórych działań, na przykład ochrony pracy. Dzięki niemu możesz obliczyć prawdopodobieństwo wystąpienia zdarzenia.
Kolejnym obszarem zastosowania tego parametru jest zarządzanie. Można go również obliczyć podczas kontroli jakości produktu. Na przykład za pomocą maty. oczekiwań, możesz obliczyć możliwą liczbę wyprodukowanych wadliwych części.
Oczekiwanie matematyczne okazuje się również niezbędne przy przeprowadzaniu statystycznego przetwarzania wyników uzyskanych w trakcie badań naukowych. Pozwala obliczyć prawdopodobieństwo pożądanego lub niepożądanego wyniku eksperymentu lub badania w zależności od poziomu osiągnięcia celu. W końcu jego osiągnięcie może wiązać się z zyskiem i korzyścią, a jego niepowodzenie może wiązać się ze stratą lub stratą.
Korzystanie z oczekiwań matematycznych na rynku Forex
Praktyczne zastosowanie tego parametru statystycznego jest możliwe przy prowadzeniu operacji na rynku walutowym. Za jego pomocą możesz analizować powodzenie transakcji handlowych. Co więcej, wzrost wartości oczekiwań wskazuje na wzrost ich sukcesu.
Należy również pamiętać, że oczekiwań matematycznych nie należy uważać za jedyny parametr statystyczny używany do analizy wyników tradera. Zastosowanie kilku parametrów statystycznych wraz z wartością średnią znacznie zwiększa dokładność analizy.
Parametr ten sprawdził się dobrze w obserwacjach monitorowania kont handlowych. Dzięki niemu przeprowadzana jest szybka ocena prac prowadzonych na rachunku lokaty. W przypadkach, gdy działalność tradera przebiega pomyślnie i unika on strat, nie zaleca się stosowania wyłącznie obliczeń oczekiwań matematycznych. W takich przypadkach ryzyko nie jest brane pod uwagę, co zmniejsza skuteczność analizy.
Przeprowadzone badania taktyki traderów wskazują, że:
- Najskuteczniejsze taktyki to te oparte na losowym wejściu;
- Najmniej skuteczne są taktyki oparte na danych wejściowych.
W osiąganiu pozytywnych wyników nie mniej ważne są:
- taktyki zarządzania pieniędzmi;
- strategie wyjścia.
Używając takiego wskaźnika jak oczekiwanie matematyczne, możesz przewidzieć, jaki będzie zysk lub strata, inwestując 1 dolara. Wiadomo, że wskaźnik ten, liczony dla wszystkich gier uprawianych w kasynie, przemawia na korzyść establishmentu. To właśnie pozwala zarabiać pieniądze. W przypadku długich serii gier prawdopodobieństwo, że klient straci pieniądze, znacznie wzrasta.
Gry rozgrywane przez profesjonalnych graczy ograniczają się do krótkich okresów czasu, co zwiększa prawdopodobieństwo wygranej i zmniejsza ryzyko przegranej. Tę samą prawidłowość można zaobserwować przy prowadzeniu działalności inwestycyjnej.
Inwestor może zarobić znaczną kwotę, mając pozytywne oczekiwania i dokonując dużej liczby transakcji w krótkim czasie.
Oczekiwanie można traktować jako różnicę między procentem zysku (PW) pomnożonym przez średni zysk (AW) a prawdopodobieństwem straty (PL) pomnożonym przez średnią stratę (AL).
Jako przykład możemy rozważyć: pozycja – 12,5 tys. dolarów, portfel – 100 tys. dolarów, ryzyko depozytu – 1%. Rentowność transakcji wynosi 40% przypadków przy średnim zysku 20%. W przypadku straty średnia strata wynosi 5%. Obliczenie matematycznego oczekiwania dla transakcji daje wartość 625 dolarów.
Kolejną najważniejszą właściwością zmiennej losowej po oczekiwaniu matematycznym jest jej rozproszenie, definiowane jako średniokwadratowe odchylenie od średniej:
Jeśli zostanie to zaznaczone, wariancja VX będzie wartością oczekiwaną. Jest to cecha „rozrzutu” rozkładu X.
Jako prosty przykład obliczenia wariancji załóżmy, że właśnie otrzymaliśmy ofertę nie do odrzucenia: ktoś dał nam dwa certyfikaty na tę samą loterię. Organizatorzy loterii sprzedają co tydzień 100 losów, biorąc udział w osobnym losowaniu. Losowanie wybiera jeden z tych losów w jednolitym procesie losowym – każdy los ma taką samą szansę na wybranie, a właściciel tego szczęśliwego losu otrzymuje sto milionów dolarów. Pozostałych 99 posiadaczy losów na loterię nie wygrywa nic.
Prezent możemy wykorzystać na dwa sposoby: kupić albo dwa losy w jednej loterii, albo po jednym, aby wziąć udział w dwóch różnych loteriach. Która strategia jest lepsza? Spróbujmy to przeanalizować. W tym celu oznaczmy przez zmienne losowe wielkość naszej wygranej na pierwszym i drugim losie. Oczekiwana wartość w milionach wynosi
i to samo dotyczy wartości oczekiwanych, które się sumują, więc nasza średnia całkowita wypłata będzie wynosić
niezależnie od przyjętej strategii.
Jednak obie strategie wydają się różne. Wyjdźmy poza wartości oczekiwane i przestudiujmy pełny rozkład prawdopodobieństwa

Jeśli kupimy dwa losy w jednej loterii, to nasze szanse na wygranie niczego wyniosą 98% i 2% - szanse na wygranie 100 milionów. Jeśli kupimy losy na różne losowania, liczby będą przedstawiały się następująco: 98,01% - szansa, że nic nie wygramy, czyli nieco większa niż dotychczas; 0,01% - szansa na wygranie 200 milionów, także nieco więcej niż dotychczas; a szansa na wygranie 100 milionów wynosi obecnie 1,98%. Zatem w drugim przypadku rozkład wielkości jest nieco bardziej rozproszony; środkowa wartość, 100 milionów dolarów, jest nieco mniej prawdopodobna, podczas gdy wartości skrajne są bardziej prawdopodobne.
Rozproszenie ma odzwierciedlać właśnie tę koncepcję rozproszenia zmiennej losowej. Mierzymy rozrzut poprzez kwadrat odchylenia zmiennej losowej od jej oczekiwań matematycznych. Zatem w przypadku 1 wariancja będzie
w przypadku 2 wariancja wynosi
Jak się spodziewaliśmy, ta druga wartość jest nieco większa, gdyż rozkład w przypadku 2 jest nieco bardziej rozłożony.
Kiedy pracujemy z wariancjami, wszystko jest podnoszone do kwadratu, więc wynikiem mogą być całkiem duże liczby. (Mnożnik wynosi jeden bilion, to powinno robić wrażenie
nawet gracze przyzwyczajeni do dużych zakładów.) Aby przeliczyć wartości na bardziej znaczącą pierwotną skalę, często bierze się pierwiastek kwadratowy z wariancji. Wynikowa liczba nazywana jest odchyleniem standardowym i jest zwykle oznaczana grecką literą a:
Standardowe odchylenia wielkości dla naszych dwóch strategii loteryjnych wynoszą . Pod pewnymi względami druga opcja jest o około 71 247 dolarów bardziej ryzykowna.
Jak wariancja pomaga w wyborze strategii? To nie jest jasne. Strategia o większej wariancji jest bardziej ryzykowna; ale co jest lepsze dla naszego portfela – ryzyko czy bezpieczna gra? Dajmy sobie szansę na zakup nie dwóch biletów, ale wszystkich na sto. Wtedy moglibyśmy zagwarantować wygraną w jednej loterii (a wariancja wynosiłaby zero); albo możesz zagrać w stu różnych losowaniach, nie otrzymując nic z prawdopodobieństwem, ale mając niezerową szansę na wygranie aż do dolarów. Wybór jednej z tych alternatyw wykracza poza zakres tej książki; jedyne, co możemy tutaj zrobić, to wyjaśnić, jak wykonać obliczenia.
W rzeczywistości istnieje prostszy sposób obliczenia wariancji niż bezpośrednie użycie definicji (8.13). (Istnieją wszelkie powody, aby podejrzewać, że kryje się tu jakaś ukryta matematyka; w przeciwnym razie dlaczego wariancja w przykładach loterii okazałaby się całkowitą wielokrotnością? Mamy
ponieważ - stała; stąd,
„Wariancja to średnia kwadratu minus kwadrat średniej”.
Np. w zadaniu loteryjnym okazuje się, że średnia wynosi czyli Odejmowanie (kwadrat średniej) daje wyniki, które uzyskaliśmy już wcześniej w trudniejszy sposób.
Istnieje jednak jeszcze prostszy wzór, który można zastosować, gdy obliczamy dla niezależnych X i Y. Mamy

ponieważ, jak wiemy, dla niezależnych zmiennych losowych Zatem

„Wariancja sumy niezależnych zmiennych losowych jest równa sumie ich wariancji.” Zatem na przykład wariancja kwoty, którą można wygrać na jednym losie na loterię, jest równa
Dlatego rozrzut całkowitych wygranych dla dwóch losów na loterię w dwóch różnych (niezależnych) loteriach będzie wynosić. Odpowiednia wartość rozrzutu dla niezależnych losów na loterię będzie wynosić
Wariancję sumy punktów wyrzuconych na dwóch kostkach można obliczyć za pomocą tego samego wzoru, ponieważ jest to suma dwóch niezależnych zmiennych losowych. Mamy
dla właściwej kostki; zatem w przypadku przesuniętego środka masy
dlatego też, jeśli obie kostki mają przesunięty środek masy. Należy zwrócić uwagę, że w tym drugim przypadku wariancja jest większa, choć częściej niż w przypadku zwykłej kostki przyjmuje wartość średnią 7. Jeśli naszym celem jest wyrzucenie większej liczby szczęśliwych siódemek, wariancja nie jest najlepszym wskaźnikiem sukcesu.
OK, ustaliliśmy, jak obliczyć wariancję. Ale nie daliśmy jeszcze odpowiedzi na pytanie, dlaczego konieczne jest obliczanie wariancji. Każdy to robi, ale dlaczego? Głównym powodem jest nierówność Czebyszewa, która ustanawia ważną właściwość dyspersji:
(Nierówność ta różni się od nierówności Czebyszewa dla sum, które napotkaliśmy w Rozdziale 2.) Na poziomie jakościowym (8.17) stwierdza, że zmienna losowa X rzadko przyjmuje wartości odległe od swojej średniej, jeśli jej wariancja VX jest mała. Dowód
zarządzanie jest niezwykle proste. Naprawdę,

dzielenie przez kończy dowód.
Jeśli oznaczymy oczekiwanie matematyczne przez a i odchylenie standardowe przez a i zastąpimy w (8.17) wtedy warunek zmieni się w zatem, otrzymamy z (8.17)
Zatem X będzie mieścić się w -krotnym odchyleniu standardowym od swojej średniej, z wyjątkiem przypadków, w których prawdopodobieństwo nie przekracza. Zmienna losowa będzie mieścić się w granicach 2a co najmniej 75% prób; od do - przynajmniej na 99%. Są to przypadki nierówności Czebyszewa.
Jeśli rzucisz raz kilkoma kostkami, całkowita suma punktów we wszystkich rzutach będzie prawie zawsze bliska. Powód tego jest następujący: wariancja niezależnych rzutów będzie wynosić. Wariancja oznacza odchylenie standardowe wszystkiego.
Zatem z nierówności Czebyszewa dowiadujemy się, że suma punktów będzie znajdować się pomiędzy
przynajmniej w 99% wszystkich rzutów poprawnymi kostkami. Na przykład wynik miliona rzutów z prawdopodobieństwem większym niż 99% będzie wynosić od 6,976 miliona do 7,024 miliona.
Ogólnie rzecz biorąc, niech X będzie dowolną zmienną losową w przestrzeni prawdopodobieństwa Π mającą skończone oczekiwanie matematyczne i skończone odchylenie standardowe a. Następnie możemy wprowadzić pod uwagę przestrzeń prawdopodobieństwa Pn, której zdarzenia elementarne są -ciągami, w których każdy , a prawdopodobieństwo definiuje się jako
Jeśli teraz zdefiniujemy zmienne losowe za pomocą wzoru
następnie wartość
będzie sumą niezależnych zmiennych losowych, co odpowiada procesowi sumowania niezależnych realizacji wartości X na P. Oczekiwanie matematyczne będzie równe, a odchylenie standardowe - ; dlatego też średnia wartość realizacji,
![]()
będzie się wahać od do przez co najmniej 99% okresu. Innymi słowy, jeśli wybierzesz wystarczająco duży, średnia arytmetyczna niezależnych testów będzie prawie zawsze bardzo bliska wartości oczekiwanej (w podręcznikach teorii prawdopodobieństwa udowadnia się jeszcze silniejsze twierdzenie, zwane mocnym prawem wielkich liczb; ale dla nas prosty wniosek nierówności Czebyszewa, który właśnie usunęliśmy.)
Czasami nie znamy charakterystyki przestrzeni prawdopodobieństwa, ale musimy oszacować matematyczne oczekiwanie zmiennej losowej X na podstawie powtarzanych obserwacji jej wartości. (Na przykład możemy chcieć średniej temperatury styczniowego południa w San Francisco lub możemy chcieć znać oczekiwaną długość życia, na której agenci ubezpieczeniowi powinni opierać swoje obliczenia.) Jeśli mamy do dyspozycji niezależne obserwacje empiryczne, możemy założyć, że prawdziwe oczekiwanie matematyczne jest w przybliżeniu równe
![]()
Możesz także oszacować wariancję za pomocą wzoru
Patrząc na tę formułę, można by pomyśleć, że zawiera ona błąd typograficzny; Wydawałoby się, że powinno być tak jak w (8.19), gdyż rzeczywistą wartość dyspersji wyznacza się w (8.15) poprzez wartości oczekiwane. Jednak zastąpienie tutaj przez pozwala nam uzyskać lepsze oszacowanie, gdyż z definicji (8.20) wynika, że
![]()
Oto dowód:

(W tych obliczeniach polegamy na niezależności obserwacji, gdy zastępujemy przez )
W praktyce, aby ocenić wyniki eksperymentu ze zmienną losową X, zwykle oblicza się średnią empiryczną i empiryczne odchylenie standardowe, a następnie zapisuje odpowiedź w postaci Tutaj są na przykład wyniki rzutu parą kostek, prawdopodobnie poprawne.