Construire un graphique des exemples de fonctions de la solution. Recherche de fonction en ligne

16.10.2019

Domaine

Afin d'explorer et de tracer une fonction, vous devez connaître quelques définitions. Une fonction est l'un des concepts de base (de base) en mathématiques. Il reflète la dépendance entre plusieurs variables (deux, trois ou plus) avec des changements. La fonction montre également la dépendance des ensembles.

Imaginez que nous ayons deux variables qui ont une certaine plage de changement. Ainsi, y est une fonction de x, à condition que chaque valeur de la seconde variable corresponde à une valeur de la seconde. Dans ce cas, la variable y est dépendante et s'appelle une fonction. Il est d'usage de dire que les variables x et y sont en Pour plus de clarté sur cette dépendance, un graphe de la fonction est construit. Qu'est-ce qu'un graphe de fonctions ? Il s'agit d'un ensemble de points sur le plan de coordonnées, où chaque valeur de x correspond à une valeur de y. Les graphiques peuvent être différents - une ligne droite, une hyperbole, une parabole, une sinusoïde, etc.

Un graphe de fonction ne peut pas être tracé sans exploration. Aujourd'hui, nous allons apprendre à effectuer des recherches et à tracer un graphique de fonction. Il est très important de prendre des notes pendant l'étude. Il sera donc beaucoup plus facile de faire face à la tâche. Le plan d'études le plus pratique:

Domaine.
Continuité.
Pair ou impair.
Périodicité.
Asymptotes.
Zéros.
Constance.
Ascendant et descendant.
Extrêmes.
Convexité et concavité.

Commençons par le premier point. Trouvons le domaine de définition, c'est-à-dire sur quels intervalles notre fonction existe: y \u003d 1/3 (x ^ 3-14x ^ 2 + 49x-36). Dans notre cas, la fonction existe pour toutes les valeurs de x, c'est-à-dire que le domaine de définition est R. Cela peut s'écrire xОR.

Continuité

Nous allons maintenant explorer la fonction de discontinuité. En mathématiques, le terme "continuité" est apparu à la suite de l'étude des lois du mouvement. Qu'est-ce que l'infini ? L'espace, le temps, certaines dépendances (un exemple est la dépendance des variables S et t dans les problèmes de mouvement), la température de l'objet chauffé (eau, poêle à frire, thermomètre, etc.), une ligne continue (c'est-à-dire une que l'on peut dessiner sans l'enlever de la feuille de crayon).

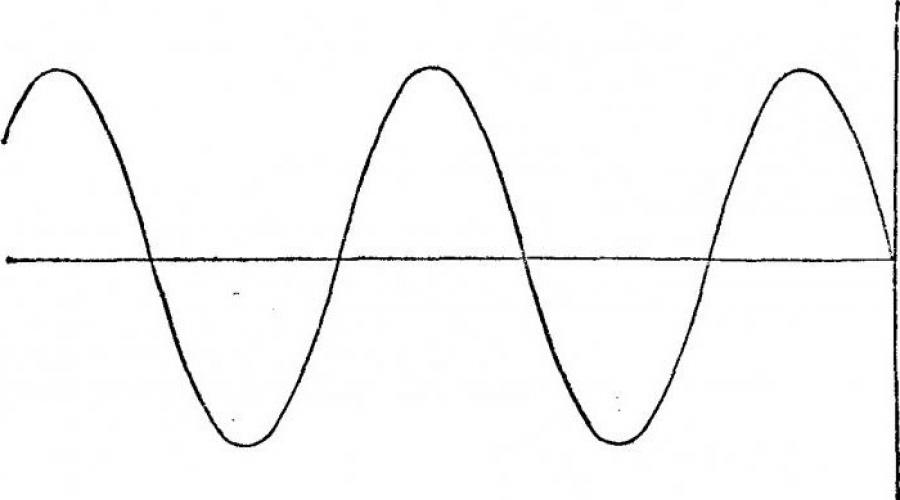
Un graphique est considéré comme continu s'il ne se brise pas à un moment donné. Un des plus bons exemples un tel graphique est une onde sinusoïdale, que vous pouvez voir dans l'image de cette section. La fonction est continue à un certain point x0 si un certain nombre de conditions sont remplies :

une fonction est définie en un point donné ;
les limites droite et gauche en un point sont égales ;
la limite est égale à la valeur de la fonction au point x0.

Si au moins une condition n'est pas remplie, la fonction est dite cassante. Et les points auxquels la fonction s'arrête sont appelés points d'arrêt. Un exemple de fonction qui "cassera" lorsqu'elle sera affichée graphiquement est : y=(x+4)/(x-3). De plus, y n'existe pas au point x = 3 (puisqu'il est impossible de diviser par zéro).

Dans la fonction que nous étudions (y \u003d 1/3 (x ^ 3-14x ^ 2 + 49x-36)), tout s'est avéré simple, puisque le graphique sera continu.

Même bizarre

Examinons maintenant la fonction de parité. Commençons par un peu de théorie. Une fonction paire est une fonction qui satisfait la condition f (-x) = f (x) pour toute valeur de la variable x (de la plage de valeurs). Les exemples sont :

module x (le graphique ressemble à un choucas, la bissectrice des premier et deuxième quarts du graphique) ;
x au carré (parabole);
cosinus x (onde cosinus).

Notez que tous ces graphiques sont symétriques lorsqu'ils sont visualisés par rapport à l'axe des ordonnées.

Qu'appelle-t-on alors une fonction impaire ? Ce sont les fonctions qui satisfont à la condition: f (-x) \u003d - f (x) pour toute valeur de la variable x. Exemples:

hyperbole;
parabole cubique ;
sinusoïde ;
tangente et ainsi de suite.

Veuillez noter que ces fonctions sont symétriques par rapport au point (0:0), c'est-à-dire l'origine. Sur la base de ce qui a été dit dans cette section de l'article, le même et fonction impaire doit avoir la propriété : x appartient à l'ensemble de définition et -x aussi.

Examinons la fonction de parité. Nous pouvons voir qu'elle ne correspond à aucune des descriptions. Par conséquent, notre fonction n'est ni paire ni impaire.

Asymptotes

Commençons par une définition. Une asymptote est une courbe aussi proche que possible du graphique, c'est-à-dire que la distance d'un point tend vers zéro. Il existe trois types d'asymptotes :

vertical, c'est-à-dire parallèle à l'axe y ;
horizontale, c'est-à-dire parallèle à l'axe des x ;
oblique.

Comme pour le premier type, ces lignes doivent être recherchées à certains endroits :

écart;
extrémités du domaine.

Dans notre cas, la fonction est continue et le domaine de définition est R. Par conséquent, il n'y a pas d'asymptotes verticales.

L'asymptote horizontale est dans le graphique de la fonction, ce qui correspond à prochaine exigence: si x tend vers l'infini ou moins l'infini, et que la limite est égale à un certain nombre (par exemple, a). À ce cas y=a est l'asymptote horizontale. Il n'y a pas d'asymptotes horizontales dans la fonction que nous étudions.

Une asymptote oblique n'existe que si deux conditions sont remplies :

lim(f(x))/x=k ;
lim f(x)-kx=b.

On peut alors le trouver par la formule : y=kx+b. Encore une fois, dans notre cas, il n'y a pas d'asymptotes obliques.

Fonction zéros

L'étape suivante consiste à examiner le graphique de la fonction pour les zéros. Il est également très important de noter que la tâche associée à la recherche des zéros d'une fonction se produit non seulement dans l'étude et le tracé d'un graphique de fonction, mais également en tant que tâche indépendante et en tant que moyen de résoudre les inégalités. Vous devrez peut-être trouver les zéros d'une fonction sur un graphique ou utiliser la notation mathématique.

Trouver ces valeurs vous aidera à tracer la fonction avec plus de précision. Si parler langage clair, alors le zéro de la fonction est la valeur de la variable x, à laquelle y=0. Si vous recherchez les zéros d'une fonction sur un graphique, vous devez faire attention aux points d'intersection du graphique avec l'axe des x.

Pour trouver les zéros de la fonction, vous devez résoudre l'équation suivante : y=1/3(x^3-14x^2+49x-36)=0. Après avoir fait les calculs nécessaires, nous obtenons la réponse suivante :

signe constance

L'étape suivante dans l'étude et la construction d'une fonction (graphique) consiste à trouver des intervalles de constance de signe. Cela signifie que nous devons déterminer sur quels intervalles la fonction prend une valeur positive, et sur quels intervalles elle prend une valeur négative. Les zéros des fonctions trouvées dans la section précédente nous aideront à le faire. Donc, nous devons tracer une ligne droite (séparée du graphique) et dans dans le bon ordre distribuez les zéros de la fonction dessus du plus petit au plus grand. Vous devez maintenant déterminer lequel des intervalles résultants a un signe "+" et lequel a un "-".

Dans notre cas, la fonction prend une valeur positive sur les intervalles :

de 1 à 4 ;
de 9 à l'infini.

Sens négatif:

de moins l'infini à 1 ;
de 4 à 9.

C'est assez facile à déterminer. Remplacez n'importe quel nombre de l'intervalle dans la fonction et voyez le signe de la réponse (moins ou plus).

Fonction croissante et décroissante

Afin d'explorer et de construire une fonction, nous devons savoir où le graphique va augmenter (monter sur Oy) et où il va baisser (ramper le long de l'axe des ordonnées).

La fonction n'augmente que si la plus grande valeur de la variable x correspond à plus grande valeur y. Autrement dit, x2 est supérieur à x1 et f(x2) est supérieur à f(x1). Et on observe un phénomène complètement opposé dans une fonction décroissante (plus il y a de x, moins il y a). Pour déterminer les intervalles d'augmentation et de diminution, vous devez trouver les éléments suivants :

portée (nous l'avons déjà);
dérivée (dans notre cas : 1/3(3x^2-28x+49) ;
résoudre l'équation 1/3(3x^2-28x+49)=0.

Après calculs, on obtient le résultat :

On obtient : la fonction croît sur les intervalles de moins l'infini à 7/3 et de 7 à l'infini, et décroît sur l'intervalle de 7/3 à 7.

Extrêmes

La fonction étudiée y=1/3(x^3-14x^2+49x-36) est continue et existe pour toutes les valeurs de la variable x. Le point extrême indique le maximum et le minimum de cette fonction. Dans notre cas, il n'y en a pas, ce qui simplifie grandement la tâche de construction. Sinon, ils sont également trouvés en utilisant la fonction dérivée. Après avoir trouvé, n'oubliez pas de les marquer sur le tableau.

Convexité et concavité

Nous continuons à étudier la fonction y(x). Maintenant, nous devons vérifier la convexité et la concavité. Les définitions de ces concepts sont assez difficiles à percevoir, mieux vaut tout analyser avec des exemples. Pour le test : une fonction est convexe si c'est une fonction non décroissante. D'accord, c'est incompréhensible !

Il faut trouver la dérivée de la fonction du second ordre. On obtient : y=1/3(6x-28). Maintenant, assimilons le côté droit à zéro et résolvons l'équation. Réponse : x=14/3. Nous avons trouvé le point d'inflexion, c'est-à-dire l'endroit où le graphe passe de convexe à concave ou vice versa. Sur l'intervalle de moins l'infini à 14/3, la fonction est convexe, et de 14/3 à plus l'infini, elle est concave. Il est également très important de noter que le point d'inflexion sur le graphique doit être lisse et doux, non coins pointus ne doit pas être présent.

Définition des points supplémentaires

Notre tâche est d'explorer et de tracer le graphe de la fonction. Nous avons terminé l'étude, il ne sera pas difficile de tracer la fonction maintenant. Pour une reproduction plus précise et détaillée d'une courbe ou d'une droite sur le plan de coordonnées, vous pouvez trouver plusieurs points auxiliaires. C'est assez facile de les calculer. Par exemple, nous prenons x=3, résolvons l'équation résultante et trouvons y=4. Ou x=5 et y=-5 et ainsi de suite. Vous pouvez prendre autant de points supplémentaires que nécessaire pour construire. Au moins 3-5 d'entre eux sont trouvés.

Traçage

Nous devions étudier la fonction (x^3-14x^2+49x-36)*1/3=y. Toutes les marques nécessaires au cours des calculs ont été faites sur le plan de coordonnées. Il ne reste plus qu'à construire un graphe, c'est-à-dire relier tous les points entre eux. Relier les points est fluide et précis, c'est une question de compétence - un peu de pratique et votre emploi du temps sera parfait.

L'étude de la fonction s'effectue selon un schéma clair et demande à l'étudiant de de solides connaissances concepts mathématiques de base tels que domaine de définition et de valeurs, continuité d'une fonction, asymptote, points extrêmes, régularité, périodicité, etc. L'élève doit librement dériver des fonctions et résoudre des équations parfois très complexes.

Autrement dit, cette tâche vérifie une couche importante de connaissances, toute lacune dans laquelle deviendra un obstacle à l'obtention bonne décision. Surtout souvent, des difficultés surviennent avec la construction de graphiques de fonctions. Cette erreur attire immédiatement l'attention de l'enseignant et peut grandement ruiner votre note, même si tout le reste a été fait correctement. Ici vous pouvez trouver tâches pour l'étude de la fonction en ligne: études d'exemples, téléchargement de solutions, commandes de missions.

Étudier une fonction et un tracé : exemples et solutions en ligne

Nous avons préparé pour vous de nombreuses études de fonctionnalités prêtes à l'emploi, à la fois payantes dans le livre de solutions et gratuites dans la section Exemples de recherche de fonctionnalités. Sur la base de ces tâches résolues, vous pourrez vous familiariser en détail avec la méthodologie pour effectuer de telles tâches, par analogie, effectuer vos propres recherches.

Nous offrons exemples prêts à l'emploi étude complète et tracer des fonctions des types les plus courants : polynômes, fraction-rationnel, irrationnel, exponentiel, logarithmique, fonctions trigonométriques. Chaque problème résolu est accompagné d'un graphique prêt à l'emploi avec des points clés sélectionnés, des asymptotes, des maxima et des minima, la solution est effectuée selon l'algorithme d'étude de la fonction.

Des exemples résolus, dans tous les cas, deviendront pour vous bonne aide, car ils couvrent les types de fonctions les plus populaires. Nous vous proposons des centaines de problèmes déjà résolus, mais, comme vous le savez, il existe un nombre infini de fonctions mathématiques dans le monde, et les enseignants sont de grands experts pour inventer des tâches de plus en plus complexes pour les élèves pauvres. Alors chers élèves, aide qualifiée ne vous dérangera pas.

Résolution de problèmes pour l'étude d'une fonction à la commande

Dans ce cas, nos partenaires vous proposeront un autre service - étude complète des fonctions en ligne commander. La tâche sera accomplie pour vous dans le respect de toutes les exigences de l'algorithme de résolution de tels problèmes, ce qui plaira grandement à votre professeur.

Nous ferons pour vous une étude complète de la fonction : nous trouverons le domaine de définition et la plage de valeurs, nous examinerons la continuité et la discontinuité, nous établirons la parité, nous vérifierons la périodicité de votre fonction, trouver des points intersections avec axes de coordonnées. Et, bien sûr, plus loin avec l'aide calculs différentiels: on va trouver des asymptotes, calculer des extrema, des points d'inflexion, construire le graphe lui-même.

Si dans la tâche il est nécessaire de réaliser une étude complète de la fonction f (x) \u003d x 2 4 x 2 - 1 avec la construction de son graphique, nous examinerons ce principe en détail.

Résoudre le problème de ce type les propriétés et les graphiques des fonctions élémentaires de base doivent être utilisés. L'algorithme de recherche comprend les étapes suivantes :

Yandex.RTB R-A-339285-1

Trouver le domaine de définition

Puisque la recherche s'effectue sur le domaine de la fonction, il faut commencer par cette étape.

Exemple 1

L'exemple donné consiste à trouver les zéros du dénominateur afin de les exclure de la DPV.

4 x 2 - 1 = 0 x = ± 1 2 ⇒ x ∈ - ∞ ; - 1 2 ∪ - 1 2 ; 1 2 ∪ 1 2 ; +∞

En conséquence, vous pouvez obtenir des racines, des logarithmes, etc. Alors on peut chercher dans l'ODZ la racine d'un degré pair de type g (x) 4 par l'inégalité g (x) ≥ 0 , le logarithme log a g (x) par l'inégalité g (x) > 0 .

Enquête sur les limites de l'ODZ et recherche d'asymptotes verticales

Il existe des asymptotes verticales sur les frontières de la fonction, lorsque les limites unilatérales en ces points sont infinies.

Exemple 2

Par exemple, considérons les points frontières égaux à x = ± 1 2 .

Ensuite, il est nécessaire d'étudier la fonction pour trouver la limite unilatérale. Alors on obtient que : lim x → - 1 2 - 0 f (x) = lim x → - 1 2 - 0 x 2 4 x 2 - 1 = = lim x → - 1 2 - 0 x 2 (2 x - 1 ) (2 x + 1) = 1 4 (- 2) - 0 = + ∞ lim x → - 1 2 + 0 f (x) = lim x → - 1 2 + 0 x 2 4 x - 1 = = lim x → - 1 2 + 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 2) (+ 0) = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 0) 2 = - ∞ lim x → 1 2 - 0 f (x) = lim X → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 ( + 0) 2 = + ∞

Cela montre que les limites unilatérales sont infinies, ce qui signifie que les droites x = ± 1 2 sont les asymptotes verticales du graphe.

Enquête sur la fonction et pour pair ou impair

Lorsque la condition y (- x) = y (x) est remplie, la fonction est considérée comme paire. Ceci suggère que le graphe est situé symétriquement par rapport à O y. Lorsque la condition y (- x) = - y (x) est remplie, la fonction est considérée comme impaire. Cela signifie que la symétrie va par rapport à l'origine des coordonnées. Si au moins une inégalité échoue, on obtient la fonction vue générale.

Le respect de l'égalité y (- x) = y (x) indique que la fonction est paire. Lors de la construction, il faut tenir compte du fait qu'il y aura symétrie par rapport à O y.

Pour résoudre l'inégalité, des intervalles d'augmentation et de diminution sont utilisés avec les conditions f "(x) ≥ 0 et f" (x) ≤ 0, respectivement.

Définition 1

Points fixes sont des points qui ramènent la dérivée à zéro.

Points critiques sont des points intérieurs du domaine où la dérivée de la fonction est égale à zéro ou n'existe pas.

Lors de la prise de décision, les points suivants doivent être pris en compte :

pour les intervalles existants d'augmentation et de diminution de l'inégalité de la forme f "(x) > 0, les points critiques ne sont pas inclus dans la solution ;
les points auxquels la fonction est définie sans dérivée finie doivent être inclus dans les intervalles d'augmentation et de diminution (par exemple, y \u003d x 3, où le point x \u003d 0 définit la fonction, la dérivée a la valeur de l'infini à ce stade, y " \u003d 1 3 x 2 3 , y " (0) = 1 0 = ∞ , x = 0 est inclus dans l'intervalle d'augmentation);
Afin d'éviter les désaccords, il est recommandé d'utiliser la littérature mathématique, ce qui est recommandé par le ministère de l'Éducation.

L'inclusion de points critiques dans les intervalles d'augmentation et de diminution dans le cas où ils satisfont le domaine de la fonction.

Définition 2

Pour déterminant les intervalles de croissance et de diminution de la fonction, il faut trouver:

dérivé;
points critiques;
diviser le domaine de définition à l'aide de points critiques en intervalles;
déterminer le signe de la dérivée à chacun des intervalles, où + est une augmentation et - est une diminution.

Exemple 3

Trouver la dérivée sur le domaine f "(x) = x 2" (4 x 2 - 1) - x 2 4 x 2 - 1 "(4 x 2 - 1) 2 = - 2 x (4 x 2 - 1) 2 .

Décision

Pour résoudre il vous faut :

trouver des points stationnaires, cet exemple a x = 0 ;
trouver les zéros du dénominateur, l'exemple prend la valeur zéro à x = ± 1 2 .

Nous exposons des points sur l'axe numérique pour déterminer la dérivée sur chaque intervalle. Pour ce faire, il suffit de prendre n'importe quel point de l'intervalle et d'effectuer le calcul. Si le résultat est positif, nous dessinons + sur le graphique, ce qui signifie une augmentation de la fonction, et - signifie sa diminution.

Par exemple, f "(- 1) \u003d - 2 (- 1) 4 - 1 2 - 1 2 \u003d 2 9\u003e 0, ce qui signifie que le premier intervalle à gauche a un signe +. Considérez sur le nombre doubler.

Répondre:

il y a augmentation de la fonction sur l'intervalle - ∞ ; - 1 2 et (- 1 2 ; 0 ] ;
il y a une diminution sur l'intervalle [ 0 ; 1 2) et 1 2 ; +∞ .

Dans le diagramme, en utilisant + et -, la positivité et la négativité de la fonction sont représentées, et les flèches indiquent une diminution et une augmentation.

Les points extrêmes d'une fonction sont les points où la fonction est définie et par lesquels la dérivée change de signe.

Exemple 4

Si nous considérons un exemple où x \u003d 0, alors la valeur de la fonction qu'il contient est f (0) \u003d 0 2 4 0 2 - 1 \u003d 0. Lorsque le signe de la dérivée passe de + à - et passe par le point x \u003d 0, le point de coordonnées (0; 0) est considéré comme le point maximum. Lorsque le signe passe de - à +, nous obtenons le point minimum.

La convexité et la concavité sont déterminées en résolvant des inégalités de la forme f "" (x) ≥ 0 et f "" (x) ≤ 0 . Moins souvent, ils utilisent le nom renflement vers le bas au lieu de concavité et renflement vers le haut au lieu de renflement.

Définition 3

Pour déterminer les écarts de concavité et de convexité nécessaire:

trouver la dérivée seconde ;
trouver les zéros de la fonction de la dérivée seconde ;
briser le domaine de définition par les points qui apparaissent en intervalles ;
déterminer le signe de l'écart.

Exemple 5

Trouvez la dérivée seconde du domaine de définition.

Décision

f "" (x) = - 2 x (4 x 2 - 1) 2 " = = (- 2 x) " (4 x 2 - 1) 2 - - 2 x 4 x 2 - 1 2 " (4 x 2 - 1) 4 = 24 x 2 + 2 (4 x 2 - 1) 3

Nous trouvons les zéros du numérateur et du dénominateur, où, en utilisant notre exemple, nous avons que les zéros du dénominateur x = ± 1 2

Vous devez maintenant placer des points sur la droite numérique et déterminer le signe de la dérivée seconde de chaque intervalle. On comprend ça

Répondre:

la fonction est convexe de l'intervalle - 1 2 ; 12 ;
la fonction est concave à partir des intervalles - ∞ ; - 1 2 et 1 2 ; +∞ .

Définition 4

point d'inflexion est un point de la forme x 0 ; f(x0) . Lorsqu'elle a une tangente au graphe de la fonction, puis lorsqu'elle passe par x 0, la fonction change de signe en l'opposé.

En d'autres termes, il s'agit d'un tel point par lequel la dérivée seconde passe et change de signe, et aux points eux-mêmes est égal à zéro ou n'existe pas. Tous les points sont considérés comme le domaine de la fonction.

Dans l'exemple, on a vu qu'il n'y a pas de points d'inflexion, puisque la dérivée seconde change de signe en passant par les points x = ± 1 2 . Ceux-ci, à leur tour, ne sont pas inclus dans le domaine de la définition.

Recherche d'asymptotes horizontales et obliques

Lors de la définition d'une fonction à l'infini, il faut rechercher les asymptotes horizontales et obliques.

Définition 5

Asymptotes obliques représenté par des lignes droites donné par l'équation y = k X + b , où k = lim X → ∞ F (x) X et b = lim X → ∞ F (x) - k X .

Pour k = 0 et b non égal à l'infini, on trouve que l'asymptote oblique devient horizontal.

En d'autres termes, les asymptotes sont les droites que le graphe de la fonction approche à l'infini. Ceci contribue à la construction rapide du graphe de la fonction.

S'il n'y a pas d'asymptotes, mais que la fonction est définie aux deux infinis, il est nécessaire de calculer la limite de la fonction à ces infinis pour comprendre comment se comportera le graphe de la fonction.

Exemple 6

A titre d'exemple, considérons que

k = lim X → ∞ F (x) X = lim X → ∞ X 2 4 X 2 - 1 X = 0 b = lim X → ∞ (f (x) - k X) = lim X → ∞ X 2 4 x 2 - 1 = 1 4 ⇒ y = 1 4

est une asymptote horizontale. Après avoir recherché la fonction, vous pouvez commencer à la construire.

Calcul de la valeur d'une fonction aux points intermédiaires

Pour rendre le tracé le plus précis, il est recommandé de trouver plusieurs valeurs de la fonction à des points intermédiaires.

Exemple 7

A partir de l'exemple que nous avons considéré, il faut trouver les valeurs de la fonction aux points x \u003d - 2, x \u003d - 1, x \u003d - 3 4, x \u003d - 1 4. Puisque la fonction est paire, nous obtenons que les valeurs coïncident avec les valeurs en ces points, c'est-à-dire que nous obtenons x \u003d 2, x \u003d 1, x \u003d 3 4, x \u003d 1 4.

Écrivons et résolvons :

F (- 2) = F (2) = 2 2 4 2 2 - 1 = 4 15 ≈ 0, 27 F (- 1) - F (1) = 1 2 4 1 2 - 1 = 1 3 ≈ 0 , 33 F - 3 4 = F 3 4 = 3 4 2 4 3 4 2 - 1 = 9 20 = 0 , 45 F - 1 4 = F 1 4 = 1 4 2 4 1 4 2 - 1 = - 1 12 ≈ - 0,08

Pour déterminer les maxima et les minima de la fonction, les points d'inflexion, les points intermédiaires, il faut construire des asymptotes. Pour une désignation pratique, les intervalles d'augmentation, de diminution, de convexité, de concavité sont fixes. Considérez la figure ci-dessous.

Il est nécessaire de tracer des lignes de graphe passant par les points marqués, ce qui vous permettra de vous rapprocher des asymptotes, en suivant les flèches.

Ceci conclut l'étude complète de la fonction. Il existe des cas de construction de certaines fonctions élémentaires pour lesquelles des transformations géométriques sont utilisées.

Si vous remarquez une erreur dans le texte, veuillez le mettre en surbrillance et appuyer sur Ctrl+Entrée

Dans cet article, nous examinerons un schéma d'étude d'une fonction et donnerons également des exemples d'étude des extrema, de la monotonie et des asymptotes d'une fonction donnée.

Schème

Le domaine d'existence (ODZ) d'une fonction.
Intersection de fonctions (le cas échéant) avec axes de coordonnées, signes de fonction, parité, périodicité.
Points d'arrêt (leur type). Continuité. Les asymptotes sont verticales.
Monotonicité et points extrêmes.
Points d'inflections. Convexe.
Etude d'une fonction à l'infini, pour les asymptotes : horizontales et obliques.
Construire un graphique.

Étude de la monotonie

Théorème. Si la fonction g continu sur , différencié par (un B) et g'(x) ≥ 0 (g'(x)≤0), xє(а; b), alors g croissant (décroissant) .

Exemple:

y = 1 : 3x 3 - 6 : 2x 2 + 5x.

ODZ : хєR

y' = x 2 + 6x + 5.

Trouver des intervalles de signes constants vous. Dans la mesure où vous - fonction élémentaire, alors il ne peut changer de signe qu'aux points où il s'évanouit ou n'existe pas. Son ODZ : хєR.

Trouvons les points où la dérivée est égale à 0 (zéro):

y' = 0;

x = -1 ; -5.

Alors, y croissant sur (-∞; -5] et sur [-une; +∞), y descendant sur .

Recherche des extrêmes

T x0 est appelé le point maximum (max) sur l'ensemble MAIS les fonctions g lorsque la valeur maximale est prise en ce point par la fonction g(x 0) ≥ g(x), xєA.

T x0 est appelé le point minimum (min) de la fonction g sur le plateau MAIS lorsque la plus petite valeur est prise par la fonction à ce point g(x 0) ≤ g(x), xєА.

Sur le plateau MAIS les points maximum (max) et minimum (min) sont appelés points extrêmes g. Ces extrema sont également appelés extrema absolus sur l'ensemble .

Si un x0- point extrême de la fonction g dans un quartier, alors x0 est appelé le point d'extremum local ou local (max ou min) de la fonction g.

Théorème (condition nécessaire). Si un x0- point extrême de la fonction (locale) g, alors la dérivée n'existe pas ou est égale à 0 (zéro) en ce point.

Définition. Les points avec une dérivée inexistante ou égale à 0 (zéro) sont dits critiques. Ce sont ces points qui sont suspects pour un extremum.

Théorème (condition suffisante n° 1). Si la fonction g est continue dans certains districts. x0 et le signe passe par ce point lorsque la dérivée passe, alors point donné il y a t. extrême g.

Théorème (condition suffisante n° 2). Soit la fonction deux fois différentiable dans un voisinage du point et g' = 0 et g'' > 0 (g''< 0) , alors ce point est le point de maximum (max) ou minimum (min) de la fonction.

Test de convexité

La fonction est appelée convexe vers le bas (ou concave) sur l'intervalle (un B) lorsque le graphique de la fonction n'est pas situé plus haut que la sécante sur l'intervalle pour tout x avec (un B) qui passe par ces points .

La fonction sera convexe strictement vers le bas sur (un B), si - le graphique se trouve en dessous de la sécante sur l'intervalle.

La fonction est appelée convexe vers le haut (convexe) sur l'intervalle (un B), si pour tout t points avec (un B) le graphique de la fonction sur l'intervalle n'est pas inférieur à la sécante passant par les abscisses en ces points .

La fonction sera strictement convexe vers le haut sur (un B), si - le graphique sur l'intervalle se situe au-dessus de la sécante.

Si la fonction est dans un voisinage du point continue et à travers t.x 0 lors de la transition, la fonction change de convexité, alors ce point est appelé point d'inflexion de la fonction.

Étude des asymptotes

Définition. La droite s'appelle l'asymptote g(x), si à une distance infinie de l'origine, le point du graphe de la fonction s'en approche : d(M,l).

Les asymptotes peuvent être verticales, horizontales ou obliques.

Ligne verticale avec équation x = x 0 sera l'asymptote du graphe vertical de la fonction g , si le point x 0 a un écart infini, alors il y a au moins une frontière gauche ou droite à ce point - l'infini.

Etude d'une fonction sur un segment pour la valeur du plus petit et du plus grand

Si la fonction est continue sur , alors d'après le théorème de Weierstrass, il y a la plus grande valeur et la plus petite valeur sur ce segment, c'est-à-dire qu'il y a t lunettes qui appartiennent tel que g(x 1) ≤ g(x)< g(x 2), x 2 є . À partir des théorèmes sur la monotonie et les extrema, nous obtenons le schéma suivant pour étudier une fonction sur un segment pour les valeurs les plus petites et les plus grandes.

Plan

Trouver la dérivée g'(x).
Rechercher la valeur d'une fonction g en ces points et aux extrémités du segment.
Comparez les valeurs trouvées et choisissez la plus petite et la plus grande.

Commenter. Si vous avez besoin d'étudier une fonction sur un intervalle fini (un B), ou sur une infinité (-∞; b); (-∞ ; +∞) sur les valeurs max et min, puis dans le plan, au lieu des valeurs de la fonction aux extrémités de l'intervalle, ils recherchent les bornes unilatérales correspondantes : au lieu de FA)à la recherche de f(a+) = limf(x), à la place de f(b)à la recherche de f(-b). Vous pouvez donc trouver la fonction ODZ sur l'intervalle, car les extrêmes absolus n'existent pas nécessairement dans ce cas.

Application de la dérivée à la solution de problèmes appliqués pour l'extremum de certaines quantités

Exprimez cette valeur en termes d'autres quantités à partir de la condition du problème afin qu'elle soit fonction d'une seule variable (si possible).
L'intervalle de changement de cette variable est déterminé.
Faire une étude de la fonction sur l'intervalle pour les valeurs max et min.

Tâche. Besoin de construire une plateforme Forme rectangulaire, en utilisant un mètre de treillis, près du mur de sorte que d'un côté il soit adjacent au mur et des trois autres il soit clôturé avec un treillis. À quel rapport d'aspect la zone d'un tel site sera-t-elle la plus grande ?

S=xy est une fonction de 2 variables.

S = x(a - 2x)- fonction de la 1ère variable ; x є .

S = ax - 2x2 ; S" = a - 4x = 0, xєR, x = a : 4.

S(a : 4) = a 2 : 8- la valeur la plus élevée ;

S(0)=0.

Trouvez l'autre côté du rectangle : à = un : 2.

Ratio d'aspect: y:x=2.

Répondre. la plus grande zone sera égal à un 2/8 si le côté parallèle au mur est 2 fois l'autre côté.

Recherche de fonction. Exemples

Exemple 1

Disponible y=x 3 : (1-x) 2 . Faire des recherches.

ODZ : хє(-∞; 1) U (1; ∞).
Une fonction générale (ni paire ni impaire) n'est pas symétrique par rapport au point 0 (zéro).
Signes de fonction. La fonction est élémentaire, elle ne peut donc changer de signe qu'aux points où elle est égale à 0 (zéro), ou n'existe pas.
La fonction est élémentaire, donc continue sur l'ODZ : (-∞; 1) U (1; ∞).

Écart: x = 1 ;

limx 3 : (1- x) 2 = ∞- Discontinuité de 2ème espèce (infinie), donc il y a une asymptote verticale au point 1 ;

x = 1- l'équation de l'asymptote verticale.

5. y' = x 2 (3 - x) : (1 - x) 3 ;

ODZ (y'): x ≠ 1 ;

x = 1 est un point critique.

y' = 0;

0; 3 sont des points critiques.

6. y'' = 6x : (1 - x) 4 ;

T. critique : 1, 0;

x= 0 - point d'inflexion, y(0) = 0.

7. limx 3 : (1 - 2x + x 2) = ∞- il n'y a pas d'asymptote horizontale, mais elle peut être oblique.

k = 1- Numéro;

b = 2- Numéro.

Il existe donc une asymptote oblique y=x+2à + ∞ et à - ∞.

Exemple 2

Donné y = (x 2 + 1) : (x - 1). Produire et enquête. Construire un graphique.

1. La zone d'existence est toute la ligne numérique, à l'exception de la soi-disant. x=1.

2. y croise OY (si possible) incl. (0;g(0)). Nous trouvons y(0) = -1 - point d'intersection OY .

Points d'intersection du graphique avec BŒUF trouver en résolvant l'équation y=0. L'équation n'a pas de racines réelles, donc cette fonction ne se coupe pas BŒUF.

3. La fonction est non périodique. Considérez l'expression

g(-x) ≠ g(x), et g(-x) ≠ -g(x). Cela signifie qu'il s'agit d'une fonction générique (ni paire ni impaire).

4. T. x=1 la discontinuité est du second type. En tous les autres points, la fonction est continue.

5. Etude de la fonction pour un extremum :

(X 2 - 2x - 1) : (x - 1)2=y"

et résoudre l'équation y" = 0.

Alors, 1 - √2, 1 + √2, 1 - points critiques ou points d'extremum possibles. Ces points divisent la droite numérique en quatre intervalles .

Sur chaque intervalle, la dérivée a un certain signe, qui peut être défini par la méthode des intervalles ou en calculant les valeurs de la dérivée à des points individuels. À intervalles (-∞; 1 - √2 ) tu (1 + √2 ; ∞) , une dérivée positive, ce qui signifie que la fonction est croissante ; si xє(1 - √2 ; 1) Tu(1; 1 + √2 ) , alors la fonction est décroissante, car la dérivée est négative sur ces intervalles. À travers. x1 pendant la transition (le mouvement suit de gauche à droite), la dérivée change de signe de "+" à "-", donc, à ce point il y a un maximum local, on trouve

y max = 2 - 2 √2 .

En passant par x2 change le signe dérivé de "-" à "+", donc, il y a un minimum local à ce point, et

y mélange = 2 + 2√2.

T x=1 pas si extrême.

6.4 : (x - 1) 3 = y"".

Sur le (-∞; 1 ) 0 > y"" , par conséquent, la courbe est convexe sur cet intervalle ; si xє (1 ; ∞) - la courbe est concave. En t point 1 aucune fonction n'est définie, donc ce point n'est pas un point d'inflexion.

7. Il résulte des résultats du paragraphe 4 que x=1 est l'asymptote verticale de la courbe.

Il n'y a pas d'asymptotes horizontales.

x + 1 = y est l'asymptote de la pente de cette courbe. Il n'y a pas d'autres asymptotes.

8. Tenant compte des études menées, nous construisons un graphique (voir la figure ci-dessus).

Pour une étude complète de la fonction et tracer son graphe, il est recommandé d'utiliser le schéma suivant :

1) trouver la portée de la fonction ;

2) trouver les points de discontinuité de la fonction et les asymptotes verticales (si elles existent) ;

3) étudier le comportement de la fonction à l'infini, trouver les asymptotes horizontales et obliques ;

4) étudier la fonction de régularité (oddity) et de périodicité (pour les fonctions trigonométriques);

5) trouver les extrema et les intervalles de monotonie de la fonction ;

6) déterminer les intervalles des points de convexité et d'inflexion ;

7) trouver des points d'intersection avec les axes de coordonnées, si possible, et quelques points supplémentaires qui affinent le graphique.

L'étude de la fonction est menée simultanément à la construction de son graphe.

Exemple 9 Explorez la fonction et construisez un graphique.

1. Domaine de définition : ;

2. La fonction se casse aux points
,
;

Nous étudions la fonction pour la présence d'asymptotes verticales.

;
,
─ asymptote verticale.

3. Nous étudions la fonction pour la présence d'asymptotes obliques et horizontales.

Droit
─ asymptote oblique, si
,
.

,
.

Droit
─ asymptote horizontale.

4. La fonction est paire parce que
. La parité de la fonction indique la symétrie du graphique par rapport à l'axe des ordonnées.

5. Trouvez les intervalles de monotonie et les extrema de la fonction.

Trouvons les points critiques, c'est-à-dire points où la dérivée est 0 ou n'existe pas :
;
. Nous avons trois points
;

. Ces points divisent l'ensemble de l'axe réel en quatre intervalles. Définissons les signes sur chacun d'eux.

Sur les intervalles (-∞ ; -1) et (-1 ; 0) la fonction augmente, sur les intervalles (0 ; 1) et (1 ; +∞) elle diminue. En passant par un point
la dérivée change de signe de plus à moins, donc, à ce stade, la fonction a un maximum
.

6. Trouvons les intervalles de convexité, les points d'inflexion.

Trouvons les points où vaut 0 ou n'existe pas.

n'a pas de vraies racines.
,
,

points
et
diviser l'axe réel en trois intervalles. Définissons le signe à chaque intervalle.

Ainsi, la courbe sur les intervalles
et
convexe vers le bas, sur l'intervalle (-1;1) convexe vers le haut ; il n'y a pas de points d'inflexion, puisque la fonction aux points
et
non spécifié.

7. Trouvez les points d'intersection avec les axes.

avec essieu
le graphique de la fonction se coupe au point (0; -1), et avec l'axe
le graphique ne se croise pas, car le numérateur de cette fonction n'a pas de racines réelles.

Le graphique de la fonction donnée est illustré à la figure 1.

Figure 1 ─ Graphique de la fonction

Application du concept de dérivée en économie. Élasticité de la fonction

Pour étudier les processus économiques et résoudre d'autres problèmes appliqués, le concept d'élasticité de fonction est souvent utilisé.

Définition.Élasticité de la fonction
est appelée la limite du rapport de l'incrément relatif de la fonction à l'incrément relatif de la variable à
, . (VII)

L'élasticité d'une fonction indique approximativement de combien de pourcentage la fonction changera
lors du changement de la variable indépendante de 1 %.

L'élasticité d'une fonction est utilisée dans l'analyse de la demande et de la consommation. Si l'élasticité de la demande (en valeur absolue)
, alors la demande est considérée comme élastique si
─ neutre si
─ inélastique par rapport au prix (ou au revenu).

Exemple 10 Calculer l'élasticité d'une fonction
et trouver la valeur de l'indice d'élasticité pour = 3.

Solution : d'après la formule (VII) l'élasticité de la fonction :

Soit x=3 alors
Cela signifie que si la variable indépendante augmente de 1 %, alors la valeur de la variable dépendante augmentera de 1,42 %.

Exemple 11 Laisser la demande fonctionner concernant le prix a la forme
, où ─ coefficient constant. Trouver la valeur de l'indice d'élasticité de la fonction de demande au prix x = 3 den. unités

Solution : calculer l'élasticité de la fonction de demande à l'aide de la formule (VII)

En supposant
unités monétaires, on obtient
. Cela signifie qu'au prix
unité monétaire une hausse de prix de 1 % entraînera une baisse de la demande de 6 %, soit la demande est élastique.