Description du graphique de fonction en ligne. Exemple complet de recherche de fonction en ligne

16.10.2019

Domaine

Afin d'explorer et de tracer une fonction, vous devez connaître quelques définitions. Une fonction est l'un des concepts de base (de base) en mathématiques. Il reflète la dépendance entre plusieurs variables (deux, trois ou plus) avec des changements. La fonction montre également la dépendance des ensembles.

Imaginez que nous ayons deux variables qui ont une certaine plage de changement. Ainsi, y est une fonction de x, à condition que chaque valeur de la seconde variable corresponde à une valeur de la seconde. Dans ce cas, la variable y est dépendante et s'appelle une fonction. Il est d'usage de dire que les variables x et y sont en Pour plus de clarté sur cette dépendance, un graphe de la fonction est construit. Qu'est-ce qu'un graphe de fonctions ? Il s'agit d'un ensemble de points sur le plan de coordonnées, où chaque valeur de x correspond à une valeur de y. Les graphiques peuvent être différents - une ligne droite, une hyperbole, une parabole, une sinusoïde, etc.

Un graphe de fonction ne peut pas être tracé sans exploration. Aujourd'hui, nous allons apprendre à effectuer des recherches et à tracer un graphique de fonction. Il est très important de prendre des notes pendant l'étude. Il sera donc beaucoup plus facile de faire face à la tâche. Le plan d'études le plus pratique:

Domaine.
Continuité.
Pair ou impair.
Périodicité.
Asymptotes.
Zéros.
Constance.
Ascendant et descendant.
Extrêmes.
Convexité et concavité.

Commençons par le premier point. Trouvons le domaine de définition, c'est-à-dire sur quels intervalles notre fonction existe: y \u003d 1/3 (x ^ 3-14x ^ 2 + 49x-36). Dans notre cas, la fonction existe pour toutes les valeurs de x, c'est-à-dire que le domaine de définition est R. Cela peut s'écrire xОR.

Continuité

Nous allons maintenant explorer la fonction de discontinuité. En mathématiques, le terme "continuité" est apparu à la suite de l'étude des lois du mouvement. Qu'est-ce que l'infini ? L'espace, le temps, certaines dépendances (un exemple est la dépendance des variables S et t dans les problèmes de mouvement), la température de l'objet chauffé (eau, poêle à frire, thermomètre, etc.), une ligne continue (c'est-à-dire une que l'on peut dessiner sans l'enlever de la feuille de crayon).

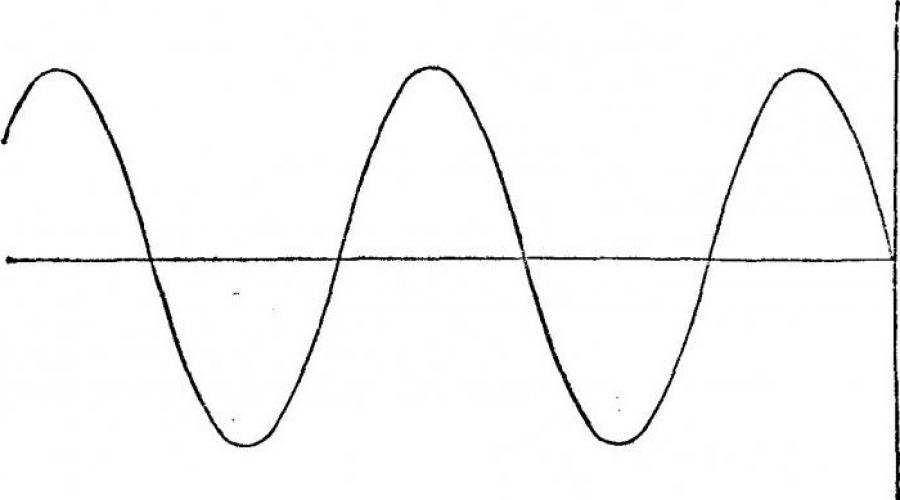
Un graphique est considéré comme continu s'il ne se brise pas à un moment donné. Un des plus bons exemples un tel graphique est une onde sinusoïdale, que vous pouvez voir dans l'image de cette section. La fonction est continue à un certain point x0 si un certain nombre de conditions sont remplies :

une fonction est définie en un point donné ;
les limites droite et gauche en un point sont égales ;
la limite est égale à la valeur de la fonction au point x0.

Si au moins une condition n'est pas remplie, la fonction est dite cassante. Et les points auxquels la fonction s'arrête sont appelés points d'arrêt. Un exemple de fonction qui "cassera" lorsqu'elle sera affichée graphiquement est : y=(x+4)/(x-3). De plus, y n'existe pas au point x = 3 (puisqu'il est impossible de diviser par zéro).

Dans la fonction que nous étudions (y \u003d 1/3 (x ^ 3-14x ^ 2 + 49x-36)), tout s'est avéré simple, puisque le graphique sera continu.

Même bizarre

Examinons maintenant la fonction de parité. Commençons par un peu de théorie. Une fonction paire est une fonction qui satisfait la condition f (-x) = f (x) pour toute valeur de la variable x (de la plage de valeurs). Les exemples sont :

module x (le graphique ressemble à un choucas, la bissectrice des premier et deuxième quarts du graphique) ;
x au carré (parabole);
cosinus x (onde cosinus).

Notez que tous ces graphiques sont symétriques lorsqu'ils sont visualisés par rapport à l'axe des ordonnées.

Qu'appelle-t-on alors une fonction impaire ? Ce sont les fonctions qui satisfont à la condition: f (-x) \u003d - f (x) pour toute valeur de la variable x. Exemples:

hyperbole;
parabole cubique ;
sinusoïde ;
tangente et ainsi de suite.

Veuillez noter que ces fonctions sont symétriques par rapport au point (0:0), c'est-à-dire l'origine. Sur la base de ce qui a été dit dans cette section de l'article, le même et fonction impaire doit avoir la propriété : x appartient à l'ensemble de définition et -x aussi.

Examinons la fonction de parité. Nous pouvons voir qu'elle ne correspond à aucune des descriptions. Par conséquent, notre fonction n'est ni paire ni impaire.

Asymptotes

Commençons par une définition. Une asymptote est une courbe aussi proche que possible du graphique, c'est-à-dire que la distance d'un point tend vers zéro. Il existe trois types d'asymptotes :

vertical, c'est-à-dire parallèle à l'axe y ;
horizontale, c'est-à-dire parallèle à l'axe des x ;
oblique.

Comme pour le premier type, ces lignes doivent être recherchées à certains endroits :

écart;
extrémités du domaine.

Dans notre cas, la fonction est continue et le domaine de définition est R. Par conséquent, il n'y a pas d'asymptotes verticales.

L'asymptote horizontale est dans le graphique de la fonction, ce qui correspond à prochaine exigence: si x tend vers l'infini ou moins l'infini, et que la limite est égale à un certain nombre (par exemple, a). À ce cas y=a est l'asymptote horizontale. Il n'y a pas d'asymptotes horizontales dans la fonction que nous étudions.

Une asymptote oblique n'existe que si deux conditions sont remplies :

lim(f(x))/x=k ;
lim f(x)-kx=b.

On peut alors le trouver par la formule : y=kx+b. Encore une fois, dans notre cas, il n'y a pas d'asymptotes obliques.

Fonction zéros

L'étape suivante consiste à examiner le graphique de la fonction pour les zéros. Il est également très important de noter que la tâche associée à la recherche des zéros d'une fonction se produit non seulement dans l'étude et le tracé d'un graphique de fonction, mais également en tant que tâche indépendante et en tant que moyen de résoudre les inégalités. Vous devrez peut-être trouver les zéros d'une fonction sur un graphique ou utiliser la notation mathématique.

Trouver ces valeurs vous aidera à tracer la fonction avec plus de précision. Si parler langage clair, alors le zéro de la fonction est la valeur de la variable x, à laquelle y=0. Si vous recherchez les zéros d'une fonction sur un graphique, vous devez faire attention aux points d'intersection du graphique avec l'axe des x.

Pour trouver les zéros de la fonction, vous devez résoudre l'équation suivante : y=1/3(x^3-14x^2+49x-36)=0. Après avoir fait les calculs nécessaires, nous obtenons la réponse suivante :

signe constance

L'étape suivante dans l'étude et la construction d'une fonction (graphique) consiste à trouver des intervalles de constance de signe. Cela signifie que nous devons déterminer sur quels intervalles la fonction prend une valeur positive, et sur quels intervalles elle prend une valeur négative. Les zéros des fonctions trouvées dans la section précédente nous aideront à le faire. Donc, nous devons tracer une ligne droite (séparée du graphique) et dans dans le bon ordre distribuez les zéros de la fonction dessus du plus petit au plus grand. Vous devez maintenant déterminer lequel des intervalles résultants a un signe "+" et lequel a un "-".

Dans notre cas, la fonction prend une valeur positive sur les intervalles :

de 1 à 4 ;
de 9 à l'infini.

Sens négatif:

de moins l'infini à 1 ;
de 4 à 9.

C'est assez facile à déterminer. Remplacez n'importe quel nombre de l'intervalle dans la fonction et voyez le signe de la réponse (moins ou plus).

Fonction croissante et décroissante

Afin d'explorer et de construire une fonction, nous devons savoir où le graphique va augmenter (monter sur Oy) et où il va baisser (ramper le long de l'axe des ordonnées).

La fonction n'augmente que si la plus grande valeur de la variable x correspond à plus grande valeur y. Autrement dit, x2 est supérieur à x1 et f(x2) est supérieur à f(x1). Et on observe un phénomène complètement opposé dans une fonction décroissante (plus il y a de x, moins il y a). Pour déterminer les intervalles d'augmentation et de diminution, vous devez trouver les éléments suivants :

portée (nous l'avons déjà);
dérivée (dans notre cas : 1/3(3x^2-28x+49) ;
résoudre l'équation 1/3(3x^2-28x+49)=0.

Après calculs, on obtient le résultat :

On obtient : la fonction croît sur les intervalles de moins l'infini à 7/3 et de 7 à l'infini, et décroît sur l'intervalle de 7/3 à 7.

Extrêmes

La fonction étudiée y=1/3(x^3-14x^2+49x-36) est continue et existe pour toutes les valeurs de la variable x. Le point extrême indique le maximum et le minimum de cette fonction. Dans notre cas, il n'y en a pas, ce qui simplifie grandement la tâche de construction. Sinon, ils sont également trouvés en utilisant la fonction dérivée. Après avoir trouvé, n'oubliez pas de les marquer sur le tableau.

Convexité et concavité

Nous continuons à étudier la fonction y(x). Maintenant, nous devons vérifier la convexité et la concavité. Les définitions de ces concepts sont assez difficiles à percevoir, mieux vaut tout analyser avec des exemples. Pour le test : une fonction est convexe si c'est une fonction non décroissante. D'accord, c'est incompréhensible !

Il faut trouver la dérivée de la fonction du second ordre. On obtient : y=1/3(6x-28). Maintenant, assimilons le côté droit à zéro et résolvons l'équation. Réponse : x=14/3. Nous avons trouvé le point d'inflexion, c'est-à-dire l'endroit où le graphe passe de convexe à concave ou vice versa. Sur l'intervalle de moins l'infini à 14/3, la fonction est convexe, et de 14/3 à plus l'infini, elle est concave. Il est également très important de noter que le point d'inflexion sur le graphique doit être lisse et doux, non coins pointus ne doit pas être présent.

Définition des points supplémentaires

Notre tâche est d'explorer et de tracer le graphe de la fonction. Nous avons terminé l'étude, il ne sera pas difficile de tracer la fonction maintenant. Pour une reproduction plus précise et détaillée d'une courbe ou d'une droite sur le plan de coordonnées, vous pouvez trouver plusieurs points auxiliaires. C'est assez facile de les calculer. Par exemple, nous prenons x=3, résolvons l'équation résultante et trouvons y=4. Ou x=5 et y=-5 et ainsi de suite. Vous pouvez prendre autant de points supplémentaires que nécessaire pour construire. Au moins 3-5 d'entre eux sont trouvés.

Traçage

Nous devions étudier la fonction (x^3-14x^2+49x-36)*1/3=y. Toutes les marques nécessaires au cours des calculs ont été faites sur le plan de coordonnées. Il ne reste plus qu'à construire un graphe, c'est-à-dire relier tous les points entre eux. Relier les points est fluide et précis, c'est une question de compétence - un peu de pratique et votre emploi du temps sera parfait.

Votre vie privée est importante pour nous. Pour cette raison, nous avons développé une politique de confidentialité qui décrit comment nous utilisons et stockons vos informations. Veuillez lire notre politique de confidentialité et faites-nous savoir si vous avez des questions.

Collecte et utilisation des informations personnelles

Les informations personnelles font référence aux données qui peuvent être utilisées pour identifier une personne spécifique ou la contacter.

Vous pouvez être invité à fournir vos informations personnelles à tout moment lorsque vous nous contactez.

Voici quelques exemples des types d'informations personnelles que nous pouvons collecter et de la manière dont nous pouvons utiliser ces informations.

Quelles informations personnelles nous collectons :

Lorsque vous soumettez une candidature sur le site, nous pouvons collecter diverses informations, notamment votre nom, votre numéro de téléphone, votre adresse E-mail etc.

Comment utilisons-nous vos informations personnelles:

Collecté par nos soins renseignements personnels nous permet de vous contacter et de vous informer des offres uniques, promotions et autres événements et événements à venir.
De temps à autre, nous pouvons utiliser vos informations personnelles pour vous envoyer des avis et des communications importants.
Nous pouvons également utiliser des informations personnelles à des fins internes telles que l'audit, l'analyse de données et diverses études pour améliorer les services que nous fournissons et pour vous fournir des recommandations concernant nos services.
Si vous participez à un tirage au sort, à un concours ou à une incitation similaire, nous pouvons utiliser les informations que vous fournissez pour administrer ces programmes.

Divulgation à des tiers

Nous ne divulguons pas les informations reçues de votre part à des tiers.

Exceptions:

Si nécessaire - conformément à la loi, ordre judiciaire, dans litige, et/ou sur la base de demandes publiques ou de demandes de organismes gouvernementaux sur le territoire de la Fédération de Russie - divulguez vos informations personnelles. Nous pouvons également divulguer des informations vous concernant si nous déterminons qu'une telle divulgation est nécessaire ou appropriée pour des raisons de sécurité, d'application de la loi ou d'autres raisons d'intérêt public.
En cas de réorganisation, de fusion ou de vente, nous pouvons transférer les informations personnelles que nous collectons au tiers successeur concerné.

Protection des informations personnelles

Nous prenons des précautions - y compris administratives, techniques et physiques - pour protéger vos informations personnelles contre la perte, le vol et l'utilisation abusive, ainsi que contre l'accès, la divulgation, l'altération et la destruction non autorisés.

Maintenir votre vie privée au niveau de l'entreprise

Pour garantir la sécurité de vos informations personnelles, nous communiquons les pratiques de confidentialité et de sécurité à nos employés et appliquons strictement les pratiques de confidentialité.