1 lección sobre el tema

Realizado:

Telegina L.B.

El propósito de la lección:

1. repetir todo el material estudiado sobre funciones.
2. presentar la definición de proporcionalidad inversa y enseñar cómo construir su gráfica.
3. Desarrollar el pensamiento lógico.
4. cultivar la atención, la exactitud, la precisión.

Plan de estudios:

1. Repetición.
2. Explicación de material nuevo.
3. Minuto de educación física.
4. Consolidación.

Equipo: carteles.

Durante las clases:

1. La lección comienza con la repetición. Se invita a los estudiantes a resolver un crucigrama (que ha sido preparado de antemano el hoja grande papel).

Preguntas de crucigramas:

1. Dependencia entre variables, en la que cada valor de la variable independiente corresponde a un único valor de la variable dependiente. [Función].

2. Variable independiente. [Argumento].

3. El conjunto de puntos del plano coordenado de abscisas, que son iguales a los valores del argumento, y las ordenadas son iguales a los valores de la función. [Cronograma].

4. Función dada por la fórmula y=kx+b. [Lineal].

5. ¿Cómo se llama coeficiente a un número? k en la fórmula y=kx+b? [Esquina].

6. ¿Cuál es la gráfica de una función lineal? [Derecho].

7. Si k≠0, entonces la gráfica y=kx+b cruza este eje, y si k=0, entonces es paralela a él. ¿Con qué letra se designa este eje? [X].

8. ¿La palabra en el nombre de la función y=kx? [Proporcionalidad].

9. Función dada por la fórmula y=x 2. [Cuadrático].

10. Título del gráfico función cuadrática. [Parábola].

11. Letra del alfabeto latino, que a menudo denota una función. [Igreco].

12. Una de las formas de especificar una función. [Fórmula].

Maestro : ¿Cuáles son las principales formas de especificar una función que conocemos?

(Un estudiante recibe una tarea en la pizarra: completar una tabla de valores de la función 12/x usando los valores dados de su argumento y luego trazar los puntos correspondientes en el plano de coordenadas).

El resto responde a las preguntas del profesor: (que están escritas previamente en la pizarra)

1. ¿Cuáles son los nombres de las siguientes funciones dadas por fórmulas: y=kx, y=kx+b, y=x? 2 , y=x 3 ?

2. Especifique el dominio de definición de las siguientes funciones: y=x 2 +8, y=1/x-7, y= 4x-1/5, y=2x, y=7-5x, y=2/x, y=x 3, y=-10/x.

Luego los estudiantes trabajan según la tabla, respondiendo las preguntas planteadas por el profesor:

1. ¿Qué figura de la tabla muestra los gráficos?

a) función lineal;

b) proporcionalidad directa;

c) función cuadrática;

d) funciones de la forma y=kx 3 ?

2. ¿Qué signo tiene el coeficiente k en fórmulas de la forma y=kx+b, que corresponden a las gráficas de las Figuras 1, 2, 4, 5 de la tabla?

3. Encuentra gráficos en la tabla. funciones lineales, cuyos coeficientes angulares son:

a) igual;

b) igual en magnitud y de signo opuesto.

(Luego toda la clase comprueba si el alumno llamado a la pizarra llenó correctamente la tabla y colocó los puntos en el plano de coordenadas).

2. La explicación comienza con la motivación.

Maestro: Como sabes, cada función describe algunos procesos que ocurren en el mundo que nos rodea.

Consideremos, por ejemplo, un rectángulo con lados x e y y área 12 cm 2 . Se sabe que x*y=12, pero ¿qué pasa si empiezas a cambiar uno de los lados del rectángulo, digamos un lado con longitud?¿X?

Longitud del lado y se puede encontrar a partir de la fórmula y=12/x. Si X aumenta 2 veces, tendrá y=12/2x, es decir lado y disminuirá 2 veces. si el valor X aumentar en 3, 4, 5... veces, entonces el valor y disminuirá en la misma cantidad. Por el contrario, si X disminuir varias veces, luego y aumentará en la misma cantidad. (Trabajar según tabla).

Por lo tanto, una función de la forma y=12/x se llama proporcionalidad inversa. EN vista general se escribe como y=k/x, donde k es una constante y k≠0.

Este es el tema de la lección de hoy, lo anotamos en nuestros cuadernos. Doy una definición estricta. Para la función y=12/x, que es un tipo especial de proporcionalidad inversa, ya hemos escrito una serie de valores del argumento y la función en la tabla y representaremos los puntos correspondientes en el plano de coordenadas. ¿Cómo es la gráfica de esta función? Es difícil juzgar todo el gráfico basándose en los puntos construidos, porque los puntos se pueden conectar de la forma que desee. Intentemos juntos sacar conclusiones sobre la gráfica de una función que surjan al considerar la tabla y la fórmula.

Preguntas para la clase:

1. ¿Cuál es el dominio de definición de la función y=12/x?
2. ¿Los valores de y son positivos o negativos si

a)x

b)x>0?

3. Cómo cambia el valor de una variable y con valor cambiante¿X?

Entonces,

1. El punto (0,0) no pertenece al gráfico, es decir. no cruza ni el eje OX ni el OY;
2. la gráfica está en los cuartos de coordenadas Ι y ΙΙΙ;
3. se acerca suavemente a los ejes de coordenadas tanto en el cuarto de coordenadas Ι como en el ΙΙΙ, y se acerca a los ejes tan cerca como se desee.

Teniendo esta información ya podemos unir los puntos de la figura (lo hace el propio profesor en la pizarra) y ver la gráfica completa de la función y=12/x. La curva resultante se llama hipérbola, que en griego significa "que pasa por algo". Esta curva fue descubierta por matemáticos de la antigua escuela griega alrededor del siglo IV a.C. El término hipérbole fue introducido por Apolonio de la ciudad de Pérgamo (Asia Menor), que vivió entre los siglos VI y VIII. ANTES DE CRISTO.

Ahora, junto a la gráfica de la función y=12/x, construiremos una gráfica de la función y=-12/x. (Los alumnos completan esta tarea en cuadernos y un alumno en el pizarrón).

Al comparar ambas gráficas, los estudiantes notan que la segunda ocupa 2 y 4 cuartos de coordenadas. Además, si la gráfica de la función y=12/x se muestra simétricamente con respecto al eje del amplificador operacional, entonces se obtendrá la gráfica de la función y=-12/x.

Pregunta: ¿Cómo depende la ubicación de la gráfica de la hipérbola y=k/x del signo y del valor del coeficiente k?

Los estudiantes están convencidos de que si k>0, entonces la gráfica se ubica en Ι Y ΙΙΙ cuartos de coordenadas, y si k

1. La lección de educación física la imparte el profesor.

1. La consolidación de lo que se está estudiando se produce al completar los números 180, 185 del libro de texto.

1. La lección está resumida, calificaciones, tarea: p.8 No. 179, 184.

Lección 2 sobre el tema.

"La función de proporcionalidad inversa y su gráfica".

Realizado:

Telegina L.B.

El propósito de la lección:

1. consolidar la habilidad de construir una gráfica de una función de proporcionalidad inversa;
2. desarrollar interés en el tema, pensamiento lógico;
3. cultivar la independencia y la atención.

Plan de estudios:

1. Comprobando el progreso tarea.
2. Trabajo oral.
3. Resolución de problemas.
4. Minuto de educación física.
5. Trabajo independiente multinivel.
6. Resumiendo, evaluaciones, tareas.

Equipo: tarjetas.

Durante las clases:

1. El profesor anuncia el tema de la lección, los objetivos y el plan de la lección.

Luego, dos estudiantes completan los números de casa asignados 179, 184 en la pizarra.

1. El resto de alumnos trabajan de forma frontal, respondiendo a las preguntas del profesor.

Preguntas:

• Defina la función de proporcionalidad inversa.
• ¿Cuál es la gráfica de una función de proporcionalidad inversa?
• ¿Cómo depende la ubicación de la gráfica de la hipérbola y=k/x del valor del coeficiente k?

Tareas:

1. Entre las funciones especificadas por las fórmulas se encuentran las funciones de proporcionalidad inversa:

a) y=x 2 +5, b) y=1/x, c) y= 4x-1, d) y=2x, e) y=7-5x, f) y=-11/x, g) y=x 3, h) y=15/x-2.

2. Para funciones de proporcionalidad inversa, nombre el coeficiente e indique en qué trimestres se encuentra la gráfica.

3. Encuentre el dominio de definición de funciones de proporcionalidad inversa.

(Luego, los estudiantes revisan la tarea de los demás con un lápiz basándose en las soluciones de los números en la pizarra verificadas por el maestro y dan una calificación).

Trabajo frontal según libro de texto nº 190, 191, 192, 193 (oral).

1. Ejecución en cuadernos y en la pizarra del libro de texto No. 186(b), 187(b), 182.

4. El profesor imparte una lección de educación física.

5. Trabajo independiente dada en tres opciones de diversa complejidad(distribuido en tarjetas).

Yo c. (ligero).

Traza una gráfica de la función de proporcionalidad inversa y=-6/x usando la tabla:

Usando el gráfico, encuentre:

a) el valor de y si x = - 1,5; 2;

b) el valor de x en el que y = - 1; 4.

ΙΙ siglo (dificultad media)

Traza una gráfica de la función de proporcionalidad inversa y=16/x, habiendo completado primero la tabla.

Usando la gráfica, encuentre en qué valores xy >0.

ΙΙΙ siglo (mayor dificultad)

Traza una gráfica de la función de proporcionalidad inversa y=10/x-2, habiendo completado primero la tabla.

Encuentre el dominio de definición de esta función.

(Los estudiantes entregan hojas con gráficos construidos para la prueba).

6. Resume la lección, evaluaciones, tareas: No. 186 (a), 187 (a).

Hoy veremos qué cantidades se llaman inversamente proporcionales, cómo se ve una gráfica de proporcionalidad inversa y cómo todo esto puede resultarle útil no solo en las lecciones de matemáticas, sino también fuera de la escuela.

Proporciones tan diferentes

Proporcionalidad Nombra dos cantidades que sean mutuamente dependientes.

La dependencia puede ser directa e inversa. En consecuencia, las relaciones entre cantidades se describen por proporcionalidad directa e inversa.

Proporcionalidad directa– se trata de una relación entre dos cantidades en la que un aumento o disminución de una de ellas conduce a un aumento o disminución de la otra. Aquellos. su actitud no cambia.

Por ejemplo, cuanto más te esfuerces en estudiar para los exámenes, mejores serán tus calificaciones. O cuantas más cosas lleves contigo de excursión, más pesada será tu mochila. Aquellos. La cantidad de esfuerzo dedicado a la preparación de los exámenes es directamente proporcional a las calificaciones obtenidas. Y la cantidad de cosas que caben en una mochila es directamente proporcional a su peso.

Proporcionalidad inversa - Este dependencia funcional, en el que una disminución o un aumento varias veces en una cantidad independiente (se llama argumento) provoca un aumento o disminución proporcional (es decir, el mismo número de veces) en una cantidad dependiente (se llama función).

Ilustremos ejemplo sencillo. Quieres comprar manzanas en el mercado. Las manzanas en el mostrador y la cantidad de dinero en tu billetera están en proporción inversa. Aquellos. Cuantas más manzanas compres, menos dinero te quedará.

Función y su gráfica.

La función de proporcionalidad inversa se puede describir como y = k/x. En el cual X≠ 0 y k≠ 0.

Esta función tiene las siguientes propiedades:

1. Su dominio de definición es el conjunto de todos los números reales excepto X = 0. D(y): (-∞; 0) U (0; +∞).
2. El rango son todos los números reales excepto y= 0. mi(y): (-∞; 0) Ud. (0; +∞) .
3. No tiene valores máximos ni mínimos.
4. Es impar y su gráfica es simétrica con respecto al origen.
5. No PERIODICO.
6. Su gráfica no corta los ejes de coordenadas.
7. No tiene ceros.
8. Si k> 0 (es decir, el argumento aumenta), la función disminuye proporcionalmente en cada uno de sus intervalos. Si k< 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
9. A medida que aumenta el argumento ( k> 0) los valores negativos de la función están en el intervalo (-∞; 0), y los valores positivos están en el intervalo (0; +∞). Cuando el argumento disminuye ( k< 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

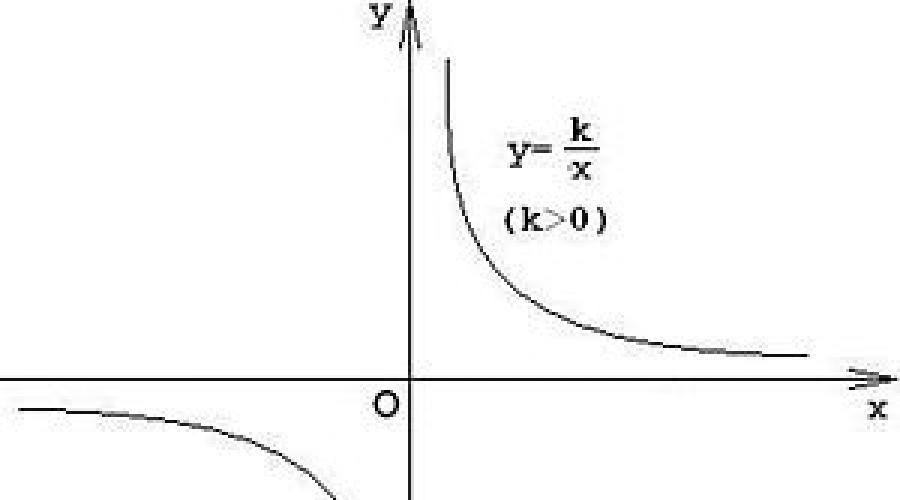
La gráfica de una función de proporcionalidad inversa se llama hipérbola. Se muestra de la siguiente manera:

Problemas de proporcionalidad inversa

Para hacerlo más claro, veamos varias tareas. No son demasiado complicados y resolverlos te ayudará a visualizar qué es la proporcionalidad inversa y cómo este conocimiento puede ser útil en tu vida ordinaria.

Tarea número 1. Un auto se mueve a una velocidad de 60 km/h. Le tomó 6 horas llegar a su destino. ¿Cuánto tiempo le tomará recorrer la misma distancia si se mueve al doble de velocidad?

Podemos empezar escribiendo una fórmula que describa la relación entre tiempo, distancia y velocidad: t = S/V. De acuerdo, nos recuerda mucho a la función de proporcionalidad inversa. E indica que el tiempo que pasa un coche en la carretera y la velocidad a la que se desplaza son inversamente proporcionales.

Para comprobarlo, encontremos V 2, que, según la condición, es 2 veces mayor: V 2 = 60 * 2 = 120 km/h. Luego calculamos la distancia usando la fórmula S = V * t = 60 * 6 = 360 km. Ahora no es difícil averiguar el tiempo t 2 que se nos exige según las condiciones del problema: t 2 = 360/120 = 3 horas.

Como puede ver, el tiempo de viaje y la velocidad son inversamente proporcionales: a una velocidad 2 veces mayor que la velocidad original, el automóvil pasará 2 veces menos tiempo en la carretera.

La solución a este problema también se puede escribir como una proporción. Así que primero hagamos este diagrama:

↓ 60 km/h – 6 h

↓120 km/h – x h

Las flechas indican una relación inversamente proporcional. También sugieren que al trazar una proporción se debe voltear el lado derecho del registro: 60/120 = x/6. ¿De dónde obtenemos x = 60 * 6/120 = 3 horas?

Tarea número 2. El taller emplea a 6 trabajadores que pueden completar una determinada cantidad de trabajo en 4 horas. Si el número de trabajadores se reduce a la mitad, ¿cuánto tiempo les tomará a los trabajadores restantes completar la misma cantidad de trabajo?

Escribamos las condiciones del problema en la forma diagrama visual:

↓ 6 trabajadores – 4 horas

↓ 3 trabajadores – x h

Escribamos esto como una proporción: 6/3 = x/4. Y obtenemos x = 6 * 4/3 = 8 horas Si hay 2 veces menos trabajadores, los restantes dedicarán 2 veces más tiempo a hacer todo el trabajo.

Tarea número 3. Hay dos tuberías que conducen a la piscina. Por una tubería fluye agua a una velocidad de 2 l/s y llena la piscina en 45 minutos. A través de otra tubería, la piscina se llenará en 75 minutos. ¿A qué velocidad entra el agua a la piscina por este tubo?

Para empezar, reduzcamos todas las cantidades que se nos dan según las condiciones del problema a las mismas unidades de medida. Para ello expresamos la velocidad de llenado de la piscina en litros por minuto: 2 l/s = 2 * 60 = 120 l/min.

Dado que la condición implica que la piscina se llena más lentamente a través de la segunda tubería, esto significa que la tasa de flujo de agua es menor. La proporcionalidad es inversa. Expresemos la velocidad desconocida a través de x y tracemos el siguiente diagrama:

↓ 120 l/min – 45 min

↓ x l/min – 75 min

Y luego hacemos la proporción: 120/x = 75/45, de donde x = 120 * 45/75 = 72 l/min.

En el problema, la velocidad de llenado de la piscina se expresa en litros por segundo, reduzcamos la respuesta que recibimos a la misma forma: 72/60 = 1,2 l/s.

Tarea número 4. Una pequeña imprenta privada imprime tarjetas de visita. Un empleado de una imprenta trabaja a una velocidad de 42 tarjetas de visita por hora y trabaja un día completo: 8 horas. Si trabajara más rápido e imprimiera 48 tarjetas de presentación en una hora, ¿cuánto antes podría regresar a casa?

Seguimos el camino probado y elaboramos un diagrama según las condiciones del problema, designando el valor deseado como x:

↓ 42 tarjetas de visita/hora – 8 horas

↓ 48 tarjetas de visita/h – x h

Tenemos una relación inversamente proporcional: la cantidad de veces más tarjetas de presentación que imprime un empleado de una imprenta por hora, la misma cantidad de veces menos tiempo que necesitará para completar el mismo trabajo. Sabiendo esto, creemos una proporción:

42/48 = x/8, x = 42 * 8/48 = 7 horas.

Así, habiendo completado el trabajo en 7 horas, el empleado de la imprenta podría irse a casa una hora antes.

Conclusión

Nos parece que estos problemas de proporcionalidad inversa son realmente sencillos. Esperamos que ahora tú también pienses en ellos de esa manera. Y lo principal es que el conocimiento sobre lo contrario. dependencia proporcional De hecho, las cantidades pueden resultarle útiles más de una vez.

No sólo en lecciones y exámenes de matemáticas. Pero aún así, cuando te preparas para salir de viaje, ir de compras, decidir ganar un dinerito extra durante las vacaciones, etc.

Cuéntanos en los comentarios qué ejemplos de relaciones proporcionales inversas y directas notas a tu alrededor. Que sea un juego así. Verás lo emocionante que es. No olvides compartir este artículo en en las redes sociales para que tus amigos y compañeros de clase también puedan jugar.

sitio web, al copiar material total o parcialmente, se requiere un enlace a la fuente.

Primer nivel

Relación inversa. Primer nivel.

Ahora hablaremos de dependencia inversa, o en otras palabras, proporcionalidad inversa, como función. ¿Recuerdas que una función es un cierto tipo de dependencia? Si aún no ha leído el tema, le recomiendo encarecidamente que lo deje todo y lo lea, porque no puede estudiar ninguna función específica sin comprender qué es: una función.

También es muy útil antes de empezar con este tema para dominar dos más. funciones simples: Y . Allí reforzarás el concepto de función y aprenderás a trabajar con coeficientes y gráficas.

Entonces, ¿recuerdas qué es una función?
Repitamos: una función es una regla según la cual cada elemento de un conjunto (argumento) está asociado con un determinado ( ¡el único!) elemento de otro conjunto (conjunto de valores de funciones). Es decir, si tienes una función, significa que todos valor aceptable una variable (llamada "argumento") corresponde a un valor de una variable (llamada "función"). ¿Qué significa "aceptable"? Si no puede responder esta pregunta, regrese al tema "" nuevamente. todo esta en el concepto "dominio": Para algunas funciones, no todos los argumentos son igualmente útiles y pueden sustituirse en dependencias. Por ejemplo, para una función, no se permiten valores de argumentos negativos.

Función que describe la relación inversa.

Esta es una función de la forma donde.

De otra forma, se llama proporcionalidad inversa: un aumento del argumento provoca una disminución proporcional de la función.
Definamos el dominio de definición. ¿A qué puede ser igual? O, en otras palabras, ¿a qué no puede ser igual?

Por lo tanto, el único número que no se puede dividir es:

o, lo que es lo mismo,

(tal notación significa que puede ser cualquier número, excepto: el signo " " denota el conjunto de números reales, es decir, todos los números posibles; el signo " " denota la exclusión de algo de este conjunto (análogo al "menos" ”signo), y un número entre llaves significa solo un número (resulta que excluimos de todos los números posibles);

Resulta que el conjunto de valores de la función es exactamente el mismo: después de todo, si, no importa por qué lo dividamos, no funcionará:

También son posibles algunas variaciones de la fórmula. Por ejemplo, esta también es una función que describe una relación inversa.
Determine usted mismo el dominio de definición y el rango de valores de esta función. Debe tener un aspecto como este:

Veamos esta función: . ¿Está inversamente relacionado?

A primera vista, es difícil decirlo: después de todo, con un aumento, tanto el denominador de la fracción como el numerador aumentan, por lo que no está claro si la función disminuirá y, de ser así, ¿disminuirá proporcionalmente? Para entender esto, necesitamos transformar la expresión para que no haya ninguna variable en el numerador:

De hecho, recibimos una relación inversa, pero con una salvedad: .

He aquí otro ejemplo: .

Aquí es más complicado: después de todo, el numerador y el denominador ahora ciertamente no se cancelan. Pero aún podemos intentar:

¿Entiendes lo que hice? En el numerador sumé y resté el mismo número (), así que no pareció cambiar nada, pero ahora hay una parte en el numerador que es igual al denominador. Ahora dividiré término por término, es decir, dividiré esta fracción en la suma de dos fracciones:

(y es verdad, si traes lo que tengo común denominador, obtenemos solo nuestra fracción inicial):

¡Guau! Funciona de nuevo relación inversa, solo que ahora se le agrega un número.
Este método nos será muy útil más adelante a la hora de construir gráficos.

Ahora transforma las expresiones tú mismo en una relación inversa:

Respuestas:

2. Aquí debes recordar cómo trinomio cuadrático se factoriza (esto se describe en detalle en el tema “”). Déjame recordarte que para ello necesitas encontrar las raíces del correspondiente. ecuación cuadrática: . Los encontraré verbalmente usando el teorema de Vieta: , . ¿Cómo está hecho? Puedes aprender esto leyendo el tema.
Entonces obtenemos: , por lo tanto:

3. ¿Has probado ya a solucionarlo tú mismo? ¿Cuál es el truco? Seguramente el hecho es que tenemos en el numerador y en el denominador, es simple. No es problema. Necesitaremos reducir por, por lo que en el numerador debemos ponerlo entre paréntesis (para que entre paréntesis quede sin el coeficiente):

Gráfico de relación inversa

Como siempre, empecemos por el caso más sencillo: .
Hagamos una tabla:

Dibujemos puntos en el plano de coordenadas:

Ahora necesitan estar conectados sin problemas, pero ¿cómo? Se puede ver que los puntos de los lados derecho e izquierdo forman líneas curvas aparentemente desconectadas. Así es. El gráfico se verá así:

Esta gráfica se llama "hipérbola"(Hay algo así como una "parábola" en ese nombre, ¿verdad?). Como una parábola, una hipérbola tiene dos ramas, solo que no están conectadas entre sí. Cada uno de ellos se esfuerza con sus extremos por acercarse a los ejes y, pero nunca los alcanza. Si miras la misma hipérbole desde lejos, obtendrás la siguiente imagen:

Esto es comprensible: ya que el gráfico no puede cruzar el eje. Pero además, la gráfica nunca tocará el eje.

Bueno, ahora veamos en qué influyen los coeficientes. Considere estas funciones:
:

¡Guau, qué belleza!
Todos los gráficos están construidos. Colores diferentes para que sea más fácil distinguirlos entre sí.

Entonces, ¿a qué debemos prestar atención primero? Por ejemplo, si una función tiene un signo menos antes de la fracción, entonces la gráfica se invierte, es decir, se muestra simétricamente con respecto al eje.

Segundo: cuanto mayor es el número en el denominador, más “se aleja” el gráfico del origen.

¿Qué pasa si la función parece más compleja, como ?

En este caso, la hipérbole será exactamente igual a la habitual, solo que se desplazará un poco. Pensemos, ¿dónde?

¿A qué no puede ser igual ahora? Bien, . Esto significa que la gráfica nunca llegará a una línea recta. ¿A qué no puede ser igual? Ahora. Esto significa que ahora la gráfica tenderá a la línea recta, pero nunca la cruzará. Ahora son heterosexuales y desempeñan el mismo papel que ellos. ejes de coordenadas para la función. Estas líneas se llaman asíntotas(líneas a las que tiende la gráfica pero no llega):

Aprenderemos más sobre cómo se construyen dichos gráficos en el tema.

Ahora intenta resolver algunos ejemplos para consolidar:

1. La figura muestra una gráfica de una función. Definir.

2. La figura muestra la gráfica de la función. Definir

3. La figura muestra la gráfica de la función. Definir.

4. La figura muestra la gráfica de la función. Definir.

5. La figura muestra gráficas de funciones y.

Elija la proporción correcta:

Respuestas:

Dependencia inversa en la vida.

¿Dónde encontramos tal función en la práctica? Hay muchos ejemplos. El más común es el movimiento: cuanto mayor sea la velocidad a la que nos desplazamos, menos tiempo nos llevará recorrer la misma distancia. De hecho, recordemos la fórmula de la velocidad: , donde es la velocidad, es el tiempo de viaje, es la distancia (camino).

Desde aquí podemos expresar el tiempo:

Ejemplo:

Un hombre va a trabajar con velocidad media km/h y llega en una hora. ¿Cuántos minutos pasará en la misma carretera si conduce a una velocidad de km/h?

Solución:

En general, ya resolviste este tipo de problemas en quinto y sexto grado. Hiciste la proporción:

Es decir, el concepto de proporcionalidad inversa ya le resulta familiar. Entonces lo recordamos. Y ahora lo mismo, sólo que de forma adulta: a través de una función.

Función (es decir, dependencia) del tiempo en minutos de la velocidad:

Se sabe que, entonces:

Necesito encontrar:

Ahora presente algunos ejemplos de la vida en los que esté presente la proporcionalidad inversa.
¿Inventado? Bien hecho si lo haces. ¡Buena suerte!

DEPENDENCIA INVERSA. BREVEMENTE SOBRE LAS COSAS PRINCIPALES

1. Definición

Función que describe la relación inversa. es una función de la forma donde.

De otra forma, esta función se llama proporcionalidad inversa, ya que un aumento en el argumento provoca una disminución proporcional de la función.

o, lo que es lo mismo,

La gráfica inversa es una hipérbola.

2. Coeficientes, y.

Responsable de “planicidad” y dirección del gráfico: cuanto mayor es este coeficiente, más lejos se encuentra la hipérbola del origen y, por tanto, “gira” menos pronunciadamente (ver figura). El signo del coeficiente afecta en qué trimestres se encuentra el gráfico:

• si, entonces las ramas de la hipérbola están ubicadas en y cuartos;
• si, entonces en y.

x=a es asíntota vertical, es decir, la vertical a la que tiende la gráfica.

El número es responsable de desplazar la gráfica de la función hacia arriba en una cantidad si y hacia abajo si.

Por lo tanto, esto es asíntota horizontal.

Repitamos la teoría sobre funciones. Una función es una regla según la cual cada elemento de un conjunto (argumento) está asociado con un determinado ( ¡el único!) elemento de otro conjunto (conjunto de valores de funciones). Es decir, si hay una función \(y = f(x)\), esto significa que para cada valor válido de la variable \(X\)(que se llama “argumento”) corresponde a un valor de la variable \(y\)(llamada "función").

Función que describe la relación inversa.

Esta es una función de la forma \(y = \frac(k)(x)\), dónde \(k\ne 0.\)

De otra forma, se llama proporcionalidad inversa: un aumento del argumento provoca una disminución proporcional de la función.
Definamos el dominio de definición. ¿A qué puede ser igual \(x\)? O, en otras palabras, ¿a qué no puede ser igual?

El único número que no se puede dividir es 0, entonces \(x\ne 0.\):

\(D(y) = (- \infty ;0) \cup (0; + \infty)\)

o, lo que es lo mismo:

\(D(y) = R\barra invertida \( 0\).\)

Esta notación significa que \(x\) puede ser cualquier número excepto 0: el signo “R” denota el conjunto de los números reales, es decir, todos los números posibles; el signo "\" indica la exclusión de algo de este conjunto (análogo al signo "menos"), y el número 0 entre llaves simplemente significa el número 0; Resulta que de todos los números posibles excluimos el 0.

Resulta que el conjunto de valores de la función es exactamente el mismo: después de todo, si \(k \ne 0.\) , entonces no importa por qué lo dividamos, 0 no funcionará:

\(E(y) = (- \infty ;0) \cup (0; + \infty)\)

o \(E(y) = R\barra invertida \( 0\).\)

También son posibles algunas variaciones de la fórmula. \(y = \frac(k)(x)\). Por ejemplo, \(y = \frac(k)((x + a))\) También es una función que describe una relación inversa. El alcance y rango de valores de esta función son los siguientes:

\(D(y) = (- \infty ; - a) \cup (- a; + \infty)\)

\(E(y) = (- \infty ;0) \cup (0; + \infty).\)

Consideremos ejemplo, reduzcamos la expresión a la forma de una relación inversa:

\(y = \frac((x + 2))((x - 3)).\)

\(y = \frac((x + 2))((x - 3)) = \frac((x - 3 + 3 + 2))((x - 3)) = \frac(((x - 3 ) + 5))((x - 3)).\)

Introdujimos artificialmente el valor 3 en el numerador, y ahora dividimos el numerador por el denominador término por término, obtenemos:

\(y = \frac(((x - 3) + 5))((x - 3)) = \frac((x - 3))((x - 3)) + \frac(5)((x - 3)) = 1 + \frac(5)((x - 3)).\)

Obtenemos la relación inversa más el número 1.

Gráfico de relación inversa

Empecemos con un caso sencillo. \(y = \frac(1)(x).\)

Creemos una tabla de valores:

Dibujemos puntos en el plano de coordenadas:

Conecte los puntos, el gráfico se verá así:

Esta gráfica se llama "hipérbola". Como una parábola, una hipérbola tiene dos ramas, solo que no están conectadas entre sí. Cada uno de ellos tiende a acercar sus extremos a los ejes. Buey Y Oye, pero nunca los alcanza.

Observemos algunas características de la función:

1. Si una función tiene un menos antes de la fracción, entonces la gráfica se invierte, es decir, se muestra simétricamente con respecto al eje. Buey.
2. Cuanto mayor es el número en el denominador, más se “aleja” el gráfico del origen.

Dependencia inversa en la vida.

¿Dónde encontramos tal función en la práctica? Hay muchos ejemplos. El más común es el movimiento: cuanto mayor sea la velocidad a la que nos desplazamos, menos tiempo nos llevará recorrer la misma distancia. Recordemos la fórmula de la velocidad:

\(v = \frac(S)(t),\)

donde v es la velocidad, t es el tiempo de viaje, S es la distancia (trayectoria).

Desde aquí podemos expresar el tiempo: \(t = \frac(S)(v).\)