تحقق من الحل الأكبر والأصغر في المقطع. أكبر وأصغر قيمة للدالة. المهمة B15 (2014)

دعونا نرى كيفية استكشاف دالة باستخدام الرسم البياني. اتضح أنه بالنظر إلى الرسم البياني ، يمكنك معرفة كل ما يثير اهتمامنا ، وهو:

• نطاق الوظيفة
• نطاق الوظيفة
• وظيفة الأصفار
• فترات الزيادة والنقصان
• النقاط العالية والمنخفضة
• أكبر وأصغر قيمة للدالة في الفترة.

دعنا نوضح المصطلحات:

الإحداثي السينيهو التنسيق الأفقي للنقطة.
تنسيق- تنسيق عمودي.
الإحداثي السيني- المحور الأفقي ، وغالبًا ما يسمى المحور.
المحور ص - محور رأسي، أو المحور.

جدال حادهو متغير مستقل تعتمد عليه قيم الوظيفة. غالبا ما يشار.
بمعنى آخر ، نحن أنفسنا نختار ونستبدل في صيغة الدالة ونحصل على.

اِختِصاصالدوال - مجموعة قيم الوسيطة التي توجد لها الوظيفة (وتلك فقط).
يشار إليه: أو.

في الشكل لدينا ، مجال الوظيفة هو قطعة. يتم رسم الرسم البياني للوظيفة في هذا الجزء. هنا فقط وظيفة معينةيوجد.

نطاق الوظيفةهي مجموعة القيم التي يأخذها المتغير. في الشكل الخاص بنا ، هذه شريحة - من أدنى قيمة إلى أعلى قيمة.

الأصفار الوظيفية- النقاط التي تكون فيها قيمة الوظيفة مساوية للصفر ، أي. في الشكل لدينا ، هذه هي النقاط و.

قيم الدالة موجبةأين . في الشكل لدينا ، هذه هي الفترات و.
قيم الدالة سالبةأين . لدينا هذه الفترة (أو الفترة) من إلى.

أهم المفاهيم - زيادة الوظائف وتناقصهافي بعض مجموعة. كمجموعة ، يمكنك أن تأخذ مقطعًا أو فاصلًا زمنيًا أو اتحادًا للفواصل الزمنية أو خط الأعداد بالكامل.

وظيفة يزيد

بمعنى آخر ، كلما انتقل الرسم البياني إلى اليمين وأعلى.

وظيفة النقصانفي المجموعة إن وجدت وتنتمي إلى المجموعة ، فإن عدم المساواة تعني عدم المساواة.

بالنسبة لدالة متناقصة ، تقابل القيمة الأكبر قيمة أصغر. يتجه الرسم البياني لليمين ولأسفل.

في الشكل الخاص بنا ، تزداد الدالة في الفترة الزمنية وتنقص في الفترات الزمنية و.

دعونا نحدد ما هو الحد الأقصى والحد الأدنى من نقاط الوظيفة.

أقصى نقطة- هذه نقطة داخلية في مجال التعريف ، بحيث تكون قيمة الوظيفة فيها أكبر من جميع النقاط القريبة منها بدرجة كافية.
بمعنى آخر ، النقطة القصوى هي نقطة ، قيمة الوظيفة التي عندها أكثرمما كانت عليه في البلدان المجاورة. هذا "تل" محلي على الرسم البياني.

في الشكل لدينا - الحد الأقصى للنقطة.

نقطة منخفضة- نقطة داخلية في مجال التعريف ، بحيث تكون قيمة الوظيفة فيها أقل من جميع النقاط القريبة منها بدرجة كافية.
أي أن الحد الأدنى للنقطة هو أن قيمة الوظيفة فيها أقل من القيم المجاورة. على الرسم البياني ، هذه "حفرة" محلية.

في الشكل لدينا - النقطة الدنيا.

النقطة هي الحدود. إنها ليست نقطة داخلية في مجال التعريف وبالتالي فهي لا تتناسب مع تعريف النقطة القصوى. بعد كل شيء ، ليس لديها جيران على اليسار. بنفس الطريقة ، لا يمكن أن يكون هناك حد أدنى على الرسم البياني الخاص بنا.

يتم استدعاء الحد الأقصى والحد الأدنى من النقاط بشكل جماعي النقاط القصوى للدالة. في حالتنا ، هذا هو و.

ولكن ماذا لو كنت بحاجة إلى البحث ، على سبيل المثال ، وظيفة الحد الأدنىعلى الخفض؟ في هذه القضيةإجابه: . لان وظيفة الحد الأدنىهي قيمتها عند الحد الأدنى.

وبالمثل ، فإن الحد الأقصى للدالة هو. يتم الوصول إليه عند هذه النقطة.

يمكننا القول أن القيم القصوى للدالة تساوي و.

في بعض الأحيان في المهام التي تحتاج إلى البحث عنها أكبر وأصغر قيم للدالةعلى جزء معين. لا تتطابق بالضرورة مع التطرف.

في حالتنا هذه أصغر قيمة للدالةفي الفترة الزمنية يساوي الحد الأدنى للدالة ويتزامن معه. لكن أكبر قيمة لها في هذا الجزء تساوي. يتم الوصول إليه في الطرف الأيسر من المقطع.

على أي حال ، يتم تحقيق أكبر وأصغر قيم للدالة المستمرة على مقطع ما إما عند النقاط القصوى أو في نهايات المقطع.

صغيرتي وجميلة مهمة بسيطةمن فئة تلك التي تكون بمثابة شريان حياة للطالب العائم. في الطبيعة ، عالم النوم الهادئ في منتصف شهر يوليو ، لذلك حان الوقت للاستقرار بجهاز كمبيوتر محمول على الشاطئ. في وقت مبكر من الصباح ، لعبت نظرية شعاع الشمس للتركيز قريبًا على الممارسة ، والتي ، على الرغم من خفتها المعلنة ، تحتوي على شظايا زجاجية في الرمال. في هذا الصدد ، أوصي بدراسة بعض الأمثلة على هذه الصفحة بضمير حي. لحل المهام العملية ، يجب أن تكون قادرًا على ذلك البحث عن المشتقاتوفهم مادة المقال فترات الرتابة والنهايات القصوى للدالة.

أولا ، باختصار عن الشيء الرئيسي. في درس عن استمرارية الوظيفةأعطيت تعريف الاستمرارية عند نقطة والاستمرارية على فترة. تتم صياغة السلوك النموذجي لوظيفة ما على مقطع بطريقة مماثلة. تكون الوظيفة متصلة على مقطع ما إذا:

1) هو مستمر على الفاصل الزمني ؛
2) مستمر عند نقطة على اليمينوفي هذه النقطة اليسار.

الفقرة الثانية تتناول ما يسمى ب استمرارية من جانب واحدوظائف عند نقطة. هناك عدة طرق لتعريفه ، لكنني سألتزم بالسطر الذي بدأ في وقت سابق:

الوظيفة متصلة عند نقطة على اليمين، إذا تم تعريفه في نقطة معينة وتوافق حده الأيمن مع قيمة الوظيفة عند نقطة معينة: . إنه مستمر عند النقطة اليسار، إذا تم تحديده في نقطة معينة وكان حده الأيسر مساويًا للقيمة عند تلك النقطة:

تخيل أن النقاط الخضراء هي المسامير التي يعلق عليها الشريط المطاطي السحري:

خذ عقليا الخط الأحمر بين يديك. من الواضح أنه بغض النظر عن مدى امتداد الرسم البياني لأعلى ولأسفل (على طول المحور) ، ستظل الوظيفة قائمة محدود- تحوط أعلاه ، وتحوط أدناه ، ومنتجنا يخدش في حقل رعي. هكذا، يتم تقييد دالة متصلة على قطعة بها. في سياق التحليل الرياضي ، تم ذكر هذه الحقيقة التي تبدو بسيطة وإثباتها بصرامة نظرية ويرشتراس الأولى.... ينزعج الكثير من الناس من أن العبارات الأولية مثبتة بشكل مضجر في الرياضيات ، ولكن هذا له معنى مهم. لنفترض أن ساكنًا معينًا من العصور الوسطى قام بسحب الرسم البياني إلى السماء بما يتجاوز حدود الرؤية ، فقد تم إدراج هذا. قبل اختراع التلسكوب ، لم تكن الوظيفة المحدودة في الفضاء واضحة على الإطلاق! في الواقع ، كيف تعرف ما ينتظرنا وراء الأفق؟ بعد كل شيء ، بمجرد اعتبار الأرض مسطحة ، لذلك اليوم حتى النقل الآني العادي يتطلب دليلًا =)

بالنسبة الى الثانية ويرستراس نظرية, مستمر على الجزءوظيفة تصل لها الحافة العلوية بالضبطكذالك هو الحافة السفلية بالضبط .

الرقم يسمى أيضا القيمة القصوى للدالة في المقطعويشار إليه بالرقم - الحد الأدنى لقيمة الوظيفة في المقطعملحوظ.

في حالتنا هذه:

ملحوظة : من الناحية النظرية ، فإن السجلات شائعة .

تحدث تقريبا، أعلى قيمةيقع حيث أعلى نقطة في الرسم البياني ، والأصغر - حيث أدنى نقطة.

الأهمية!كما سبق أن أشرنا في المقال على القيم القصوى للوظيفة, أكبر قيمة للدالةو أصغر قيمة للدالة – ليس نفس الشيء، ماذا او ما وظيفة كحد أقصىو وظيفة الحد الأدنى. إذن ، في هذا المثال ، الرقم هو الحد الأدنى للدالة ، ولكن ليس الحد الأدنى للقيمة.

بالمناسبة ، ماذا يحدث خارج المقطع؟ نعم ، حتى الطوفان ، في سياق المشكلة قيد النظر ، هذا لا يهمنا على الإطلاق. تتضمن المهمة إيجاد رقمين فقط وهذا كل شيء!

علاوة على ذلك ، فإن الحل تحليلي بحت ، لذلك ، لا حاجة للرسم!

الخوارزمية تقع على السطح وتقترح نفسها من الشكل أعلاه:

1) ابحث عن قيم الدالة في نقاط حرجة, التي تنتمي إلى هذه الشريحة.

قبض على قطعة أخرى من الأشياء الجيدة: ليست هناك حاجة للتحقق من حالة كافية لأقصى حد ، نظرًا لوجود حد أدنى أو أقصى ، كما هو موضح للتو ليست مضمونة بعدما هي القيمة الدنيا أو القصوى. تصل وظيفة العرض إلى الحد الأقصى لها ، ووفقًا لإرادة القدر ، يكون نفس الرقم هو أكبر قيمة للدالة في الفترة الزمنية. لكن ، بالطبع ، مثل هذه المصادفة لا تحدث دائمًا.

لذلك ، في الخطوة الأولى ، يكون من الأسرع والأسهل حساب قيم الوظيفة في النقاط الحرجة التي تنتمي إلى المقطع ، دون القلق بشأن ما إذا كانت تحتوي على قيمة قصوى أم لا.

2) نحسب قيم الوظيفة في نهايات المقطع.

3) من بين قيم الوظيفة الموجودة في الفقرتين الأولى والثانية ، نختار الأصغر والأكثر رقم ضخماكتب الجواب.

نجلس على شاطئ البحر الأزرق ونضرب الكعبين في المياه الضحلة:

مثال 1

أوجد أكبر وأصغر قيم دالة في مقطع

قرار:
1) احسب قيم الوظيفة عند النقاط الحرجة التي تنتمي إلى هذا المقطع:

دعونا نحسب قيمة الوظيفة في النقطة الحرجة الثانية:

2) احسب قيم الوظيفة في نهايات المقطع:

3) تم الحصول على نتائج "جريئة" باستخدام الأس واللوغاريتمات ، مما يعقد بشكل كبير مقارنتها. لهذا السبب ، سنسلح أنفسنا بآلة حاسبة أو Excel ونحسب القيم التقريبية ، دون أن ننسى ما يلي:

الآن كل شيء واضح.

إجابه:

مثال كسري منطقي ل قرار مستقل:

مثال 6

أوجد الحد الأقصى و الحد الأدنى للقيمةوظائف في الفترة

تذكرنا عملية العثور على أصغر وأكبر قيم لدالة ما على مقطع ما برحلة رائعة حول كائن (رسم بياني لوظيفة) على طائرة هليكوبتر بإطلاق النار من مدفع بعيد المدى في نقاط معينة والاختيار من بينها هذه النقاط خاصة جدا لطلقات التحكم. يتم تحديد النقاط بطريقة معينة ووفقًا لقواعد معينة. بأية قواعد؟ سوف نتحدث عن هذا أكثر.

إذا كانت الوظيفة ذ = F(x) مستمر على المقطع [ أ, ب] ، ثم تصل إلى هذا الجزء الأقل و أعلى القيم . يمكن أن يحدث هذا إما في النقاط القصوىأو في نهايات المقطع. لذلك ، لتجد الأقل و أكبر قيم الدالة ، مستمر على الفاصل الزمني [ أ, ب] ، تحتاج إلى حساب قيمها بالكامل نقاط حرجةوفي نهايات المقطع ، ثم اختر أصغرها وأكبرها.

دعنا ، على سبيل المثال ، مطلوب تحديد الحد الأقصى لقيمة الوظيفة F(x) في المقطع [ أ, ب]. للقيام بذلك ، ابحث عن جميع نقاطه الحرجة التي تقع على [ أ, ب] .

نقطة حرجة يسمى النقطة التي وظيفة محددة، وهي المشتقإما أن يكون صفرًا أو غير موجود. ثم يجب عليك حساب قيم الوظيفة عند النقاط الحرجة. وأخيرًا ، يجب على المرء أن يقارن قيم الوظيفة عند النقاط الحرجة وفي نهايات المقطع ( F(أ) و F(ب)). سيكون أكبر هذه الأرقام أكبر قيمة للدالة في الفترة [أ, ب] .

مشكلة البحث أصغر قيم الدالة .

نحن نبحث عن أصغر وأكبر قيم للدالة معًا

مثال 1. أوجد أصغر وأكبر قيم للدالة في الجزء [-1, 2] .

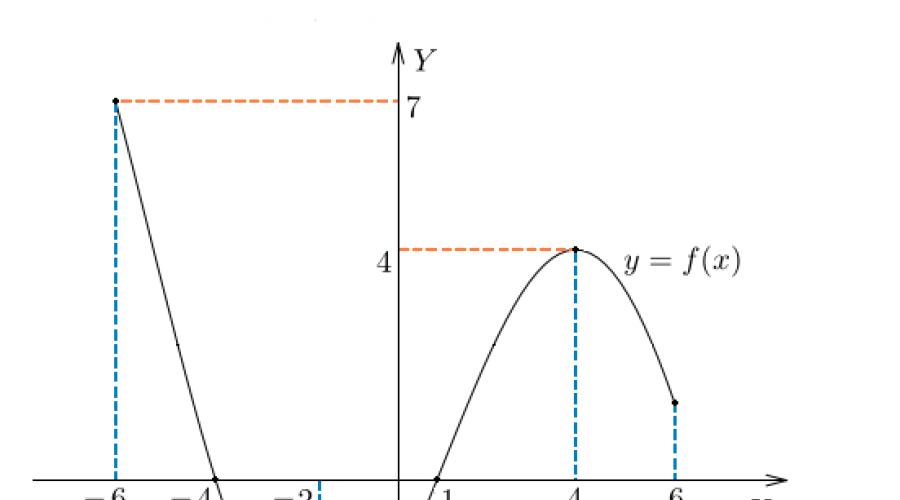
قرار. نجد مشتقة هذه الدالة. ساوي المشتق بصفر () واحصل على نقطتين حرجتين: و. للعثور على أصغر وأكبر قيم دالة في مقطع معين ، يكفي حساب قيمها في نهايات المقطع وعند النقطة ، نظرًا لأن النقطة لا تنتمي إلى المقطع [-1 ، 2]. قيم الوظائف هذه هي كما يلي: ، ،. إنه يتبع هذا أصغر قيمة للدالة(مميزة باللون الأحمر على الرسم البياني أدناه) ، تساوي -7 ، يتم الوصول إليها في الطرف الأيمن من المقطع - عند النقطة ، و أعظم(أحمر أيضًا على الرسم البياني) يساوي 9 ، - عند النقطة الحرجة.

إذا كانت الوظيفة متصلة في فاصل زمني معين ولم يكن هذا الفاصل الزمني مقطعًا (ولكنه ، على سبيل المثال ، فاصل زمني ؛ الفرق بين الفاصل الزمني والمقطع: لم يتم تضمين نقاط حدود الفاصل في الفاصل الزمني ، ولكن يتم تضمين نقاط حدود المقطع في المقطع) ، ثم من بين قيم الوظيفة قد لا يكون هناك أصغر وأكبر. لذلك ، على سبيل المثال ، الوظيفة الموضحة في الشكل أدناه متصلة على]-، + ∞ [وليس لها أكبر قيمة.

ومع ذلك ، بالنسبة لأي فترة زمنية (مغلقة أو مفتوحة أو لانهائية) ، فإن الخاصية التالية للوظائف المستمرة تبقى ثابتة.

مثال 4. أوجد أصغر وأكبر قيم للدالة في الجزء [-1, 3] .

قرار. نجد مشتق هذه الدالة كمشتق من حاصل القسمة:

.

نحن نساوي المشتقة بالصفر ، وهو ما يعطينا نقطة حرجة واحدة:. إنه ينتمي إلى الفاصل الزمني [-1 ، 3]. للعثور على أصغر وأكبر قيم دالة في مقطع معين ، نجد قيمها في نهايات المقطع وعند النقطة الحرجة التي تم العثور عليها:

دعونا نقارن هذه القيم. الخلاصة: تساوي -5 / 13 عند النقطة و أعظم قيمةيساوي 1 عند هذه النقطة.

نواصل البحث عن القيم الأصغر والأكبر للوظيفة معًا

يوجد مدرسون ، فيما يتعلق بموضوع العثور على أصغر وأكبر قيم للدالة ، لا يقدمون للطلاب أمثلة أكثر تعقيدًا من تلك التي تم أخذها في الاعتبار للتو ، أي تلك التي تكون فيها الوظيفة كثيرة الحدود أو الكسر ، البسط ومقامها كثيرات الحدود. لكننا لن نقتصر على مثل هذه الأمثلة ، حيث يوجد بين المعلمين عشاق لجعل الطلاب يفكرون بالكامل (جدول المشتقات). لذلك ، سيتم استخدام اللوغاريتم والدالة المثلثية.

مثال 6. أوجد أصغر وأكبر قيم للدالة في الجزء .

قرار. نجد مشتقة هذه الدالة كـ مشتق من المنتج :

نحن نساوي المشتق بالصفر ، وهو ما يعطينا نقطة حرجة واحدة:. إنه ينتمي إلى الجزء. للعثور على أصغر وأكبر قيم دالة في مقطع معين ، نجد قيمها في نهايات المقطع وعند النقطة الحرجة التي تم العثور عليها:

نتيجة جميع الإجراءات: تصل الدالة إلى أدنى قيمة لها، تساوي 0 ، عند نقطة وعند نقطة و أعظم قيمةيساوي ه² ، عند هذه النقطة.

مثال 7. أوجد أصغر وأكبر قيم للدالة في الجزء .

قرار. نجد مشتق هذه الوظيفة:

يساوي المشتق بصفر:

النقطة الحرجة الوحيدة تنتمي إلى المقطع. للعثور على أصغر وأكبر قيم دالة في مقطع معين ، نجد قيمها في نهايات المقطع وعند النقطة الحرجة التي تم العثور عليها:

خاتمة: تصل الدالة إلى أدنى قيمة لها، يساوي ، عند النقطة و أعظم قيمة، يساوي ، عند هذه النقطة.

في المسائل المتطرفة المطبقة ، يتم تقليل إيجاد أصغر (أكبر) قيم دالة ، كقاعدة عامة ، لإيجاد الحد الأدنى (الحد الأقصى). لكن ليست الحدود الدنيا أو القصوى نفسها هي التي لها أهمية عملية أكبر ، ولكن قيم الحجة التي يتم تحقيقها من خلالها. عند حل المشكلات التطبيقية ، تنشأ صعوبة إضافية - تجميع الوظائف التي تصف الظاهرة أو العملية قيد الدراسة.

المثال 8يجب أن يكون الخزان بسعة 4 ، على شكل خط متوازي بقاعدة مربعة ومفتوح من الأعلى ، معلبًا. ماذا يجب أن تكون أبعاد الخزان لتغطيته بأقل كمية من المواد؟

قرار. اسمحوا ان x- جانب القاعدة ح- ارتفاع الخزان ، س- مساحة سطحه بدون غطاء ، الخامس- حجمه. يتم التعبير عن مساحة سطح الخزان بالصيغة ، أي هي دالة لمتغيرين. للتعبير سكدالة لمتغير واحد ، نستخدم حقيقة أنه من أين. استبدال التعبير الموجود حفي صيغة س:

دعونا نفحص هذه الوظيفة لأقصى حد. يتم تعريفه وقابل للتفاضل في كل مكان في] 0 و + [و

.

نحن نساوي المشتق بصفر () ونوجد النقطة الحرجة. بالإضافة إلى ذلك ، في ، المشتق غير موجود ، ولكن هذه القيمة غير مدرجة في مجال التعريف وبالتالي لا يمكن أن تكون نقطة قصوى. لذا ، - النقطة الحرجة الوحيدة. دعنا نتحقق من وجود الحد الأقصى باستخدام الثانية علامة كافية. لنجد المشتق الثاني. عندما يكون المشتق الثاني أكبر من صفر (). هذا يعني أنه عندما تصل الوظيفة إلى الحد الأدنى . لأن هذا الحد الأدنى - الحد الأقصى الوحيد لهذه الوظيفة ، هو أصغر قيمة لها. لذلك ، يجب أن يكون جانب قاعدة الخزان مساويًا لـ 2 متر وارتفاعه.

المثال 9من فقرة أ، الواقعة على خط السكة الحديد ، حتى هذه النقطة مع، على مسافة منه ليجب نقل البضائع. تكلفة نقل وحدة وزن لكل وحدة مسافة بالسكك الحديدية تساوي وتساوي تكلفة نقلها بالطرق السريعة. إلى أي نقطة مخطوط سكة حديديةيجب بناء طريق سريع بحيث يتم نقل البضائع من لكنفي معكان الأكثر اقتصادا ABمن المفترض أن تكون السكة الحديدية مستقيمة)؟

من الناحية العملية ، من الشائع استخدام المشتق لحساب أكبر وأصغر قيمة للدالة. نقوم بهذا الإجراء عندما نتوصل إلى كيفية تقليل التكاليف وزيادة الأرباح والحساب الحمل الأمثلللإنتاج ، وما إلى ذلك ، أي في الحالات التي يكون فيها من الضروري تحديد القيمة المثلىأي معلمة. لحل هذه المشكلات بشكل صحيح ، يجب أن يكون لدى المرء فهم جيد لما هي أكبر وأصغر قيمة للدالة.

Yandex.RTB R-A-339285-1

عادةً ما نحدد هذه القيم ضمن فترة زمنية معينة x ، والتي بدورها يمكن أن تتوافق مع النطاق الكامل للوظيفة أو جزء منها. يمكن أن يكون إما مقطعًا [a ؛ ب] ، وفترة مفتوحة (أ ؛ ب) ، (أ ؛ ب] ، [أ ؛ ب) ، فاصل لانهائي (أ ؛ ب) ، (أ ؛ ب] ، [أ ؛ ب) أو فاصل لانهائي - ؛ أ ، (- ∞ ؛ أ] ، [أ ؛ +) ، (- ∞ ؛ + ∞).

في هذه المقالة ، سنشرح كيف يتم حساب القيم الأكبر والأصغر بشكل صريح. وظيفة معينةبمتغير واحد y = f (x) y = f (x).

التعاريف الأساسية

نبدأ ، كما هو الحال دائمًا ، بصياغة التعاريف الرئيسية.

التعريف 1

أكبر قيمة للدالة y = f (x) في بعض الفترات x هي القيمة m a x y = f (x 0) x ∈ X ، والتي ، لأي قيمة x x ∈ X ، x ≠ x 0 ، تجعل المتباينة f (x ) ≤ و (× 0).

التعريف 2

أصغر قيمة للدالة y = f (x) في بعض الفترات x هي القيمة m i n x ∈ X y = f (x 0) ، والتي ، لأي قيمة x ∈ X ، x ≠ x 0 ، تجعل المتباينة f (X و (س) ≥ و (س 0).

هذه التعريفات واضحة إلى حد ما. أسهل من ذلك ، يمكنك قول هذا: أكبر قيمة للدالة هي أكثرها أهمية عظيمةفي فترة معروفة عند الحد الأقصى × 0 ، والأصغر هي أصغر قيمة مقبولة على نفس الفترة عند x 0.

التعريف 3

النقاط الثابتة هي قيم وسيطة الوظيفة التي يصبح فيها مشتقها 0.

لماذا نحتاج إلى معرفة ما هي النقاط الثابتة؟ للإجابة على هذا السؤال ، علينا أن نتذكر نظرية فيرما. ويترتب على ذلك أن النقطة الثابتة هي النقطة التي يقع عندها الحد الأقصى لوظيفة قابلة للتفاضل (أي الحد الأدنى أو الحد الأقصى المحلي). وبالتالي ، ستأخذ الوظيفة أصغر أو أكبر قيمة في فترة زمنية معينة بالضبط عند إحدى النقاط الثابتة.

يمكن أن تأخذ وظيفة أخرى أكبر أو أصغر قيمة في تلك النقاط التي تكون فيها الوظيفة نفسها محددة ، ومشتقها الأول غير موجود.

السؤال الأول الذي يطرح نفسه عند دراسة هذا الموضوع هو: في جميع الحالات ، هل يمكننا تحديد الحد الأقصى أو الحد الأدنى لقيمة دالة في فترة زمنية معينة؟ لا ، لا يمكننا القيام بذلك عندما تتطابق حدود الفترة الزمنية مع حدود مجال التعريف ، أو إذا كنا نتعامل مع فترة لا نهائية. يحدث أيضًا أن الوظيفة في فترة زمنية معينة أو في اللانهاية سوف تستغرق متناهية الصغر أو لانهائية قيم كبيرة. في هذه الحالات ، لا يمكن تحديد القيمة الأكبر و / أو الأصغر.

ستصبح هذه اللحظات أكثر قابلية للفهم بعد الصورة على الرسوم البيانية:

يوضح لنا الشكل الأول دالة تأخذ أكبر وأصغر القيم (m a x y و m i n y) عند نقاط ثابتة تقع في الفترة [- 6 ؛ 6].

دعونا نفحص بالتفصيل الحالة المشار إليها في الرسم البياني الثاني. دعنا نغير قيمة المقطع إلى [1 ؛ 6] ونحصل على أن أكبر قيمة للدالة ستتحقق عند النقطة التي تكون فيها الإحداثيات في الحد الأيمن للفاصل الزمني ، والأصغر - عند النقطة الثابتة.

في الشكل الثالث ، تمثل أحواف النقاط نقاط حدود المقطع [- 3 ؛ 2]. تتوافق مع أكبر وأصغر قيمة للدالة المحددة.

الآن دعونا نلقي نظرة على الصورة الرابعة. في ذلك ، تأخذ الوظيفة m a x y (أكبر قيمة) و m i n y (أصغر قيمة) عند نقاط ثابتة في الفترة المفتوحة (- 6 ؛ 6).

إذا أخذنا الفاصل الزمني [1؛ 6) ، فيمكننا القول أنه سيتم الوصول إلى أصغر قيمة للوظيفة الموجودة عليها عند نقطة ثابتة. لن نعرف القيمة القصوى. يمكن أن تأخذ الدالة أكبر قيمة عند x تساوي 6 إذا كانت x = 6 تنتمي إلى الفترة الزمنية. هذه هي الحالة الموضحة في الشكل 5.

في الرسم البياني 6 ، تكتسب هذه الوظيفة أصغر قيمة في الحد الأيمن من الفترة الزمنية (- 3 ؛ 2] ، ولا يمكننا استخلاص استنتاجات محددة حول القيمة الأكبر.

في الشكل 7 ، نلاحظ أن الدالة سيكون لها m a x y عند النقطة الثابتة ، بحيث يساوي الإحداثي السيني 1. تصل الدالة إلى أدنى قيمة لها عند حد الفاصل الزمني على الجانب الأيمن. عند طرح ما لا نهاية ، ستقترب قيم الدالة بشكل مقارب من y = 3.

إذا أخذنا فترة x ∈ 2؛ + ∞ ، سنرى أن الوظيفة المعينة لن تأخذها سواء أصغر أو أكبر قيمة. إذا كانت x تميل إلى 2 ، فإن قيم الدالة تميل إلى سالب ما لا نهاية ، لأن الخط المستقيم x = 2 هو خط مقارب رأسي. إذا كانت الإحداثيات تميل إلى زائد اللانهاية ، فإن قيم الدالة ستقترب بشكل مقارب من y = 3. هذه هي الحالة الموضحة في الشكل 8.

في هذه الفقرة ، سنقدم سلسلة من الإجراءات التي يجب القيام بها للعثور على أكبر أو أصغر قيمة للدالة في فترة زمنية معينة.

1. أولًا ، لنجد مجال الدالة. دعنا نتحقق مما إذا كان المقطع المحدد في الشرط مدرجًا فيه.
2. الآن لنحسب النقاط التي يحتوي عليها هذا المقطع والتي لا يوجد عندها المشتق الأول. في أغلب الأحيان يمكن العثور عليها في الوظائف التي تكتب حججها تحت علامة الوحدة أو في وظائف الطاقة، الذي يمثل الأس عددًا كسريًا.
3. بعد ذلك ، نكتشف النقاط الثابتة التي تقع في مقطع معين. للقيام بذلك ، تحتاج إلى حساب مشتق الدالة ، ثم مساواتها بالصفر وحل المعادلة الناتجة ، ثم اختيار الجذور المناسبة. إذا لم نحصل على نقطة ثابتة واحدة أو لم تقع في جزء معين ، فإننا ننتقل إلى الخطوة التالية.
4. دعونا نحدد القيم التي ستتخذها الوظيفة عند النقاط الثابتة المعينة (إن وجدت) ، أو في تلك النقاط التي لا يوجد فيها المشتق الأول (إن وجد) ، أو نحسب قيم x = a و x = ب.
5. 5. لدينا سلسلة من قيم الدالة ، والتي نحتاج الآن إلى اختيار الأكبر والأصغر منها. ستكون هذه أكبر وأصغر قيم للدالة التي نحتاج إلى إيجادها.

دعونا نرى كيفية تطبيق هذه الخوارزمية بشكل صحيح عند حل المشكلات.

مثال 1

شرط:الدالة y = x 3 + 4 x 2 معطاة. تحديد أكبر وأصغر قيمة لها على المقاطع [1؛ 4] و [- 4 ؛ - واحد ] .

قرار:

لنبدأ بإيجاد مجال هذه الوظيفة. في هذه الحالة ، ستكون مجموعة جميع الأعداد الحقيقية باستثناء 0. بمعنى آخر ، D (y): x ∈ (- ∞ ؛ 0) ∪ 0 ؛ + ∞. سيكون كلا الجزأين المحددين في الشرط داخل منطقة التعريف.

الآن نحسب مشتق الدالة وفقًا لقاعدة اشتقاق الكسر:

y "= x 3 + 4 x 2" = x 3 + 4 "x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3-4) 2 x x 4 = x 3-8 × 3

تعلمنا أن مشتق الوظيفة سيكون موجودًا في جميع نقاط المقاطع [1 ؛ 4] و [- 4 ؛ - واحد ] .

نحتاج الآن إلى تحديد النقاط الثابتة للدالة. لنفعل هذا بالمعادلة x 3 - 8 x 3 = 0. لها جذر حقيقي واحد فقط ، وهو 2. ستكون نقطة ثابتة للوظيفة وستندرج في المقطع الأول [1 ؛ 4].

دعونا نحسب قيم الوظيفة في نهايات المقطع الأول وعند نقطة معينة ، أي بالنسبة إلى x = 1 و x = 2 و x = 4:

ص (1) = 1 3 + 4 1 2 = 5 ص (2) = 2 3 + 4 2 2 = 3 ص (4) = 4 3 + 4 4 2 = 4 1 4

لقد حصلنا على أكبر قيمة للدالة m a x y x ∈ [1؛ 4] = y (2) = 3 ستتحقق عند x = 1 ، والأصغر m i n y x ∈ [1؛ 4] = y (2) = 3 - عند x = 2.

لا يتضمن المقطع الثاني أي نقاط ثابتة ، لذلك نحتاج إلى حساب قيم الوظيفة فقط في نهايات المقطع المحدد:

ص (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

ومن ثم ، m a x y x ∈ [- 4 ؛ - 1] = y (- 1) = 3، m i n y x ∈ [- 4 ؛ - 1] = ص (- 4) = - 3 3 4.

إجابه:لشريحة [1 ؛ 4] - م أ س ص س ∈ [1 ؛ 4] = y (2) = 3، m i n y x ∈ [1؛ 4] = y (2) = 3 ، للقطاع [- 4 ؛ - 1] - م أ س ص س ∈ [- 4 ؛ - 1] = y (- 1) = 3، m i n y x ∈ [- 4 ؛ - 1] = ص (- 4) = - 3 3 4.

انظر الصورة:

قبل الدراسة من هناننصحك بتكرار كيفية حساب الحد من جانب واحد والنهاية بشكل صحيح عند اللانهاية ، وكذلك تعلم الطرق الأساسية للعثور عليها. للعثور على أكبر و / أو أصغر قيمة للدالة في فترة مفتوحة أو لانهائية ، نقوم بتنفيذ الخطوات التالية بالتسلسل.

1. تحتاج أولاً إلى التحقق مما إذا كان الفاصل الزمني المحدد سيكون مجموعة فرعية من مجال الوظيفة المحددة.
2. دعونا نحدد جميع النقاط الموجودة في الفترة الزمنية المطلوبة والتي لا يوجد فيها المشتق الأول. عادةً ما تكون للوظائف التي تكون فيها الوسيطة محاطة بعلامة المقياس ، وللوظائف الأسرية ذات الكسور مؤشر منطقي. إذا كانت هذه النقاط مفقودة ، فيمكنك المتابعة إلى الخطوة التالية.
3. الآن نحدد النقاط الثابتة التي تقع في فترة زمنية معينة. أولًا ، نساوي المشتق بالصفر ، ونحل المعادلة ونوجد الجذور المناسبة. إذا لم يكن لدينا نقطة ثابتة واحدة أو لم تقع في فترة زمنية معينة ، فإننا ننتقل على الفور إلى مزيد من العمل. يتم تحديدها حسب نوع الفاصل الزمني.

• إذا كان الفاصل الزمني يشبه [a ؛ ب) ، ثم نحتاج إلى حساب قيمة الوظيفة عند النقطة x = a والحد من جانب واحد lim x → b - 0 f (x).
• إذا كان الفاصل الزمني له الشكل (أ ؛ ب] ، فإننا نحتاج إلى حساب قيمة الوظيفة عند النقطة س = ب والحد من جانب واحد lim x → a + 0 f (x).
• إذا كان الفاصل الزمني له الشكل (أ ؛ ب) ، فنحن بحاجة إلى حساب الحدود من جانب واحد lim x → b - 0 f (x) ، lim x → a + 0 f (x).
• إذا كان الفاصل الزمني يشبه [a ؛ + ∞) ، إذن من الضروري حساب القيمة عند النقطة x = a والحد من زائد اللانهاية lim x → + ∞ f (x).
• إذا كان الفاصل الزمني يشبه (- ∞ ؛ ب] ، نحسب القيمة عند النقطة x = b والحد عند سالب اللانهاية lim x → - ∞ f (x).
• إذا - ∞ ؛ ب ، ثم نعتبر الحد من جانب واحد lim x → b - 0 f (x) والحد عند ناقص اللانهاية lim x → - f (x)
• إذا - ∞ ؛ + ∞ ، ثم نعتبر حدود سالب زائد اللانهاية lim x → + ∞ f (x) ، lim x → - ∞ f (x).

1. في النهاية ، تحتاج إلى استخلاص نتيجة بناءً على القيم التي تم الحصول عليها للوظيفة والحدود. هناك العديد من الخيارات هنا. لذا ، إذا كان الحد من جانب واحد يساوي سالب ما لا نهاية أو زائد ما لا نهاية ، فمن الواضح على الفور أنه لا يمكن قول أي شيء عن أصغر وأكبر قيمة للدالة. أدناه سننظر في مثال نموذجي واحد. الأوصاف التفصيليةتساعدك على فهم ما هو. إذا لزم الأمر ، يمكنك العودة إلى الأشكال من 4 إلى 8 في الجزء الأول من المادة.

الشرط: معطى دالة y = 3 e 1 x 2 + x - 6-4. احسب أكبر وأصغر قيمة لها في الفترات - ∞ ؛ - 4 ، - ∞ ؛ - 3 ، (- 3 ؛ 1] ، (- 3 ؛ 2) ، [1 ؛ 2) ، 2 ؛ + ∞ ، [4 ؛ + ∞).

قرار

أولًا ، نجد مجال الدالة. مقام الكسر هو ثلاثي الحدود مربع، والتي لا يجب أن تتحول إلى 0:

س 2 + س - 6 = 0 د = 1 2-4 1 (- 6) = 25 × 1 = - 1-5 2 = - 3 × 2 = - 1 + 5 2 = 2 د (ص): س ∈ (- ∞ ؛ - 3) ∪ (- 3 ؛ 2) ∪ (2 ؛ +)

لقد حصلنا على نطاق الوظيفة التي تنتمي إليها جميع الفترات الزمنية المحددة في الشرط.

الآن دعنا نفرق الدالة ونحصل على:

y "= 3 e 1 x 2 + x - 6-4" = 3 e 1 x 2 + x - 6 "= 3 e 1 x 2 + x - 6 1 x 2 + x - 6" == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6-1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + س - 6 2

وبالتالي ، توجد مشتقات الوظيفة في النطاق الكامل لتعريفها.

دعنا ننتقل إلى إيجاد النقاط الثابتة. يصبح مشتق الدالة 0 عند x = - 1 2. هذه نقطة ثابتة تقع في الفواصل الزمنية (- 3 ؛ 1] و (- 3 ؛ 2).

دعنا نحسب قيمة الدالة عند x = - 4 للفترة (- ∞ ؛ - 4] ، وكذلك الحد عند سالب ما لا نهاية:

ص (- 4) \ u003d 3 e 1 (- 4) 2 + (- 4) - 6-4 \ u003d 3 e 1 6-4 ≈ - 0. 456 ليم س → - ∞ 3 ه 1 س 2 + س - 6 = 3 ه 0 - 4 = - 1

بما أن 3 e 1 6-4> - 1 ، ثم m a x y x ∈ (-؛ - 4] = y (- 4) = 3 e 1 6 - 4. هذا لا يسمح لنا بتحديد أصغر قيمة للدالة بشكل فريد. يمكننا فقط أن نستنتج أن هناك حدًا أقل من - 1 ، نظرًا لأن هذه القيمة تقترب من التقارب عند سالب اللانهاية.

من سمات الفاصل الزمني الثاني أنه لا يحتوي على نقطة ثابتة واحدة وليس حدًا صارمًا واحدًا. لذلك ، لا يمكننا حساب أكبر قيمة للدالة أو أصغرها. من خلال تحديد الحد عند سالب ما لا نهاية وبما أن الوسيطة تميل إلى - 3 على الجانب الأيسر ، نحصل فقط على نطاق القيم:

ليم س → - 3 - 0 3 ه 1 س 2 + س - 6-4 = ليم س → - 3-0 3 ه 1 (س + 3) (س - 3) - 4 = 3 ه 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + - 4 = + lim x → - ∞ 3 e 1 x 2 + x - 6-4 = 3 e 0-4 = - 1

هذا يعني أن قيم الوظيفة ستكون موجودة في الفاصل الزمني - 1 ؛ + ∞

للعثور على القيمة القصوى للدالة في الفترة الثالثة ، نحدد قيمتها عند النقطة الثابتة x = - 1 2 إذا كانت x = 1. نحتاج أيضًا إلى معرفة الحد من جانب واحد للحالة عندما تميل الوسيطة إلى - 3 على الجانب الأيمن:

ص - 1 2 = 3 هـ 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 ه 4 25 - 4 ≈ - 1. 444 ص (1) = 3 هـ 1 1 2 + 1 - 6 - 4 ≈ - 1. 644 ليم x → - 3 + 0 3 e 1 x 2 + x - 6-4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1-3 + 0 + 3 (- 3 + 0-2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0-4 = - 4

اتضح أن الوظيفة ستأخذ أكبر قيمة عند نقطة ثابتة m a x y x ∈ (3 ؛ 1] = y - 1 2 = 3 e - 4 25-4. أما بالنسبة لأصغر قيمة ، فلا يمكننا تحديدها. كل هذا نحن تعرف ، هو وجود حد أدنى لـ - 4.

بالنسبة للفاصل الزمني (- 3 ؛ 2) ، دعنا نأخذ نتائج الحساب السابق ونحسب مرة أخرى ما يساوي الحد من جانب واحد عند الاتجاه إلى 2 من الجانب الأيسر:

ص - 1 2 = 3 هـ 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 هـ - 4 25 - 4 ≈ - 1. 444 ليم x → - 3 + 0 3 e 1 x 2 + x - 6-4 = - 4 ليم x → 2-0 3 e 1 x 2 + x - 6-4 = lim x → - 3 + 0 3 e 1 (س + 3) (س - 2) - 4 = 3 هـ 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = 3 هـ 1 - 0 - 4 = 3 هـ - ∞ - 4 = 3 0-4 = - 4

ومن ثم ، م أ س ص س ∈ (- 3 ؛ 2) = ص - 1 2 = 3 هـ - 4 25-4 ، ولا يمكن تحديد أصغر قيمة ، وقيم الوظيفة مقيدة من أسفل بالرقم - 4.

بناءً على ما فعلناه في الحسابين السابقتين ، يمكننا التأكيد على ذلك في الفترة [1 ؛ 2) تأخذ الدالة أكبر قيمة عند x = 1 ، ومن المستحيل إيجاد أصغرها.

في الفاصل الزمني (2 ؛ + ∞) ، لن تصل الوظيفة إلى القيمة الأكبر أو الأصغر ، أي سيأخذ القيم من الفاصل الزمني - 1 ؛ + ∞.

ليم س → 2 + 0 3 ه 1 س 2 + س - 6-4 = ليم س → - 3 + 0 3 ه 1 (س + 3) (س - 2) - 4 = 3 ه 1 (2 + 0 + 3 ) (2 + 0-2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + lim x → + 3 e 1 x 2 + x - 6-4 = 3 e 0-4 = - 1

بعد حساب قيمة الدالة عند x = 4 ، نجد أن m a x y x ∈ [4؛ + ∞) = y (4) = 3 e 1 14-4 ، والدالة المعطاة عند زائد اللانهاية ستقترب بشكل مقارب من الخط y = - 1.

لنقارن ما حصلنا عليه في كل عملية حسابية بالرسم البياني للدالة المحددة. في الشكل ، تظهر الخطوط المقاربة بخطوط منقطة.

هذا كل ما أردنا التحدث عنه حول إيجاد أكبر وأصغر قيمة للدالة. ستساعدك تسلسلات الإجراءات التي قدمناها على إجراء الحسابات اللازمة بأسرع ما يمكن وببساطة. لكن تذكر أنه غالبًا ما يكون من المفيد أولاً معرفة الفواصل الزمنية التي ستنخفض فيها الوظيفة وفي الفترات الزمنية التي ستزيد فيها ، وبعد ذلك يمكن استخلاص المزيد من الاستنتاجات. حتى تتمكن من تحديد أكبر وأصغر قيمة للدالة بشكل أكثر دقة وتبرير النتائج.

إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter