Ko'p yuzli qismlarni qurish bilan bog'liq muammolar muhim o'rin tutadi maktab kursi o'rta maktab uchun geometriya va turli darajadagi imtihonlarda. Ushbu turdagi muammolarni hal qilish stereometriya aksiomalarini o'zlashtirishga, bilim va ko'nikmalarni tizimlashtirishga, fazoviy tushunish va konstruktiv ko'nikmalarni rivojlantirishga yordam beradi. Bo'limlarni qurish bilan bog'liq muammolarni hal qilishda yuzaga keladigan qiyinchiliklar yaxshi ma'lum.

Erta bolalikdan biz bo'limlarga duch kelamiz. Biz non, kolbasa va boshqa mahsulotlarni kesib, pichoq bilan tayoq yoki qalamni rejalashtiramiz. Bu barcha holatlarda kesish tekisligi pichoq tekisligidir. Bo'limlar (bo'laklarni kesish) boshqacha bo'lib chiqadi.

Qavariq ko‘pburchak kesimi qavariq ko‘pburchak bo‘lib, uning uchlari umumiy holatda kesuvchi tekislikning ko‘pburchak chetlari bilan kesishish nuqtalari, yon tomonlari esa kesuvchi tekislikning yuzlar bilan kesishish chiziqlari hisoblanadi. .

Ikki tekislikning kesishgan to'g'ri chizig'ini qurish uchun ikkitasini topish kifoya umumiy nuqtalar bu tekisliklar va ular orqali to'g'ri chiziq o'tkazing. Bu quyidagi bayonotlarga asoslanadi:

1. agar chiziqning ikkita nuqtasi tekislikka tegishli bo'lsa, u holda butun chiziq shu tekislikka tegishlidir;

2. agar ikki xil tekislikning umumiy nuqtasi bo‘lsa, u holda ular shu nuqtadan o‘tuvchi to‘g‘ri chiziq bo‘ylab kesishadi.

Yuqorida aytib o'tganimdek, ko'p yuzli kesimlarni qurish stereometriya aksiomalari va chiziqlar va tekisliklarning parallelligi haqidagi teoremalar asosida amalga oshirilishi mumkin. Shu bilan birga, ko'pburchakning tekis qismlarini qurishning ma'lum usullari mavjud. Quyidagi uchta usul eng samarali hisoblanadi:

Izlash usuli

Ichki dizayn usuli

Kombinatsiyalangan usul.

Geometriyani o'rganishda, xususan, uning geometrik figuralarning tasvirlari ko'rib chiqiladigan bo'limlarida, geometrik figuralarning tasvirlari kompyuter taqdimotlaridan foydalanishga yordam beradi. Kompyuter yordamida ko'plab geometriya darslari vizual va dinamik bo'ladi. Aksiomalar, teoremalar, isbotlar, qurish masalalari, kesma qurish masalalari monitor ekranida ketma-ket konstruktsiyalar bilan birga bo'lishi mumkin. Kompyuter yordamida chizilgan chizmalar saqlanishi va boshqa hujjatlarga kiritilishi mumkin.

Men "Geometrik jismlarda kesmalarni qurish" mavzusida bir nechta slaydlarni ko'rsatmoqchiman.

Chiziq va tekislikning kesishish nuqtasini qurish uchun tekislikda berilgan chiziqni kesib o'tuvchi chiziqni toping. Keyin kerakli nuqta topilgan chiziqning berilgan bilan kesishish nuqtasidir. Buni keyingi slaydlarda ko'rib chiqamiz.

Vazifa 1.

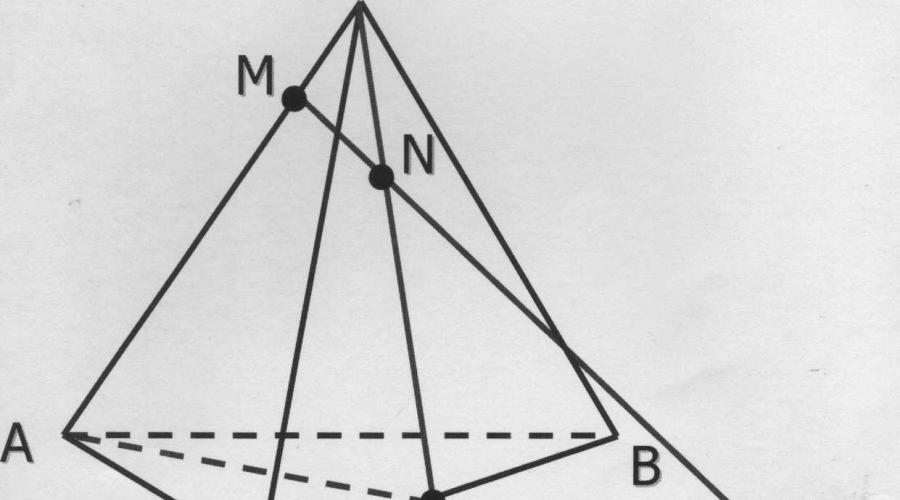
DABC tetraedrining chetlarida ikkita M va N nuqtalar belgilangan; M GAD, N b DC. MN to‘g‘ri chiziqning asos tekisligi bilan kesishish nuqtasini ko‘rsating.

Yechish: MN chiziqning tekislik bilan kesishgan nuqtasini topish uchun

Biz bazani AC va MN segmenti bilan davom ettiramiz. Bu chiziqlarning X orqali kesishgan nuqtasini belgilaymiz. X nuqta MN to'g'ri chiziq va AC yuziga tegishli, AC esa asos tekisligida yotadi, demak X nuqta ham asos tekisligida yotadi. Demak, X nuqta MN to'g'ri chiziqning asos tekisligi bilan kesishgan nuqtasidir.

Keling, ikkinchi muammoni ko'rib chiqaylik. Keling, buni biroz murakkablashtiraylik.

Vazifa 2.

M va N nuqtalarning DABC tetraedri berilgan, bu erda M € DA, N C (DBC). MN to‘g‘ri chiziqning ABC tekislik bilan kesishgan nuqtasini toping.

Yechish: MN to‘g‘rining ABC tekisligi bilan kesishgan nuqtasi MN chiziqni o‘z ichiga olgan tekislikda va asos tekisligida yotishi kerak. DN segmentini DC chekkasi bilan kesishish nuqtasiga qadar davom ettiramiz. Biz kesishish nuqtasini E orqali belgilaymiz. AE va MN chizig'ini ularning kesishish nuqtasiga davom ettiramiz. X ni belgilaymiz. X nuqta MN ga tegishli, demak u MN chiziqni o'z ichiga olgan tekislikda va X AE ga tegishli, AE esa ABC tekislikda yotadi. Demak, X ham ABC tekisligida yotadi. Shuning uchun X MN to'g'ri chiziq bilan ABC tekislikning kesishish nuqtasidir.

Keling, vazifani murakkablashtiramiz. Berilgan uchta nuqtadan o'tuvchi tekisliklar bo'yicha geometrik figuralarning kesimini ko'rib chiqaylik.

Muammo 3

DABC tetraedrining AC, AD va DB chekkalarida M, N va P nuqtalar belgilangan. MNP tekisligidan foydalanib tetraedrning kesimini tuzing.

Yechish: tekislik MNP bo'lgan to'g'ri chiziqni qurish. ABC yuz tekisligini kesib o'tadi. M nuqtasi bu tekisliklarning umumiy nuqtasidir. Yana bir umumiy nuqtani qurish uchun biz AB va NP segmentini davom ettiramiz. Biz kesishish nuqtasini X orqali belgilaymiz, bu MNP va ABC tekisliklarining ikkinchi umumiy nuqtasi bo'ladi. Demak, bu tekisliklar MX to‘g‘ri chiziq bo‘ylab kesishadi. MX BC qirrasini qaysidir E nuqtasida kesib o'tadi. E MX ustida joylashgani uchun va MX MNP tekisligiga tegishli chiziq bo'lganligi sababli, PE MNP ga tegishli. To'rtburchak MNPE - kerakli qism.

Muammo 4

ABCA1B1C1 to'g'ri prizmaning P nuqtalardan o'tuvchi tekislik bilan kesmasini quramiz. , Q,R, bu yerda R tegishli ( A.A. 1C 1C), R tegishli IN 1C1,

Q ABga tegishli

Yechim: Uchalasi ham P, Q, R nuqtalari turli yuzlarda yotadi, shuning uchun biz prizmaning biron bir yuzi bilan kesish tekisligining kesishish chizig'ini hali qura olmaymiz. Keling, bir nuqtani topaylik PRning ABC bilan kesishishi. P va R nuqtalarning BC ga perpendikulyar PP1 asos tekisligiga va AC ga perpendikulyar RR1 proyeksiyalarini topamiz. P1R1 chizig'i PR chizig'ini X nuqtada kesib o'tadi. X - PR to'g'ri chiziqning ABC tekisligi bilan kesishish nuqtasi. U kerakli K tekislikda va Q nuqtasi kabi asos tekisligida yotadi. XQ - K ni asos tekisligi bilan kesib o'tuvchi to'g'ri chiziq. XQ AC ni K nuqtada kesib o'tadi. Demak, KQ X tekislikning ABC yuzi bilan kesishgan segmentidir. K va R X tekislikda va yuzning AA1S1S tekisligida yotadi. KR to'g'ri chiziq chizamiz va A1Q E bilan kesishgan nuqtani belgilaymiz. KE - X tekislikning shu yuz bilan kesishish chizig'i. X tekislikning BB1A1A yuzlar tekisligi bilan kesishish chizig‘ini topamiz. KE A1A bilan Y nuqtada kesishadi.QY to'g'ri chiziq kesuvchi tekislikning AA1B1B tekislik bilan kesishish chizig'idir. FPEKQ - kerakli bo'lim.

Stereometriyada ko'p yuzli kesimlar usuli qurilish masalalarida qo'llaniladi. U ko'pburchakning kesimini qurish va kesma turini aniqlash qobiliyatiga asoslangan.

Ushbu material quyidagi xususiyatlar bilan ajralib turadi:

1. Bo'limlar usuli faqat ko'pburchaklar uchun qo'llaniladi, chunki aylanish jismlarining turli xil murakkab (qiyshiq) turlari o'rta maktab o'quv dasturiga kiritilmagan.
2. Muammolar, asosan, eng oddiy polihedradan foydalanadi.
3. Muammolar ko'p martalik foydalanish imkoniyatini yaratish uchun asosan raqamli ma'lumotlarsiz taqdim etiladi.

Ko'pburchak kesimini qurish masalasini hal qilish uchun talaba bilishi kerak:

• ko'pburchakning tekislik bilan kesmasini qurish nimani anglatadi;
• ko'pburchak va tekislikni bir-biriga nisbatan qanday joylashtirish mumkin;
• tekislik qanday aniqlanadi;
• ko'pburchak kesimini tekislik bilan qurish masalasi hal qilingan deb hisoblanganda.

Chunki tekislik aniqlangan:

• uch ball;
• to'g'ri chiziq va nuqta;
• ikkita parallel chiziq;
• ikkita kesishgan chiziq,

Bo'lim tekisligining qurilishi ushbu tekislikning spetsifikatsiyasiga bog'liq. Shuning uchun ko'pburchaklar kesimlarini qurishning barcha usullarini usullarga bo'lish mumkin.

Mavjud uchta asosiy usul ko'p yuzli qismlarni qurish:

1. Izlash usuli.
2. Yordamchi bo'limlar usuli.
3. Kombinatsiyalangan usul.

Birinchi ikkita usul o'zgaruvchanlikdir Aksiomatik usul bo'limlarni qurish.

Shuningdek, biz ko'pburchaklar bo'limlarini qurishning quyidagi usullarini ajratib ko'rsatishimiz mumkin:

• tekislik o'tadigan ko'pburchakning kesimini qurish berilgan nuqta berilgan tekislikka parallel;
• berilgan chiziqdan boshqa berilgan chiziqqa parallel ravishda o'tuvchi kesmani qurish;
• berilgan nuqtadan ikkita berilgan kesishuvchi chiziqqa parallel ravishda o‘tuvchi kesmani qurish;
• berilgan tekislikka perpendikulyar berilgan chiziqdan o'tuvchi tekislik bilan ko'pburchakning kesmasini qurish;
• berilgan to‘g‘ri chiziqqa perpendikulyar berilgan nuqtadan o‘tuvchi tekislik bilan ko‘pburchak kesimini qurish.

10-11-sinflar uchun geometriya darsliklarining federal ro'yxati quyidagi mualliflarning darsliklarini o'z ichiga oladi:

• Atanasyan L.S., Butuzova V.F., Kadomtseva S.B. va boshqalar (Geometriya, 10-11);
• Pogorelova A.V. (Geometriya, 7-11);
• Aleksandrova A.D., Vernera A.L., Ryjik V.I. (Geometriya, 10-11);
• Smirnova I.M. (Geometriya, 10-11);
• Sharygina I.F. (Geometriya, 10-11).

Keling, L.S., Atanasyan va A.V. Pogorelovning darsliklarini batafsil ko'rib chiqaylik.

Darslikda L.S. Atanasyanga “Ko‘p yuzli bo‘limlarni qurish” mavzusiga ikki soat vaqt ajratildi. 10-sinfda “Chiziqlar va tekisliklarning parallelligi” mavzusida tetraedr va parallelepipedni o‘rgangach, “Kesmalarni qurish masalalari” bandini taqdim etishga bir soat vaqt ajratiladi. Tetraedr va parallelepipedning kesimlari ko'rib chiqiladi. “Chiziqlar va tekisliklarning parallelligi” mavzusi esa bir yoki ikki soat ichida masalalar yechish bilan tugaydi (darslikda bo‘limlar qurish uchun jami sakkizta masala bor).

Darslikda Pogorelov A.V. "Ko'p yuzli" bo'limida bo'limlarni qurish uchun taxminan uch soat ajratilgan: biri "Prizma tasviri va uning kesmalarini qurish" mavzusini o'rganish uchun, ikkinchisi "Piramida va uning tekislik kesimlarini qurish" mavzusini o'rganish uchun va uchinchi soat. muammolarni hal qilish uchun. Mavzudan keyin berilgan masalalar ro'yxatida faqat o'nga yaqin kesma masalalari mavjud.

Pogorelov A.V. darsligi uchun "Ko'p yuzli kesimlarni qurish" mavzusidagi darslar tizimini taklif qilamiz.

Materialni talabalarga o'qitishda foydalanish mumkin bo'lgan ketma-ketlikda joylashtirish taklif etiladi. “Polyhedra” mavzusi taqdimotidan tizimlashtirish uchun quyidagi bandlarni chiqarib tashlash taklif etiladi: “Prizma kesmalarini qurish” va “Piramida kesmalarini qurish”. bu material ushbu mavzu oxirida "Polyhedra". Taxminan "oddiydan murakkabga" tamoyiliga rioya qilgan holda, vazifalarning predmetiga ko'ra, uni quyidagicha tasniflash mumkin:

1. Ko'pburchaklar kesimini aniqlash.
2. Prizma, parallelepiped, piramida kesmalarini iz usuli yordamida qurish. (Stereometriya bo'yicha maktab kursida, qoida tariqasida, asosiy usullar bilan echilgan ko'pburchak kesimlarini qurish uchun masalalar qo'llaniladi. Boshqa usullar, ularning ko'proqligi tufayli. yuqori daraja murakkabligi bo'lsa, o'qituvchi uni tanlov darslarida ko'rib chiqish yoki mustaqil ta'lim uchun qoldirishi mumkin. Qurilish muammolarida asosiy usullar uch nuqtadan o'tuvchi qism tekisligini qurishni talab qiladi).
3. Ko'pburchakda ko'ndalang kesim maydonini topish (ko'pburchakning ortogonal proyeksiyasi maydoni haqidagi teoremadan foydalanmasdan).
4. Ko'pburchakda ko'ndalang kesim maydonini topish (ko'pburchakning ortogonal proyeksiyasi maydoni haqidagi teoremadan foydalanish).

KO'P YO'LLI BO'LIMLARNI QURUSH UCHUN STEREOMETRIK MASALALARI VA ULARNING 10-11-SINF DARSLARIDA FOYDALANISH USULLARI.

("Ko'p yuzli bo'limlarni qurish" mavzusidagi darslar va fakultativ darslar tizimi)

1-DARS.

Dars mavzusi: "Ko'p yuzli qismlarni qurish."

Darsning maqsadi: ko'p yuzli kesimlarni qurish usullari bilan tanishish.

Dars bosqichlari:

1. Asosiy bilimlarni yangilash.
2. Muammoni shakllantirish.
3. Yangi materialni o'rganish:

A) Bo‘limning ta’rifi.

B) Bo'limlarni qurish usullari:

a) kuzatuv usuli;

b) yordamchi bo'limlar usuli;

c) qo'shma usul.

1. Materialni tuzatish.

Iz usuli yordamida kesmalarni qurishga misollar.

1. Darsni yakunlash.

Darslar davomida.

1. Asosiy bilimlarni yangilash.

Keling, eslaylik:
- to'g'ri chiziqning tekislik bilan kesishishi;
- tekisliklarning kesishishi;
- parallel tekisliklarning xossalari.

2. Muammoni shakllantirish.

Sinf uchun savollar:
- Ko'pburchakning tekislik bilan kesmasini qurish nimani anglatadi?
- Ko'pburchak va tekislikni bir-biriga nisbatan qanday joylashtirish mumkin?
- Samolyot qanday ta'riflanadi?
- Ko'pburchak kesimini tekislik bilan yasash masalasi qachon hal qilingan deb hisoblanadi?

3. Yangi materialni o'rganish.

A) Demak, vazifa ikki figuraning: ko‘pburchak va tekislikning kesishuvini qurishdan iborat (1-rasm). Bular bo'lishi mumkin: bo'sh shakl (a), nuqta (b), segment (c), ko'pburchak (d). Agar ko'pburchak va tekislikning kesishishi ko'pburchak bo'lsa, bu ko'pburchak deyiladi ko'pburchakning tekislik bilan kesmasi.

Biz faqat tekislik ko'pburchakni uning ichki qismi bo'ylab kesib o'tgan holatni ko'rib chiqamiz. Bunday holda, bu tekislikning ko'pburchakning har bir yuzi bilan kesishishi ma'lum bir segment bo'ladi. Shunday qilib, tekislik ko'pburchak yuzlarini kesib o'tadigan barcha segmentlar topilsa, muammo hal qilingan hisoblanadi.

Kubning bo'limlarini ko'rib chiqing (2-rasm) va quyidagi savollarga javob bering:

Kub tekislik bilan kesilganda qanday ko'pburchaklar olinadi? (Ko'pburchakning tomonlar soni muhim);

[Tavsiya etilgan javoblar: uchburchak, to'rtburchak, beshburchak, olti burchakli.]

Kubni samolyot bilan yettiburchak qilib kesish mumkinmi? Sakkizburchak va boshqalar haqida nima deyish mumkin? Nega?

Prizma va uning mumkin bo'lgan kesimlarini tekislik bo'yicha ko'rib chiqamiz (model bo'yicha). Qanday turdagi ko'pburchaklar olinadi?

Qanday xulosa qilish mumkin? Ko'pburchakni tekislik bilan kesish natijasida olingan ko'pburchakning eng ko'p tomonlari qancha?

[ Eng katta raqam Ko'pburchakni tekislik bilan kesish natijasida olingan ko'pburchakning tomonlari ko'pburchak yuzlari soniga teng.]

B) a) Izlash usuli ko'pburchakning har bir yuzining tekisligiga kesish tekisligining izlarini qurishdan iborat. Ko'pburchakning bir qismini iz usuli yordamida qurish odatda kesish tekisligining asosiy izi deb ataladigan qurilishdan boshlanadi, ya'ni. ko'pburchak asosi tekisligida kesish tekisligining izi.

b) Yordamchi bo'limlar usuli ko'p yuzli qismlarni qurish juda universaldir. Kesuvchi tekislikning kerakli izi (yoki izlari) chizmadan tashqarida bo'lgan hollarda, bu usul hatto ma'lum afzalliklarga ega. Shu bilan birga, shuni yodda tutish kerakki, ushbu usul yordamida amalga oshirilgan konstruktsiyalar ko'pincha "olomon" bo'lib chiqadi. Shunga qaramay, ba'zi hollarda yordamchi bo'limlar usuli eng oqilona bo'lib chiqadi.

Iz usuli va yordamchi bo'lim usuli o'zgarishlardir aksiomatik usul tekislik bilan ko'pburchak kesimlarini qurish.

c) mohiyati birlashgan usul ko'p yuzli kesimlarni qurish fazoda to'g'ri va tekisliklarning parallelligi haqidagi teoremalarni aksiomatik usul bilan birgalikda qo'llashdan iborat.

Keling, muammoni hal qilish misolidan foydalanib, ko'rib chiqaylik kuzatish usuli

4. Materialni mahkamlash.

Vazifa 1.

ABCDA 1 B 1 C 1 D 1 prizmasining P, Q, R nuqtalardan o'tuvchi tekislik bilan kesmasini tuzing (nuqtalar chizmada ko'rsatilgan (3-rasm)).

Yechim.

Guruch. 3

1. Prizmaning pastki asosi tekisligiga kesuvchi tekislikning izini yasaymiz. AA 1 B 1 B yuzini ko'rib chiqaylik. Bu yuzda P va Q kesma nuqtalari yotadi, PQ to'g'ri chiziq chizamiz.
2. Kesimga tegishli bo'lgan PQ chizig'ini AB chizig'ini kesib o'tguncha davom ettiramiz. Biz izga tegishli S 1 nuqtani olamiz.
3. Xuddi shunday, biz S 2 nuqtani QR va BC chiziqlarining kesishishi orqali olamiz.
4. S 1 S 2 to'g'ri chiziq - prizmaning pastki poydevori tekisligiga kesuvchi tekislikning izi.
5. S 1 S 2 to'g'ri chiziq AD tomonini U nuqtada, CD yon tomonini T nuqtada kesib o'tadi. P va U nuqtalarni bog'laymiz, chunki ular yuzning bir xil tekisligida AA 1 D 1 D. Biz ham xuddi shunday olamiz. TU va RT.
6. PQRTU - bu zarur bo'lim.

M, N, P nuqtalardan o'tuvchi tekislik bilan ABCDA 1 B 1 C 1 D 1 parallelepiped kesmasini tuzing (nuqtalar chizmada ko'rsatilgan (4-rasm)).

Yechim.

1. N va P nuqtalar kesma tekislikda va parallelepipedning pastki asosi tekisligida yotadi. Keling, ushbu nuqtalar orqali to'g'ri chiziq quramiz. Bu to'g'ri chiziq kesuvchi tekislikning parallelepiped asosi tekisligiga qo'yilgan izidir.
2. AB parallelepipedning qaysi tomonida yotgan to'g'ri chiziqni davom ettiramiz. AB va NP chiziqlar qaysidir S nuqtada kesishadi. Bu nuqta kesma tekisligiga tegishli.
3. Chunki M nuqta ham kesma tekisligiga tegishli va AA 1 chiziqni qaysidir X nuqtada kesib o'tadi.
4. X va N nuqtalar AA 1 D 1 D yuzining bir tekisligida yotib, ularni birlashtirib, XN to'g'ri chiziqni oling.
5. Parallelepipedning yuzlari tekisliklari parallel bo'lganligi sababli, M nuqta orqali NP chizig'iga parallel A 1 B 1 C 1 D 1 yuziga chiziq chizishimiz mumkin. Bu to'g'ri chiziq B 1 C 1 tomonini Y nuqtada kesib o'tadi.
6. Xuddi shunday, XN to'g'ri chiziqqa parallel ravishda YZ to'g'ri chiziq chizamiz. Biz Z ni P bilan bog'laymiz va kerakli bo'limni olamiz - MYZPNX.

3-masala (mustaqil yechim uchun).

M, N, P nuqtalardan o'tuvchi tekislik bilan DACB tetraedri kesmasini tuzing (nuqtalar chizmada ko'rsatilgan (5-rasm)).

5. Darsni yakunlash.

Savolga javob bering: PQR tekisligida tasvirlangan ko'pburchakning soyali figuralari bo'limlarimi? Va to'g'ri qurilishni bajaring (6-rasm).

Variant 1.

Variant 2.

Dars mavzusi: SEKSIONAL MAYODNI TOPISH.

Darsning maqsadi: ko'pburchakning kesma maydonini topish usullari bilan tanishtirish.

Dars bosqichlari:

1. Asosiy bilimlarni yangilash.

Ko'pburchakning ortogonal proyeksiyasi maydoni haqidagi teoremani eslang.

2. Ko'ndalang kesimlar maydonini topishga oid masalalarni yechish:

Ko'pburchakning ortogonal proyeksiyasi maydoni haqidagi teoremadan foydalanmasdan;

Ko'pburchakning ortogonal proyeksiyasi maydoni haqidagi teoremadan foydalanish.

3. Darsni yakunlash.

Darslar davomida.

1. Asosiy bilimlarni yangilash.

Keling, eslaylik ko'pburchakning ortogonal proyeksiyasi maydoni haqidagi teorema: Ko'pburchakning tekislikka ortogonal proyeksiyasining maydoni uning maydoni va ko'pburchak tekisligi bilan proyeksiya tekisligi orasidagi burchak kosinusining mahsulotiga teng.

2. Muammoni hal qilish.

ABCD - to'g'ri uchburchak piramida tayanch tomoni AB bilan teng A va balandligi DH teng h. Piramidaning tekisligi D, C va M nuqtalardan o'tuvchi kesmani tuzing, bu erda M AB tomonining o'rtasi bo'lib, uning maydonini toping (7-rasm).

Piramidaning kesimi MCD uchburchagidir. Keling, uning maydonini topamiz.

S = 1/2 DH CM = 1/2 =

ABCDA 1 B 1 C 1 D 1 qirrali kubning ko‘ndalang kesimini toping. A D cho'qqisidan o'tuvchi tekislik va A 1 D 1 va C 1 D 1 qirralarning E va F nuqtalari, agar A 1 E = k D 1 E va C 1 F = k D 1 F bo'lsa.

Bo'limning qurilishi:

1. E va F nuqtalar kesma tekisligiga va yuzning A 1 B 1 C 1 D 1 tekisligiga tegishli bo'lgani uchun va ikkala tekislik to'g'ri chiziq bo'ylab kesishganligi sababli, EF to'g'ri chiziq kesma tekisligining tekislikdagi izi bo'ladi. yuzning A 1 B 1 C 1 D 1 (8-rasm).
2. To'g'ridan-to'g'ri ED va FD xuddi shu tarzda olinadi.
3. EDF zarur bo'limdir.

3-masala (mustaqil yechim uchun).

ABCDA 1 B 1 C 1 D 1 kubining yon tomoni bilan kesmasini tuzing A B, M va N nuqtalardan o'tuvchi tekislik, bu erda L - AA 1 chetining o'rtasi va N - CC 1 chetining o'rtasi.

Bo'limni iz usuli yordamida tuzamiz.

Ko'pburchakning ortogonal proyeksiyasining maydoni haqidagi teoremadan foydalanib, ko'ndalang kesim maydonini topamiz. Javob: S = 1/2 · a 2.

CHIZMALAR BO'YICHA BO'LMA VA BO'LIMLARNI QURISH

Qism chizmasini shakllantirish kerakli proyeksiyalar, bo'limlar va bo'limlarni ketma-ket qo'shish orqali amalga oshiriladi. Dastlab, foydalanuvchi tomonidan ko'rsatilgan model bilan maxsus ko'rinish yaratiladi va asosiy ko'rinish uchun eng mos bo'lgan modelning yo'nalishi o'rnatiladi. Keyinchalik, ushbu va keyingi ko'rinishlardan foydalanib, kerakli kesmalar va bo'limlar yaratiladi.

Asosiy ko'rinish (old ko'rinish) qismning shakllari va o'lchamlari haqida eng to'liq tasavvurni beradigan tarzda tanlangan.

Chizmalardagi bo'limlar

Kesish tekisligining holatiga qarab, mavjud quyidagi turlar kesmalar:

A) gorizontal, agar kesuvchi tekislik proyeksiyalarning gorizontal tekisligiga parallel joylashgan bo'lsa;

B) vertikal, agar kesuvchi tekislik proyeksiyalarning gorizontal tekisligiga perpendikulyar bo'lsa;

C) qiya - kesuvchi tekislik proyeksiya tekisliklariga qiya.

Vertikal qismlar quyidagilarga bo'linadi:

· frontal - kesish tekisligi proyeksiyalarning frontal tekisligiga parallel;

· profil - kesish tekisligi proyeksiyalarning profil tekisligiga parallel.
Kesish tekisliklari soniga qarab, kesmalar:

· oddiy - bitta kesish tekisligi bilan (107-rasm);

· murakkab - ikki yoki undan ortiq kesish tekisliklari bilan (108-rasm)
Standart quyidagi murakkab kesish turlarini nazarda tutadi:

· pog'onali, kesish tekisliklari parallel (108-rasm a) va singan bo'lsa - kesish tekisliklari kesishadi (108-rasm b).

107-rasm Oddiy kesma

A) b)

108-rasm Murakkab kesmalar

Kesishlarni belgilash

Agar oddiy kesmada ajralish tekisligi ob'ektning simmetriya tekisligiga to'g'ri keladigan bo'lsa, kesma ko'rsatilmaydi (107-rasm). Boshqa barcha holatlarda, qisqartirishlar rus alifbosining bosh harflari bilan, A harfi bilan boshlanadi, masalan, A-A.

Chizmadagi kesish tekisligining holati kesma chizig'i - qalin ochiq chiziq bilan ko'rsatilgan. Murakkab kesish bo'lsa, kesishmalar chiziq chizig'ining egilish joylarida ham amalga oshiriladi. O'qlarni ko'rish yo'nalishini ko'rsatadigan dastlabki va oxirgi zarbalarga qo'yish kerak, strelkalar zarbalarning tashqi uchlaridan 2-3 mm masofada bo'lishi kerak; Ko'rish yo'nalishini ko'rsatadigan har bir o'qning tashqi tomonida bir xil bosh harf qo'llaniladi.

KOMPAS tizimidagi kesmalar va bo'limlarni belgilash uchun xuddi shu tugma ishlatiladi Belgilash sahifasida joylashgan kesish chizig'i (109-rasm).

109-rasm Chiziqni kesish tugmasi

Yarim ko'rinishni yarim qism bilan ulash

Agar ko'rinish va bo'lim nosimmetrik figuralar bo'lsa (110-rasm), u holda siz ko'rinishning yarmini va kesmaning yarmini simmetriya o'qi bo'lgan nozik chiziqli nuqta bilan ajratib, ulashingiz mumkin. Bo'limning bir qismi odatda simmetriya o'qining o'ng tomonida joylashgan bo'lib, u ko'rinishning bir qismini kesma qismidan ajratib turadi yoki simmetriya o'qi ostidadir. Ko'rinish va kesimning birlashtiruvchi qismlarida yashirin kontur chiziqlari odatda ko'rsatilmaydi. Agar biron-bir chiziqning proyeksiyasi, masalan, fasetli figuraning qirrasi ko'rinish va kesimni ajratib turuvchi eksenel chiziqqa to'g'ri kelsa, u holda ko'rinish va kesma o'qning chap tomoniga chizilgan qattiq to'lqinli chiziq bilan ajratiladi. simmetriya, agar chekka yotsa ichki yuzasi, yoki cheti tashqi bo'lsa, o'ngga ko'proq.

Guruch. 110 Ko‘rinish va bo‘limning bir qismini ulash

Bo'limlarni qurish

Biz KOMPAS tizimida kesimlarni qurishni prizma chizmasini qurish misolida o'rganamiz, uning vazifasi 111-rasmda ko'rsatilgan.

Chizish ketma-ketligi quyidagicha:

1. Berilgan o'lchamlar asosida prizmaning yaxlit modelini quramiz (109 b-rasm). Modelni kompyuter xotirasida "Prizma" nomli faylda saqlaymiz.

112-rasm Chiziqlar paneli

3. Profil uchastkasini qurish uchun (113-rasm) chiziq chizamiz A-A bo'limi tugmasi yordamida asosiy ko'rinishda Kesilgan chiziq.

113-rasm Profil uchastkasining qurilishi

Ko'rish yo'nalishi va belgi matni ekranning pastki qismidagi buyruqlar boshqaruv panelida tanlanishi mumkin (114-rasm). Kesish chizig'ini qurish Ob'ektni yaratish tugmasini bosish bilan yakunlanadi.

114-rasm Bo'limlar va bo'limlarni qurish buyrug'ining boshqaruv paneli

4. Assotsiativ ko'rinishlar panelida (115-rasm) Cut Line tugmasini tanlang, so'ngra kesish chizig'ini ko'rsatish uchun ekranda paydo bo'ladigan tuzoqdan foydalaning. Har bir narsa to'g'ri bajarilgan bo'lsa (kesilgan chiziq faol shaklda chizilgan bo'lishi kerak), keyin kesilgan chiziq qizil rangga aylanadi. A-A kesma chizig'ini ko'rsatgandan so'ng, ekranda umumiy to'rtburchak ko'rinishidagi xayoliy tasvir paydo bo'ladi.

115-rasm Panelning assotsiativ ko'rinishlari

Xususiyatlar panelidagi Bo'lim/bo'lim kaliti yordamida siz tasvir turini - Bo'lim (116-rasm) va ko'rsatilgan qismning masshtabini tanlaysiz.

116-rasm Bo'limlar va bo'limlarni qurish buyrug'ining boshqaruv paneli

Profil qismi avtomatik ravishda proektsion ulanishda va standart belgi bilan quriladi. Agar kerak bo'lsa, proektsion aloqa kalit bilan o'chirilishi mumkin Proyeksiyali ulanish (116-rasm). Yaratilgan bo'limda (bo'limda) qo'llaniladigan lyukka parametrlarini sozlash uchun Hatching yorlig'idagi boshqaruv elementlaridan foydalaning.

117-rasm Gorizontalni qurish B-B bo'limi va B-B bo'limlari

Agar uchastkani qurishda tanlangan kesish tekisligi qismning simmetriya tekisligiga to'g'ri kelsa, standartga muvofiq bunday qism belgilanmaydi. Ammo agar siz shunchaki bo'limning belgilanishini o'chirib tashlasangiz, u holda ko'rinish va kompyuter xotirasidagi bo'lim o'zaro bog'langanligi sababli butun bo'lim o'chiriladi. Shuning uchun, belgini o'chirish uchun birinchi navbatda ko'rinish va bo'lim o'rtasidagi aloqani yo'q qilish kerak. Buning uchun sichqonchaning chap tugmasi bosilib, bo‘lim tanlanadi, so‘ngra sichqonchaning o‘ng tugmasi bosilib kontekst menyusi ochiladi, undan “Ko‘rishni yo‘q qilish” bandi tanlanadi (97-rasm). Endi kesish belgisini olib tashlash mumkin.

5. Gorizontal kesimni qurish uchun oldingi ko'rinishdagi teshikning pastki tekisligi orqali B-B kesish chizig'ini o'tkazing. Avval sichqonchaning chap tugmachasini ikki marta bosish orqali oldingi ko'rinishni joriy qilishingiz kerak. Keyin gorizontal qism quriladi (117-rasm).

6. Frontal qismni qurishda ko'rinishning bir qismini va kesimning bir qismini birlashtiring, chunki bu simmetrik raqamlar. Prizmaning tashqi qirrasi ko'rinish va kesimni ajratib turuvchi chiziqqa proyeksiyalanadi, shuning uchun biz ajratamiz. simmetriya o'qining o'ng tomoniga chizilgan qattiq ingichka to'lqinli chiziqli ko'rinish va kesma, chunki tashqi qovurg'a. To'lqinli chiziq chizish uchun tugmani ishlating Bezier egri chizig'i Geometriya panelida joylashgan, For break chizig'i uslubi bilan chizilgan (118-rasm). Bezier egri chizig'i o'tishi kerak bo'lgan nuqtalarni ketma-ket belgilang. Buyruqning bajarilishini Ob'ekt yaratish tugmasini bosish orqali tugatishingiz mumkin.

118-rasm. Tanaffus uchun chiziq uslubini tanlash

Bo'limlarni qurish

Kesim - bu ob'ektni tekislik bilan aqliy ravishda kesish natijasida olingan ob'ektning tasviri. Bo'lim faqat kesish tekisligida joylashgan narsalarni ko'rsatadi.

Kesish tekisligining joylashuvi, uning yordamida bo'lim hosil bo'ladi, xuddi kesmalar uchun bo'lgani kabi, chizmada kesma chizig'i bilan ko'rsatilgan.

Bo'limlar, chizmalardagi joylashishiga qarab, kengaytirilgan va ustiga qo'yilgan bo'linadi. Chiqarilgan bo'limlar ko'pincha chizmaning bo'sh maydonida joylashgan va asosiy chiziq bilan belgilanadi. Ustiga qo'yilgan bo'limlar to'g'ridan-to'g'ri ob'ekt tasviriga joylashtiriladi va ingichka chiziqlar bilan chiziladi (119-rasm).

119-rasm Bo'limlarni qurish

Nishab o'zgarishi bilan prizma chizmasini qurish ketma-ketligini ko'rib chiqaylik. B-B bo'limi(117-rasm).

1. Ko'rinishda sichqonchaning chap tugmachasini faol ravishda ikki marta bosish orqali old ko'rinish hosil qiling va tugma yordamida kesma chizig'ini chizing. Kesilgan chiziq . V-V yozuvining matnini tanlang.

2. Assotsiativ ko'rinishlar panelida joylashgan Chiziqni kesish tugmasi yordamida (115-rasm) paydo bo'lgan tuzoq sekant chizig'ini ko'rsatadi. samolyot B-B. Xususiyatlar panelidagi Bo'lim/bo'lim tugmasidan foydalanib, tasvir turini - Bo'limni tanlang (116-rasm), ko'rsatilgan qismning masshtabi Scale oynasidan tanlanadi.

Tuzilgan bo'lim proyeksiya havolasida joylashgan bo'lib, bu uning chizmadagi harakatini cheklaydi, ammo proyeksiya havolasini tugma yordamida o'chirib qo'yish mumkin. Proyeksiya aloqasi.

Tayyor chizmada siz eksenel chiziqlarni chizishingiz va kerak bo'lganda o'lchamlarni qo'shishingiz kerak.

Geometriyaning butun tarixi va matematikaning boshqa ba'zi bo'limlari geometrik konstruktsiyalar nazariyasining rivojlanishi bilan chambarchas bog'liq. Miloddan avvalgi 300-yillarda Evklid tomonidan shakllantirilgan geometriyaning eng muhim aksiomalari geometriyaning shakllanishida geometrik konstruktsiyalarning rolini aniq ko'rsatib beradi.

Maktab geometriyasida siz aql bovar qilmaydigan uchrashuvni kutayotgan maxsus mavzular mavjud chiroyli material. Bunday mavzular "Polyhedra va ularning bo'limlarini qurish" bu erda nafaqat ochiladi ajoyib dunyo noyob xususiyatlarga ega geometrik jismlar, lekin ayni paytda qiziqarli ilmiy farazlar. Va keyin geometriya darsi tanish maktab mavzusining kutilmagan tomonlarini o'rganishning bir turiga aylanadi.

Bu yilgi geometriya darslarida biz “Ko‘p yuzli kesimlarni yasash” mavzusini o‘rgandik. Dasturning bir qismi sifatida biz bo'limlarni qurishning bitta usulini o'rgandik, ammo men yana qanday usullar mavjudligi bilan qiziqib qoldim.

Mening ishimning maqsadi: Ko'pburchaklar kesimlarini qurishning barcha usullarini o'rganing.

Hech bir geometrik jismlar ko'p yuzli kabi mukammallik va go'zallikka ega emas. "Ko'p yuzlilarning hayratlanarli darajada kam soni bor, - deb yozgan edi L.Kerroll, - ammo bu juda kamtarona bo'linma turli fanlarning chuqurligiga kirishga muvaffaq bo'ldi".

Hozirgi vaqtda geometrik konstruktsiyalar nazariyasi matematikaning boshqa sohalariga kiradigan turli fundamental masalalarni hal qilish bilan bog'liq bo'lgan matematikaning keng va chuqur rivojlangan sohasini ifodalaydi.

1. Chizma geometriya tarixi

Qadim zamonlarda ham odamlar toshlar, toshlar, devorlar va uy-ro'zg'or buyumlariga narsalar, daraxtlar, hayvonlar va odamlarning tasvirlarini chizib, chizganlar. U buni o'zining ehtiyojlarini, shu jumladan estetik ehtiyojlarini qondirish uchun qildi. Bundan tashqari, bunday tasvirlarga qo'yiladigan asosiy talab, tasvir tasvirlangan ob'ektning shakli to'g'risida to'g'ri vizual fikrni uyg'otishi edi.

Amaliy va o'sishi bilan texnik ilovalar tasvirlar (binolar va boshqa fuqarolik va harbiy inshootlarni qurishda va hokazo) ularga shunday talablar qo'yila boshlandiki, tasvirdan geometrik xususiyatlar, o'lchamlar va nisbiy pozitsiyani hukm qilish uchun foydalanish mumkin edi. individual elementlar ma'lum bir mavzu. Bunday talablar bugungi kungacha saqlanib qolgan ko'plab qadimiy yodgorliklar tomonidan baholanishi mumkin. Biroq, fazoviy figuralarni tasvirlashning qat'iy geometrik asosli qoidalari va usullari (perspektivga nisbatan) faqat Uyg'onish davrida rassomlar, me'morlar va haykaltaroshlar tomonidan muntazam ravishda ishlab chiqila boshlandi: Leonardo da Vinchi, Dyurer, Rafael, Mikelanjelo, Titian va boshqalar.

Tasviriy geometriya fan sifatida yaratilgan XVIII oxiri asrning buyuk frantsuz geometriyachisi va muhandisi Gaspard Monge (1746 - 1818). 1637 yilda frantsuz geometriyachisi va faylasufi Rene Dekart (1596 - 1650) koordinata usulini yaratdi va analitik geometriyaga asos soldi va uning vatandoshi, muhandis va matematik Jirard Desages (1593 - 1662) ushbu koordinataviy loyihani amalga oshirish uchun foydalangan. va aksonometrik proyeksiyalar nazariyasini asoslab berdi.

17-asrda miqyosda rejalar va profillar ko'rinishida tuzilgan texnik chizmalar Rossiyada muvaffaqiyatli rivojlandi. Bu erda, birinchi navbatda, taniqli rus mexanik va ixtirochi I.P.ning chizmalarini eslatib o'tishimiz kerak. Kulibin (1735 - 1818). Uning yog'ochdan yasalgan kamar ko'prik loyihasi ortogonal proektsiyalardan birinchi marta foydalangan (1773). (Samolyotning unda yotgan chiziqqa yoki fazoning tekislikka ortogonal proyeksiyasi maxsus holat parallel proyeksiya, bunda proyeksiya yo'nalishi ular proyeksiya qilayotgan to'g'ri chiziq yoki tekislikka perpendikulyar bo'ladi.)

Ortogonal proyeksiyalarning rivojlanishiga fransuz muhandisi A. Frezier (1682–1773) katta hissa qo‘shgan bo‘lib, u birinchi bo‘lib jismni ikkita tekislikka - gorizontal va frontalga proyeksiyalashni ko‘rib chiqdi.

G. Monjning eng katta xizmati o‘zidan oldingi olimlarning barcha ilmiy ishlarini, fazoviy figuralarni tasvirlash usullarining butun nazariyasini umumlashtirish va ortogonal proyeksiyaning yagona matematik fani — chizma geometriyani yaratishda bo‘ldi.

Buning tug'ilishi yangi fan deyarli Sankt-Peterburgda Rossiyaning birinchi oliy transporti tashkil etilganiga to'g'ri keldi ta'lim muassasasi- Temir yo'l muhandislari korpusi instituti (1809 yil 2 dekabr)

Ushbu institut bitiruvchilari, professor-o‘qituvchilari, olimlar tasvirlashning geometrik usullarini, chizma geometriya nazariyasi va amaliyotini rivojlantirishga katta hissa qo‘shdilar.

1. Ko'p yuzlilarga ta'riflar

Stereometriyada kosmosdagi raqamlar o'rganiladi, deyiladi jismlar . Vizual ravishda (geometrik) jismni egallagan makonning bir qismi sifatida tasavvur qilish kerak jismoniy tana va sirt bilan chegaralanadi.

Ko'p yuzli - bu yuzasi bir nechta tekis ko'pburchaklardan iborat bo'lgan jism. Ko'pburchak deyiladi qavariq , agar uning yuzasida har bir tekislik ko'pburchak tekisligining bir tomonida joylashgan bo'lsa. Bunday tekislikning umumiy qismi va qavariq ko'pburchak yuzasi deyiladi chekka . Qavariq ko'pburchakning yuzlari tekis qavariq ko'pburchaklardir. Yuzlarning yon tomonlari deyiladiko'pburchakning qirralari, va uchlari ko'pburchakning uchlari.

Bo'lim ko'pburchak tekislik deyiladi geometrik shakl, bu bir vaqtning o'zida berilgan ko'pburchak va tekislikka tegishli bo'lgan fazodagi barcha nuqtalar to'plamidir; tekislik kesuvchi tekislik deyiladi.

Ko'pburchakning yuzasi tekis ko'pburchaklarning qirralari, segmentlari va yuzlaridan iborat. To'g'ri chiziq va tekislik bir nuqtada kesishganligi sababli va ikkita tekislik to'g'ri chiziq bo'ylab kesishganligi sababli, ko'pburchakning tekislik bilan kesmasi bo'ladi.tekis ko'pburchak; bu ko'pburchakning uchlari kesuvchi tekislikning ko'pburchak qirralari bilan kesishish nuqtalari, tomonlari esa kesuvchi tekislik yuzlarini kesib o'tadigan segmentlardir. Demak, berilgan ko‘pburchakning kerakli kesimini a tekislik bilan qurish uchun uning ko‘pburchak chetlari bilan kesishish nuqtalarini qurish kifoya. Keyin ushbu nuqtalarni ketma-ket segmentlar bilan bog'lang, shu bilan birga hosil bo'lgan ko'pburchak kesimining ko'rinadigan va chiziqli ko'rinmas tomonlarini qattiq chiziqlar bilan ajratib ko'rsating.

III. Ko'p yuzli kesimlarni qurish usullari

Stereometriyada ko'p yuzli kesimlar usuli qurilish masalalarida qo'llaniladi. U ko'pburchakning kesimini qurish va kesma turini aniqlash qobiliyatiga asoslangan.

Ushbu material quyidagi xususiyatlar bilan ajralib turadi:

• Bo'limlar usuli faqat ko'pburchaklar uchun qo'llaniladi, chunki inqilob organlarining turli xil murakkab (qiyshiq) turlari o'rta maktab o'quv dasturiga kiritilmagan.
• Muammolar, asosan, eng oddiy polihedradan foydalanadi.
• Muammolar ko'p martalik foydalanish imkoniyatini yaratish uchun asosan raqamli ma'lumotlarsiz taqdim etiladi.

Ko'pburchak kesimini qurish masalasini hal qilish uchun talaba bilishi kerak:

• Ko'pburchakning tekislik bilan kesmasini qurish nimani anglatadi;
• Ko'pburchak va tekislikni bir-biriga nisbatan qanday joylashtirish mumkin?
• Samolyot qanday aniqlanadi;
• Ko'pburchak kesimini tekislik bilan qurish masalasi hal qilingan deb hisoblansa.

Chunki tekislik aniqlangan:

• Uch ball;
• To'g'ri va nuqta;
• Ikki parallel chiziq;
• Ikkita kesishuvchi chiziq

Bo'lim tekisligining qurilishi ushbu tekislikning spetsifikatsiyasiga bog'liq. Shuning uchun ko'pburchaklar kesimlarini qurishning barcha usullarini usullarga bo'lish mumkin.

3.1 Stereometriya aksiomalari tizimi asosida ko'p yuzli kesimlarni qurish

Muammo 1 . RABC piramidasining a = (MKH) tekislik bilan kesmasini tuzing, bu erda M, K va H mos ravishda RS, PB va AB qirralarning ichki nuqtalaridir (1-rasm, a).

Yechim.

1-qadam . M va K nuqtalar a va RVS ikkita tekislikning har birida yotadi. Demak, ikkita tekislikning kesishish aksiomasi bo'yicha a tekislik RVS tekislikni MK to'g'ri chiziq bo'ylab kesib o'tadi. Binobarin, MK segmenti kerakli kesimning tomonlaridan biri hisoblanadi (1-rasm, b).

2-qadam . Xuddi shunday, KN segmenti kerakli qismning boshqa tomonidir (1-rasm, c).

3-qadam . M va H nuqtalari bir vaqtning o'zida RABC piramidasining biron bir yuzida yotmaydi, shuning uchun MH segmenti ushbu piramida kesmasining bir tomoni emas. KN va RA to'g'ri chiziqlar AVR yuzining tekisligida yotadi va kesishadi. T= KH ∩AP nuqtasini quramiz (1-rasm, d).

KN to'g'ri chiziq a tekislikda joylashgani uchun T nuqta a tekislikda yotadi. Endi biz a va APC tekisliklari M va T umumiy nuqtalarga ega ekanligini ko'ramiz. Binobarin, ikkita tekislikning kesishish aksiomasiga ko'ra, a tekislik va APC tekislik MT to'g'ri chiziq bo'ylab kesishadi, bu esa o'z navbatida AC chekkasini R nuqtada kesib o'tadi ( 1-rasm, d).

4-bosqich . Endi, xuddi 1-bosqichda bo'lgani kabi, biz a tekislik ACP va ABC yuzlarini mos ravishda MR va HR segmentlari bo'ylab kesib o'tishini aniqlaymiz. Binobarin, kerakli bo'lim to'rtburchak MKHR (1-rasm, f).

Guruch. 2

Vazifa 2. MABCD piramidasining a = (CN) tekislik bilan kesmasini tuzing, bu erda K, H va P mos ravishda MA, MV va MD qirralarning ichki nuqtalaridir (2-rasm, a).

Yechim. Birinchi ikki qadam oldingi muammoning 1 va 2 bosqichlariga o'xshaydi. Natijada, biz kerakli qismning KR va KN tomonlarini (2-rasm, b) olamiz. Ko'pburchakning qolgan uchlari va tomonlarini - kesmalarni quramiz.

3-qadam . KR segmentini F nuqtada AD to‘g‘ri chiziq bilan kesishguncha davom ettiramiz (2-rasm, v). KR to'g'ri chiziq kesuvchi a tekislikda joylashganligi uchun F= KR ∩ AD = KR ∩ (ABC) nuqta a va ABC tekisliklari uchun umumiydir.

4-bosqich . KH segmentini L nuqtada AB to'g'ri chiziq bilan kesishguncha davom ettiramiz (2-rasm, d). KN to'g'ri chiziq kesuvchi a tekislikda joylashgani uchun a va AVS tekisliklar uchun L = KN ∩ AV = KN ∩ (AVS) nuqta umumiydir.

Shunday qilib , F va L nuqtalar a va ABC tekisliklari uchun umumiydir. Demak, a tekislik piramida asosining ABC tekisligini FL to'g'ri chiziq bo'ylab kesib o'tadi.

5-qadam . FL to'g'ri chiziq chizamiz. Bu to'g'ri chiziq BC va DC qirralarini mos ravishda R va T nuqtalarida kesib o'tadi (2-rasm, e), ular kerakli kesimning uchlari bo'lib xizmat qiladi. Bu shuni anglatadiki, a tekislik ABCD asosining yuzini RT segmenti - kerakli kesma tomoni bo'ylab kesib o'tadi.

6-qadam . Endi biz RH va PT segmentlarini chizamiz (2-rasm, f), ular bo'ylab a tekislik ushbu piramidaning BMC va MCD yuzlarini kesib o'tadi. Biz PKHRT beshburchakni - MABCD piramidasining kerakli qismini olamiz (2-rasm, f).

Keling, yanada murakkab muammoni ko'rib chiqaylik.

Muammo 3 . PABCDE beshburchakli piramidasining a = (KQR) tekislik bilan kesmasini tuzing, bu erda K, Q mos ravishda RA va RS qirralarning ichki nuqtalari, R nuqtasi esa DPE yuzining ichida joylashgan (3-rasm, a).

Yechim . To'g'ri chiziqlar (QK va AC bir xil ACP tekisligida yotadi (to'g'ri chiziq va tekislik aksiomasiga ko'ra) va T1, (3 b-rasm) biron bir nuqtada kesishadi), T1 ê a, chunki QK ê a.

PR to'g'ri chiziq DE ni qandaydir F nuqtada kesib o'tadi (3-rasm, c), bu piramida asosining ARR tekisligi va DE tomonining kesishish nuqtasidir. Keyin KR va AF toʻgʻri chiziqlar bir xil APR tekisligida yotib, qandaydir T2 nuqtada (3-rasm, d), T2 ê a toʻgʻri chiziq nuqtasi sifatida KR ê a (toʻgʻri aksioma boʻyicha) kesishadi. chiziq va tekislik).

Olingan: T1 T2 toʻgʻri chiziq ajralish tekisligida va piramida asosi tekisligida (toʻgʻri chiziq va tekislik aksiomasiga koʻra) yotadi, toʻgʻri chiziq esa piramidaning ABCDE asosining DE va ​​AE tomonlarini kesib oʻtadi, mos ravishda, M va N nuqtalarida (3-rasm, e), ular piramidaning DE va ​​AE qirralari bilan kesishish nuqtalari a tekisligi bo'lib, kerakli kesimning tepalari bo'lib xizmat qiladi.

Keyinchalik , to'g'ri chiziq MR yuzi DPE tekisligida va kesish tekisligida yotadi a (to'g'ri chiziq va tekislikning aksiomasiga ko'ra), PD qirrasini biron bir H nuqtasida kesishganda - istalgan kesimning boshqa cho'qqisi ( 3-rasm, f).

Keyinchalik, T3 - T1T2 ∩ AB nuqtasini quramiz (3-rasm, g), u T1T2 ê a to'g'ri chiziqning nuqtasi sifatida a tekislikda yotgan (to'g'ri chiziq va tekislik aksiomasiga ko'ra). Endi RAB yuzining tekisligi ikkita T3 nuqtaga va kesuvchi a tekisligiga tegishli, ya'ni T3K to'g'ri chiziq bu tekisliklarning kesishgan to'g'ri chizig'idir. T3K to'g'ri chiziq RV chekkasini L nuqtada kesib o'tadi (3-rasm, h), u kerakli kesmaning keyingi cho'qqisi bo'lib xizmat qiladi.

Guruch. 3

Shunday qilib, kerakli qismni qurish ketma-ketligining "zanjiri" quyidagicha:

1 . T1 = QK ∩AC;

2. F = PR ∩ DE;

3. T2 = KR ∩ AF;

4 . M = T1T2 ∩ DE;

5 . N = T1T2 ∩ AE;

6. N = MR ∩ PD;

7. T3 = T1T2 ∩ AB;

8 . L = T3K ∩ PB.

Olti burchakli MNKLQH kerakli bo'limdir.

Rasmdagi piramidaning kesimi. 1 va shakldagi kubning kesimi. 2 faqat stereometriya aksiomalari asosida tuzilgan.

Shu bilan birga, parallel tekisliklarning xossalaridan foydalanib, ko'pburchakning parallel yuzli (prizma, parallelepiped, kub) kesimini qurish mumkin.

3.2 Ko'p yuzlilarning tekis kesimlarini qurishda iz usuli

Kesuvchi tekislik a ko‘pburchak asosi tekisligini kesib o‘tuvchi to‘g‘ri chiziq shu asos tekisligidagi a tekislikning izi deyiladi.

Izning ta'rifidan biz quyidagilarni olamiz: uning har bir nuqtasida to'g'ri chiziqlar kesishadi, ulardan biri kesuvchi tekislikda, ikkinchisi asos tekisligida yotadi. Izning ana shu xossasi iz usuli yordamida ko‘pburchakning tekis kesimlarini qurishda qo‘llaniladi. Bundan tashqari, sekant tekisligida ko'pburchakning qirralarini kesib o'tadigan to'g'ri chiziqlardan foydalanish qulay.

Birinchidan, sekant tekislikni uning prizma asosi (piramida) tekisligidagi izi va prizma yuzasiga (piramida) tegishli nuqta orqali aniqlaymiz.

Muammo 1 . Prizma asosining ABC tekisligidagi l izi va DD1 chetiga tegishli M nuqta bilan aniqlangan a tekislik orqali AVSVEA1V1S1D1E1 prizma kesimini tuzing.

Yechim. Tahlil . Faraz qilaylik, beshburchak MNPQR kerakli kesma (4-rasm). Ushbu tekis beshburchakni qurish uchun uning N, P, Q, R uchlarini (M nuqtasi berilgan) - berilgan prizmaning CC1, BB1, AA1, EE1 qirralari bilan kesuvchi a tekislikning kesishish nuqtalarini qurish kifoya. mos ravishda.

E1 D1

N =a ∩ CC1 nuqtani qurish uchun kesuvchi a tekislikning SDD1C1 yuz tekisligi bilan kesishgan to'g'ri chizig'ini qurish kifoya. Buning uchun, o'z navbatida, bu yuzning tekisligida kesuvchi a tekisligiga tegishli yana bir nuqtani qurish kifoya. Bunday nuqtani qanday qurish mumkin?

l to'g'ri chiziq prizma asosi tekisligida yotganligi sababli u SDD1C1 yuz tekisligini faqat CD = (CDD1) ∩ (AVS) to'g'ri chiziqqa tegishli nuqtada kesishi mumkin, ya'ni. nuqta X = l ∩ SD = l ∩ (CDD1) kesuvchi tekislik a ga tegishli. Shunday qilib, N = a ∩ CC1 nuqtasini qurish uchun X = l ∩ CD nuqtasini qurish kifoya.

Xuddi shunday, P = a ∩ BB1, Q = a ∩ AA1 va R = a ∩ EE1 nuqtalarini qurish uchun mos ravishda nuqtalarni qurish kifoya: Y = l ∩ BC, Z = 1 ∩ AB va T =1 ∩ AE. .

Qurilish. Biz quramiz (5-rasm):

1. X = l ∩ CD (5-rasm, b);

2. N = MX ∩ CC1 (5-rasm, c);

3. U = l ∩ VS (5-rasm, d);

4. P = NY ∩ BB1 (5-rasm, e);

5. Z = 1 ∩ AB (5-rasm, f);

6. Q= PZ ∩ AA1 (5-rasm, g);

7. T= l ∩ AE (5-rasm, h);

8. R= QT ∩ EE1 (5-rasm, i).

Pentagon MNPQR - kerakli bo'lim (5-rasm, j).

Isbot. l to'g'ri chiziq a kesuvchi tekislikning izi bo'lgani uchun X = l ∩ CD, Y = l ∩ BC, Z = 1 ∩ AB va T= l ∩ AE nuqtalari shu tekislikka tegishli.

Shuning uchun bizda:

M Ê a, X Ê a => MX ê a, keyin MX ∩ SS1 = N ê a, ya’ni N = a ∩ SS1;

N Ê a, Y Ê a => NY Ê a, keyin NY ∩ BB1= P Ê a, ya'ni P = a ∩ BB1;

R Ê a, Z Ê a => RZ Ê a, keyin PZ ∩ AA1 = Q Ê a, ya'ni Q = a ∩ AA1;

Q Ê a, T Ê a => QT Ê a, keyin QT ∩ EE1 =R Ê a, ya'ni R = a ∩ EE1.

Shuning uchun MNPQR kerakli bo'limdir.

O'qish. Kesuvchi tekislik a ning l izi prizma asosini kesmaydi va kesuvchi tekislikning M nuqtasi prizmaning DD1 yon chetiga tegishli. Shuning uchun kesuvchi tekislik a yon qirralarga parallel emas. Binobarin, bu tekislikning prizmaning lateral qirralari (yoki bu qirralarning kengaytmalari) bilan kesishgan N, P, Q va R nuqtalari doimo mavjud. Va bundan tashqari, M nuqta l iziga tegishli emasligi sababli, ular tomonidan aniqlangan a tekislik yagonadir. Bu muammo (har doim) o'ziga xos echimga ega ekanligini anglatadi.

3.3 Ko'pburchakning tekis kesimlarini qurish uchun ichki dizayn usuli

Ba'zi darsliklarda biz hozir ko'rib chiqamiz ko'pburchak kesimlarini qurish usuli ichki proyeksiyalar usuli yoki yozishmalar usuli yoki diagonal kesmalar usuli deb ataladi.

Muammo 1 . PABCDE piramidasining a = (MFR) tekislik bilan kesmasini tuzing, agar M, F va R nuqtalar mos ravishda RA, RS va PE qirralarning ichki nuqtalari bo'lsa. (6-rasm)

Yechim . Piramida asosining tekisligini b deb belgilaymiz. Kerakli kesimni qurish uchun kesuvchi tekislik a ning piramida qirralari bilan kesishish nuqtalarini quramiz.

Ushbu piramidaning PD qirrasi bilan kesuvchi tekislikning kesishish nuqtasini quramiz.

APD va CPE tekisliklari b tekislikni AD va CE toʻgʻri chiziqlar boʻylab kesib oʻtadi, ular qaysidir K nuqtada kesishadi. RK = (ARD) ∩(SPE) toʻgʻri chiziq FR ê a toʻgʻri chiziqni K1: K1 nuqtada kesib oʻtadi. = RK ∩ FR, bu vaqtda K1 ê a. Unda: M ê a, K1 ê a => to'g'ri chiziq MK ê a. Demak, Q = MK1 ∩ PD nuqta PD chekkasi va kesish tekisligining kesishish nuqtasidir: Q =a ∩ PD. Q nuqtasi - kerakli bo'limning tepasi. Xuddi shunday, biz a tekislikning kesishish nuqtasini va PB chekkasini quramiz. BPE va AD tekisliklari H nuqtada kesishgan BE va AD toʻgʻri chiziqlar boʻylab b tekislikni kesishadi. Toʻgʻri RN = (VRE) ∩ (ARD) toʻgʻri chiziqni N1 nuqtada kesib oʻtadi = a ∩ RV - bo'limning yuqori qismi.

Shunday qilib , kerakli qismni qurish bosqichlari ketma-ketligi quyidagicha:

1 . K = AD ∩ EC; 2. K1 = RK ∩ RF;

3. Q = MK1 ∩ RD; 4. H = BE ∩ AD;

5 . N1 = RN ∩ MQ; 6. N = RN1 ∩ RV.

Pentagon MNFQR zarur bo'limdir.

3.4 Ko'pburchaklarning tekis kesimlarini qurishda kombinatsiyalangan usul

Ko'pburchaklar kesimlarini qurishning kombinatsiyalangan usulining mohiyati quyidagicha. Kesmani qurishning ayrim bosqichlarida yo iz usuli yoki ichki loyihalash usuli, bir xil kesmani qurishning boshqa bosqichlarida esa parallellik, to'g'ri chiziqlar va tekisliklarning perpendikulyarligi haqidagi o'rganilgan teoremalardan foydalaniladi.

Ushbu usulni qo'llashni ko'rsatish uchun quyidagi muammoni ko'rib chiqing.

Vazifa 1.

ABCDA1B1C1D1 parallelepipedining kesmasini P, Q va R nuqtalari bilan belgilangan a tekislik bo'yicha quring, agar P nuqta A1C1 diagonali, Q nuqtasi BB1 chetida va R nuqtasi DD1 chetida bo'lsa. (7-rasm)

Yechim

Bu masalani chiziq va tekisliklarning parallelligi haqidagi iz usuli va teoremalaridan foydalanib yechamiz.

Avvalo, ABC tekisligida a = (RQR) kesuvchi tekislikning izini tuzamiz. T1T2 izini qurib, biz P nuqta ABC tekisligiga parallel bo'lgan A1B1C1 tekisligida yotishini ko'ramiz. Demak, a tekislik A1B1C1 tekislikni P nuqtadan o‘tuvchi va T1T2 to‘g‘ri chiziqqa parallel bo‘lgan to‘g‘ri chiziq bo‘ylab kesib o‘tadi. Bu chiziqni chizamiz va uning A1B1 va A1D1 qirralari bilan kesishgan nuqtalarini mos ravishda M va E bilan belgilaymiz: M = a ∩ A1B1, E = a∩ A1D1. Keyin ER va QM segmentlari kerakli bo'limning tomonlari hisoblanadi.

Bundan tashqari, BCC1 tekisligi ADD1A1 yuz tekisligiga parallel bo'lganligi sababli, a tekislik BCC1B1 yuzini QF (F= a ∩ CC1) segmenti bo'ylab, ER to'g'ri chiziqqa parallel ravishda kesib o'tadi. Shunday qilib, ERFQM beshburchak talab qilinadigan qismdir. (F nuqtasini RF║ MQ bajarish orqali olish mumkin)

Bu masalani ichki proyeksiyalash usuli va chiziqlar va tekisliklarning parallelligi haqidagi teoremalardan foydalanib yechamiz.(8-rasm)

Guruch. 8

H=AC ∩ BD bo‘lsin. NN1 to'g'ri chiziqni V1 chetiga (N1 ê RQ) parallel qilib, F nuqtani quramiz: F=RN1 ∩ CC1 F nuqta - a tekislikning CC1 qirrasi bilan kesishish nuqtasi, chunki RN1 ê a. Keyin a tekislik ushbu parallelepipedning mos ravishda CC1D1D va VSS1V1 yuzlarini kesib o'tadigan RF va QF segmentlari uning kerakli kesimining tomonlari hisoblanadi.

ABB1 tekisligi CDD1 tekisligiga parallel bo'lgani uchun a tekislik va ABB1A1 yuzining kesishishi FR segmentiga parallel bo'lgan QM (M Ê A1B1) segmentidir; segment QM - bo'limning tomoni. Bundan tashqari, E = MP ∩ A1D1 nuqtasi a tekislikning kesishish nuqtasi va A1D1 chekkasi, chunki MP ê a. Shuning uchun E nuqtasi kerakli bo'limning boshqa cho'qqisidir. Shunday qilib, ERFQM beshburchak talab qilinadigan qismdir. (E nuqtani RE ║ FQ to'g'ri chiziq chizish orqali qurish mumkin. Keyin M = PE ∩ A1B1).

IV. Xulosa

Ushbu ish tufayli men bu yilgi geometriya kursida olingan bilimlarni umumlashtirdim va tizimlashtirdim, bajarish qoidalari bilan tanishdim. ijodiy ish, yangi bilimlarga ega bo'ldi va ularni amalda qo'lladi.

Yangi olgan bilimlarimni amaliyotda tez-tez ishlatib turmoqchiman.

Afsuski, men ko'p yuzli qismlarni qurishning barcha usullarini ko'rib chiqmadim. Yana ko'p maxsus holatlar mavjud:

• ko'pburchakning berilgan nuqtadan o'tadigan tekislikka parallel bo'lgan kesimini qurish;
• berilgan chiziqdan boshqa berilgan chiziqqa parallel ravishda o'tuvchi kesmani qurish;
• berilgan nuqtadan ikkita berilgan kesishuvchi chiziqqa parallel ravishda o‘tuvchi kesmani qurish;
• berilgan tekislikka perpendikulyar berilgan chiziqdan o'tuvchi tekislik bilan ko'pburchakning kesmasini qurish;
• ko‘pburchakning berilgan to‘g‘riga perpendikulyar berilgan nuqtadan o‘tuvchi tekislik bilan kesimini qurish va h.k.

Kelajakda ilmiy izlanishlarimni kengaytirish va yuqorida sanab o‘tilgan maxsus holatlar tahlili bilan ishimni to‘ldirishni rejalashtirmoqdaman.

Mening ishim dolzarb, deb o'ylayman, chunki undan o'rta va o'rta maktab o'quvchilari foydalanishi mumkin o'z-o'zini o'rganish matematikadan Yagona davlat imtihonini topshirish uchun, tanlov bo'yicha materialni chuqur o'rganish va yosh o'qituvchilarning o'z-o'zini tarbiyalash uchun. O'rta maktab bitiruvchilari nafaqat materialni o'zlashtirishlari kerak maktab dasturlari, balki uni ijodiy qo‘llay olish va har qanday muammoga yechim topa olish.

V. Adabiyot

1. Potoskuev E.V., Zvavich L.I. Geometriya. 10-sinf: uchun darslik ta'lim muassasalari matematikani chuqur va maxsus o'rganish bilan. - M.: Bustard, 2008 yil.
2. Potoskuev E.V., Zvavich L.I. Geometriya. 10-sinf: Matematika fanini chuqurlashtirilgan va ixtisoslashtirilgan umumta’lim muassasalari uchun muammoli kitob. - M.: Bustard, 2008 yil.
3. Potoskuev E.V. Samolyotdagi fazoviy figuralarning tasviri. Ko'pburchaklar kesimlarini qurish. Qo'llanma Pedagogika universitetining fizika-matematika fakulteti talabalari uchun. - Tolyatti: TDU, 2004 yil.
4. O'rta maktab o'quvchilari uchun ilmiy-amaliy jurnal "Matematika o'quvchilari uchun", 2009, № 2 / No 3, 1-64.
5. Jadvallardagi geometriya - O'rta maktab o'quvchilari uchun darslik - Nelin E.P.
6. Geometriya, 7-11 sinflar, Ma'lumotnomalar, Bezrukova G.K., Litvinenko V.N., 2008 y.
7. Matematika, Ma'lumotnoma, O'rta maktab o'quvchilari va universitetlarga kiruvchilar uchun, Ryvkin A.A., Ryvkin A.Z., 2003 yil.
8. Jadval va diagrammalarda algebra va geometriya, Roganin A.N., Dergachev V.A., 2006 yil.

Tekislik yordamida kubning kesmalarini qurish bilan bog'liq masalalar, qoida tariqasida, masalan, piramida kesimlari bilan bog'liq masalalarga qaraganda oddiyroqdir.

Ikki nuqta bir tekislikda yotsa, ular orqali to'g'ri chiziq o'tkazishimiz mumkin. Kubning qismlarini qurishda, kesish tekisligining izini qurish uchun boshqa variant ham mumkin. Uchinchi tekislik ikkita parallel tekislikni parallel to'g'ri chiziqlar bo'ylab kesib o'tganligi sababli, agar yuzlarning birida to'g'ri chiziq allaqachon qurilgan bo'lsa, ikkinchisida esa kesma o'tadigan nuqta bo'lsa, biz parallel to'g'ri chiziq chizishimiz mumkin. bu nuqta orqali bu nuqta.

Keling, ko'rib chiqaylik aniq misollar tekislik yordamida kubning kesmalarini yasash.

1) A, C va M nuqtalardan o'tuvchi tekislik bilan kubning kesmasini tuzing.

Ushbu turdagi masalalar kubning kesimlarini qurish uchun eng oddiy masalalardir. A va C nuqtalar bir tekislikda (ABC) yotganligi sababli ular orqali to'g'ri chiziq o'tkazishimiz mumkin. Uning izi AC segmentidir. Bu ko'rinmas, shuning uchun biz ACni zarba bilan tasvirlaymiz. Xuddi shunday, biz bir tekislikda yotuvchi M va C nuqtalarni (CDD1) va bir tekislikda joylashgan A va M nuqtalarni (ADD1) bog'laymiz. Uchburchak ACM - kerakli qism.

2) M, N, P nuqtalardan o'tuvchi tekislik bilan kubning kesmasini tuzing.

Bu erda faqat M va N nuqtalar bir tekislikda yotadi (ADD1), shuning uchun biz ular orqali to'g'ri chiziq o'tkazamiz va MN (ko'rinmas) izini olamiz. Kubning qarama-qarshi tomonlari joylashganligi sababli parallel tekisliklar, keyin kesish tekisligi parallel tekisliklar (ADD1) va (BCC1) parallel chiziqlar bo'ylab kesishadi. Biz allaqachon parallel chiziqlardan birini qurdik - bu MN.

P nuqta orqali MN ga parallel chiziq chizamiz. U BB1 chetini S nuqtada kesib o'tadi. PS - yuzdagi kesish tekisligining izi (BCC1).

Bir tekislikda yotgan M va S nuqtalar orqali to'g'ri chiziq o'tkazamiz (ABB1). Biz MS izini oldik (ko'rinadigan).

Samolyotlar (ABB1) va (CDD1) parallel. Tekislikda (ABB1) allaqachon MS to'g'ri chiziq mavjud, shuning uchun tekislikdagi N nuqta (CDD1) orqali MS ga parallel to'g'ri chiziq o'tkazamiz. Bu chiziq D1C1 chetini L nuqtada kesib o'tadi. Uning izi NL (ko'rinmas). P va L nuqtalar bir tekislikda yotadi (A1B1C1), shuning uchun biz ular orqali to'g'ri chiziq o'tkazamiz.

Pentagon MNLPS - bu zarur bo'lim.

3) M, N, P nuqtalardan o'tuvchi tekislik bilan kubning kesmasini tuzing.

M va N nuqtalar bir tekislikda yotadi (VSS1), shuning uchun ular orqali to'g'ri chiziq o'tkazish mumkin. Biz MN izini olamiz (ko'rinadigan). Tekislik (BCC1) tekislikka (ADD1) parallel, shuning uchun (ADD1) da yotgan P nuqta orqali MN ga parallel chiziq chizamiz. U E nuqtada AD qirrasini kesib o'tadi. Biz iz PE (ko'rinmas) oldik.

Endi bitta tekislikda yotadigan nuqtalar yoki parallel tekisliklarda to'g'ri chiziq va nuqtalar yo'q. Shuning uchun, qo'shimcha nuqta olish uchun mavjud chiziqlardan birini davom ettirishimiz kerak.

Agar MN chizig'ini davom ettirsak, u holda u (BCC1) tekislikda yotganligi uchun MN ning shu tekislik chiziqlaridan biri bilan kesishish nuqtasini izlash kerak. CC1 va B1C1 bilan kesishish nuqtalari allaqachon mavjud - bular M va N. Qolgan narsa BC va BB1 to'g'ri chiziqlardir. BC va MN ni K nuqtada kesishguncha davom ettiramiz. K nuqta BC to‘g‘rida yotadi, ya’ni u tekislikka (ABC) tegishli ekanligini bildiradi, shuning uchun biz u orqali to‘g‘ri chiziq o‘tkazamiz va shu tekislikda joylashgan E nuqtani o‘tkazamiz. CD qirrasini H nuqtada kesib o'tadi. EH - uning izi (ko'rinmas). H va N bir tekislikda (CDD1) yotganligi uchun ular orqali to'g'ri chiziq o'tkazish mumkin. Biz HN (ko'rinmas) izini olamiz.

Samolyotlar (ABC) va (A1B1C1) parallel. Ularning birida EH chizig'i, ikkinchisida M nuqta bor. M orqali EH ga parallel chiziq o'tkazishimiz mumkin. Biz MF izini olamiz (ko'rinadigan). M va F nuqtalar orqali to'g'ri chiziq o'tkazing.

Olti burchakli MNHEPF talab qilinadigan qismdir.

Agar MN toʻgʻri chiziqni boshqa toʻgʻri tekislik (BCC1) BB1 bilan kesishguncha davom ettirsak, (ABB1) tekislikka tegishli G nuqtani olgan boʻlamiz. Bu shuni anglatadiki, G va P orqali biz izi PF bo'lgan to'g'ri chiziq chizishimiz mumkin. Keyinchalik, parallel tekisliklarda yotgan nuqtalar orqali to'g'ri chiziqlar o'tkazamiz va bir xil natijaga erishamiz.

To'g'ri PE bilan ishlash bir xil bo'lim MNHEPFni beradi.

4) M, N, P nuqtadan o'tuvchi tekislik bilan kubning kesmasini tuzing.

Bu yerda bir tekislikda (A1B1C1) yotgan M va N nuqtalar orqali toʻgʻri chiziq oʻtkazish mumkin. Uning izi MN (ko'rinadigan). Xuddi shu tekislikda yoki parallel tekisliklarda yotadigan nuqtalar qolmaydi.

MN to'g'ri chiziqni davom ettiramiz. U (A1B1C1) tekislikda yotadi, shuning uchun u faqat shu tekislikning chiziqlaridan biri bilan kesishishi mumkin. A1D1 va C1D1 - N va M bilan kesishish nuqtalari allaqachon mavjud. Ushbu tekislikning yana ikkita to'g'ri chizig'i - A1B1 va B1C1. A1B1 va MN ning kesishish nuqtasi S. U A1B1 toʻgʻrida yotganligi uchun u tekislikka (ABB1) tegishli, yaʼni u orqali toʻgʻri chiziq oʻtkazish mumkin va bir tekislikda yotgan P nuqta. PS chizig'i AA1 chekkasini E nuqtasida kesib o'tadi. PE - uning izi (ko'rinadigan). Bir tekislikda (ADD1) yotgan N va E nuqtalari orqali siz to'g'ri chiziq chizishingiz mumkin, uning izi NE (ko'rinmas). Tekislikda (ADD1) NE chiziq bor, unga parallel tekislikda (BCC1) P nuqta mavjud. P nuqta orqali NE ga parallel PL chizig'ini o'tkazishimiz mumkin. U CC1 chetini L nuqtada kesib o'tadi. PL - bu chiziqning izi (ko'rinadigan). M va L nuqtalar bir tekislikda yotadi (CDD1), ya'ni ular orqali to'g'ri chiziq o'tkazish mumkin. Uning izi ML (ko'rinmas). Pentagon MLPEN zarur bo'limdir.

NM toʻgʻri chiziqni har ikki yoʻnalishda davom ettirish va uning kesishish nuqtalarini nafaqat A1B1 toʻgʻri chiziq bilan, balki tekislikda (A1B1C1) yotuvchi B1C1 toʻgʻri chiziq bilan ham izlash mumkin edi. Bunday holda, P nuqta orqali biz bir vaqtning o'zida ikkita to'g'ri chiziq chizamiz: biri tekislikda (ABB1) P va S nuqtalari orqali, ikkinchisi esa tekislikda (BCC1), P va R nuqtalari orqali. Shundan so'ng ulanish qoladi. bir tekislikda yotgan nuqtalar: M c L, E - N bilan.