Sinus kosinus tangens kotangensi uchun formulalar. O'tkir burchakning sinus, kosinus, tangensi, kotangensi. Trigonometrik funktsiyalar
Trigonometriya - trigonometrik funktsiyalar va ularning geometriyada qo'llanilishini o'rganadigan matematika fanining bir tarmog'i. Trigonometriyaning rivojlanishi kunlarda boshlangan qadimgi Yunoniston. Oʻrta asrlarda bu fanning rivojlanishiga Yaqin Sharq va Hindiston olimlari muhim hissa qoʻshgan.
Ushbu maqola bag'ishlangan asosiy tushunchalar va trigonometriyaning ta'riflari. Unda asosiy trigonometrik funktsiyalarning ta'riflari muhokama qilinadi: sinus, kosinus, tangens va kotangens. Ularning ma'nosi geometriya kontekstida tushuntiriladi va tasvirlanadi.
Yandex.RTB R-A-339285-1
Dastlab argumenti burchak boʻlgan trigonometrik funksiyalarning taʼriflari toʻgʻri burchakli uchburchak tomonlari nisbati bilan ifodalangan.
Trigonometrik funksiyalarning ta’riflari
Burchakning sinusi (sin a) - bu burchakka qarama-qarshi bo'lgan oyoqning gipotenuzaga nisbati.
Burchakning kosinusu (cos a) - qo'shni oyoqning gipotenuzaga nisbati.
Burchak tangensi (t g a) - qarama-qarshi tomonning qo'shni tomonga nisbati.
Burchak kotangenti (c t g a) - qo'shni tomonning qarama-qarshi tomoniga nisbati.
Ushbu ta'riflar uchun berilgan o'tkir burchak to'g'ri uchburchak!
Keling, misol keltiraylik.
To'g'ri burchakli C burchakli ABC uchburchakda A burchakning sinusi nisbatga teng BC oyog'idan AB gipotenuzasiga.
Sinus, kosinus, tangens va kotangensning ta'riflari ushbu funktsiyalarning qiymatlarini uchburchak tomonlarining ma'lum uzunliklaridan hisoblash imkonini beradi.
Esda tutish muhim!
Sinus va kosinus qiymatlari diapazoni -1 dan 1 gacha. Boshqacha qilib aytganda, sinus va kosinus -1 dan 1 gacha qiymatlarni oladi. Tangens va kotangens qiymatlari diapazoni butun son chizig'idir, ya'ni bu funktsiyalar har qanday qiymatlarni qabul qilishi mumkin.
Yuqorida keltirilgan ta'riflar o'tkir burchaklarga tegishli. Trigonometriyada burilish burchagi tushunchasi kiritiladi, uning qiymati o'tkir burchakdan farqli o'laroq, 0 dan 90 gradusgacha bo'lgan burilish burchagi - ∞ dan + ∞ gacha bo'lgan har qanday haqiqiy son bilan ifodalanadi. .
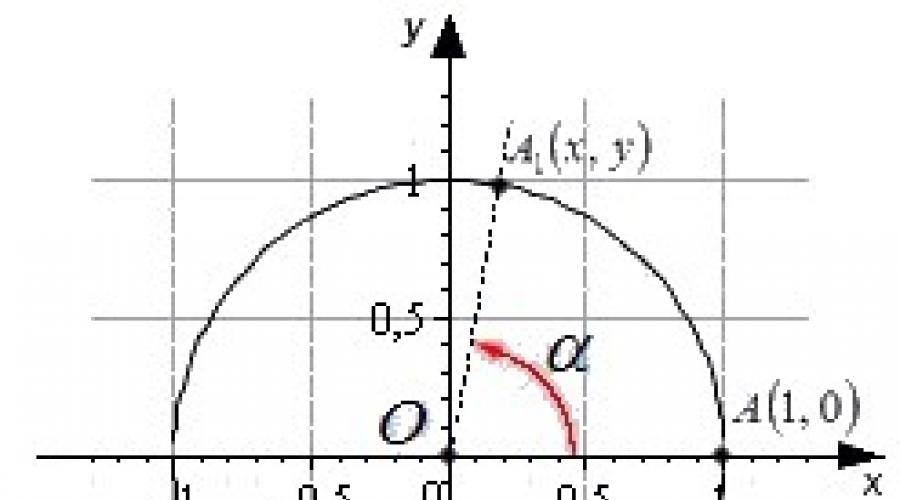
Shu nuqtai nazardan, biz ixtiyoriy kattalikdagi burchakning sinusini, kosinusini, tangensini va kotangensini aniqlashimiz mumkin. Markazi Dekart koordinata tizimining boshida joylashgan birlik doirani tasavvur qilaylik.

Koordinatalari (1, 0) bo'lgan boshlang'ich A nuqta ma'lum a burchak orqali birlik doira markazi atrofida aylanadi va A 1 nuqtaga boradi. Ta'rif A 1 (x, y) nuqtaning koordinatalari bo'yicha berilgan.
Aylanish burchagining sinus (sin).
Aylanish burchagi a sinusi A nuqtaning ordinatasi 1 (x, y). sin a = y
Aylanish burchagining kosinusu (cos).
Aylanish burchagi a kosinusu A 1 (x, y) nuqtaning abssissasidir. cos a = x
Aylanish burchagining tangensi (tg).
A burilish burchagi tangensi A 1 (x, y) nuqta ordinatasining uning abssissasiga nisbati hisoblanadi. t g a = y x
Aylanish burchagining kotangenti (ctg).
Aylanish burchagi a kotangensi A 1 (x, y) nuqta abssissasining uning ordinatasiga nisbati hisoblanadi. c t g a = x y
Har qanday aylanish burchagi uchun sinus va kosinus aniqlanadi. Bu mantiqan to'g'ri, chunki aylanmadan keyin nuqtaning abscissa va ordinatasi istalgan burchakda aniqlanishi mumkin. Tangens va kotangens bilan vaziyat boshqacha. Aylanishdan keyin nuqta nol abscissa (0, 1) va (0, - 1) nuqtaga o'tganda tangens aniqlanmagan. Bunday hollarda t g a = y x tangensi ifodasi shunchaki ma'noga ega emas, chunki u nolga bo'linishni o'z ichiga oladi. Vaziyat kotangent bilan o'xshash. Farqi shundaki, nuqta ordinatasi nolga tushgan hollarda kotangent aniqlanmaydi.
Esda tutish muhim!
Har qanday a burchak uchun sinus va kosinus aniqlanadi.
Tangens a = 90° + 180° k, k ∈ Z (a = p 2 + p k, k ∈ Z) dan tashqari barcha burchaklar uchun aniqlanadi.
Kotangent a = 180° k, k ∈ Z (a = p k, k ∈ Z) dan tashqari barcha burchaklar uchun aniqlanadi.
Qaror qabul qilganda amaliy misollar"aylanish burchagi sinusi a" demang. "Aylanish burchagi" so'zlari shunchaki olib tashlandi, bu esa kontekstdan nima muhokama qilinayotgani allaqachon aniq ekanligini anglatadi.
Raqamlar
Aylanish burchagi emas, balki sonning sinus, kosinus, tangens va kotangens ta'rifi haqida nima deyish mumkin?
Sonning sinus, kosinus, tangensi, kotangensi
Sonning sinus, kosinus, tangensi va kotangensi t-da mos ravishda sinus, kosinus, tangens va kotangensga teng bo'lgan son t radian.
Masalan, 10 p sonining sinusi sinusga teng aylanish burchagi 10 p rad.
Sonning sinus, kosinus, tangens va kotangensini aniqlashning yana bir usuli mavjud. Keling, buni batafsil ko'rib chiqaylik.
Har qanday haqiqiy raqam t birlik doiradagi nuqta to'rtburchaklar Dekart koordinata tizimining boshidagi markaz bilan bog'langan. Bu nuqtaning koordinatalari orqali sinus, kosinus, tangens va kotangens aniqlanadi.
Doiradagi boshlang'ich nuqta koordinatalari (1, 0) bo'lgan A nuqtadir.
Ijobiy raqam t
Salbiy raqam t aylana bo'ylab soat sohasi farqli ravishda harakatlansa, boshlang'ich nuqtasi ketadigan nuqtaga to'g'ri keladi va yo'ldan boradi t.
Aylanadagi son bilan nuqta o‘rtasidagi bog‘lanish o‘rnatilgandan so‘ng, biz sinus, kosinus, tangens va kotangens ta’rifiga o‘tamiz.
t ning sinusi (gunohi).
Raqamning sinusi t- songa mos keladigan birlik doiradagi nuqtaning ordinatasi t. sin t = y
Kosinus (cos) t
Sonning kosinusu t- songa mos keladigan birlik aylana nuqtasining abssissasi t. cos t = x
Tangensi (tg) t
Sonning tangensi t- songa mos keladigan birlik doiradagi nuqtaning abssissasiga ordinataning nisbati t. t g t = y x = sin t cos t
Eng so'nggi ta'riflar ushbu bandning boshida berilgan ta'rifga mos keladi va unga zid kelmaydi. Raqamga mos keladigan aylanaga ishora qiling t, burchak bilan burilgandan keyin boshlang'ich nuqtasi ketadigan nuqtaga to'g'ri keladi t radian.
Burchak va son argumentning trigonometrik funktsiyalari
Burchakning har bir qiymati a bu burchakning sinusi va kosinusining ma'lum bir qiymatiga mos keladi. Xuddi a = 90 ° + 180 ° k dan boshqa barcha a burchaklar kabi, k ∈ Z (a = p 2 + p k, k ∈ Z) ma'lum bir tangens qiymatiga mos keladi. Kotangent, yuqorida aytib o'tilganidek, a = 180° k, k ∈ Z (a = p k, k ∈ Z) dan tashqari barcha a uchun aniqlanadi.
Aytishimiz mumkinki, sin a, cos a, t g a, c t g a alfa burchakning funksiyalari yoki burchak argumentining funksiyalaridir.
Xuddi shunday, sonli argumentning funktsiyalari sifatida sinus, kosinus, tangens va kotangens haqida gapirishimiz mumkin. Har bir haqiqiy raqam t sonning sinus yoki kosinusining ma'lum bir qiymatiga mos keladi t. p 2 + p · k, k ∈ Z dan boshqa barcha raqamlar tangens qiymatiga mos keladi. Xuddi shunday kotangent p · k, k ∈ Z dan boshqa barcha sonlar uchun aniqlanadi.
Trigonometriyaning asosiy funktsiyalari
Sinus, kosinus, tangens va kotangens asosiy trigonometrik funktsiyalardir.
Odatda kontekstdan trigonometrik funktsiyaning qaysi argumenti aniq bo'ladi ( burchak argumenti yoki raqamli argument) biz bilan shug'ullanamiz.
Keling, eng boshida berilgan ta'riflarga va 0 dan 90 darajagacha bo'lgan alfa burchagiga qaytaylik. Trigonometrik ta'riflar sinus, kosinus, tangens va kotangens to'liq mos keladi geometrik ta'riflar, to'g'ri burchakli uchburchakning tomonlar nisbati yordamida berilgan. Keling, ko'rsataylik.

To'g'ri to'rtburchaklar Dekart koordinatalari tizimida markazi bo'lgan birlik doirani olaylik. A (1, 0) boshlang'ich nuqtasini 90 gradusgacha burchakka aylantiramiz va hosil bo'lgan A 1 (x, y) nuqtadan abscissa o'qiga perpendikulyar chizamiz. Olingan to'g'ri burchakli uchburchakda A 1 O H burchak burchakka teng a burilish, oyoqning uzunligi O H A 1 (x, y) nuqtasi abssissasiga teng. Burchakka qarama-qarshi turgan oyoqning uzunligi A 1 (x, y) nuqtaning ordinatasiga teng, gipotenuzaning uzunligi esa bir ga teng, chunki u birlik doirasining radiusi.
Geometriya ta'rifiga ko'ra, a burchakning sinusi qarama-qarshi tomonning gipotenuzaga nisbatiga teng.
sin a = A 1 H O A 1 = y 1 = y
Bu shuni anglatadiki, to'g'ri burchakli uchburchakdagi o'tkir burchakning sinusini tomonlar nisbati orqali aniqlash, alfa 0 dan 90 darajagacha bo'lgan oraliqda joylashgan aylanish burchagining sinusini aniqlashga teng.
Xuddi shunday, ta'riflarning mosligini kosinus, tangens va kotangens uchun ko'rsatish mumkin.

Agar siz matnda xatolikni sezsangiz, uni belgilang va Ctrl+Enter tugmalarini bosing
To'g'ri burchakli uchburchakni echish bo'yicha masalalar ko'rib chiqilganda, men sinus va kosinus ta'riflarini yodlash texnikasini taqdim etishga va'da berdim. Undan foydalanib, siz har doim qaysi tomon gipotenuzaga tegishli ekanligini tezda eslaysiz (qo'shni yoki qarama-qarshi). Men buni uzoq vaqtga qoldirmaslikka qaror qildim, zarur material pastda, o'qing 😉
Gap shundaki, men 10-11-sinf o‘quvchilari bu ta’riflarni eslab qolishda qiynalayotganliklarini bir necha bor kuzatganman. Ular oyoqning gipotenuzaga tegishli ekanligini juda yaxshi eslashadi, lekin qaysi biri- ular unutishadi va chalkash. Xatoning narxi, siz imtihonda bilganingizdek, yo'qolgan balldir.
Men to'g'ridan-to'g'ri taqdim etadigan ma'lumotlarning matematikaga hech qanday aloqasi yo'q. U bilan bog'langan xayoliy fikrlash, va og'zaki-mantiqiy muloqot usullari bilan. Aynan shunday, men buni bir marta va umuman eslaymanta'rif ma'lumotlari. Agar siz ularni unutib qo'ysangiz, taqdim etilgan usullardan foydalangan holda ularni har doim osongina eslab qolishingiz mumkin.
To'g'ri burchakli uchburchakda sinus va kosinus ta'riflarini eslatib o'taman:
Kosinus To'g'ri burchakli uchburchakdagi o'tkir burchak qo'shni oyoqning gipotenuzaga nisbati:

Sinus To'g'ri burchakli uchburchakdagi o'tkir burchak qarama-qarshi tomonning gipotenuzaga nisbati:

Xo'sh, siz kosinus so'zi bilan qanday bog'liqliklarga egasiz?
Balki har kimning o'ziga xos 😉Havolani eslang:
Shunday qilib, ibora darhol sizning xotirangizda paydo bo'ladi -
«… QO'SHAN oyoqning gipotenuzaga nisbati».
Kosinusni aniqlash muammosi hal qilindi.
Agar siz to'g'ri uchburchakda sinusning ta'rifini eslab qolishingiz kerak bo'lsa, u holda kosinus ta'rifini eslab, to'g'ri burchakli uchburchakdagi o'tkir burchakning sinusi qarama-qarshi tomonning gipotenuzaga nisbati ekanligini osongina aniqlashingiz mumkin. Axir, faqat ikkita oyoq bor, agar qo'shni oyoq kosinus bilan "ishg'ol qilingan" bo'lsa, u holda faqat qarama-qarshi oyoq sinus bilan qoladi.
Tangens va kotangens haqida nima deyish mumkin? Chalkashlik ham xuddi shunday. Talabalar bu oyoqlarning munosabatlari ekanligini bilishadi, ammo muammo qaysi biri qaysi biri bilan bog'liqligini eslab qolishdir - qo'shniga qarama-qarshi yoki aksincha.
Ta'riflar:
Tangent To'g'ri burchakli uchburchakdagi o'tkir burchak qarama-qarshi tomonning qo'shni tomonga nisbati:

Kotangent To'g'ri burchakli uchburchakdagi o'tkir burchak qo'shni tomonning qarama-qarshi tomoniga nisbati:

Qanday eslash kerak? Ikki yo'l bor. Birida og'zaki-mantiqiy bog'lanish ham qo'llaniladi, ikkinchisi matematikadan foydalanadi.
MATEMATIK USUL
Bunday ta'rif mavjud - o'tkir burchakning tangensi - bu burchak sinusining uning kosinusiga nisbati:

*Formulani yodlab, siz har doim to'g'ri burchakli uchburchakdagi o'tkir burchakning tangensi qarama-qarshi tomonning qo'shni tomonga nisbati ekanligini aniqlashingiz mumkin.
Xuddi shunday.O'tkir burchakning kotangensi bu burchak kosinusining sinusiga nisbati:

Shunday ekan! Ushbu formulalarni eslab, siz har doim quyidagilarni aniqlashingiz mumkin:
- to'g'ri burchakli uchburchakdagi o'tkir burchakning tangensi - qarama-qarshi tomonning qo'shni tomonga nisbati
- to'g'ri burchakli uchburchakdagi o'tkir burchakning kotangensi qo'shni tomonning qarama-qarshi tomoniga nisbati.
SO`Z-MANTIQ METOD
Tangens haqida. Havolani eslang:

Ya'ni, agar siz tangensning ta'rifini eslab qolishingiz kerak bo'lsa, ushbu mantiqiy aloqadan foydalanib, uning nima ekanligini osongina eslab qolishingiz mumkin
"... qarama-qarshi tomonning qo'shni tomonga nisbati"
Agar biz kotangens haqida gapiradigan bo'lsak, unda tangens ta'rifini eslab, siz kotangentning ta'rifini osongina aytishingiz mumkin -
"... qo'shni tomonning qarama-qarshi tomonga nisbati"
Veb-saytda tangens va kotangensni eslab qolish uchun qiziqarli hiyla mavjud " Matematik tandem " , qarang.
UNIVERSAL USUL
Siz shunchaki eslab qolishingiz mumkin.Ammo amaliyot shuni ko'rsatadiki, og'zaki-mantiqiy aloqalar tufayli odam nafaqat matematik ma'lumotlarni, balki uzoq vaqt davomida ma'lumotni eslab qoladi.
Umid qilamanki, material siz uchun foydali bo'ldi.
Hurmat bilan, Aleksandr Krutitskix
P.S: Ijtimoiy tarmoqlardagi sayt haqida ma'lumot bersangiz, minnatdor bo'lardim.
Sinusni qanday topish mumkin?



Geometriyani o'rganish fikrlashni rivojlantirishga yordam beradi. Bu fan maktab ta'limiga majburiy ravishda kiritiladi. Kundalik hayotda ushbu mavzu bo'yicha bilim foydali bo'lishi mumkin - masalan, kvartirani rejalashtirishda.
Tarixdan
Geometriya kursi trigonometrik funktsiyalarni o'rganuvchi trigonometriyani ham o'z ichiga oladi. Trigonometriyada biz burchaklarning sinuslari, kosinuslari, tangenslari va kotangenslarini o'rganamiz.
Lekin davom bu daqiqa Eng oddiy narsadan boshlaylik - sinus. Keling, eng birinchi tushunchani - geometriyadagi burchak sinusini batafsil ko'rib chiqaylik. Sinus nima va uni qanday topish mumkin?
"Sinus burchak" va sinusoidlar tushunchasi
Burchakning sinusi - bu qarama-qarshi tomonning qiymatlari va to'g'ri burchakli uchburchakning gipotenuzasi nisbati. Bu to'g'ridan-to'g'ri trigonometrik funktsiya bo'lib, u "sin (x)" deb yoziladi, bu erda (x) - uchburchakning burchagi.
Grafikda burchakning sinusi o'ziga xos xususiyatlarga ega sinus to'lqin bilan ko'rsatilgan. Sinus to'lqin koordinata tekisligida ma'lum chegaralar ichida joylashgan doimiy to'lqinli chiziqqa o'xshaydi. Funktsiya g'alati, shuning uchun u koordinata tekisligida 0 ga yaqin simmetrikdir (u koordinatalarning boshidan chiqadi).
Ushbu funktsiyani aniqlash sohasi Dekart koordinata tizimida -1 dan +1 gacha bo'lgan oraliqda joylashgan. Sinus burchak funksiyasining davri 2 Pi ga teng. Bu shuni anglatadiki, har 2 Pida naqsh takrorlanadi va sinus to'lqin to'liq tsikldan o'tadi.
Sinus to'lqin tenglamasi
- sin x = a/c
- bu yerda a - uchburchak burchagiga qarama-qarshi oyoq
- c - to'g'ri burchakli uchburchakning gipotenuzasi
Burchak sinusining xossalari
- sin(x) = - sin(x). Bu xususiyat funktsiyaning simmetrik ekanligini ko'rsatadi va agar x va (-x) qiymatlari koordinatalar tizimida har ikki yo'nalishda chizilgan bo'lsa, u holda bu nuqtalarning ordinatalari qarama-qarshi bo'ladi. Ular bir-biridan teng masofada joylashgan bo'ladi.
- Bu funksiyaning yana bir xususiyati shundaki, [- P/2 + 2 Pn] segmentida funksiya grafigi ortadi; [P/2 + 2Pn], bu erda n har qanday butun son. Segmentda burchak sinusining grafigida pasayish kuzatiladi: [P/2 + 2Pn]; [3P/2 + 2Pn].
- x oraliqda bo'lganda sin(x) > 0 (2Pn, P + 2Pn)
- (x)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)
Burchak sinuslarining qiymatlari maxsus jadvallar yordamida aniqlanadi. Sanoq jarayonini osonlashtirish uchun bunday jadvallar yaratilgan murakkab formulalar va tenglamalar. Foydalanish oson va nafaqat ma'nolarni o'z ichiga oladi vazifalari gunoh(x), balki boshqa funksiyalarning qiymatlari ham.
Bundan tashqari, ushbu funktsiyalar uchun standart qiymatlar jadvali ilovaga kiritilgan majburiy o'qish xotira uchun, ko'paytirish jadvali kabi. Bu, ayniqsa, fizikaviy va matematik jihatdan moyil bo'lgan sinflar uchun to'g'ri keladi. Jadvalda trigonometriyada ishlatiladigan asosiy burchaklarning qiymatlarini ko'rishingiz mumkin: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 va 360 daraja.
Shuningdek, nostandart burchaklarning trigonometrik funktsiyalari qiymatlarini belgilaydigan jadval mavjud. Foyda olish turli jadvallar, siz ba'zi burchaklarning sinusi, kosinusu, tangensi va kotangensini osongina hisoblashingiz mumkin.
Tenglamalar trigonometrik funksiyalar bilan tuziladi. Agar oddiy tenglamalarni bilsangiz, bu tenglamalarni yechish oson trigonometrik identifikatsiyalar va funksiyalarning qisqarishi, masalan, sin (P/2 + x) = cos (x) va boshqalar. Bunday qisqartirishlar uchun alohida jadval ham tuzilgan.
Burchakning sinusini qanday topish mumkin
Vazifa burchakning sinusini topish bo'lsa va shartga ko'ra, biz faqat burchakning kosinus, tangensi yoki kotangensiga egamiz, biz trigonometrik identifikatsiyalar yordamida kerakli narsani osongina hisoblashimiz mumkin.
- sin 2 x + cos 2 x = 1
Ushbu tenglamadan qaysi qiymat noma'lumligiga qarab sinus va kosinusni topishimiz mumkin. Biz qila olamiz trigonometrik tenglama bitta noma'lum bilan:
- sin 2 x = 1 - cos 2 x
- sin x = ± √ 1 - cos 2 x
- karavot 2 x + 1 = 1 / gunoh 2 x
Bu tenglamadan burchak kotangensining qiymatini bilib, sinusning qiymatini topish mumkin. Soddalashtirish uchun sin 2 x = y ni almashtiring va sizda oddiy tenglama mavjud. Masalan, kotangent qiymati 1 ga teng, keyin:
- 1 + 1 = 1/y
- 2 = 1/y
- 2u = 1
- y = 1/2
Endi biz o'yinchini teskari almashtirishni amalga oshiramiz:
- gunoh 2 x = ½
- sin x = 1 / √2
Standart burchak uchun kotangent qiymatini olganimiz sababli (45 0), olingan qiymatlarni jadvalda tekshirish mumkin.
Agar sizga tangens qiymat berilsa va sinusni topishingiz kerak bo'lsa, boshqa trigonometrik identifikatsiya yordam beradi:
- tg x * ctg x = 1
Bundan kelib chiqadiki:
- karavot x = 1 / tg x
Nostandart burchakning sinusini topish uchun, masalan, 240 0, burchakni qisqartirish formulalaridan foydalanish kerak. Bilamizki, p 180 0 ga mos keladi. Shunday qilib, biz tengligimizni standart burchaklar yordamida kengaytirish orqali ifodalaymiz.
- 240 0 = 180 0 + 60 0
Biz quyidagilarni topishimiz kerak: gunoh (180 0 + 60 0). Trigonometriyada kamaytirish formulalari mavjud Ushbu holatda yordam beradi. Bu formula:
- gunoh (p + x) = - gunoh (x)
Shunday qilib, 240 graduslik burchakning sinusi quyidagilarga teng:
- gunoh (180 0 + 60 0) = - gunoh (60 0) = - √3/2
Bizning holatda, x = 60 va P, mos ravishda, 180 daraja. Biz standart burchaklar funktsiyalari qiymatlari jadvalidan (-√3/2) qiymatini topdik.
Shu tarzda biz parchalanishimiz mumkin nostandart burchaklar, masalan: 210 = 180 + 30.
Sinus (), kosinus (), tangens (), kotangens () tushunchalari burchak tushunchasi bilan uzviy bog'liqdir. Bularni, birinchi qarashda, murakkab tushunchalarni (ko'pgina maktab o'quvchilarida dahshatga soladigan) yaxshi tushunish uchun va "iblis u chizilgandek dahshatli emas"ligiga ishonch hosil qilish uchun keling, keling, "shayton" dan boshlaylik. juda boshlang'ich va burchak tushunchasini tushunish.
Burchak tushunchasi: radian, daraja
Keling, rasmga qaraylik. Vektor nuqtaga nisbatan ma'lum miqdorda "aylangan". Shunday qilib, bu aylanishning boshlang'ich pozitsiyasiga nisbatan o'lchovi bo'ladi burchak.
Burchak tushunchasi haqida yana nimani bilishingiz kerak? Albatta, burchak birliklari!
Geometriyada ham, trigonometriyada ham burchakni daraja va radian bilan o'lchash mumkin.
Burchak (bir daraja) aylananing bir qismiga teng dumaloq yoy bilan qoplangan aylanadagi markaziy burchak. Shunday qilib, butun doira dumaloq yoylarning "bo'laklari" dan iborat yoki aylana tasvirlangan burchak tengdir.

Ya'ni, yuqoridagi rasmda teng burchak ko'rsatilgan, ya'ni bu burchak aylana o'lchamidagi aylana yoyga tayanadi.
Radianlardagi burchak uzunligi aylananing radiusiga teng bo'lgan aylana yoyi bilan qoplangan doiradagi markaziy burchakdir. Xo'sh, tushundingizmi? Agar yo'q bo'lsa, keling, buni rasmdan aniqlaylik.

Demak, rasmda radianga teng burchak ko'rsatilgan, ya'ni bu burchak aylana yoyiga tayanadi, uning uzunligi aylananing radiusiga teng (uzunligi uzunlik yoki radiusga teng). uzunligiga teng yoylar). Shunday qilib, yoy uzunligi quyidagi formula bo'yicha hisoblanadi:
Radianlarda markaziy burchak qayerda.
Xo'sh, buni bilib, aylana tasvirlangan burchakda qancha radian borligiga javob bera olasizmi? Ha, buning uchun siz aylana formulasini eslab qolishingiz kerak. Mana u:
Xo'sh, endi bu ikki formulani o'zaro bog'laymiz va aylana tasvirlangan burchak teng ekanligini topamiz. Ya'ni, qiymatni darajalar va radyanlardagi o'zaro bog'lash orqali biz buni olamiz. Tegishli ravishda, . Ko'rib turganingizdek, "daraja" dan farqli o'laroq, "radian" so'zi olib tashlandi, chunki o'lchov birligi odatda kontekstdan aniq.
Qancha radian bor? Hammasi to'g'ri!
Tushundim? Keyin davom eting va uni tuzating:
Qiyinchiliklar bormi? Keyin qarang javoblar:
To'g'ri burchakli uchburchak: sinus, kosinus, tangens, burchak kotangensi
Shunday qilib, biz burchak tushunchasini aniqladik. Lekin burchakning sinus, kosinus, tangensi, kotangensi nima? Keling, buni aniqlaylik. Buning uchun bizga to'g'ri burchakli uchburchak yordam beradi.

To'g'ri burchakli uchburchakning tomonlari nima deyiladi? To'g'ri, gipotenuza va oyoqlar: gipotenuza qarama-qarshi tomonda joylashgan to'g'ri burchak(bizning misolimizda bu tomon); oyoqlari qolgan ikkita tomon va (to'g'ri burchakka qo'shni bo'lganlar) va agar biz burchakka nisbatan oyoqlarni ko'rib chiqsak, u holda oyoq qo'shni oyoq, oyoq esa aksincha. Xo'sh, endi savolga javob beraylik: burchakning sinus, kosinus, tangensi va kotangensi nima?
Burchak sinusi- bu qarama-qarshi (uzoq) oyoqning gipotenuzaga nisbati.
Bizning uchburchakda.
Burchak kosinusi- bu qo'shni (yaqin) oyoqning gipotenuzaga nisbati.
Bizning uchburchakda.
Burchak tangensi- bu qarama-qarshi (uzoq) tomonning qo'shni (yaqin) nisbati.
Bizning uchburchakda.
Burchak kotangensi- bu qo'shni (yaqin) oyoqning qarama-qarshi (uzoq) nisbati.
Bizning uchburchakda.
Bu ta'riflar zarur eslab qoling! Qaysi oyoqni nimaga bo'lish kerakligini eslab qolishni osonlashtirish uchun siz buni aniq tushunishingiz kerak tangens Va kotangent faqat oyoqlar o'tiradi va gipotenuz faqat ichida paydo bo'ladi sinus Va kosinus. Va keyin siz birlashmalar zanjiri bilan kelishingiz mumkin. Masalan, bu:
Kosinus → teginish → teginish → ulashgan;
Kotangent → teginish → teginish → qo‘shni.
Avvalo, sinus, kosinus, tangens va kotangens uchburchak tomonlarining nisbati bu tomonlarning uzunligiga (bir xil burchak ostida) bog'liq emasligini yodda tutishingiz kerak. Ishonma? Keyin rasmga qarab ishonch hosil qiling:

Masalan, burchakning kosinusini ko'rib chiqaylik. Ta'rifga ko'ra, uchburchakdan: , lekin biz uchburchakdan burchakning kosinusini hisoblashimiz mumkin: . Ko'ryapsizmi, tomonlarning uzunligi har xil, lekin bir burchakning kosinus qiymati bir xil. Shunday qilib, sinus, kosinus, tangens va kotangens qiymatlari faqat burchakning kattaligiga bog'liq.
Agar siz ta'riflarni tushunsangiz, davom eting va ularni birlashtiring!
Quyidagi rasmda ko'rsatilgan uchburchak uchun biz topamiz.

Xo'sh, tushundingizmi? Keyin o'zingizni sinab ko'ring: burchak uchun xuddi shunday hisoblang.
Birlik (trigonometrik) doira
Darajalar va radianlar tushunchalarini tushunib, biz radiusi teng bo'lgan doirani ko'rib chiqdik. Bunday doira deyiladi yagona. Bu trigonometriyani o'rganishda juda foydali bo'ladi. Shuning uchun, keling, buni biroz batafsilroq ko'rib chiqaylik.

Ko'rib turganingizdek, bu aylana Dekart koordinata tizimida qurilgan. Doira radiusi birga teng, aylananing markazi koordinatalarning boshida joylashgan bo'lsa, radius vektorining boshlang'ich pozitsiyasi o'qning musbat yo'nalishi bo'ylab o'rnatiladi (bizning misolimizda bu radius).
Doiradagi har bir nuqta ikkita raqamga to'g'ri keladi: o'q koordinatasi va o'q koordinatasi. Bu koordinata raqamlari nima? Va umuman olganda, ularning mavzuga qanday aloqasi bor? Buning uchun biz ko'rib chiqilgan to'g'ri burchakli uchburchak haqida eslashimiz kerak. Yuqoridagi rasmda siz ikkita to'g'ri burchakli uchburchakni ko'rishingiz mumkin. Uchburchakni ko'rib chiqing. U to'rtburchaklar, chunki u o'qga perpendikulyar.
Uchburchak nimaga teng? Hammasi to'g'ri. Bundan tashqari, biz bilamizki, bu birlik doirasining radiusi, ya'ni . Keling, bu qiymatni kosinus formulamizga almashtiramiz. Mana nima sodir bo'ladi:
Uchburchak nimaga teng? Xo'sh, albatta,! Ushbu formulaga radius qiymatini almashtiring va quyidagilarni oling:
Demak, nuqta qanday koordinatalarga ega ekanligini ayta olasizmi? doiraga tegishli? Xo'sh, yo'qmi? Agar buni tushunsangiz va shunchaki raqamlar bo'lsa-chi? U qaysi koordinataga mos keladi? Albatta, koordinatalar! Va u qaysi koordinataga mos keladi? To'g'ri, koordinatalar! Shunday qilib, davr.

Xo'sh, nimaga teng va nimaga teng? To'g'ri, keling, tangens va kotangensning tegishli ta'riflaridan foydalanamiz va buni olamiz, a.
Agar burchak kattaroq bo'lsa-chi? Masalan, ushbu rasmdagi kabi:

Ushbu misolda nima o'zgardi? Keling, buni aniqlaylik. Buning uchun yana to'g'ri burchakli uchburchakka o'taylik. To'g'ri uchburchakni ko'rib chiqing: burchak (burchakka qo'shni sifatida). Burchak uchun sinus, kosinus, tangens va kotangensning qiymatlari qanday? To'g'ri, biz trigonometrik funktsiyalarning tegishli ta'riflariga amal qilamiz:
Ko'rib turganingizdek, burchak sinusining qiymati hali ham koordinataga to'g'ri keladi; burchak kosinusining qiymati - koordinata; va mos keladigan nisbatlarga tangens va kotangens qiymatlari. Shunday qilib, bu munosabatlar radius vektorining har qanday aylanishiga taalluqlidir.
Radius vektorining boshlang'ich pozitsiyasi o'qning ijobiy yo'nalishi bo'ylab joylashganligi allaqachon aytib o'tilgan. Hozirgacha biz bu vektorni soat sohasi farqli ravishda aylantirdik, lekin agar biz uni soat yo'nalishi bo'yicha aylantirsak nima bo'ladi? Hech qanday g'ayrioddiy narsa yo'q, siz ham ma'lum bir qiymatga ega burchakka ega bo'lasiz, lekin faqat salbiy bo'ladi. Shunday qilib, radius vektorini soat sohasi farqli ravishda aylantirganda, biz olamiz ijobiy burchaklar, va soat yo'nalishi bo'yicha aylanganda - salbiy.
Shunday qilib, biz bilamizki, radius vektorining aylana atrofida butun aylanishi yoki. Radius vektorini burish mumkinmi? Xo'sh, albatta qila olasiz! Birinchi holda, shuning uchun radius vektori bitta to'liq aylanishni amalga oshiradi va yoki pozitsiyasida to'xtaydi.
Ikkinchi holda, ya'ni radius vektori uchta to'liq aylanishni amalga oshiradi va yoki holatida to'xtaydi.
Shunday qilib, yuqoridagi misollardan xulosa qilishimiz mumkinki, bir-biridan farq qiladigan burchaklar yoki (bu erda har qanday butun son) radius vektorining bir xil holatiga mos keladi.
Quyidagi rasmda burchak ko'rsatilgan. Xuddi shu rasm burchakka mos keladi va hokazo. Ushbu ro'yxatni cheksiz davom ettirish mumkin. Bu burchaklarning barchasi umumiy formula yoki (bu yerda har qanday butun son) bilan yozilishi mumkin.

Endi, asosiy trigonometrik funktsiyalarning ta'riflarini bilib, birlik doirasidan foydalanib, qiymatlar nima ekanligiga javob berishga harakat qiling:
Mana sizga yordam beradigan birlik doirasi:

Qiyinchiliklar bormi? Keyin buni aniqlaylik. Shunday qilib, biz buni bilamiz:
Bu erdan ma'lum burchak o'lchovlariga mos keladigan nuqtalarning koordinatalarini aniqlaymiz. Keling, tartibda boshlaylik: burchak koordinatali nuqtaga to'g'ri keladi, shuning uchun:
Mavjud emas;
Bundan tashqari, xuddi shu mantiqqa rioya qilgan holda, biz burchaklar mos ravishda koordinatali nuqtalarga mos kelishini aniqlaymiz. Buni bilib, tegishli nuqtalarda trigonometrik funktsiyalarning qiymatlarini aniqlash oson. Avval o'zingiz sinab ko'ring, keyin javoblarni tekshiring.
Javoblar:
Mavjud emas
Mavjud emas
Mavjud emas
Mavjud emas
Shunday qilib, biz quyidagi jadvalni tuzishimiz mumkin:

Bu barcha qadriyatlarni eslab qolishning hojati yo'q. Birlik aylanasidagi nuqtalar koordinatalari va trigonometrik funktsiyalar qiymatlari o'rtasidagi muvofiqlikni eslash kifoya:
Ammo burchaklarning trigonometrik funktsiyalarining qiymatlari va quyidagi jadvalda keltirilgan, eslash kerak:

Qo'rqmang, endi biz sizga bitta misol keltiramiz mos keladigan qiymatlarni eslab qolish juda oddiy:
Ushbu usuldan foydalanish uchun burchakning barcha uch o'lchovi uchun sinus qiymatlarini (), shuningdek burchak tangensining qiymatini eslab qolish juda muhimdir. Ushbu qiymatlarni bilib, butun jadvalni tiklash juda oddiy - kosinus qiymatlari o'qlarga muvofiq uzatiladi, ya'ni:
Buni bilib, siz uchun qiymatlarni tiklashingiz mumkin. Numerator " " mos keladi va maxraj " " mos keladi. Kotangent qiymatlari rasmda ko'rsatilgan o'qlarga muvofiq o'tkaziladi. Agar siz buni tushunsangiz va o'qlar bilan diagrammani eslab qolsangiz, jadvaldagi barcha qiymatlarni eslab qolish kifoya qiladi.
Doiradagi nuqtaning koordinatalari
Aylanada nuqtani (uning koordinatalarini) topish mumkinmi? aylana markazining koordinatalarini, uning radiusini va burilish burchagini bilish?
Xo'sh, albatta qila olasiz! Keling, chiqaraylik umumiy formula nuqtaning koordinatalarini topish uchun.
Masalan, oldimizda aylana bor:

Bizga nuqta aylananing markazi ekanligi berilgan. Doira radiusi teng. Nuqtani gradusga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
Rasmdan ko'rinib turibdiki, nuqta koordinatasi segment uzunligiga to'g'ri keladi. Segmentning uzunligi aylana markazining koordinatasiga to'g'ri keladi, ya'ni u tengdir. Segment uzunligini kosinus ta'rifi yordamida ifodalash mumkin:
Keyin biz nuqta koordinatasini olamiz.
Xuddi shu mantiqdan foydalanib, nuqta uchun y koordinata qiymatini topamiz. Shunday qilib,
Shunday qilib, ichida umumiy ko'rinish Nuqtalarning koordinatalari quyidagi formulalar bilan aniqlanadi:
Doira markazining koordinatalari,
Doira radiusi,
Vektor radiusining burilish burchagi.
Ko'rib turganingizdek, biz ko'rib chiqayotgan birlik doirasi uchun bu formulalar sezilarli darajada kamayadi, chunki markazning koordinatalari nolga va radius birga teng:
Xo'sh, keling, aylana bo'ylab nuqtalarni topishni mashq qilib, ushbu formulalarni sinab ko'raylik?
1. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
2. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
3. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
4. Nuqta aylananing markazidir. Doira radiusi teng. Dastlabki radius vektorini ga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
5. Nuqta aylananing markazidir. Doira radiusi teng. Dastlabki radius vektorini ga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
Aylanadagi nuqtaning koordinatalarini topishda muammo bormi?
Ushbu beshta misolni yeching (yoki ularni echishni yaxshi biling) va siz ularni topishni o'rganasiz!
1.
Siz buni sezishingiz mumkin. Ammo biz boshlang'ich nuqtaning to'liq inqilobiga nima mos kelishini bilamiz. Shunday qilib, kerakli nuqta burilish paytida bo'lgani kabi bir xil holatda bo'ladi. Buni bilib, biz nuqtaning kerakli koordinatalarini topamiz:
2. Birlik doirasi nuqtada markazlashtirilgan, ya'ni biz soddalashtirilgan formulalardan foydalanishimiz mumkin:
Siz buni sezishingiz mumkin. Biz boshlang'ich nuqtaning ikkita to'liq inqilobiga nima mos kelishini bilamiz. Shunday qilib, kerakli nuqta burilish paytida bo'lgani kabi bir xil holatda bo'ladi. Buni bilib, biz nuqtaning kerakli koordinatalarini topamiz:
Sinus va kosinus jadval qiymatlari. Biz ularning ma'nolarini eslaymiz va olamiz:
Shunday qilib, kerakli nuqta koordinatalarga ega.
3. Birlik doirasi nuqtada markazlashtirilgan, ya'ni biz soddalashtirilgan formulalardan foydalanishimiz mumkin:
Siz buni sezishingiz mumkin. Keling, ushbu misolni rasmda tasvirlaymiz:

Radius o'qga teng va o'q bilan burchaklarni hosil qiladi. Kosinus va sinusning jadval qiymatlari teng ekanligini bilib, bu erda kosinus manfiy, sinus esa ijobiy qiymat olishini aniqlab, biz:
Mavzu bo'yicha trigonometrik funktsiyalarni kamaytirish formulalarini o'rganishda bunday misollar batafsilroq muhokama qilinadi.
Shunday qilib, kerakli nuqta koordinatalarga ega.
4.
Vektor radiusining burilish burchagi (shart bo'yicha)
Sinus va kosinusning tegishli belgilarini aniqlash uchun biz birlik doira va burchakni quramiz:

Ko'rib turganingizdek, qiymat, ya'ni ijobiy, qiymat esa, ya'ni salbiy. Tegishli trigonometrik funktsiyalarning jadval qiymatlarini bilib, biz quyidagilarni olamiz:
Olingan qiymatlarni formulamizga almashtiramiz va koordinatalarni topamiz:
Shunday qilib, kerakli nuqta koordinatalarga ega.
5. Ushbu muammoni hal qilish uchun biz umumiy shakldagi formulalardan foydalanamiz, bu erda
Doira markazining koordinatalari (bizning misolimizda,
Doira radiusi (shart bo'yicha)
Vektor radiusining burilish burchagi (shart bo'yicha).
Keling, barcha qiymatlarni formulaga almashtiramiz va olamiz:
va - jadval qiymatlari. Keling, eslaylik va ularni formulaga almashtiramiz:
Shunday qilib, kerakli nuqta koordinatalarga ega.
XULOSA VA ASOSIY FORMULALAR
Burchakning sinusi - bu qarama-qarshi (uzoq) oyoqning gipotenuzaga nisbati.
Burchakning kosinusu - qo'shni (yaqin) oyoqning gipotenuzaga nisbati.
Burchakning tangensi - qarama-qarshi (uzoq) tomonning qo'shni (yaqin) tomonga nisbati.
Burchakning kotangensi - qo'shni (yaqin) tomonning qarama-qarshi (uzoq) tomonga nisbati.
Ko'rsatmalar
Agar burchakning qiymatini bilsangiz, burchakning qiymatini darajalarda hisoblash uchun arcsine funktsiyasidan foydalaning. Agar burchak a harfi bilan belgilanadi, umuman yechimni quyidagicha yozish mumkin: a = arcsin(sin(a)).
Agar sizda kompyuterdan foydalanish imkoniyati mavjud bo'lsa, amaliy hisob-kitoblarni amalga oshirishning eng oson yo'li o'rnatilgan operatsion tizimdan foydalanishdir. Windows OS ning so'nggi ikki versiyasida siz uni quyidagicha ishga tushirishingiz mumkin: Win tugmasini bosing, "ka" ni kiriting va Enter tugmasini bosing. Ushbu OTning oldingi versiyalarida tizimning asosiy menyusidagi "Barcha dasturlar" bo'limining "Standart" bo'limida "Kalkulyator" havolasini qidiring.
Ilovani ishga tushirgandan so'ng, uni trigonometrik funktsiyalar bilan ishlashga imkon beruvchi rejimga o'tkazing. Buni kalkulyator menyusining "Ko'rish" bo'limida "Muhandislik" qatorini tanlash yoki Alt + 2 tugmalarini bosish orqali amalga oshirish mumkin.
Sinus qiymatini kiriting. Odatiy bo'lib, kalkulyator interfeysida arksinusni hisoblash tugmasi mavjud emas. Ushbu funktsiyadan foydalanish uchun siz standart tugma qiymatlarini o'zgartirishingiz kerak - dastur oynasida Inv tugmachasini bosing. Ko'proq oldingi versiyalar bu tugma bir xil belgiga ega bo'lgan katakcha bilan almashtiriladi - uni tekshiring.
Hisob-kitoblarda siz turli xil xizmatlardan foydalanishingiz mumkin, ularning Internetda ko'pi etarli. Misol uchun, http://planetcalc.com/326/ saytiga o'ting, biroz pastga aylantiring va Kirish maydoniga sinus qiymatini kiriting. Hisoblash jarayonini boshlash uchun Hisoblash deb nomlangan tugma mavjud - ustiga bosing. Hisoblash natijasini jadvalning birinchi qatorida ushbu tugma ostida topasiz. Yoy sinusiga qo'shimcha ravishda u kiritilgan qiymatning kattaliklarini ham, yoy tangensini ham ko'rsatadi.
Sinusning teskarisi trigonometrik funktsiya deyiladi arksin. U Pi sonining yarmida ham ijobiy, ham salbiy qiymatlarni qabul qilishi mumkin. salbiy tomoni radianlarda o'lchanganda. Darajalarda o'lchanganda, bu qiymatlar mos ravishda -90 ° dan +90 ° gacha bo'ladi.
Ko'rsatmalar
Ba'zi "dumaloq" qiymatlarni hisoblashning hojati yo'q, ularni eslab qolish osonroq; Masalan: - funktsiya argumenti nolga teng bo'lsa, uning yoyi ham nolga teng - 1/2 ga teng 30° yoki 1/6 Pi, -1/2 ning yoyi -30°; yoki Pi sonidan -1/ 6 - 1 ning yoyi radiandagi Pi sonining 1/2 qismiga teng; -1 ning yoyi -90° yoki -1/2 ga teng; radiandagi Pi soni;
Ushbu funktsiyaning qiymatlarini boshqa argumentlardan o'lchashning eng oson yo'li, agar qo'lingizda bo'lsa, standart Windows kalkulyatoridan foydalanishdir. Boshlash uchun "Ishga tushirish" tugmachasidagi asosiy menyuni oching (yoki WIN tugmachasini bosib), "Barcha dasturlar" bo'limiga, so'ngra "Aksessuarlar" bo'limiga o'ting va "Kalkulyator" ni bosing.
Kalkulyator interfeysini trigonometrik funktsiyalarni hisoblash imkonini beruvchi ish rejimiga o'tkazing. Buning uchun uning menyusidagi "Ko'rish" bo'limini oching va "Muhandislik" yoki "Ilmiy" ni tanlang (ishlatilgan operatsion tizimga qarab).
Arktangentni hisoblash kerak bo'lgan argumentning qiymatini kiriting. Buni kalkulyator interfeysi tugmachalarini sichqoncha bilan bosish yoki tugmachalarini bosish yoki qiymatni (CTRL + C) nusxalash va keyin uni (CTRL + V) kalkulyator kiritish maydoniga joylashtirish orqali amalga oshirish mumkin.
Funktsiyani hisoblash natijasini olishingiz kerak bo'lgan o'lchov birliklarini tanlang. Kirish maydoni ostida uchta variant mavjud, ulardan birini tanlash kerak (sichqoncha bilan bosish orqali) - , radian yoki rad.
Kalkulyator interfeysi tugmalarida ko'rsatilgan funktsiyalarni o'zgartiradigan katakchani belgilang. Uning yonida Inv degan qisqa yozuv bor.
Gunoh tugmasini bosing. Kalkulyator u bilan bog'liq funktsiyani o'zgartiradi, hisob-kitobni amalga oshiradi va natijani belgilangan birliklarda sizga taqdim etadi.
Mavzu bo'yicha video
To'g'ri uchburchakda, eng oddiy ko'pburchak sifatida, turli olimlar trigonometriya sohasidagi bilimlarini hech kim matematikaning bu sohasini bu so'z bilan atamagan kunlarda yaxshilagan. Shuning uchun, ushbu tekislikdagi tomonlar uzunligi va burchak qiymatlari nisbatlarida naqshlarni aniqlagan muallifni ko'rsating geometrik shakl, bugungi kunda mumkin emas. Bunday munosabatlar trigonometrik funktsiyalar deb ataladi va bir nechta guruhlarga bo'linadi, ularning asosiylari shartli ravishda "to'g'ridan-to'g'ri" funktsiyalar deb hisoblanadi. Bu guruh faqat ikkita funktsiyani o'z ichiga oladi va ulardan biri sinusdir.

Ko'rsatmalar
Ta'rifga ko'ra, to'g'ri burchakli uchburchakda burchaklardan biri 90 ° ga teng va Evklid geometriyasidagi burchaklarining yig'indisi 180 ° ga teng bo'lishi kerakligi sababli, qolgan ikkita burchak (ya'ni 90 °). Aynan shu burchaklar va yon uzunliklar orasidagi munosabatlar naqshlari trigonometrik funktsiyalarni tavsiflaydi.
O'tkir burchak sinusi deb ataladigan funktsiya to'g'ri burchakli uchburchakning ikki tomonining uzunliklari orasidagi nisbatni aniqlaydi, ulardan biri o'tkir burchakka qarama-qarshi, ikkinchisi esa unga qo'shni va to'g'ri burchakka qarama-qarshi yotadi. Bunday uchburchakda to'g'ri burchakka qarama-qarshi yotgan tomon gipotenuza, qolgan ikkitasi esa oyoqlar deb ataladiganligi sababli, sinus funktsiyani oyoq va gipotenuzaning uzunliklari orasidagi nisbat sifatida shakllantirish mumkin.
Ushbu trigonometrik funktsiyaning eng oddiy ta'rifiga qo'shimcha ravishda, yanada murakkablari mavjud: dekart koordinatalarida aylana orqali, ketma-ketlik orqali, differentsial va funktsional tenglamalar orqali. Bu funktsiya uzluksiz, ya'ni uning argumentlari ("domen") har qanday raqam bo'lishi mumkin - cheksiz salbiydan cheksiz ijobiygacha. Va bu funktsiyaning maksimal qiymatlari -1 dan +1 gacha bo'lgan oraliq bilan cheklangan - bu "uning qiymatlari diapazoni". Minimal qiymat sinus 270 ° burchak ostida joylashadi, bu 3/Pi ga to'g'ri keladi va maksimal 90 ° (Pi ning ½) da olinadi. Funktsiya qiymatlari 0°, 180°, 360° va hokazolarda nolga aylanadi. Bularning barchasidan kelib chiqadiki, sinus davriy funktsiya bo'lib, uning davri 360 ° ga teng yoki Pi sonining ikki barobariga teng.
Berilgan argument bo'yicha ushbu funktsiyaning qiymatlarini amaliy hisoblash uchun siz ularning katta qismidan (shu jumladan o'rnatilgan dasturiy kalkulyatordan) foydalanishingiz mumkin. operatsion tizim kompyuteringiz) tegishli variantga ega.
Mavzu bo'yicha video
Sinus Va kosinus- bu to'g'ridan-to'g'ri trigonometrik funktsiyalar bo'lib, ular uchun bir nechta ta'riflar mavjud - Dekart koordinata tizimidagi aylana orqali, echimlar orqali differensial tenglama, to'g'ri uchburchakdagi o'tkir burchaklar orqali. Ushbu ta'riflarning har biri bizga ushbu ikki funktsiya o'rtasidagi munosabatni aniqlashga imkon beradi. Quyida ifodalashning eng oddiy usuli keltirilgan kosinus sinus orqali - to'g'ri burchakli uchburchakning o'tkir burchaklari uchun ularning ta'riflari orqali.

Ko'rsatmalar
To'g'ri burchakli uchburchakning o'tkir burchagi sinusini ushbu rasmning tomonlari uzunligi bilan ifodalang. Ta'rifga ko'ra, burchakning sinusi (a) uning qarshisida yotgan tomonning (a) uzunligi - oyoq - to'g'ri burchakka qarama-qarshi tomonning uzunligi (c) - gipotenuza nisbati bo'lishi kerak: sin(a) = a/c.
ga o'xshash formulani toping kosinus lekin bir xil burchak. Ta'rifga ko'ra, bu qiymat bu burchakka (ikkinchi oyoq) ulashgan tomonning (b) uzunligining to'g'ri burchakka qarama-qarshi yotgan tomonning (c) uzunligiga nisbati sifatida ifodalanishi kerak: cos (a) = a. /c.
Pifagor teoremasidan kelib chiqadigan tenglikni qayta yozing, shunda u oldingi ikki bosqichda olingan oyoqlar va gipotenuza o'rtasidagi munosabatlarni o'z ichiga oladi. Buning uchun avval asl teoremaning ikkalasini (a² + b² = c²) gipotenuzaning kvadratiga (a²/c² + b²/c² = 1) boʻling, soʻngra hosil boʻlgan tenglikni quyidagi koʻrinishda qayta yozing: (a/c) )² + (b/c )² = 1.
Hosil boʻlgan ifodada birinchi va ikkinchi bosqich formulalari asosida oyoq va gipotenuzaning uzunliklari nisbatini trigonometrik funksiyalar bilan almashtiring: sin²(a) + cos²(a) = 1. Ekspress. kosinus olingan tenglikdan: cos(a) = √(1 - sin²(a)). Bu bilan muammoni umumiy shaklda hal qilish mumkin.
Agar umumiy natijaga qo'shimcha ravishda siz raqamli natija olishingiz kerak bo'lsa, masalan, operatsiya xonasiga o'rnatilgan kalkulyatordan foydalaning. Windows tizimi. Uni OS menyusining "Barcha dasturlar" bo'limining "Standart" bo'limida ishga tushirish uchun havola. Ushbu havola qisqacha tuzilgan - "Kalkulyator". Ushbu dastur yordamida trigonometrik funktsiyalarni hisoblash uchun uning "muhandislik" interfeysini yoqing - Alt + 2 tugmalar birikmasini bosing.
Shartlarda burchak sinusining qiymatini kiriting va x² bilan belgilangan interfeys tugmachasini bosing - bu asl qiymatni kvadratga aylantiradi. Keyin klaviaturada *-1 ni kiriting, Enter tugmasini bosing, +1 kiriting va yana Enter tugmasini bosing - shu tarzda siz sinusning kvadratini bittadan ayirasiz. Kvadratni ajratib olish va yakuniy natijani olish uchun radikal tugmachani bosing.
Uchburchaklarni o'rganish bir necha ming yillar davomida matematiklar tomonidan amalga oshirilgan. Uchburchaklar fani - trigonometriya maxsus kattaliklardan foydalanadi: sinus va kosinus.

To'g'ri uchburchak
Sinus va kosinus dastlab to'g'ri burchakli uchburchaklardagi miqdorlarni hisoblash zaruratidan kelib chiqqan. Agar to'g'ri burchakli uchburchakdagi burchaklarning daraja o'lchovi o'zgarmasa, tomonlarning nisbati, bu tomonlar uzunligi qanchalik o'zgarmasin, har doim bir xil bo'lib qolishi ta'kidlandi.
Shunday qilib sinus va kosinus tushunchalari kiritildi. To'g'ri burchakli uchburchakdagi o'tkir burchakning sinusi qarama-qarshi tomonning gipotenuzaga nisbati, kosinus esa gipotenuzaga qo'shni tomonning nisbati.
Kosinuslar va sinuslar teoremalari
Ammo kosinuslar va sinuslar faqat to'g'ri burchakli uchburchaklar uchun emas, balki ko'proq uchun ishlatilishi mumkin. Har qanday uchburchakning o'tkir yoki o'tkir burchagi yoki tomonining qiymatini topish uchun kosinuslar va sinuslar teoremasini qo'llash kifoya.
Kosinus teoremasi juda oddiy: "Uchburchakning bir tomonining kvadrati boshqa ikki tomonning kvadratlari yig'indisiga, bu tomonlarning ikki baravar ko'paytmasiga va ular orasidagi burchakning kosinusiga tengdir."
Sinus teoremasining ikkita talqini mavjud: kichik va kengaytirilgan. Kichkintoyning so'zlariga ko'ra: "Uchburchakda burchaklar qarama-qarshi tomonlarga proportsionaldir." Ushbu teorema ko'pincha uchburchakning aylanasi xususiyati tufayli kengaytiriladi: "Uchburchakda burchaklar qarama-qarshi tomonlarga proportsionaldir va ularning nisbati aylananing diametriga tengdir."
Hosilalar
Hosila - bu argumentning o'zgarishiga nisbatan funktsiya qanchalik tez o'zgarishini ko'rsatadigan matematik vositadir. Hosilalar geometriyada va bir qator texnik fanlarda qo'llaniladi.
Muammolarni hal qilishda siz trigonometrik funktsiyalarning hosilalarining jadval qiymatlarini bilishingiz kerak: sinus va kosinus. Sinusning hosilasi kosinus, kosinus esa sinus, lekin minus belgisi bilan.
Matematikada qo'llash
Ayniqsa, sinuslar va kosinuslar yechishda tez-tez ishlatiladi to'g'ri uchburchaklar va ular bilan bog'liq vazifalar.
Sinuslar va kosinuslarning qulayligi texnologiyada ham namoyon bo'ladi. Burchaklar va tomonlarni kosinus va sinus teoremalari yordamida baholash oson edi, murakkab shakllar va ob'ektlarni "oddiy" uchburchaklarga bo'lishdi. Ko'pincha tomonlar nisbati va daraja o'lchovlarini hisoblash bilan shug'ullanadigan muhandislar jadvalsiz burchaklarning kosinuslari va sinuslarini hisoblash uchun ko'p vaqt va kuch sarfladilar.
Keyin sinuslar, kosinuslar, tangenslar va kotangentlarning minglab qiymatlarini o'z ichiga olgan Bradis jadvallari yordamga keldi. turli burchaklar. Sovet davrida ba'zi o'qituvchilar o'z shogirdlarini Bradis jadvallari sahifalarini yodlashga majbur qilishgan.
Radian - burchak kattaligi yoylar, uzunlik radiusga teng yoki 57,295779513 ° daraja.
Daraja (geometriyada) aylananing 1/360 qismi yoki toʻgʻri burchakning 1/90 qismidir.
p = 3,141592653589793238462… (Pi ning taxminiy qiymati).
Burchaklar uchun kosinuslar jadvali: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| x burchak (gradusda) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x burchak (radianlarda) | 0 | p/6 | p/4 | p/3 | p/2 | 2 x p/3 | 3 x p/4 | 5 x p/6 | π | 7 x p/6 | 5 x p/4 | 4 x p/3 | 3 x p/2 | 5 x p/3 | 7 x p/4 | 11 x p/6 | 2 x p |
| chunki x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |