Značenje izvedenice. Derivacija funkcije. Geometrijsko značenje derivacije

10.10.2019

Pročitajte također

Aforizmi, citati, izreke, fraze Sir Isaac Newton Newtonove fraze

Citati i fraze o postupcima i ponašanju Citati o lošim djelima

Citati i aforizmi o školi i studiju

Zlatni citati o obrazovanju i aforizmi za učenje

Kako pravilno i brzo filetirati haringu od kostiju i kože?

Što je derivat?
Definicija i značenje derivacije funkcije

Mnogi će biti iznenađeni neočekivanim postavljanjem ovog članka u moj autorski kolegij o izvodu funkcije jedne varijable i njegovim primjenama. Uostalom, kako je to još od školske klupe: standardni udžbenik prije svega daje definiciju derivacije, njezino geometrijsko, mehaničko značenje. Zatim učenici pronalaze izvode funkcija po definiciji i zapravo tek tada usavršavaju tehniku diferenciranja pomoću tablice izvedenica.

Ali s moje točke gledišta, sljedeći pristup je pragmatičniji: prije svega, preporučljivo je DOBRO RAZUMIJETI granica funkcije, a posebno, infinitezimalne količine. Činjenica je da definicija derivacije temelji se na konceptu granice, što se slabo razmatra u školski tečaj. Zato značajan dio mladih konzumenata granita znanja ne razumije samu bit derivata. Dakle, ako ste loše orijentirani u diferencijalni račun ili mudar mozak za duge godine uspješno se riješio ove prtljage, počnite s granice funkcije. Istovremeno savladajte/zapamtite njihovo rješenje.

Isti praktični smisao nalaže da je prvo prednost naučiti pronalaziti izvedenice, uključujući izvode složenih funkcija. Teorija je teorija, ali, kako kažu, uvijek se želi razlikovati. U tom smislu, bolje je proraditi navedene osnovne lekcije, a možda majstor diferencijacije a da i ne shvaćaju bit svojih postupaka.

Preporučujem da počnete s materijalima na ovoj stranici nakon čitanja članka. Najjednostavniji problemi s izvedenicama, gdje se posebno razmatra problem tangente na graf funkcije. Ali možete čekati. Činjenica je da mnoge primjene derivata ne zahtijevaju njegovo razumijevanje, te ne čudi da se teorijska lekcija pojavila prilično kasno - kada sam trebao objasniti pronalaženje rastućih/opadajućih intervala i ekstrema funkcije. Štoviše, on je bio na toj temi dosta dugo. Funkcije i grafovi”, dok ga konačno nisam odlučio staviti ranije.

Stoga, dragi čajnici, nemojte poput gladnih životinja žuriti upijati esenciju derivata jer će zasićenje biti neukusno i nepotpuno.

Pojam rastućeg, opadajućeg, maksimuma, minimuma funkcije

Puno nastavna sredstva dovesti do koncepta derivata koristeći neke praktične probleme, a također sam ih smislio zanimljiv primjer. Zamislite da ćemo putovati u grad do kojeg se može doći na različite načine. Odmah odbacimo zakrivljene vijugave staze i razmotrimo samo ravne autoceste. Međutim, pravocrtni pravci su također različiti: do grada možete doći glatkom autocestom. Ili uz brdovitu autocestu - gore-dolje, gore-dolje. Drugi put ide samo uzbrdo, a drugi stalno nizbrdo. Ljubitelji ekstrema odabrat će rutu kroz klanac sa strmom liticom i strmim usponom.

No bez obzira na vaše želje, preporučljivo je poznavati područje ili ga barem locirati topografska karta. Što ako takve informacije nedostaju? Uostalom, možete odabrati, na primjer, glatku stazu, ali kao rezultat toga naletjeti na skijašku stazu s veselim Fincima. Nije činjenica da će navigator ili čak satelitska slika dati pouzdane podatke. Stoga bi bilo lijepo formalizirati reljef staze pomoću matematike.

Pogledajmo neku cestu (bočni pogled):

Za svaki slučaj, podsjećam vas na elementarnu činjenicu: putovanja se događaju s lijeva na desno. Radi jednostavnosti, pretpostavljamo da funkcija stalan u području koje se razmatra.

Koje značajke ima ovaj grafikon?

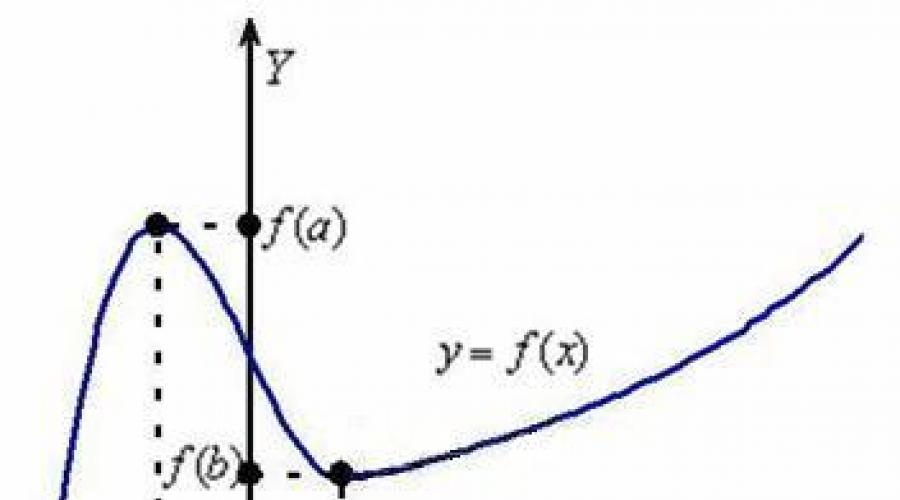
U intervalima funkcija povećava se, odnosno svaka njegova sljedeća vrijednost više prethodni. Ugrubo rečeno, raspored ide dolje gore(penjemo se na brdo). A na intervalu funkcija smanjuje se– svaka sljedeća vrijednost manje prethodni, a naš raspored je na vrh prema dolje(spuštamo se niz padinu).

Obratimo pozornost i na singularne točke. Na točki do koje dolazimo maksimum, to je postoji takav dio puta gdje će vrijednost biti najveća (najviša). U istoj točki se postiže minimum, I postoji njegovo susjedstvo u kojem je vrijednost najmanja (najniža).

U nastavi ćemo pogledati strožu terminologiju i definicije. o ekstremima funkcije, ali za sada proučimo još jedno važna značajka: u intervalima funkcija se povećava, ali se povećava S različitim brzinama . I prva stvar koja upada u oči je da graf raste tijekom intervala mnogo više cool, nego na intervalu . Je li moguće izmjeriti strminu ceste pomoću matematičkih alata?

Stopa promjene funkcije

Ideja je sljedeća: uzmimo neku vrijednost (čitaj "delta x"), koju ćemo nazvati povećanje argumenta, i počnimo ga "isprobavati" na raznim točkama na našem putu:

1) Pogledajmo krajnju lijevu točku: prolazeći udaljenost, penjemo se uz padinu do visine (zelena linija). Količina se zove prirast funkcije, i u u ovom slučaju ovaj prirast je pozitivan (razlika u vrijednostima duž osi je veća od nule). Napravimo omjer koji će biti mjera strmine naše ceste. Očito, ovo je vrlo specifičan broj, a budući da su oba povećanja pozitivna, tada .

Pažnja! Oznake su JEDAN simbol, odnosno ne možete "otkinuti" "deltu" od "X" i razmatrati ova slova odvojeno. Naravno, komentar se odnosi i na simbol inkrementa funkcije.

Istražimo prirodu dobivenog razlomka smislenije. Neka se u početku nalazimo na visini od 20 metara (na lijevoj crnoj točki). Nakon što smo prevalili udaljenost od metara (lijeva crvena linija), naći ćemo se na visini od 60 metara. Tada će prirast funkcije biti metara (zelena linija) i: . Tako, na svakom metru ovaj dio puta povećava se visina prosjek za 4 metra...zaboravili ste opremu za penjanje? =) Drugim riječima, konstruirani odnos karakterizira PROSJEČNU STOPU PROMJENE (u ovom slučaju rasta) funkcije.

Bilješka : Brojčane vrijednosti predmetnog primjera samo približno odgovaraju proporcijama crteža.

2) Sada idemo na istu udaljenost od krajnje desne crne točke. Ovdje je uspon postupniji, pa je prirast (grmizna linija) relativno malen, a omjer u odnosu na prethodni slučaj bit će vrlo skroman. Relativno govoreći, metara i stopa rasta funkcije je . To jest, ovdje za svaki metar staze postoje prosjek pola metra uspona.

3) Mala avantura na planini. Pogledajmo vrh crna točka, koji se nalazi na osi ordinata. Pretpostavimo da je ovo oznaka od 50 metara. Ponovno svladavamo udaljenost, zbog čega se nalazimo niže - na razini od 30 metara. Budući da se kretanje provodi vrh prema dolje(u “kontra” smjeru osi), zatim završni prirast funkcije (visine) bit će negativan: metara (smeđi segment na crtežu). A u ovom slučaju već govorimo o stopa smanjenja Značajke: , odnosno za svaki metar staze ove dionice visina se smanjuje prosjek za 2 metra. Pazite na svoju odjeću u petoj točki.

Postavimo si sada pitanje: koju je vrijednost “mjernog etalona” najbolje koristiti? Potpuno je razumljivo, 10 metara je vrlo grubo. Na njih lako stane dobar tucet humova. Bez obzira na neravnine, dolje može biti dubok klanac, a nakon nekoliko metara njegova druga strana s daljnjim strmim usponom. Dakle, desetmetrom nećemo dobiti razumljiv opis takvih dionica puta kroz omjer .

Iz gornje rasprave slijedi sljedeći zaključak: kako manje vrijednosti , što točnije opisujemo topografiju ceste. Štoviše, istinite su sljedeće činjenice:

– Za bilo koga točke dizanja možete odabrati vrijednost (čak i ako je vrlo mala) koja odgovara granicama određenog porasta. To znači da će odgovarajući prirast visine biti zajamčeno pozitivan, a nejednakost će ispravno pokazati rast funkcije u svakoj točki ovih intervala.

- Isto tako, za bilo koji točka nagiba postoji vrijednost koja će u potpunosti stati na ovaj nagib. Posljedično, odgovarajući porast visine je jasno negativan, a nejednadžba će ispravno pokazati smanjenje funkcije u svakoj točki zadanog intervala.

– Posebno je zanimljiv slučaj kada je brzina promjene funkcije nula: . Prvo, nulti prirast visine () je znak glatke putanje. I drugo, postoje i druge zanimljive situacije čije primjere vidite na slici. Zamislite da nas je sudbina dovela na sam vrh brda gdje lebde orlovi ili na dno gudure s kreketom žaba. Napravite li mali korak u bilo kojem smjeru, promjena visine bit će zanemariva i možemo reći da je brzina promjene funkcije zapravo nula. Upravo se takva slika uočava na točkama.

Dakle, došli smo do nevjerojatne prilike da savršeno točno karakteriziramo brzinu promjene funkcije. Uostalom, matematička analiza omogućuje usmjeravanje povećanja argumenta na nulu: , tj. infinitezimalnog.

Kao rezultat toga, postavlja se još jedno logično pitanje: je li moguće pronaći cestu i njen raspored drugu funkciju, koji javio bi nam o svim ravnim dionicama, usponima, spustovima, vrhovima, dolinama, kao i stopi rasta/smanjenja na svakoj točki puta?

Što je derivat? Definicija derivata.
Geometrijsko značenje derivacije i diferencijala

Čitajte pažljivo i ne prebrzo - materijal je jednostavan i dostupan svima! U redu je ako na nekim mjestima nešto nije jasno, uvijek se možete kasnije vratiti na članak. Reći ću više, korisno je proučiti teoriju nekoliko puta kako biste temeljito razumjeli sve točke (savjet je posebno relevantan za studente "techie" koji imaju viša matematika ima značajnu ulogu u obrazovnom procesu).

Naravno, u samoj definiciji derivacije u točki zamjenjujemo je s:

Do čega smo došli? I došli smo do zaključka da za funkciju po zakonu stavlja se u skladu druga funkcija, koji se zove izvodna funkcija(ili jednostavno izvedenica).

Izvedenica karakterizira stopa promjene funkcije Kako? Ideja se provlači kao crvena nit od samog početka članka. Razmotrimo neke točke domena definicije funkcije Neka je funkcija diferencijabilna u danoj točki. Zatim:

1) Ako je , tada funkcija raste u točki . A očito postoji interval(čak i vrlo malen), koji sadrži točku u kojoj funkcija raste, a njezin graf ide "odozdo prema gore".

2) Ako je , tada funkcija opada u točki . I postoji interval koji sadrži točku u kojoj funkcija opada (graf ide "od vrha do dna").

3) Ako je , tada beskrajno blizu u blizini točke funkcija održava svoju brzinu konstantnom. To se događa, kao što je navedeno, s konstantnom funkcijom i na kritičnim točkama funkcije, posebno u minimalnim i maksimalnim točkama.

Malo semantike. Što u u širem smislu znači li glagol "razlikovati"? Razlikovati znači istaknuti značajku. Diferenciranjem funkcije “izoliramo” brzinu njezine promjene u obliku derivacije funkcije. Što se, usput, podrazumijeva pod riječju "derivat"? Funkcija dogodilo se od funkcije.

Pojmovi se vrlo uspješno tumače mehaničkim značenjem izvedenice :
Razmotrimo zakon promjene koordinata tijela ovisno o vremenu i funkciju brzine gibanja zadanog tijela. Funkcija karakterizira brzinu promjene koordinata tijela, stoga je prva derivacija funkcije u odnosu na vrijeme: . Da koncept "kretanja tijela" ne postoji u prirodi, onda ga ne bi ni bilo izvedenica koncept "brzine tijela".

Ubrzanje tijela je brzina promjene brzine, dakle: . Da početni pojmovi "gibanja tijela" i "brzine tijela" ne postoje u prirodi, onda ne bi postojali izvedenica koncept “ubrzanja tijela”.

Prilikom odlučivanja razne zadatke geometrija, mehanika, fizika i druge grane znanja postale su neophodne korištenjem istog analitičkog procesa iz ove funkcije y=f(x) pozvati novu funkciju izvodna funkcija(ili jednostavno izvod) zadane funkcije f(x) i označava se simbolom

Proces kojim se iz zadane funkcije f(x) dobiti novu značajku f" (x), nazvao diferencijacija a sastoji se od sljedeća tri koraka: 1) dati argument x prirast  x te odrediti pripadni prirast funkcije  y = f(x+ x) -f(x); 2) uspostaviti odnos

3) brojanje x konstantan i  x0, nalazimo
, što označavamo sa f" (x), kao da naglašava da rezultirajuća funkcija ovisi samo o vrijednosti x, pri čemu idemo do granice. Definicija: Derivacija y " =f " (x) dana funkcija y=f(x) za dati x naziva se granica omjera prirasta funkcije i prirasta argumenta, pod uvjetom da priraštaj argumenta teži nuli, ako, naravno, ta granica postoji, tj. konačan. Tako,
, ili

Imajte na umu da ako pri nekoj vrijednosti x, na primjer kada x=a, stav
na  x0 ne teži konačnoj granici, onda u ovom slučaju kažu da funkcija f(x) na x=a(ili u točki x=a) nema derivaciju ili nije diferencijabilna u točki x=a.

2. Geometrijsko značenje derivacije.

Razmotrimo graf funkcije y = f (x), diferencijabilne u blizini točke x 0

f(x)

Promotrimo proizvoljnu ravnu liniju koja prolazi točkom na grafu funkcije - točkom A(x 0, f (x 0)) i siječe graf u nekoj točki B(x;f(x)). Takav pravac (AB) naziva se sekantom. Iz ∆ABC: AC = ∆x; VS =∆u; tgβ=∆y/∆x.

Budući da je AC || Ox, tada je ALO = BAC = β (kao što odgovara za paralelu). Ali ALO je kut nagiba sekante AB prema pozitivnom smjeru osi Ox. To znači tanβ = k - nagib ravna AB.

Sada ćemo smanjiti ∆x, tj. ∆h→ 0. U tom slučaju će se točka B približiti točki A prema grafu, a sekanta AB će se zarotirati. Granični položaj sekante AB na ∆x→ 0 bit će ravna crta (a), koja se naziva tangenta na graf funkcije y = f (x) u točki A.

Ako idemo do limita kao ∆x → 0 u jednakosti tgβ =∆y/∆x, dobivamo
ortg =f "(x 0), jer
-kut nagiba tangente na pozitivan smjer osi Ox
, po definiciji izvedenice. Ali tg = k je kutni koeficijent tangente, što znači k = tg = f "(x 0).

Dakle, geometrijsko značenje izvoda je sljedeće:

Derivacija funkcije u točki x 0 jednak nagibu tangente na graf funkcije nacrtan u točki s apscisom x 0 .

3. Fizičko značenje izvedenice.

Razmotrimo kretanje točke po ravnoj liniji. Neka je dana koordinata točke u bilo kojem trenutku x(t). Poznato je (iz tečaja fizike) da je prosječna brzina u određenom vremenskom razdoblju jednaka omjeru prijeđene udaljenosti u tom vremenskom razdoblju prema vremenu, tj.

Vav = ∆x/∆t. Idemo do granice u posljednjoj jednakosti kao ∆t → 0.

lim Vav (t) = (t 0) - trenutna brzina u trenutku t 0, ∆t → 0.

i lim = ∆x/∆t = x"(t 0) (po definiciji derivacije).

Dakle, (t) =x"(t).

Fizičko značenje derivacije je sljedeće: derivacija funkcijeg = f(x) u točkix 0 je brzina promjene funkcijef(x) u točkix 0

Derivacija se koristi u fizici za pronalaženje brzine iz poznate funkcije koordinata u odnosu na vrijeme, ubrzanja iz poznate funkcije brzine u odnosu na vrijeme.

(t) = x"(t) - brzina,

a(f) = "(t) - ubrzanje, odn

Ako je poznat zakon gibanja materijalne točke u krugu, tada se mogu pronaći kutna brzina i kutna akceleracija tijekom rotacijskog gibanja:

φ = φ(t) - promjena kuta tijekom vremena,

ω = φ"(t) - kutna brzina,

ε = φ"(t) - kutno ubrzanje, odnosno ε = φ"(t).

Ako je poznat zakon raspodjele mase nehomogenog štapa, tada se linearna gustoća nehomogenog štapa može naći:

m = m(x) - masa,

x  , l - duljina štapa,

p = m"(x) - linearna gustoća.

Pomoću derivacije rješavaju se problemi iz teorije elastičnosti i harmonijskih vibracija. Dakle, prema Hookeovom zakonu

F = -kx, x – promjenljiva koordinata, k – koeficijent elastičnosti opruge. Stavljajući ω 2 =k/m, dobivamo diferencijalnu jednadžbu opružnog njihala x"(t) + ω 2 x(t) = 0,

gdje je ω = √k/√m frekvencija oscilacija (l/c), k - krutost opruge (H/m).

Jednadžba oblika y" + ω 2 y = 0 naziva se jednadžba harmonijskih oscilacija (mehaničkih, električnih, elektromagnetskih). Rješenje takvih jednadžbi je funkcija

y = Asin(ωt + φ 0) ili y = Acos(ωt + φ 0), gdje je

A - amplituda oscilacija, ω - ciklička frekvencija,

φ 0 - početna faza.

(\large\bf Derivacija funkcije)

Razmotrite funkciju y=f(x), naveden na intervalu (a, b). Neka x- bilo koja fiksna točka intervala (a, b), A Δx- proizvoljan broj takav da vrijednost x+Δx također pripada intervalu (a, b). Ovaj broj Δx zove se povećanje argumenta.

Definicija. Povećanje funkcije y=f(x) u točki x, što odgovara prirastu argumenta Δx, nazovimo broj

Δy = f(x+Δx) - f(x).

Vjerujemo u to Δx ≠ 0. Razmotrite na danoj fiksnoj točki x omjer inkrementa funkcije u ovoj točki i odgovarajućeg inkrementa argumenta Δx

Ovu relaciju ćemo nazvati relacijom razlike. Budući da je vrijednost x smatramo fiksnim, omjer razlike je funkcija argumenta Δx. Ova je funkcija definirana za sve vrijednosti argumenata Δx, koji pripada nekoj dovoljno maloj okolini točke Δx=0, osim same točke Δx=0. Dakle, imamo pravo razmotriti pitanje postojanja limita navedene funkcije na Δx → 0.

Definicija. Derivacija funkcije y=f(x) u datoj fiksnoj točki x nazvana granica na Δx → 0 omjer razlike, tj

Pod uvjetom da ta granica postoji.

Oznaka. y'(x) ili f'(x).

Geometrijsko značenje derivacije: Derivacija funkcije f(x) u ovom trenutku x jednaka tangensu kuta između osi Vol i tangenta na graf ove funkcije u odgovarajućoj točki:

f′(x 0) = \tgα.

Mehaničko značenje derivata: Derivacija puta po vremenu jednaka je brzini pravocrtnog gibanja točke:

Jednadžba tangente na pravac y=f(x) u točki M 0 (x 0, y 0) poprima oblik

y-y 0 = f′(x 0) (x-x 0).

Normala na krivulju u nekoj točki je okomica na tangentu u istoj točki. Ako f′(x 0)≠ 0, zatim jednadžba normale na pravac y=f(x) u točki M 0 (x 0, y 0) piše ovako:

Pojam diferencijabilnosti funkcije

Neka funkcija y=f(x) definiran u određenom intervalu (a, b), x- neka fiksna vrijednost argumenta iz ovog intervala, Δx- svako povećanje argumenta tako da vrijednost argumenta x+Δx ∈ (a, b).

Definicija. Funkcija y=f(x) koji se naziva diferencijabilnim u datoj točki x, ako se povećava Δy ovu funkciju u točki x, što odgovara prirastu argumenta Δx, može se predstaviti u obliku

Δy = A Δx +αΔx,

Gdje A- neki broj neovisan o Δx, A α - funkcija argumenta Δx, što je infinitezimalno pri Δx→ 0.

Budući da je umnožak dviju infinitezimalnih funkcija αΔx je infinitezimal višeg reda od Δx(svojstvo 3 infinitezimalne funkcije), tada možemo napisati:

Δy = A Δx +o(Δx).

Teorema. Kako bi funkcija y=f(x) bilo diferencijabilno u datoj točki x, potrebno je i dovoljno da ima konačnu derivaciju u ovoj točki. pri čemu A=f′(x), to je

Δy = f′(x) Δx +o(Δx).

Operacija nalaženja derivacije obično se naziva diferenciranje.

Teorema. Ako funkcija y=f(x) x, onda je kontinuirana u ovoj točki.

Komentar. Iz neprekidnosti funkcije y=f(x) u ovom trenutku x, općenito govoreći, diferencijabilnost funkcije ne slijedi f(x) u ovom trenutku. Na primjer, funkcija y=|x|- kontinuirano u točki x=0, ali nema izvedenicu.

Pojam diferencijalne funkcije

Definicija. Funkcijski diferencijal y=f(x) naziva se umnožak derivacije te funkcije i prirasta nezavisne varijable x:

dy = y′ Δx, df(x) = f′(x) Δx.

Za funkciju y=x dobivamo dy=dx=x′Δx = 1· Δx= Δx, to je dx=Δx- diferencijal nezavisne varijable jednak je prirastu ove varijable.

Dakle, možemo pisati

dy = y′ dx, df(x) = f′(x) dx

Diferencijal dy i prirast Δy funkcije y=f(x) u ovom trenutku x, oba odgovaraju istom prirastu argumenta Δx, općenito govoreći, nisu međusobno jednaki.

Geometrijsko značenje diferencijala: Diferencijal funkcije jednak je prirastu ordinate tangente na graf ove funkcije kada se argument povećava Δx.

Pravila razlikovanja

Teorema. Ako svaka od funkcija u(x) I v(x) diferencijabilan u datoj točki x, zatim zbroj, razlika, umnožak i kvocijent tih funkcija (kvocijent pod uvjetom da v(x)≠ 0) su također diferencijabilne u ovoj točki, a formule vrijede:

Razmotrite složenu funkciju y=f(φ(x))≡ F(x), Gdje y=f(u), u=φ(x). U ovom slučaju u nazvao posredni argument, x - neovisna varijabla.

Teorema. Ako y=f(u) I u=φ(x) su diferencijabilne funkcije svojih argumenata, zatim izvod složena funkcija y=f(φ(x)) postoji i jednak je umnošku ove funkcije s obzirom na posredni argument i derivacije posrednog argumenta s obzirom na nezavisnu varijablu, tj.

Komentar. Za složenu funkciju koja je superpozicija triju funkcija y=F(f(φ(x))), pravilo diferenciranja ima oblik

y′ x = y′ u u′ v v′ x,

gdje su funkcije v=φ(x), u=f(v) I y=F(u)- diferencijabilne funkcije svojih argumenata.

Teorema. Neka funkcija y=f(x) raste (ili opada) i kontinuirana je u nekoj okolini točke x 0. Neka je, osim toga, ova funkcija diferencijabilna u navedenoj točki x 0 i njegov derivat u ovom trenutku f′(x 0) ≠ 0. Zatim u nekoj okolini odgovarajuće točke y 0 =f(x 0) inverz je definiran za y=f(x) funkcija x=f -1 (y), i naznačeno inverzna funkcija diferencijabilan u odgovarajućoj točki y 0 =f(x 0) a za njegov derivat u ovom trenutku g formula vrijedi

Tablica izvedenica

Invarijantnost oblika prvog diferencijala

Razmotrimo diferencijal složene funkcije. Ako y=f(x), x=φ(t)- funkcije svojih argumenata su diferencijabilne, zatim izvod funkcije y=f(φ(t)) izražen formulom

y′ t = y′ x x′ t.

A-priorat dy=y′ t dt, onda dobivamo

dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,

dy = y′ x dx.

Dakle, dokazali smo

Svojstvo invarijantnosti oblika prvog diferencijala funkcije: kao u slučaju kada argument x je nezavisna varijabla, a u slučaju kada je argument x sama je diferencijabilna funkcija nove varijable, diferencijala dy funkcije y=f(x) jednaka je derivaciji ove funkcije pomnoženoj s diferencijalom argumenta dx.

Primjena diferencijala u aproksimativnim proračunima

Pokazali smo da diferencijal dy funkcije y=f(x), općenito govoreći, nije jednako priraštaju Δy ovu funkciju. Međutim, do infinitezimalne funkcije višeg reda malenosti od Δx, vrijedi približna jednakost

Δy ≈ dy.

Omjer se naziva relativna pogreška jednakosti ove jednakosti. Jer Δy-dy=o(Δx), To relativna pogreška ove jednakosti postaje proizvoljno mala kako se smanjujemo |Δh|.

S obzirom na to Δy=f(x+δ x)-f(x), dy=f′(x)Δx, dobivamo f(x+δ x)-f(x) ≈ f′(x)Δx ili

f(x+δ x) ≈ f(x) + f′(x)Δx.

Ova približna jednakost dopušta s greškom o(Δx) zamijeniti funkciju f(x) u malom susjedstvu točke x(tj. za male vrijednosti Δx) linearna funkcija argument Δx, stojeći s desne strane.

Izvodnice višeg reda

Definicija. Drugi izvod (ili izvod drugog reda) funkcije y=f(x) naziva se derivacija svoje prve derivacije.

Zapis za drugu derivaciju funkcije y=f(x):

Mehaničko značenje druge derivacije. Ako funkcija y=f(x) opisuje zakon gibanja materijalna točka u pravoj liniji, zatim drugu izvodnicu f″(x) jednaka ubrzanju pokretne točke u trenutku vremena x.

Slično se određuju treća i četvrta derivacija.

Definicija. n izvedenica (ili izvedenica n-th reda) funkcije y=f(x) naziva se njegova izvedenica n-1 derivacija:

y (n) =(y (n-1))', f (n) (x)=(f (n-1) (x))'.

Oznake: y″′, y IV, y V itd.

Zadatak B9 daje graf funkcije ili derivacije iz kojeg trebate odrediti jednu od sljedećih veličina:

Vrijednost derivacije u nekoj točki x 0,
Maksimalni ili minimalni bodovi (ekstremni bodovi),
Intervali rastućih i padajućih funkcija (intervali monotonosti).

Funkcije i derivacije predstavljene u ovom problemu uvijek su kontinuirane, što rješenje čini puno lakšim. Unatoč tome što zadatak pripada sekciji matematička analiza, to je sasvim unutar mogućnosti čak i najslabijih učenika, budući da ovdje nije potrebno duboko teorijsko znanje.

Za pronalaženje vrijednosti derivacije, točaka ekstrema i intervala monotonosti, postoje jednostavni i univerzalni algoritmi - svi će biti raspravljeni u nastavku.

Pažljivo pročitajte uvjete zadatka B9 kako biste izbjegli glupe pogreške: ponekad naiđete na prilično dugačke tekstove, ali važni uvjeti, koji utječu na tijek odluke, malo je.

Izračun vrijednosti derivata. Metoda dvije točke

Ako je problemu dan graf funkcije f(x), tangenta na taj graf u nekoj točki x 0, i potrebno je pronaći vrijednost derivacije u toj točki, primjenjuje se sljedeći algoritam:

Pronađite dvije “odgovarajuće” točke na grafu tangente: njihove koordinate moraju biti cijeli brojevi. Označimo te točke kao A (x 1 ; y 1) i B (x 2 ; y 2). Ispravno zapišite koordinate - ovo je ključni trenutak rješenja, a svaka pogreška ovdje rezultira netočnim odgovorom.
Poznavajući koordinate, lako je izračunati priraštaj argumenta Δx = x 2 − x 1 i priraštaj funkcije Δy = y 2 − y 1 .
Konačno, nalazimo vrijednost derivacije D = Δy/Δx. Drugim riječima, trebate podijeliti prirast funkcije s prirastom argumenta - i to će biti odgovor.

Napomenimo još jednom: točke A i B potrebno je tražiti upravo na tangenti, a ne na grafu funkcije f(x), kako se često događa. Tangenta će nužno sadržavati najmanje dvije takve točke - inače problem neće biti ispravno formuliran.

Promotrimo točke A (−3; 2) i B (−1; 6) i pronađi priraštaje:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Nađimo vrijednost derivacije: D = Δy/Δx = 4/2 = 2.

Zadatak. Na slici je prikazan graf funkcije y = f(x) i tangenta na nju u točki s apscisom x 0. Odredite vrijednost derivacije funkcije f(x) u točki x 0 .

Razmotrite točke A (0; 3) i B (3; 0), pronađite priraštaje:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Sada nalazimo vrijednost derivacije: D = Δy/Δx = −3/3 = −1.

Zadatak. Na slici je prikazan graf funkcije y = f(x) i tangenta na nju u točki s apscisom x 0. Odredite vrijednost derivacije funkcije f(x) u točki x 0 .

Razmotrite točke A (0; 2) i B (5; 2) i pronađite priraštaje:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Ostaje pronaći vrijednost derivacije: D = Δy/Δx = 0/5 = 0.

Iz posljednjeg primjera možemo formulirati pravilo: ako je tangenta paralelna s osi OX, derivacija funkcije u točki dodirivanja je nula. U ovom slučaju ne morate ništa ni brojati - samo pogledajte grafikon.

Izračunavanje maksimalnih i minimalnih bodova

Ponekad, umjesto grafa funkcije, zadatak B9 daje graf derivacije i zahtijeva pronalaženje maksimalne ili minimalne točke funkcije. U ovoj situaciji metoda dvije točke je beskorisna, ali postoji još jedan, još jednostavniji algoritam. Prvo, definirajmo terminologiju:

Točku x 0 nazivamo točkom maksimuma funkcije f(x) ako u nekoj okolini te točke vrijedi nejednakost: f(x 0) ≥ f(x).
Točku x 0 nazivamo točkom minimuma funkcije f(x) ako u nekoj okolini te točke vrijedi nejednakost: f(x 0) ≤ f(x).

Kako biste pronašli maksimalne i minimalne točke iz grafa izvedenica, samo slijedite ove korake:

Ponovno nacrtajte graf izvedenica, uklanjajući sve nepotrebne podatke. Kao što praksa pokazuje, nepotrebni podaci samo ometaju odluku. Stoga napominjemo koordinatna os nule izvoda - to je sve.
Utvrdite predznake izvoda na intervalima između nula. Ako je za neku točku x 0 poznato da je f'(x 0) ≠ 0, tada su moguće samo dvije opcije: f'(x 0) ≥ 0 ili f'(x 0) ≤ 0. Predznak derivacije je lako odrediti iz izvornog crteža: ako derivacijski graf leži iznad OX osi, tada je f'(x) ≥ 0. I obrnuto, ako derivacijski graf leži ispod OX osi, tada je f'(x) ≤ 0.
Ponovno provjeravamo nule i predznake izvoda. Tamo gdje se predznak mijenja iz minusa u plus je minimalna točka. Obrnuto, ako se predznak derivacije mijenja s plusa na minus, to je najveća točka. Brojanje se uvijek vrši s lijeva na desno.

Ova shema radi samo za kontinuirane funkcije - nema drugih u zadatku B9.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definirane na intervalu [−5; 5]. Pronađite točku minimuma funkcije f(x) na tom segmentu.

Riješimo se nepotrebne informacije— ostavimo samo granice [−5; 5] i nulte derivacije x = −3 i x = 2,5. Također bilježimo znakove:

Očito se u točki x = −3 predznak derivacije mijenja s minusa na plus. Ovo je minimalna točka.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definirane na intervalu [−3; 7]. Pronađite točku maksimuma funkcije f(x) na tom segmentu.

Ponovno nacrtajmo graf, ostavljajući samo granice [−3; 7] i nule derivacije x = −1.7 i x = 5. Zabilježimo predznake derivacije na dobivenom grafu. Imamo:

Očito, u točki x = 5 znak derivacije se mijenja iz plusa u minus - to je maksimalna točka.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x), definirane na intervalu [−6; 4]. Odredite broj maksimalnih točaka funkcije f(x) koje pripadaju segmentu [−4; 3].

Iz uvjeta zadatka proizlazi da je dovoljno razmotriti samo dio grafa ograničen segmentom [−4; 3]. Stoga gradimo novi graf na kojem označavamo samo granice [−4; 3] i nule derivacije unutar njega. Naime, točke x = −3,5 i x = 2. Dobivamo:

Na ovom grafu postoji samo jedna maksimalna točka x = 2. U toj točki se predznak derivacije mijenja iz plusa u minus.

Mala napomena o točkama s necijelobrojnim koordinatama. Na primjer, u prošlom zadatku razmatrana je točka x = −3,5, ali s istim uspjehom možemo uzeti x = −3,4. Ako je problem ispravno sastavljen, takve promjene ne bi trebale utjecati na odgovor, budući da bodovi "bez stalnog mjesta stanovanja" ne sudjeluju izravno u rješavanju problema. Naravno, ovaj trik neće raditi s cjelobrojnim točkama.

Određivanje intervala rastućih i padajućih funkcija

U takvom problemu, poput točaka maksimuma i minimuma, predlaže se korištenje grafa derivacije za pronalaženje područja u kojima sama funkcija raste ili opada. Prvo, definirajmo što su povećanje i opadanje:

Kaže se da je funkcija f(x) rastuća na segmentu ako za bilo koje dvije točke x 1 i x 2 iz tog segmenta vrijedi sljedeća izjava: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Drugim riječima, što je veća vrijednost argumenta, to je veća vrijednost funkcije.
Kaže se da je funkcija f(x) opadajuća na segmentu ako za bilo koje dvije točke x 1 i x 2 iz tog segmenta vrijedi sljedeća izjava: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . Oni. višu vrijednost argument odgovara manjoj vrijednosti funkcije.

Formulirajmo dovoljne uvjete za povećanje i smanjenje:

Da bi kontinuirana funkcija f(x) rasla na segmentu dovoljno je da njezina derivacija unutar segmenta bude pozitivna, tj. f’(x) ≥ 0.
Da bi kontinuirana funkcija f(x) opadala na segmentu dovoljno je da njezina derivacija unutar segmenta bude negativna, tj. f’(x) ≤ 0.

Prihvatimo ove izjave bez dokaza. Dakle, dobivamo shemu za pronalaženje intervala povećanja i opadanja, koja je na mnogo načina slična algoritmu za izračunavanje ekstremnih točaka:

Uklonite sve nepotrebne podatke. U izvornom grafu derivacije nas prvenstveno zanimaju nule funkcije pa ćemo ostaviti samo njih.
Označite predznake izvoda na razmacima između nula. Gdje je f’(x) ≥ 0, funkcija raste, a gdje je f’(x) ≤ 0, opada. Ako problem postavlja ograničenja na varijablu x, dodatno ih označavamo na novom grafu.
Sada kada znamo ponašanje funkcije i ograničenja, ostaje izračunati količinu potrebnu u problemu.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definirane na intervalu [−3; 7.5]. Odredite intervale opadanja funkcije f(x). U svom odgovoru naznačite zbroj cijelih brojeva uključenih u ove intervale.

Kao i obično, ponovno nacrtajmo graf i označimo granice [−3; 7.5], kao i nulte derivacije x = −1.5 i x = 5.3. Zatim bilježimo predznake izvedenice. Imamo:

Budući da je derivacija negativna na intervalu (− 1,5), to je interval opadajuće funkcije. Ostaje zbrojiti sve cijele brojeve koji se nalaze unutar ovog intervala:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x), definirane na intervalu [−10; 4]. Odredite intervale porasta funkcije f(x). U odgovoru navedite duljinu najvećeg od njih.

Oslobodimo se nepotrebnih informacija. Ostavimo samo granice [−10; 4] i nulte derivacije kojih je ovoga puta bilo četiri: x = −8, x = −6, x = −3 i x = 2. Označimo predznake derivacije i dobijemo sljedeću sliku:

Zanimaju nas intervali rastuće funkcije, tj. tako da je f’(x) ≥ 0. Dva su takva intervala na grafu: (−8; −6) i (−3; 2). Izračunajmo njihove duljine:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Budući da trebamo pronaći duljinu najvećeg od intervala, zapisujemo vrijednost l 2 = 5 kao odgovor.

Derivacija funkcije jedne varijable.

Uvod.

Stvaran metodološki razvoj namijenjen studentima Fakulteta za industriju i građevinarstvo. Sastavljeni su u odnosu na program kolegija matematike u odjeljku "Diferencijalni račun funkcija jedne varijable".

Razvoj predstavlja jedinstven metodološki vodič, uključujući: kratke teorijske informacije; “standardne” zadatke i vježbe s detaljnim rješenjima i objašnjenjima tih rješenja; mogućnosti testiranja.

Na kraju svakog odlomka nalaze se dodatne vježbe. Ova struktura razvoja čini ih pogodnim za samostalno savladavanje dionice uz minimalnu pomoć učitelja.

§1. Definicija derivata.

Mehaničko i geometrijsko značenje

izvedenica.

Pojam derivacije jedan je od najvažnijih pojmova matematičke analize. Nastao je još u 17. stoljeću. Formiranje pojma derivacije povijesno je povezano s dva problema: problemom brzine izmjeničnog gibanja i problemom tangente na krivulju.

Ovi zadaci, unatoč različitom sadržaju, dovode do iste matematičke operacije koju je potrebno izvršiti nad funkcijom. Ova operacija je dobila poseban naziv u matematici. Zove se operacija diferenciranja funkcije. Rezultat operacije diferenciranja naziva se derivacija.

Dakle, derivacija funkcije y=f(x) u točki x0 je granica (ako postoji) omjera prirasta funkcije i prirasta argumenta
na
.

Derivat se obično označava na sljedeći način:
.

Dakle, po definiciji

Simboli se također koriste za označavanje izvedenica
.

Mehaničko značenje derivata.

Ako je s=s(t) zakon pravocrtnog gibanja materijalne točke, tada
je brzina ove točke u trenutku t.

Geometrijsko značenje derivacije.

Ako funkcija y=f(x) ima derivaciju u točki , zatim kutni koeficijent tangente na graf funkcije u točki
jednaki
.

Primjer.

Pronađite izvod funkcije
u točki =2:

1) Recimo to =2 povećanje
. Primijeti da.

2) Pronađite prirast funkcije u točki =2:

3) Kreirajmo omjer prirasta funkcije i prirasta argumenta:

Nađimo granicu omjera pri
:

Tako,
.

§ 2. Izvedenice nekih

najjednostavnije funkcije.

Učenik treba naučiti kako izračunati derivacije određenih funkcija: y=x,y= i općenito= .

Nađimo izvod funkcije y=x.

oni. (x)′=1.

Nađimo izvod funkcije

Izvedenica

Neka
Zatim

Lako je uočiti obrazac u izrazima za derivacije potencije
s n=1,2,3.

Stoga,

. (1)

Ova formula vrijedi za svaki realni n.

Konkretno, koristeći formulu (1), imamo:

;

Primjer.

Pronađite izvod funkcije

Ova funkcija je poseban slučaj funkcije oblika

na
.

Koristeći formulu (1), imamo

Derivacije funkcija y=sin x i y=cos x.

Neka je y=sinx.

Podijelimo s ∆x, dobivamo

Prelazeći na limit pri ∆x→0, imamo

Neka je y=cosx.

Prelaskom na limit pri ∆x→0 dobivamo

;
. (2)

§3. Osnovna pravila razlikovanja.

Razmotrimo pravila razlikovanja.

Teorema1 . Ako su funkcije u=u(x) i v=v(x) diferencijabilne u danoj točki x, tada je u toj točki i njihov zbroj diferencijabilan, a derivacija zbroja jednaka je zbroju derivacija članova : (u+v)"=u"+v".(3 )

Dokaz: razmotrite funkciju y=f(x)=u(x)+v(x).

Prirast ∆x argumenta x odgovara priraštajima ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) funkcija u i v. Tada će funkcija y rasti

∆y=f(x+∆x)-f(x)=

=--=∆u+∆v.

Stoga,

Dakle, (u+v)"=u"+v".

Teorema2. Ako su funkcije u=u(x) i v=v(x) diferencijabilne u danoj točkix, tada je njihov umnožak diferencijabilan u istoj točki. U ovom slučaju, derivacija umnoška nalazi se sljedećom formulom: ( uv)"=u"v+uv". ( 4)

Dokaz: Neka je y=uv, gdje su u i v neke diferencijabilne funkcije od x. Dajmo x povećanje od ∆x; tada će u dobiti povećanje od ∆u, v će dobiti povećanje od ∆v, a y će dobiti povećanje od ∆y.

Imamo y+∆y=(u+∆u)(v+∆v), odn

y+∆y=uv+u∆v+v∆u+∆u∆v.

Prema tome, ∆y=u∆v+v∆u+∆u∆v.

Odavde

Prelaskom na granicu pri ∆x→0 i uzimajući u obzir da u i v ne ovise o ∆x, imat ćemo

Teorem 3. Derivacija kvocijenta dviju funkcija jednaka je razlomku čiji je nazivnik jednak kvadratu djelitelja, a brojnik je razlika umnoška derivacije djelitelja s djeliteljem i umnoška djelitelja. dividendu izvodom djelitelja, tj.

Ako
Da
(5)