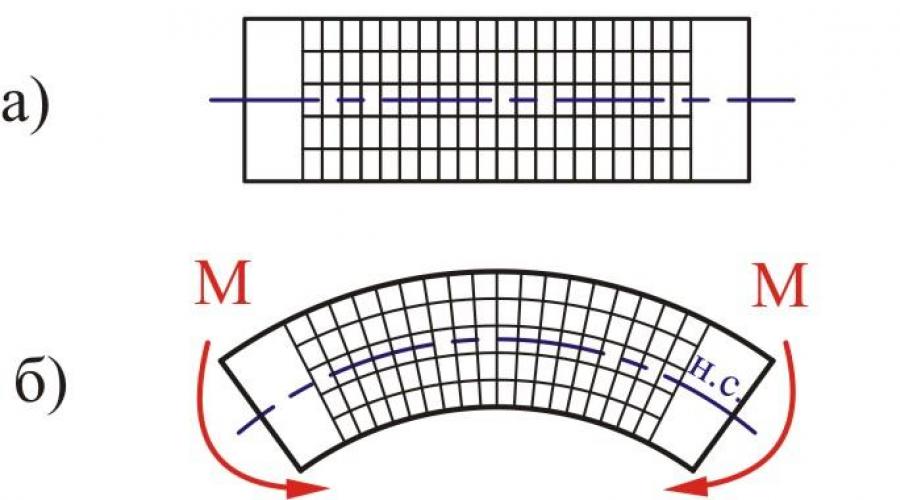
Deformacija savijanjem sastoji se u zakrivljenosti osi ravna šipka ili u promjeni početne zakrivljenosti ravnog štapa (slika 6.1). Upoznajmo se s osnovnim pojmovima koji se koriste pri razmatranju deformacije savijanjem.

Šipke koje se savijaju nazivaju se grede.

Čist nazvano savijanje, u kojem je moment savijanja jedini faktor unutarnje sile koji nastaje u presjeku grede.

Češće se u presjeku štapa uz moment savijanja javlja i poprečna sila. Ovo savijanje naziva se poprečnim.

Ravno (ravno) naziva se savijanje kada ravnina djelovanja momenta savijanja u presjeku prolazi kroz jednu od glavnih središnjih osi poprečnog presjeka.

Na kosi zavoj ravnina djelovanja momenta savijanja siječe poprečni presjek grede po liniji koja se ne poklapa ni s jednom glavnom središnjom osi poprečnog presjeka.

Naše proučavanje deformacije savijanjem počinjemo sa slučajem čistog ravninskog savijanja.

Normalna naprezanja i deformacije pri čistom savijanju.

Kao što je već spomenuto, s čistim ravnim zavojem u presjeku od šest unutarnje sile novi faktori, samo moment savijanja nije nula (slika 6.1, c):

Eksperimenti provedeni na elastičnim modelima pokazuju da ako se mreža linija nanese na površinu modela (slika 6.1, a), tada se s čistim savijanjem deformira na sljedeći način (slika 6.1, b):

a) uzdužne linije su zakrivljene duž oboda;

b) konture presjeci ostati ravan;

c) konturne linije presjeka posvuda se sijeku s uzdužnim vlaknima pod pravim kutom.

Na temelju toga može se pretpostaviti da kod čistog savijanja poprečni presjeci grede ostaju ravni i rotiraju se tako da ostaju normalni na zakrivljenu os grede (ravni presjeci u hipotezi savijanja).

Riža. 6.1

Mjerenjem duljine uzdužnih linija (slika 6.1, b), možete utvrditi da se gornja vlakna produljuju kada se greda savija, a donja se skraćuju. Očito je moguće pronaći vlakna čija duljina ostaje nepromijenjena. Naziva se skup vlakana koja ne mijenjaju svoju duljinu kada se greda savija neutralni sloj (n.s.). Neutralni sloj siječe presjek grede u ravnoj liniji, što se tzv neutralna linija (n.l.) dionica.

Za izvođenje formule koja određuje veličinu normalnih naprezanja koja nastaju u presjeku, razmotrite dio grede u deformiranom i nedeformiranom stanju (slika 6.2).

Riža. 6.2

Pomoću dva infinitezimalna presjeka odabiremo element duljine
. Prije deformacije, dijelovi koji ograničavaju element
, bile su paralelne jedna s drugom (sl. 6.2, a), a nakon deformacije lagano su se savile, tvoreći kut
. Duljina vlakana koja leže u neutralnom sloju ne mijenja se pri savijanju
. Označimo polumjer zakrivljenosti traga neutralnog sloja na ravnini crtanja slovom . Odredimo linearnu deformaciju proizvoljnog vlakna
, koji se nalazi na udaljenosti iz neutralnog sloja.

Duljina ovog vlakna nakon deformacije (duljina luka
) jednako je
. S obzirom da su prije deformacije sva vlakna bila iste duljine
, nalazimo da je apsolutno izduženje vlakna koje se razmatra

Njegova relativna deformacija

Očito je da
, budući da se duljina vlakna koje leži u neutralnom sloju nije promijenila. Zatim nakon zamjene
dobivamo

(6.2)

Stoga je relativna uzdužna deformacija proporcionalna udaljenosti vlakna od neutralne osi.

Uvedimo pretpostavku da pri savijanju uzdužna vlakna ne pritišću jedno drugo. Pod ovom pretpostavkom, svako se vlakno deformira zasebno, doživljavajući jednostavnu napetost ili kompresiju, u kojoj
. Uzimajući u obzir (6.2)

, (6.3)

odnosno normalna naprezanja izravno su proporcionalna udaljenostima razmatranih točaka presjeka od neutralne osi.

Zamijenimo ovisnost (6.3) u izraz za moment savijanja
u presjeku (6.1)

.

Prisjetimo se da je integral
predstavlja moment tromosti presjeka u odnosu na os

.

(6.4)

Ovisnost (6.4) predstavlja Hookeov zakon za savijanje, budući da povezuje deformaciju (zakrivljenost neutralnog sloja
) s trenutkom koji djeluje u presjeku. Raditi
naziva se krutost presjeka tijekom savijanja, N m 2.

Zamijenimo (6.4) u (6.3)

(6.5)

Ovo je potrebna formula za određivanje normalnih naprezanja tijekom čistog savijanja grede u bilo kojoj točki njezinog poprečnog presjeka.

Da bismo ustanovili gdje se nalazi neutralna linija u presjeku, zamijenimo vrijednost normalnih naprezanja u izraz uzdužna sila
i moment savijanja

Jer
,

;

(6.6)

(6.7)

Jednakost (6.6) pokazuje da je os – neutralna os presjeka – prolazi kroz težište presjeka.

Jednakost (6.7) to pokazuje I - glavni središnje osi odjeljci.

Prema (6.5), najveći napon se postiže u vlaknima koja su najudaljenija od neutralne linije

Stav predstavlja aksijalni moment otpora presjeka u odnosu na svoju središnju os , Sredstva

Značenje za najjednostavnije presjeke sljedeće:

Za pravokutni presjek

, (6.8)

Gdje - strana presjeka okomita na os ;

- strana presjeka paralelna s osi ;

Za okrugli presjek

, (6.9)

Gdje - promjer kružnog presjeka.

Uvjet čvrstoće za normalna naprezanja na savijanje može se napisati u obliku

(6.10)

Sve dobivene formule dobivene su za slučaj čistog savijanja ravnog štapa. Djelovanje transverzalne sile dovodi do činjenice da hipoteze na kojima se temelje zaključci gube snagu. Međutim, proračunska praksa pokazuje da čak i tijekom poprečnog savijanja greda i okvira, kada su u presjeku, osim momenta savijanja
postoji i uzdužna sila
i sila smicanja , možete koristiti formule dane za čisto savijanje. Greška je beznačajna.

Savijte se je vrsta opterećenja grede pri kojoj se na gredu primjenjuje moment koji leži u ravnini koja prolazi kroz uzdužnu os. U presjecima grede javljaju se momenti savijanja. Kod savijanja nastaje deformacija pri kojoj se os ravne grede savija ili se mijenja zakrivljenost zakrivljene grede.

Greda koja se savija naziva se greda . Konstrukcija koja se sastoji od više savitljivih šipki, najčešće međusobno povezanih pod kutom od 90°, naziva se okvir .

Zavoj se zove ravna ili ravna , ako ravnina opterećenja prolazi kroz glavnu središnju os tromosti presjeka (slika 6.1).

sl.6.1

Kada u gredi dođe do ravnog poprečnog savijanja, javljaju se dvije vrste unutarnjih sila: poprečna sila Q i moment savijanja M. U okviru s ravnim poprečnim savijanjem nastaju tri sile: uzdužna N, poprečno Q sile i moment savijanja M.

Ako je moment savijanja jedini faktor unutarnje sile, tada se takvo savijanje naziva čist (Slika 6.2). Kada postoji posmična sila, naziva se savijanje poprečni . Strogo govoreći, jednostavne vrste otpora uključuju samo čisti zavoj; poprečno savijanje se konvencionalno klasificira kao jednostavna vrsta otpora, budući da se u većini slučajeva (za dovoljno duge grede) učinak poprečne sile može zanemariti pri proračunu čvrstoće.

22.Ravan poprečno savijanje. Diferencijalne ovisnosti između unutarnjih sila i vanjskog opterećenja. Postoje diferencijalni odnosi između momenta savijanja, posmične sile i intenziteta raspodijeljenog opterećenja, temeljeni na teoremu Žuravskog, nazvanom po ruskom inženjeru mostova D.I. Žuravskom (1821.-1891.).

Ovaj teorem je formuliran na sljedeći način:

Poprečna sila jednaka je prvoj izvodnici momenta savijanja po apscisi presjeka grede.

23. Ravni poprečni zavoj. Crtanje dijagrama posmičnih sila i momenata savijanja. Određivanje posmičnih sila i momenata savijanja - dio 1

Odbacimo desnu stranu grede i zamijenimo njezino djelovanje s lijeva strana sila smicanja i moment savijanja. Radi lakšeg izračuna, pokrijmo odbačenu desnu stranu grede komadom papira, poravnavajući lijevi rub lista s odjeljkom 1 koji se razmatra.

Transverzalna sila u presjeku 1 grede jednaka je algebarskom zbroju svih vanjske sile, koje vidimo nakon zatvaranja

Vidimo samo reakciju oslonca usmjerenu prema dolje. Dakle, sila smicanja je:

kN.

Uzeli smo znak "minus" jer sila rotira dio grede koji nam je vidljiv u odnosu na prvi presjek u smjeru suprotnom od kazaljke na satu (ili zato što je u istom smjeru kao i smjer transverzalne sile prema pravilu predznaka)

Moment savijanja u presjeku 1 grede jednak je algebarskom zbroju momenata svih sila koje vidimo nakon zatvaranja odbačenog dijela grede, u odnosu na presjek 1 koji se razmatra.

Vidimo dvije sile: reakciju oslonca i moment M. Međutim, sila ima rame koje je praktički jednako nuli. Stoga je moment savijanja jednak:

kNm.

Ovdje smo uzeli znak "plus" jer vanjski moment M savija nama vidljivi dio grede konveksom prema dolje. (ili zato što je suprotan smjeru momenta savijanja prema pravilu predznaka)

Određivanje posmičnih sila i momenata savijanja - dio 2

Za razliku od prvog odjeljka, sila reakcije sada ima rame jednako a.

posmična sila:

kN;

moment savijanja:

Određivanje posmičnih sila i momenata savijanja - dio 3

posmična sila:

moment savijanja:

Određivanje posmičnih sila i momenata savijanja - dio 4

Sada je praktičnije pokrij lijevu stranu grede plahtom.

posmična sila:

moment savijanja:

Određivanje posmičnih sila i momenata savijanja - dio 5

posmična sila:

moment savijanja:

Određivanje posmičnih sila i momenata savijanja - dio 1

sila smicanja i moment savijanja:

.

Koristeći pronađene vrijednosti, konstruiramo dijagram poprečnih sila (slika 7.7, b) i momenata savijanja (slika 7.7, c).

KONTROLA ISPRAVNOSTI IZRADE DIJAGRAMA

Uvjerimo se da su dijagrami ispravno konstruirani na temelju vanjskih obilježja, koristeći pravila za konstruiranje dijagrama.

Provjera dijagrama posmične sile

Uvjereni smo: pod neopterećenim područjima dijagram poprečnih sila ide paralelno s osi grede, a pod raspodijeljenim opterećenjem q - duž ravne linije nagnute prema dolje. Na dijagramu uzdužne sile postoje tri skoka: pod reakcijom - dolje za 15 kN, pod silom P - dolje za 20 kN i pod reakcijom - gore za 75 kN.

Provjera dijagrama momenta savijanja

Na dijagramu momenata savijanja vidimo pregibe pod koncentriranom silom P i pod reakcijama oslonca. Kutovi loma su usmjereni prema tim silama. Pod raspodijeljenim opterećenjem q mijenja se dijagram momenata savijanja duž kvadratne parabole, čija je konveksnost usmjerena prema opterećenju. U odjeljku 6 na dijagramu momenta savijanja postoji ekstrem, budući da dijagram poprečne sile na ovom mjestu prolazi kroz nultu vrijednost.

Čisti zavoj Ova vrsta savijanja naziva se u kojoj se radnja odvija samo moment savijanja(Sl. 3.5, A). Mentalno nacrtajmo presječnu ravninu I-I okomito na uzdužnu os grede na udaljenosti * od slobodnog kraja grede na koji se primjenjuje vanjski moment m z . Provedimo radnje slične onima koje smo izvršili pri određivanju naprezanja i deformacija tijekom torzije, naime:

• 1) sastavimo jednadžbe ravnoteže za mentalno odsječeni dio dijela;
• 2) određujemo deformaciju materijala dijela na temelju uvjeta kompatibilnosti deformacija elementarnih volumena danog presjeka;
• 3) riješiti jednadžbe ravnoteže i kompatibilnosti deformacija.

Iz uvjeta ravnoteže odsječenog dijela grede (Sl. 3.5, b)

nalazimo da moment unutarnjih sila Mz jednak momentu vanjskih sila t: M = t.

Riža. 3.5.

Moment unutarnjih sila stvaraju normalna naprezanja o v usmjerena duž x osi. Kod čistog savijanja nema vanjskih sila, dakle zbroj projekcija unutarnjih sila na bilo koju koordinatna os jednaka nuli. Na temelju toga uvjete ravnoteže zapisujemo u obliku jednakosti

Gdje A- površina poprečnog presjeka grede (šipke).

Kod čistog savijanja vanjske sile Fx, F, Fv kao i momenti vanjskih sila t x, t y jednaki su nuli. Stoga su preostale jednadžbe ravnoteže identički jednake nuli.

Iz uvjeta ravnoteže kada o^O slijedi da

normalni napon c x u presjeku poprimaju i pozitivne i negativne vrijednosti. (Iskustvo pokazuje da prilikom savijanja materijal donje strane grede na sl. 3.5, A rastegnut, a gornji je sabijen.) Posljedično, u presjeku pri savijanju postoje takvi elementarni volumeni (prijelaznog sloja iz tlačnog u vlačni) u kojima nema istezanja niti kompresije. ovo - neutralni sloj. Linija presjeka neutralnog sloja s ravninom presjeka naziva se neutralna linija.

Uvjeti kompatibilnosti deformacija elementarnih volumena tijekom savijanja formiraju se na temelju hipoteze ravnih presjeka: poprečni presjeci grede su ravni prije savijanja (vidi sl. 3.5, b) ostat će ravna čak i nakon savijanja (slika 3.6).

Kao rezultat djelovanja vanjskog momenta greda se savija, a ravnine odjeljci I-I i II-II zakrenuti jedan prema drugom za kut dy(Sl. 3.6, b). Kod čistog savijanja deformacija svih presjeka duž osi grede je ista, stoga je polumjer pk zakrivljenosti neutralnog sloja grede duž osi x isti. Jer dx= str K pad, tada je zakrivljenost neutralnog sloja jednaka 1 / p k = umočiti / dx i konstantna je duž duljine grede.

Neutralni sloj nije deformiran; njegova duljina prije i poslije deformacije jednaka je dx. Ispod ovog sloja materijal je rastegnut, iznad je sabijen.

Riža. 3.6.

Vrijednost istezanja istegnutog sloja koji se nalazi na udaljenosti y od neutralnog jednaka je ydq. Relativno izduženje ovog sloja:

Tako je u usvojenom modelu dobivena linearna raspodjela deformacija ovisno o udaljenosti zadanog elementarnog volumena od neutralnog sloja, tj. po visini presjeka grede. Pod pretpostavkom da ne postoji međusobni pritisak paralelnih slojeva materijala jedan na drugi (o y = 0, a, = 0), pišemo Hookeov zakon za linearno rastezanje:

Prema (3.13) normalni naponi u presjeku grede raspoređeni su po linearnom zakonu. Naprezanje elementarnog volumena materijala najudaljenijeg od neutralnog sloja (Sl. 3.6, V), maksimalno i jednako

? Problem 3.6

Odredite granicu elastičnosti čelične oštrice debljine / = 4 mm i duljine / = 80 cm, ako njezino savijanje u polukrug ne uzrokuje zaostalu deformaciju.

Riješenje

Napon savijanja o v = Ej/ r k. Uzmimo y max = t/ 2i r k = / / Do.

Granica elastičnosti mora odgovarati uvjetu s up > c v = 1/2 kE t/1.

Odgovor: o = ] / 2 do 2 10 11 4 10 _3 / 0,8 = 1570 MPa; Granica razvlačenja ovog čelika je a t > 1800 MPa, što premašuje a t najčvršćih čelika za opruge. ?

? Problem 3.7

Odrediti minimalni radijus bubnja za namotavanje trake debljine / = 0,1 mm grijaće tijelo izrađena od legure nikla, u kojoj materijal trake nije plastično deformiran. Modul E= 1,6 10 5 MPa, granica elastičnosti oko yp = 200 MPa.

Odgovor: minimalni radijus r = V 2 ?ir/a yM = U? 1,6-10 11 0,1 10 -3 / (200 10 6) = = 0,04 m?

1. Kada zajedno rješavamo prvu jednadžbu ravnoteže (3.12) i jednadžbu kompatibilnosti deformacije (3.13), dobivamo

Značenje E/ r k φ 0 i isti za sve elemente dA integracijska područja. Prema tome, ova jednakost je zadovoljena samo pod uvjetom

Ovaj integral se zove statički moment površine poprečnog presjeka oko osiz? Koje je fizičko značenje ovog integrala?

Uzmimo rekord stalne debljine/, ali proizvoljnog profila (sl. 3.7). Objesimo ovu ploču na jednu točku S tako da bude u vodoravnom položaju. Označimo simbolom y m specifična gravitacija materijal ploče, zatim težina elementarnog volumena s površinom dA jednaki dq= g JdA. Budući da je ploča u stanju ravnoteže, tada iz jednakosti na nulu projekcija sila na os na dobivamo

Gdje G= g M tA- težina zapisa.

Riža. 3.7.

Zbroj momenata sila svih sila oko osi z prolazeći kroz bilo koji dio ploče također je nula:

S obzirom na to Y c = G, zapišimo

Dakle, ako je integral oblika J xdA po površini A jednaki

nula, dakle x c = 0. To znači da se točka C poklapa s težištem ploče. Dakle, iz jednakosti S z = J ydA = 0 kada dospije

savijanja proizlazi da je težište presjeka grede na neutralnoj liniji.

Prema tome, vrijednost y s presjek grede je nula.

• 1. Neutralna linija pri savijanju prolazi kroz težište presjeka grede.
• 2. Težište presjeka je središte redukcije momenata vanjskih i unutarnjih sila.

Problem 3.8

Problem 3.9

2. Kada zajedno rješavamo drugu jednadžbu ravnoteže (3.12) i jednadžbu kompatibilnosti deformacije (3.13), dobivamo

Sastavni Jz= J y 2 dA nazvao moment tromosti poprečnog

presjek grede (šipke) u odnosu na os z, koja prolazi kroz težište presjeka.

Tako, M z = E J z / r k. S obzirom na to c x = Ee x = Ey/ r k i E/ r k = a x / y, dobivamo ovisnost normalnih naprezanja Oh pri savijanju:

1. Naprezanje na savijanje u određenoj točki presjeka ne ovisi o normalnom modulu elastičnosti E, ali ovisi o geometrijski parametar poprečni presjek Jz i udaljenosti na od zadane točke do težišta presjeka.

2. Maksimalni napon tijekom savijanja, javlja se u elementarnim volumenima najudaljenijim od neutralne linije (vidi sl. 3.6, V):

Gdje W z- moment otpora poprečnog presjeka u odnosu na os Z-

Uvjet za čvrstoću pri čistom savijanju sličan je uvjetu za čvrstoću pri linearnoj napetosti:

gdje [a m | - dopušteno naprezanje na savijanje.

Očito je da unutarnji volumeni materijala, posebno u blizini neutralne osi, praktički nisu opterećeni (vidi sl. 3.6, V). To je u suprotnosti sa zahtjevom da se smanji potrošnja materijala za konstrukciju. U nastavku ćemo pokazati neke načine za prevladavanje ove kontradikcije.

10.1. Opći pojmovi i definicije

Savijte se- ovo je vrsta opterećenja u kojoj je šipka opterećena momentima u ravninama koje prolaze kroz uzdužnu os šipke.

Šipka koja se savija naziva se greda (ili drvo). U budućnosti ćemo razmatrati pravocrtne grede čiji presjek ima barem jednu os simetrije.

Otpornost materijala dijelimo na ravno, koso i složeno savijanje.

Ravni zavoj– savijanje, kod kojeg sve sile koje savijaju gredu leže u jednoj od ravnina simetrije grede (u jednoj od glavnih ravnina).

Glavne tromosti grede su ravnine koje prolaze kroz glavne osi poprečnih presjeka i geometrijsku os grede (x-os).

Kosi zavoj– savijanje, kod kojeg opterećenja djeluju u jednoj ravnini koja se ne poklapa s glavnim ravninama tromosti.

Složeni zavoj– savijanje, kod kojeg opterećenja djeluju u različitim (proizvoljnim) ravninama.

10.2. Određivanje unutarnjih sila savijanja

Razmotrimo dva tipična slučaja savijanja: u prvom je konzolna greda savijena koncentriranim momentom Mo; u drugom - koncentrirana sila F.

Metodom mentalnih presjeka i sastavljanjem jednadžbi ravnoteže za odsječene dijelove grede određujemo unutarnje sile u oba slučaja:

Ostale jednadžbe ravnoteže očito su identički jednake nuli.

Dakle, u općem slučaju ravnog savijanja u presjeku grede, od šest unutarnjih sila nastaju dvije - moment savijanja Mz i sila smicanja Qy (ili kod savijanja u odnosu na drugu glavnu os - moment savijanja My i posmična sila Qz).

Štoviše, u skladu s dva razmatrana slučaja opterećenja, ravninsko savijanje može se podijeliti na čisto i poprečno.

Čisti zavoj– ravno savijanje, kod kojeg u presjecima štapa od šest unutarnjih sila nastaje samo jedna – moment savijanja (vidi prvi slučaj).

Poprečni zavoj– savijanje, kod kojeg u presjecima štapa, osim unutarnjeg momenta savijanja, nastaje i poprečna sila (vidi drugi slučaj).

Strogo govoreći, jednostavne vrste otpora uključuju samo čisto savijanje; poprečno savijanje se konvencionalno klasificira kao jednostavna vrsta otpora, budući da se u većini slučajeva (za dovoljno duge grede) učinak poprečne sile može zanemariti pri proračunu čvrstoće.

Pri određivanju unutarnjih napora pridržavat ćemo se sljedećeg pravila znakova:

1) poprečna sila Qy smatra se pozitivnom ako nastoji rotirati dotični element grede u smjeru kazaljke na satu;

2) moment savijanja Mz smatra se pozitivnim ako su pri savijanju grednog elementa gornja vlakna elementa komprimirana, a donja rastegnuta (pravilo kišobrana).

Stoga ćemo rješenje problema određivanja unutarnjih sila tijekom savijanja izgraditi prema sljedećem planu: 1) u prvoj fazi, uzimajući u obzir uvjete ravnoteže konstrukcije kao cjeline, odredimo, ako je potrebno, nepoznate reakcije oslonaca (imajte na umu da za konzolnu gredu reakcije u ugradnji mogu biti i ne pronađene ako razmatramo gredu sa slobodnog kraja); 2) u drugoj fazi odabiremo karakteristične dijelove grede, uzimajući kao granice presjeka točke primjene sila, točke promjene oblika ili veličine grede, točke pričvršćivanja grede; 3) u trećoj fazi određujemo unutarnje sile u presjecima grede, uzimajući u obzir uvjete ravnoteže elemenata grede u svakom presjeku.

10.3. Diferencijalne ovisnosti pri savijanju

Ustanovimo neke odnose između unutarnjih sila i vanjskih opterećenja savijanja, kao i karakteristike dijagrami Q i M, čije će poznavanje olakšati konstrukciju dijagrama i omogućiti vam kontrolu njihove ispravnosti. Radi lakšeg označavanja, označit ćemo: M≡Mz, Q≡Qy.

Izaberimo mali element dx u presjeku grede s proizvoljnim opterećenjem na mjestu gdje nema koncentriranih sila i momenata. Budući da je cijela greda u ravnoteži, element dx će također biti u ravnoteži pod djelovanjem posmičnih sila, momenata savijanja i vanjskog opterećenja koje djeluje na njega. Budući da Q i M općenito variraju

osi grede, tada će se u presjecima elementa dx pojaviti transverzalne sile Q i Q+dQ, kao i momenti savijanja M i M+dM. Iz uvjeta ravnoteže odabranog elementa dobivamo

Prva od dvije napisane jednadžbe daje uvjet

Iz druge jednadžbe, zanemarujući član q·dx·(dx/2) kao infinitezimalnu veličinu drugog reda, nalazimo

Promatrajući zajedno izraze (10.1) i (10.2) možemo dobiti

Relacije (10.1), (10.2) i (10.3) nazivamo diferencijalnim ovisnosti D.I. Zhuravskog tijekom savijanja.

Analiza gornjih diferencijalnih ovisnosti tijekom savijanja omogućuje nam uspostavljanje nekih značajki (pravila) za konstruiranje dijagrama momenata savijanja i poprečnih sila: a - u područjima gdje nema raspodijeljenog opterećenja q, dijagrami Q su ograničeni na ravne linije paralelne s bazom , a dijagrami M ograničeni su na nagnute ravne linije; b – u područjima gdje je greda pričvršćena raspodijeljeno opterećenje q, dijagrami Q ograničeni su nagnutim ravnim crtama, a dijagrami M kvadratnim parabolama.

Štoviše, ako konstruiramo dijagram M "na rastegnutom vlaknu", tada će konveksnost parabole biti usmjerena u smjeru djelovanja q, a ekstrem će se nalaziti u dijelu gdje dijagram Q siječe osnovnu liniju; c – u presjecima gdje na gredu djeluje koncentrirana sila, na dijagramu Q će biti skokova po veličini i smjeru te sile, a na dijagramu M će biti pregiba, vrh usmjeren u smjeru djelovanja ova sila; d – u presjecima gdje je na gredu primijenjen koncentrirani moment neće biti promjena na dijagramu Q, a na dijagramu M doći će do skokova u veličini ovog momenta; d – u područjima gdje Q>0, u trenutku kada M raste, au područjima gdje Q<0, момент М убывает (см. рисунки а–г).

10.4. Normalna naprezanja pri čistom savijanju ravne grede

Razmotrimo slučaj čistog ravnog savijanja grede i izvedimo formulu za određivanje normalnih naprezanja za taj slučaj.

Imajte na umu da je u teoriji elastičnosti moguće dobiti točnu ovisnost za normalna naprezanja tijekom čistog savijanja, ali ako se ovaj problem rješava pomoću metoda čvrstoće materijala, potrebno je uvesti neke pretpostavke.

Postoje tri takve hipoteze za savijanje:

a – hipoteza ravnih presjeka (Bernoullijeva hipoteza) – ravni presjeci prije deformacije ostaju ravni nakon deformacije, ali se samo okreću u odnosu na određenu liniju, koja se naziva neutralna os presjeka grede. U tom će se slučaju vlakna grede koja leže s jedne strane neutralne osi rastegnuti, a s druge strane stisnuti; vlakna koja leže na neutralnoj osi ne mijenjaju svoju duljinu;

b – hipoteza o postojanosti normalnih naprezanja - naprezanja koja djeluju na istoj udaljenosti y od neutralne osi konstantna su po širini grede;

c – hipoteza o nepostojanju bočnih pritisaka – susjedna uzdužna vlakna ne pritišću jedno drugo.

Statička strana problema

Za određivanje naprezanja u presjecima grede razmatramo prije svega statičke strane problema. Metodom mentalnih presjeka i sastavljanjem jednadžbi ravnoteže za odsječeni dio grede pronaći ćemo unutarnje sile pri savijanju. Kao što je ranije pokazano, jedina unutarnja sila koja djeluje u presjeku grede tijekom čistog savijanja je unutarnji moment savijanja, što znači da će se ovdje pojaviti normalna naprezanja povezana s njim.

Pronaći ćemo odnos između unutarnjih sila i normalnih naprezanja u presjeku grede razmatranjem naprezanja na elementarnoj površini dA, odabranoj u presjeku A grede u točki s koordinatama y i z (os y je usmjerena prema dolje za pogodnost analize):

Kao što vidimo, problem je interno statički neodređen, budući da je priroda raspodjele normalnih naprezanja po presjeku nepoznata. Za rješavanje problema razmotrite geometrijsku sliku deformacija.

Geometrijska strana problema

Razmotrimo deformaciju grednog elementa duljine dx, odvojenog od šipke za savijanje u proizvoljnoj točki s koordinatom x. Uzimajući u obzir prethodno prihvaćenu hipotezu o ravnim presjecima, nakon savijanja presjek grede zarotirati će se u odnosu na neutralnu os (n.o.) za kut dϕ, dok će se vlakno ab, udaljeno od neutralne osi na udaljenosti y, pretvoriti u luk kružnice a1b1, a njegova duljina će se promijeniti za neku veličinu. Prisjetimo se ovdje da se duljina vlakana koja leže na neutralnoj osi ne mijenja, pa stoga luk a0b0 (čiji je polumjer zakrivljenosti označen s ρ) ima istu duljinu kao segment a0b0 prije deformacije a0b0=dx .

Nađimo relativnu linearnu deformaciju εx vlakna ab zakrivljene grede.

Prilikom gradnje dijagrami momenata savijanjaM na graditelji prihvaćeno: ordinate koje izražavaju u određenom mjerilu pozitivan vrijednosti momenata savijanja, odvojene rastegnut vlakna, tj. - dolje, A negativno - gore od osi grede. Stoga kažu da graditelji konstruiraju dijagrame na rastegnutim vlaknima. Kod mehaničara pozitivne vrijednosti posmične sile i momenta savijanja su odgođene gore. Mehaničari crtaju dijagrame na komprimiran vlakna.

Glavni naponi pri savijanju. Ekvivalentni naponi.

U općem slučaju izravnog savijanja u presjecima grede, normalan I tangentenapon. Ovi naponi variraju i po duljini i po visini grede.

Dakle, u slučaju savijanja postoji ravno stanje naprezanja.

Razmotrimo dijagram gdje je greda opterećena silom P

Najveća normalna javljaju se napetosti u ekstremno, točke najudaljenije od neutralne crte, i U njima nema posmičnih naprezanja. Stoga, za ekstreman vlakna glavna naprezanja različita od nule su normalna naprezanja u presjeku.

Na razini neutralne linije u presjeku grede nalaze se najveći smični napon, A normalni naponi su nula. znači u vlaknima neutralan sloj glavna naprezanja određena su vrijednostima tangencijalnih naprezanja.

U ovoj shemi dizajna, gornja vlakna grede će biti rastegnuta, a donja će biti komprimirana. Za određivanje glavnih naprezanja koristimo dobro poznati izraz:

puna analiza naprezanja Zamislimo to na slici.

Analiza naprezanja na savijanje

Maksimalno glavno naprezanje σ 1 Nalazi se Gornji ekstremna vlakna i jednaka nuli na donjim vanjskim vlaknima. Glavno naprezanje σ 3 Ima najveća apsolutna vrijednost je na donjim vlaknima.

Trajektorija glavnih naprezanja ovisi o vrsta opterećenja I način učvršćivanja grede.

Kod rješavanja problema to je dovoljno odvojenoček normalan I odvojeno tangencijalni naponi. Međutim ponekad najstresnije ispasti da jesu srednji vlakna u kojima postoje i normalni i posmični naponi. To se događa u dijelovima gdje Istodobno, i moment savijanja i posmična sila dostižu velike vrijednosti- to može biti u ugradnji konzolne grede, na nosaču grede s konzolom, u dijelovima pod koncentriranom silom ili u dijelovima s oštrim promjenama širine. Na primjer, u I-presjeku najopasniji spoj zida i police- tamo su značajna normalna i posmična naprezanja.

Materijal je u stanju ravnog naprezanja i potreban je provjerite ekvivalentne napone.

Uvjeti čvrstoće greda od plastičnih materijala Po treći(teorija maksimalnih tangencijalnih naprezanja) I Četvrta(teorija energije promjena oblika) teorije snage.

U pravilu, u valjanim gredama ekvivalentna naprezanja ne prelaze normalna naprezanja u krajnjim vanjskim vlaknima i nije potrebno posebno ispitivanje. Druga stvar - kompozitne metalne grede, koji zid je tanji nego kod valjanih profila na istoj visini. Češće se koriste zavarene spregnute grede od čeličnog lima. Proračun takvih greda na čvrstoću: a) izbor presjeka - visina, debljina, širina i debljina tetiva grede; b) provjera čvrstoće normalnim i tangencijalnim naprezanjima; c) provjera čvrstoće pomoću ekvivalentnih naprezanja.

Određivanje posmičnih naprezanja u I-presjeku. Razmotrimo odjeljak I-zraka S x = 96,9 cm3; Yh=2030 cm 4 ; Q=200 kN

Za određivanje posmičnog naprezanja koristi se formula,gdje je Q posmična sila u presjeku, S x 0 je statički moment dijela presjeka koji se nalazi s jedne strane sloja u kojem su određena tangencijalna naprezanja, I x je moment tromosti cijelog sloja. presjeka, b je širina presjeka na mjestu gdje se određuje posmično naprezanje

Izračunajmo maksimum smično naprezanje:

Izračunajmo statički moment za najgornja polica:

Sada izračunajmo smično naprezanje:

Mi gradimo dijagram smičnih naprezanja:

Razmotrimo presjek standardnog profila u obliku I-zraka i definirati smično naprezanje, koja djeluje paralelno sa silom smicanja:

Idemo izračunati statički momenti jednostavne figure:

Ova se vrijednost može izračunati i inače, koristeći činjenicu da je za presjeke I-nosača i žlijeba zadan statički moment polovice presjeka. Za to je potrebno od poznate vrijednosti statičkog momenta oduzeti vrijednost statičkog momenta na liniji A 1 B 1:

Tangencijalni naponi na spoju prirubnice i stijenke se mijenjaju grčevito, jer oštar debljina stijenke varira od t st prije b.

Dijagrami tangencijalnih naprezanja u stijenkama koritastih, šupljih pravokutnih i drugih presjeka imaju isti oblik kao i kod I-prosjeka. Formula uključuje statički moment osjenčanog dijela presjeka u odnosu na os X, au nazivniku širinu presjeka (neto) u sloju u kojem se određuje posmično naprezanje.

Odredimo tangencijalna naprezanja za kružni presjek.

Budući da posmična naprezanja na konturi presjeka moraju biti usmjerena tangenta na konturu, zatim u točkama A I U na krajevima bilo koje tetive paralelne s promjerom AB, naponi smicanja su usmjereni okomito na polumjere OA I OV. Stoga, pravcima tangencijalni naponi u točkama A, VC konvergirati u nekoj točki N na Y osi.

Statički moment odsječenog dijela:

Odnosno, posmični naponi se mijenjaju prema parabolični zakona i bit će maksimum na razini neutralne crte, kada y 0 =0

Formula za određivanje smičnog naprezanja (formula)

Razmotrimo pravokutni presjek

Na daljinu y 0 od središnje osi povlačimo odjeljak 1-1 te odrediti tangencijalna naprezanja. Statički moment područje odrezani dio:

Treba imati na umu da je temeljna ravnodušan, uzmite statički moment površine osjenčani ili preostali dio poprečni presjek. Oba statička momenta jednaki i suprotni predznakom, dakle njihov iznos, koji predstavlja statički moment površine cijelog presjeka u odnosu na neutralnu liniju, točnije središnju os x, bit će jednak nula.

Moment inercije pravokutnog presjeka:

Zatim smično naprezanje prema formuli

Varijabla y 0 uključena je u formulu u drugi stupnjeva, tj. tangencijalni naponi u pravokutnom presjeku variraju prema zakon kvadratne parabole.

Dostignuti smični napon maksimum na razini neutralne linije, tj. Kada y 0 =0:

, Gdje A je područje cijelog odjeljka.

Uvjet čvrstoće za tangencijalna naprezanja ima oblik:

, Gdje S x 0– statički moment dijela poprečnog presjeka koji se nalazi s jedne strane sloja u kojem se određuju posmična naprezanja, Ix– moment tromosti cijelog presjeka, b– širina presjeka na mjestu gdje se određuje posmično naprezanje, Q- bočna sila, τ - smično naprezanje, [τ] — dopušteno tangencijalno naprezanje.

Ovo stanje čvrstoće omogućuje nam proizvodnju tri vrsta proračuna (tri vrste problema pri proračunu čvrstoće):

1. Proračun provjere ili ispitivanje čvrstoće temeljeno na tangencijalnim naprezanjima:

2. Odabir širine presjeka (za pravokutni presjek):

3. Određivanje dopuštene bočne sile (za pravokutni presjek):

Za određivanje tangente naprezanja, razmotrite gredu opterećenu silama.

Zadatak određivanja naprezanja je uvijek statički neodređen i zahtijeva uključenost geometrijski I fizički jednadžbe. Međutim, to je moguće prihvatiti hipoteze o prirodi raspodjele naprezanja da će zadatak postati statički odrediv.

Po dva beskonačno bliska presjeka 1-1 i 2-2 biramo dz element, Prikažimo ga u velikom mjerilu, a zatim nacrtajte uzdužni presjek 3-3.

U odjeljcima 1–1 i 2–2, normalni σ 1, σ 2 naprezanja, koji se određuju dobro poznatim formulama:

Gdje M - moment savijanja u presjeku, dM - prirast moment savijanja po duljini dz

Bočna sila u presjecima 1–1 i 2–2 usmjeren je duž glavne središnje osi Y i, očito, predstavlja zbroj vertikalnih komponenti unutarnjih tangencijalnih naprezanja raspoređenih po presjeku. U čvrstoći materijala obično se uzima pretpostavka njihove ravnomjerne raspodjele po širini presjeka.

Za određivanje veličine posmičnih naprezanja u bilo kojoj točki poprečnog presjeka koja se nalazi na udaljenosti y 0 od neutralne X osi, nacrtajte ravninu paralelnu s neutralnim slojem (3-3) kroz ovu točku i uklonite odrezani element. Odredit ćemo napon koji djeluje preko područja ABCD.

Projicirajmo sve sile na Z os

Rezultanta unutarnjih uzdužnih sila duž desne strane bit će jednaka:

Gdje A 0 – površina ruba fasade, S x 0 – statički moment odsječenog dijela u odnosu na X os. Slično na lijevoj strani:

Obje rezultante usmjereni jedni prema drugima, budući da je element in komprimiran područje snopa. Njihova razlika je uravnotežena tangencijalnim silama na donjem rubu 3-3.

Hajdemo to pretvarati smično naprezanje τ raspoređen po širini presjeka grede b ravnomjerno. Ova pretpostavka je vjerojatnija što je širina manja u usporedbi s visinom presjeka. Zatim rezultanta tangencijalnih sila dT jednaka vrijednosti naprezanja pomnoženoj s površinom lica:

Sastavljajmo sada jednadžba ravnoteže Σz=0:

ili odakle

Prisjetimo se diferencijalne ovisnosti, prema kojem Tada dobivamo formulu:

Ova formula se zove formule. Ova formula je dobivena 1855. Ovdje S x 0 – statički moment dijela poprečnog presjeka, koji se nalazi s jedne strane sloja u kojem se određuju posmična naprezanja, I x – moment tromosti cijeli presjek, b – širina presjeka na mjestu gdje se određuje smično naprezanje, Q - sila smicanja u presjeku.

— stanje čvrstoće na savijanje, Gdje

- najveći moment (modulo) iz dijagrama momenata savijanja; - aksijalni moment otpora presjeka, geometrijski karakteristika; - dopušteno naprezanje (σ adm)

- najveći normalni napon.

Ako se obračun provodi prema metoda graničnog stanja, tada umjesto dopuštenog napona ulazimo u izračun proračunska otpornost materijala R.

Vrste proračuna čvrstoće na savijanje

1. Ček proračun ili ispitivanje čvrstoće pomoću normalnih naprezanja

2. Oblikovati obračun ili odabir odjeljka

3. Definicija dopušteno opterećenje (definicija kapacitet dizanja i ili operativni prijevoznik sposobnosti)

Prilikom izvođenja formule za izračunavanje normalnih naprezanja, razmatramo slučaj savijanja, kada se unutarnje sile u presjecima grede svode samo na moment savijanja, A posmična sila ispada nula. Ovaj slučaj savijanja zove se čisto savijanje. Razmotrite srednji dio grede, koji je podložan čistom savijanju.

Pri opterećenju greda se savija tako da se Donja vlakna se izdužuju, a gornja se skraćuju.

Budući da je dio vlakana grede rastegnut, a dio sabijen, dolazi do prijelaza iz napetosti u kompresiju glatko, bez skokova, V prosjek nalazi se dio grede sloj čija se vlakna samo savijaju, ali ne doživljavaju ni napetost ni kompresiju. Ovaj sloj se zove neutralan sloj. Pravac po kojem neutralni sloj siječe presjek grede naziva se neutralna linija ili neutralna os odjeljci. Na osi grede nanizane su neutralne linije. Neutralna linija je linija u kojoj normalni naponi su nula.

Linije povučene na bočnoj površini grede okomito na os ostaju ravan pri savijanju. Ovi eksperimentalni podaci omogućuju temeljenje zaključaka formula hipoteza ravnih presjeka (konjektura). Prema ovoj hipotezi, presjeci grede su ravni i okomiti na svoju os prije savijanja, ostaju ravni i ispadaju okomiti na zakrivljenu os grede kada se savija.

Pretpostavke za izvođenje formula za normalno naprezanje: 1) Hipoteza ravninskih presjeka je ispunjena. 2) Uzdužna vlakna ne pritišću jedno drugo (hipoteza o netlaku) i stoga je svako od vlakana u stanju jednoosne napetosti ili kompresije. 3) Deformacije vlakana ne ovise o njihovom položaju po širini presjeka. Posljedično, normalni naponi, koji se mijenjaju po visini presjeka, ostaju isti po širini. 4) Greda ima najmanje jednu ravninu simetrije i sve vanjske sile leže u toj ravnini. 5) Materijal grede pokorava se Hookeovom zakonu, a modul elastičnosti na napetost i pritisak je isti. 6) Odnos između dimenzija grede je takav da radi u uvjetima ravnog savijanja bez savijanja ili uvijanja.

Razmotrimo gredu proizvoljnog presjeka, ali koja ima os simetrije. Moment savijanja predstavlja rezultantni moment unutarnjih normalnih sila, koja nastaje na beskonačno malim površinama i može se izraziti u sastavni oblik: (1), gdje je y krak elementarne sile u odnosu na os x

Formula (1) izražava statički strana problema savijanja ravne grede, ali duž nje u poznatom momentu savijanja Nemoguće je odrediti normalna naprezanja dok se ne utvrdi zakon njihove raspodjele.

Odaberimo grede u srednjem dijelu i razmotrimo dionica duljine dz, podložni savijanju. Prikažimo to u uvećanom mjerilu.

Dijelovi koji ograničavaju područje dz, međusobno paralelni dok se ne deformiraju, i nakon primjene opterećenja rotirati oko svojih neutralnih linija za kut . Duljina segmenta vlakana neutralnog sloja neće se promijeniti. i bit će jednako: , gdje je radijus zakrivljenosti zakrivljena os grede. Ali bilo koje drugo vlakno laže niži ili viši neutralni sloj, promijenit će svoju duljinu. Izračunajmo relativno produljenje vlakana koja se nalaze na udaljenosti y od neutralnog sloja. Relativno istezanje je omjer apsolutne deformacije prema izvornoj duljini, zatim:

Smanjimo za i dovedimo slične članove, tada ćemo dobiti: (2) Ova formula izražava geometrijski strana čistog problema savijanja: Deformacije vlakana izravno su proporcionalne njihovoj udaljenosti od neutralnog sloja.

Sada prijeđimo na naglašava, tj. razmotrit ćemo fizički stranu zadatka. u skladu s pretpostavka bez pritiska koristimo vlakna pod aksijalnom napetosti-kompresijom: tada uzimajući u obzir formulu (2) imamo (3), oni. normalan stres kod savijanja po visini presjeka linearno raspoređena. Na krajnjim vanjskim vlaknima normalna naprezanja postižu najveću vrijednost, au težištu presjeka jednaka su nuli. Zamijenimo (3) u jednadžbu (1) i uzmemo razlomak iz znaka integrala kao konstantnu vrijednost, tada imamo . Ali izraz je aksijalni moment tromosti presjeka u odnosu na os x - ja x. Njegova dimenzija cm 4, m 4

Zatim ,gdje (4) ,gdje je zakrivljenost zakrivljene osi grede, a je krutost presjeka grede tijekom savijanja.

Zamijenimo dobiveni izraz zakrivljenost (4) u izraz (3) i dobivamo formula za izračunavanje normalnih naprezanja u bilo kojoj točki poprečnog presjeka: (5)

Da. maksimum javljaju se napetosti u točkama najudaljenijim od neutralne linije. Stav (6) nazvao aksijalni moment otpora presjeka. Njegova dimenzija cm 3, m 3. Moment otpora karakterizira utjecaj oblika i dimenzija poprečnog presjeka na veličinu naprezanja.

Zatim maksimalni naponi: (7)

Uvjet čvrstoće na savijanje: (8)

Kada dođe do poprečnog savijanja ne samo normalna, već i posmična naprezanja, jer dostupno sila smicanja. Smično naprezanje kompliciraju sliku deformacije, dovode do zakrivljenost poprečni presjeci grede, što rezultira narušena je hipoteza ravninskih presjeka. Međutim, istraživanja pokazuju da izobličenja uvedena posmičnim naprezanjima malo utječu na normalna naprezanja izračunata formulom (5) . Dakle, pri određivanju normalnih naprezanja u slučaju poprečnog savijanja Teorija čistog savijanja sasvim je primjenjiva.

Neutralna linija. Pitanje o položaju neutralne linije.

Pri savijanju nema uzdužne sile, pa možemo pisati Zamijenimo ovdje formulu za normalna naprezanja (3) i dobivamo Budući da modul uzdužne elastičnosti materijala grede nije jednak nuli, a zakrivljena os grede ima konačan polumjer zakrivljenosti, ostaje pretpostaviti da je ovaj integral statički moment površine presjek grede u odnosu na neutralnu os x , i od jednaka je nuli, tada neutralna linija prolazi kroz težište presjeka.

Uvjet (odsutnost momenta unutarnjih sila u odnosu na liniju polja) će dati ili uzimajući u obzir (3) . Iz istih razloga (vidi gore) . U integrandu - centrifugalni moment tromosti presjeka u odnosu na osi x i y jednak je nuli, što znači da su ove osi glavni i središnji i našminkati se ravno kutak. Stoga, Silna i neutralna linija u ravnom zavoju međusobno su okomite.

Nakon instaliranja položaj neutralne linije, lako se gradi dijagram normalnog naprezanja po visini presjeka. Nju linearni karakter je određen jednadžba prvog stupnja.

Priroda dijagrama σ za simetrične presjeke u odnosu na neutralnu liniju, M<0