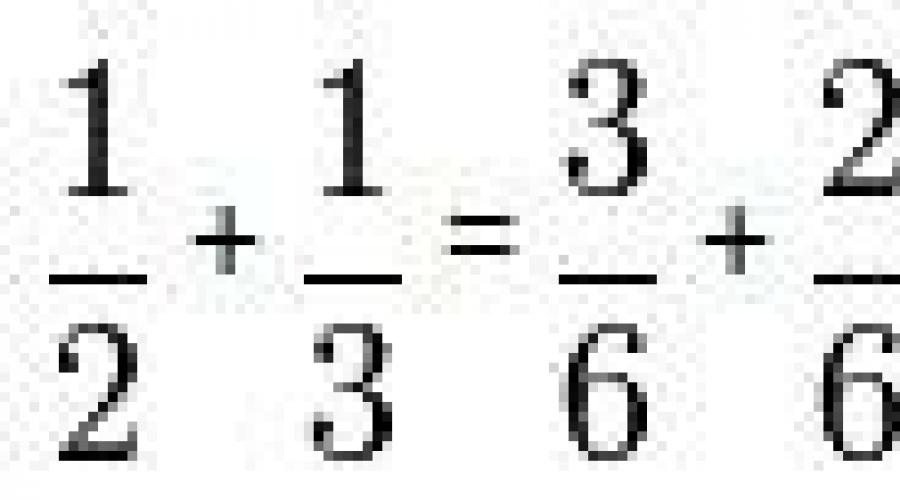
U članku ćemo pokazati kako riješiti razlomke na jednostavnom jasni primjeri. Shvatimo što je razlomak i razmotrimo rješavanje razlomaka!

Koncept razlomci uvodi se u nastavu matematike od 6. razreda srednje škole.

Razlomci imaju oblik: ±X/Y, gdje je Y nazivnik, govori na koliko je dijelova cijela podijeljena, a X je brojnik, govori koliko je takvih dijelova uzeto. Radi jasnoće, uzmimo primjer s tortom:

U prvom slučaju kolač je izrezan na jednake dijelove i uzeta je jedna polovica, tj. 1/2. U drugom slučaju kolač je izrezan na 7 dijelova, od kojih su uzeta 4 dijela, tj. 4/7.

Ako dio dijeljenja jednog broja s drugim nije cijeli broj, piše se kao razlomak.

Na primjer, izraz 4:2 = 2 daje cijeli broj, ali 4:7 nije djeljiv cjelinom, pa se ovaj izraz piše kao razlomak 4/7.

Drugim riječima frakcija je izraz koji označava dijeljenje dvaju brojeva ili izraza, a koji se piše razlomačkom kosom crtom.

Ako brojnik manji od nazivnika- razlomak je točan, ako je obrnuto netočan. Razlomak može sadržavati cijeli broj.

Na primjer, 5 cijelih 3/4.

Ovaj unos znači da za dobivanje cijelog 6 nedostaje jedan dio od četiri.

Ako želiš zapamtiti, kako riješiti razlomke za 6. razred, morate to razumjeti rješavanje razlomaka, u osnovi, svodi se na razumijevanje nekoliko jednostavnih stvari.

• Razlomak je u biti izraz razlomka. To je brojčani izraz koji je dio date vrijednosti jedne cjeline. Na primjer, razlomak 3/5 izražava da ako smo nešto cijelo podijelili na 5 dijelova i broj dionica ili dijelova te cjeline je tri.
• Razlomak može biti manji od 1, na primjer 1/2 (ili u biti polovica), tada je točan. Ako je razlomak veći od 1, npr. 3/2 (tri polovice ili jedan i pol), onda je netočan i radi pojednostavljenja rješenja bolje nam je odabrati cijeli dio 3/2 = 1 cijeli 1 /2.
• Razlomci su isti brojevi kao 1, 3, 10, pa čak i 100, samo što ti brojevi nisu cijeli brojevi nego razlomci. S njima možete izvoditi sve iste operacije kao i s brojevima. Brojanje razlomaka nije teže, i dalje konkretni primjeri mi ćemo to pokazati.

Kako riješiti razlomke. Primjeri.

Širok izbor aritmetičkih operacija primjenjiv je na razlomke.

Svođenje razlomka na zajednički nazivnik

Na primjer, trebate usporediti razlomke 3/4 i 4/5.

Da bismo riješili problem, prvo pronalazimo najmanji zajednički nazivnik, tj. najmanji broj, koji je djeljiv bez ostatka sa svakim od nazivnika razlomaka

Najmanji zajednički nazivnik (4,5) = 20

Tada se nazivnik oba razlomka svede na najmanji zajednički nazivnik

Odgovor: 15/20

Zbrajanje i oduzimanje razlomaka

Ako je potrebno izračunati zbroj dvaju razlomaka, oni se prvo dovode na zajednički nazivnik, zatim se zbrajaju brojnici, dok nazivnik ostaje nepromijenjen. Razlika između razlomaka izračunava se na isti način, jedina razlika je što se brojnici oduzimaju.

Na primjer, trebate pronaći zbroj razlomaka 1/2 i 1/3

Nađimo sada razliku između razlomaka 1/2 i 1/4

Množenje i dijeljenje razlomaka

Ovdje rješavanje razlomaka nije teško, ovdje je sve vrlo jednostavno:

• Množenje - brojnici i nazivnici razlomaka se međusobno množe;
• Dijeljenje - prvo dobijemo razlomak inverzan drugom razlomku, tj. Zamijenimo njegov brojnik i nazivnik, nakon čega pomnožimo dobivene razlomke.

Na primjer:

To je otprilike to kako riješiti razlomke, Svi. Ako još uvijek imate pitanja o rješavanje razlomaka, ako vam nešto nije jasno, napišite u komentarima i svakako ćemo vam odgovoriti.

Ako ste nastavnik, onda je moguće preuzeti prezentaciju za osnovna škola(http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) dobro će vam doći.

Aritmetičke operacije s običnim razlomcima

1. Zbrajanje.

Da biste zbrojili razlomke s istim nazivnicima, morate zbrojiti njihove brojnike, a nazivnik ostaviti isti.

Primjer. .

Za zbrajanje razlomaka sa različite nazivnike, potrebno ih je dovesti do najmanjeg zajedničkog nazivnika, a zatim dobivene brojnike zbrojiti i zajednički nazivnik potpisati ispod zbroja.

Primjer.

Ukratko piše ovako:

Za zbrajanje mješovitih brojeva potrebno je zasebno pronaći zbroj cijelih brojeva i zbroj razlomaka. Akcija je napisana ovako:

2. Oduzimanje.

Da biste oduzeli razlomke s istim nazivnicima, trebate oduzeti brojnik umanjenika od brojnika umanjenika i ostaviti isti nazivnik. Akcija je napisana ovako:

Da biste oduzeli razlomke s različitim nazivnicima, prvo ih morate svesti na najmanji zajednički nazivnik, zatim od brojnika umanjenika oduzeti brojnik umanjenika i zajednički nazivnik potpisati ispod njihove razlike. Akcija je napisana ovako:

Ako trebate oduzeti jedan mješoviti broj od drugog mješovitog broja, onda, ako je moguće, oduzmite razlomak od razlomka, a cjelinu od cjeline. Radnja je ovako napisana:

Ako je razlomak oduzetog veći od razlomka umanjenika, tada se od cijelog broja umanjenika uzima jedna jedinica, dijeli na odgovarajuće dijelove i dodaje razlomku umanjenika, nakon čega se nastavlja kako je gore opisano. . Akcija je napisana ovako:

Učinite istu stvar kada trebate oduzeti razlomak od cijelog broja.

Primjer. .

3. Proširenje svojstava zbrajanja i oduzimanja na razlomke.Svi zakoni i svojstva zbrajanja i oduzimanja prirodni brojevi vrijede i za razlomke. Njihova uporaba u mnogim slučajevima uvelike pojednostavljuje proces izračuna.

4. Množenje.

Da biste pomnožili razlomak s razlomkom, trebate pomnožiti brojnik s brojnikom, a nazivnik s nazivnikom, te da prvi umnožak bude brojnik, a drugi umnožak nazivnik.

Kod množenja treba (ako je moguće) smanjiti.

Primjer. .

Ako uzmemo u obzir da je cijeli broj razlomak s nazivnikom 1, tada se množenje razlomka cijelim brojem i cijelog broja razlomkom može slijediti istim pravilom.

Primjeri.

5. Množenje mješoviti brojevi.

Da biste množili mješovite brojeve, prvo ih morate pretvoriti u nepravi razlomci a zatim pomnoži prema pravilu za množenje razlomaka.

Primjer. .

6. Dijeljenje razlomka razlomkom.

Da biste razlomak podijelili na razlomak, potrebno je brojnik prvog razlomka pomnožiti s nazivnikom drugog, a nazivnik prvog s brojnikom drugog te prvi umnožak napisati kao brojnik, a drugi kao nazivnik.

Primjer. .

Koristeći isto pravilo, možete podijeliti razlomak s cijelim brojem i cijeli broj s razlomkom, ako cijeli broj predstavite kao razlomak s nazivnikom 1.

Primjeri.

7. Dijeljenje mješovitih brojeva.

Za dijeljenje mješovitih brojeva prvo se pretvaraju u neprave razlomke, a zatim dijele prema pravilu za dijeljenje razlomaka.

Primjer. .

8. Zamjena dijeljenja množenjem.

Ako u razlomku zamijenite brojnik i nazivnik, dobit ćete novi razlomak, obrnuto od ovog. Na primjer, za razlomakrecipročni razlomak će biti.

Očito je umnožak dvaju međusobno inverznih razlomaka jednak 1.

1. Nalaženje razlomka iz broja.

Postoje mnogi problemi koji zahtijevaju da pronađete dio ili razlomak zadanog broja. Takvi se problemi rješavaju množenjem.

Zadatak. Domaćica je imala 20 rubalja;Potrošila ih je na kupovinu. Koliko košta kupovina?

Ovdje morate pronaćibroj 20. Možete to učiniti ovako:

Odgovor. Domaćica je potrošila 8 rubalja.

Primjeri. Pronađite od 30. Rješenje. .

Pronađite iz. Riješenje. .

1. Pronalaženje broja prema poznatoj veličini njegovog razlomka.

Ponekad je potrebno odrediti cijeli broj pomoću poznatog dijela broja i razlomka koji izražava taj dio. Takvi se problemi rješavaju diobom.

Zadatak. U razredu ima 12 komsomolaca, što jedijelovi svih učenika u razredu. Koliko učenika ima u razredu?

Riješenje. .

Odgovor. 20 učenika.

Primjer. Pronađite brojšto je 34.

Riješenje. .

Odgovor. Traženi broj je.

1. Pronalaženje omjera dvaju brojeva.

Razmotrite problem: radnik je proizveo 40 dijelova u jednom danu. Koji dio mjesečnog zadatka je radnik izvršio ako je mjesečni plan 400 dijelova?

Riješenje. .

Odgovor. Radnik je završiodio mjesečnog plana.

U u ovom slučaju dio (40 dijelova) izražava se kao razlomak cjeline (400 dijelova). Također kažu da je pronađen omjer broja proizvedenih dijelova dnevno i mjesečnog plana.

1. Pretvaranje decimalnog razlomka u obični razlomak.

Preobratiti se decimal u obični, piše se s nazivnikom i po mogućnosti skraćeno:

Primjeri.

1. Pretvaranje razlomka u decimalu.

Postoji nekoliko načina pretvaranja razlomka u decimalu.

Prvi način. Da biste razlomak pretvorili u decimalu, podijelite brojnik s nazivnikom.

Primjeri. .

Drugi način. Da biste razlomak pretvorili u decimalu, trebate pomnožiti brojnik i nazivnik razlomka s takvim brojem da nazivnik na kraju bude jedan s nulama (ako je moguće).

Primjer.

1. Usporedba decimala po veličini. Da biste saznali koji je od dva decimalna razlomka veći, potrebno je usporediti njihove cijele dijelove, desetinke, stotinke itd. Kad su cijeli dijelovi jednaki, veći je razlomak koji ima više desetina; ako su cijeli brojevi i decimale jednaki, veći je onaj s više stotinki itd.

Primjer. Od tri razlomka 2,432; 2,41 i 2,4098 je najveći prvi, jer ima najviše stotinki, a cijeli i deseti su isti u svim razlomcima.

Operacije s decimalama

1. Množenje i dijeljenje decimala s 10, 100, 1000 itd.

Za množenje decimale s 10, 100, 1000 itd. trebate premjestiti zarez na jedan, dva, tri itd. znak desno. Ako u broju nema dovoljno znakova, tada se dodjeljuju nule.

Primjer. 15,45 10 = 154,5; 32,3 · 100 = 3230.

Da biste podijelili decimalni razlomak s 10, 100, 1000 itd., trebate premjestiti decimalni zarez na jedan, dva, tri itd. znak lijevo. Ako nema dovoljno znakova za pomicanje zareza, njihov broj se nadopunjuje odgovarajućim brojem nula s lijeve strane.

Primjeri. 184,35 : 100 = 1,8435; 3,5 : 100 = 0,035.

1. Zbrajanje i oduzimanje decimala.

Decimale se zbrajaju i oduzimaju na gotovo isti način kao što se zbrajaju i oduzimaju prirodni brojevi. Znamenka je napisana ispod znamenke, zarez je napisan ispod zareza.

Primjeri.

1. Množenje decimala.

Za množenje dva decimalna razlomka dovoljno ih je, ne obazirući se na zareze, pomnožiti kao cijele brojeve i u umnošku zarezom s desne strane odvojiti onoliko decimala koliko ih je bilo u množeniku i množitelju zajedno.

Primjer 1. 2.064 · 0.05.

Množimo cijele brojeve 2064 · 5 = 10320. Prvi faktor je imao tri decimale, a drugi dvije. Proizvod mora imati pet decimala. Odvojimo ih s desne strane i dobijemo 0,10320. Nula na kraju se može odbaciti: 2,064 · 0,05 = 0,1032.

Primjer 2. 1,125 · 0,08; 1125 · 8 = 9000.

Broj decimala treba biti 3 + 2 = 5. Na 9000 s lijeve strane dodamo nule (009000), a s desne odvojimo pet decimala. Dobivamo 1,125 · 0,08 = 0,09000 = 0,09.

1. Dijeljenje decimala.

Razmatraju se dva slučaja dijeljenja decimalnih razlomaka bez ostatka: 1) dijeljenje decimalnog razlomka cijelim brojem; 2) dijeljenje broja (cijelog ili razlomka) decimalnim razlomkom.

Dijeljenje decimale cijelim brojem vrši se na isti način kao i dijeljenje cijelih brojeva; rezultirajući ostaci se sekvencijalno dijele na manje decimalne dijelove i dijeljenje se nastavlja sve dok ostatak ne bude nula.

Primjeri.

Dijeljenje broja (cijelog ili razlomka) decimalnim razlomkom u svim slučajevima rezultira dijeljenjem cijelim brojem. Da biste to učinili, povećajte djelitelj za 10, 100, 1000 itd. puta, a da se kvocijent ne mijenja, dividenda se uvećava isto toliko puta, a zatim se dijeli cijelim brojem (kao u prvom slučaju).

Primjer. 47,04 : 0,0084 = 470400 : 84 = 5600;

1. Primjeri na suradnja s običnim i decimalnim razlomcima.

Razmotrimo najprije primjer svih operacija s decimalnim razlomcima.

Primjer 1. Izračunajte:

Ovdje se koristi svođenje dividende i djelitelja na cijeli broj, uzimajući u obzir činjenicu da se kvocijent ne mijenja. Zatim imamo:

Kod rješavanja primjera zajedničkih radnji s običnim i decimalnim razlomcima, neke se radnje mogu izvoditi u decimalnim razlomcima, a neke u običnim. Mora se imati na umu da nije uvijek obični razlomak može se pretvoriti u konačni decimalni razlomak. Stoga se zapisivanje decimalnog razlomka može učiniti samo ako se potvrdi da je takva pretvorba moguća.

Primjer 2. Izračunajte:

Interes

Pojam postotka.Postotak broja je stoti dio tog broja. Na primjer, umjesto da kažemo "54 stotinke svih stanovnika naše zemlje su žene", moglo bi se reći "54 posto svih stanovnika naše zemlje su žene". Umjesto riječi "postotak" pišu i znak %, na primjer 35% znači 35 posto.

Budući da je postotak stoti dio, slijedi da je postotak razlomak s nazivnikom 100. Dakle, razlomak je 0,49, odn., može se pročitati kao 49 posto i napisati bez nazivnika kao 49%. Općenito, nakon što ste odredili koliko stotinki ima u određenom decimalnom razlomku, lako ga je napisati kao postotak. Da biste to učinili, upotrijebite pravilo: da biste zapisali decimalni razlomak kao postotak, morate pomaknuti decimalnu točku u ovom razlomku dva mjesta udesno.

Primjeri. 0,33 = 33%; 1,25 = 125%; 0,002 = 0,2%; 21 = 2100%.

I obrnuto: 7% = 0,07; 24,5% = 0,245; 0,1% = 0,001; 200% = 2.

1. Pronalaženje postotka zadanog broja

Zadatak. Prema planu, ekipa traktorista mora potrošiti 9 tona goriva. Vozači traktora su se društveno obvezali uštedjeti 20% goriva. Odredite uštedu goriva u tonama.

Ako u ovom zadatku umjesto 20% napišemo njemu jednak broj 0,2, dobivamo zadatak za pronalaženje razlomka broja. A takvi problemi se rješavaju množenjem. Ovo je rješenje:

20% = 0,2; 9 · 0,2 = 1,8 (m).

Izračuni se mogu napisati ovako:

(m)

Da biste pronašli nekoliko postotaka zadanog broja, dovoljno je zadani broj podijeliti sa 100 i rezultat pomnožiti s brojem postotaka.

Zadatak. Radnik je 1963. primao 90 rubalja mjesečno, a 1964. počeo je primati 30% više. Koliko je zaradio 1964.?

Rješenje (prva metoda).

1) Koliko je više rubalja dobio radnik?

(trljati.)

90 + 27 = 117 (utrljati).

Drugi način.

1) Koliki je postotak prethodne zarade radnik počeo primati 1964. godine?

100% + 30% = 130%.

2) Kolika je bila mjesečna plaća radnika 1964. godine?

(trljati.)

2. Pronalaženje broja iz zadane vrijednosti njegovog postotka.

Zadatak. Zadruga je zasijala kukuruz na površini od 280 hektara, što je 14% ukupne zasijane površine. Odredite sjetvenu površinu kolektivne farme.

Ako u ovom zadatku umjesto 14% napišemo 0,14 odn, tada dobivamo zadatak pronaći broj iz poznate vrijednosti njegovog razlomka. A takvi se problemi rješavaju diobom.

Riješenje. 14% = 0,14; 280: 0,14 = 2000 (ha). Ova se otopina može formulirati i ovako:

(Ha)

Da biste pronašli broj na temelju zadane vrijednosti od nekoliko postotaka, dovoljno je tu vrijednost podijeliti s brojem postotaka i rezultat pomnožiti sa 100.

Zadatak. U ožujku je tvornica istopila 125,4 T metala, premašivši plan za 4,5%. Koliko je tona metala tvornica trebala istopiti u ožujku prema planu?

Riješenje.

1) U kojem postotku je tvornica ispunila plan u ožujku?

100% + 4,5% = 104,5%.

2) Koliko tona metala bi postrojenje trebalo rastaliti?

(Ha)

1. Određivanje postotnog odnosa između dva broja.

Zadatak. Moramo preorati 300 hektara zemlje. Prvog dana poorano je 120 hektara. Koliki je postotak zadatka obavljen prvog dana?

Riješenje.

Prvi način. 300 hektara je 100%, što znači da 1% čini 3 hektara. Određivanjem koliko puta 3 hektara, što čini 1%, sadrži 120 hektara, saznajemo koliki je postotak zadatka zemlja obrađena prvog dana

120: 3 = 40(%).

Drugi način. Nakon što smo utvrdili koji je dio zemlje bio preoran prvog dana, taj udio izražavamo u postotku.

Zapišimo izračun:

Za izračunavanje postotka broja a do broja b , morate pronaći odnos a do b i pomnožite sa 100.

Ovaj članak govori o obični razlomci. Ovdje ćemo uvesti pojam razlomka cjeline, što će nas dovesti do definicije običnog razlomka. Zatim ćemo se zadržati na prihvaćenom zapisu za obične razlomke i dati primjere razlomaka, recimo o brojniku i nazivniku razlomka. Nakon toga dat ćemo definicije pravih i nepravih, pozitivnih i negativnih razlomaka, te razmotriti položaj razlomaka na koordinatna zraka. Zaključno navodimo glavne operacije s razlomcima.

Navigacija po stranici.

Udjeli cjeline

Prvo predstavljamo koncept udjela.

Pretpostavimo da imamo neki objekt sastavljen od nekoliko potpuno identičnih (odnosno jednakih) dijelova. Radi jasnoće, možete zamisliti, na primjer, jabuku izrezanu na nekoliko dijelova jednake dijelove, ili naranča koja se sastoji od nekoliko jednakih segmenata. Svaki od tih jednakih dijelova koji čine cijeli predmet naziva se dijelovi cjeline ili jednostavno dionice.

Imajte na umu da su dionice različite. Objasnimo ovo. Uzmimo dvije jabuke. Prvu jabuku prerežite na dva jednaka dijela, a drugu na 6 jednakih dijelova. Jasno je da će se udio prve jabuke razlikovati od udjela druge jabuke.

Ovisno o broju dionica koje čine cijeli objekt, te dionice imaju svoja imena. Idemo to riješiti imena otkucaja. Ako se predmet sastoji od dva dijela, bilo koji od njih se naziva jednim drugim dijelom cijelog predmeta; ako se predmet sastoji od tri dijela, onda se bilo koji od njih naziva jedan treći dio, i tako dalje.

Jedna druga dionica ima posebno ime - pola. Jedna trećina je pozvana treći, i jedna četvrtina dijela - četvrtina.

Radi sažetosti uvedeno je sljedeće: pobijediti simbole. Jedna druga dionica označena je kao ili 1/2, jedna trećina dionice označena je kao ili 1/3; jedna četvrtina dionice - like ili 1/4, i tako dalje. Imajte na umu da se oznaka s vodoravnom crtom koristi češće. Da bismo pojačali gradivo, navedimo još jedan primjer: natuknica označava sto šezdeset sedmi dio cjeline.

Koncept udjela prirodno se proteže od objekata do količina. Na primjer, jedna od mjera za duljinu je metar. Za mjerenje duljina kraćih od metra mogu se koristiti djelići metra. Tako možete koristiti, na primjer, pola metra ili desetinku ili tisućinku metra. Udjeli ostalih količina primjenjuju se na sličan način.

Obični razlomci, definicija i primjeri razlomaka

Za opis broja dionica koje koristimo obični razlomci. Navedimo primjer koji će nam omogućiti da se približimo definiciji običnih razlomaka.

Neka se naranča sastoji od 12 dijelova. Svaka dionica u ovom slučaju predstavlja jednu dvanaestinu cijele naranče, tj. Dva otkucaja označavamo kao , tri otkucaja kao , i tako dalje, 12 otkucaja označavamo kao . Svaki od navedenih unosa naziva se običnim razlomkom.

Sada dajmo generalku definicija običnih razlomaka.

Izražena definicija običnih razlomaka omogućuje nam davanje primjeri običnih razlomaka: 5/10, , 21/1, 9/4, . A evo i zapisa ne odgovaraju navedenoj definiciji običnih razlomaka, odnosno nisu obični razlomci.

Brojnik i nazivnik

Radi praktičnosti razlikuju se obični razlomci brojnik i nazivnik.

Definicija.

Brojnik obični razlomak (m/n) je prirodni broj m.

Definicija.

Nazivnik obični razlomak (m/n) je prirodni broj n.

Dakle, brojnik se nalazi iznad crte razlomka (lijevo od kose crte), a nazivnik se nalazi ispod crte razlomka (desno od kose crte). Na primjer, uzmimo obični razlomak 17/29, brojnik tog razlomka je broj 17, a nazivnik je broj 29.

Ostaje da raspravimo značenje sadržano u brojniku i nazivniku običnog razlomka. Nazivnik razlomka pokazuje od koliko se dijelova sastoji jedan objekt, a brojnik, pak, označava broj takvih udjela. Na primjer, nazivnik 5 razlomka 12/5 znači da se jedan objekt sastoji od pet dionica, a brojnik 12 znači da je uzeto 12 takvih dionica.

Prirodni broj kao razlomak s nazivnikom 1

Nazivnik običnog razlomka može biti jednak jedinici. U ovom slučaju možemo smatrati da je predmet nedjeljiv, drugim riječima, predstavlja nešto cjelovito. Brojnik takvog razlomka pokazuje koliko je cijelih predmeta uzeto. Dakle, obični razlomak oblika m/1 ima značenje prirodnog broja m. Time smo potkrijepili valjanost jednakosti m/1=m.

Prepišimo posljednju jednakost na sljedeći način: m=m/1. Ova jednakost nam omogućuje da svaki prirodni broj m predstavimo kao običan razlomak. Na primjer, broj 4 je razlomak 4/1, a broj 103,498 jednak je razlomku 103,498/1.

Tako, bilo koji prirodni broj m može se predstaviti kao običan razlomak s nazivnikom 1 kao m/1, a svaki obični razlomak oblika m/1 može se zamijeniti prirodnim brojem m.

Crta razlomka kao znak dijeljenja

Predstavljanje izvornog objekta u obliku n dionica nije ništa drugo nego podjela na n jednakih dijelova. Nakon što je predmet podijeljen na n dionica, možemo je jednako podijeliti među n ljudi - svaki će dobiti jednu dionicu.

Ako na početku imamo m identičnih objekata, od kojih je svaki podijeljen na n dionica, tada možemo jednako podijeliti tih m objekata između n ljudi, dajući svakoj osobi po jednu dionicu od svakog od m objekata. U ovom slučaju, svaka osoba će imati m dionica od 1/n, a m dionica od 1/n daje obični razlomak m/n. Dakle, obični razlomak m/n može se koristiti za označavanje podjele m predmeta između n ljudi.

Tako smo dobili eksplicitnu vezu između običnih razlomaka i dijeljenja (vidi opću ideju dijeljenja prirodnih brojeva). Ova veza se izražava na sljedeći način: razlomka se može shvatiti kao znak dijeljenja, odnosno m/n=m:n.

Pomoću običnog razlomka možete napisati rezultat dijeljenja dvaju prirodnih brojeva za koje se ne može izvesti cijelo dijeljenje. Na primjer, rezultat dijeljenja 5 jabuka s 8 ljudi može se napisati kao 5/8, odnosno svi će dobiti pet osmina jabuke: 5:8 = 5/8.

Jednaki i nejednaki razlomci, usporedba razlomaka

Prilično prirodna radnja je uspoređivanje razlomaka, jer je jasno da se 1/12 naranče razlikuje od 5/12, a 1/6 jabuke je isto što i druga 1/6 ove jabuke.

Usporedbom dva obična razlomka dobiva se jedan od rezultata: razlomci su jednaki ili nejednaki. U prvom slučaju imamo jednaki obični razlomci, a u drugom – nejednaki obični razlomci. Dajmo definiciju jednakih i nejednakih običnih razlomaka.

Definicija.

jednak, ako je istinita jednakost a·d=b·c.

Definicija.

Dva obična razlomka a/b i c/d nejednak, ako ne vrijedi jednakost a·d=b·c.

Evo nekoliko primjera jednakih razlomaka. Na primjer, obični razlomak 1/2 jednak je razlomku 2/4, jer je 1·4=2·2 (po potrebi pogledajte pravila i primjere množenja prirodnih brojeva). Radi jasnoće, možete zamisliti dvije identične jabuke, prva je prerezana na pola, a druga na 4 dijela. Očito je da su dvije četvrtine jabuke jednake 1/2 udjela. Drugi primjeri jednakih običnih razlomaka su razlomci 4/7 i 36/63, te par razlomaka 81/50 i 1,620/1,000.

Ali obični razlomci 4/13 i 5/14 nisu jednaki, jer je 4·14=56, a 13·5=65, odnosno 4·14≠13·5. Drugi primjeri nejednakih običnih razlomaka su razlomci 17/7 i 6/4.

Ako se pri usporedbi dvaju običnih razlomaka pokaže da nisu jednaki, tada ćete možda morati otkriti koji od tih običnih razlomaka manje drugačiji, a koji - više. Da bi se to saznalo, koristi se pravilo za usporedbu običnih razlomaka, čija je bit uspoređivane razlomke dovesti do zajedničkog nazivnika i zatim usporediti brojnike. Detaljne informacije o ovoj temi prikupljene su u članku usporedba razlomaka: pravila, primjeri, rješenja.

Razlomački brojevi

Svaki razlomak je zapis razlomački broj. Odnosno, razlomak je samo "ljuska" frakcijskog broja, njegov izgled, a svo semantičko opterećenje sadržano je u frakcijskom broju. Međutim, radi sažetosti i praktičnosti, koncepti razlomka i frakcijskog broja kombinirani su i jednostavno se nazivaju razlomkom. Prikladno je ovdje preformulirati poznata izreka: kažemo razlomak - mislimo razlomački broj, kažemo razlomački broj - mislimo na razlomak.

Razlomci na koordinatnoj zraci

Svi razlomački brojevi koji odgovaraju običnim razlomcima imaju svoje jedinstveno mjesto na, to jest, postoji korespondencija jedan na jedan između razlomaka i točaka koordinatne zrake.

Da biste došli do točke na koordinatnoj zraci koja odgovara razlomku m/n, potrebno je od ishodišta u pozitivnom smjeru odvojiti m odsječaka čija je duljina 1/n razlomak jediničnog odsječka. Takvi se segmenti mogu dobiti dijeljenjem jediničnog segmenta na n jednakih dijelova, što se uvijek može učiniti pomoću šestara i ravnala.

Na primjer, pokažimo točku M na koordinatnoj zraci, koja odgovara razlomku 14/10. Duljina segmenta s krajevima u točki O i točki koja je njoj najbliža, označena malom crticom, iznosi 1/10 jediničnog segmenta. Točka s koordinatom 14/10 udaljena je od ishodišta na udaljenosti od 14 takvih segmenata.

Jednaki razlomci odgovaraju istom razlomačkom broju, tj. jednaki razlomci su koordinate iste točke na koordinatnoj zraci. Na primjer, koordinate 1/2, 2/4, 16/32, 55/110 odgovaraju jednoj točki na koordinatnoj zraci, budući da su svi napisani razlomci jednaki (nalazi se na udaljenosti od pola jediničnog segmenta položenog od ishodišta u pozitivnom smjeru).

Na vodoravnoj i desno usmjerenoj koordinatnoj zraci točka čija je koordinata veći razlomak nalazi se desno od točke čija je koordinata manji razlomak. Slično, točka s manjom koordinatom leži lijevo od točke s većom koordinatom.

Pravi i nepravi razlomci, definicije, primjeri

Među običnim razlomcima postoje pravi i nepravi razlomci. Ova se podjela temelji na usporedbi brojnika i nazivnika.

Definirajmo prave i neprave obične razlomke.

Definicija.

Pravilan razlomak je običan razlomak čiji je brojnik manji od nazivnika, tj. ako je m

Definicija.

Nepravilan razlomak je običan razlomak u kojem je brojnik veći ili jednak nazivniku, odnosno ako je m≥n, tada je obični razlomak nepravilan.

Evo nekoliko primjera pravih razlomaka: 1/4, , 32,765/909,003. Doista, u svakom od napisanih običnih razlomaka brojnik je manji od nazivnika (po potrebi pogledajte članak usporedbe prirodnih brojeva), pa su oni točni po definiciji.

Evo primjera nepravih razlomaka: 9/9, 23/4, . Doista, brojnik prvog od napisanih običnih razlomaka jednak je nazivniku, a kod ostalih razlomaka brojnik je veći od nazivnika.

Postoje i definicije pravih i nepravih razlomaka, koje se temelje na usporedbi razlomaka s jedinicom.

Definicija.

ispraviti, ako je manji od jedan.

Definicija.

Obični razlomak naziva se pogrešno, ako je ili jednak jedan ili veći od 1.

Dakle, obični razlomak 7/11 je točan, budući da je 7/11<1 , а обыкновенные дроби 14/3 и 27/27 – неправильные, так как 14/3>1, i 27/27=1.

Razmislimo o tome kako obični razlomci s brojnikom većim ili jednakim nazivniku zaslužuju takvo ime - "nepravilni".

Na primjer, uzmimo nepravi razlomak 9/9. Ovaj razlomak znači da se od predmeta koji se sastoji od devet dijelova uzima devet dijelova. Odnosno, od dostupnih devet dijelova možemo sastaviti cijeli objekt. To jest, nepravi razlomak 9/9 u biti daje cijeli predmet, to jest, 9/9 = 1. Općenito, nepravi razlomci s brojnikom jednakim nazivniku označavaju jedan cijeli predmet, a takav se razlomak može zamijeniti prirodnim brojem 1.

Sada razmotrite neprave razlomke 7/3 i 12/4. Sasvim je očito da od tih sedam trećina možemo sastaviti dva cijela objekta (jedan cijeli objekt sastoji se od 3 dijela, onda će nam za sastavljanje dva cijela objekta trebati 3 + 3 = 6 dijelova) i još će ostati jedna trećina . To jest, nepravi razlomak 7/3 u biti znači 2 objekta i također 1/3 takvog objekta. A od dvanaest četvrtinskih dijelova možemo napraviti tri cijela predmeta (tri predmeta sa po četiri dijela). Odnosno, razlomak 12/4 u biti znači 3 cijela objekta.

Razmotreni primjeri dovode nas do sljedećeg zaključka: neprave razlomke možemo zamijeniti ili prirodnim brojevima, kada se brojnik ravnomjerno podijeli s nazivnikom (npr. 9/9=1 i 12/4=3), ili zbrojem prirodnog broja i pravilnog razlomka, kada brojnik nije ravnomjerno djeljiv s nazivnikom (npr. 7/3=2+1/3). Možda je upravo to ono zbog čega su nepravi razlomci dobili naziv "nepravilni".

Posebno je zanimljiv prikaz nepravog razlomka kao zbroja prirodnog broja i pravog razlomka (7/3=2+1/3). Taj se postupak naziva odvajanje cijelog dijela od nepravog razlomka i zaslužuje posebno i pažljivije razmatranje.

Također je vrijedno napomenuti da postoji vrlo bliska veza između nepravilnih razlomaka i mješovitih brojeva.

Pozitivni i negativni razlomci

Svaki obični razlomak odgovara pozitivnom razlomačkom broju (vidi članak o pozitivnim i negativnim brojevima). Odnosno, obični razlomci su pozitivni razlomci. Na primjer, obični razlomci 1/5, 56/18, 35/144 su pozitivni razlomci. Kada trebate istaknuti pozitivnost razlomka, ispred njega se stavlja znak plus, na primjer, +3/4, +72/34.

Ako stavite znak minus ispred običnog razlomka, tada će ovaj unos odgovarati negativnom razlomku. U ovom slučaju možemo razgovarati o negativni razlomci. Evo nekoliko primjera negativnih razlomaka: −6/10, −65/13, −1/18.

Pozitivni i negativni razlomci m/n i −m/n su suprotni brojevi. Na primjer, razlomci 5/7 i −5/7 su suprotni razlomci.

Pozitivni razlomci, kao i pozitivni brojevi općenito, označavaju dodatak, prihod, promjenu bilo koje vrijednosti naviše itd. Negativni razlomci odgovaraju trošku, dugu ili smanjenju bilo koje količine. Na primjer, negativni razlomak −3/4 može se protumačiti kao dug čija je vrijednost jednaka 3/4.

U vodoravnom i desnom smjeru, negativni razlomci nalaze se lijevo od ishodišta. Točke koordinatnog pravca čije su koordinate pozitivni razlomak m/n i negativni razlomak −m/n nalaze se na istoj udaljenosti od ishodišta, ali na suprotnim stranama točke O.

Ovdje vrijedi spomenuti razlomke oblika 0/n. Ti razlomci su jednaki broju nula, odnosno 0/n=0.

Pozitivni razlomci, negativni razlomci i 0/n razlomci kombiniraju se u racionalne brojeve.

Operacije s razlomcima

Već smo raspravljali o jednoj radnji s običnim razlomcima - usporedbi razlomaka - gore. Definirane su još četiri aritmetičke funkcije operacije s razlomcima– zbrajanje, oduzimanje, množenje i dijeljenje razlomaka. Pogledajmo svaki od njih.

Opća bit operacija s razlomcima slična je biti odgovarajućih operacija s prirodnim brojevima. Napravimo analogiju.

Množenje razlomaka može se zamisliti kao radnja pronalaženja razlomka iz razlomka. Da pojasnimo, navedimo primjer. Uzmimo 1/6 jabuke i trebamo uzeti 2/3. Dio koji nam treba je rezultat množenja razlomaka 1/6 i 2/3. Rezultat množenja dva obična razlomka je obični razlomak (koji je u posebnom slučaju jednak prirodnom broju). Zatim preporučujemo da proučite informacije u članku Množenje razlomaka - pravila, primjeri i rješenja.

Bibliografija.

• Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S., Shvartsburd S.I. Matematika: udžbenik za 5. razred. obrazovne ustanove.
• Vilenkin N.Ya. i drugi. 6. razred: udžbenik za općeobrazovne ustanove.
• Gusev V.A., Mordkovich A.G. Matematika (priručnik za polaznike tehničkih škola).

Online kalkulator.
Izračunajte izraz s numeričkim razlomcima.
Množenje, oduzimanje, dijeljenje, zbrajanje i smanjivanje razlomaka s različitim nazivnicima.

S ovim online kalkulatorom možete množenje, oduzimanje, dijeljenje, zbrajanje i smanjivanje razlomaka s različitim nazivnicima.

Program radi s regularnim, nepravilnim i mješovitim brojevima.

Ovaj program (online kalkulator) može:
- izvoditi zbrajanje mješovitih razlomaka s različitim nazivnicima
- izvoditi oduzimanje mješovitih razlomaka s različitim nazivnicima
- dijeliti mješovite razlomke s različitim nazivnicima
- množenje mješovitih razlomaka s različitim nazivnicima
- svesti razlomke na zajednički nazivnik
- pretvoriti mješovite razlomke u neprave razlomke
- smanjiti razlomke

Također možete unijeti ne izraz s razlomcima, već jedan jedini razlomak.
U tom slučaju, frakcija će se smanjiti i cijeli dio će biti odvojen od rezultata.

Online kalkulator za izračunavanje izraza s numeričkim razlomcima ne daje samo odgovor na problem, on nudi detaljno rješenje s objašnjenjima, tj. prikazuje proces pronalaženja rješenja.

Ovaj program može biti koristan za učenike srednjih škola u općim školama kada se pripremaju za testove i ispite, kada testiraju znanje prije Jedinstvenog državnog ispita, a roditeljima za kontrolu rješenja mnogih problema iz matematike i algebre. Ili vam je možda preskupo unajmiti učitelja ili kupiti nove udžbenike? Ili samo želite završiti svoju zadaću iz matematike ili algebre što je brže moguće? U tom slučaju također možete koristiti naše programe s detaljnim rješenjima.

Na taj način možete provoditi vlastitu obuku i/ili obuku svoje mlađe braće ili sestara, dok se razina edukacije u području rješavanja problema povećava.

Ako niste upoznati s pravilima za unos izraza s numeričkim razlomcima, preporučujemo da se s njima upoznate.

Pravila za upisivanje izraza s brojevnim razlomcima

Samo cijeli broj može biti brojnik, nazivnik i cijeli broj razlomka.

Nazivnik ne može biti negativan.

Pri unosu brojčanog razlomka brojnik se od nazivnika odvaja znakom dijeljenja: /
Unos: -2/3 + 7/5
Rezultat: \(-\frac(2)(3) + \frac(7)(5)\)

Cijeli dio je odvojen od razlomka znakom ampersand: &
Unos: -1&2/3 * 5&8/3
Rezultat: \(-1\frac(2)(3) \cdot 5\frac(8)(3)\)

Dijeljenje razlomaka uvodi se znakom dvotočke: :
Unos: -9&37/12: -3&5/14
Rezultat: \(-9\frac(37)(12) : \lijevo(-3\frac(5)(14) \desno) \)
Zapamtite da ne možete dijeliti s nulom!

Možete koristiti zagrade kada unosite izraze s numeričkim razlomcima.
Ulazni: -2/3 * (6&1/2-5/9) : 2&1/4 + 1/3
Rezultat: \(-\frac(2)(3) \cdot \left(6 \frac(1)(2) - \frac(5)(9) \desno) : 2\frac(1)(4) + \frac(1)(3)\)

Otkriveno je da neke skripte potrebne za rješavanje ovog problema nisu učitane i program možda neće raditi.
Možda imate omogućen AdBlock.
U tom slučaju, onemogućite ga i osvježite stranicu.

Jer Puno je ljudi voljnih riješiti problem, vaš zahtjev je u redu čekanja.
Za nekoliko sekundi rješenje će se pojaviti ispod.
Molimo pričekajte sekund...

Ako ti uočio grešku u rješenju, onda o tome možete pisati u obrascu za povratne informacije.
Ne zaboravi navesti koji zadatak ti odluči što unesite u polja.

Naše igre, zagonetke, emulatori:

Malo teorije.

Obični razlomci. Dijeljenje s ostatkom

Ako trebamo podijeliti 497 s 4, tada ćemo pri dijeljenju vidjeti da 497 nije ravnomjerno djeljivo s 4, tj. ostatak diobe ostaje. U takvim slučajevima se kaže da je završeno dijeljenje s ostatkom, a rješenje je zapisano na sljedeći način:
497: 4 = 124 (1 ostatak).

Komponente dijeljenja na lijevoj strani jednakosti nazivaju se isto kao i kod dijeljenja bez ostatka: 497 - dividenda, 4 - šestar. Rezultat dijeljenja pri dijeljenju s ostatkom naziva se nepotpuno privatno. U našem slučaju to je broj 124. I na kraju, posljednja komponenta koja nije u običnom dijeljenju je ostatak. U slučajevima kada nema ostatka, kaže se da je jedan broj podijeljen drugim bez traga ili potpuno. Vjeruje se da je s takvim dijeljenjem ostatak nula. U našem slučaju, ostatak je 1.

Ostatak je uvijek manji od djelitelja.

Dijeljenje se može provjeriti množenjem. Ako, na primjer, postoji jednakost 64: 32 = 2, tada se provjera može učiniti ovako: 64 = 32 * 2.

Često je u slučajevima kada se izvodi dijeljenje s ostatkom zgodno koristiti jednakost
a = b * n + r,
gdje je a dividenda, b je djelitelj, n je djelomični kvocijent, r je ostatak.

Kvocijent prirodnih brojeva može se napisati kao razlomak.

Brojnik razlomka je dividenda, a nazivnik je djelitelj.

Budući da je brojnik razlomka dividenda, a nazivnik djelitelj, vjeruju da crta razlomka znači radnju dijeljenja. Ponekad je zgodno napisati dijeljenje kao razlomak bez upotrebe znaka ":".

Kvocijent dijeljenja prirodnih brojeva m i n može se napisati kao razlomak \(\frac(m)(n)\), gdje je brojnik m djelitelj, a nazivnik n djelitelj:
\(m:n = \frac(m)(n)\)

Sljedeća pravila su istinita:

Da biste dobili razlomak \(\frac(m)(n)\), trebate jedinicu podijeliti na n jednakih dijelova (dijelova) i uzeti m takvih dijelova.

Da biste dobili razlomak \(\frac(m)(n)\), trebate broj m podijeliti s brojem n.

Da biste pronašli dio cjeline, trebate broj koji odgovara cjelini podijeliti s nazivnikom i rezultat pomnožiti s brojnikom razlomka koji izražava taj dio.

Da biste pronašli cjelinu iz njezinog dijela, trebate podijeliti broj koji odgovara ovom dijelu s brojnikom i pomnožiti rezultat s nazivnikom razlomka koji izražava ovaj dio.

Ako se i brojnik i nazivnik razlomka pomnože s istim brojem (osim nule), vrijednost razlomka se neće promijeniti:
\(\veliki \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

Ako su i brojnik i nazivnik razlomka podijeljeni s istim brojem (osim nule), vrijednost razlomka se neće promijeniti:
\(\veliki \frac(a)(b) = \frac(a: m)(b: m) \)
Ovo svojstvo se zove glavno svojstvo razlomka.

Posljednje dvije transformacije nazivaju se smanjivanje razlomka.

Ako razlomke treba predstaviti kao razlomke s istim nazivnikom, tada se ova akcija poziva svođenje razlomaka na zajednički nazivnik.

Pravi i nepravi razlomci. Mješoviti brojevi

Već znate da se razlomak može dobiti tako da se cjelina podijeli na jednake dijelove i uzme nekoliko takvih dijelova. Na primjer, razlomak \(\frac(3)(4)\) znači tri četvrtine jedan. U mnogim zadacima iz prethodnog odlomka razlomci su korišteni za predstavljanje dijelova cjeline. Zdrav razum nalaže da bi dio uvijek trebao biti manji od cjeline, ali što je s razlomcima kao što su \(\frac(5)(5)\) ili \(\frac(8)(5)\)? Jasno je da ovo više nije dio jedinice. Vjerojatno se zato nazivaju razlomci čiji je brojnik veći ili jednak nazivniku nepravi razlomci. Preostale razlomke, tj. razlomke čiji je brojnik manji od nazivnika, nazivamo pravilni razlomci.

Kao što znate, bilo koji obični razlomak, i pravilan i nepravilan, može se smatrati rezultatom dijeljenja brojnika nazivnikom. Dakle, u matematici, za razliku od običnog jezika, izraz “nepravi razlomak” ne znači da smo nešto pogriješili, već samo da je brojnik tog razlomka veći ili jednak nazivniku.

Ako se broj sastoji od cijelog dijela i razlomka, tada razlomci se nazivaju mješoviti.

Na primjer:
\(5:3 = 1\frac(2)(3) \) : 1 je cijeli broj, a \(\frac(2)(3) \) je razlomački dio.

Ako je brojnik razlomka \(\frac(a)(b) \) djeljiv s prirodnim brojem n, tada da bi se taj razlomak podijelio s n, njegov brojnik mora biti podijeljen s ovim brojem:
\(\veliki \frac(a)(b) : n = \frac(a:n)(b) \)

Ako brojnik razlomka \(\frac(a)(b)\) nije djeljiv s prirodnim brojem n, tada da biste taj razlomak podijelili s n, trebate pomnožiti njegov nazivnik ovim brojem:
\(\veliki \frac(a)(b) : n = \frac(a)(bn) \)

Imajte na umu da je drugo pravilo također istinito kada je brojnik djeljiv s n. Stoga ga možemo koristiti kada je na prvi pogled teško odrediti je li brojnik razlomka djeljiv s n ili nije.

Akcije s razlomcima. Zbrajanje razlomaka.

Možete izvoditi aritmetičke operacije s razlomačkim brojevima, baš kao i s prirodnim brojevima. Pogledajmo prvo zbrajanje razlomaka. Lako je zbrajati razlomke s istim nazivnicima. Nađimo, na primjer, zbroj \(\frac(2)(7)\) i \(\frac(3)(7)\). Lako je razumjeti da \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

Da biste zbrojili razlomke s istim nazivnicima, morate zbrojiti njihove brojnike, a nazivnik ostaviti isti.

Koristeći slova, pravilo za zbrajanje razlomaka s istim nazivnicima može se napisati na sljedeći način:
\(\veliki \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

Ako trebate zbrajati razlomke s različitim nazivnicima, prvo ih morate svesti na zajednički nazivnik. Na primjer:
\(\veliki \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

Za razlomke, kao i za prirodne brojeve, vrijede komutativnost i asocijativnost zbrajanja.

Zbrajanje mješovitih razlomaka

Pozivaju se zapisi poput \(2\frac(2)(3)\). mješovite frakcije. U ovom slučaju poziva se broj 2 cijeli dio mješoviti razlomak, a broj \(\frac(2)(3)\) je njegov razlomački dio. Zapis \(2\frac(2)(3)\) čita se na sljedeći način: "dvije i dvije trećine."

Kada broj 8 podijelite s brojem 3, možete dobiti dva odgovora: \(\frac(8)(3)\) i \(2\frac(2)(3)\). Oni izražavaju isti razlomački broj, tj. \(\frac(8)(3) = 2 \frac(2)(3)\)

Stoga je nepravi razlomak \(\frac(8)(3)\) predstavljen kao mješoviti razlomak \(2\frac(2)(3)\). U takvim slučajevima kažu da iz nepravog razlomka istaknuo cijeli dio.

Oduzimanje razlomaka (frakcijski brojevi)

Oduzimanje razlomačkih brojeva, kao i prirodnih brojeva, određuje se na temelju radnje zbrajanja: oduzeti drugi od jednog broja znači pronaći broj koji, kada se zbroji s drugim, daje prvi. Na primjer:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) jer \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9)\)

Pravilo za oduzimanje razlomaka s istim nazivnicima slično je pravilu za zbrajanje takvih razlomaka:
Da biste pronašli razliku između razlomaka s istim nazivnicima, morate od brojnika prvog razlomka oduzeti brojnik drugog, a nazivnik ostaviti isti.

Koristeći slova, ovo pravilo je napisano ovako:
\(\veliki \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Množenje razlomaka

Da biste pomnožili razlomak s razlomkom, potrebno je pomnožiti njihove brojnike i nazivnike i prvi umnožak napisati kao brojnik, a drugi kao nazivnik.

Koristeći slova, pravilo za množenje razlomaka može se napisati na sljedeći način:
\(\veliki \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

Pomoću formuliranog pravila možete pomnožiti razlomak prirodnim brojem, mješovitim razlomkom, a također i mješovite razlomke. Za to je potrebno prirodni broj napisati kao razlomak s nazivnikom 1, a mješoviti razlomak kao nepravi razlomak.

Rezultat množenja treba pojednostaviti (ako je moguće) smanjivanjem razlomka i izdvajanjem cijelog dijela nepravog razlomka.

Za razlomke, kao i za prirodne brojeve, vrijede svojstva komutativnosti i kombinativnosti množenja, kao i svojstvo distributivnosti množenja u odnosu na zbrajanje.

Dijeljenje razlomaka

Uzmimo razlomak \(\frac(2)(3)\) i "okrenimo" ga, zamijenivši brojnik i nazivnik. Dobivamo razlomak \(\frac(3)(2)\). Ovaj se razlomak zove obrnuti razlomci \(\frac(2)(3)\).

Ako sada “obrnemo” razlomak \(\frac(3)(2)\), dobit ćemo izvorni razlomak \(\frac(2)(3)\). Stoga se razlomci kao što su \(\frac(2)(3)\) i \(\frac(3)(2)\) nazivaju međusobno inverzni.

Na primjer, razlomci \(\frac(6)(5) \) i \(\frac(5)(6) \), \(\frac(7)(18) \) i \(\frac (18 )(7)\).

Recipročni razlomci mogu se pisati slovima na sljedeći način: \(\frac(a)(b) \) i \(\frac(b)(a) \)

Jasno je da umnožak recipročnih razlomaka jednak je 1. Na primjer: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

Koristeći recipročne razlomke, možete svesti dijeljenje razlomaka na množenje.

Pravilo za dijeljenje razlomka razlomkom je:
Da biste podijelili jedan razlomak drugim, trebate pomnožiti dividendu s recipročnom vrijednošću djelitelja.

Frakcija- broj koji se sastoji od cijelog broja razlomaka jedinice i prikazuje se u obliku: a/b

Brojnik razlomka (a)- broj koji se nalazi iznad razlomka i pokazuje broj dionica na koje je udjel podijeljen.

Nazivnik razlomka (b)- broj koji se nalazi ispod razlomka i pokazuje na koliko je dijelova jedinica podijeljena.

2. Svođenje razlomaka na zajednički nazivnik

3. Aritmetičke operacije nad običnim razlomcima

3.1. Zbrajanje običnih razlomaka

3.2. Oduzimanje razlomaka

3.3. Množenje običnih razlomaka

3.4. Dijeljenje razlomaka

4. Recipročni brojevi

5. Decimale

6. Aritmetičke operacije nad decimalama

6.1. Zbrajanje decimala

6.2. Oduzimanje decimala

6.3. Množenje decimala

6.4. Decimalno dijeljenje

#1. Glavno svojstvo razlomka

Ako se brojnik i nazivnik razlomka pomnože ili podijele istim brojem koji nije jednak nuli, dobiva se razlomak jednak zadanom.

3/7=3*3/7*3=9/21, odnosno 3/7=9/21

a/b=a*m/b*m - ovako izgleda glavno svojstvo razlomka.

Drugim riječima, razlomak jednak zadanom dobivamo množenjem ili dijeljenjem brojnika i nazivnika izvornog razlomka s istim prirodnim brojem.

Ako oglas=bc, tada su dva razlomka a/b =c /d smatraju se jednakima.

Na primjer, razlomci 3/5 i 9/15 bit će jednaki, jer je 3*15=5*9, odnosno 45=45

Smanjenje razlomka je postupak zamjene razlomka u kojem je novi razlomak jednak izvornom, ali s manjim brojnikom i nazivnikom.

Uobičajeno je skratiti razlomke na temelju osnovnog svojstva razlomka.

Na primjer, 45/60=15/ ​ ​20 =9/12=3/4 ​ ​ ​ (brojnik i nazivnik dijele se s brojem 3, s 5 i s 15).

Nesvodivi razlomak je razlomak oblika 3/4 ​ ​ , gdje su brojnik i nazivnik međusobno prosti brojevi. Glavna svrha smanjivanja razlomka je učiniti razlomak nesvodivim.

2. Svođenje razlomaka na zajednički nazivnik

Da biste dva razlomka doveli na zajednički nazivnik, trebate:

1) rastavite nazivnik svakog razlomka na proste faktore;

2) brojnik i nazivnik prvog razlomka pomnoži s onima koji nedostaju

faktori iz proširenja drugog nazivnika;

3) pomnožite brojnik i nazivnik drugog razlomka faktorima koji nedostaju iz prvog proširenja.

Primjeri: Svođenje razlomaka na zajednički nazivnik.

Rastavimo nazivnike na jednostavne faktore: 18=3∙3∙2, 15=3∙5

Pomnožite brojnik i nazivnik razlomka faktorom 5 koji nedostaje iz drugog proširenja.

brojnik i nazivnik razlomka na nedostajuće faktore 3 i 2 iz prvog proširenja.

= , 90 – zajednički nazivnik razlomaka.

3. Aritmetičke operacije nad običnim razlomcima

3.1. Zbrajanje običnih razlomaka

a) Ako su nazivnici isti, brojnik prvog razlomka pribraja se brojniku drugog razlomka, a nazivnik ostaje isti. Kao što možete vidjeti u primjeru:

a/b+c/b=(a+c)/b ​ ​ ;

b) Za različite nazivnike razlomci se prvo svedu na zajednički nazivnik, a zatim se brojnici zbrajaju prema pravilu a):

7/3+1/4=7*4/12+1*3/12=(28+3)/12=31/12

3.2. Oduzimanje razlomaka

a) Ako su nazivnici isti, oduzmite brojnik drugog razlomka od brojnika prvog razlomka, a nazivnik ostavite isti:

a/b-c/b=(a-c)/b ​ ​ ;

b) Ako su nazivnici razlomaka različiti, tada se razlomci prvo svedu na zajednički nazivnik, a zatim se ponavljaju koraci kao u točki a).

3.3. Množenje običnih razlomaka

Množenje razlomaka slijedi sljedeće pravilo:

a/b*c/d=a*c/b*d,

odnosno odvojeno množe brojnike i nazivnike.

Na primjer:

3/5*4/8=3*4/5*8=12/40.

3.4. Dijeljenje razlomaka

Razlomci se dijele na sljedeći način:

a/b:c/d=a*d/b*c,

odnosno razlomak a/b pomnožimo obrnutim razlomkom danog, odnosno pomnožimo s d/c.

Primjer: 7/2:1/8=7/2*8/1=56/2=28

4. Recipročni brojevi

Ako a*b=1, tada je broj b recipročni broj za broj a.

Primjer: za broj 9 recipročna vrijednost je 1/9 ​ ​ , od 9*1/9 = 1 , za broj 5 - inverzni broj 1/5 ​ ​ , jer 5* ​ 1/5 ​ ​ = 1 .

5. Decimale

Decimal je pravi razlomak čiji je nazivnik jednak 10, 1000, 10 000, …, 10^n 1 0 , 1 0 0 0 , 1 0 0 0 0 , . . . , 1 0 ​ n​ ​ .

Na primjer: 6/10 =0,6; 44/1000=0,044 ​ .

Na isti način pišu se i netočni s nazivnikom 10^n ili mješoviti brojevi.

Na primjer: 51/10= 5,1; 763/100=7,63

Svaki obični razlomak s nazivnikom koji je djelitelj određene potencije broja 10 predstavlja se kao decimalni razlomak.

mjenjač, ​​koji je djelitelj određene potencije broja 10.

Primjer: 5 je djelitelj od 100, pa je razlomak 1/5=1 *20/5*20=20/100=0,2 ​ 0 = 0 , 2 .

6. Aritmetičke operacije nad decimalama

6.1. Zbrajanje decimala

Da biste zbrojili dva decimalna razlomka, potrebno ih je posložiti tako da jedna ispod druge budu iste znamenke, a ispod zareza zarez, a zatim razlomke zbrajati kao obične brojeve.

6.2. Oduzimanje decimala

Izvodi se na isti način kao i zbrajanje.

6.3. Množenje decimala

Kod množenja decimalnih brojeva dovoljno je pomnožiti zadane brojeve, ne pazeći na zareze (kao prirodni brojevi), a u dobivenom odgovoru zarez s desne strane odvaja onoliko znamenki koliko iza decimalne točke stoji u oba faktora. ukupno.

Pomnožimo 2,7 sa 1,3. Imamo 27\cdot 13=351 2 7 ⋅ 1 3 = 3 5 1 . Dvije znamenke s desne strane odvajamo zarezom (prvi i drugi broj imaju jednu znamenku iza decimalne točke; 1+1=2 1 + 1 = 2 ). Kao rezultat dobivamo 2,7\cdot 1,3=3,51 2 , 7 ⋅ 1 , 3 = 3 , 5 1 .

Ako dobiveni rezultat sadrži manje znamenki nego što ih treba odvojiti zarezom, tada se nule koje nedostaju pišu ispred, na primjer:

Da biste pomnožili s 10, 100, 1000, trebate pomaknuti decimalnu točku za 1, 2, 3 znamenke udesno (ako je potrebno, određeni broj nula dodijeljen je udesno).

Na primjer: 1,47\cdot 10 000 = 14 700 1 , 4 7 ⋅ 1 0 0 0 0 = 1 4 7 0 0 .

6.4. Decimalno dijeljenje

Dijeljenje decimalnog razlomka prirodnim brojem vrši se na isti način kao i dijeljenje prirodnog broja prirodnim brojem. Zarez u količniku stavlja se nakon što je završeno dijeljenje cijelog dijela.

Ako je cjelobrojni dio dividende manji od djelitelja, tada je odgovor nula cijelih brojeva, na primjer:

Pogledajmo dijeljenje decimale decimalom. Recimo da trebamo podijeliti 2,576 s 1,12. Najprije pomnožimo djelitelj i djelitelj razlomka sa 100, odnosno pomaknimo decimalnu točku udesno u djelitelju i djelitelju za onoliko znamenki koliko ih ima u djelitelju iza decimalne točke (u ovom primjeru dva). Tada trebate razlomak 257,6 podijeliti s prirodnim brojem 112, odnosno problem se svodi na već razmatrani slučaj:

Dešava se da se konačni decimalni razlomak ne dobije uvijek kada se jedan broj dijeli drugim. Rezultat je beskonačni decimalni razlomak. U takvim slučajevima prelazimo na obične razlomke.

Na primjer, 2,8: 0,09= 28/10: 9/100= 28*100/10*9=2800/90=280/9= ​ 31 1/9 ​ ​ .