Principaux exemples de solutions de D'Alembert. Principe de mécanique théorique de D'Alembert. Définition du principe de d'Alembert
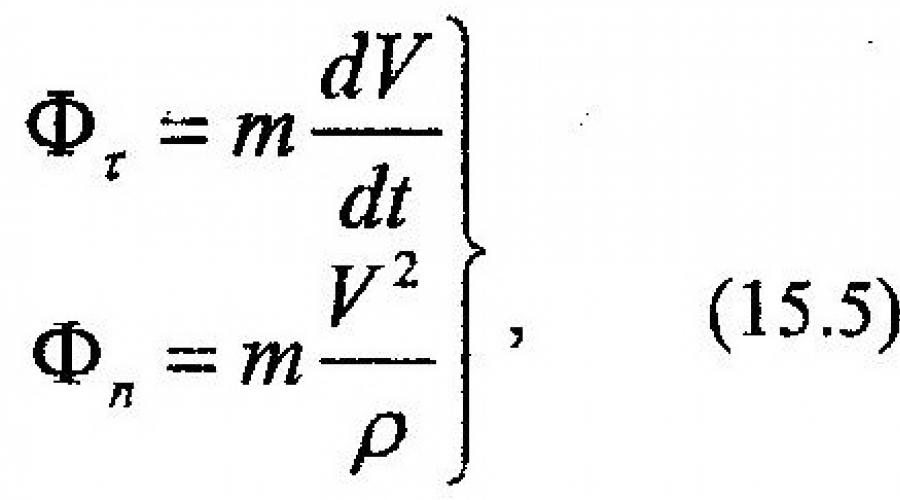
Lire aussi
Le domaine d'application du principe de d'Alembert est la dynamique des systèmes mécaniques contraints. d'Alembert a proposé une méthode originale de résolution de problèmes de dynamique, qui permet d'utiliser suffisamment équations simples statique. Il a écrit: " Cette règle conduit tous les problèmes liés au mouvement des corps à plus tâches simples sur l'équilibre."
La base cette méthode des forces d'inertie sont appliquées. Introduisons ce concept.
La force d'inertie est la somme géométrique des forces d'opposition d'une particule matérielle en mouvement aux corps qui lui confèrent une accélération.
Expliquons cette définition. En figue. 15.1 montre une particule matérielle M , interagir avec n objets matériels. En figue. 15.1 montre les forces d'interaction : sans
qui en réalité ne concernent pas la particule, mais les corps ayant des masses m 1 , …, m n . Il est clair que la résultante de ce système de forces contraires convergentes, R ’ = ΣF’ k , modulo égal R. et est dirigé à l'opposé de l'accélération, c'est-à-dire : R’ =-ma. Ce pouvoir et est la force d'inertie mentionnée dans la définition. Dans ce qui suit nous le désignerons par la lettre F , c'est à dire.:
En général mouvement curviligne l'accélération ponctuelle est la somme de deux composantes :
D'après (15.4), il ressort clairement que les composantes de la force d'inertie sont dirigées à l'opposé des directions des composantes correspondantes de l'accélération du point. Les modules des composantes de la force d'inertie sont déterminés par les formules suivantes :

Où ρ – rayon de courbure de la trajectoire du point.
Après avoir déterminé la force d'inertie, considérez principe de d'Alembert.
Soit un système mécanique constitué de n points matériels (Fig. 15.2). Prenons-en un. Toutes les forces agissant sur k ème point, nous le classons en groupes :
L'expression (15.6) reflète l'essence du principe de d'Alembert, écrit pour un point matériel. Répéter les étapes ci-dessus pour chaque point Système mécanique, on peut écrire le système n des équations similaires à (15.6), qui seront une représentation mathématique du principe de d'Alembert appliqué à un système mécanique. Formulons donc Principe de d'Alembert pour un système mécanique :
Si à chaque point du système mécanique à tout moment, à l'exception de l'extérieur et Forces internes, appliquez la force d'inertie appropriée, alors l'ensemble du système de forces sera mis dans un état d'équilibre et toutes les équations statiques pourront lui être appliquées.
S'il vous plaît gardez en tête:
Le principe de D'Alembert peut être appliqué aux processus dynamiques se produisant dans
systèmes de référence inertiels. La même exigence, comme indiqué précédemment, doit être respectée lors de l'application des lois de la dynamique ;
Les forces d’inertie qui, selon la méthodologie du principe de d’Alembert, doivent être appliquées
vivent aux points du système, en fait ils ne sont pas affectés. En effet, s'ils existaient, alors l'ensemble des forces appliquées à chaque point serait en équilibre, et la formulation même du problème de la dynamique serait absente.
Pour un système de forces à l’équilibre, les équations suivantes peuvent être écrites :

ceux. somme géométrique de toutes les forces du système, y compris les forces d'inertie, et la somme géométrique des moments de toutes les forces par rapport à un centre arbitraire sont égales à zéro.
Considérant les propriétés des efforts internes du système :
les expressions (15.7) peuvent être considérablement simplifiées.
Présentation de la principale notation vectorielle
et le point principal
les expressions (15.7) apparaîtront sous la forme :

Les équations (15.11) sont une continuation directe du principe de d'Alembert, mais ne contiennent pas de forces internes, ce qui constitue leur avantage incontestable. Leur utilisation est plus efficace lors de l'étude de la dynamique des systèmes mécaniques constitués de solides.
Le principe de D'Alembert permet de formuler des problèmes de dynamique des systèmes mécaniques comme des problèmes de statique. Dans ce cas, les équations différentielles dynamiques du mouvement prennent la forme d’équations d’équilibre. Cette méthode est appelée méthode kinétostatique .
principe de d'Alembert pour point matériel: « A chaque instant, le mouvement d'un point matériel, les forces actives agissant effectivement sur lui, les réactions de connexions et la force d'inertie appliquée conditionnellement au point forment un système de forces équilibré.»
Par la force d'inertie d'un point appelé quantité vectorielle qui a une dimension de force égale en ampleur au produit de la masse d'un point et de son accélération et dirigée à l'opposé du vecteur accélération
 .
(3.38)
.
(3.38)
En considérant un système mécanique comme un ensemble de points matériels sur lesquels chacun est sollicité, selon le principe de d'Alembert, par un système de forces équilibré, nous avons les conséquences de ce principe appliqué au système. Vecteur principal et le point principal concernant tout centre rattaché au système forces externes et les forces d'inertie de tous ses points sont égales à zéro :
 (3.39)
(3.39)
Ici, les forces externes sont les forces actives et les réactions des connexions.
Principal vecteur des forces d'inertie d'un système mécanique est égale au produit de la masse du système par l'accélération de son centre de masse et est dirigée dans la direction opposée à cette accélération
 .
(3.40)
.
(3.40)
Moment principal des forces d'inertie systèmes par rapport à un centre arbitraire À PROPOS est égal à la dérivée temporelle prise avec le signe opposé de son moment cinétique par rapport au même centre
 .
(3.41)
.
(3.41)
Pour solide, tournant autour d'un axe fixe Oz, trouvons le moment principal des forces d'inertie par rapport à cet axe
 .
(3.42)
.
(3.42)
3.8. Éléments de mécanique analytique
La section « Mécanique analytique » examine les principes généraux et les méthodes analytiques pour résoudre des problèmes de mécanique des systèmes matériaux.
3.8.1. Mouvements possibles du système. Classification
quelques connexions
Mouvements de points possibles
 d'un système mécanique sont tous les mouvements imaginaires et infinitésimaux autorisés par les connexions imposées au système à un instant donné. Un prieuré, nombre de degrés de liberté
Un système mécanique est appelé le nombre de ses mouvements indépendants possibles.
d'un système mécanique sont tous les mouvements imaginaires et infinitésimaux autorisés par les connexions imposées au système à un instant donné. Un prieuré, nombre de degrés de liberté
Un système mécanique est appelé le nombre de ses mouvements indépendants possibles.
Les connexions imposées au système sont appelées idéal , si la somme des travaux élémentaires de leurs réactions sur l'un des déplacements possibles des points du système est égale à zéro
 .
(3. 43)
.
(3. 43)
Les connexions pour lesquelles les restrictions qu'elles imposent sont conservées dans n'importe quelle position du système sont appelées holding . Les relations qui ne changent pas dans le temps et dont les équations n'incluent pas explicitement le temps sont appelées Stationnaire . Les connexions qui limitent uniquement les mouvements des points du système sont appelées géométrique , et les vitesses limites sont cinématique . Dans ce qui suit, nous considérerons uniquement les connexions géométriques et celles cinématiques qui peuvent être réduites à des connexions géométriques par intégration.
3.8.2. Le principe des mouvements possibles
Pour l'équilibre d'un système mécanique avec maintien de connexions idéales et stationnaires, il est nécessaire et suffisant que
la somme des travaux élémentaires de toutes les forces actives agissant sur lui, pour les éventuels déplacements du système, était égale à zéro
 .
(3.44)
.
(3.44)
En projections sur les axes de coordonnées :
 .
(3.45)
.
(3.45)
Le principe des mouvements possibles permet d'établir Forme générale conditions d'équilibre de tout système mécanique, sans considérer l'équilibre de ses parties individuelles. Dans ce cas, seules les forces actives agissant sur le système sont prises en compte. Les réactions inconnues des liaisons idéales ne sont pas incluses dans ces conditions. En même temps, ce principe permet de déterminer des réactions inconnues de liaisons idéales en écartant ces liaisons et en introduisant leurs réactions dans le nombre de forces actives. En rejetant les liaisons dont les réactions doivent être déterminées, le système acquiert un nombre correspondant supplémentaire de degrés de liberté.
Exemple 1
.
Trouver la relation entre les forces  Et
Et  jack, si l'on sait qu'à chaque tour de poignée AB = l, vis AVEC s'étend du montant h(Fig. 3.3).
jack, si l'on sait qu'à chaque tour de poignée AB = l, vis AVEC s'étend du montant h(Fig. 3.3).
Solution
Les mouvements possibles du mécanisme sont la rotation de la poignée et le déplacement de la charge h. La condition pour que le travail élémentaire des forces soit égal à zéro :
PL– Qh = 0;

Alors  . Depuis h
0, alors
. Depuis h
0, alors 
|
|
3.8.3. Équation générale de dynamique variationnelle
Considérons le mouvement d'un système composé de n points. Les forces actives agissent sur lui  et réactions des connexions
et réactions des connexions  .(k
= 1,…,n) Si on ajoute les forces d'inertie des points aux forces agissantes
.(k
= 1,…,n) Si on ajoute les forces d'inertie des points aux forces agissantes  , alors, selon le principe de d’Alembert, le système de forces résultant sera en équilibre et, par conséquent, l’expression écrite sur la base du principe des déplacements possibles (3.44) est valable :
, alors, selon le principe de d’Alembert, le système de forces résultant sera en équilibre et, par conséquent, l’expression écrite sur la base du principe des déplacements possibles (3.44) est valable :

 .
(3.46)
.
(3.46)
Si toutes les connexions sont idéales, alors la 2ème somme est égale à zéro et dans les projections sur les axes de coordonnées, l'égalité (3.46) ressemblera à ceci :
La dernière égalité est une équation variationnelle générale de la dynamique en projections sur les axes de coordonnées, qui permet de composer des équations différentielles du mouvement d'un système mécanique.
L'équation variationnelle générale de la dynamique est une expression mathématique principe d'Alembert-Lagrange: « Lorsqu'un système se déplace, soumis à des connexions stationnaires, idéales et restrictives, à un instant donné, la somme des travaux élémentaires de toutes les forces actives appliquées au système et des forces d'inertie sur tout mouvement possible du système est nulle.».
Exemple 2 . Pour un système mécanique (Fig. 3.4) composé de trois corps, déterminer l'accélération de la charge 1 et la tension du câble 1-2 si : m 1 = 5m; m 2 = 4m; m 3 = 8m; r 2 = 0,5R. 2 ; rayon de giration du bloc 2 je = 1,5r 2. Le rouleau 3 est un disque homogène continu.

Solution
Décrivons les forces qui effectuent un travail élémentaire sur déménagement possible s charge 1 :
Notons les mouvements possibles de tous les corps à travers le mouvement possible de la charge 1 :
Exprimons les accélérations linéaires et angulaires de tous les corps à travers l'accélération souhaitée de la charge 1 (les relations sont les mêmes que dans le cas des déplacements possibles) :
 .
.
L’équation variationnelle générale pour ce problème a la forme :
En remplaçant les expressions obtenues précédemment pour les forces actives, les forces d'inertie et les déplacements possibles, après de simples transformations, nous obtenons
Depuis s 0, donc l'expression entre parenthèses contenant l'accélération est égale à zéro UN 1 , où un 1 = 5g/8,25 = 0,606g.
Pour déterminer la tension du câble retenant la charge, nous libérons la charge du câble, en remplaçant son action par la réaction souhaitée  . Sous l'influence de forces données
. Sous l'influence de forces données  ,
, et la force d'inertie appliquée à la charge
et la force d'inertie appliquée à la charge  il est en équilibre. Par conséquent, le principe de d’Alembert est applicable à la charge (point) en question, c’est-à-dire écrivons ça
il est en équilibre. Par conséquent, le principe de d’Alembert est applicable à la charge (point) en question, c’est-à-dire écrivons ça  . D'ici
. D'ici  .
.
3.8.4. Équation de Lagrange du 2ème type
Coordonnées généralisées et vitesses généralisées. Tous les paramètres mutuellement indépendants qui déterminent de manière unique la position d'un système mécanique dans l'espace sont appelés coordonnées généralisées . Ces coordonnées, notées q 1 ,....q je peux avoir n'importe quelle dimension. En particulier, les coordonnées généralisées peuvent être des déplacements ou des angles de rotation.
Pour les systèmes considérés, le nombre de coordonnées généralisées est égal au nombre de degrés de liberté. Position de chaque point du système  est une fonction à valeur unique de coordonnées généralisées
est une fonction à valeur unique de coordonnées généralisées

Ainsi, le mouvement du système en coordonnées généralisées est déterminé par les dépendances suivantes :
Les dérivées premières des coordonnées généralisées sont appelées vitesses généralisées
:
 .
.
Forces généralisées. Expression du travail de force élémentaire  sur un éventuel déménagement
sur un éventuel déménagement  a la forme :
a la forme :
 .
.
Pour le fonctionnement élémentaire du système de forces, on écrit

En utilisant les dépendances obtenues, cette expression peut s’écrire :
 ,
,
où est la force généralisée correspondant à je la coordonnée généralisée,

 .
(3.49)
.
(3.49)
Ainsi,
force généralisée correspondant jeème coordonnée généralisée, est le coefficient de variation de cette coordonnée dans l'expression de la somme des travaux élémentaires des forces actives sur le déplacement possible du système .
Pour calculer la force généralisée, il faut informer le système des déplacements possibles, au cours desquels seule la coordonnée généralisée change q je. Coefficient à  et sera la force généralisée souhaitée.
et sera la force généralisée souhaitée.
Équations de mouvement d'un système en coordonnées généralisées.
Donnons-nous un système mécanique avec s degrés de liberté. Connaissant les forces agissant sur lui, il est nécessaire d'établir des équations différentielles du mouvement en coordonnées généralisées  . Appliquons la procédure de composition des équations différentielles du mouvement du système - équations de Lagrange du 2ème type - par analogie avec la dérivation de ces équations pour un point matériel libre. En nous basant sur la 2ème loi de Newton, nous écrivons
. Appliquons la procédure de composition des équations différentielles du mouvement du système - équations de Lagrange du 2ème type - par analogie avec la dérivation de ces équations pour un point matériel libre. En nous basant sur la 2ème loi de Newton, nous écrivons
Obtenons un analogue de ces équations en utilisant la notation pour énergie cinétique point matériel,

Dérivée partielle de l'énergie cinétique par rapport à la projection de la vitesse sur l'axe  égal à la projection de la quantité de mouvement sur cet axe, c'est-à-dire
égal à la projection de la quantité de mouvement sur cet axe, c'est-à-dire

Pour obtenir les équations nécessaires, on calcule les dérivées par rapport au temps :

Le système d'équations résultant est les équations de Lagrange du 2ème type pour un point matériel.
Pour un système mécanique, nous présentons les équations de Lagrange du 2ème type sous forme d'équations dans lesquelles au lieu de projections de forces actives P. X , P. oui , P. z utiliser des forces généralisées Q 1 , Q 2 ,...,Q je et prends généralement en compte la dépendance de l'énergie cinétique sur les coordonnées généralisées.
Les équations de Lagrange du 2ème type pour un système mécanique ont la forme :
 .
(3.50)
.
(3.50)
Ils peuvent être utilisés pour étudier le mouvement de tout système mécanique avec des contraintes géométriques, idéales et restrictives.
Exemple 3 . Pour un système mécanique (Fig. 3.5), dont les données sont données dans l'exemple précédent, créer une équation différentielle du mouvement en utilisant l'équation de Lagrange du 2ème type,

Solution
Un système mécanique possède un degré de liberté. Prenons le mouvement linéaire de la charge comme coordonnée généralisée q 1 = s; vitesse généralisée –  . En tenant compte de cela, nous écrivons l'équation de Lagrange du 2ème type
. En tenant compte de cela, nous écrivons l'équation de Lagrange du 2ème type
 .
.
Créons une expression pour l'énergie cinétique du système
 .
.

Exprimons tous les angles et vitesses linéaires via vitesse généralisée :

Maintenant nous obtenons
Calculons la force généralisée en composant une expression pour le travail élémentaire sur le déplacement possible s tout le monde forces actives. Sans tenir compte des forces de frottement, le travail dans le système est effectué uniquement par la force de gravité de la charge 1  Écrivons la force généralisée en s, comme coefficient dans le travail élémentaire Q 1
=
5mg. Nous trouverons ensuite
Écrivons la force généralisée en s, comme coefficient dans le travail élémentaire Q 1
=
5mg. Nous trouverons ensuite
Finalement, l'équation différentielle du mouvement du système aura la forme : 
Lorsqu'un point matériel se déplace, son accélération à chaque instant est telle que les forces données (actives) appliquées au point, les réactions des connexions et la force fictive d'Alembert Ф = - м forment un système de forces équilibré.
Preuve. Considérons le mouvement d'un point matériel non libre de masse T dans un référentiel inertiel. Selon la loi fondamentale de la dynamique et le principe de libération des connexions, nous avons :
où F est la résultante des forces (actives) données ; N est la résultante des réactions de toutes les liaisons imposées sur le point.
Il est facile de transformer (13.1) sous la forme :
Vecteur Ф = - que appelée force d'inertie de d'Alembert, force d'inertie ou simplement Le pouvoir de D'Alembert. Ci-dessous, nous utiliserons uniquement le dernier terme.
L'équation (13.3), exprimant le principe de d'Alembert sous forme symbolique, s'appelle équation kinétostatique point matériel.
Il est facile d'obtenir une généralisation du principe de d'Alembert pour un système mécanique (système P. points matériels).
Pour tout le monde Àème point du système mécanique, l'égalité (13.3) est satisfaite :
Où ? À - résultante de forces (actives) données agissant sur À le point; N À - résultant des réactions des obligations imposées à k-ième indiquer; F k = - donc k- Le pouvoir de D'Alembert À le point.
Il est évident que si les conditions d'équilibre (13.4) sont satisfaites pour chaque triplet de forces F*, N* : , Ф* (À = 1,. .., P.), puis tout le système 3 P. force
est équilibré.
Par conséquent, lorsqu'un système mécanique se déplace à chaque instant du temps, les forces actives qui lui sont appliquées, les réactions de liaisons et les forces de D'Alembert des points du système forment un système de forces équilibré.
Les forces du système (13.5) ne convergent plus, donc, comme le sait la statique (section 3.4), les conditions nécessaires et suffisantes pour son équilibre ont la forme suivante :

Les équations (13.6) sont appelées équations kinétostatiques d'un système mécanique. Pour les calculs, des projections de ces équations vectorielles sur des axes passant par le point de moment sont utilisées À PROPOS DE.
Remarque 1. Puisque la somme de toutes les forces internes du système, ainsi que la somme de leurs moments par rapport à n'importe quel point, sont égales à zéro, alors dans les équations (13.6) il suffit de prendre en compte uniquement les réactions externe Connexions.
Les équations kinétostatiques (13.6) sont habituellement utilisées pour déterminer les réactions des connexions d'un système mécanique lorsque le mouvement du système est donné, et donc les accélérations des points du système et les forces de D'Alembert qui en dépendent sont connu.

Exemple 1. Trouver des réactions d'assistance UN Et DANS arbre lorsqu'il tourne uniformément à une fréquence de 5000 tr/min.
Les masses ponctuelles sont reliées rigidement à l'arbre généraliste= 0,1 kg, t 2 = 0,2 kg. Tailles connues CA - CD - DB = 0,4 m, h= 0,01 m. La masse du puits est considérée comme négligeable.

Solution. Pour utiliser le principe de D'Alembert pour un système mécanique constitué de deux masses ponctuelles, nous indiquons dans le diagramme (Fig. 13.2) les forces données (forces de gravité) Gi, G 2, réactions de liaison N4, N# et forces de D'Alembert Ф |, F 2.
Les directions des forces de D'Alambsrov sont opposées aux accélérations des masses ponctuelles T b t 2u qui décrivent uniformément des cercles de rayon h autour de l'axe UN B arbre
On retrouve les grandeurs de gravité et les forces de Dalambrov :
Ici la vitesse angulaire de l'arbre co- 5000* l/30 = 523,6 s Projection des équations kinétostatiques (13.6) sur des axes cartésiens Ah, oui, Az, on obtient les conditions d'équilibre système plat forces parallèles Gi, G 2, 1Chd, N tf, Фь Ф 2 :

A partir du moment où l'on trouve l'équation N dans = - + - 1 - - - 2 --- =
(0,98 + 274) 0,4 - (548 -1,96) 0,8 w „
272 N, et de l'équation de projection sur
axe Oui : Nune = -N B +G,+G 2 +F,-F 2 = 272 + 0,98 +1,96 + 274-548 =0,06 N.
Les équations kinétostatiques (13.6) peuvent également être utilisées pour obtenir des équations différentielles du mouvement du système, si elles sont composées de telle manière que les réactions de contrainte soient exclues et, par conséquent, il devient possible d'obtenir la dépendance des accélérations sur des valeurs données. les forces.
Dans les cours précédents, les méthodes de résolution de problèmes de dynamique basées sur les lois de Newton ont été discutées. En mécanique théorique, d'autres méthodes ont été développées pour résoudre des problèmes dynamiques, basées sur d'autres points de départ, appelés principes de la mécanique.
Le plus important des principes de la mécanique est le principe de D'Alembert. La méthode kinétostatique est étroitement liée au principe de d'Alembert - une méthode de résolution de problèmes de dynamique dans laquelle les équations dynamiques sont écrites sous la forme d'équations d'équilibre. La méthode kinétostatique est largement utilisée dans des disciplines d'ingénierie générales telles que la résistance des matériaux, la théorie des mécanismes et des machines, ainsi que dans d'autres domaines de la mécanique appliquée. Le principe de D'Alembert est également utilisé efficacement au sein même de la mécanique théorique, où ils ont été créés avec son aide. moyens efficaces résoudre des problèmes de dynamique.
Le principe de D'Alembert pour un point matériel
Supposons qu'un point de masse matériel effectue un mouvement non libre par rapport à système inertiel coordonne Oxyz sous l'action de la force active et de la réaction de la liaison R (Fig. 57).

Définissons le vecteur
![]()
numériquement égal au produit de la masse d'un point et de son accélération et dirigé à l'opposé du vecteur accélération. Un vecteur a la dimension d'une force et est appelé force d'inertie (D'Alembert) d'un point matériel.
Le principe de D’Alembert pour un point matériel se résume à l’énoncé suivant : si l’on ajoute conditionnellement la force d’inertie du point aux forces agissant sur le point matériel, on obtient un système de forces équilibré, c’est-à-dire
![]()
Rappelant de la statique la condition d’équilibre des forces convergentes, le principe de d’Alembert peut aussi s’écrire sous la forme suivante :
![]()
Il est facile de voir que le principe de D'Alembert est équivalent à l'équation de base de la dynamique, et vice versa, de l'équation de base de la dynamique découle le principe de D'Alembert. En effet, en transférant le vecteur de la dernière égalité vers l'autre partie de l'égalité et en le remplaçant par , on obtient l'équation de base de la dynamique. Au contraire, en déplaçant le terme m dans l’équation principale de la dynamique du côté des forces et en utilisant la notation , on obtient une notation du principe de d’Alembert.
Le principe de D'Alembert pour un point matériel, étant tout à fait équivalent à la loi fondamentale de la dynamique, exprime cette loi sous une forme complètement différente - sous la forme d'une équation de la statique. Cela permet d'utiliser des méthodes statiques lors de la composition d'équations dynamiques, appelées méthode kinétostatique.
La méthode kinétostatique est particulièrement pratique pour résoudre le premier problème de dynamique.
Exemple. Du point le plus élevé d'un dôme sphérique lisse de rayon R, un point matériel M de masse de masse négligeable glisse vitesse initiale(Fig. 58). Déterminez où la pointe quittera le dôme.

Solution. Le point se déplacera le long de l’arc d’un méridien. Supposons qu'à un moment donné (actuel), le rayon OM fasse un angle avec la verticale. En développant l'accélération du point a en tangente ) et normale, nous représentons également la force d'inertie du point comme la somme de deux composantes :
![]()
La composante tangentielle de la force d'inertie a un module et est dirigée à l'opposé de l'accélération tangentielle, la composante normale a un module et est dirigée à l'opposé de l'accélération normale.
En ajoutant ces forces à la force active et à la réaction du dôme N agissant réellement sur la pointe, nous composons l'équation kinétostatique
Définition 1
Le principe de D'Alembert est l'un des principes fondamentaux de la dynamique en mécanique théorique. Selon ce principe, à condition d'ajouter la force d'inertie aux forces agissant activement sur les points d'un système mécanique et aux réactions des liaisons superposées, on obtient un système équilibré.
Ce principe doit son nom au scientifique français J. d'Alembert, qui a proposé pour la première fois sa formulation dans son ouvrage « Dynamics ».
Définition du principe de d'Alembert
Note 1
Le principe de D'Alembert est le suivant : si une force d'inertie supplémentaire est appliquée à la force active agissant sur le corps, le corps restera dans un état d'équilibre. Dans ce cas, la valeur totale de toutes les forces agissant dans le système, complétée par le vecteur d'inertie, recevra une valeur nulle.
Selon ce principe, pour chaque i-ième point du système, l'égalité devient vraie :
$F_i+N_i+J_i=0$, où :
- $F_i$ est la force agissant activement sur ce point,
- $N_i$ - réaction de la connexion imposée au point ;
- $J_i$ est la force d'inertie, déterminée par la formule $J_i=-m_ia_i$ (elle est dirigée à l'opposé de cette accélération).
En fait, séparément pour chaque point matériel considéré $ma$ est transféré de droite à gauche (deuxième loi de Newton) :
$F=ma$, $F-ma=0$.
$ma$ dans ce cas est appelé force d'inertie de d'Alembert.
Le concept de force d'inertie a été introduit par Newton. Selon le raisonnement du scientifique, si un point se déplace sous l'influence d'une force $F=ma$, le corps (ou le système) devient la source de cette force. Dans ce cas, selon la loi d'égalité d'action et de réaction, le point accéléré influencera le corps en l'accélérant avec une force $Ф=-ma$. Newton a donné à cette force le nom de système d'inertie d'un point.
Les forces $F$ et $Ф$ seront égales et opposées, mais appliquées à différents corps, ce qui exclut leur ajout. La force d'inertie n'affecte pas directement le point, puisqu'elle représente pour lui une force fictive. Dans ce cas, le point resterait au repos si, en plus de la force $F$, le point était également affecté par la force $Ф$.
Note 2
Le principe de D'Alembert permet d'utiliser des méthodes statiques plus simplifiées pour résoudre des problèmes de dynamique, ce qui explique son large application dans la pratique de l'ingénierie. La méthode kinétostatique est basée sur ce principe. Il est particulièrement pratique de l'utiliser pour établir les réactions des connexions dans une situation où la loi du mouvement en cours est connue ou est obtenue en résolvant les équations correspondantes.
Une variante du principe de d’Alembert est le principe d’Hermann-Euler, qui était en fait une forme de ce principe, mais découvert avant la publication des travaux du scientifique en 1743. En même temps, le principe d’Euler n’a pas été considéré par son auteur (contrairement au principe de d’Alembert) comme base pour méthode générale résoudre des problèmes de mouvement de systèmes mécaniques avec connexions. Le principe de D'Alembert est considéré comme plus approprié à utiliser lorsqu'il est nécessaire de déterminer des forces inconnues (pour résoudre le premier problème de dynamique).
Le principe de D'Alembert pour un point matériel
La variété des types de problèmes résolus en mécanique doit être développée techniques efficacesélaboration d'équations de mouvement pour des systèmes mécaniques. L'une de ces méthodes, qui permet de décrire le mouvement de systèmes arbitraires au moyen d'équations, est considérée comme le principe de d'Alembert en mécanique théorique.
En nous basant sur la deuxième loi de la dynamique, pour un point matériel non libre nous écrivons la formule :
$m\bar(a)=\bar(F)+\bar(R)$,
où $R$ représente la réaction de couplage.
En prenant la valeur :
$\bar(Ф)=-m\bar(a)$, où $Ф$ est la force d'inertie, on obtient :
$\bar(F)+\bar(R)+\bar(Ф)=0$
Cette formule est une expression du principe de d'Alembert pour un point matériel, selon lequel, pour un point en mouvement à tout instant, la somme géométrique des forces actives agissant sur lui et de la force d'inertie prend une valeur nulle. Ce principe permet d'écrire des équations statiques pour un point en mouvement.
Le principe de D'Alembert pour un système mécanique
Pour un système mécanique constitué de $n$-points, on peut écrire $n$-équations de la forme :
$\bar(F_i)+ \bar(R_i)+\bar(Ф_i)=0$
En sommant toutes ces équations et en introduisant la notation suivante :
qui sont respectivement les principaux vecteurs des forces extérieures, des réactions de couplage et des forces d'inertie, on obtient :
$\sum(F_i)+\sum(R_i)+\sum(Ф_i)=0$, c'est-à-dire
$FE + R + Ф = 0$
La condition de l'état d'équilibre d'un corps solide est la valeur nulle du vecteur principal et du moment des forces agissantes. Compte tenu de cette position et du théorème de Varignon sur le moment de la résultante, on écrit alors la relation suivante :
$\sum(riF_i)+\sum(riR_i)+\sum(riФ_i) = 0$
Prenons la notation suivante :
$\somme(riF_i)=MOF$
$\somme(riR_i)=MOR$
$\sum(riФ_i)=MOФ$
les principaux moments des forces extérieures, réaction des connexions et forces d'inertie, respectivement.
En conséquence nous obtenons :
$\bar(F^E)+\bar(R)+\bar(Ф)=0$
$\bar(M_0^F)+\bar(M_0^R)+\bar(M_0^Ф)=0$
Ces deux formules sont une expression du principe de d'Alembert pour un système mécanique. A tout moment pour un système mécanique en mouvement, la somme géométrique du vecteur principal des réactions des connexions, des forces externes et des forces d'inertie reçoit une valeur nulle. La somme géométrique des moments principaux des forces d'inertie, des forces externes et des réactions de couplage sera également nulle.
Les formules résultantes sont équations différentielles second ordre en raison de la présence dans chacun d'eux d'une accélération des forces d'inertie (la dérivée seconde de la loi du mouvement d'un point).
Le principe de D'Alembert permet de résoudre des problèmes dynamiques en utilisant des méthodes statiques. Pour un système mécanique, les équations du mouvement peuvent s'écrire sous forme d'équations d'équilibre. A partir de telles équations, il est possible de déterminer des forces inconnues, en particulier les réactions des liaisons (le premier problème de la dynamique).
