Las propiedades de la función son el valor mayor y menor. Cómo encontrar el valor más pequeño de una función

Y para resolverlo, necesitas un conocimiento mínimo del tema. El próximo año académico está terminando, todos quieren irse de vacaciones, y para acercar este momento, inmediatamente me pongo manos a la obra:

Comencemos con el área. El área a que se refiere la condición es limitado cerrado conjunto de puntos en el plano. Por ejemplo, un conjunto de puntos delimitados por un triángulo, incluido el triángulo ENTERO (si de fronteras"Asomar" al menos un punto, entonces el área ya no estará cerrada). En la práctica, también hay áreas de forma rectangular, redonda y un poco más formas complejas. Cabe señalar que en teoría Análisis matemático se dan definiciones estrictas limitaciones, aislamiento, fronteras, etc., pero creo que todo el mundo es consciente de estos conceptos en un nivel intuitivo, y no se necesita más ahora.

El área plana se denota estándar con la letra y, como regla, se da analíticamente, mediante varias ecuaciones. (no necesariamente lineal); menos a menudo las desigualdades. Una rotación verbal típica: "área cerrada limitada por líneas".

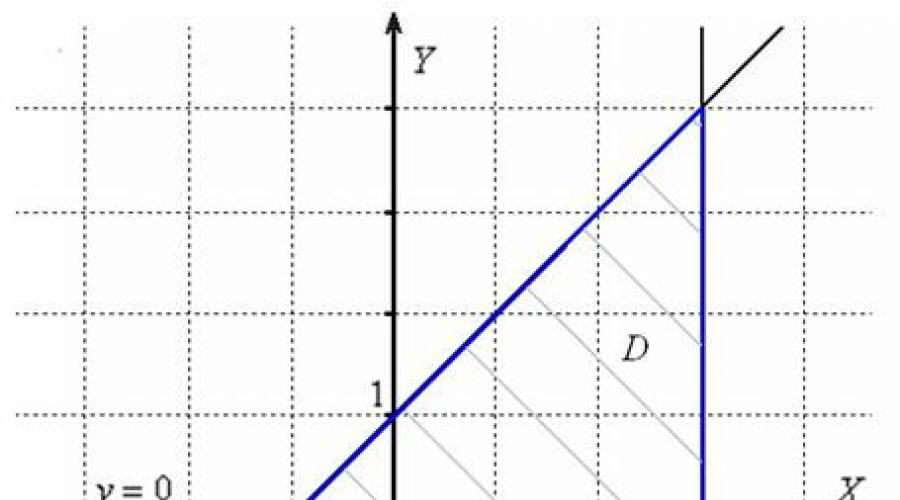
Una parte integral de la tarea en consideración es la construcción del área en el dibujo. ¿Cómo hacerlo? Es necesario dibujar todas las líneas enumeradas (en este caso 3 derecho) y analizar lo sucedido. El área deseada generalmente está ligeramente sombreada y su borde está resaltado con una línea en negrita:


Se puede establecer la misma área desigualdades lineales: , que por alguna razón se escriben más a menudo como una lista de enumeración, y no sistema.
Dado que el límite pertenece a la región, entonces todas las desigualdades, por supuesto, no estricto.

Y ahora el quid de la cuestión. Imagina que el eje va directo hacia ti desde el origen de coordenadas. Considere una función que continuo en cada punto de área. La gráfica de esta función es superficie, y la pequeña felicidad es que para resolver el problema de hoy, no necesitamos saber cómo es esta superficie en absoluto. Se puede ubicar arriba, abajo, cruzar el plano; todo esto no es importante. Y lo siguiente es importante: según Teoremas de Weierstrass, continuo en cerrado limitadoárea, la función alcanza su máximo (del "alto") y menos (de los "más bajos") valores a encontrar. Estos valores se consiguen o en puntos estacionarios, perteneciente a la regiónD , o en los puntos que se encuentran en el límite de esta región. De lo cual se sigue un algoritmo de solución simple y transparente:

Ejemplo 1

En un área cerrada limitada

Decisión: En primer lugar, debe representar el área en el dibujo. Desafortunadamente, es técnicamente difícil para mí hacer un modelo interactivo del problema y, por lo tanto, daré inmediatamente la ilustración final, que muestra todos los puntos "sospechosos" encontrados durante el estudio. Por lo general, se colocan uno tras otro a medida que se encuentran:

Con base en el preámbulo, la decisión se puede dividir convenientemente en dos puntos:

I) Busquemos puntos estacionarios. Esta es una acción estándar que hemos realizado repetidamente en la lección. sobre los extremos de varias variables:

Punto estacionario encontrado perteneceáreas: (márcalo en el dibujo), lo que significa que debemos calcular el valor de la función en un punto dado:

- como en el artículo Los valores mayor y menor de una función en un segmento, resaltaré los resultados importantes en negrita. En un cuaderno, es conveniente rodearlos con un lápiz.

Preste atención a nuestra segunda felicidad: no tiene sentido verificar condición suficiente para un extremo. ¿Por qué? Incluso si en el punto que alcanza la función, por ejemplo, mínimo local, entonces esto NO SIGNIFICA que el valor resultante será mínimo en toda la región (ver el principio de la lección sobre los extremos incondicionales) .

¿Qué pasa si el punto estacionario NO pertenece al área? ¡Casi nada! Cabe señalar que y pasar al siguiente párrafo.

II) Investigamos la frontera de la región.

Dado que el borde está formado por los lados de un triángulo, es conveniente dividir el estudio en 3 subpárrafos. Pero es mejor hacerlo no de todos modos. Desde mi punto de vista, es más ventajoso considerar primero segmentos paralelos a ejes de coordenadas, y, en primer lugar, los mismos que yacen en las hachas. Para captar toda la secuencia y la lógica de las acciones, intente estudiar el final "de una vez":

1) Tratemos con el lado inferior del triángulo. Para hacer esto, sustituimos directamente en la función:

Alternativamente, puedes hacerlo así:

Geométricamente, esto significa que el plano de coordenadas (que también viene dada por la ecuación)"cortar" de superficies parábola "espacial", cuya parte superior cae inmediatamente bajo sospecha. Vamos a averiguar donde esta ella:

- el valor resultante "golpea" en el área, y bien puede ser que en el punto (marca en el dibujo) la función alcanza el valor más grande o más pequeño en toda el área. De todos modos, hagamos los cálculos:

Otros "candidatos" son, por supuesto, los extremos del segmento. Calcular los valores de la función en los puntos (marca en el dibujo):

Aquí, por cierto, puede realizar una mini-comprobación oral en la versión "reducida":

2) Para estudiar el lado derecho del triángulo, lo sustituimos en la función y “ordenamos ahí”:

Aquí realizamos inmediatamente una verificación aproximada, "sonando" el final del segmento ya procesado:
, Perfecto.

La situación geométrica está relacionada con el punto anterior:

- el valor resultante también "entró en el ámbito de nuestros intereses", lo que significa que necesitamos calcular a qué es igual la función en el punto que ha aparecido:

Examinemos el segundo extremo del segmento:

Usando la función , vamos a revisar:

3) Probablemente todos saben cómo explorar el lado restante. Sustituimos en la función y hacemos simplificaciones:

Finales de línea ya se han investigado, pero en el borrador aún verificamos si encontramos la función correctamente :
– coincidió con el resultado del primer párrafo;
– coincidió con el resultado del segundo párrafo.

Queda por saber si hay algo interesante dentro del segmento:

- ¡hay! Sustituyendo una línea recta en la ecuación, obtenemos la ordenada de este "interés":

Marcamos un punto en el dibujo y encontramos el valor correspondiente de la función:

Controlemos los cálculos según la versión "presupuestaria" :
, pedido.

Y el paso final: Mire CUIDADOSAMENTE todos los números "gordos", recomiendo incluso a los principiantes que hagan una sola lista:

de donde elegimos los valores mayor y menor. Responder escribir en el estilo del problema de encontrar los valores mayor y menor de la función en el segmento:

Vuelvo a comentar por si acaso. sentido geométrico resultado:
– aquí está el punto más alto de la superficie en la región;
- aquí está el punto más bajo de la superficie en el área.

En el problema analizado, encontramos 7 puntos “sospechosos”, pero su número varía de una tarea a otra. Para una región triangular, el "conjunto de exploración" mínimo consiste en Tres puntos. Esto sucede cuando la función, por ejemplo, establece avión- está bastante claro que no hay puntos estacionarios, y la función puede alcanzar los valores máximos / mínimos solo en los vértices del triángulo. Pero no hay tales ejemplos una vez, dos veces; por lo general, tiene que lidiar con algún tipo de superficie de segundo orden.

Si resuelve un poco esas tareas, entonces los triángulos pueden hacer que su cabeza dé vueltas y, por lo tanto, lo he preparado para usted. ejemplos inusuales para hacerlo cuadrado :)

Ejemplo 2

Encuentra los valores mayor y menor de una función en un área cerrada delimitada por líneas

Ejemplo 3

Encuentra los valores mayor y menor de una función en un área cerrada acotada.

Atención especial preste atención al orden racional y la técnica de estudiar el límite del área, así como a la cadena de controles intermedios, que evitarán casi por completo los errores de cálculo. En términos generales, puede resolverlo como desee, pero en algunos problemas, por ejemplo, en el mismo Ejemplo 2, existe la posibilidad de complicar significativamente su vida. Muestra Muestra terminar las tareas al final de la lección.

Sistematizamos el algoritmo de solución, de lo contrario, con mi diligencia de araña, de alguna manera se perdió en un largo hilo de comentarios del 1er ejemplo:

- En el primer paso, construimos un área, es deseable sombrearla y resaltar el borde con una línea en negrita. Durante la solución, aparecerán puntos que deben colocarse en el dibujo.

– Encuentra puntos estacionarios y calcula los valores de la función solo en esos, que pertenecen a la zona . Los valores obtenidos se resaltan en el texto (por ejemplo, en un círculo con un lápiz). Si el punto estacionario NO pertenece al área, entonces marcamos este hecho con un icono o verbalmente. Si no hay ningún punto estacionario, entonces sacamos una conclusión por escrito de que están ausentes. En cualquier caso, ¡este elemento no se puede omitir!

– Exploración de la zona fronteriza. Primero, es ventajoso tratar con líneas rectas que son paralelas a los ejes de coordenadas (si hay alguno). También se resaltan los valores de función calculados en puntos "sospechosos". Mucho se ha dicho sobre la técnica de solución anterior y algo más se dirá a continuación: ¡lea, relea, profundice!

- De los números seleccionados, seleccione los valores más grandes y más pequeños y dé una respuesta. A veces sucede que la función alcanza tales valores en varios puntos a la vez; en este caso, todos estos puntos deberían reflejarse en la respuesta. Deje, por ejemplo, y resultó que valor más pequeño. Entonces escribimos que

Los ejemplos finales están dedicados a otros. ideas útilesútil en la práctica:

Ejemplo 4

Encuentra los valores mayor y menor de una función en un área cerrada .

He mantenido la formulación del autor, en la que el área se da como una doble desigualdad. Esta condición se puede escribir en un sistema equivalente o en una forma más tradicional para este problema:

te recuerdo que con no lineal encontramos desigualdades en , y si no comprende el significado geométrico de la entrada, no se demore y aclare la situación ahora mismo ;-)

Decisión, como siempre, comienza con la construcción del área, que es una especie de "suela":

Hmm, a veces hay que roer no solo el granito de la ciencia ...

I) Encontrar puntos estacionarios:

El sistema de sueños del idiota :)

El punto estacionario pertenece a la región, es decir, se encuentra en su límite.

Y así, no es nada... fue una lección divertida: eso es lo que significa beber el té correcto =)

II) Investigamos la frontera de la región. Sin más preámbulos, comencemos con el eje x:

1) Si , entonces

Encuentra dónde está la parte superior de la parábola:
- Aprecie esos momentos - "golpee" justo en el punto, desde el cual todo ya está claro. Pero no olvides revisar:

Calculemos los valores de la función en los extremos del segmento:

2) C abajo Averigüemos las "suelas" "de una vez": sin complejos, las sustituimos en la función, además, solo nos interesará el segmento:

El control:

Ahora bien, esto ya está reviviendo el monótono viaje en una pista con estrías. Encontremos los puntos críticos:

Nosotros decidimos ecuación cuadrática¿Recuerdas esto? ... Sin embargo, recuerda, por supuesto, de lo contrario no leerías estas líneas =) Si en los dos ejemplos anteriores los cálculos fueran convenientes en fracciones decimales(que, por cierto, es raro), entonces aquí estamos esperando lo habitual fracciones comunes. Encontramos las raíces "x" y, usando la ecuación, determinamos las coordenadas correspondientes del "juego" de los puntos "candidatos":


Calculemos los valores de la función en los puntos encontrados:

Compruebe la función usted mismo.

Ahora estudiamos cuidadosamente los trofeos ganados y anotamos responder:

¡Aquí están los "candidatos", entonces los "candidatos"!

Para una solución independiente:

Ejemplo 5

Encuentra los valores más pequeños y más grandes de una función en un área cerrada

Una entrada con llaves se lee así: “un conjunto de puntos tal que”.

A veces, en tales ejemplos, usan Método del multiplicador de Lagrange, pero verdadera necesidad es poco probable que se use. Entonces, por ejemplo, si se da una función con la misma área "de", luego de sustituirla, con una derivada sin dificultades; además, todo está trazado en “una línea” (con signos) sin necesidad de considerar los semicírculos superior e inferior por separado. Pero, por supuesto, hay más casos dificiles, donde sin la función de Lagrange (donde , por ejemplo, es la misma ecuación circular) es difícil pasar - ¡qué difícil es pasar sin un buen descanso!

¡Todo lo mejor para pasar la sesión y hasta pronto la próxima temporada!

Soluciones y respuestas:

Ejemplo 2: Decisión: dibuje el área en el dibujo:

A veces, en los problemas B15 hay funciones "malas" para las que es difícil encontrar la derivada. Anteriormente, esto era solo en las pruebas, pero ahora estas tareas son tan comunes que ya no se pueden ignorar al prepararse para este examen.

En este caso, funcionan otros trucos, uno de los cuales es: monótono.

La función f (x) se llama monótonamente creciente en el segmento, si para cualquier punto x 1 y x 2 de este segmento se cumple lo siguiente:

x1< x 2 ⇒ f (x1) < f (x2).

La función f (x) se llama monótonamente decreciente en el segmento si para cualquier punto x 1 y x 2 de este segmento se cumple lo siguiente:

x1< x 2 ⇒ f (x1) > f ( x2).

En otras palabras, para una función creciente, cuanto mayor es x, mayor es f(x). Para una función decreciente, lo contrario es cierto: cuanto más x, más menor f(x).

Por ejemplo, el logaritmo crece monótonamente si la base a > 1 y decrece monótonamente si 0< a < 1. Не забывайте про область valores permitidos logaritmo: x > 0.

f (x) = log a x (a > 0; a ≠ 1; x > 0)

La raíz cuadrada aritmética (y no solo cuadrada) aumenta monótonamente en todo el dominio de definición:

La función exponencial se comporta de manera similar al logaritmo: crece para a > 1 y decrece para 0< a < 1. Но в отличие от логарифма, funcion exponencial definido para todos los números, no solo x > 0:

f (x) = a x (a > 0)

Finalmente, grados con exponente negativo. Puedes escribirlos como una fracción. Tienen un punto de quiebre donde se rompe la monotonía.

Todas estas características nunca se encuentran en forma pura. Se les agregan polinomios, fracciones y otras tonterías, por lo que se vuelve difícil calcular la derivada. Lo que sucede en este caso, ahora lo analizaremos.

Coordenadas del vértice de la parábola

Muy a menudo, el argumento de la función se reemplaza con trinomio cuadrado de la forma y = ax 2 + bx + c . Su gráfica es una parábola estándar, en la que nos interesa:

1. Ramas de parábola: pueden subir (para a > 0) o bajar (a< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. El vértice de una parábola es el punto extremo de una función cuadrática, en el cual esta función toma su menor (para a > 0) o su mayor (a< 0) значение.

De mayor interés es parte superior de una parábola, cuya abscisa se calcula mediante la fórmula:

Entonces, hemos encontrado el punto extremo de la función cuadrática. Pero si la función original es monótona, para ella el punto x 0 será también un punto extremo. Por lo tanto, formulamos la regla clave:

puntos extremos trinomio cuadrado y función compleja, en el que entra, son los mismos. Por lo tanto, puedes buscar x 0 para un trinomio cuadrado y olvidarte de la función.

Del razonamiento anterior, no queda claro qué tipo de punto obtenemos: un máximo o un mínimo. Sin embargo, las tareas están diseñadas específicamente para que no importe. Juzga por ti mismo:

1. No hay ningún segmento en la condición del problema. Por lo tanto, no es necesario calcular f(a) y f(b). Queda por considerar sólo los puntos extremos;
2. Pero solo hay uno de esos puntos: esta es la parte superior de la parábola x 0, cuyas coordenadas se calculan literalmente de forma oral y sin derivadas.

Así, la solución del problema se simplifica enormemente y se reduce a tan solo dos pasos:

1. Escribe la ecuación de la parábola y = ax 2 + bx + c y encuentra su vértice usando la fórmula: x 0 = −b /2a;
2. Encuentra el valor de la función original en este punto: f (x 0). Si no hay condiciones adicionales, esta será la respuesta.

A primera vista, este algoritmo y su justificación pueden parecer complicados. Deliberadamente no publico un esquema de solución "desnudo", ya que la aplicación irreflexiva de tales reglas está plagada de errores.

Consideremos los problemas reales de examen de prueba en matemáticas: aquí es donde esta técnica ocurre con mayor frecuencia. Al mismo tiempo, nos aseguraremos de que de esta manera muchos problemas de B15 se vuelvan casi verbales.

Debajo de la raíz está función cuadrática y \u003d x 2 + 6x + 13. El gráfico de esta función es una parábola con ramas hacia arriba, ya que el coeficiente a \u003d 1\u003e 0.

Parte superior de la parábola:

x 0 \u003d -b / (2a) \u003d -6 / (2 1) \u003d -6 / 2 \u003d -3

Dado que las ramas de la parábola se dirigen hacia arriba, en el punto x 0 \u003d −3, la función y \u003d x 2 + 6x + 13 toma el valor más pequeño.

La raíz es monótonamente creciente, por lo que x 0 es el punto mínimo de toda la función. Tenemos:

Tarea. Encuentre el valor más pequeño de la función:

y = registro 2 (x 2 + 2x + 9)

Debajo del logaritmo hay nuevamente una función cuadrática: y \u003d x 2 + 2x + 9. El gráfico es una parábola con ramas hacia arriba, porque a = 1 > 0.

Parte superior de la parábola:

x 0 \u003d -b / (2a) \u003d -2 / (2 1) \u003d -2/2 \u003d -1

Entonces, en el punto x 0 = −1, la función cuadrática toma el valor más pequeño. Pero la función y = log 2 x es monótona, entonces:

y mín = y (−1) = log 2 ((−1) 2 + 2 (−1) + 9) = ... = log 2 8 = 3

El exponente es una función cuadrática y = 1 − 4x − x 2 . Reescribámoslo en forma normal: y = −x 2 − 4x + 1.

Obviamente, la gráfica de esta función es una parábola, se ramifica hacia abajo (a = −1< 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 (−1)) = 4/(−2) = −2

La función original es exponencial, es monótona, entonces valor más alto estará en el punto encontrado x 0 = −2:

Un lector atento seguramente notará que no escribimos el área de valores permisibles de la raíz y el logaritmo. Pero esto no era obligatorio: dentro hay funciones cuyos valores son siempre positivos.

Consecuencias del alcance de una función

A veces, para resolver el problema B15, no basta con encontrar el vértice de la parábola. El valor deseado puede estar al final del segmento, pero no en el punto extremo. Si la tarea no especifica un segmento en absoluto, mire rango de tolerancia función original. A saber:

Presta atención de nuevo: el cero bien puede estar debajo de la raíz, pero nunca en el logaritmo o denominador de una fracción. Veamos cómo funciona con ejemplos específicos:

Tarea. Encuentre el mayor valor de la función:

Debajo de la raíz hay nuevamente una función cuadrática: y \u003d 3 - 2x - x 2. Su gráfica es una parábola, pero se ramifica hacia abajo ya que a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический Raíz cuadrada de un número negativo no existe.

Escribimos el área de valores permisibles (ODZ):

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; uno]

Ahora encuentra el vértice de la parábola:

x 0 = −b /(2a ) = −(−2)/(2 (−1)) = 2/(−2) = −1

El punto x 0 = −1 pertenece al segmento ODZ, y esto es bueno. Ahora consideramos el valor de la función en el punto x 0, así como en los extremos de la ODZ:

y(−3) = y(1) = 0

Entonces, obtuvimos los números 2 y 0. Se nos pide que encontremos el más grande: este es el número 2.

Tarea. Encuentre el valor más pequeño de la función:

y = registro 0,5 (6x - x 2 - 5)

Dentro del logaritmo hay una función cuadrática y = 6x − x 2 − 5. Esta es una parábola con ramas hacia abajo, pero en el logaritmo no puede ser números negativos, entonces escribimos la ODZ:

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Tenga en cuenta: la desigualdad es estricta, por lo que los extremos no pertenecen a la ODZ. De esta forma, el logaritmo se diferencia de la raíz, donde los extremos del segmento nos vienen bastante bien.

Buscando el vértice de la parábola:

x 0 = −b /(2a ) = −6/(2 (−1)) = −6/(−2) = 3

La parte superior de la parábola se ajusta a lo largo de la ODZ: x 0 = 3 ∈ (1; 5). Pero como los extremos del segmento no nos interesan, consideramos el valor de la función solo en el punto x 0:

y mín = y (3) = log 0,5 (6 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2

Con punto práctico De mayor interés es el uso de la derivada para encontrar los valores mayor y menor de una función. ¿Con qué está conectado? Maximizar beneficios, minimizar costes, determinar la carga óptima de los equipos... En otras palabras, en muchos ámbitos de la vida hay que resolver el problema de optimizar algunos parámetros. Y este es el problema de encontrar los valores mayor y menor de la función.

Cabe señalar que el valor mayor y menor de una función generalmente se busca en algún intervalo X, que es todo el dominio de la función o parte del dominio. El intervalo X en sí mismo puede ser un segmento de línea, un intervalo abierto , un intervalo infinito .

En este artículo, hablaremos sobre cómo encontrar los valores más grandes y más pequeños de manera explícita. función dada una variable y=f(x) .

Navegación de página.

El valor más grande y más pequeño de una función: definiciones, ilustraciones.

Detengámonos brevemente en las principales definiciones.

El mayor valor de la función. , que para cualquier la desigualdad es verdadera.

El valor más pequeño de la función. y=f(x) en el intervalo X se llama tal valor , que para cualquier la desigualdad es verdadera.

Estas definiciones son intuitivas: el valor mayor (menor) de una función es el valor mayor (menor) aceptado en el intervalo considerado con la abscisa.

Puntos estacionarios son los valores del argumento en los que se anula la derivada de la función.

¿Por qué necesitamos puntos estacionarios al encontrar los valores más grandes y más pequeños? La respuesta a esta pregunta viene dada por el teorema de Fermat. De este teorema se sigue que si una función diferenciable tiene un extremo (mínimo local o máximo local) en algún punto, entonces ese punto es estacionario. Por lo tanto, la función a menudo toma su valor máximo (menor) en el intervalo X en uno de los puntos estacionarios de este intervalo.

Además, una función a menudo puede tomar los valores más grandes y más pequeños en los puntos donde la primera derivada de esta función no existe y la función en sí está definida.

Respondamos de inmediato una de las preguntas más comunes sobre este tema: "¿Siempre es posible determinar el valor más grande (más pequeño) de una función"? No, no siempre. A veces los límites del intervalo X coinciden con los límites del dominio de la función, o el intervalo X es infinito. Y algunas funciones en el infinito y en los límites del dominio de definición pueden tomar valores infinitamente grandes e infinitamente pequeños. En estos casos, no se puede decir nada sobre el valor mayor y menor de la función.

Para mayor claridad, damos una ilustración gráfica. Mire las imágenes, y mucho se aclarará.

en el segmento

En la primera figura, la función toma los valores mayor (max y ) y menor (min y ) en puntos estacionarios dentro del segmento [-6;6] .

Considere el caso que se muestra en la segunda figura. Cambia el segmento a . En este ejemplo, el valor más pequeño de la función se logra en un punto estacionario y el más grande, en un punto con una abscisa que corresponde al límite derecho del intervalo.

En la figura No. 3, los puntos límite del segmento [-3; 2] son ​​las abscisas de los puntos correspondientes al mayor y menor valor de la función.

en el campo abierto

En la cuarta figura, la función toma los valores mayor (max y ) y menor (min y ) en puntos estacionarios dentro del intervalo abierto (-6;6).

En el intervalo , no se pueden sacar conclusiones sobre el valor más grande.

en el infinito

En el ejemplo que se muestra en la séptima figura, la función toma el valor más grande (max y ) en un punto estacionario con la abscisa x=1, y el valor más pequeño (min y ) se alcanza en el límite derecho del intervalo. En menos infinito, los valores de la función se aproximan asintóticamente a y=3.

En el intervalo, la función no alcanza ni el valor más pequeño ni el más grande. Como x=2 tiende a la derecha, los valores de la función tienden a menos infinito (la recta x=2 es una asíntota vertical), y como la abscisa tiende a más infinito, los valores de la función tienden asintóticamente a y=3 . En la Figura 8 se muestra una ilustración gráfica de este ejemplo.

Algoritmo para encontrar los valores mayor y menor de una función continua sobre el segmento.

Escribimos un algoritmo que nos permite encontrar el valor más grande y más pequeño de una función en un segmento.

1. Encontramos el dominio de la función y verificamos si contiene el segmento completo.
2. Encontramos todos los puntos en los que no existe la primera derivada y que están contenidos en el segmento (por lo general tales puntos ocurren en funciones con un argumento bajo el signo del módulo y en funciones de poder con un exponente racional fraccionario). Si no hay tales puntos, entonces vaya al siguiente punto.
3. Determinamos todos los puntos estacionarios que caen en el segmento. Para ello, lo igualamos a cero, resolvemos la ecuación resultante y elegimos las raíces adecuadas. Si no hay puntos estacionarios o ninguno de ellos cae en el segmento, vaya al siguiente paso.
4. Calculamos los valores de la función en los puntos estacionarios seleccionados (si los hay), en los puntos donde no existe la primera derivada (si los hay), y también en x=a y x=b.
5. De los valores obtenidos de la función, seleccionamos el más grande y el más pequeño; serán los valores máximo y más pequeño deseados de la función, respectivamente.

Analicemos el algoritmo al resolver un ejemplo para encontrar los valores más grandes y más pequeños de una función en un segmento.

Ejemplo.

Encuentra el valor mayor y menor de una función

• en el segmento;
• en el intervalo [-4;-1] .

Decisión.

El dominio de la función es todo el conjunto de los números reales, excepto el cero, es decir, . Ambos segmentos caen dentro del dominio de la definición.

Encontramos la derivada de la función con respecto a:

Obviamente, la derivada de la función existe en todos los puntos de los segmentos y [-4;-1] .

Los puntos estacionarios se determinan a partir de la ecuación. La única raíz real es x=2. Este punto estacionario cae en el primer segmento.

Para el primer caso, calculamos los valores de la función en los extremos del segmento y en un punto estacionario, es decir, para x=1, x=2 y x=4:

Por lo tanto, el mayor valor de la función se alcanza en x=1, y el valor más pequeño – en x=2 .

Para el segundo caso, calculamos los valores de la función solo en los extremos del segmento [-4;-1] (ya que no contiene puntos estacionarios):

Dada una función definida y continua en algún intervalo. Se requiere encontrar el valor más grande (más pequeño) de la función en este intervalo.

Bases teóricas.
Teorema (Segundo Teorema de Weierstrass):

Si una función es definida y continua en un intervalo cerrado, entonces alcanza sus valores máximo y mínimo en este intervalo.

La función puede alcanzar sus valores máximos y mínimos ya sea en los puntos internos del intervalo o en sus límites. Ilustremos todo posibles opciones.

Explicación:
1) La función alcanza su valor máximo en el borde izquierdo del intervalo en el punto , y su valor mínimo en el borde derecho del intervalo en el punto .
2) La función alcanza su valor máximo en el punto (este es el punto máximo), y su valor mínimo en el límite derecho del intervalo en el punto.
3) La función alcanza su valor máximo en el borde izquierdo del intervalo en el punto , y su valor mínimo en el punto (este es el punto mínimo).
4) La función es constante en el intervalo, es decir alcanza sus valores mínimo y máximo en cualquier punto del intervalo, y los valores mínimo y máximo son iguales entre sí.
5) La función alcanza su valor máximo en el punto , y su valor mínimo en el punto (a pesar de que la función tiene un máximo y un mínimo en este intervalo).
6) La función alcanza su valor máximo en un punto (este es el punto máximo), y su valor mínimo en un punto (este es el punto mínimo).
Comentario:

"Máximo" y "valor máximo" son cosas diferentes. Esto se deriva de la definición del máximo y la comprensión intuitiva de la frase "valor máximo".

Algoritmo para resolver el problema 2.



4) Elija de los valores obtenidos el mayor (menor) y anote la respuesta.

Ejemplo 4:

Determinar el valor mayor y menor de una función en el segmento.
Decisión:
1) Encuentra la derivada de la función.

2) Encuentra puntos estacionarios (y puntos que son sospechosos de un extremo) resolviendo la ecuación. Preste atención a los puntos donde no hay derivada finita de dos lados.

3) Calcular los valores de la función en puntos estacionarios y en los límites del intervalo.

4) Elija de los valores obtenidos el mayor (menor) y anote la respuesta.

La función sobre este segmento alcanza su valor máximo en el punto con coordenadas .

La función sobre este segmento alcanza su valor mínimo en el punto con coordenadas .

Puede verificar la exactitud de los cálculos mirando el gráfico de la función en estudio.


Comentario: La función alcanza su valor máximo en el punto máximo y su valor mínimo en el límite del segmento.

Caso especial.

Supongamos que queremos encontrar el máximo y valor mínimo alguna función en el intervalo. Después de la ejecución del primer párrafo del algoritmo, es decir cálculo de la derivada, queda claro que, por ejemplo, toma solo valores negativos en todo el segmento bajo consideración. Recuerda que si la derivada es negativa, entonces la función es decreciente. Encontramos que la función es decreciente en todo el intervalo. Esta situación se muestra en el cuadro N° 1 al inicio del artículo.

La función decrece en el intervalo, es decir no tiene puntos extremos. Se puede ver en la imagen que la función tomará el valor más pequeño en el borde derecho del segmento y el valor más grande en el izquierdo. si la derivada en el intervalo es positiva en todas partes, entonces la función es creciente. El valor más pequeño está en el borde izquierdo del segmento, el más grande está a la derecha.

En este artículo hablaré de algoritmo para encontrar el valor mayor y menor función, puntos mínimos y máximos.

Desde la teoría, definitivamente necesitaremos tabla de derivadas y reglas de diferenciación. Todo está en este tablero:

Algoritmo para encontrar los valores mayor y menor.

me resulta mas facil de explicar ejemplo específico. Considerar:

Ejemplo: Encuentra el valor más grande de la función y=x^5+20x^3–65x en el segmento [–4;0].

Paso 1. Tomamos la derivada.

Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Paso 2 Búsqueda de puntos extremos.

punto extremo nombramos aquellos puntos en los que la función alcanza su valor máximo o mínimo.

Para encontrar los puntos extremos, es necesario igualar la derivada de la función a cero (y "= 0)

5x^4 + 60x^2 - 65 = 0

Ahora resolvamos esto ecuación cuadrática y las raíces encontradas son nuestros puntos extremos.

Resuelvo tales ecuaciones reemplazando t = x^2, luego 5t^2 + 60t - 65 = 0.

Reducimos la ecuación por 5, obtenemos: t^2 + 12t - 13 = 0

D = 12^2 - 4*1*(-13) = 196

T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

Hacemos la sustitución inversa x^2 = t:

X_(1 y 2) = ±raíz cuadrada(1) = ±1
x_(3 y 4) = ±sqrt(-13) (excluimos, no puede haber números negativos debajo de la raíz, a menos, por supuesto, que estemos hablando de números complejos)

Total: x_(1) = 1 y x_(2) = -1 - estos son nuestros puntos extremos.

Paso 3 Determinar el valor mayor y menor.

Método de sustitución.

En la condición, nos dieron el segmento [b][–4;0]. El punto x=1 no está incluido en este segmento. Así que no lo consideramos. Pero además del punto x=-1, también debemos considerar los bordes izquierdo y derecho de nuestro segmento, es decir, los puntos -4 y 0. Para hacer esto, sustituimos estos tres puntos en la función original. Observe que el original es el que se da en la condición (y=x^5+20x^3–65x), algunos comienzan a sustituir en la derivada...

Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

Esto significa que el valor máximo de la función es [b]44 y se alcanza en los puntos [b]-1, lo que se denomina punto máximo de la función en el segmento [-4; 0].

Decidimos y obtuvimos una respuesta, somos geniales, puedes relajarte. ¡Pero detente! ¿No crees que contar y(-4) es demasiado complicado? En condiciones de tiempo limitado, es mejor usar otro método, lo llamo así:

A través de intervalos de constancia.

Estos huecos se encuentran para la derivada de la función, es decir, para nuestra ecuación bicuadrática.

Lo hago de la siguiente manera. Dibujo una línea direccional. Establecí los puntos: -4, -1, 0, 1. A pesar de que 1 no está incluido en el segmento dado, aún debe tenerse en cuenta para determinar correctamente los intervalos de constancia. Tomemos un número muchas veces mayor que 1, digamos 100, sustituyémoslo mentalmente en nuestra ecuación bicuadrática 5(100)^4 + 60(100)^2 - 65. Incluso sin contar nada, se vuelve obvio que en el punto 100 la función tiene signo más. Esto significa que para los intervalos del 1 al 100 tiene un signo más. Al pasar por 1 (vamos de derecha a izquierda), la función cambiará de signo a menos. Al pasar por el punto 0, la función conservará su signo, ya que este es solo el límite del segmento, y no la raíz de la ecuación. Al pasar por -1, la función volverá a cambiar de signo a más.

De la teoría, sabemos que donde está la derivada de la función (y dibujamos esto para ello) cambia el signo de más a menos (punto -1 en nuestro caso) función alcanza su máximo local (y(-1)=44 como se calculó anteriormente) sobre este segmento (esto es lógicamente muy claro, la función ha dejado de aumentar, ya que alcanzó su máximo y comenzó a disminuir).

En consecuencia, donde la derivada de la función cambia el signo de menos a más, logrado mínimo local de una función. Sí, sí, también encontramos el punto mínimo local, que es 1, y y(1) es el valor mínimo de la función en el intervalo, digamos de -1 a +∞. Tenga en cuenta que esto es solo un MÍNIMO LOCAL, es decir, un mínimo en un segmento determinado. Dado que la función mínima real (global) llegará a algún lugar allí, en -∞.

En mi opinión, el primer método es más simple teóricamente y el segundo es más simple en términos de operaciones aritméticas, pero mucho más difícil en términos teóricos. Después de todo, a veces hay casos en los que la función no cambia de signo al pasar por la raíz de la ecuación, y de hecho puedes confundirte con estos máximos y mínimos locales y globales, aunque tendrás que dominar esto bien de todos modos si planeas. para ingresar a una universidad técnica (y para qué más hacer el examen de perfil y resolver esta tarea). Pero la práctica y sólo la práctica te enseñará cómo resolver esos problemas de una vez por todas. Y puedes entrenar en nuestra web. Aquí .

Si tiene alguna pregunta, o algo no está claro, asegúrese de preguntar. Estaré encantado de responderle y hacer cambios, adiciones al artículo. ¡Recuerde que estamos haciendo este sitio juntos!