Nok 34 and 2 solution. How to find the least common multiple of two numbers

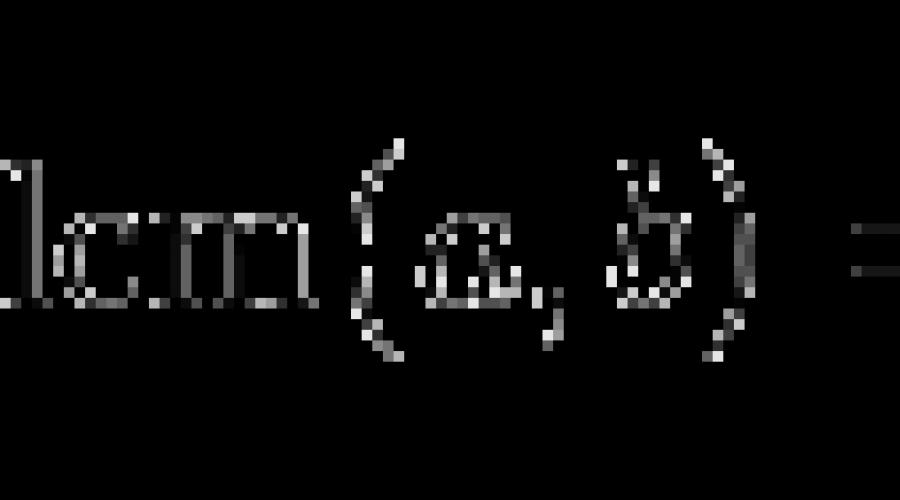
Greatest common divisor and least common multiple are key arithmetic concepts that allow you to operate effortlessly ordinary fractions. LCM and are most often used to find the common denominator of several fractions.

Basic Concepts

The divisor of an integer X is another integer Y by which X is divided without leaving a remainder. For example, the divisor of 4 is 2, and 36 is 4, 6, 9. A multiple of an integer X is a number Y that is divisible by X without a remainder. For example, 3 is a multiple of 15, and 6 is a multiple of 12.

For any pair of numbers we can find their common divisors and multiples. For example, for 6 and 9, the common multiple is 18, and the common divisor is 3. Obviously, pairs can have several divisors and multiples, so the calculations use the largest divisor GCD and the smallest multiple LCM.

The least divisor is meaningless, since for any number it is always one. The greatest multiple is also meaningless, since the sequence of multiples goes to infinity.

Finding gcd

There are many methods for finding the greatest common divisor, the most famous of which are:

• sequential search of divisors, selection of common ones for a pair and search for the largest of them;
• decomposition of numbers into indivisible factors;
• Euclidean algorithm;
• binary algorithm.

Today at educational institutions the most popular are decomposition methods into prime factors and the Euclidean algorithm. The latter, in turn, is used when solving Diophantine equations: searching for GCD is required to check the equation for the possibility of resolution in integers.

Finding the NOC

The least common multiple is also determined by sequential search or decomposition into indivisible factors. In addition, it is easy to find the LCM if the greatest divisor has already been determined. For numbers X and Y, the LCM and GCD are related by the following relationship:

LCD(X,Y) = X × Y / GCD(X,Y).

For example, if GCM(15,18) = 3, then LCM(15,18) = 15 × 18 / 3 = 90. The most obvious example of using LCM is to find the common denominator, which is the least common multiple of given fractions.

Coprime numbers

If a pair of numbers has no common divisors, then such a pair is called coprime. The gcd for such pairs is always equal to one, and based on the connection between divisors and multiples, the gcd for coprime pairs is equal to their product. For example, the numbers 25 and 28 are relatively prime, because they have no common divisors, and LCM(25, 28) = 700, which corresponds to their product. Any two indivisible numbers will always be relatively prime.

Common divisor and multiple calculator

Using our calculator you can calculate GCD and LCM for an arbitrary number of numbers to choose from. Tasks on calculating common divisors and multiples are found in 5th and 6th grade arithmetic, but GCD and LCM are key concepts in mathematics and are used in number theory, planimetry and communicative algebra.

Real life examples

Common denominator of fractions

Least common multiple is used when finding the common denominator of several fractions. Let's say in an arithmetic problem you need to sum 5 fractions:

1/8 + 1/9 + 1/12 + 1/15 + 1/18.

To add fractions, the expression must be reduced to common denominator, which reduces to the problem of finding the LCM. To do this, select 5 numbers in the calculator and enter the values ​​of the denominators in the appropriate cells. The program will calculate the LCM (8, 9, 12, 15, 18) = 360. Now you need to calculate additional factors for each fraction, which are defined as the ratio of the LCM to the denominator. So the additional multipliers would look like:

• 360/8 = 45
• 360/9 = 40
• 360/12 = 30
• 360/15 = 24
• 360/18 = 20.

After this, we multiply all the fractions by the corresponding additional factor and get:

45/360 + 40/360 + 30/360 + 24/360 + 20/360.

We can easily sum such fractions and get the result as 159/360. We reduce the fraction by 3 and see the final answer - 53/120.

Solving linear Diophantine equations

Linear Diophantine equations are expressions of the form ax + by = d. If the ratio d / gcd(a, b) is an integer, then the equation is solvable in integers. Let's check a couple of equations to see if they have an integer solution. First, let's check the equation 150x + 8y = 37. Using a calculator, we find GCD (150.8) = 2. Divide 37/2 = 18.5. The number is not an integer, therefore the equation does not have integer roots.

Let's check the equation 1320x + 1760y = 10120. Use a calculator to find GCD(1320, 1760) = 440. Divide 10120/440 = 23. As a result, we get an integer, therefore, the Diophantine equation is solvable in integer coefficients.

Conclusion

GCD and LCM play a big role in number theory, and the concepts themselves are widely used in the most different areas mathematics. Use our calculator to calculate the greatest divisors and least multiples of any number of numbers.

But many natural numbers are also divisible by other natural numbers.

For example:

The number 12 is divisible by 1, by 2, by 3, by 4, by 6, by 12;

The number 36 is divisible by 1, by 2, by 3, by 4, by 6, by 12, by 18, by 36.

The numbers by which the number is divisible by a whole (for 12 these are 1, 2, 3, 4, 6 and 12) are called divisors of numbers. Divisor of a natural number a- is a natural number that divides a given number a without a trace. A natural number that has more than two divisors is called composite .

Please note that the numbers 12 and 36 have common factors. These numbers are: 1, 2, 3, 4, 6, 12. The greatest divisor of these numbers is 12. The common divisor of these two numbers a And b- this is the number by which both given numbers are divided without remainder a And b.

Common multiples several numbers is a number that is divisible by each of these numbers. For example, the numbers 9, 18 and 45 have a common multiple of 180. But 90 and 360 are also their common multiples. Among all common multiples there is always a smallest one, in in this case this is 90. This number is called the smallestcommon multiple (CMM).

The LCM is always a natural number that must be greater than the largest of the numbers for which it is defined.

Least common multiple (LCM). Properties.

Commutativity:

Associativity:

In particular, if and are coprime numbers, then:

Least common multiple of two integers m And n is a divisor of all other common multiples m And n. Moreover, the set of common multiples m, n coincides with the set of multiples for LCM( m, n).

The asymptotics for can be expressed in terms of some number-theoretic functions.

So, Chebyshev function. And:

This follows from the definition and properties of the Landau function g(n).

What follows from the law of distribution of prime numbers.

Finding the least common multiple (LCM).

NOC( a, b) can be calculated in several ways:

1. If the greatest common divisor is known, you can use its connection with the LCM:

2. Let the canonical decomposition of both numbers into prime factors be known:

Where p 1 ,...,p k- various prime numbers, A d 1 ,...,d k And e 1 ,...,e k— non-negative integers (they can be zeros if the corresponding prime is not in the expansion).

Then NOC ( a,b) is calculated by the formula:

In other words, the LCM decomposition contains all prime factors included in at least one of the decompositions of numbers a, b, and the largest of the two exponents of this multiplier is taken.

Example:

Calculating the least common multiple of several numbers can be reduced to several sequential calculations of the LCM of two numbers:

Rule. To find the LCM of a series of numbers, you need:

- decompose numbers into prime factors;

- transfer the largest expansion (the product of the factors of the desired product) into the factors of the desired product large number from the given ones), and then add factors from the expansion of other numbers that do not appear in the first number or appear in it fewer times;

— the resulting product of prime factors will be the LCM of the given numbers.

Any two or more natural numbers have their own NOC. If the numbers are not multiples of each other or do not have the same factors in the expansion, then their LCM is equal to the product of these numbers.

The prime factors of the number 28 (2, 2, 7) are supplemented with the factor 3 (the number 21), the resulting product (84) will be the smallest number, which is divisible by 21 and 28.

The prime factors of the largest number 30 are supplemented by the factor 5 of the number 25, the resulting product 150 is greater than the largest number 30 and is divisible by all given numbers without a remainder. This is the smallest possible product (150, 250, 300...) that is a multiple of all given numbers.

The numbers 2,3,11,37 are prime numbers, so their LCM is equal to the product of the given numbers.

Rule. To calculate the LCM of prime numbers, you need to multiply all these numbers together.

Another option:

To find the least common multiple (LCM) of several numbers you need:

1) represent each number as a product of its prime factors, for example:

504 = 2 2 2 3 3 7,

2) write down the powers of all prime factors:

504 = 2 2 2 3 3 7 = 2 3 3 2 7 1,

3) write down all the prime divisors (multipliers) of each of these numbers;

4) choose the greatest degree of each of them, found in all expansions of these numbers;

5) multiply these powers.

Example. Find the LCM of the numbers: 168, 180 and 3024.

Solution. 168 = 2 2 2 3 7 = 2 3 3 1 7 1,

180 = 2 2 3 3 5 = 2 2 3 2 5 1,

3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1.

We write down the greatest powers of all prime divisors and multiply them:

NOC = 2 4 3 3 5 1 7 1 = 15120.

A multiple is a number that is divisible by a given number without a remainder. The least common multiple (LCM) of a group of numbers is the smallest number that is divisible by each number in the group without leaving a remainder. To find the least common multiple, you need to find the prime factors of given numbers. The LCM can also be calculated using a number of other methods that apply to groups of two or more numbers.

Steps

Series of multiples

Look at these numbers. The method described here is best used when given two numbers, each of which is less than 10. If larger numbers are given, use a different method.

• For example, find the least common multiple of 5 and 8. These are small numbers, so you can use this method.

1. A multiple is a number that is divisible by a given number without a remainder. Multiples can be found in the multiplication table.

   • For example, numbers that are multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40.

2. Write down a series of numbers that are multiples of the first number. Do this under multiples of the first number to compare two sets of numbers.

   • For example, numbers that are multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, and 64.

3. Find the smallest number that is present in both sets of multiples. You may have to write long series of multiples to find total number. The smallest number that is present in both sets of multiples is the least common multiple.

   • For example, the smallest number that appears in the series of multiples of 5 and 8 is the number 40. Therefore, 40 is the least common multiple of 5 and 8.

   Prime factorization

   1. Look at these numbers. The method described here is best used when given two numbers, each of which is greater than 10. If smaller numbers are given, use a different method.

      • For example, find the least common multiple of the numbers 20 and 84. Each of the numbers is greater than 10, so you can use this method.

   2. Factor the first number into prime factors. That is, you need to find such prime numbers that, when multiplied, will result in a given number. Once you have found the prime factors, write them as equalities.

      • For example, 2 × 10 = 20 (\displaystyle (\mathbf (2) )\times 10=20) And 2 × 5 = 10 (\displaystyle (\mathbf (2) )\times (\mathbf (5) )=10). Thus, the prime factors of the number 20 are the numbers 2, 2 and 5. Write them as an expression: .

   3. Factor the second number into prime factors. Do this in the same way as you factored the first number, that is, find such prime numbers that, when multiplied, will yield the given number.

      • For example, 2 × 42 = 84 (\displaystyle (\mathbf (2) )\times 42=84), 7 × 6 = 42 (\displaystyle (\mathbf (7) )\times 6=42) And 3 × 2 = 6 (\displaystyle (\mathbf (3) )\times (\mathbf (2) )=6). Thus, the prime factors of the number 84 are the numbers 2, 7, 3 and 2. Write them as an expression: .

   4. Write down the factors common to both numbers. Write such factors as a multiplication operation. As you write each factor, cross it out in both expressions (expressions that describe factorizations of numbers into prime factors).

      • For example, both numbers have a common factor of 2, so write 2 × (\displaystyle 2\times ) and cross out the 2 in both expressions.
      • What both numbers have in common is another factor of 2, so write 2 × 2 (\displaystyle 2\times 2) and cross out the second 2 in both expressions.

   5. Add the remaining factors to the multiplication operation. These are factors that are not crossed out in both expressions, that is, factors that are not common to both numbers.

      • For example, in the expression 20 = 2 × 2 × 5 (\displaystyle 20=2\times 2\times 5) Both twos (2) are crossed out because they are common factors. The factor 5 is not crossed out, so write the multiplication operation like this: 2 × 2 × 5 (\displaystyle 2\times 2\times 5)
      • In expression 84 = 2 × 7 × 3 × 2 (\displaystyle 84=2\times 7\times 3\times 2) both twos (2) are also crossed out. The factors 7 and 3 are not crossed out, so write the multiplication operation like this: 2 × 2 × 5 × 7 × 3 (\displaystyle 2\times 2\times 5\times 7\times 3).

   6. Calculate the least common multiple. To do this, multiply the numbers in the written multiplication operation.

      • For example, 2 × 2 × 5 × 7 × 3 = 420 (\displaystyle 2\times 2\times 5\times 7\times 3=420). So the least common multiple of 20 and 84 is 420.

   Finding common factors

   1. Draw a grid like for a game of tic-tac-toe. Such a grid consists of two parallel lines that intersect (at right angles) with another two parallel lines. This will give you three rows and three columns (the grid looks a lot like the # icon). Write the first number in the first line and second column. Write the second number in the first row and third column.

      • For example, find the least common multiple of the numbers 18 and 30. Write the number 18 in the first row and second column, and write the number 30 in the first row and third column.

   2. Find the divisor common to both numbers. Write it down in the first row and first column. It is better to look for prime factors, but this is not a requirement.

      • For example, 18 and 30 are even numbers, so their common factor is 2. So write 2 in the first row and first column.

   3. Divide each number by the first divisor. Write each quotient under the appropriate number. A quotient is the result of dividing two numbers.

      • For example, 18 ÷ 2 = 9 (\displaystyle 18\div 2=9), so write 9 under 18.
      • 30 ÷ 2 = 15 (\displaystyle 30\div 2=15), so write down 15 under 30.

   4. Find the divisor common to both quotients. If there is no such divisor, skip the next two steps. Otherwise, write the divisor in the second row and first column.

      • For example, 9 and 15 are divisible by 3, so write 3 in the second row and first column.

   5. Divide each quotient by its second divisor. Write each division result under the corresponding quotient.

      • For example, 9 ÷ 3 = 3 (\displaystyle 9\div 3=3), so write 3 under 9.
      • 15 ÷ 3 = 5 (\displaystyle 15\div 3=5), so write 5 under 15.

   6. If necessary, add additional cells to the grid. Repeat the described steps until the quotients have a common divisor.

   7. Circle the numbers in the first column and last row of the grid. Then write the selected numbers as a multiplication operation.

      • For example, the numbers 2 and 3 are in the first column, and the numbers 3 and 5 are in the last row, so write the multiplication operation like this: 2 × 3 × 3 × 5 (\displaystyle 2\times 3\times 3\times 5).

   8. Find the result of multiplying numbers. This will calculate the least common multiple of two given numbers.

      • For example, 2 × 3 × 3 × 5 = 90 (\displaystyle 2\times 3\times 3\times 5=90). So the least common multiple of 18 and 30 is 90.

   Euclid's algorithm

   1. Remember the terminology associated with the division operation. The dividend is the number that is being divided. The divisor is the number that is being divided by. A quotient is the result of dividing two numbers. A remainder is the number left when two numbers are divided.

      • For example, in the expression 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) ost. 3:
        15 is the dividend
        6 is a divisor
        2 is quotient
        3 is the remainder.

The material presented below is logical continuation theories from the article entitled LCM - least common multiple, definition, examples, connection between LCM and GCD. Here we will talk about finding the least common multiple (LCM), And Special attention Let's focus on solving examples. First, we will show how the LCM of two numbers is calculated using the GCD of these numbers. Next, we'll look at finding the least common multiple by factoring numbers into prime factors. After this, we will focus on finding the LCM of three and more numbers, and also pay attention to calculating the LCM of negative numbers.

Page navigation.

Calculating Least Common Multiple (LCM) via GCD

One way to find the least common multiple is based on the relationship between LCM and GCD. The existing connection between LCM and GCD allows us to calculate the least common multiple of two positive integers through a known greatest common divisor. The corresponding formula is LCM(a, b)=a b:GCD(a, b) . Let's look at examples of finding the LCM using the given formula.

Example.

Find the least common multiple of two numbers 126 and 70.

Solution.

In this example a=126 , b=70 . Let us use the connection between LCM and GCD, expressed by the formula LCM(a, b)=a b:GCD(a, b). That is, first we have to find the greatest common divisor of the numbers 70 and 126, after which we can calculate the LCM of these numbers using the written formula.

Let's find GCD(126, 70) using the Euclidean algorithm: 126=70·1+56, 70=56·1+14, 56=14·4, therefore, GCD(126, 70)=14.

Now we find the required least common multiple: GCD(126, 70)=126·70:GCD(126, 70)= 126·70:14=630.

Answer:

LCM(126, 70)=630 .

Example.

What is LCM(68, 34) equal to?

Solution.

Because 68 is divisible by 34, then GCD(68, 34)=34. Now we calculate the least common multiple: GCD(68, 34)=68·34:GCD(68, 34)= 68·34:34=68.

Answer:

LCM(68, 34)=68 .

Note that the previous example fits the following rule for finding the LCM for positive integers a and b: if the number a is divisible by b, then the least common multiple of these numbers is a.

Finding the LCM by factoring numbers into prime factors

Another way to find the least common multiple is based on factoring numbers into prime factors. If you compose a product from all the prime factors of given numbers, and then exclude from this product all the common prime factors present in the decompositions of the given numbers, then the resulting product will be equal to the least common multiple of the given numbers.

The stated rule for finding the LCM follows from the equality LCM(a, b)=a b:GCD(a, b). Indeed, the product of numbers a and b is equal to the product of all factors involved in the expansion of numbers a and b. In turn, GCD(a, b) is equal to the product of all prime factors simultaneously present in the expansions of numbers a and b (as described in the section on finding GCD using the expansion of numbers into prime factors).

Let's give an example. Let us know that 75=3·5·5 and 210=2·3·5·7. Let's compose the product from all the factors of these expansions: 2·3·3·5·5·5·7 . Now from this product we exclude all the factors present in both the expansion of the number 75 and the expansion of the number 210 (these factors are 3 and 5), then the product will take the form 2·3·5·5·7. The value of this product is equal to the least common multiple of 75 and 210, that is, NOC(75, 210)= 2·3·5·5·7=1,050.

Example.

Factor the numbers 441 and 700 into prime factors and find the least common multiple of these numbers.

Solution.

Let's factor the numbers 441 and 700 into prime factors:

We get 441=3·3·7·7 and 700=2·2·5·5·7.

Now let’s create a product from all the factors involved in the expansion of these numbers: 2·2·3·3·5·5·7·7·7. Let us exclude from this product all factors that are simultaneously present in both expansions (there is only one such factor - this is the number 7): 2·2·3·3·5·5·7·7. Thus, LCM(441, 700)=2·2·3·3·5·5·7·7=44 100.

Answer:

NOC(441, 700)= 44 100 .

The rule for finding the LCM using factorization of numbers into prime factors can be formulated a little differently. If the missing factors from the expansion of number b are added to the factors from the expansion of the number a, then the value of the resulting product will be equal to the least common multiple of the numbers a and b.

For example, let's take the same numbers 75 and 210, their decompositions into prime factors are as follows: 75=3·5·5 and 210=2·3·5·7. To the factors 3, 5 and 5 from the expansion of the number 75 we add the missing factors 2 and 7 from the expansion of the number 210, we obtain the product 2·3·5·5·7, the value of which is equal to LCM(75, 210).

Example.

Find the least common multiple of 84 and 648.

Solution.

We first obtain the decompositions of the numbers 84 and 648 into prime factors. They look like 84=2·2·3·7 and 648=2·2·2·3·3·3·3. To the factors 2, 2, 3 and 7 from the expansion of the number 84 we add the missing factors 2, 3, 3 and 3 from the expansion of the number 648, we obtain the product 2 2 2 3 3 3 3 7, which is equal to 4 536 . Thus, the desired least common multiple of 84 and 648 is 4,536.

Answer:

LCM(84, 648)=4,536 .

Finding the LCM of three or more numbers

The least common multiple of three or more numbers can be found by sequentially finding the LCM of two numbers. Let us recall the corresponding theorem, which gives a way to find the LCM of three or more numbers.

Theorem.

Let positive integer numbers a 1 , a 2 , …, a k be given, the least common multiple m k of these numbers is found by sequentially calculating m 2 = LCM(a 1 , a 2) , m 3 = LCM(m 2 , a 3) , … , m k = LCM(m k−1 , a k) .

Let's consider the application of this theorem using the example of finding the least common multiple of four numbers.

Example.

Find the LCM of four numbers 140, 9, 54 and 250.

Solution.

In this example, a 1 =140, a 2 =9, a 3 =54, a 4 =250.

First we find m 2 = LOC(a 1 , a 2) = LOC(140, 9). To do this, using the Euclidean algorithm, we determine GCD(140, 9), we have 140=9·15+5, 9=5·1+4, 5=4·1+1, 4=1·4, therefore, GCD(140, 9)=1 , from where GCD(140, 9)=140 9:GCD(140, 9)= 140·9:1=1,260. That is, m 2 =1 260.

Now we find m 3 = LOC (m 2 , a 3) = LOC (1 260, 54). Let's calculate it through GCD(1 260, 54), which we also determine using the Euclidean algorithm: 1 260=54·23+18, 54=18·3. Then gcd(1,260, 54)=18, from which gcd(1,260, 54)= 1,260·54:gcd(1,260, 54)= 1,260·54:18=3,780. That is, m 3 =3 780.

All that remains is to find m 4 = LOC(m 3, a 4) = LOC(3 780, 250). To do this, we find GCD(3,780, 250) using the Euclidean algorithm: 3,780=250·15+30, 250=30·8+10, 30=10·3. Therefore, GCM(3,780, 250)=10, whence GCM(3,780, 250)= 3 780 250: GCD(3 780, 250)= 3,780·250:10=94,500. That is, m 4 =94 500.

So the least common multiple of the original four numbers is 94,500.

Answer:

LCM(140, 9, 54, 250)=94,500.

In many cases, it is convenient to find the least common multiple of three or more numbers using prime factorizations of the given numbers. In this case, you should adhere to the following rule. The least common multiple of several numbers is equal to the product, which is composed as follows: the missing factors from the expansion of the second number are added to all the factors from the expansion of the first number, the missing factors from the expansion of the third number are added to the resulting factors, and so on.

Let's look at an example of finding the least common multiple using prime factorization.

Example.

Find the least common multiple of the five numbers 84, 6, 48, 7, 143.

Solution.

First, we obtain decompositions of these numbers into prime factors: 84=2·2·3·7, 6=2·3, 48=2·2·2·2·3, 7 (7 is a prime number, it coincides with its decomposition into prime factors) and 143=11·13.

To find the LCM of these numbers, to the factors of the first number 84 (they are 2, 2, 3 and 7), you need to add the missing factors from the expansion of the second number 6. The decomposition of the number 6 does not contain missing factors, since both 2 and 3 are already present in the decomposition of the first number 84. Next, to the factors 2, 2, 3 and 7 we add the missing factors 2 and 2 from the expansion of the third number 48, we get a set of factors 2, 2, 2, 2, 3 and 7. There will be no need to add multipliers to this set in the next step, since 7 is already contained in it. Finally, to the factors 2, 2, 2, 2, 3 and 7 we add the missing factors 11 and 13 from the expansion of the number 143. We get the product 2·2·2·2·3·7·11·13, which is equal to 48,048.

Greatest common divisor

Definition 2

If a natural number a is divisible by a natural number $b$, then $b$ is called a divisor of $a$, and $a$ is called a multiple of $b$.

Let $a$ and $b$ be natural numbers. The number $c$ is called the common divisor of both $a$ and $b$.

The set of common divisors of the numbers $a$ and $b$ is finite, since none of these divisors can be greater than $a$. This means that among these divisors there is a largest one, which is called the greatest common divisor of the numbers $a$ and $b$ and is denoted by the following notation:

$GCD\(a;b)\ or \D\(a;b)$

To find the greatest common divisor of two numbers you need:

1. Find the product of the numbers found in step 2. The resulting number will be the desired greatest common divisor.

Example 1

Find the gcd of the numbers $121$ and $132.$

$242=2\cdot 11\cdot 11$

$132=2\cdot 2\cdot 3\cdot 11$

Choose the numbers that are included in the expansion of these numbers

$242=2\cdot 11\cdot 11$

$132=2\cdot 2\cdot 3\cdot 11$

Find the product of the numbers found in step 2. The resulting number will be the desired greatest common divisor.

$GCD=2\cdot 11=22$

Example 2

Find the gcd of the monomials $63$ and $81$.

We will find according to the presented algorithm. For this:

Let's factor the numbers into prime factors

$63=3\cdot 3\cdot 7$

$81=3\cdot 3\cdot 3\cdot 3$

We select the numbers that are included in the expansion of these numbers

$63=3\cdot 3\cdot 7$

$81=3\cdot 3\cdot 3\cdot 3$

Let's find the product of the numbers found in step 2. The resulting number will be the desired greatest common divisor.

$GCD=3\cdot 3=9$

You can find the gcd of two numbers in another way, using a set of divisors of numbers.

Example 3

Find the gcd of the numbers $48$ and $60$.

Solution:

Let's find the set of divisors of the number $48$: $\left\((\rm 1,2,3.4.6,8,12,16,24,48)\right\)$

Now let's find the set of divisors of the number $60$:$\ \left\((\rm 1,2,3,4,5,6,10,12,15,20,30,60)\right\)$

Let's find the intersection of these sets: $\left\((\rm 1,2,3,4,6,12)\right\)$ - this set will determine the set of common divisors of the numbers $48$ and $60$. Largest element in given set the number will be $12$. This means that the greatest common divisor of the numbers $48$ and $60$ is $12$.

Definition of NPL

Definition 3

Common multiples of natural numbers$a$ and $b$ is a natural number that is a multiple of both $a$ and $b$.

Common multiples of numbers are numbers that are divisible by the original numbers without a remainder. For example, for the numbers $25$ and $50$, the common multiples will be the numbers $50,100,150,200$, etc.

The smallest common multiple will be called the least common multiple and will be denoted LCM$(a;b)$ or K$(a;b).$

To find the LCM of two numbers, you need to:

1. Factor numbers into prime factors
2. Write down the factors that are part of the first number and add to them the factors that are part of the second and are not part of the first

Example 4

Find the LCM of the numbers $99$ and $77$.

We will find according to the presented algorithm. For this

Factor numbers into prime factors

$99=3\cdot 3\cdot 11$

Write down the factors included in the first

add to them multipliers that are part of the second and not part of the first

Find the product of the numbers found in step 2. The resulting number will be the desired least common multiple

$NOK=3\cdot 3\cdot 11\cdot 7=693$

Compiling lists of divisors of numbers is often a very labor-intensive task. There is a way to find GCD called the Euclidean algorithm.

Statements on which the Euclidean algorithm is based:

If $a$ and $b$ are natural numbers, and $a\vdots b$, then $D(a;b)=b$

If $a$ and $b$ are natural numbers such that $b

Using $D(a;b)= D(a-b;b)$, we can successively reduce the numbers under consideration until we reach a pair of numbers such that one of them is divisible by the other. Then the smaller of these numbers will be the desired greatest common divisor for the numbers $a$ and $b$.

Properties of GCD and LCM

1. Any common multiple of $a$ and $b$ is divisible by K$(a;b)$
2. If $a\vdots b$ , then К$(a;b)=a$

If K$(a;b)=k$ and $m$ is a natural number, then K$(am;bm)=km$

If $d$ is a common divisor for $a$ and $b$, then K($\frac(a)(d);\frac(b)(d)$)=$\ \frac(k)(d) $

If $a\vdots c$ and $b\vdots c$ , then $\frac(ab)(c)$ is the common multiple of $a$ and $b$

For any natural numbers $a$ and $b$ the equality holds

$D(a;b)\cdot К(a;b)=ab$

Any common divisor of the numbers $a$ and $b$ is a divisor of the number $D(a;b)$